The Fraction of Myosin Motors That Participate in Isometric Contraction of Rabbit Muscle Fibers at Near-Physiological Temperature

Abstract

The duty ratio, or the part of the working cycle in which a myosin molecule is strongly attached to actin, determines motor processivity and is required to evaluate the force generated by each molecule. In muscle, it is equal to the fraction of myosin heads that are strongly, or stereospecifically, bound to the thin filaments. Estimates of this fraction during isometric contraction based on stiffness measurements or the intensities of the equatorial or meridional x-ray reflections vary significantly. Here, we determined this value using the intensity of the first actin layer line, A1, in the low-angle x-ray diffraction patterns of permeable fibers from rabbit skeletal muscle. We calibrated the A1 intensity by considering that the intensity in the relaxed and rigor states corresponds to 0% and 100% of myosin heads bound to actin, respectively. The fibers maximally activated with Ca²⁺ at 4°C were heated to 31–34°C with a Joule temperature jump (T-jump). Rigor and relaxed-state measurements were obtained on the same fibers. The intensity of the inner part of A1 during isometric contraction compared with that in rigor corresponds to 41–43% stereospecifically bound myosin heads at near-physiological temperature, or an average force produced by a head of ∼6.3 pN.

Introduction

The fraction of myosin heads that participate in force production during muscle contraction is an essential characteristic of the myosin motor in muscle. This value is important in calculations of unitary force and efficiency of the motor. A similar characteristic, the duty ratio, is the fraction of the working cycle in which a myosin head is attached to an actin filament (1,2). However, this term is often used without specification as to whether a head produces force or not. In muscle, the duty ratio is equal to the fraction of attached heads if each myosin head is able to find and bind actin. This is the case for skeletal muscle, where in rigor (i.e., in the absence of ATP), all myosin heads are bound to actin (3). In mechanical experiments, the fraction is calculated from the ratio of fiber stiffness during isometric contraction to that in rigor, assuming that all attached heads have the same stiffness. This approach gives a fraction of bound heads in intact frog muscle of 22–43% depending on estimates of the compliance of the actin and myosin filaments (2,4), and 33% ± 5% in rabbit muscle fibers (2).

There is evidence that myosin heads can bind actin in different ways. Weakly bound heads detected in rabbit muscle fibers at low temperature in the absence of Ca²⁺ contribute to fiber stiffness, but are unable to produce active force (5), i.e., such heads are attached to actin, but are not on duty, or, more precisely, they do not contribute to active force development. Direct observations of myosin heads on electron microscopy tomograms of isometrically contracting insect flight muscle fibers revealed that only some myosin heads are bound to actin strongly (or stereospecifically), and most are attached weakly (nonstereospecifically) with a wide range of axial and azimuthal angles between their catalytic domains and the actin filaments (6,7). The term “stereospecific binding” refers to a fixed position of the catalytic domain of the heads with respect to actin. Electron paramagnetic resonance (EPR) spectroscopy showed that during isometric contraction of rabbit muscle fibers at 20°C, only 12–20% of myosin heads were ordered in a rigor-like manner (8,9). This fraction is even less at lower temperatures (9). Tension of contracting skeletal muscle increases with temperature, whereas stiffness remains constant (2,10,11). These findings can be explained by assuming that the whole population of attached myosin heads in contracting muscle consists of both force-generating and nonforce-generating ones. Although the total number of attached heads remains constant, the fraction of force-generating heads increases with temperature. Previous studies suggested that contractile force in muscle is produced only by stereospecifically bound heads (12,13).

These observations suggest that in contracting muscle, a more informative characteristic of myosin motor functionality than the duty ratio is the fraction of myosin heads that are strongly (stereospecifically) bound to actin. This fraction cannot be determined from stiffness measurements, because nonstereospecifically bound heads also contribute to stiffness. Therefore, structural methods that are able to distinguish between stereo- and nonstereospecifically bound myosin heads are required.

In isometrically contracting muscle, the intensity of the first actin layer line, A1, at ∼(36 nm)⁻¹ on the x-ray diffraction pattern increases simultaneously with tension (13). Model calculations show that the A1 intensity, I_A1, results mostly from stereospecific binding of catalytic domains of the heads to actin and is almost independent of the orientation of their light chain domains, called lever arms (14,15). Strongly bound heads contribute to the inner part of A1, with a peak at the radial spacing of ∼0.045 nm⁻¹, whereas actin and the regulatory proteins of the thin filaments give rise to I_A1 at higher reciprocal radii of ∼0.12 nm⁻¹ (16,17). These useful features make I_A1 a robust and reliable index of the fraction of stereospecifically bound heads, although care is required in the analysis to remove the overlap with the neighbor myosin M1 layer line at (∼43 nm)⁻¹ and in the choice of the radial integration area to minimize the contribution of the thin filament proteins to A1.

In this work, we estimated the fraction of stereospecifically bound heads in fast permeable fibers from rabbit skeletal muscle during isometric contraction at near physiological temperature. We derived the fraction from measured A1 intensities in contracting muscle fibers and in the same fibers in rigor and relaxed states using direct modeling (14,15). We previously used this approach to estimate this fraction in muscle fibers treated with ethyl-dimethyl-carbodiimide (EDC) (15), which could have affected the results of those experiments. Here, the fibers were activated and relaxed without any extra treatment.

Materials and Methods

Fiber preparation and solution

Bundles of fibers from rabbit m. psoas were prepared, permeabilized, and stored at −20°C in 50% glycerol relaxing solution as previously described (13). Samples of two or three fibers at least 10 mm long were dissected so that they could be divided into two segments of at least 5 mm each. One segment was used to record the active diffraction patterns at low and high temperatures. The relaxed and rigor patterns were taken from the second segment. A low-tension, highly ordered rigor state was obtained as previously described (18). The composition of the solutions was as described previously (13) except that 80 mM dithiothreitol (DTT) was added to all solutions to minimize radiation damage. The DTT had no impact on the diffraction pattern or fiber mechanical performance.

Apparatus

The T-jump apparatus and its use were described previously (10). The x-ray beam of ∼0.1 nm wavelength at beam line ID02 (ESRF, Grenoble, France) was focused on the FReLoN CCD detector operating at 2048 × 256 (meridian × equator) pixels, 3.5 m from the sample. The beam size on the sample was 70 × 400 μm (full width at half-maximum) with a flux of ∼3.8 × 10¹³ photons/s.

The experimental setup allowed us to record the x-ray diffraction pattern from vertically mounted fibers with the force transducer on top and the motor to change the fiber length beneath the preparation (Fig. 1). This improved the meridional spatial resolution compared with horizontally mounted fibers used previously. We mounted a fiber bundle in the open trough (trough 1) by gluing its ends to nickel electrodes with shellac (14). This trough had a glass bottom and no lid (Fig. 1). Narrow troughs (troughs 2 and 4) with glass windows were filled with 40 μl of experimental solutions. An unglazed trough (trough 3) was used to expose the bundle to x-rays, avoiding any scattering from the windows and surrounding solution. During x-ray exposure, the bundle was surrounded by a cold, wet atmosphere to minimize drying and condensation (10). The trough assembly was motorized so that we could activate or relax the fibers remotely in a fraction of a second without entering the synchrotron hutch.

Figure 1.

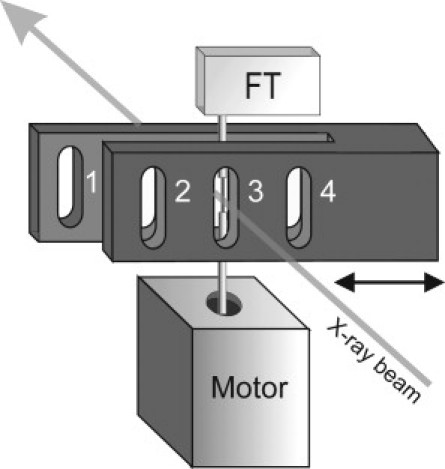
Diagram of the remotely controlled trough assembly. A fiber bundle is glued to a force transducer (FT) and a length motor (Motor). Trough 1 is used only for fiber mounting. All other troughs are 0.7 mm wide. Troughs 2 and 4 have glass windows and are filled with experimental solutions. The solution in these troughs is held in place by surface tension, even when the assembly is turned so that the fibers are vertical. Trough 3 has no windows and is used for x-ray exposure. The double arrow shows the direction of movement of the trough assembly. By moving the troughs horizontally, we could change the solution bathing the fibers and activate or relax them.

Experimental protocol

Fiber bundles were activated at 0–1°C with 32 μM Ca²⁺, suspended in air at ∼4°C, and heated to 31–34°C with a T-jump (Fig. 2). X-ray diffraction patterns were recorded during the steady-state isometric contraction before and after the T-jump. Framing (∼30 ms exposures) was controlled by two fast shutters, and the precise timing of the x-ray exposure was determined from a PIN diode signal (Fig. 2). A length step release was applied after the end of the exposure to monitor the force response and check the mechanical state of the fibers. Active x-ray diffraction patterns during contraction at each temperature were collected from three to 10 runs of the protocol in three bundles (the total number of runs was 21). Data collection was stopped when the tension rise induced by the T-jump slowed down by >30% or when the post-T-jump isometric tension was <80% of that after the first T-jump. Relaxed and rigor patterns were recorded at 4–5°C from other segments of the same bundles in 60 ms long frames for a total of 300–480 ms in each state. The patterns were then scaled for x-ray exposure of their partner bundles in the active state and added together. Data analysis was performed as previously described (13,15).

Figure 2.

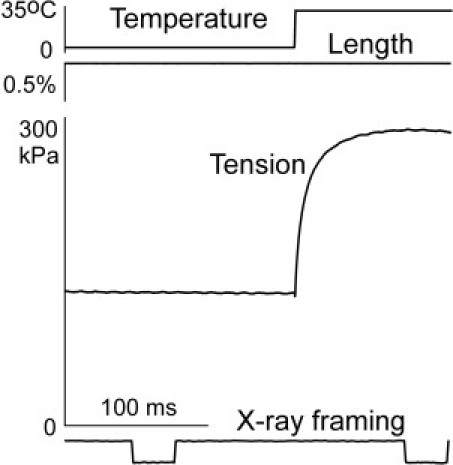
A representative record of a run of the experimental protocol in a bundle of two fibers (2.92 mm long, 7500 μm², sarcomere length: 2.45 μm). Top to bottom: temperature, length, tension, and x-ray exposure framing recorded with a PIN diode in the x-ray pipe.

Results

The T-jumps from 4–5°C to 31–34°C induced tension rise by an average factor of 2.48 (range: 2.19–2.81; Fig. 2). The four summed two-dimensional (2D) diffraction patterns collected from three pairs of bundles are shown in Fig. 3. The quality of the patterns was good enough to distinguish by eye the neighbor M1 and A1 layer lines.

Figure 3.

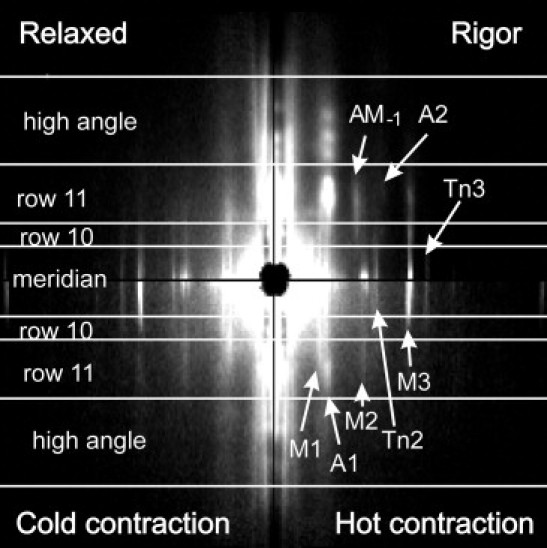
2D x-ray diffraction patterns collected from six segments of three bundles. Each quadrant is a mirrored pattern collected in the state shown in its corner. The equator is vertical, high intensity is white. The horizontal lines (0.018 nm⁻¹, 0.031 nm⁻¹, 0.061 nm⁻¹, and 0.105 nm⁻¹) show the intervals of radial integration for Fig. 4. The layer lines of interest, namely, the first (M1), second (M2), and third (M3) myosin layer lines, the first actin layer line (A1), a beating actin-myosin layer line (AM_-1), and the troponin meridional reflections (Tn2 and Tn3) are labeled.

The meridional profiles of the meridional and off-meridional intensity sliced at different reciprocal radii for all four 2D patterns shown in Fig. 3 are plotted in Fig. 4. The off-meridional slices include the 10, 11 row lines and a high-angle region. The 11 row line also includes the position of the 20 equatorial reflection, and the high-angle region covers the positions of the 21, 30, 22, and 31 equatorials. The integration range for the 11 row line is wider than that used by Bordas and colleagues (19), to cover the whole range of the major peak at A1 in rigor.

Figure 4.

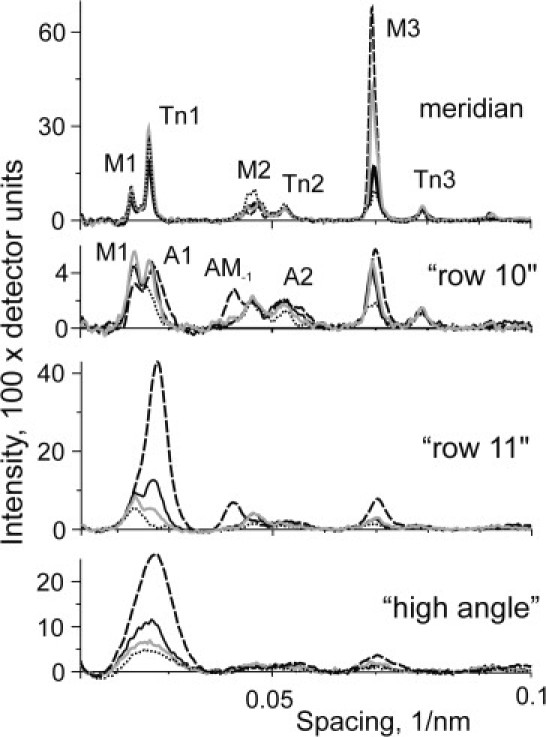
Meridional profiles of the off-meridional intensities obtained from the four patterns shown in Fig. 3. The meridional profiles were integrated within the range of ±0.018 nm⁻¹ on both sides of the meridian. The 10 and 11 row lines were obtained by integration within intervals (0.018–0.031 nm⁻¹) and (0.031–0.61 nm⁻¹). The high-angle slice was obtained by integration at reciprocal radii of 0.061–0.105 nm⁻¹. Some layer lines of interest are labeled. Rigor, high- and low-temperature contractions, and relaxed patterns are shown by dashed, solid black, gray, and dotted lines, respectively.

The T-jump caused a 54% increase in the intensity of the meridional peak of the M3 reflection (Fig. 4), in similarity to the 60% described previously for rabbit muscle fibers mildly cross-linked with EDC (13,16). The radial width of the M3 layer line in contracting muscle was significantly higher than that in rigor or in relaxed fibers (Figs. 3 and 4, and Fig. S1 in the Supporting Material). Increasing the temperature of contracting fibers induced a complex change in the radial profile of M3: no change was found in the narrow peak of the reflection in the region of ±0.015 nm⁻¹ from the meridian, whereas at higher reciprocal radii of 0.015–0.035 nm⁻¹, including the 10 row line, the M3 became narrower at the higher temperature (Fig. S1). During isometric contraction at the low and high temperatures, the peaks of the A1 and M1 layer lines were clearly separated from each other in row lines 10 and 11, whereas at the higher reciprocal radii they overlapped (Fig. 4).

Modeling (15) suggests that the A1 intensity can be used to estimate the fraction of myosin heads stereospecifically bound to actin. Two different approaches were exploited to extract the intensity of the A1 layer line from the complex M1/A1 layer line profile integrated radially in the region of the 10 and 11 row lines. Outside this range, on the meridian and at reciprocal radii > 0.61 nm⁻¹, proteins of the thin filaments may significantly contribute to the A1 intensity (17). Results from the two methods used to estimate the A1 intensity are given below.

Method 1: integration of the high-angle region of the A1 peak

To minimize the influence of the M1 layer line, the intensity of the high-angle region of the A1 layer line was integrated from the position of the A1 peak to 0.035 nm⁻¹, where the intensity vanishes. The position of the A1 peak was 0.0277 nm⁻¹ in rigor, 0.0268 nm⁻¹ during isometric contraction at 31–34°C, and 0.0263 nm⁻¹ during contraction at low temperature (Fig. 5 A). Because the A1 peak position in the relaxed state could not be determined precisely, its position during low-temperature isometric contraction was used for this state. The results of the integration give estimates of the A1 intensity normalized for its rigor value of 11.1%, 23.8%, and 36.3% for relaxed, low-temperature, and high-temperature contraction patterns, respectively (Table 1).

Figure 5.

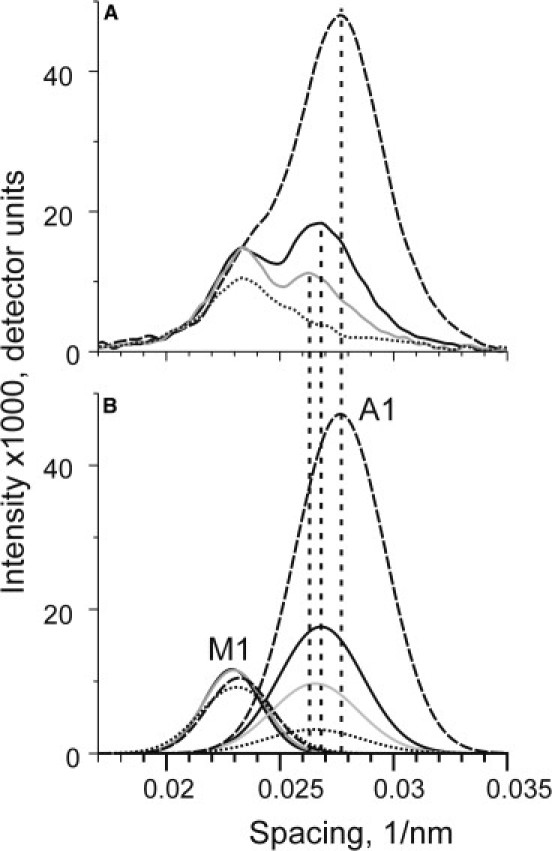
(A) The profiles of the M1/A1 layer lines in four different states of muscle bundles in the region of the M1 and A1 layer lines integrated in the region of the 10 and 11 row lines. (B) Gaussians for the M1 (dotted lines) and A1 (continuous lines) layer lines obtained by curve fitting (method 2). The parameters of the Gaussians and calculated M1 and A1 intensities are given in Table 2. Rigor, high- and low-temperature contractions, and relaxed patterns are shown by dashed, solid black, gray, and dotted lines, respectively. Vertical dashed lines are the positions of the A1 peaks used for integration of the high-angle regions of A1, respectively (method 1).

Table 1.

A1 intensity determined by integrating the high-angle regions of the A1 profiles

State	High-angle intensity∗	Estimated total A1 intensity∗	Normalized A1 intensity
Contraction, ∼4°C	0.0289	0.0578	0.238
Contraction, 31–34°C	0.0441	0.0882	0.363
Relaxed, ∼4°C	0.0135	0.0270	0.111
Rigor, ∼4°C	0.1214	0.2428	1

^∗Intensities here and in Table 2 are expressed in 1000 units of the CCD detector × nm⁻¹.

Method 2: fitting of the intensity profiles with two Gaussians

The intensity profiles shown in Fig. 5 A were fitted by the sum of two Gaussians of varying amplitudes, peak positions, and standard deviations with a nonlinear least-square routine incorporated into GIM software (Dr. Achev Development, Tempe, AZ) as shown in Fig. 5 B. All parameters were set free for a least mean-square optimization, except for the position and the standard deviation of the A1 peak for the relaxed profile, which were forced to have the same values as in the high-temperature isometric contraction (otherwise, the fitting procedure became unstable and unreliable). The results of the fit are shown in Fig. 5 B and presented in Table 2. It is worth noting that despite a difference in the height of the M1 peaks in different states of the bundles, the change in width compensated for this, and thus the total M1 intensity was the same in all four profiles within a 7% accuracy (Table 2). The normalized A1 intensities obtained from the fits were 7.3%, 19.2%, and 36.5% for relaxed, low-temperature, and high-temperature contractions, respectively, (i.e., close to those found using method 1).

Table 2.

Intensity of the M1 and A1 layer line calculated from the fit to two Gaussians

State	AM1	SM1	σM1	IM1	AA1	SA1	σA1	IA1	Norm. IA1
Contraction, ∼4°C	11.57	0.023	0.00133	0.0386	9.7	0.0265	0.00185	0.0445	0.192
Contraction, 31–34°C	11.67	0.0229	0.00126	0.0369	17.56	0.0268	0.00192	0.0846	0.365
Relaxed, ∼4°C	8.97	0.0231	0.0016	0.036	3.49	0.0268∗	0.00192∗	0.0168	0.073
Rigor, ∼4°C	10.48	0.0232	0.00141	0.037	47.12	0.0277	0.00196	0.2315	1

^∗Fixed values. All other parameters were set free during curve fitting. A_M1, A_A1, S_M1, S_M1, σ_M1, and σ_A1 are the amplitude, spacing, and standard deviations of Gaussians for the M1 and A1 layer lines, respectively.

It should be noted that the observed meridional position of the A1 peak on the low-temperature pattern on Fig. 5 A is affected by the presence of the neighbor myosin layer line M1. When the complex M1/A1 layer line in contracting muscle was fitted by the sum of two Gaussians that represent M1 and A1, the position of the A1 peak during the low-temperature isometric contraction was very close to that observed during the high-temperature contraction. This means that the A1 intensity evaluated with method 1 was possibly overestimated. If the position of the A1 peak at low temperature was forced to be the same as at the higher temperature, the normalized A1 intensity estimated with method 1 was reduced from 0.238 (Table 1) to 0.197, which is close to the 0.192 found with method 2 (Table 2). In the relaxed state, the same change in the A1 peak position resulted in a reduction of the normalized A1 intensity to 0.096 (from 0.111).

To estimate the fraction of stereospecifically bound heads, we used the results of model calculations described previously (15,17), which showed that the A1 intensity is independent of the tilt of the lever arms of myosin heads stereospecifically bound to actin (15). The calculated relationship between the fraction of stereospecifically bound heads and the A1 intensity is plotted in Fig. 6. The A1 intensity obtained by methods 1 and 2 corresponds to 41–43% of the heads bound stereospecifically during high-temperature isometric contraction (Tables 1 and 2, and Fig. 6).

Figure 6.

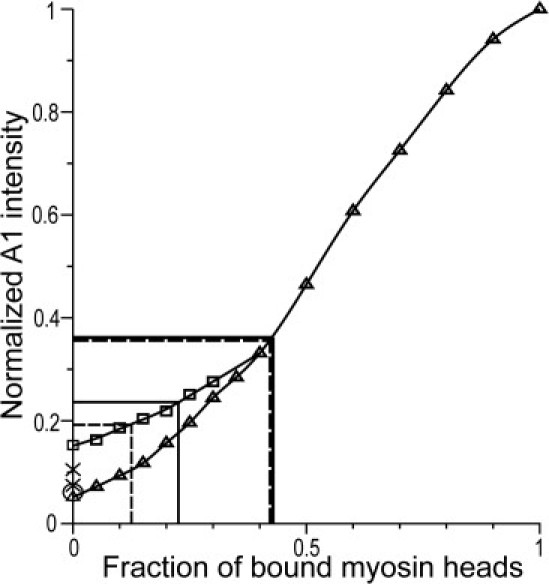
Calculated dependence of the A1 intensity on the fraction of stereospecifically bound heads obtained with a previously described model (15,17). The off-meridional A1 intensity was integrated at reciprocal radii of 0.014–0.061 nm⁻¹ and normalized for its rigor value. Triangles: Calculations made for different fractions of stereospecifically bound heads assuming that all other heads are detached. Squares: Calculations for different fractions of stereospecifically bound heads (0–40%) assuming that the total number of heads bound to actin either stereo- or nonstereospecifically is constant and equal to 40%. The circle on the ordinate axis is the A1 intensity calculated for relaxed muscle, where troponin and tropomyosin are in the blocked state (17); all other calculations were made for the open conformation of the regulatory proteins on the thin filaments. Straight solid lines show the estimates of the fraction of bound heads using method 1, dashed lines show the same estimates for method 2, thin lines correspond to low-temperature isometric contraction, and thick lines correspond to high-temperature contraction. Crosses on the ordinate axis show normalized A1 intensities in the relaxed state estimated from experimental data with methods 1 and 2. See text for details.

The dynamic stiffness of isometrically contracting muscle fibers is temperature-independent (10,2). We therefore assumed that during a low-temperature contraction, the total fraction of attached heads is the same as at high temperature (∼40%), but some heads are attached nonstereospecifically with a wide range of azimuthal (±80°) and axial (±30°) binding angles between their catalytic domains and actin. We then calculated the dependence of I_A1 on the fraction of stereospecifically bound heads for this mixture of differently attached heads (squares in Fig. 6). Using this plot, we estimate 10–13.5% heads stereospecifically bound during low-temperature isometric contraction (Tables 1 and 2, and Fig. 6). Note that the estimates of A1 intensity in the experimental diffraction pattern in the relaxed state obtained with methods 1 and 2—11.1% (9.6%) and 7.3%, respectively—are higher than the 6% predicted by the mathematical model (Fig. 6).

Discussion

The tensions and intensities of A1 and M3 x-ray reflections during contraction at low and high temperatures observed here were similar to those found for EDC cross-linked rabbit fibers (13,15). This establishes that the mild cross-linking used in those experiments did not affect the mechanical or structural properties of the fibers. The increase in I_M3 and I_A1 with temperature was also similar, although somewhat higher than in intact frog muscle fibers (20). The smaller increase in I_M3 and I_A1 in frog fibers with respect to those reported here correlates with the smaller increase in tension upon a temperature rise in frog muscles compared with rabbit fibers.

Different experimental approaches give estimates for the fraction of attached heads ranging from 10% to 70% (1,2,4,7,21,22). The estimates, which are based on the equatorial and meridional Bragg x-ray reflections of the x-ray diffraction pattern of contracting muscle, vary widely, mainly because the intensities of these reflections strongly depend on the degree of crystallinity of the filament lattice in sarcomeres, which changes during development of active force and with a change in temperature (16) (Fig. S1). Furthermore, the intensities of both equatorial and meridional Bragg reflections do not provide information about stereo- and nonstereospecific binding of myosin heads. The estimates obtained from EPR spectroscopy (8,9) are similar to, albeit somewhat lower than, those obtained here, probably because of the differences in experimental conditions.

Actin-based layer lines in the x-ray diffraction pattern arise not only from actin, tropomyosin, and troponin associated with the thin filaments in sarcomeres but also from myosin heads bound to actin, which contribute to the diffraction pattern with an actin-based helical periodicity. The contribution of stereospecifically bound heads to the actin layer lines is higher than that of nonstereospecifically bound ones (15). Changes in the intensity of the bright sixth actin layer line, A6, at ∼(5.9 nm)⁻¹ are difficult to interpret because the thin filament proteins contribute largely to its intensity, and the intensity is also very sensitive to the tilt of the lever arm (the light chain domain) of the myosin heads (14,15,17) and the movement of actin domains, troponin, and tropomyosin (23). The structure of F-actin also changes upon strong binding of myosin heads (24). For these reasons, estimates based on the A6 intensity (22) may overestimate the fraction of stereospecifically bound heads.

Unlike the Bragg reflections, I_A1 is independent of the degree of crystallinity of the filament lattice (14). Methods 1 and 2, used to determine ΔI_A1 in contracting muscle, both have flaws and rely on assumptions. Nevertheless, they give a consistent estimate of 41–43% for the fraction of myosin motor domains stereospecifically bound to actin at high temperature. This figure is higher than the fraction of bound heads of 33% ± 5% derived from stiffness measurements at 4–20°C, also in rabbit muscle (2). The stiffness of both permeable fibers from rabbit (10) and intact frog (11) muscles remains nearly independent of temperature. This means that within experimental error, all myosin heads that are attached to actin during isometric contraction at physiological temperature are bound stereospecifically.

At the lower temperature, I_A1 and thus the fraction of stereospecifically bound heads decrease approximately proportionally with tension (Figs. 2–6) (13,15), although the total number of heads bound to actin either stereo- or nonstereospecifically remains nearly constant (2,10,11). This suggests that the force produced by a stereospecifically bound head is temperature-independent.

With 154 μM heads in permeable rabbit fibers (25), and taking the average fraction of stereospecifically bound heads of 42%, we have 0.154 × 6.02 × 10²³ m⁻³ = 9.3 × 10²² heads × m⁻³. At a sarcomere length of 2.45 μm (Fig. 2), there are (9.3 × 10²² m⁻³) × (2.45/2 × 10⁻⁶ m) × 0.42 = 4.78 × 10¹⁶ stereospecifically bound heads per half-sarcomere per m². To hold 300 kPa tension (Fig. 2), each of these heads should produce an average force of ∼6.3 pN.

This figure is similar to the 6 pN estimate derived from x-ray and mechanical experiments with intact frog muscle fibers at 4°C (26), but significantly higher than the 1.7–4 pN found in single-molecule experiments, possibly because of the extra compliance that is unavoidably present in such experiments (27).