A procedure to statistically evaluate agreement of differential expression for cross-species genomics

Abstract

Motivation: Animal models play a pivotal role in translation biomedical research. The scientific value of an animal model depends on how accurately it mimics the human disease. In principle, microarrays collect the necessary data to evaluate the transcriptomic fidelity of an animal model in terms of the similarity of expression with the human disease. However, statistical methods for this purpose are lacking.

Results: We develop the agreement of differential expression (AGDEX) procedure to measure and determine the statistical significance of the similarity of the results of two experiments that measure differential expression across two groups. AGDEX defines a metric of agreement and determines statistical significance by permutation of each experiment's group labels. Additionally, AGDEX performs a comprehensive permutation-based analysis of differential expression for each experiment, including gene-set analyses and meta-analytic integration of results across studies. As an example, we show how AGDEX was recently used to evaluate the similarity of the transcriptome of a novel model of the brain tumor ependymoma in mice to that of a subtype of the human disease. This result, combined with other observations, helped us to infer the cell of origin of this devastating human cancer.

Availability: An R package is currently available from www.stjuderesearch.org/site/depts/biostats/agdex and will shortly be available from www.bioconductor.org.

Contact: stanley.pounds@stjude.org

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Microarray technology has enabled researchers to simultaneously measure the expression of thousands of genes in a biological tissue specimen. These data are commonly used to compare gene expression among biological conditions within the same species. For example, the experiments may compare the transcriptomes of tumors and host normal tissue or between tumors arising in the same tissue. However, translating this wealth of data into other experimental systems has proven difficult because of limitations in comparing transcriptome data generated with different microarray platforms or from different species.

Here, we present a statistically rigorous procedure (called AGDEX for agreement of differential expression) to combine transcriptome information across two experiments that compare expression across two biological conditions. Each experiment may utilize different microarray platforms or even study different species. The AGDEX procedure determines whether the differential expression profile of one experiment has statistically significant similarity to that of the other experiment. In our studies, we used AGDEX analysis results and other experimental data to validate a novel mouse model of a human brain tumor. We have successfully used AGDEX for this purpose in published studies of ependymoma (Johnson et al., 2010) and medulloblastoma (Gibson et al., 2010) to identify the cell of origin for each of these two brain cancers. We describe the method in detail and illustrate it with our analysis of the data from our ependymoma study.

2 METHODS

The AGDEX procedure enables investigators to perform a rigorous and comprehensive analysis of data from a pair of experiments that each compares expression across two biological conditions. In total, the AGDEX procedure performs the following analyses:

1. identify individual genes that are differentially expressed in each experiment;

2. identify gene-sets that are differentially expressed in each experiment;

3. meta-analytically integrate results across experiments to identify differentially expressed genes;

4. meta-analytically integrate results across experiments to identify differentially expressed gene-sets; and

5. characterize and determine the statistical significance of similarities of differential expression profiles across the two experiments for the entire transcriptome and for specific gene-sets.

Below, we provide details for how AGDEX performs each of these analyses.

2.1 Differential expression of individual probe-sets for one experiment

Suppose an array measures the expression of j=1,…,m probe−sets for each of g=1,2 groups defined by distinct biological conditions. Now, for each probe-set j, define

(1)

as the difference between the average 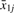log-signal for group 1 and the average 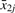for group 2. Let d={d₁,…,d_m} be the vector of d_j for all probe-sets j.

For each probe-set j, compute a P-value for d_j by permutation of the group labels (Good, 2010; Gadbury et al., 2003). Let b=1,…,B index a set of permutations of assignment of the group labels to the arrays. For b=1,…,B, let d_jb be the value of (1) obtained by permutation b of the group labels. For each d_j, the permutation P-value is the proportion of permuted group labels that yield an absolute value of (1) than does the original assignment of group labels. Mathematically, the P-value for d_j is given by

(2)

where d_j0 is the value of d_j computed using the original group assignments, and I(·) is the indicator function that equals 1 if the enclosed statement is true and equals 0 otherwise. In practice, all possible permutations are used whenever it is computationally feasible to do so. Otherwise, a large number of randomly selected permutations are utilized. In some applications, the permutations should be restricted to preserve important stratification features of the experimental design.

2.2 Differential expression of gene-sets for one experiment

Suppose the probe-sets are annotated according to membership in a gene-set s. Let j_s=1,…,m_s index the m_s probe-sets that belong to gene-set s. The gene-set differential expression statistic

(3)

is the average of the absolute value of the differential expression statistics of probe-sets belonging to gene-set s.

The statistic defined in (3) is a function only of the data of genes that belong to the gene-set and thus is self-contained by Goeman and Bühlmann's (2007) definition. Goeman and Bühlmann's (2007) show that self-contained gene-set testing procedures have greater statistical power than competitive testing procedures that compare the differential expression results of genes belonging to a gene-set to those of genes that do not belong to a gene-set.

A P-value for h_s may be determined by permutation of the group labels (Barry et al., 2005). Let b=1,…,B index a set of permutations of the group labels. Let h_s0 be the value of (3) obtained using the original group labels. Also, let h_sb be the value (3) obtained by permutation b=1,…,B. The permutation P-value

(4)

is the proportion of permuted assignments of labels that yield a greater value of (3) than does the original assignment of labels. The same set of permutations is used to compute P-values for each of the differential expression statistics for individual probe-sets and each gene-set.

2.3 Meta-analytic integration of probe-set results

Now, suppose that data have been collected in two experiments that perform biologically analogous comparisons of expression across two biological conditions. Additionally, suppose that we wish to perform a meta-analysis that combines the analysis results to identify differentially expressed probe-sets. Without loss of generality, assume that the probe-sets from each study have been matched and ordered so that the index j=1,…,m corresponds to the probe-sets that query the same gene in both studies. Let d_1j and d_2j represent the vectors differential expression statistics computed for probe-set j in the analysis of data from studies 1 and 2, respectively. Also, let P(d_1j) and P(d_2j) be the P-values computed from B₁ and B₂ permutations for each study, respectively.

Now, define

and

where Φ⁻¹(·) is the quantile function of the standard normal distribution. Note that the definitions for the z-statistics incorporate information about the direction (sign) and significance (P-value) of differential expression from each study and include a correction for discrete permutation P-values by adding 0.5 to the numerator and adding 1 to the denominator of the fraction. If the null hypothesis is true for both studies, then the P-values are approximately uniform. Thus, the z-statistics are independent and each z-statistic approximately follows a standard normal distribution. Therefore, Z(d_1j)+Z(d_2j) is approximately normal with mean 0 and variance 2. Stouffer et al., (1949) show that a meta-analysis P-value is then

where Φ(·) is the cumulative distribution function of the standard normal distribution.

2.4 Meta-analytic integration of gene-set results

Now, suppose that (3) has been used to compute statistics h_1s and h_2s and their corresponding P-values P(h_1s) and P(h_2s) for differential expression analysis of gene-set s for study 1 and study 2. Define

and

as z-statistic that characterize the statistical significance of h_1s and h_2s, respectively. Recall that h_1s≥0 and h_2s≥0 by definition (3). If the null hypothesis is true for both studies, then Z(h_1s)+Z(h_2s) approximately follows a normal distribution with mean 0 and variance 2. Therefore,

is a meta-analysis P-value for the gene-set analysis that combines the analysis results from the two studies.

2.5 Agreement of differential expression

Now we describe how AGDEX evaluates the agreement of differential expression among probe-sets that belong to a gene-set s and evaluate its statistical significance by permutation. Again, suppose that data has been collected for two studies that each compare expression across two groups. For simplicity of notation, assume in this section that the data have already been limited to probe-sets that are members of gene-set s and that the order of these probe-sets has been matched across the two studies. Let j_s=1,…,m_s index the probe-sets. For simplicity of notation, the subscript s will be omitted from j_s and m_s in this section. For each probe−set j, let d_1j and d_2j be the values of (1) from study 1 and study 2, respectively. Let d₁={d_1j,…,d_1m} and d₂={d_2j,…,d_2m}.

The AGDEX procedure uses two statistics to measure the agreement of d₁ and d₂. The first statistic is the cosine of the angle between d₁ and d₂ in multivariate space (Fitzpatrick, 1996), i.e.

(5)

The second statistic is the difference of proportions (dop). Formally, the second statistic is defined as

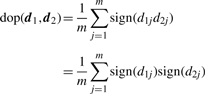(6)

which is the difference between the proportion of probe-sets that show agreement and the proportion that show disagreement in the direction of differential expression. Both statistics have range [−1,+1] with +1 indicating the greatest agreement of differential expression results and −1 indicating the greatest disagreement of differential expression results.

A P-value can be computed for each statistic by permutation of the group labels for either study. Let a₀ be the value of the cosine or dop statistic obtained from the original assignment of group labels in both studies. Let u=1,…,B₁ index permutations of the group labels from study 1 and let v=1,…,B₂ index permutations of the group labels from study 2. Let d_1u be the vector of differential expression statistics obtained from permutation u of the group labels of Study 1. For each u, let a_1u be computed using d_1u and the observed d₂. Thus,

(7)

is a P-value obtained by permutation of the group labels in study 1. This P-value compares the observed value a₀ of the agreement statistic to the distribution of agreement statistics obtained under the null hypothesis that there is no differential expression in Experiment 1.

Similarly, for each v, let d_2v be the vector of differential expression statistics obtained by permutation v of group labels for Study 2. Also, define a_2v as the value of the agreement statistic obtained using d_2v. This yields

(8)

as a P-value for a₀ based on permutation of group assignments for Study 2.

2.6 Statistical Properties

For each study s=1,2 and each probe−set j=1,…,m, let the expected value of the differential expression statistic be E(d_sj)=δ_sj. Also, let δ₁ and δ₂ be the vectors of true difference between means for Experiments 1 and 2, respectively. Recall that d₁ and d₂ are independent because they are estimated from datasets collected in separate studies. Therefore,

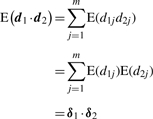(9)

and thus the expected value of the numerator of the cosine statistic in (5) is zero if d₁ and d₂ are orthogonal. Similarly, the expected value of the dop statistic in (6) is zero if sign(d₁) and sign(d₂) are orthogonal. In the specific orthogonal case, none of the genes with differential expression in Study 1 are differentially expressed in Study 2 (δ_2j=0 for each j with δ_1j≠0), the expected value of the dop statistic is 0 and the expected value of the cosine statistic is approximately zero. Consequently, for analyses with this type of orthogonal differential expression, the P-values are not likely to be significant because they compare the absolute value of the observed statistic to that of statistics obtained by permutation.

In non-orthogonal cases, the probability of a significant result increases with sample size of each group in each study. As the sample sizes increase, the variance of d_sj decreases for each s and j and thus the variances of the agreement statistics also decrease. The probability of a significant result also increases with the magnitude of

(10)

for the cosine agreement statistic and with the magnitude of

(11)

for the dop statistic.

2.7 Statistical and biological interpretation

The statistical interpretation of AGDEX results must consider the magnitude and sign of each agreement statistic and the sample sizes of each group in each differential expression analysis comparison. Analyses with large sample sizes may have power to detect some subtle but biologically uninteresting agreements as statistically significant. In such cases, AGDEX will give small agreement statistics with small P-values. Conversely, analyses with small sample sizes may not have sufficient power to detect strong agreements as statistically significant. With very small sample sizes, it is impossible for permutation procedures to give very small P-values. For example, a 3 versus 3 comparison cannot yield a permutation P-value smaller than 1/10 (Gadbury et al., 2003; Pounds and Dyer 2008). In these cases, large agreement statistics with moderate P-values may be of biological interest. In some analyses, one comparison may have large sample size and the other comparison may have a small sample size. In these analyses, one may wish to focus attention on the P-values from permuting the labels of the study with the larger sample size. In analyses where both comparisons have large sample size, one may take the maximum of the four P-values (one P-value for each of two agreement statistics by permutation of group labels from each of two studies) to focus attention on the most robust results.

The biological interpretation of AGDEX results must consider that the parameters Δ and Δ′ are functions of the differential expression status of j=1,…,m genes for each of two studies that each compare expression between two groups. A significant result may be driven by a subset of genes with statistically influential patterns of agreement. The genes with statistically influential data may not have the greatest biological relevance. Also, the P-values evaluate significance against the null hypothesis that there is no differential expression in the experiment for which the group labels are permuted. Permutation simulates values of a test statistic under the null hypothesis that group labels are random and arbitrary. Thus, significant agreement may not indicate biologically meaningful agreement. Therefore, a significant AGDEX result alone does not necessarily indicate that an animal model accurately recapitulates the biologically important characteristics of a human disease.

Nevertheless, a significant AGDEX result can help direct additional biological studies to more thoroughly evaluate the fidelity of an animal model. We used the AGDEX procedure to characterize the transcriptional similarity of novel brain tumors in mice with a series of types of human brain tumors. We found that one mouse tumor showed significant transcriptomic agreement with one subtype of human ependymoma (Johnson et al., 2010) and another mouse model showed significant transcriptomic agreement with one subtype of human medulloblastoma (Gibson et al., 2010). AGDEX did not find significant agreement with other human brain tumor subtypes. Thus, we compared the histological characteristics of the mouse tumors to those of their AGDEX-matched human tumors. In each case, the animal model and human tumors showed striking histological similarities. The combination of histological and transcriptomic evidence supports our assertion that these animal models may be a useful resource for understanding the biology of these tumors and performing preclinical evaluations of new therapies.

2.8 Comparison with other procedures

The AGDEX procedure addresses a different biological question than other methods proposed to evaluate the transcriptional similarity of a model system (cell line or animal tissue) to a human tissue. Sandberg and Ernberg (2005) and Zheng-Bradley et al., (2010) apply dimension reduction techniques such as singular value decomposition or principal components analysis to expression data matrices that include arrays from both the human tissues and the model systems. The similarity of expression is measured by proximity of the different systems' samples in the lower dimensional space. These methods are useful for describing similarities in a dataset that includes a very diverse set of biological systems (multiple tissue types and multiple species). However, these approaches do not formally evaluate statistical significance and their results depend on arbitrary user choices of tuning parameters such as the number of dimensions in the reduced dataset. Poisson and Ghosh (2007) propose a method to determine whether the profile of genes that differentiate between two model systems is useful for developing a predictor of an outcome for humans. In contrast, AGDEX addresses the specific biological question of whether the difference between tumor and control in mice is similar to the difference between tumor and control in humans.

2.9 Adaptive permutation to reduce computational burden

Permutation testing is a computationally intensive procedure. We have developed an adaptive permutation procedure that retains the statistical rigor of permutation testing while greatly reducing its computational cost for many genomics applications (Pounds et al., 2011). Adaptive permutation testing computes permutation statistics until observing a minimum of B_min permutation statistics that exceed the observed value of the test statistic or until a maximum of B_max permutation statistics have been computed. In this way, the number of permutations B is a random variable with a truncated negative binomial distribution. The success probability of the truncated negative binomial distribution is the exact P-value π based on all possible permutations and the number of required successes is B_min. The expected number of permutations is approximately min(B_max, B_min)/π. The effect is that a small number of permutations are performed for tests with large π (and thus not of much interest) and a very large number of permutations are performed to achieve the desired precision for tests with very small π. In many genomics applications, adaptive permutation testing greatly reduces the computational effort because most tests have insignificant P-values.

AGDEX allows users the option to utilize adaptive permutation to compute the gene-set differential expression P-value of Section 2.2 and the agreement of differential expression P-values of Section 2.5 for gene-sets. For AGDEX, the adaptive permutation is modified so that at least B_min permutations yield extreme values for each of the 3 gene-set statistics: the gene-set differential expression statistic in (3), the cosine agreement statistic in (5) and the difference of proportions agreement statistic in (6).

3 RESULTS

As an example, we apply AGDEX to the data from our published study of the expression of murine neural stem/progenitor cells, murine brain tumors and the human brain tumor ependymoma (Johnson et al., 2010). The Affymetrix 430v2 array was used to profile the expression of 45 037 probe-sets for 13 brain tumors from mice and a collection of 179 normal mouse stem cells. Additionally, the Affymetrix U133+2 array was used to profile the expression of 54 613 probe-sets for 83 human ependymoma tumors. The human tumors were classified as belonging to the novel subgroup ‘D’ or another subgroup. The expression data were normalized with the MAS 5.0 algorithm. We downloaded the 1454 biological process gene-set definitions from the gene-set enrichment analysis website (www.broadinstitute.org/gsea) for the U133+2 array. We used the Affymetrix best-match dataset (available from www.affymetrix.com) to define 76 061 pairs of ortholog-matched probe-sets across the two arrays. We used the best-match dataset to define the gene-sets for the mouse array probe-sets. Adaptive permutation with B_min=100 and B_max=10 000 was used to compute P-values for gene-set statistics. P-values for individual probe-set statistics and the genome-wide dop and cosine statistics were determined using 10 000 permutations. Here, we report statistical summaries of the results and refer readers to our previous publication (Johnson et al., 2010) for more detailed results and biological interpretations of the findings.

3.1 Differential expression analysis results

The methods described in Sections 2.1 and 2.2 were used to compare the expression of the mouse tumors to the mouse stem cells. The large sample size and biological distinctiveness of the tumor provided exceptional statistical power for this comparison. A total of 18 974 probe-sets and 1452 gene-sets showed significant differential expression at the P=0.0001 level.

We also compared the expression of the recently described ependymoma subtype ‘D’ to that of other human ependymomas because the ideal control of normal human brain stem cells was not available. A total of 986 probe-sets and 419 gene-sets showed significant differential expression at the P=0.0001 level (Supplementary Fig. S1).

3.2 Meta-analytic integration of differential expression results

The methods of Sections 2.3 and 2.4 were used to meta-analytically integrate the differential expression results obtained in Sections 3.1 and 3.2. A total of 1257 gene-sets and 12 560 ortholog-matched pairs of probe-sets (among 76 061 pairs defined by the best-match dataset) showed significant differential expression at the P=0.0001 level.

3.3 Agreement of differential expression

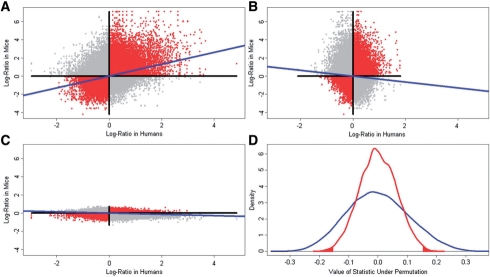
Figure 1 plots the differential expression statistic for the mouse comparison (x-axis) and human comparison (y-axis) for each of the 76 061 probe-set pairs. The paired differential expression statistics give cos(d₁,d₂)=0.305 which is very significant because only 18 of 10 000 permutations of the human group labels (P=0.0018) and 51 of 10 000 permutations of the mouse group labels (P=0.0051) yield |cos(d₁,d₂)|≥0.305. Also, dop(d₁,d₂)=0.157 is statistically significant because only 82 of 10 000 permutations of the human group labels (P=0.0082) and 118 of 10 000 permutations of the mouse group labels yield |dop(d₁,d₂)|≥0.157. Thus, the agreement of differential expression across the two experiments is significantly different from what may be expected if the human group labels are randomly assigned and from what may be expected if the mouse group labels are randomly assigned. This significant transcriptomic similarity prompted subsequent investigations which found that the mouse model shared several microscopic and submicroscopic cellular features with the human disease (Johnson et al., 2010).

Fig. 1.

Genome-Wide AGDEX analysis. (A) Plots the differential expression statistics from the human experiment (x-axis) and mouse experiment (y-axis) for each pair of matched probe-sets computed using the observed data. These results are also plotted for one permutation of the human group labels (B) and mouse group labels (C). (D) Shows the distribution of the cosine statistic (blue curve) and the dop statistic (red curve) obtained by 10 000 permutations of the human group labels.

We also computed the agreement statistics and P-values for each gene-set. A total of 29 gene-sets had the robust result of showing significance at the P=0.01 level in each of the four permutation tests performed by computing each of two agreement statistics across permutations of group labels for each of two agreement statistics (Supplementary Fig. S2).

3.4 Computing time

This analysis was completed in 2.5 h using R version 2.10.1 on a desktop computer with 2.00 GHz Intel Xeon CPU, 3.25 GB of RAM and Windows XP. This is approximately an upper limit for computing time for other applications with similar sample size and number of probe-sets. Adaptive permutation computed a large number of permutation statistics for most gene-sets in this example with such highly significant genome-wide agreement of differential expression. In particular, the statistics were computed for B_max=10 000 permutations of the mouse group labels for all gene-sets. Also, the average number of permutations of human data for gene-set analyses was 7784. In general, computing time for AGDEX will increase with sample size, number of genes, number of gene-sets and statistical significance of the gene-sets.

3.5 Results using robust multichip averaging normalization

We also applied AGDEX to data normalized by robust multichip averaging (RMA; Irizarry et al., 2003). The results were similar to those obtained using MAS 5.0 to normalize signal data (Supplementary Table S1).

4 DISCUSSION

We have developed the agreement of differential expression (AGDEX) procedure to integrate differential expression analysis results across two experiments that may utilize different platforms or even different species. The AGDEX procedure can be used to examine the transcriptional fidelity of animal models of human disease by evaluating the similarities of transcriptome-wide differential expression profiles across species. AGDEX may also be used to integrate differential expression results that use different platforms for the same species. In our studies, the AGDEX procedure enabled us to confirm the transcriptomic fidelity of newly generated mouse models and thereby infer the cell of origin of two distinct human brain cancers (Gibson et al., 2010; Johnson et al., 2010).

The AGDEX procedure also performs a comprehensive and statistically rigorous permutation-based analysis to address other biologically important questions. For each experiment, the AGDEX procedure performs differential expression analysis at the probe-set and gene-set levels. Additionally, the AGDEX procedure meta-analytically integrates differential expression results at the probe-set and gene-set levels to improve statistical power to identify genes or pathways that are important in one or both experiments. Finally, the AGDEX procedure also evaluates similarity of differential expression across the two experiments for predefined gene-sets.

The AGDEX procedure computes P-values by permuting assignments of group labels within each experiment. Permutation is computationally demanding but yet is critical to obtain an accurate measure of statistical significance, especially for identifying differentially expressed gene-sets and evaluating the agreement of differential expression. Some computationally simple approaches for gene-set analyses utilize statistical models of chance that inappropriately use final results for genes as the unit of analysis. For example, in our setting, one might use the binomial distribution to model the number of ortholog pairs that have the same sign for differential expression analysis in both experiments. Such an approach grossly exaggerates statistical significant by inappropriately using the number of ortholog pairs as the “sample size” and ignoring the correlation among genes. Permutation of group labels preserves correlation among genes by keeping gene expression values for each subject together during the random reassignment, is explicitly linked to the experimental design and uses the correct sample size by retaining the correct number of group labels and expression data vectors (Allison et al., 2006; Barry et al., 2005).

Nevertheless, the AGDEX procedure is computationally feasible. Our example analysis was completed on a desktop computer in 2.5 h. The sample size and number of genes and gene-sets are similar to those of other contemporary applications. Additionally, utilization of adaptive permutation will help reduce computational burden by performing fewer permutations for gene-sets with insignificant results (Pounds et al., 2011). This may be especially useful if the more statistically robust and computationally demanding distance-based statistic of Nettleton et al., (2008) for differential expression analysis of gene-sets is incorporated into later versions of AGDEX.

The example analysis also shows that the AGDEX procedure and our previously published results are robust against the strategy used to select the ortholog pairs that are included in the analysis. In our previously published study, the expression data were used to select which ortholog pairs from the Affymetrix best match definitions were retained for the AGDEX analysis. In this work, no such filtering was applied. The results of the analyses based on the cosine statistic are qualitatively similar to the previously published findings. The robustness of AGDEX results against filtering of ortholog pairs is concordant with earlier work that questions the merit of gene filtering in other contexts (Pounds and Cheng, 2005a).

Methodological extensions of AGDEX may enable researchers to explore more complex and biologically interesting questions. It would be interesting to generalize the procedure to handle multiple two-group experiments or manage experiments that examine differential expression across three or more groups. Differential expression analysis may be generalized to an analysis that examines the association of expression with one or more phenotypes (Pounds et al., 2009b; Pounds et al., 2011). Additionally, use of different metrics of agreement across two or more experiments may improve statistical power to make meaningful biological discoveries. These questions should be explored more thoroughly in future research.

A number of statistical issues related to AGDEX should also be explored. Normalization can have a profound impact on the accuracy of copy number analysis of tumors (Mullighan et al., 2007; Pounds et al., 2009a) and may have a substantial impact on the analysis of expression data as well. Additionally, a fundamental experimental design question is how to determine a large enough sample size to ensure adequate statistical power (Pounds and Cheng, 2005b). Finally, the question of how to adjust for multiple testing via control or estimation of the false discovery rate (Pounds, 2006) for this type of analysis should also be explicitly addressed. The AGDEX procedure performs multiple sets of related multiple tests and thus introduces a challenge for estimating or controlling the false discovery rate.

The bioinformatic issue of how to best match genes and gene-sets across species for AGDEX should also be explored. The results of the agreement analysis clearly depend on how accurately genes and gene-sets are matched across species. In our study, we matched genes and probe-sets across arrays using the Affymetrix homolog dataset. We also used the Affymetrix homolog dataset to define gene-sets for mice as those probe-sets that match genes in human gene-sets. This Affymetrix homolog dataset is based on the NCBI Homologene database, which is reasonable for many applications. Nevertheless, the matching definitions in the NCBI or any other homolog database depend on definitions, metrics and thresholds for sequence similarity. Alternative definitions, metrics or thresholds could impact the results of AGDEX and other cross-species analyses.