Abstract
Cytochrome c oxidase (CytcO) is a membrane-bound enzyme, which catalyzes the reduction of di-oxygen to water and uses a major part of the free energy released in this reaction to pump protons across the membrane. In the Rhodobacter sphaeroides aa3 CytcO all protons that are pumped across the membrane, as well as one half of the protons that are used for O2 reduction, are transferred through one specific intraprotein proton pathway, which holds a highly conserved Glu286 residue. Key questions that need to be addressed in order to understand the function of CytcO at a molecular level are related to the timing of proton transfers from Glu286 to a “pump site” and the catalytic site, respectively. Here, we have investigated the temperature dependencies of the H/D kinetic-isotope effects of intramolecular proton-transfer reactions in the wild-type CytcO as well as in two structural CytcO variants, one in which proton uptake from solution is delayed and one in which proton pumping is uncoupled from O2 reduction. These processes were studied for two specific reaction steps linked to transmembrane proton pumping, one that involves only proton transfer (peroxy–ferryl, P→F, transition) and one in which the same sequence of proton transfers is also linked to electron transfer to the catalytic site (ferryl–oxidized, F→O, transition). An analysis of these reactions in the framework of theory indicates that that the simpler, P→F reaction is rate-limited by proton transfer from Glu286 to the catalytic site. When the same proton-transfer events are also linked to electron transfer to the catalytic site (F→O), the proton-transfer reactions are gated by a protein structural change, which presumably ensures that the proton-pumping stoichiometry is maintained also in the presence of a transmembrane electrochemical gradient.
Keywords: Respiration, Electron transfer, Cytochrome aa3, Membrane protein, Electrostatics, Energy transduction
1. Introduction
Cytochrome c oxidases (CytcOs) catalyze the oxidation of cytochrome c and reduction of O2 to H2O, and use the free energy derived from this reaction to pump protons across a membrane. CytcO from Rhodobacter (R.) sphaeroides is composed of four subunits1 (SUs) and it carries four redox-active sites. The functional core of the CytcO is composed of SUs I and II, which hold all four cofactors. Electrons from cytochrome c are initially donated to a copper site composed of two copper ions (CuA) from which the electron is transferred to a heme group, heme a, and then to the catalytic site composed of a heme group, heme a3, and a copper ion, CuB (for recent reviews on structure and function of CytcOs, see [1–9]). Even though SUIII does not hold any redox-active co-factors, it is functionally important in providing amino-acid residues that are used for proton uptake [10,11] (see also below). SUIV is composed of a single transmembrane helix and its function, if any, is unknown.
In order to translocate protons all the way across the membrane a proton pump must harbor a proton pathway that spans the entire distance across the membrane. However, the barriers within the pathway must change during the course of the reaction in order to drive proton transfer unidirectionally against the proton electrochemical potential, and in order to prevent proton leaks driven by the proton gradient. Changes in the barrier heights may be modulated by the intraprotein electron-transfer reactions [12]. Alternatively, proton transfer may be controlled by means of structural changes that would also involve changes in pKas of the donors and acceptors such that in different conformational states proton uptake would take place exclusively from the more negative (N) side of the membrane and proton release to the other, more positive (P) side of the membrane. This phenomenon is often referred to as proton gating. Irrespectively of the mechanism, the design of a proton pump requires involvement of a proton-loading site (PLS), which becomes protonated from the more negative side of the membrane and then releases its proton to the other side (for a general discussion on design principles of proton pumps, see [5,6,13,14]).
In the A-type oxidases (for a discussion of a classification of the oxidases, see [15,16]), to which the mitochondrial and R. sphaeroides CytcOs belong, two proton pathways are used for proton uptake during O2 reduction, the K and D pathways (Fig. 1). A third (H) pathway has also been suggested to be used in the mitochondrial CytcO [17], but it is not functional in the R. sphaeroides CytcO [18] and therefore it is not discussed here. The K pathway is used for uptake of two substrate protons upon reduction of the catalytic site (“substrate” refers to the protons being used for reduction of O2 to water at the catalytic site, c.f. “pumped protons”), while the D pathway is used to transfer the remaining two substrate protons as well as all four protons that are pumped across the membrane [19–21]. The D pathway starts near a highly conserved Asp residue (Asp132) and leads to another highly conserved residue, Glu286. The two proto-natable residues are connected by a chain of 10–12 water molecules, which form a hydrogen-bonded chain. The PLS of CytcO has not been identified, however, there is consensus in the field that the trajectory leads via one of the heme a3 propionates (propionate D), “above” Glu286, and propionate A is a possible candidate for a PLS [22–25] (see Fig. 1).
Fig. 1.
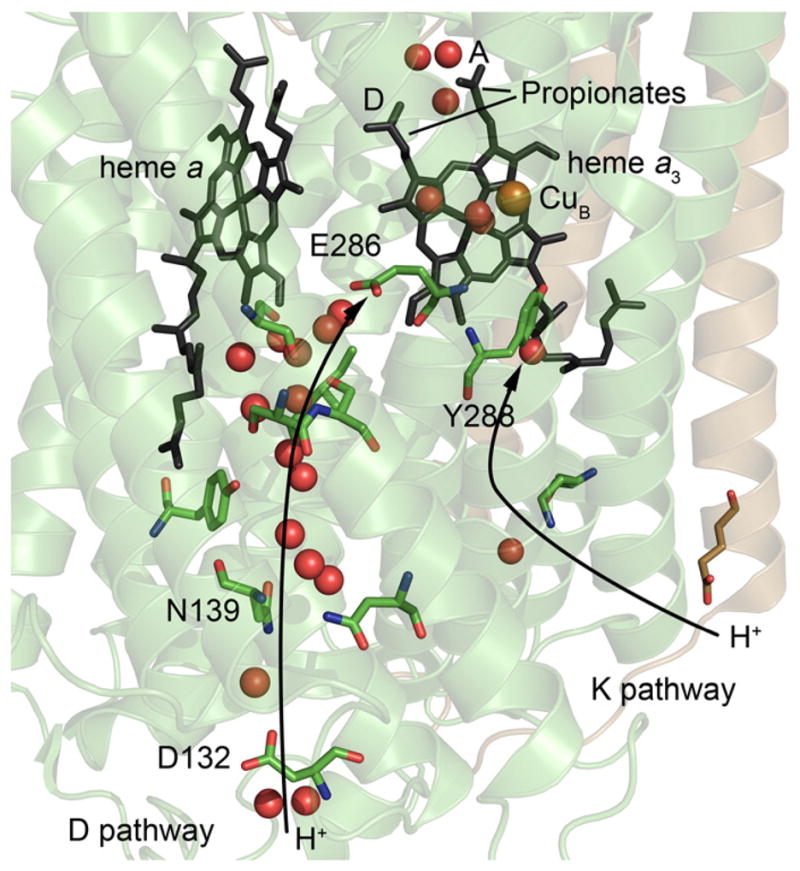
Structures of the D and K proton pathways in CytcO from R. sphaeroides. The positions of amino-acid residues discussed in this work are indicated. The red spheres are water molecules. During CytcO turnover electrons are transferred from CuA (not seen in this figure, located above heme a) to heme a and then to the catalytic site, which consists of heme a3 and CuB. Protons that are pumped across the membrane are transferred through the D pathway. The figure was prepared using the program PyMOL [90] (cytochrome c oxidase (PDB ID: 1M56)). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
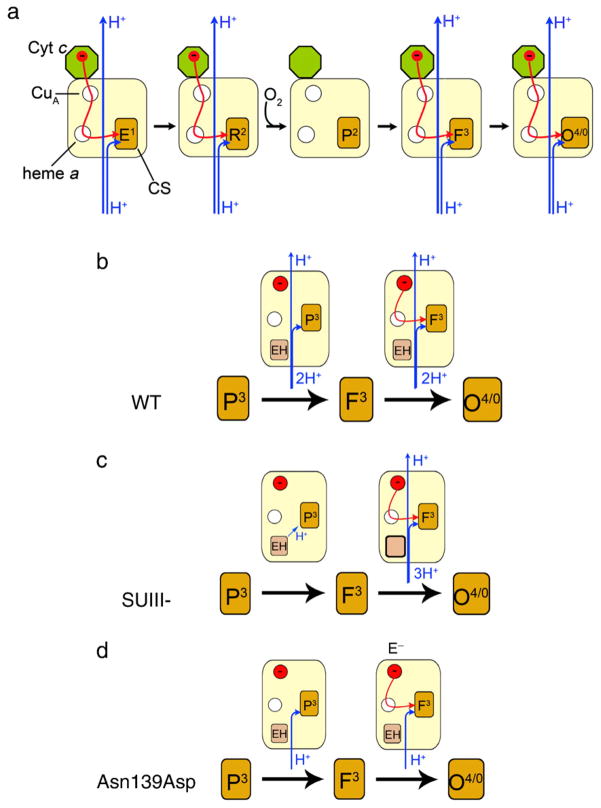
Proton pumping in CytcO takes place in four well-defined reaction steps where electrons are transferred consecutively, one-by-one to the catalytic site (see Fig. 2a) [13,26–28]. Upon transfer of the first electron to CytcO, the state that is formed is denoted E1 (where the superscript denotes the number of electrons transferred to the catalytic site). Upon transfer of the second electron the catalytic site, both heme a3 and CuB are reduced (R2) and oxygen binds to heme a3 forming state A2 (not shown in Fig. 2a). In the next step the O–O bond is broken, which results in formation in a state called peroxy (for historical reasons), denoted P2 (also PM). Transfer of a third electron to the catalytic site results in formation of the ferryl state F3. Finally, transfer of a fourth electron results in formation of the oxidized CytcO, O4: O0→E1→(R2→A2→P2)→F3→O4, where the reaction in parentheses involves only O2 binding and O–O bond cleavage. Each of the steps outside of the parentheses involves electron and proton transfers to the catalytic site, which drives the proton translocation in each of these four steps (note that states O0 and O4 are equivalent when considering the number of electrons residing at the catalytic site. This is because in both cases heme a3 and CuB are oxidized).
Fig. 2.
Schematic representation of electron and proton-transfer reactions in CytcO. The CytcO is illustrated by colored boxes where the circles represent the redox-active metal sites (empty and filled circles represent oxidized and reduced sites, respectively). In (b)–(d), EH and E− are the protonated and deprotonated forms of Glu286, respectively. (a) During turnover when electrons are transferred to the catalytic site one-by-one. (b) During reaction of the four-electron (fully) reduced wild-type CytcO with O2. In the P3→F3 reaction there is no internal electron transfer and the transition is only accompanied by proton uptake and pumping. During F3→O4 there is electron transfer to the catalytic site (in reality the electron at CuA equilibrates with heme a in F3, but for simplicity it is indicated to be present at CuA) as well as proton uptake and pumping (c.f. the corresponding reactions during turnover in (a)). (c) SUIII– CytcO, same reaction as in (b). Here, there is no proton uptake from solution during P3→F3 and during F3→O4 two protons are taken up (to the catalytic site and to re-protonate Glu286) and there is presumably also proton pumping. (d) Asn139Asp CytcO, same reaction as in (b), except that here there is no proton pumping. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Because residue Glu286 is located at the end of the D proton pathway, it defines a branching point from which protons are transferred along different trajectories to the catalytic site and the PLS, respectively (see Fig. 1). A possibility to study these proton transfers separately from the electron transfer is offered when investigating the reaction of the four-electron reduced CytcO with O2 (for review see e.g. [3]). Here, after binding of O2 to the catalytic site, an electron is transferred directly from heme a forming a state that is chemically similar to P2 (PM), but which carries one more electron at the catalytic site. This state is formed with a time constant of ~30 μs and it is called P3 (also PR) (Fig. 2b). Because in P3 there is one more electron at the catalytic than in the P2 (PM) state, the P3→F3 reaction does not involve any electron transfer, but only proton transfer to the catalytic site, as well as proton pumping, both with a time constant of ~100 μs at pH 7 [29], which is rate-limited by proton transfer from Glu286 to the catalytic site [30,31]. During steps P3→F3 and F3→O4 the substrate as well as pumped protons transferred through the D pathway [21]. In other words, in each of these reactions two protons are transferred through the D pathway, where one is transferred to the catalytic site while the other is transferred to the PLS.
In order to elucidate these processes, in the present study we have investigated the temperature dependencies of reactions associated with proton and deuteron-transfer through the D pathway in the wild-type four-subunit CytcO, in the two-subunit CytcO (lacking SUIII, SUIII–) in which proton uptake to the D pathway is impaired during the P3→F3 reaction and occurs over the same time scale as the F3→O4 transition (see Fig. 2c) [11,32] and in a mutant of the CytcO (Asn139Asp) in which proton pumping is impaired [33,34] (see Fig. 2d). The kinetic (deuterium) isotope effects (KIE2, i.e. the ratio of a specific reaction rate measured in H2O and in D2O) for the wild-type and N139D mutant CytcO have been reported previously, but not their temperature dependencies. The KIEs for the SUIII–CytcO have not been reported previously. We noted that earlier studies of KIEs have provided major functional insight into enzymatic systems [35,36]. In addition, the temperature dependence of nuclear quantum mechanical effects (NQM) can provide valuable information about the potential of mean force for the donor–acceptor distance [37] and thus can help in understanding proton-transfer mechanisms in CytcO.
2. Materials and methods
2.1. Preparation of R. sphaeroides CytcO
The R. sphaeroides bacteria were grown aerobically in shaker incubators and the His-tagged wild-type and Asn139Asp mutant (obtained from R.B. Gennis, [33]) variants of CytcO were purified using affinity chromatography as described in [38]. To obtain enzyme lacking subunit III (SUIII–), wild-type CytcO was treated with Triton X-100 [39] and the absence of SUIII was confirmed using SDS-PAGE. The purified enzyme was stored in −80 °C until use.
2.2. Preparation of fully reduced CytcO
The CytcO buffer in which the enzyme was stored was replaced by buffer containing HEPES (0.1 M, pH 7.5) or CAPS (0.1 M, pH 10.0), 100 μM EDTA and 0.05% n-dodecyl-β-D-maltoside (DDM) using concentration tubes (Amicon Ultra, Ultracel 100K, 1.16 Millipore). The CytcO was found to be stable at pH 10 as after lowering the pH from 10 to ~7 the same behavior was observed as with the pH 7 samples. Samples to be used in D2O experiments were prepared in the same way (the fraction of H2O remaining after buffer exchange was estimated to be less than one percent). The samples were diluted to a final concentration of 10 μM and transferred to an anaerobic cuvette. The air in the cuvette was exchanged for N2 on a vacuum line and CytcO was reduced by adding 2 mM reductant and 1 μM redox mediator (for samples in H2O ascorbate and hexaammineruthenium (III) chloride, and for samples in D2O ascorbate and phenazine methosulfate was used). When the enzyme was fully reduced the N2 gas was removed and replaced by CO. The reduction of the enzyme as well as binding of CO was verified using UV–vis spectroscopy.
The experiments in H2O and in D2O were done at the same pH-meter reading (pHobs). Due to the deuterium-isotope effect on the pH-glass electrode, pD=pHobs +0.4 (see [40]). The deuterium-isotope effect on the pKa of a titratable group has a similar magnitude (i.e., pKaD =pKaH +0.4). Thus, at a given pH-meter reading the “protonation” state of the group is approximately the same in H2O and D2O. However, the concentration of deuterons in D2O or protons in H2O is different at a given pH-meter reading. Consequently, the major fraction of the experiments in this study was done at pHobs =7.5 where the pH dependence of the reactions that were studied is small.
2.3. Temperature dependence studies using flow-flash spectroscopy
Fully reduced, CO-bound CytcO was transferred to a modified stopped-flow apparatus (Applied photophysics) and rapidly mixed (<10 ms) with a buffer saturated with oxygen at a ratio of 1:5 (~1 mM O2 after mixing at room temperature). The CO ligand was removed using a short laser flash (~8 ns pulse, 200 mJ, 532 nm, Nd-YAG Quantel Brilliant B) after which O2 could bind to the catalytic site of CytcO. The reaction between CytcO and oxygen was monitored by measuring absorbance changes at specific wavelengths. To be able to study the temperature dependence of this reaction, the temperature was controlled around the cuvette using a thermostated water-circulating bath. The temperature was measured around the reaction cuvette. We also verified that the effect on the measured rates as a result of temperature-induced pH changes of the solutions (c.f. temperature coefficient of the buffer) was negligible.
The solubility of O2 in water changes by a factor of two between 0 °C and 30 °C and the O2 concentration determines the rate of O2 binding to heme a3 in CytcO. However, in a saturated O2 solution at 20 °C this reaction rate is at least a factor of ~10 faster than that of the reactions studied in this work. Therefore, changes in O2 solubility do not affect the results from the present study.
3. Theory
The proton transfer from Glu286 to the catalytic site during the P3→F3 reaction is the most likely rate determining process of the overall reaction and exploration of the temperature dependence of the KIE can in principle shed light on the details of this proton transfer path. The results from our previous study of this path [41] indicated that it most likely involves a bridge of two water molecules where the proton-transfer reaction is coupled to a rotation of Glu286. In the present work we focus on a parametric examination of the KIE and on relating the results to specific molecular factors.
The theoretical analysis can be done by evaluating the actual empirical valence bond (EVB) surface of the proton-transfer process [42] and using the quantum classical path3 (QCP) centroid path integral approach developed in previous studies of nuclear quantum mechanical (NQM) effects in chemical reactions in solution and proteins [43,44]. This strategy has been adopted recently by other research groups as well (see e.g. [45–47]).
In the QCP approach, the nuclear quantum mechanical rate constant is expressed as
| (1) |
where Fqm, kB, T, h, and β are, respectively, the transmission factor, the Boltzmann constant, the temperature, the Planck constant, and β=1/kBT. The quantum mechanical activation barrier, , includes almost all the nuclear quantum mechanical effects, whereas only small effects originate from the pre-exponential transmission factor in the case of systems with a significant activation barrier [48,49].
The quantum mechanical free energy barrier, , can be evaluated using Feynman’s path integral formulation [50], where each classical coordinate is replaced by a ring of quasiparticles that are subjected to the effective “quantum mechanical” potential:
| (2) |
Here, Δxk = xk + 1 −xk (where xp + 1 = x1), Ω=p/β, p is the number of quasiparticles, M is the mass, and U is the actual potential used in the classical simulation. The total quantum mechanical partition function can then be obtained by running classical trajectories of the quasiparticles with the potential Uqm. The probability of being at the transition state is this way approximated by a probability distribution of the center of mass of the quasiparticles (the centroid) rather than the classical single point. Thus, we follow the strategy of the centroid path integral method [51–53]. However, the regular centroid approach requires one to consider the trajectory of all the quasiparticles and thus the use of this approach in condensed phase reactions are very challenging and may have major convergence problems. The QCP approach offers an effective and rather simple way for evaluating this probability without changing the simulation program significantly. This is done by propagating classical trajectories on the classical potential energy surface of the reacting system and using the positions of the atom of the system to generate the centroid position for the quantum mechanical partition function. This treatment is based on the finding that the quantum mechanical partition function, Zq, can be expressed as [43,44,54,55]:
| (3) |
coincides with the current position of the corresponding classical particle, and 〈…〉U designates an average over the classical potential U. Using Eq. (3), we can obtain the quantum mechanical free energy surface by evaluating the corresponding probability by the combined free energy perturbation umbrella sampling (FEP-US) approach of the EVB method [42]. Now we use the double average of Eq. (3) rather than an average over a regular classical potential. At any rate, the main point of the QCP is that the quantum-mechanical free energy function can be evaluated by a centroid approach that is constrained to move on the classical potential. This provides stable and relatively fast converging results that have been shown to be quite accurate in studies of well defined test potentials, where the exact quantum mechanical results are known (e.g. [43]).
In order to obtain the NQM effect we run classical trajectories of the quasiparticles on the “quantum mechanical” potential given by Eq. (2). For these trajectories, we have used 18 particles (less than 10 particles gives unstable results). Also, since any reliable protein investigation should average the relevant energies over different protein configurations, the energy of the quasiparticle trajectory has been averaged for every 0.5 fs of a 20 ps protein simulation. In the end, the term is averaged over 20,000 protein and quasiparticle configurations. In order to compensate for the comparatively short simulation over the protein configurations (it turns out to be very time consuming to average both over protein and quasiparticle configurations with an 18 particle system), the system was first equilibrated thoroughly for 500 ps.
While the QCP can be very effective we can also obtain significant insights by using a simplified vibronic approach [45,56–60] in a parametric way. The vibronic treatment provides a quasiharmonic rate constant which involves a Boltzmann sum from contributions (kam, bm) of transitions between vibronic states. The high temperature limit of each vibronic rate constant is given by [56,57].
| (4) |
where we consider the activation barriers Δg≠ relative to the minimum of the reactant state, instead of the ΔG≠ that reflects all the available configurations in the reactant state (see [36]), and the effect of the reactant state configuration is assumed to be included in the vibronic sum. Here λ is the “reorganization energy” defined by
| (5) |
where Δεba and ΔG0 are the energy gap between the potentials of state b and a (averaged over trajectories on state a) and standard free energy. Eq. (4) reflects the probability of a vibronic transition from the reactant well to the product well (as determined by the vibrational overlap integrals (the Smm′) modulated by the chance that Δε would be zero). This chance is determined by the activation free energy, Δg≠, whose value can be approximated by
| (6) |
where ωr is the vibrational frequency of the X–H bond. This relationship is only applicable if the system can be described by the linear response approximation (see [56]), but this does not require the system to be harmonic. The above vibronic treatment is similar to the expression developed by Kuznetsov and Ulstrup [60]. However, the treatment that leads to Eq. (13), which was developed by Warshel and coworkers [61]} [56,57], is based on a more microscopic approach and leads to much more consistent treatment of Δg≠, where we can use rigorously ΔG0 rather than ΔE. Furthermore, our dispersed polaron (spin boson) treatment [56] gives a clear connection between the spectral distribution of the solvent fluctuations and the low temperature limit of the rate constant. It is also useful to note that Borgis and Hynes [62] and Antoniou and Schwartz [63] have used a similar treatment but considered only the lowest vibrational levels of the proton.
As we repeatedly noted (e.g. [37]), the use of the above vibronic treatment is only valid in the diabatic limit when is sufficiently small. Now, in cases of proton transfer, hydrogen transfer and hydride transfer (HT) processes, Hab is far too large to allow for a diabatic treatment. However, it is more significant to ask what is the magnitude of . Here we note that for 0→0 transitions, Smn may be quite small, since it is given by S00 =exp{−Δ2/4} where Δ is the dimension-less origin shift. Now, using the fact that Δis 6.5 for Δr=0.6 Å and the proper dimensionless conversion (e.g. [64,65]), we obtain for proton and hydrogen transfer (or the corresponding deuterated system) the relationship [37]:
| (7) |
With this we can write
| (8) |
This expression is given for single Δr and a more consistent expression can be obtained by integrating the vibronic rate constant over the “soft” coordinates, and in particular the X···Y distance R, which is related to Δr as Δr=R–2b, where b is the X–H bond length, which is typically 1.05 Å. This can be done by writing:
| (9) |
where w(R) is the potential of mean force (PMF for the donor–acceptor) distance. If the main contribution to kab originates from ka0,b0, then we can approximate the KIE by
| (10) |
where
| (11) |
If we assume that λ and Hab are independent of R in the region with the largest contribution to k00 we can write
| (12) |
where . Eq. (12) can be used as a qualitative guide, but we must keep in mind that we are dealing with a very qualitative approximation here (see [37]).
In order to obtain useful parametric representation for the above equations we introduced the following approximations:
| (13) |
where, K and R0 are the force constant and position of the minimum, respectively, for the potential of mean force (PMF) between the donor and acceptor. The first (exponential) term signifies the repulsive part of the PMF and A is the corresponding pre-exponential factor. In the presented results we have used K = 7.0 kcal/mol−1 Å−2 and R0 =4.0 Å. Also, we have used ΔG0=0.
In the adiabatic limit we have to use the QCP approach, writing
| (14) |
where is the quantum correction. We can also write
| (15) |
where
| (16) |
is the classical probability of being at the transition state for different values of the donor and acceptor distance and w is the potential of mean force, PMF, for the distance between the donor and acceptor.
4. Experimental results
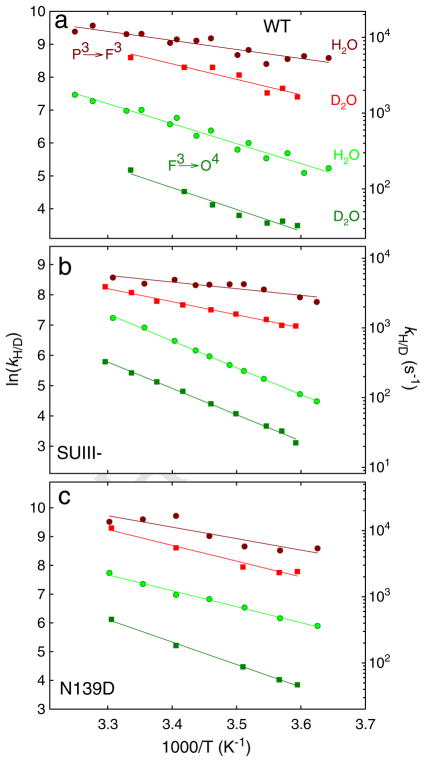
In Fig. 3 are shown absorbance changes at 580 nm during oxidation of the four-electron reduced CytcO in H2O and D2O. The increase in absorbance in the time range 100–300 μs is associated with formation of the F3 state from P3 (PR) (τ ≅100 μs) while the following decrease in absorbance (in the time range >300 μs) is associated with the F3→O4 reaction. The ratio of the P3→F3 and F3→O4 rates measured in H2O (kH) and in D2O (kD), i.e. the KIE was ~2.0 and 7.7 at ~20 °C (i.e. at room temperature, RT), respectively, consistent with previous observations [66–71]. The temperature dependence of the P3→F3 and F3→O4 transition rates for the wild-type CytcO in H2O and D2O is shown in Fig. 4a, and the parameters extracted from these data are summarized in Table 1.
Fig. 3.
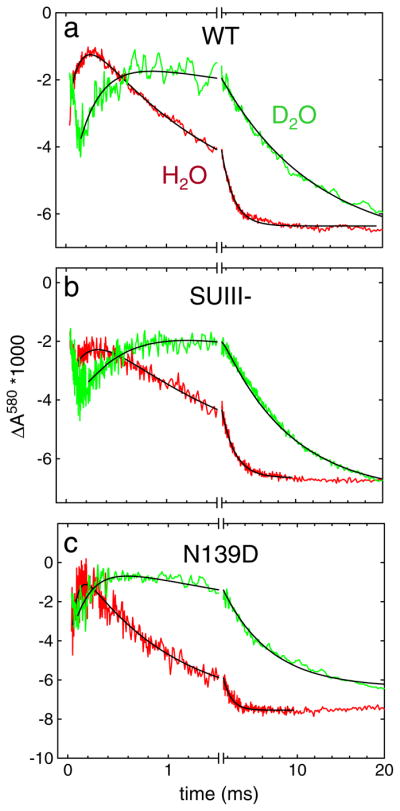
Absorbance changes at 580 nm associated with reaction of the four-electron reduced CytcO with O2: (a) wild-type CytcO (b) SUIII (–) CytcO and (c) Asn139Asp mutant CytcO in H2O (green) and D2O (red). The increase in absorbance is associated with the P3→F3 reaction, while the following decrease in absorbance is associated with the F3→O4 reaction. The rate constants of the P3→F3 and F3→O4 reactions were extracted from these data at 580 nm (as well as at 445 nm in the case of the F3→O4) by fitting the traces to sums of exponential functions. The black solid lines show such fits. The rate constants are plotted in Fig. 4. Experimental conditions: ~2 μM reacting enzyme, 0.1 M HEPES pH-meter reading 7.5, 100 μM EDTA, 0.05% DDM, ~1 mM O2 (at RT) and the temperature was ~20 °C. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Fig. 4.
Temperature dependence of the P3→F3 and F3→O4 rates with (a) wild-type CytcO (b) SUIII (–) CytcO and (c) Asn139Asp mutant CytcO in H2O and D2O at a pH meter reading of 7.5. The experiments in H2O and D2O were done at the same pH-meter reading because the deuterium-isotope effect on the pH-glass electrode has about the same magnitude as that on the pKa of protonatable groups. Thus, at a given pH-meter reading in H2O and D2O, respectively, the protonation state of the protonatable groups is approximately the same. The rates were extracted from absorbance changes at 580 nm and 445 nm.
Table 1.
Kinetic-isotope effects and thermodynamic and kinetic parameters of the P3→F3 and F3→O4 reactions in the wild-type (WT), two-subunit (SUIII–) and Asn139Asp (N139D) mutant CytcOs. The parameters are extracted from the data shown in Fig. 4. The data with the Asn139Asp mutant CytcO at pH 10 are not shown in that figure.
| CytcO | H2O or D2O (pH meter) |
P3→F3 |
F3→O4 |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| KIE at RT | Ea (kcal/mol) | ΔH≠ (kcal/mol) | −TΔS (kcal/mol) | ΔG≠ (kcal/mol) | KIE at RT | Ea (kcal/mol) | ΔH≠ (kcal/mol) | −TΔS≠ (kcal/mol) | ΔG≠ (kcal/mol) | ||
| WT | H2O (7.5) | 5.4±0.6 | 4.8±0.6 | 6.3±0.4 | 11±1 | 12.0±0.8 | 11.4±0.8 | 1.07±0.05 | 12.5±1 | ||
| WT | D2O (7.5) | ~2.0 | 9.3±1.3 | 8.7±1.3 | 2.7±0.3 | 11±2 | ~7.7 | 13.0±0.9 | 12.4±0.9 | 1.19±0.09 | 13.6±1 |
| SUIII– | H2O (7.5) | 4.3±0.7 | 3.7±0.7 | 7.8±0.7 | 12±2 | 17.5±0.2 | 16.9±0.2 | –4.52±0.05 | 12.4±0.3 | ||
| SUIII– | D2O (7.5) | ~2.2 | 8.5±0.4 | 7.9±0.4 | 3.9±0.1 | 12±0.5 | ~5.2 | 17.2±0.4 | 16.6±0.4 | –3.27±0.07 | 13.3±0.5 |
| N139D | H2O (7.5) | 7.9±1.6 | 7.3±1.6 | 3.6±0.5 | 11±2 | 11.0±0.4 | 10.4±0.4 | 1.79±0.06 | 12.2±0.5 | ||
| N139D | D2O (7.5) | ~2.0 | 11±1 | 10±1 | 1.0±0.07 | 11±1.2 | ~7.0 | 15.5±0.4 | 14.9±0.4 | –1.79±0.05 | 13.1±0.5 |
| N139D | H2O (10) | 7±2 | 6±2 | 5±1 | 11±3 | 13.6±1 | 13±1 | 1.0±0.1 | 14.0±1.1 | ||
The same reaction was also investigated with CytcO in which SUIII was removed (SUIII-) (Fig. 2c). Without SUIII proton uptake through the D pathway is slowed such that after proton transfer from Glu286 to the catalytic site during the P3→F3 transition, re-protonation of the Glu from solution is delayed by a factor of >10 [11,32]. In other words, the P3→F3 transition occurs only as a result of internal proton transfer to the catalytic site and the reaction is not accompanied by proton uptake from solution [32]. The next reaction, F3→O4 thus involves a net uptake of at least two protons (see Fig. 2c), one proton is transferred to the catalytic site, a second proton is transferred to re-protonate Glu286. The SUIII– CytcO pumps protons with a stoichiometry of ~65% of that of the wild-type CytcO [72]. Because there is no proton uptake in P3→F3 reaction, in Fig. 2c we have assumed that one proton is pumped during the F3→O4 reaction. This assumption does not affect the conclusions from the present study. For the SUIII–CytcO the KIE for the P3→F3 and F3→O4 rates was ~2.2 and 5.2 at RT, respectively, i.e. similar to the values obtained with the intact wild-type CytcO. Fig. 4b shows the temperature dependence of the P3→F3 and F3→O4 transition rates in H2O and in D2O, and the parameters extracted from these data are summarized in Table 1.
We also investigated the P3→F3 and F3→O4 reactions in a CytcO mutant that is fully active, but in which proton pumping is uncoupled from O2 reduction, Asn139Asp [33,73–77]. In this mutant CytcO each of these transitions is linked to the uptake of one proton to the catalytic site, but there is no uptake or release of protons that are pumped (see Fig. 2d). For the Asn139Asp CytcO the KIE for the P3→F3 and F3→O4 rates was ~2.0 and 7.0 at RT, respectively, i.e. similar to the values obtained with the intact wild-type CytcO. The temperature dependence of the reactions in H2O and in D2O is shown in Fig. 4c. The reaction was also investigated at pH 10 because in this mutant CytcO the Glu286 pKa is increased from 9.4 in the wild-type (data not shown, but the parameters are given in Table 1 along with all other parameters for this mutant CytcO) [31] to ~11 [73].
4.1. Determination of the thermodynamic parameters from the data
The empirical, experimentally determined Arrhenius activation energies, Ea, were calculated from the slope of:
| (17) |
where kH/D represents the reaction rate in H2O (subscript “H”) or D2O (subscript “D”), A is a constant, R is the molar gas constant and T is the temperature. The Ea values for all experiments outlined above are summarized in Table 1.
The transition state theory gives:
| (18a) |
| (18b) |
| (19) |
| (20) |
| (21) |
where ΔH≠, ΔS≠ and ΔG≠ are the standard enthalpy, entropy and Gibbs energy of activation, respectively. It has been established that in condensed phase and in biological systems Eq. (18a) is extremely useful and that it only needs to be multiplied by a transmission factor to give the exact classical term (see [78]). Furthermore, there is now consensus in the field that the transmission factor is close to one when ΔG≠>5 kcal/mol (see references in [55] and [49]). In addition, even the inclusion of NQM does not change these conclusions because the main NQM corrections are included in the quantum free energy (see [43,53]) and the quantum transmission factor also appears to be close to one [79].
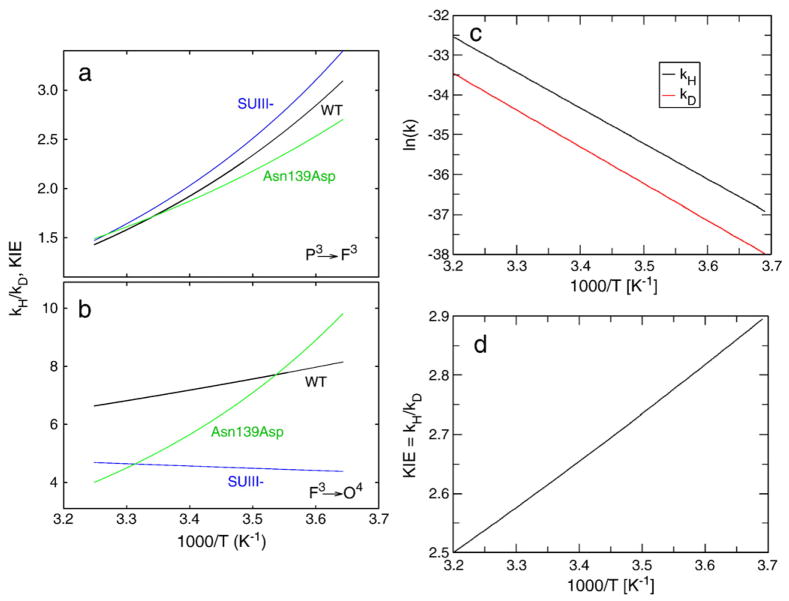
In view of the discussion above, ΔH≠ was determined from Eq. (19), –TΔS≠ from ln kH/D at 1/T=0 (see Fig. 4) and ΔG≠ from Eq. (20). The data are summarized in Table 1. From these data we can also estimate the KIE as a function of 1/T, which is shown for the P3→F3 and F3→O4 reactions in Fig. 5a and b.
Fig. 5.
The observed kinetic isotope effect (KIE), defined as kH/kD, as a function of the inverse temperature (1/T) for the (a) P3→F3 and (b) F3→O4 reactions. In (a) and (b) the rates were determined using the parameters shown in Table 1. (c) The logarithm of rate constants kH and kD as function of 1/T and (d) the KIE, defined as kH/kD, as function of 1/T. In c and d the rate constants were determined from calculations.
5. Discussion
We have investigated the temperature dependencies of the H/D KIEs of the P3→F3 and F3→O4 reactions in the wild-type CytcO as well as in two structural CytcO variants, one in which proton uptake from solution is delayed and one in which proton pumping is uncoupled from O2 reduction. As discussed below, an analysis of these reactions in the framework of theory indicates that that the simpler, P3→F3 reaction is rate-limited by proton transfer from Glu286 to the catalytic site. This proton transfer involves a change in the configuration of the Glu286 side chain, but this movement is not suggested to be involved in proton gating. When the same proton-transfer events are also linked to electron transfer to the catalytic site, i.e. the F3→O4 reaction, the proton-transfer reactions are gated by a protein structural change, presumably controlling the release of the pumped proton from the PLS.
In this section, we start with a general discussion of proton transfer and pumping in the investigated reaction steps of CytcO and then we continue to a more detailed discussion in the framework of theory.
5.1. Background
Results from earlier studies showed that the kinetic-isotope effects (KIEs) are distinctly different for the P3→F3 (τ ≅ 100 μs at pH 7.5) and F3→O4 (τ ≅ 1 ms at pH 7.5) reactions. First, we recapitulate the differences and similarities of these two reactions (see Fig. 2). The F3→O4 reaction involves all events that occur during CytcO turnover, i.e. electron transfer via heme a to the catalytic site, proton uptake to the catalytic site as well as the uptake and release of a proton that is pumped. In contrast, for the preceding step, P3→F3, the electron is already present at the catalytic site (in P3) and the reaction only involves proton transfer to the catalytic site as well as the uptake and release of a proton that is pumped across the membrane. In other words, the difference between the P3→F3 and F3→O4 reactions is that only the latter involves intramolecular electron transfer to the catalytic site.
The P3→F3 reaction, which in the wild-type CytcO is accompanied by proton uptake from solution, displays a small KIE of ~2, which is typical for a proton (deuteron) transfer from a donor to a nearby acceptor. The F3→O4 reaction displays a much bigger KIE of 7–8 in the R. sphaeroides CytcO [67,69,80] and it was found that this large KIE is associated with an event (possibly a structural change) that controls both electron transfer to the catalytic site and the release of the proton that is pumped across the membrane [70]. This structural change is also likely to be linked to a re-orientation of the Glu286 side chain [81]. These conclusions are based on the following additional observations, which are relevant for the discussion below:
Even though the uptake of the substrate proton, pumped proton and formation of the F3 state during in the P3→F3 reaction display a KIE of ~2, the release of the pumped proton in this reaction step displays a KIE of ~7, i.e. the same KIE as that observed for the F3→O4 reaction [70]. In other words, the release of the pumped proton is delayed in D2O. One interpretation of this observation is that the F3→O4 rate is determined by the proton release.
During the F3→O4 transition, as already mentioned above, all reaction steps display the same large KIE of 7–8 (τ ≅ 1 ms in H2O and ~7 ms in D2O at pH/pD 7). If intramolecular electron transfer is slowed by more than a factor 100 to ~150 ms (in the Met263Leu mutant CytcO [69]), the reaction still slows by a factor of ~8 in D2O (τ ≅ 1.3 s). However, if proton uptake is slowed by a factor of ~500 to yield a time constant of ~0.5 s (in the Asp132Asn mutant CytcO), the KIE was only 1.6 [71]. In other words, it appears that the large KIE of 7–8 is associated with reactions that control electron transfer and proton transfer within CytcO itself; if the F3→O4 reaction is slowed due to proton uptake from the outside solution, no further slowing in D2O is observed.
5.2. Thermodynamic parameters for the different types of CytcO
The data from this study show that for the P3→F3 reaction in the wild-type CytcO the ΔH≠ values are almost a factor of ~2 larger in D2O than in H2O, while the opposite is observed for –TΔS≠, yielding similar ΔG≠ values. This difference between the ΔH≠ and –TΔS≠ parameters is discussed in more detail below. Essentially the same KIE, ΔH≠ and –TΔS≠ values were obtained for the two-subunit CytcO where the P3→F3 transition is only associated with internal proton transfer from Glu286 to the catalytic site and is not followed by immediate re-protonation of Glu286 (Glu286 is left in the ionized state) (see Fig. 2c). Also with the non-pumping Asn139Asp mutant CytcO the KIE for the P3→F3 reaction was about the same as for the wild-type CytcO. Furthermore, as with the wild-type and SUIII–CytcOs, the ΔH≠ values were smaller in H2O than in D2O while the –TΔS≠ values were larger in H2O than in D2O. However, for the Asn139Asp mutant CytcO the ΔH≠ and –TΔS≠ values were in general slightly larger and smaller, respectively, than the corresponding values in the wild-type CytcO. This difference is not surprising given that the configuration of Glu286, the internal proton donor to the catalytic site, is likely to be different [41,81].
The situation is notably different for the F3→O4 reaction. Here, the ΔH≠ and –TΔS≠ values were within the error the same in H2O and D2O for both the wild-type and two-subunit (SUIII–) CytcOs, i.e. for each type of CytcO the two thermodynamic parameters were insensitive to isotopic exchange. When considering the difference between the wild-type and the SUIII– CytcOs, we note that ΔH≠ was larger for the former and that in the latter case the value of –TΔS≠ was negative (see more detailed discussion below).
As already mentioned above, the observation of a much larger KIE for the F3→O4 than for the P3→F3 reaction suggest that these reactions are likely to be rate-limited by proton transfer process of different nature. Furthermore, the observation that the thermodynamic parameters associated with the F3 →O4 reaction were insensitive to the isotopic exchange indicates that the reaction involves significant structural changes around the donor and/or acceptor.
A different situation was obtained in the non-pumping Asn139Asp mutant CytcO where the activation enthalpy values were different in H2O and D2O for the F3 →O4 reaction; ΔH ≠ was smaller in H2O (~10 kcal/mol) than in D2O (~ 15 kcal/mol). Furthermore, in D2O the –TΔS≠ value was negative (while it was positive in H2O). These data indicate that for the F3→O4 transition the rate-limiting reaction(s) is different in the non-pumping Asn139Asp mutant than in the wild-type CytcO. Furthermore, the data with the Asn139Asp mutant CytcO support the conclusion that in the wild-type CytcO the rate-limiting reaction is closely linked to the release of pumped protons (the Asn139Asp mutant CytcO does not pump protons in H2O, but in D2O it displays a pumping stoichiometry of ~30%).
5.3. Computational results, the P3→F3 reaction
We first discuss the P3→F3 reaction, which is rate-limited by internal proton transfer from Glu286 to the catalytic site. Using Eqs. (9), (12) and (13) above, and looking for the best parameters to reproduce the observed experimental data in Figs. 4 and 5 we obtained the results presented in Fig. 5c and d. The calculated slope in Fig. 5d that reproduced the observed slope for the KIE for the Asn139Asp mutant in the P3→F3 transition was obtained with R0 =4.0 Å. A PMF with slightly larger R0 was needed for the wild-type CytcO, which means that in this case the equilibrium distance between the proton donor and acceptor is larger than for the Asn139Asp mutant CytcO. This would be the case, for example, if in the wild-type CytcO the Glu286 side chain points away from the catalytic site compared to the Asn139Asp CytcO (see [41]) as observed in the X-ray crystal structure of the mutant CytcO from P. denitrificans [82].
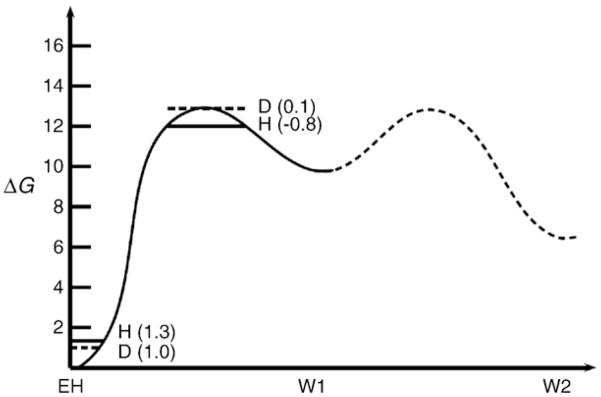
Although we have not performed here systematic QCP calculations of the temperature dependence (because the analysis is not straightforward (see [37])), it is useful to point here to the potential of this approach in the analysis of reactions in CytcO. For example, our recent study for the Asn139Asp mutant [41] has generated the surface shown in Fig. 6 for the proton transfer from Glu286 to the catalytic site through a bridge of two water molecules (W1 and W2 in Fig. 6). This surface reflects also the PMF of rotating Glu286 to a position, which brings the donor and acceptor to an optimal distance (R0 =3.0 Å). The figure also includes the NQM correction calculated by the QCP approach for protons and deuterons, leading to a KIE of ~2. When the donor and acceptor distance increases to 3.5 Å the KIE becomes ~3.
Fig. 6.
Calculated free energy profile for the proton transfer between Glu286 and the OH−in the catalytic site for the Asn139Asp mutant CytcO. We indicate the calculated QCP NQM corrections for hydrogen (H) and deuteron (D) for both ground and transition states. The corresponding total NQM corrections lead to an isotope effect of ~2.
5.4. Computational results, analysis of the thermodynamic parameters
The slope of the temperature (1/T) dependence of the KIE for the F3→O4 transition in the Asn139Asp mutant CytcO is similar to the corresponding dependence in the case of the P3→F3 transition (compare ratios of Ea values in H2O and D2O, Table 1), which is consistent with the same proton transfer being rate limiting, i.e. the absence of proton pumping by this mutant CytcO. However, in order to obtain more accurate data, this issue must be explored with QCP calculations and with EVB free energy surface for the F3→O4 transition.
The decomposition of the activation free energy change, ΔG≠, to the entropic and enthalpy components (Table 1) can potentially offer insights into the molecular nature of the proton-transfer process. For example, for the P3→F3 reaction the activation entropy is negative in all cases (positive –TΔS≠). This means that the reacting system has a smaller available configurational space at the transition state. The reduction in configurational space is fully consistent with the fact that the proton transfer involves a change from a neutral pair (Glu286 – H2O) to an ion pair (Glu286− – H3O+). In the transition state the water molecules and polar protein residues are partially oriented towards the charges of the ion pair and this reduces the entropy of the system. An additional factor is associated with the constraint on the rotation of Glu286, which is relatively fixed at the transition state.
Another feature is the fact that the entropic contribution is larger in H2O than in D2O. Here, we can invoke entropy–enthalpy compensation, since the nuclear quantum mechanical (NQM) effect leads to a larger reduction in ΔH≠ for the proton than for the deuteron. The resulting compensation by the activation entropy is reflected in the overall activation entropy (which includes a NQM contribution and a classical contribution). However, we can also obtain this trend from the vibronic treatment (see below). It should also be noted that the same behavior for the proton and deuteron NQM entropies has been observed with other systems such as e.g. lypoxygenase [83] and alcohol dehydrogenase [84]. However, the trend in the classical treatment is expected to be different (e.g. negative activation entropy in ADH, see [55]) due to the different charge distributions in the transition and ground states.
The general behavior of the quantum contribution to the activation free energy can be explored by using the vibronic treatment discussed above. In doing so it is useful to consider a harmonic approximation for the effective barrier using:
| (22) |
Substituting this expression in Eq. (9) gives:
| (23) |
Note that for simplicity the integration range has been extended over (−∞,∞). This is a reasonable approximation because the integral has almost no contribution for R<0. Using Eq. (23) we obtain:
| (24) |
One can easily verify from the above expression that for physically meaningful numerical values, the first two terms have very small contribution. Consequently, we can approximate −TΔS as:
| (25) |
5.5. Computational results, comparison to experiments
The above relation provides a few important physical insights, namely (i) –TΔS≠ increases rapidly with increasing R0, where the position of the minimum of w#(R) moves to higher values, and (ii) for intermediate values of the force constant K, we can find that –TΔS≠ is lower in deuterium than in hydrogen. Thus, –TΔS≠ (D)–(–TΔS≠ (H)) becomes negative, i.e. there is agreement between experiment and theory (Table 1) for the P3→F3 reaction, but not the F3→O4 reaction, which indicates that the latter is rate-limited by another event than a pure proton transfer (see below).
It should be clarified that the above general behavior depends strongly on the PMF used and it suffers from the fact that the vibronic treatment is invalid in the range for R values <2.6 Å (see analysis in [85]). Thus a more general verification would require QCP path integral calculations at different temperatures but this is left to subsequent studies.
Our main point in the discussion of the quantum entropic effect is to establish that the trend in the sign of –TΔS≠ (D)–(–TΔS≠ (H)) is consistent with the observed trend in the KIE for different enzymes and with qualitative considerations. The details of this behavior can provide information on the PMF for the donor–acceptor distance, but extracting the quantitative trend is challenging and can only be done with full QCP type analysis. On the other hand, the observation of a large KIE and its temperature dependence is easier to analyze because it reflects large donor–acceptor distances where the vibronic treatment is valid. In addition, the classical –TΔS≠ does provide important information on changes in the environment of the donor and acceptor system.
At this point it is useful to turn to the observed temperature dependence of the KIE. As was derived from an analysis of mutants of dihydrofolate reductase (DHFR) [37] there is considerable temperature dependence in cases where the contribution is large from configurations with large donor–acceptor distances. In the case of CytcO one has to be careful with the analysis because a specific reaction step may involve several proton-transfer events [41]. Thus, it is most straightforward to start with the Asn139Asp mutant CytcO, which does not pump protons.
The simplest explanation for the larger KIE for the F3→O4 than for the P3→F3 reaction is that the proton donor–acceptor distance is larger in the F3→O4 than in the P3→F3 reaction. However, this scenario is unlikely because the two reactions involve proton transfer through the same (D) pathway to the catalytic site. Alternatively, the exotermicities of the proton-transfer reactions may be different due to different proton acceptors at the catalytic site [23] and thereby the electrostatic effects on the proton transfer would be different. However, we exclude this possibility as the larger KIE appears to be linked to proton transfer on the proton-release (P) side of the CytcO and not proton transfer to the catalytic site (see discussion above). Yet another possibility, which is consistent with other results discussed above, is that the PMF for rotating Glu286 is steeper in the F3→O4 than in the P3→F3 reaction. This explanation is consistent with the proton transfer during the F3→O4 reaction being controlled by a change in structure above the hemes if such a change is tightly linked to a reorientation of the Glu286 side chain (as discussed in detail in [81]).
Another major effect is the disappearance of the temperature dependence of the KIE for the SUIII– CytcO in the F3→O4 reaction. Here, it is possible that rate-determining proton-transfer step is different than in the intact wild-type CytcO. We note that while for the wild-type CytcO at the initiation of the F3→O4 reaction Glu286 is protonated, for the two-subunit CytcO Glu286 is likely to be in the ionized state because there is no proton uptake during the P3→F3 reaction [32] (Fig. 2c). Consequently, the F3→O4 reaction involves proton transfer all the way through the D pathway, rather than from Glu286 followed by reprotonation of the residue (as in the wild-type CytcO). Furthermore, with the SUIII– CytcO, two substrate protons are taken up on the time scale of the F3→O4 reaction (c.f. one with the wild-type CytcO) (c.f. Fig. 2b and c); one proton to the catalytic site and one to re-protonate the ionized Glu286. Interestingly, in the F3→O4 step with the SUIII– CytcO the sign of the activation entropy (–TΔS≠) is different from that obtained with the wild-type CytcO (see Table 1), which indicates that the proton-transfer transition state is different for the SUIII– CytcO. One explanation of this result is that the system moves from a charged ground state to less polar transition state, which is consistent with Glu286 carrying a charge upon initiation of the F3→O4 reaction (see Fig. 2c). Even though the proton transfer to the catalytic site requires Glu286 to be re-protonated, because of the different initial state, the proton transfer may involve a different pathway, e.g. via a water molecule. Alternatively, in this case proton transfer to the ionized Glu286 may be rate limiting for the overall process.
6. Summary and concluding remarks
The data show that for the P3→F3 reaction qualitatively the same or similar KIEs, thermodynamic parameters (or the ratio of these parameters in H2O and D2O) (Table 1) and temperature dependencies of the KIE (Fig. 5) were observed for the wild-type, SUIII– and Asn139Asp CytcOs. This indicates that the same proton-transfer reaction is rate limiting irrespectively if the reaction involves (i) proton transfer all the way through the D pathway to the catalytic site and proton pumping (wild-type CytcO, see Fig. 2b), (ii) internal proton transfer from Glu286 to the catalytic site, no proton transfer through the D pathway to re-protonate Glu286 and presumably no proton pumping (SUIII– CytcO, see Fig. 2c), and (iii) proton transfer all the way through the D pathway to the catalytic site, but no proton pumping (Asn139Asp mutant CytcO, see Fig. 2d). Thus, the data are consistent with the proton transfer from Glu286 to the catalytic site being rate-limiting for this reaction.
The situation is strikingly different for the F3→O4 reaction, which in the wild-type CytcO involves the same proton-transfer events as the P3→F3 step and differs from the latter only in that it involves internal electron transfer to the catalytic site. First, the F3→O4 reaction displays a significantly larger KIE in all investigated CytcO variants. Next, for the (pumping) wild-type and SUIII– CytcOs, the ΔH≠ and –TΔS≠ values were the same in H2O and D2O, although they differed between the two enzyme types. For the Asn139Asp mutant CytcO, which does not pump protons in H2O but pumps to some extent in D2O [73], the ΔH≠ and –TΔS ≠ were different in H2O and D2O. Furthermore, in all cases the ΔH≠ contributions were significantly larger and the –TΔS≠ were significantly smaller for the F3→O4 than for the P3→F3 step. In addition, while the temperature dependencies of the KIE were similar for all enzyme forms in the P3→F3 step (Fig. 5a), significant differences were observed for the F3→O4 reaction (Fig. 5b). Thus, a comparison of the thermodynamic parameters for the P3→F3 and F3→O4 reactions indicates that these reactions involve different rate-determining steps. Furthermore, the theoretical analysis indicates that while the P3→F3 reaction is rate-limited by proton transfer to the catalytic site, the F3→O4 reaction is rate-limited by a structural change, presumably related to the function of CytcO as a proton pump. It should be noted that the computational results discussed above indicate a slight movement of the Glu286 side chain during the P3→F3 reaction, but this change in configuration is only part of the proton-transfer event and it is not implied to be the structural change that is suggested to be rate-determining for the F3→O4 reaction.
As described in the “Introduction” section, the operation of any redox-driven proton pump requires control of internal electron and proton-transfer reactions to prevent leaks and assure that at any step of the reaction protons are taken up from the “correct”, N side, of the membrane. Controlling internal electron transfer and proton transfer from the N-side of the membrane to the catalytic site by the release of the pumped proton to the P-side (as suggested here for the F3→O4 reaction) is one way to solve this problem. In an early discussion of the P3→F3 reaction it was pointed out [86] that it is “artificial” in that it occurs only in the four-electron (fully) reduced CytcO where electron transfer from heme a to the catalytic site is faster than the proton transfer to the catalytic site (see discussion above). Even though the conclusion that proton pumping does not occur [86] in this reaction was proven to be incorrect [29,87] (these are technically difficult measurements and was not straightforward to demonstrate proton pumping in a single, specific reaction of CytcO), it is a fact that the P3→F3 reaction is unique in that it is the only reaction step in CytcO that does not involve simultaneous electron transfer to the catalytic site (c.f. Fig. 2). As already mentioned above, the electron transfer to form the P3 state (i) is not linked to any proton uptake from solution [88] and (ii) it occurs also when the internal proton donor to the catalytic site, Glu286, is removed by mutation (Glu286Gln mutant CytcO) [89]. Because the state of the CytcO upon initiation of the P3→F3 is different from that upon initiation of the F3→O4 reaction (as well as other steps during CytcO turnover, which all involve simultaneous electron transfer to the catalytic site), it is possible that the mechanism of proton gating during P3→F3 is different. In other words, the sequence of events during P3→F3 leads to proton pumping by the same mechanism as in any other step of the reaction, only that in this case the reaction is not controlled (rate-limited) by the structural changes referred to above. A corollary of this statement is that proton pumping during P3→F3 may be more sensitive to changes in the transmembrane electrochemical potential because it is not controlled (as tightly as) the other steps of the CytcO reaction (it should be noted that all measurements of proton pumping during P3→F3 so far have been made in the absence of a transmembrane potential).
In summary, the discussion above suggests that understanding the (simpler) P3→F3 reaction offers insights into internal proton-transfer reactions that eventually lead to pumping while during the F3→O4 reaction, which is representative of any other reaction step during turnover, there is an additional level of control, which ensures that the proton-pumping stoichiometry is maintained also in the presence of a transmembrane electrochemical gradient.
Acknowledgments
The study was supported by grants from the Swedish Research Council (to PB), the Center for Biomembrane Research (to PB & MH) and NIH grant GM40283 (to AW). The authors gratefully acknowledge the University of Southern California’s High Performance Computing and Communications Center for computer time.
Abbreviations
- CytcO
cytochrome c oxidase
- N
P-side, negative and positive sides of the membrane, respectively
- SU
subunit; time constants are given as (rate constant)–1
- PLS
proton-loading site
- KIE
kinetic isotope effect
- PMF
potential of mean force
- QCP
quantum classical path
- kB
Boltzmann constant
- h
Planck constant
- T
temperature
- Ea
Arrhenius activation energy
- M
mass
- U
potential used in the classical simulation
- Fqm
transmission factor
- λ
the “reorganization energy”
- kH
kD, proton or deuteron-transfer rate constants
- ΔH≠
standard enthalpy of activation
- ΔS≠
standard entropy of activation
- ΔG≠
standard Gibbs energy of activation
- Δg‡
the quantum mechanical activation barrier
- Δg≠
activation free energy relative to the minimum of the reactant state
- P
number of quasiparticles
- Δεba
“energy gap” between the reactant and product states
- Zq
quantum mechanical partition function
- ω
effective vibrational frequency
- w
potential of mean force
- Smm
vibrational overlap integral
- R
distance between the proton donor and acceptor
Footnotes
The ratio of proton/deuteron transfer rates in H2O and in D2O, respectively.
If not otherwise indicated, amino-acid residues are numbered according to the Rhodobacter sphaeroides CytcO sequence.
References
- 1.Belevich I, Verkhovsky MI. Molecular mechanism of proton translocation by cytochrome c oxidase, Antioxid. Redox Signal. 2008;10:1–29. doi: 10.1089/ars.2007.1705. [DOI] [PubMed] [Google Scholar]
- 2.Gennis RB. Coupled proton and electron transfer reactions in cytochrome oxidase. Front Biosci. 2004;9:581–591. doi: 10.2741/1237. [DOI] [PubMed] [Google Scholar]
- 3.Brzezinski P, Gennis RB. Cytochrome c oxidase: exciting progress and remaining mysteries. J Bioenerg Biomembr. 2008;40:521–531. doi: 10.1007/s10863-008-9181-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Brändén G, Gennis RB, Brzezinski P. Transmembrane proton translocation by cytochrome c oxidase. Biochim Biophys Acta. 2006;1757:1052–1063. doi: 10.1016/j.bbabio.2006.05.020. [DOI] [PubMed] [Google Scholar]
- 5.Brzezinski P, Ädelroth P. Design principles of proton-pumping haem-copper oxidases. Curr Opin Struct Biol. 2006;16:465–472. doi: 10.1016/j.sbi.2006.06.012. [DOI] [PubMed] [Google Scholar]
- 6.Wikström M, Verkhovsky MI. Mechanism and energetics of proton translocation by the respiratory heme-copper oxidases. Biochim Biophys Acta BBA Bioenerg. 2007;1767:1200–1214. doi: 10.1016/j.bbabio.2007.06.008. [DOI] [PubMed] [Google Scholar]
- 7.Wikström M, Verkhovsky MI. Towards the mechanism of proton pumping by the haem-copper oxidases. Biochim Biophys Acta Bioenerg. 2006;1757:1047–1051. doi: 10.1016/j.bbabio.2006.01.010. [DOI] [PubMed] [Google Scholar]
- 8.Hosler JP, Ferguson-Miller S, Mills DA. Energy transduction: proton transfer through the respiratory complexes. Annu Rev Biochem. 2006;75:165–187. doi: 10.1146/annurev.biochem.75.062003.101730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Brunori M, Giuffre A, Sarti P. Cytochrome c oxidase, ligands and electrons. J Inorg Biochem. 2005;99:324–336. doi: 10.1016/j.jinorgbio.2004.10.011. [DOI] [PubMed] [Google Scholar]
- 10.Hosler JP. The influence of subunit III of cytochrome c oxidase on the D pathway, the proton exit pathway and mechanism-based inactivation in subunit I. Biochim Biophys Acta. 2004:332–339. doi: 10.1016/j.bbabio.2003.06.009. [DOI] [PubMed] [Google Scholar]
- 11.Ädelroth P, Hosler J. Surface proton donors for the D-pathway of cytochrome c oxidase in the absence of subunit III. Biochemistry. 2006;45:8308–8318. doi: 10.1021/bi0605843. [DOI] [PubMed] [Google Scholar]
- 12.Olsson MHM, Siegbahn PEM, Blomberg MRA, Warshel A. Exploring pathways and barriers for coupled ET/PT in cytochrome c oxidase: a general framework for examining energetics and mechanistic alternatives. Biochim Biophys Acta Bioenerg. 2007;1767:244–260. doi: 10.1016/j.bbabio.2007.01.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wikström M. Cytochrome c oxidase: 25 years of the elusive proton pump. Biochim Biophys Acta. 2004;1655:241–247. doi: 10.1016/j.bbabio.2003.07.013. [DOI] [PubMed] [Google Scholar]
- 14.Rich PR. Towards an understanding of the chemistry of oxygen reduction and proton translocation in the iron–copper respiratory oxidases. Aust J Plant Physiol. 1995;22:479–486. [Google Scholar]
- 15.Hemp J, Gennis RB. Diversity of the heme-copper superfamily in archaea: insights from genomics and structural modeling. Results Probl Cell Differ. 2008;45:1–31. doi: 10.1007/400_2007_046. [DOI] [PubMed] [Google Scholar]
- 16.Pereira MM, Santana M, Teixeira M. A novel scenario for the evolution of haem-copper oxygen reductases. Biochim Biophys Acta Bioenerg. 2001;1505:185–208. doi: 10.1016/s0005-2728(01)00169-4. [DOI] [PubMed] [Google Scholar]
- 17.Yoshikawa S, Muramoto K, Shinzawa-Itoh K, Aoyama H, Tsukihara T, Ogura T, Shimokata K, Katayama Y, Shimada H. Reaction mechanism of bovine heart cytochrome c oxidase. Biochim Biophys Acta Bioenerg. 2006;1757:395–400. doi: 10.1016/j.bbabio.2006.04.028. [DOI] [PubMed] [Google Scholar]
- 18.Lee HM, Das TK, Rousseau DL, Mills D, Ferguson-Miller S, Gennis RB. Mutations in the putative H-channel in the cytochrome c oxidase from Rhodobacter sphaeroides show that this channel is not important for proton conduction but reveal modulation of the properties of heme a. Biochemistry. 2000;39:2989–2996. doi: 10.1021/bi9924821. [DOI] [PubMed] [Google Scholar]
- 19.Konstantinov AA, Siletsky S, Mitchell D, Kaulen A, Gennis RB. The roles of the two proton input channels in cytochrome c oxidase from Rhodobacter sphaeroides probed by the effects of site-directed mutations on time-resolved electrogenic intraprotein proton transfer. Proc Natl Acad Sci U S A. 1997;94:9085–9090. doi: 10.1073/pnas.94.17.9085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wikström M, Jasaitis A, Backgren C, Puustinen A, Verkhovsky MI. The role of the D- and K-pathways of proton transfer in the function of the haem-copper oxidases. Biochim Biophys Acta. 2000;1459:514–520. doi: 10.1016/s0005-2728(00)00191-2. [DOI] [PubMed] [Google Scholar]
- 21.Brzezinski P, Ädelroth P. Pathways of proton transfer in cytochrome c oxidase. J Bioenerg Biomembr. 1998;30:99–107. doi: 10.1023/a:1020567729941. [DOI] [PubMed] [Google Scholar]
- 22.Sugitani R, Medvedev ES, Stuchebrukhov AA. Theoretical and computational analysis of the membrane potential generated by cytochrome c oxidase upon single electron injection into the enzyme. Biochim Biophys Acta Bioenerg. 2008;1777:1129–1139. doi: 10.1016/j.bbabio.2008.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Siegbahn PEM, Blomberg MRA, Blomberg ML. Theoretical study of the energetics of proton pumping and oxygen reduction in cytochrome oxidase. J Phys Chem B. 2003;107:10946–10955. [Google Scholar]
- 24.Lee HJ, Öjemyr L, Vakkasoglu A, Brzezinski P, Gennis RB. Properties of Arg481 mutants of the aa3-type cytochrome c oxidase from Rhodobacter sphaeroides suggest that neither R481 nor the nearby D-propionate of heme a3 is likely to be the proton loading site of the proton pump. Biochemistry. 2009;48:7123–7131. doi: 10.1021/bi901015d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pisliakov AV, Sharma PK, Chu ZT, Haranczyk M, Warshel A. Electrostatic basis for the unidirectionality of the primary proton transfer in cytochrome c oxidase. Proc Natl Acad Sci U S A. 2008;105:7726–7731. doi: 10.1073/pnas.0800580105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Michel H. Cytochrome c oxidase: catalytic cycle and mechanisms of proton pumping—a discussion. Biochemistry. 1999;38:15129–15140. doi: 10.1021/bi9910934. [DOI] [PubMed] [Google Scholar]
- 27.Ruitenberg M, Kannt A, Bamberg E, Fendler K, Michel H. Reduction of cytochrome c oxidase by a second electron leads to proton translocation. Nature. 2002;417:99–102. doi: 10.1038/417099a. [DOI] [PubMed] [Google Scholar]
- 28.Bloch D, Belevich I, Jasaitis A, Ribacka C, Puustinen A, Verkhovsky MI, Wikström M. The catalytic cycle of cytochrome c oxidase is not the sum of its two halves. Proc Natl Acad Sci U S A. 2004;101:529–533. doi: 10.1073/pnas.0306036101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Faxén K, Gilderson G, Ädelroth P, Brzezinski P. A mechanistic principle for proton pumping by cytochrome c oxidase. Nature. 2005;437:286–289. doi: 10.1038/nature03921. [DOI] [PubMed] [Google Scholar]
- 30.Brzezinski P, Johansson AL. Variable proton-pumping stoichiometry in structural variants of cytochrome c oxidase. Biochim Biophys Acta Bioenerg. 2010;1797:710–723. doi: 10.1016/j.bbabio.2010.02.020. [DOI] [PubMed] [Google Scholar]
- 31.Namslauer A, Aagaard A, Katsonouri A, Brzezinski P. Intramolecular proton-transfer reactions in a membrane-bound proton pump: the effect of pH on the peroxy to ferryl transition in cytochrome c oxidase. Biochemistry. 2003;42:1488–1498. doi: 10.1021/bi026524o. [DOI] [PubMed] [Google Scholar]
- 32.Gilderson G, Salomonsson L, Aagaard A, Gray J, Brzezinski P, Hosler J. Subunit III of Cytochrome c Oxidase of Rhodobacter sphaeroides is required to maintain rapid proton uptake through the D pathway at physiologic pH. Biochemistry. 2003;42:7400–7409. doi: 10.1021/bi0341298. [DOI] [PubMed] [Google Scholar]
- 33.Pawate AS, Morgan J, Namslauer A, Mills D, Brzezinski P, Ferguson-Miller S, Gennis RB. A mutation in subunit I of cytochrome oxidase from Rhodobacter sphaeroides results in an increase in steady-state activity but completely eliminates proton pumping. Biochemistry. 2002;41:13417–13423. doi: 10.1021/bi026582+. [DOI] [PubMed] [Google Scholar]
- 34.Pfitzner U, Hoffmeier K, Harrenga A, Kannt A, Michel H, Bamberg E, Richter OMH, Ludwig B. Tracing the D-pathway in reconstituted site-directed mutants of cytochrome c oxidase from Paracoccus denitrificans. Biochemistry. 2000;39:6756–6762. doi: 10.1021/bi992235x. [DOI] [PubMed] [Google Scholar]
- 35.Klinman JP. A new model for the origin of kinetic hydrogen isotope effects. J Phys Org Chem. 2010;23:606–612. [Google Scholar]
- 36.Warshel A. Computer Modeling of Chemical Reactions in Enzymes and Solutions. John Wiley & Sons; New York: 1991. [Google Scholar]
- 37.Liu H, Warshel A. Origin of the temperature dependence of isotope effects in enzymatic reactions: the case of dihydrofolate reductase. J Phys Chem B. 2007;111:7852–7861. doi: 10.1021/jp070938f. [DOI] [PubMed] [Google Scholar]
- 38.Mitchell DM, Gennis RB. Rapid purification of wildtype and mutant cytochrome c oxidase from Rhodobacter sphaeroides by Ni(2+)-NTA affinity chromatography. FEBS Lett. 1995;368:148–150. doi: 10.1016/0014-5793(95)00626-k. [DOI] [PubMed] [Google Scholar]
- 39.Bratton MR, Pressler MA, Hosler JP. Suicide inactivation of cytochrome c oxidase: catalytic turnover in the absence of subunit III alters the active site. Biochemistry. 1999;38:16236–16245. doi: 10.1021/bi9914107. [DOI] [PubMed] [Google Scholar]
- 40.Schowen KB, Schowen RL. Solvent isotope effects on enzyme systems. Methods Enzymol. 1982;87:551–606. [PubMed] [Google Scholar]
- 41.Chakrabarty S, Namslauer I, Brzezinski P, Warshel A. Exploration of the cytochrome c oxidase pathway puzzle and examination of the origin of elusive mutational effects. Biochim Biophys Acta Bioenerg. 2011;1807:413–426. doi: 10.1016/j.bbabio.2011.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Åqvist J, Warshel A. Simulation of enzyme reactions using valence bond force fields and other hybrid quantum/classical approaches. Chem Rev. 1993;93:2523–2544. [Google Scholar]
- 43.Hwang J-K, Warshel A. A quantized classical path approach for calculations of quantum mechanical rate constants. J Phys Chem. 1993;97:10053–10058. [Google Scholar]
- 44.Hwang J-K, Warshel A. How important are quantum mechanical nuclear motions in enzyme catalysis? J Am Chem Soc. 1996;118:11745–11751. [Google Scholar]
- 45.Wang Q, Hammes-Schiffer S. Hybrid quantum/classical path integral approach for simulation of hydrogen transfer reactions in enzymes. J Chem Phys. 2006;126(1–11):184102. doi: 10.1063/1.2362823. [DOI] [PubMed] [Google Scholar]
- 46.Wang M, Lu Z, Yang W. Nuclear quantum effects on an enzyme-catalyzed reaction with reaction path potential: proton transfer in triosephosphate isomerase. J Chem Phys. 2006;124(1–8):124516. doi: 10.1063/1.2181145. [DOI] [PubMed] [Google Scholar]
- 47.Major DT, Gao JL. A combined quantum mechanical and molecular mechanical study of the reaction mechanism and α-amino acidity in alanine racemase. J Am Chem Soc. 2006;128:16345–16357. doi: 10.1021/ja066334r. [DOI] [PubMed] [Google Scholar]
- 48.Billeter SR, Webb SP, Agarwal PK, Iordanov T, Hammes-Schiffer S. Hydride transfer in liver alcohol dehydrogenase: quantum dynamics, kinetic isotope effects, and role of enzyme motion. J Am Chem Soc. 2001;123:11262–11272. doi: 10.1021/ja011384b. [DOI] [PubMed] [Google Scholar]
- 49.Warshel A, Parson WW. Dynamics of biochemical and biophysical reactions: insight from computer simulations. Q Rev Biophys. 2001;34:563–670. doi: 10.1017/s0033583501003730. [DOI] [PubMed] [Google Scholar]
- 50.Feynman RP. Statistical Mechanics. Benjamin; New York: 1972. [Google Scholar]
- 51.Gillan MJ. Quantum classical crossover of the transition rate in the damped double well. J Phys C Solid State Phys. 1987;20:3621–3641. [Google Scholar]
- 52.Voth GA. Path-integral centroid methods in quantum statistical mechanics and dynamics. Adv Chem Phys. 1996;93:135–218. [Google Scholar]
- 53.Voth GA, Chandler D, Miller WH. Rigorous formulation of quantum transition state theory and its dynamical corrections. J Chem Phys. 1989;91:7749. [Google Scholar]
- 54.Hwang J-K, Chu ZT, Yadav A, Warshel A. Simulations of quantum mechanical corrections for rate constants of hydride-transfer reactions in enzymes and solutions. J Phys Chem. 1991;95:8445–8448. [Google Scholar]
- 55.Olsson MHM, Parson WW, Warshel A. Dynamical contributions to enzyme catalysis: critical tests of a popular hypothesis. Chem Rev. 2006;106:1737–1756. doi: 10.1021/cr040427e. [DOI] [PubMed] [Google Scholar]
- 56.Warshel A, Hwang J-K. Simulation of the dynamics of electron transfer reactions in polar solvents: semiclassical trajectories and dispersed polaron approaches. J Chem Phys. 1986;84:4938–4957. [Google Scholar]
- 57.Warshel A, Chu ZT. Quantum corrections for rate constants of diabatic and adiabatic reactions in solutions. J Chem Phys. 1990;93:4003–4015. [Google Scholar]
- 58.Knapp MJ, Klinman JP. Environmentally coupled hydrogen tunneling — linking catalysis to dynamics. Eur J Biochem. 2002;269:3113–3121. doi: 10.1046/j.1432-1033.2002.03022.x. [DOI] [PubMed] [Google Scholar]
- 59.Hatcher E, Soudackov AV, Hammes-Schiffer S. Proton-coupled electron transfer in soybean lipoxygenase. J Am Chem Soc. 2004;126:5763–5775. doi: 10.1021/ja039606o. [DOI] [PubMed] [Google Scholar]
- 60.Kuznetsov AM, Ulstrup J. Proton and hydrogen atom tunnelling in hydrolytic and redox enzyme catalysis. Can J Chem Rev Canadian De Chimie. 1999;77:1085–1096. [Google Scholar]
- 61.Warshel A. Dynamics of reactions in polar solvents. Semiclassical trajectory studies of electron-transfer and proton-transfer reactions. J Phys Chem. 1982;86:2218–2224. [Google Scholar]
- 62.Borgis D, Hynes JT. Molecular-dynamics simulation for a model nonadiabatic proton transfer reaction in solution. J Chem Phys. 1991;94:3619–3628. [Google Scholar]
- 63.Antoniou D, Schwartz SD. Large kinetic isotope effects in enzymatic proton transfer and the role of substrate oscillations. Proc Natl Acad Sci U S A. 1997;94:12360–12365. doi: 10.1073/pnas.94.23.12360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Manneback C. Computation of the intensities of vibrational spectra of electronic bands in diatomic molecules. Physica. 1951;17:1001–1010. [Google Scholar]
- 65.Warshel A. Interpretation of resonance raman spectra of biological molecules. Annu Rev Biophys Bioeng. 1977;6:273–300. doi: 10.1146/annurev.bb.06.060177.001421. [DOI] [PubMed] [Google Scholar]
- 66.Zaslavsky D, Sadoski RC, Wang KF, Durham B, Gennis RB, Millett F. Single electron reduction of cytochrome c oxidase compound F: resolution of partial steps by transient spectroscopy. Biochemistry. 1998;37:14910–14916. doi: 10.1021/bi981490z. [DOI] [PubMed] [Google Scholar]
- 67.Karpefors M, Ädelroth P, Brzezinski P. Localized control of proton transfer through the D-pathway in cytochrome c oxidase: application of the proton-inventory technique. Biochemistry. 2000;39:6850–6856. doi: 10.1021/bi992719t. [DOI] [PubMed] [Google Scholar]
- 68.Karpefors M, Ädelroth P, Brzezinski P. The onset of the deuterium isotope effect in cytochrome c oxidase. Biochemistry. 2000;39:5045–5050. doi: 10.1021/bi9925221. [DOI] [PubMed] [Google Scholar]
- 69.Ädelroth P, Karpefors M, Gilderson G, Tomson FL, Gennis RB, Brzezinski P. Proton transfer from glutamate 286 determines the transition rates between oxygen intermediates in cytochrome c oxidase. Biochim Biophys Acta. 2000;1459:533–539. doi: 10.1016/s0005-2728(00)00194-8. [DOI] [PubMed] [Google Scholar]
- 70.Salomonsson L, Faxén K, Ädelroth P, Brzezinski P. The timing of proton migration in membrane-reconstituted cytochrome c oxidase. Proc Natl Acad Sci U S A. 2005;102:17624–17629. doi: 10.1073/pnas.0505431102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Salomonsson L, Brändén G, Brzezinski P. Deuterium isotope effect of proton pumping in cytochrome c oxidase. Biochim Biophys Acta Bioenerg. 2008;1777:343–350. doi: 10.1016/j.bbabio.2007.09.009. [DOI] [PubMed] [Google Scholar]
- 72.Mills DA, Tan Z, Ferguson-Miller S, Hosler J. A role for subunit III in proton uptake into the D pathway and a possible proton exit pathway in Rhodobacter sphaeroides cytochrome c oxidase. Biochemistry. 2003;42:7410–7417. doi: 10.1021/bi0341307. [DOI] [PubMed] [Google Scholar]
- 73.Namslauer A, Pawate AS, Gennis RB, Brzezinski P. Redox-coupled proton translocation in biological systems: Proton shuttling in cytochrome c oxidase. Proc Natl Acad Sci U S A. 2003;100:15543–15547. doi: 10.1073/pnas.2432106100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Siletsky SA, Pawate AS, Weiss K, Gennis RB, Konstantinov AA. Transmembrane charge separation during the ferryl–oxo→oxidized transition in a nonpumping mutant of cytochrome c oxidase. J Biol Chem. 2004;279:52558–52565. doi: 10.1074/jbc.M407549200. [DOI] [PubMed] [Google Scholar]
- 75.Brändén G, Pawate AS, Gennis RB, Brzezinski P. Controlled uncoupling and recoupling of proton pumping in cytochrome c oxidase. Proc Natl Acad Sci U S A. 2006;103:317–322. doi: 10.1073/pnas.0507734103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Olsson MH, Warshel A. Monte Carlo simulations of proton pumps: on the working principles of the biological valve that controls proton pumping in cytochrome c oxidase. Proc Natl Acad Sci U S A. 2006;103:6500–6505. doi: 10.1073/pnas.0510860103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Henry RM, Yu CH, Rodinger T, Pomès R. Functional hydration and conformational gating of proton uptake in cytochrome c oxidase. J Mol Biol. 2009;387:1165–1185. doi: 10.1016/j.jmb.2009.02.042. [DOI] [PubMed] [Google Scholar]
- 78.Olsson MH, Mavri J, Warshel A. Transition state theory can be used in studies of enzyme catalysis: lessons from simulations of tunnelling and dynamical effects in lipoxygenase and other systems. Philos Trans R Soc Lond B Biol Sci. 2006;361:1417–1432. doi: 10.1098/rstb.2006.1880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Billeter SR, Webb SP, Agarwal PK, Iordanov T, Hammes-Schiffer S. Hydride transfer in liver alcohol dehydrogenase: quantum dynamics, kinetic isotope effects, and role of enzyme motion. J Am Chem Soc. 2001;123:11262–11272. doi: 10.1021/ja011384b. [DOI] [PubMed] [Google Scholar]
- 80.Karpefors M, Ädelroth P, Aagaard A, Smirnova IA, Brzezinski P. The deuterium isotope effect as a tool to investigate enzyme catalysis: proton-transfer control mechanisms in cytochrome c oxidase. Isr J Chem. 1999;39:427–437. [Google Scholar]
- 81.Brzezinski P, Larsson G. Redox-driven proton pumping by heme-copper oxidases. Biochim Biophys Acta. 2003;1605:1–13. doi: 10.1016/s0005-2728(03)00079-3. [DOI] [PubMed] [Google Scholar]
- 82.Durr KL, Koepke J, Hellwig P, Muller H, Angerer H, Peng G, Olkhova E, Richter OM, Ludwig B, Michel H. A D-pathway mutation decouples the Paracoccus denitrificans cytochrome c oxidase by altering the side-chain orientation of a distant conserved glutamate. J Mol Biol. 2008;384:865–877. doi: 10.1016/j.jmb.2008.09.074. [DOI] [PubMed] [Google Scholar]
- 83.Olsson MHM, Siegbahn PEM, Warshel A. Simulations of the large kinetic isotope effect and the temperature dependence of the hydrogen atom transfer in lipoxygenase. J Am Chem Soc. 2004;126:2820–2828. doi: 10.1021/ja037233l. [DOI] [PubMed] [Google Scholar]
- 84.Warshel A, Sharma PK, Kato M, Xiang Y, Liu H, Olsson MHM. Electrostatic basis for enzyme catalysis. Chem Rev. 2006;106:3210–3235. doi: 10.1021/cr0503106. [DOI] [PubMed] [Google Scholar]
- 85.Liu HB, Warshel A. Origin of the temperature dependence of isotope effects in enzymatic reactions: the case of dihydrofolate reductase. J Phys Chem B. 2007;111:7852–7861. doi: 10.1021/jp070938f. [DOI] [PubMed] [Google Scholar]
- 86.Babcock GT, Wikström M. Oxygen activation and the conservation of energy in cell respiration. Nature. 1992;356:301–309. doi: 10.1038/356301a0. [DOI] [PubMed] [Google Scholar]
- 87.Verkhovsky MI, Morgan JE, Verkhovskaya ML, Wikström M. Translocation of electrical charge during a single turnover of cytochrome-c oxidase. Biochim Biophys Acta. 1997;1318:6–10. [Google Scholar]
- 88.Ädelroth P, Ek M, Brzezinski P. Factors determining electron-transfer rates in cytochrome c oxidase: investigation of the oxygen reaction in the R. sphaeroides and bovine enzymes. Biochim Biophys Acta. 1998;1367:107–117. doi: 10.1016/s0005-2728(98)00142-x. [DOI] [PubMed] [Google Scholar]
- 89.Gorbikova EA, Belevich I, Wikström M, Verkhovsky MI. The proton donor for O–O bond scission by cytochrome c oxidase. Proc Natl Acad Sci U S A. 2008;105:10733–10737. doi: 10.1073/pnas.0802512105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.M . The PyMOL Molecular Graphics System. Schrödinger, LLC; 2006. [Google Scholar]