Additive Mixed Effect Model for Clustered Failure Time Data

Summary

We propose an additive mixed effect model to analyze clustered failure time data. The proposed model assumes an additive structure and include a random effect as an additional component. Our model imitates the commonly used mixed effect models in repeated measurement analysis but under the context of hazards regression; our model can also be considered as a parallel development of the gamma-frailty model in additive model structures. We develop estimating equations for parameter estimation and propose a way of assessing the distribution of the latent random effect in the presence of large clusters. We establish the asymptotic properties of the proposed estimator. The small sample performance of our method is demonstrated via a large number of simulation studies. Finally, we apply the proposed model to analyze data from a diabetic study and a treatment trial for congestive heart failure.

1. Introduction

Clustered failure time data are commonly seen in biomedical studies. A popular model for analyzing clustered failure time data is the gamma-frailty model, which models the intra-cluster dependence by incorporating an unobserved random effect, the so-called frailty, into the Cox (1972) proportional hazards model. The asymptotic distribution of the maximum likelihood estimator for the gamma frailty model has been rigorously established by Murphy (1994; 1995) and by Parner (1998).

The multiplicative hazards model focuses on estimating hazard ratios and its multiplicative structure may not model real data well in many situations. In some cases, an additive effect could be a more reasonable association. Such an effect can be modeled using the so-called additive hazards model (Aalen, 1989; Huffer and McKeague, 1991; Lin and Ying, 1994; and McKeague and Sasieni, 1994; among others). In this model, an additive structure of a baseline hazards function and a covariate effect is assumed via the expression dΛ(t|X) = dΛ(t) + X(t)^T βdt, where Λ(t|X) denotes the cumulative hazard function for the given, possibly time-dependent, covariates X and (t) is the baseline cumulative hazard function. The regression coefficient β in the additive model is interpreted as risk difference and it has been eloquently advocated and successfully utilized for right-censored independent survival data in many papers, e.g., Andersen, Borgan, Gill, and Keiding (1993, pp. 563–566), Lin and Ying (1994), McKeague and Sasieni (1994), Shen and Cheng (1999), and Gandy and Jensen (2005a; 2005b). The multivariate version of the above additive model has been used to model clustered failure time data in Yin and Cai (2004): dΛ_ij(t|X) = dΛ(t) + X_ij(t)^T βdt, where Λ_ij(t|X) denotes the cumulative hazard function for subject j in cluster i and X_ij is the associated covariate. Yin (2007) further developed a test for checking the additive structure using clustered data.

All the previous additive models assume the marginal relationship between covariates and survival times. In other words, they do not model the dependence among these events explicitly. Therefore, the marginal models cannot be used for individual prediction given the status of other individuals in the same cluster; neither can they be used to assess the dependence between individuals. In this paper, we propose an additive mixed effect model for clustered failure times. Our model includes a cluster-specific random effect as an additional component. Thus, our model imitates the commonly used mixed effect models in repeated measurement analysis but under the context of hazards regression; our model can also be considered as a parallel development of the gamma-frailty model in additive model structures. However, different from the gamma-frailty model, the proposed model still induces an additive marginal model. In Section 2, we introduce the proposed model and provide estimation procedure of the model parameters. We then establish the asymptotic distribution of the estimators. In Section 3, we demonstrate small-sample performance via a large number of simulation studies. When cluster size is large, we propose a consistent testing procedure in Section 4 to evaluate the distribution of random effects. The application to a diabetic study and the SOLVD treatment trial (SOLVD Investigators, 1990) is given in Section 5.

2. Model and Inference Procedure

2.1 Models and data

Suppose that data are collected from n i.i.d clusters. Within cluster i (i = 1, …, n), there are n_i subjects and we use T_ij to denote the failure time of subject j in this cluster. We denote X_ij as the covariates associated with this subject.

Since the failure times from the same cluster may be correlated, in order to account for such dependence, we introduce a cluster-specific random effect ξ_i which is independent of covariates. We assume that T_i1, …, T_ini are conditionally independent given all the covariates and the random effect ξ_i. Additionally, if letting Λ_ij(t) be the cumulative hazards function given all the covariates and the cluster-specific random effect, our semiparametric additive mixed effect model assumes

$${d\mathrm{\Lambda }}_{ij}(t)=d\mathrm{\Lambda }(t)+{\mathbf{X}}_{ij}{(t)}^T\mathit{\beta }dt+{\xi }_{i}dt.$$ (1)

Here, Λ(t) is an unknown baseline function and β is an unknown coefficient vector. We also assume ξ_i follows a one-parameter distribution with density function f (x; θ) which has mean zero and a finite moment generating function. Note that our model (1) imitates the usual mixed effect model with a random intercept in the analysis of longitudinal data; more interestingly, it can be considered as an additive counterpart of the usual multiplicative frailty model for clustered failure time.

In practice, failure time T_ij may be right censored. We denote C_ij as the censoring time for subject j in cluster i and assume (C_i1, …, C_ini) are independent of (T_i1, …, T_ini) and ξ_i given all the covariates. Subject to censoring, the actual observations from these clusters are (Z_ij = T_ij Λ C_ij, X_ij, Δ_ij = I(T_ij ≤ C_ij)), j = 1, …, n_i, i = 1, …, n, where a Λ b = min(a, b) and I(·) is the indicator function. We let τ be the study duration.

2.2 Parameter estimation and inference

To estimate parameters (β, θ) and Λ (t), we use the moment methods to construct estimating equations. First, from model (1), it is easy to calculate the marginal survival function T_ij given covariates X_ij which is given by

$$\begin{array}{l}P(T_{ij}>t\mid {\mathbf{X}}_{ij})=E_{{\xi }_i}\left[exp\left\{-\mathrm{\Lambda }(t)-{\int }_0^t{\mathbf{X}}_{ij}{(u)}^T\mathit{\beta }du-{\xi }_{i}t\right\}\mid {\mathbf{X}}_{ij}\right]\\ =exp\left\{-\mathrm{\Lambda }(t)-{\int }_0^t{\mathbf{X}}_{ij}{(u)}^T\mathit{\beta }du-G(t;\theta )\right\},\end{array}$$ (2)

where exp{−G(t; θ)} = ∫ e^−xt f (x; θ)dx. Equivalently, if N_ij(t) denotes the counting process Δ_ijI(Z_ij ≤ t) and Y_ij denotes the at-risk process I (Z_ij ≥ t), then the relationship in (2) implies

$$E[{dN}_{ij}(t)\mid {\mathbf{X}}_{ij},Z_{ij}\ge t]=Y_{ij}(t)\left\{dH(t)+{\mathbf{X}}_{ij}{(t)}^T\mathit{\beta }dt\right\},$$ (3)

where H(t) = Λ(t) + G(t; θ).

Since equation (2) implies another marginal additive model studied in Lin and Ying (1994), the estimating equations developed in their paper can be used here. Following Lin and Ying (1994), we can construct the following estimating equation to estimate β and H:

$$\sum _{i=1}^n\sum _{j=1}^{n_i}{\int }_0^{\tau }{Y}_{ij}(t)I(t\le s)\left\{{dN}_{ij}(t)-dH(t)-{\mathbf{X}}_{ij}{(t)}^T\mathit{\beta }dt\right\}=0,s>0,$$ (4)

and

$$\sum _{i=1}^n\sum _{j=1}^{n_i}{\int }_0^{\tau }{Y}_{ij}(t){\mathbf{X}}_{ij}(t)\left\{{dN}_{ij}(t)-dH(t)-{\mathbf{X}}_{ij}{(t)}^T\mathit{\beta }dt\right\}=0.$$ (5)

The solutions to these equations have an explicit expression and we denote them as β̂ and Ĥ respectively. Specifically,

$$\widehat{\mathit{\beta }}={\left[\sum _{i=1}^n\sum _{j=1}^{n_i}{\int }_0^{\tau }{Y}_{ij}(t){\{{\mathbf{X}}_{ij}(t)-\overline{\mathbf{X}}(t)\}}^{\otimes 2}dt\right]}^{-1}\left[\sum _{i=1}^n\sum _{j=1}^{n_i}{\int }_0^{\tau }{Y}_{ij}(t)\{{\mathbf{X}}_{ij}(t)-\overline{\mathbf{X}}(t)\}{dN}_{ij}(t)\right],$$

where a^⊗2 = aa^T and $\overline{\mathbf{X}}(t)={\sum }_{k=1}^n{\sum }_{l=1}^{n_k}{Y}_{kl}(t){\mathbf{X}}_{kl}(t)/{\sum }_{k=1}^n{\sum }_{l=1}^{n_k}{Y}_{kl}(t)$. Additionally,

$$\widehat{H}(s)={\int }_0^s\frac{{\sum }_{i=1}^n{\sum }_{j=1}^{n_i}{Y}_{ij}(t)\{{dN}_{ij}(t)-{\mathbf{X}}_{ij}{(t)}^T\widehat{\mathit{\beta }}dt\}}{{\sum }_{i=1}^n{\sum }_{j=1}^{n_i}{Y}_{ij}(t)}.$$

From (3), Ĥ(t) estimates the function which involves both Λ(t) and θ. Thus, we need additional information to be able to discriminate between these two parameters. Note that θ describes the dependence among the failure times within the same cluster. This motivates us to consider the cross-moment among the marginal residual process (dN_ij(t) − dH(t) − X_ij(t)^T βdt), also denoted as dε_ij(t). First, suppose X_i. denotes the vector covariate (X_i1, …, X_ini). Then for j ≠ l,

$$\begin{array}{l}E\{{d\epsilon }_{ij}(t){d\epsilon }_{il}(s)\mid Z_{ij}\ge t,Z_{ij}\ge s,{\mathbf{X}}_{i·}\}\\ =\frac{E\left[\{-dG(t;\theta )+{\xi }_{i}dt\}\{-dG(s;\theta )+{\xi }_{i}ds\}I(Z_{ij}\ge t)I(Z_{il}\ge s)\mid {\mathbf{X}}_{i·}\right]}{E\left\{I(Z_{ij}\ge t)I(Z_{il}\ge s)\mid {\mathbf{X}}_{i·}\right\}}\\ =\frac{P(C_{ij}\ge t,C_{il}\ge s\mid {\mathbf{X}}_{i·})E[\{-dG(t;\theta )+{\xi }_{i}dt\}\{-dG(s;\theta )+{\xi }_{i}ds\}I(T_{ij}\ge t)I(T_{il}\ge s)\mid {\mathbf{X}}_{i·}]}{P(C_{ij}\ge t,C_{il}\ge s\mid {\mathbf{X}}_{i·})P(T_{ij}\ge t,T_{il}\ge s\mid {\mathbf{X}}_{i·})}\\ =\frac{E[\{-dG(t;\theta )+{\xi }_{i}dt\}\{-dG(s;\theta )+{\xi }_{i}ds\}I(T_{ij}\ge t)I(T_{il}\ge s)\mid {\mathbf{X}}_{i·}]}{P(T_{ij}\ge t,T_{il}\ge s\mid {\mathbf{X}}_{i·})}.\end{array}$$

On the other hand,

$$\begin{array}{l}E[\{-dG(t;\theta )+{\xi }_{i}dt\}\{-dG(s;\theta )+{\xi }_{i}ds\}I(T_{ij}\ge t)I(T_{il}\ge s)\mid {\mathbf{X}}_{i·}]\\ =E[\{-dG(t;\theta )+{\xi }_{i}dt\}\{-dG(s;\theta )+{\xi }_{i}ds\}E\{I(T_{ij}\ge t)\mid {\mathbf{X}}_{i·},{\xi }_i\}E\{I(T_{il}\ge s)\mid {\mathbf{X}}_{i·},{\xi }_i\}]\\ =E_{{\xi }_i}\left[\{-dG(t;\theta )+{\xi }_{i}dt\}\{-dG(s;\theta )+{\xi }_{i}ds\}{e}^{-{\xi }_i(t+s)}\right]\times exp\left[-\{\mathrm{\Lambda }(t)+{\int }_0^t{\mathbf{X}}_{ij}{(u)}^T\mathit{\beta }du\}-\{\mathrm{\Lambda }(s)+{\int }_0^s{\mathbf{X}}_{il}{(u)}^T\mathit{\beta }du\}\right],\end{array}$$

and

$$P(T_{ij}\ge t,T_{il}\ge s\mid {\mathbf{X}}_{i·})=E_{{\xi }_i}\left(exp\left[-\{\mathrm{\Lambda }(t)+{\int }_0^t{\mathbf{X}}_{ij}{(u)}^T\mathit{\beta }du+{\xi }_{i}t\}-\{\mathrm{\Lambda }(s)+{\int }_0^s{\mathbf{X}}_{il}{(u)}^T\mathit{\beta }du+{\xi }_{i}s\}\right]\right).$$

Thus, we have

$$E\{{d\epsilon }_{ij}(t){d\epsilon }_{il}(s)\mid Z_{ij}\ge t,Z_{il}\ge s,{\mathbf{X}}_{i·}\}=\frac{E_{{\xi }_i}\left[\{-dG(t;\theta )+{\xi }_{i}dt\}\{-dG(s;\theta )+{\xi }_{i}ds\}{e}^{-{\xi }_i(t+s)}\right]}{E_{{\xi }_i}\{e^{-{\xi }_i(t+s)}\}}.$$

. Since E(ξ_ie^−tξ_i) = G′(t; θ) exp{−G(t; θ)} and $E({\xi }_i^2{e}^{-t{\xi }_i})=\{G^{\prime }{(t;\theta )}^2-G^{″}(t;\theta )\}exp\{-G(t;\theta )\}$, where G′ (t; θ) and G″ (t; θ) denote the first and the second derivative of G(t; θ), respectively, with respect to t, some algebra yields

$$E\{{d\epsilon }_{ij}(t){d\epsilon }_{ij}(s)\mid Z_{ij}\ge t,Z_{il}\ge s,{\mathbf{X}}_{i·}\}=dG(t;\theta )dG(s;\theta )-G^{\prime }(t+s;\theta )dG(t;\theta )ds-G^{\prime }(t+s;\theta )dG(s;\theta )dt+\{G^{\prime }{(t+s;\theta )}^2-G^{″}(t+s;\theta )\}\mathit{dtds}.$$ (6)

After replacing H(t) and β with their estimators, we can estimate θ by solving the following estimating equation

$$\sum _{i=1}^n\sum _{j\ne l,j,l=1}^{n_i}{\int }_0^{\tau }{\int }_0^{\tau }{Y}_{ij}(t)Y_{il}(s)\{{d\widehat{\epsilon }}_{ij}(t){d\widehat{\epsilon }}_{il}(s)-Q(t,s;\theta )\mathit{dtds}\}=0,$$ (7)

where dε̂_ij(t) = dN_ij(t) − dĤ(t) − X_ij(t)^T β̂dt and

$$Q(t,s;\theta )=G^{\prime }(t;\theta )G^{\prime }(s;\theta )-G^{\prime }(t+s;\theta )\{G^{\prime }(t;\theta )+G^{\prime }(s;\theta )\}+G^{\prime }{(t+s;\theta )}^2-G^{″}(t+s;\theta ).$$

We denote the solution to (7) as θ̂. Then an estimator for Λ(t) is given by Λ̂(t) = Ĥ(t) − G(t; θ̂).

In equation (7), G(t; θ) and its derivatives can be evaluated for each specific distribution for ξ_i. For example, if ξ_i is assumed to be from a normal distribution with mean zero and variance θ, then G(t; θ) = −t²θ/2, G′(t, θ) = − tθ and G″(t; θ) = −θ. Then, with time independent covariates, equation (7) becomes

$$\sum _{i=1}^n\sum _{j\ne l,j,l=1}^{n_i}\left[\left\{{\mathrm{\Delta }}_{ij}-\widehat{H}(Z_{ij})-{\mathbf{X}}_{ij}^T\widehat{\mathit{\beta }}{Z}_{ij}\right\}\left\{{\mathrm{\Delta }}_{ij}-\widehat{H}(Z_{ij})-{\mathbf{X}}_{ij}^T\widehat{\mathit{\beta }}{Z}_{ij}\right\}-\left({\theta }^2{Z}_{ij}^2{Z}_{il}^2/4+\theta Z_{ij}{Z}_{il}\right)\right]=0,$$

which has an explicit solution. If (ξ_i + θ) is assumed to be from an exponential distribution with mean θ, then G(t; θ) = log(1 + θt), G′ (t; θ) = θ (1 + θt)⁻¹ and G″(t; θ) = −θ²(1 + θt)⁻². Under this case, the solution to equation (7) can be obtained via Newton-Raphson iteration.

In Appendix, we will show that the estimators β̂, Ĥ and θ̂ are all asymptotic linear estimators for the respective true parameters. Thus, the asymptotic covariance can be consistently estimated using the empirical covariance of the corresponding estimated influence functions. The details are given in Web Appendix.

2.3 Asymptotic properties

The technical conditions for obtaining the asymptotic properties of the proposed estimators are given in Web Appendix. Let β₀, θ₀, and Λ₀(t) denote the true values for β, θ, and Λ₀(t), respectively. Under those conditions, we obtain the following results.

Theorem 1

Under conditions (C.1)–(C.4) in Web Appendix and assuming that the true density for ξ is f(ξ; θ), there exits a local consistent estimator θ̂ solving equation (7). Moreover, β̂ →_p β₀ and Λ̂(t) →_p Λ₀(t) uniformly in [0, τ].

Theorem 2

Under conditions (C.1)–(C.4) in Web Appendix and assuming that the true density for ξ is f(ξ; θ), $\sqrt{n}(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0,\widehat{\theta }-{\theta }_0,\widehat{\mathrm{\Lambda }}(t)-{\mathrm{\Lambda }}_0(t))$ converges in distribution to a mean-zero Gaussian process in the metric space R^d+1 × l^∞ [0, τ], where d is the dimension of β₀ and l^∞ [0, τ] is the space of bounded functions in [0, τ] equipped with the uniform bounded norm.

The proofs of Theorem 1 and Theorem 2 are given in Appendix. In addition, we provide a consistent estimator of the asymptotic covariance in Web Appendix.

3. Simulation Studies

In the first simulation study, covariate X_ij contains one Bernoulli random variable and the other random variable is from the uniform distribution in [0, 1]. The survival time T_ij is generated using model (1), where Λ(t) = 2t² + 3t and ξ_i follows a standard normal distribution. The true value for β is set to be (0.5, 1) and θ₀ = 1. The censoring time is generated from the uniform distribution in [0, 3], which yields the average censoring rate of 23%. Finally, the cluster size is chosen randomly from 2, 3 and 4. Since in many multi-center studies, the center size can be large, we also consider the cluster size to be as large as 50 while the number of clusters is relatively small.

For each simulated data set, we solve equations (4) and (5) to estimate β and H then solve equation (7) for θ. Since ξ_i follows the normal distribution, the function Q(t, s; θ) is equal to θ²t²s²/4 + θts. Thus, solving equation (7) is equivalent to solving a quadratic equation, which may have two solutions. To ensure θ to be positive, we choose the maximum between 0 and the larger of these two solutions as the estimate for θ. To estimate the asymptotic variance, we first estimate the influence functions as given in Appendix then calculate the empirical variance of these influence functions.

Table 1 summarizes the results from 1,000 replicates for each choice of sample size and cluster size. In the table, column “Est” is the average of the estimates from 1,000 replicates; column “SE” is the sample standard deviations of these estimates; column “ESE” is the average of the estimated standard errors; column “CP” is the coverage probabilities of 95% confidence intervals, which are given using the asymptotic normality. Table 1 reports the results for estimating β and θ. In addition, we also summarize the results for Λ(t) for some t values which are chosen to be some quantiles of Z_ij. The table shows that the estimators for the regression coefficient β and the cumulative baseline functions Λ(t) have negligible bias and the inference appears to be correct with the estimated variance being close to the empirical variance and with proper confidence interval coverage. Moreover, we observe that even if the number of clusters is as small as 20, the estimators for the regression coefficients and the baseline cumulative hazard functions still perform well when the cluster size is large. There seems to be some bias in estimating the frailty parameter, due to the small number of the clusters or small cluster size.

Table 1.

Results from the simulation study with normal frailty

n	Cluster Size	Parameter	True value	Est	SE	ESE	CP
100	2 ~ 5	β1	0.5	0.506	0.631	0.613	0.94
		β2	1.0	1.015	1.091	1.059	0.95
		θ	1.0	1.043	1.096	1.424	0.97
		Λ (t1)	0.473	0.477	0.103	0.103	0.95
		Λ (t2)	1.076	1.094	0.213	0.215	0.94
		Λ (t3)	1.958	2.000	0.377	0.397	0.96
200	2 ~ 5	β1	0.5	0.504	0.445	0.433	0.94
		β2	1.0	1.018	0.769	0.747	0.94
		θ	1.0	0.976	0.857	1.044	0.98
		Λ (t1)	0.473	0.473	0.075	0.073	0.93
		Λ (t2)	1.076	1.082	0.158	0.153	0.94
		Λ (t3)	1.958	1.964	0.281	0.281	0.95
400	2 ~ 5	β1	0.5	0.490	0.310	0.306	0.95
		β2	1.0	1.001	0.549	0.528	0.94
		θ	1.0	0.921	0.655	0.761	0.98
		Λ (t1)	0.473	0.474	0.054	0.052	0.94
		Λ (t2)	1.076	1.079	0.111	0.108	0.94
		Λ (t3)	1.958	1.959	0.200	0.200	0.94
20	25	β1	0.5	0.509	0.430	0.416	0.94
		β2	1.0	1.015	0.757	0.714	0.92
		θ	1.0	0.856	0.491	0.449	0.86
		Λ (t1)	0.473	0.470	0.078	0.076	0.93
		Λ (t2)	1.076	1.078	0.162	0.155	0.93
		Λ (t3)	1.958	1.952	0.284	0.269	0.93
20	50	β1	0.5	0.502	0.314	0.292	0.93
		β2	1.0	0.992	0.554	0.503	0.91
		θ	1.0	0.817	0.404	0.328	0.79
		Λ (t1)	0.473	0.476	0.064	0.058	0.91
		Λ (t2)	1.076	1.080	0.128	0.117	0.92
		Λ (t3)	1.958	1.953	0.220	0.204	0.92

We also conduct a second simulation study, in which the data are generated using the same model except that the cluster-specific frailty (ξ_i +3) is from an exponential distribution with mean θ = 3. In this case, G(t; θ) = log(1 + θt) and

$$Q(t,s;\theta )=\frac{{\theta }^2}{(1+\theta t)(1+\theta s)}-\frac{{\theta }^2}{\{1+\theta (t+s)\}}\left(\frac{1}{1+\theta t}+\frac{1}{1+\theta s}\right)+\frac{2{\theta }^2}{{\{1+\theta (t+s)\}}^2}.$$

Then the double integration of Q(t, s; θ) in equation (7) is equivalent to

$${\int }_0^a{\int }_0^{b}Q(t,s;\theta )\mathit{dtds}=log(1+\theta a)log(1+\theta b)+2log\frac{(1+\theta a)(1+\theta b)}{1+\theta (a+b)}-{\left\{zlog(1-e^{-z})+\frac{z^2}{2}-\sum _{k=1}^{\infty }\frac{e^{-kz}}{k^2}\right\}|}_{log\{1+\theta (b+a)\}-log(1+\theta a)}^{log(1+\theta b)}-{\left\{zlog(1-e^{-z})+\frac{z^2}{2}-\sum _{k=1}^{\infty }\frac{e^{-kz}}{k^2}\right\}|}_{log\{1+\theta (b+a)\}-log(1+\theta b)}^{log(1+\theta a)}.$$

Thus, we can solve equation (7) for θ̂ via one-dimensional numerical search algorithm. In our simulations, we find that for sample size 200, the proportion of equation (7) having no solution is about 5%; however, this number reduces to 0.5% for sample size 400. Table 2 summarizes the simulation results from 1,000 replicates after excluding these non-convergence cases. The same conclusion as in the previous simulation study can be made.

Table 2.

Results from the simulation study with exponential frailty

n	Cluster Size	Parameter	True value	Est	SE	ESE	CP
100	2 ~ 5	β1	0.5	0.526	0.658	0.643	0.95
		β2	1.0	1.002	1.107	1.104	0.95
		θ	3.0	2.889	1.192	1.264	0.99
		Λ (t1)	0.111	0.116	0.069	0.077	0.98
		Λ (t2)	0.298	0.307	0.157	0.173	0.98
		Λ (t3)	0.549	0.579	0.259	0.281	0.98
200	2 ~ 5	β1	0.5	0.501	0.462	0.455	0.95
		β2	1.0	1.015	0.796	0.779	0.95
		θ	3.0	2.913	0.939	0.914	0.97
		Λ (t1)	0.111	0.118	0.052	0.056	0.97
		Λ (t2)	0.298	0.315	0.117	0.125	0.98
		Λ (t3)	0.549	0.577	0.188	0.202	0.97
400	2 ~ 5	β1	0.5	0.484	0.329	0.320	0.95
		β2	1.0	1.016	0.568	0.552	0.95
		θ	3.0	2.929	0.660	0.653	0.95
		Λ (t1)	0.111	0.114	0.040	0.040	0.96
		Λ (t2)	0.298	0.308	0.088	0.089	0.96
		Λ (t3)	0.549	0.564	0.140	0.143	0.96
20	25	β1	0.5	0.534	0.514	0481	0.94
		β2	1.0	0.980	0.867	0.810	0.93
		θ	3.0	2.805	0.865	0.859	0.91
		Λ (t1)	0.111	0.118	0.045	0.051	0.95
		Λ (t2)	0.298	0.316	0.107	0.117	0.96
		Λ (t3)	0.549	0.569	0.191	0.197	0.95
20	50	β1	0.5	0.489	0.344	0.334	0.93
		β2	1.0	1.011	0.625	0.576	0.91
		θ	3.0	2.826	0.772	0.790	0.90
		Λ (t1)	0.111	0.118	0.033	0.042	0.97
		Λ (t2)	0.298	0.317	0.080	0.096	0.97
		Λ (t3)	0.549	0.586	0.140	0.161	0.97

Finally, in another simulation study, we simulate data using the same setting as in the second simulation study. However, we misspecify the frailty distribution as a normal distribution. The simulation results which are reported in Table 3 indicate that due to the misspecification of the frailty distribution, the estimators for the baseline cumulative hazard function have more than 100% bias and the coverage probabilities are as low as 10%. However, the estimators for β’s and also H(t)’s are the same as before. This is because the estimating equations for β’s and H’s are independent of the frailty distribution.

Table 3.

Results from the simulation study with misspecified frailty

n	Cluster Size	Parameter	True value	Est	SE	ESE	CP
100	2 ~ 5	β1	0.5	0.521	0.659	0.645	0.95
		β2	1.0	1.014	1.125	1.112	0.95
		θ	3.0	2.559	1.390	1.345	0.93
		Λ (t1)	0.111	0.272	0.050	0.051	0.09
		Λ (t2)	0.298	0.695	0.117	0.117	0.05
		Λ (t3)	0.549	1.251	0.214	0.213	0.05
200	2 ~ 5	β1	0.5	0.510	0.462	0.454	0.95
		β2	1.0	1.004	0.796	0.782	0.95
		θ	3.0	2.685	1.034	0.966	0.92
		Λ (t1)	0.111	0.271	0.035	0.036	0.00
		Λ (t2)	0.298	0.699	0.082	0.083	0.00
		Λ (t3)	0.549	1.255	0.149	0.150	0.00
20	25	β1	0.5	0.524	0.514	0.485	0.94
		β2	1.0	1.004	0.867	0.824	0.93
		θ	3.0	2.680	1.041	0.985	0.85
		Λ (t1)	0.111	0.270	0.051	0.049	0.06
		Λ (t2)	0.298	0.699	0.119	0.115	0.03
		Λ (t3)	0.549	1.255	0.208	0.203	0.03
20	50	β1	0.5	0.487	0.347	0.340	0.93
		β2	1.0	1.002	0.621	0.582	0.91
		θ	3.0	2.724	0.928	0.900	0.86
		Λ (t1)	0.111	0.270	0.043	0.041	0.01
		Λ (t2)	0.298	0.701	0.103	0.098	0.00
		Λ (t3)	0.549	1.263	0.180	0.173	0.00

4. Assessing Frailty Distribution

In practice, it is impossible to know what distribution the frailty follows and our numerical experience showed that misspecifying the frailty distribution leads to large bias in the aforementioned approaches. Therefore, an important issue is how to assess the frailty distribution using empirical data.

By examining our approach, we have the following relationship H(t) = Λ(t)+G(t; θ), where G(t; θ) is the Laplace transformation of ξ’s density. Moreover, we find that the estimators for H(t) and β are obtained from equations (4) and (5), which never use the information about the distribution of the frailty. In fact, the proof of Theorem 1 shows that Ĥ(t) and β̂ are always consistent estimators of H₀(t) and β₀ respectively, no matter how the frailty distribution is assumed in the models. Hence, if we can obtain a consistent estimator of Λ(t) disregarding the frailty distribution and denote it as Λ̃(t), then the difference between Ĥ(t) and Λ̃(t) should be close to G(t; θ) when the frailty distribution is correctly specified.

To obtain such an estimator Λ̃, we use the following fact:

$$E\{{dN}_{ij}(t)-{\mathbf{X}}_{ij}{(t)}^T\mathit{\beta }dt\mid Y_{ij}(t),{\mathbf{X}}_{ij},{\xi }_i\}=Y_{ij}(t)\{d\mathrm{\Lambda }(t)+{\xi }_i(dt)\},j=1,\dots ,n_i.$$

Thus, using the observations from cluster i and substituting β by β̂, we can estimate dΛ(t)+ ξ_idt by ${\sum }_{j=1}^{n_i}{Y}_{ij}(t)\{{dN}_{ij}(t)-{\mathbf{X}}_{ij}{(t)}^T\widehat{\mathit{\beta }}dt\}/{\sum }_{j=1}^{n_i}{Y}_{ij}(t)$. After taking the average over all the clusters, we have

$$d\mathrm{\Lambda }(t)=\frac{1}{n}\sum _{i=1}^n\frac{{\sum }_{j=1}^{n_i}{Y}_{ij}(t)\{{dN}_{ij}(t)-{\mathbf{X}}_{ij}{(t)}^T\widehat{\mathit{\beta }}dt\}}{{\sum }_{j=1}^{n_i}{Y}_{ij}(t)}-\frac{1}{n}\sum _{i=1}^n{\xi }_{i}dt.$$

Since $n^{-1}{\sum }_{i=1}^n{\xi }_i$ converges to zero, we thus drop the second term on the right-hand side and obtain an estimator for Λ(t) as

$$\stackrel{\sim }{\mathrm{\Lambda }}(t)={\int }_0^t\frac{1}{n}\sum _{i=1}^n\frac{{\sum }_{j=1}^{n_i}{Y}_{ij}(u)\{{dN}_{ij}(u)-{\mathbf{X}}_{ij}{(u)}^T\widehat{\mathit{\beta }}du\}}{{\sum }_{j=1}^{n_i}{Y}_{ij}(u)}.$$

Hence, we compare D̂(t) ≡ {Ĥ(t) − Λ̃(t)} with G(t; θ̂) to examine the validity of assuming ξ’s density as f(ξ; θ). Additionally, we can obtain a confidence interval of {D̂(t) − G(t; θ̂)} using the following result.

Theorem 3

Under conditions (C.1)–(C.4) in Web Appendix, sup_{t∈[0, τ]} |Λ̃(t) − Λ₀(t) |→_p 0. Furthermore, if assume that ξ_i’s density is f (ξ; θ₀), $\sqrt{n}\{\widehat{D}(t)-G(t;\widehat{\theta })\}$ converges in distribution to a zero-mean Gaussian process in l^∈ [0, τ].

In the proof of Theorem 3, we obtain $\sqrt{n}\{\widehat{D}(t)-G(t;\widehat{\theta })\}=n^{-1/2}{\sum }_{i=1}^n{W}_i(t)+o_p(1)$, where

$$W_i(t)=S_{H,i}(t)-{\int }_0^t\frac{{\sum }_{j=1}^{n_i}{Y}_{ij}(u)\{{dN}_{ij}(u)-{d\mathrm{\Lambda }}_0(u)-{\mathbf{X}}_{ij}{(u)}^T{\mathit{\beta }}_{0}du\}}{{\sum }_{j=1}^{n_i}{Y}_{ij}(u)}+E\left\{{\int }_0^t\frac{{\sum }_{j=1}^{n_i}{Y}_{ij}(u){\mathbf{X}}_{ij}{(u)}^{T}du}{{\sum }_{j=1}^{n_i}{Y}_{ij}(u)}\right\}{S}_{\mathit{\beta },i}-\frac{\partial }{\partial \theta }G(t;{\theta }_0)S_{\theta ,i}$$

with S_{H, i}(t), S_{β, i} and S_{θ,, i} being the respective influence functions for Ĥ(t), β̂ and θ̂ from the ith cluster observations. To construct a uniform confidence band for the true function of {D(t) − G(t; θ̂)}, we use a resampling method: we generate ω₁,…, ω_n independently from the standard normal distribution and calculate ${sup}_{t\in [0,\tau ]}\mid \widehat{D}(t)-G(t;\widehat{\theta })+n^{-1}{\sum }_{i=1}^n{\omega }_i{\widehat{W}}_i(t)\mid$, where Ŵ_i(t) has the same expression as W_i(t) except that we replace Λ₀ and β₀ by Λ̃ and β̂ and use consistent estimators for S_{β, i} and S_{θ, i}. We repeat this resampling procedure many times and determine the 95%-percentile of the calculated values, denoted by c_0.95. Then a uniform 95% confidence band is given by {D̂(t) − G(t; θ̂) − c_0.95, D̂(t) − G(t; θ̂) + c_0.95}, t ∈ [0, τ]. If the band contains the horizontal line at zero, then there is no significant evidence to reject the assumed frailty distribution.

Finally, we conduct simulation studies to examine the performance of this assessment approach. The setting is similar to Section 4 but we only look at the case with large cluster size of 25. We simulate the frailty ξ from either normal or exponential distribution but we estimate all the parameters treating ξ as from a normal distribution. This way, we can examine both the type I error and power of the proposed method. The results show that under the nominal level of 0.05, if using the correct frailty distribution, the type I error for the test statistic ${\int }_0^{t_0}\mid \widehat{D}(t)-G(t;\widehat{\theta })\mid dt$, where t₀ is the median time of the observed events, is 0.067 for both n = 20 and n = 50; while if using the incorrect frailty distribution, the power becomes 0.214 for n = 20 and increases to 0.520 for n = 50. Our additional numerical experience indicates that the proposed procedure may not work well if the cluster size is as small as 5. This is because in the estimation of each cluster-specific hazards function may Λ̃ be very inaccurate with small clusters. However, the above simulation study shows that the procedure is valid when the cluster size is at least 25.

5. Applications

5.1 Diabetic study

We now apply the proposed model to analyze the well-known Diabetic Retinopathy Study (Huster et al. 1989), which was conducted to assess the effectiveness of laser photocoagulation in delaying visual loss among patients with diabetic retinopathy. One eye of each patient was randomly selected to receive the laser treatment while the other eye was used as a control. The failure time of interest is the time to visual loss as measured by visual acuity less than 5/200. We confine our analysis to a subset of 197 high-risk patients, and consider three covariates: X_1ij indicates, by the values 1 versus 0, whether or not the jth eye (j = 1 for the left eye and j = 2 for the right eye) of the ith patient was treated with laser photocoagulation, X_2i1 = X_2i2 indicates, by the values 1 versus 0, whether the ith patient had adult-onset or juvenile-onset diabetics, and X_3ij = X_1ij * X_2ij.

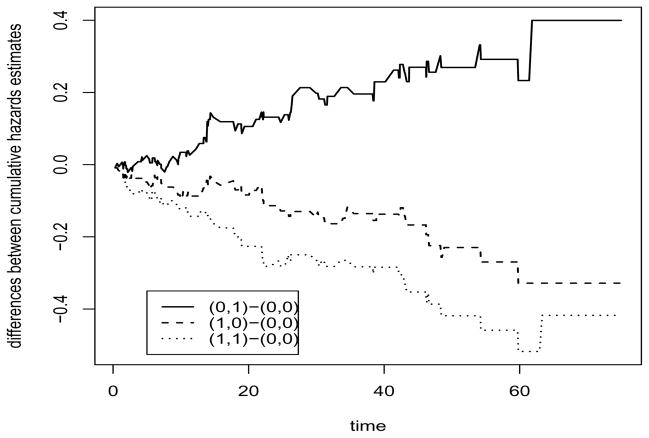
To justify why the covariates may have additive effects, we plot the differences among the cumulative hazards estimates for each combination of (X_1ij, X_2ij) (a total of four combinations), where the estimates are the Breslow-estimates of the cumulative hazards function within each group. The plot as shown in Figure 1 indicates that the differences are clearly linear in time, which imply that additive effects of the covariates may be plausible. Thus, we fit model (1) with these three covariates, along with ξ_i to account for the correlation between the two eyes of the same patient. We consider fitting the model with ξ_i from the normal distribution or the exponential distribution. The results are given in Table 4. They show that there is a high degree of dependence between the failure times of the two eyes from the same patient. Both the treatment indicator and the interaction term are significant, whereas the diabetic type is not. These findings agree with the results fitting the gamma-frailty proportional hazards model or proportional odds model (Zeng, Lin and Yin, 2005).

Figure 1.

Differences among the estimated cumulative hazard functions versus time in the DRS study

Table 4.

Results of analyzing DRS data

Covariates	Est	SE	Z	p-value
treated vs untreated	−.0046	.0020	−2.2847	.022
diabetic type	.0057	.0034	1.705	.088
treat*type	−.0091	.0034	−2.673	.007
Normal frailty	−.000066	.000018	3.741	<.001
Exponential frailty	.0545	.0092	5.944	<.001

Another nice feature for our model is to make individual prediction. For example, we can predict the conditional survival probabilities of the treated eye given that it has not failed before 30 months while the untreated eye failed between 24 and 30 months, i.e., Pr(T₂ > t|T₂ ≥ 30, 24 < T₁ < 30, X₁₁ = 0, X₁₂ = 1, X₂) for t > 30, where T₂ is the failure time for the treated eye and T₁ is the failure time for the untreated eye, X_1k is the treatment status for the kth eye (k=1, 2), and X₂ is the diabetic type for this patient. It is straightforward to show that

$$Pr(T_2>t\mid T_2\ge 30,24<T_1<30,{\mathbf{X}}_1,{\mathbf{X}}_2)=\frac{{\int }_u{e}^{-\mathrm{\Lambda }(t)-t{\mathbf{X}}_2^T\mathit{\beta }-ut}\{e^{-\mathrm{\Lambda }(24)-24{\mathbf{X}}_1^T\mathit{\beta }-24u}-e^{-\mathrm{\Lambda }(30)-30{\mathbf{X}}_1^T\mathit{\beta }-30u}\}f(u;\theta )du}{{\int }_u{e}^{-\mathrm{\Lambda }(30)-30{\mathbf{X}}_2^T\mathit{\beta }-30u}\{e^{-\mathrm{\Lambda }(24)-24{\mathbf{X}}_1^T\mathit{\beta }-24u}-e^{-\mathrm{\Lambda }(30)-30{\mathbf{X}}_1^T\mathit{\beta }-30u}\}f(u;\theta )du}.$$

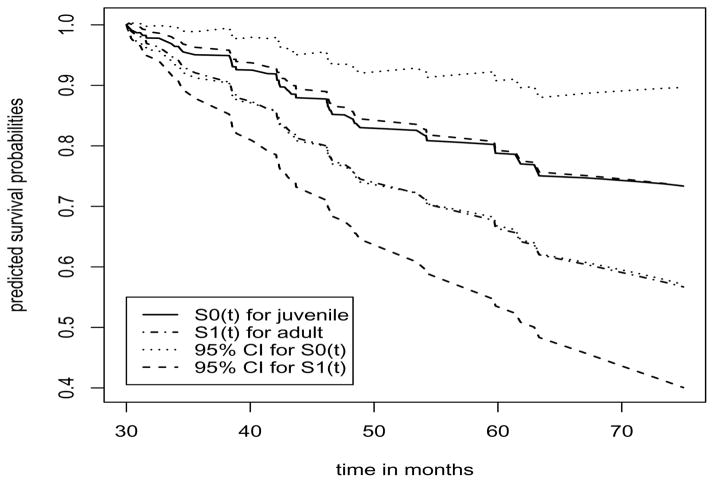
We can estimate this probability function by replacing β, θ and Λ by their respective estimates. The variance function is given by the Delta method. Figure 2 displays the estimated survival curves along with the 95% confidence intervals for the two diabetic types using model (1) with the normally distributed frailty, where the solid curve is the survival function for the patient with the juvenile-onset type, the dot-dash curve is for the patient with the adult-onset type, both the dashed and dotted curves are the confidence bands.

Figure 2.

Predicted survival functions in the DRS study

5.2 SOLVD study

We also apply our method to analyze the SOLVD (SOLVD Investigators, 1990) Treatment Trial data. This study was a randomized, double-masked, placebo-controlled trial conducted between 1986 and 1991. The participants were of age 21 to 80 years old, inclusive, with overt symptoms of congestive heart failure and left ventricular ejection fraction less than 35%. The latter is a measure of the efficiency of the heart in ejecting blood and is a number between 0 and 100%. The study was done at 23 medical centers in US, Canada and Belgium and the average number of patients per center was slightly over 100. The event of interest was the number of years to the first hospitalization for congestive heart failure or death from all causes, whichever happened first. The goal was to examine the effect of treatment by enalapril versus placebo but the participants’ age, gender and ejection fraction could be potential confounders so they should also be adjusted for in the analysis. We fit our proposed model for this data, assuming that the frailty follows a normal distribution. Because of the large size in each cluster, the test process in Section 5 can be used to assess the goodness-of-fit of the assumed frailty model. It shows that there exists little evidence to reject the normal frailty (p-value is 0.33). The results are summarized in Table 5.

Table 5.

Results of analyzing SOLVD data

Covariates	Est	SE	p-value	Est	SE	p-value
Results using data from all 23 centers
	Additive model			Multiplicative model
Treatment vs placebo	−.0628	.0135	< .001	−.4590	.0717	< .001
Age	.0076	.0034	.03	.0645	.0201	.001
Male vs female	−.0211	.0154	.17	−.1314	.0861	.13
Ejection fraction	−.0040	.0007	< .001	−.0284	.0054	< .001
Frailty parameter	.0008	.0006	.083	.0449	.0125	< .001
Results using data after excluding one center
	Additive model			Multiplicative model
Treatment vs placebo	−.0662	.0134	< .001	−.5013	.0751	< .001
Age	.0099	.0027	< .001	.0751	.0208	< .001
Male vs female	−.0172	.0159	.278	−.1254	.0902	.16
Ejection fraction	−.0039	.0007	< .001	−.0287	.0056	< .001
Frailty parameter	.0002	.0003	.404	.0144	.0274	.17

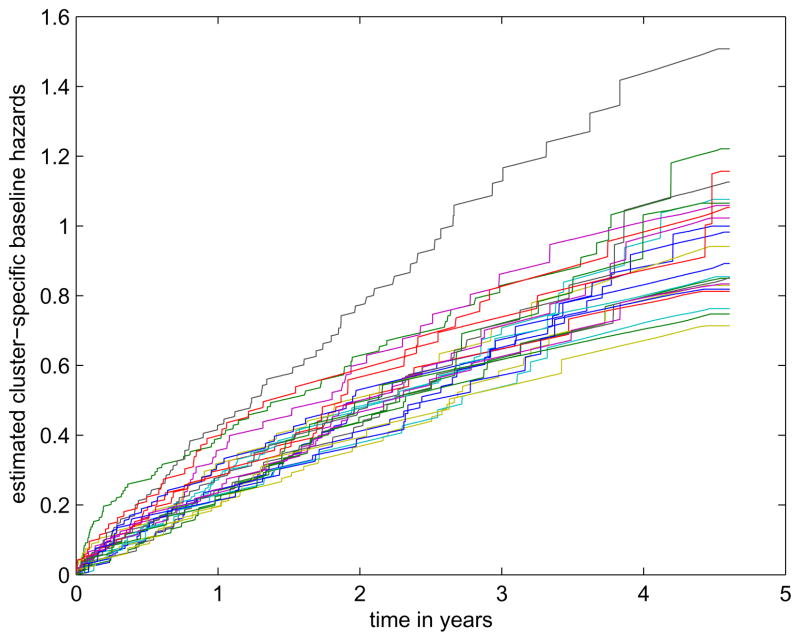
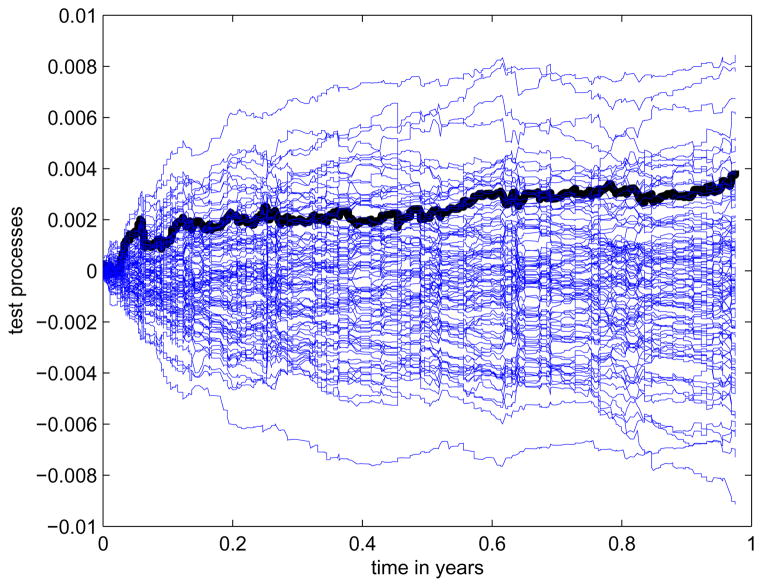
The results indicate that the treatment had a significant effect in reducing the risk of first hospitalization for congestive heart failure or death from all causes; younger patients had lower risk; patients with higher ejection fraction had lower risk as well. There is no strong evidence that significant difference exists between the two gender groups. The non-significance of the frailty parameter implies that the survival behaviors among all these centers were similar to one another. In fact, we plot the estimated cumulative hazards functions from all 23 centers in Figure 3 and they have very small differences except that one particulary medical center had a relatively larger baseline hazards. In Figure 4, we plot the proposed test process (the bold black curves) and the randomly simulated 100 curves from the null distribution. The figure indicates that using the normal frailty distribution may be appropriate.

Figure 3.

Estimated baseline hazards functions from all medical centers in the SOLVD study

Figure 4.

Plot of the test process and simulated curves under the null in the SOLVD study

Finally, we exclude that particular center identified from Figure 3 and re-do the analysis. The p-value for assessing the normality frailty assumption is around 0.30. The fitted results are also given in Table 5 and the conclusion are similar to before. For comparison, we also report the results by fitting the data using multiplicative gamma frailty models. The results show that the direction and significance of the estimates for the covariate effects are similar, although the interpretation of the coefficients is very different.

6. Discussion

We have proposed an additive model with random effects for clustered survival times. The proposed model takes a similar expression as one would fit longitudinal data via mixed effect models. Thus, the parameters in our model enjoy similar nice interpretations as in the usual mixed effect models, but in terms of hazard risks. The inference approach we have proposed can be treated as a generalization of the generalized estimating equations to the hazards models. As the result, any working dependence matrices can be used as weights in equations (4) and (5) to construct consistent estimators of regression parameters. One natural question is how to obtain the most efficient weight matrices; however, although in the longitudinal data analysis, the true dependence covariance matrices should give the most efficient estimation, it is unclear how the covariance matrices are even defined under survival context.

One limitation of the additive structure is that the estimated hazards rate function may not always be positive so the derived survival functions, S̃(t), are not necessarily non-increasing. With an additional random effect introduced in our proposed model, the non-positive hazards problem may be lessened or worsened depending on the monotonicity of G(t; θ). For example, in a normal frailty case, H(t) = Λ(t) − θt²/2, where H(t) is the baseline after integrating out the random effect. Then even though H(t) may be estimated to have negative jumps at some t, the estimator for Λ(t) may not. In the exponential case, H(t) = Λ(t) + log(1 + θt)/θ. Then Λ(t) can have more negative jumps but this also depends on the scale of θ. To fix the non-monotonicity problem in the estimated survival function, we can make a minor modification and define a new estimator as inf_s≤t S̃(s). Theoretically, if S̃(t) is a consistent estimator, the latter should also be consistent due to the increasing property of the truth. This type of modification has been employed in the literature for additive rate models (Lin and Yin, 1994; Yin and Cai, 2004).

In comparison to the multiplicative frailty model, the proposed model can be viewed as a parallel generalization of the additive hazards model to clustered data. Thus, when data (as shown in the diabetic study and seen in Figure 1) really present additive structure and cluster heterogeneity, the proposed model is more appropriate as the multiplicative assumption for the multiplicative model could be violated and may not fit the data well. Our proposed model provides information on hazard differences instead of hazard ratios. Additionally, the frailty variance represents the variability of the baseline hazards rates across clusters and therefore provide us information on the heterogenity of the hazard rate across clusters.

With the specified random effect distribution, the observed likelihood function can be expressed in terms of all the parameters. Therefore, some possible maximum likelihood approaches can be applicable to obtain the efficient parameter estimators. Unfortunately, due to the additive model structure as well as the semiparametric model structure, such inference and computation will be more complicated than the multiplicative frailty model. Further research is being investigated by us.

In model (1), we can further allow for heterogeneity of mixed effects among subjects. This can be achieved by including the interaction between random effects and some covariates. The proposed estimating equations should be applicable but in more complex forms. Finally, as a counterpart to the usual gamma-frailty multiplicative model, developing a valid test to discriminate our model from the gamma-frailty model is an important problem in practice.

Appendix

Proofs of Theorems 1–3

Proof of Theorem 1

We first show the consistency of the estimators. Clearly, since {Y_kl(t): t ∈ [0, τ]} is a P-Glivenko-Cantelli class, we obtain that uniformly in t ∈ [0, τ],

$$n^{-1}\sum _{k=1}^n\sum _{l=1}^{n_k}{Y}_{kl}(t){\mathbf{X}}_{kl}(t){\to }_{a.s.}E\left\{\sum _{l=1}^{n_k}{Y}_{kl}(t){\mathbf{X}}_{kl}(t)\right\},n^{-1}\sum _{k=1}^n\sum _{l=1}^{n_k}{Y}_{kl}(t){\to }_{a.s.}E\left\{\sum _{l=1}^{n_k}{Y}_{kl}(t)\right\}$$

and the second limit is strictly positive from condition (C.2) in Web Appendix. Thus,

$$\overline{\mathbf{X}}(t){\to }_{a.s.}\frac{E\{{\sum }_{l=1}^{n_k}{Y}_{kl}(t){\mathbf{X}}_{kl}(t)\}}{E\{{\sum }_{l=1}^{n_k}{Y}_{kl}(t)\}}\equiv \mathit{\mu }(t)$$

uniformly in t ∈ [0, τ]. As a result,

$$n^{-1}\sum _{i=1}^n\sum _{j=1}^{n_i}{\int }_0^{\tau }{Y}_{ij}(t){\{{\mathbf{X}}_{ij}(t)-\overline{\mathbf{X}}(t)\}}^{\otimes 2}dt{\to }_{a.s}E\left[{\int }_0^{\tau }{Y}_{ij}(t){\{{\mathbf{X}}_{ij}(t)-\mathit{\mu }(t)\}}^{\otimes 2}dt\right]\equiv \mathbf{\sum }.$$

In Web Appendix, we show Σ is invertible. Therefore, from the expression of β̂ and equation (3), we have

$$\widehat{\mathit{\beta }}{\to }_{a.s.}{\mathbf{\sum }}^{-1}E\left[\sum _{j=1}^{n_i}{\int }_0^{\tau }{Y}_{ij}(t)\{{\mathbf{X}}_{ij}(t)-\mathit{\mu }(t)\}{dN}_{ij}(t)\right],$$

which is also equal to

$${\mathbf{\sum }}^{-1}E\left[\sum _{j=1}^{n_i}{\int }_0^{\tau }{Y}_{ij}(t)\{{\mathbf{X}}_{ij}(t)-\mathit{\mu }(t)\}\{{dH}_0(t)+{\mathbf{X}}_{ij}{(t)}^T{\mathit{\beta }}_{0}dt\}\right]={\mathit{\beta }}_0.$$

Similarly, for fixed s ∈ [0, τ],

$$\widehat{H}(s)={\int }_0^s\frac{{\sum }_{i=1}^n{\sum }_{j=1}^{n_i}{Y}_{ij}(t)\{{dN}_{ij}(t)-{\mathbf{X}}_{ij}{(t)}^T{\mathit{\beta }}_{0}dt\}}{{\sum }_{i=1}^n{\sum }_{j=1}^{n_i}{Y}_{ij}(t)}+o(1){\to }_{a.s}{\int }_0^s\frac{E\left[{\sum }_{j=1}^{n_i}{Y}_{ij}\{{dN}_{ij}(t)-{\mathbf{X}}_{ij}{(t)}^T{\mathit{\beta }}_0\}dt\right]}{E\{{\sum }_{j=1}^{n_i}{Y}_{ij}(t)\}},$$

which is equal to H₀(s). Since H₀(s) is continuous in [0, τ], the pointwise consistency can be strengthened to the uniform convergence in [0, τ].

The consistency of θ̂ is based on the estimating equation for θ̂ as given in (7), i.e.,

$$n^{-1}\sum _{i=1}^n\sum _{j\ne l,j,l=1}^{n_i}{\int }_0^{\tau }{\int }_0^{\tau }{Y}_{ij}(t)Y_{il}(s)\{{d\widehat{\epsilon }}_{ij}(t){d\widehat{\epsilon }}_{il}(s)-Q(t,s;\theta )\mathit{dtds}\}=0.$$

From the consistency of (β̂, Ĥ), it is clear that the left-hand side of the above equation converges to

$$E\left[\sum _{j\ne l,j,l=1}^{n_i}{\int }_0^{\tau }{\int }_0^{\tau }{Y}_{ij}(t)Y_{il}(s)\{{d\epsilon }_{ij0}(t){d\epsilon }_{il0}(s)-Q(t,s;\theta )\mathit{dtds}\}\right],$$

where dε_ij0(t) = dN_ij(t) − dH₀(t) − X_ij(t)^T β₀dt. The above limit, by the derivation in Section 2, is also equal to

$$E\left[\sum _{j\ne l,j,l=1}^{n_i}{\int }_0^{\tau }{\int }_0^{\tau }{Y}_{ij}(t)Y_{il}(s)\{Q(t,s;{\theta }_0)-Q(t,s;\theta )\}\mathit{dtds}\right].$$

Moreover, this convergence is uniformly in for in a compact set. By condition (C.4) in Web Appendix,

$$E\left[\sum _{j\ne l,j,l=1}^{n_i}{\int }_0^{\tau }{\int }_0^{\tau }{Y}_{ij}(t)Y_{il}(s){\nabla }_{\theta }Q(t,s;\theta )\mathit{dtds}\right]$$

is non-singular in a neighborhood of θ₀. Thus, from the inverse mapping theorem, for any small ε, there exists a unique solution θ̂ to equation (7) such that |θ̂ − θ₀| < ε. This proves the consistency of θ̂.

Proof of Theorem 2

We use P_n to denote the empirical measure from n i.i.d clustered data and use P to denote the true probability measure. From the expression of β̂, we obtain

$$\widehat{\mathit{\beta }}-{\mathit{\beta }}_0={\left[n^{-1}\sum _{i=1}^n\sum _{j=1}^{n_i}{\int }_0^{\tau }{Y}_{ij}(t){\{{\mathbf{X}}_{ij}(t)-\overline{\mathbf{X}}(t)\}}^{\otimes 2}dt\right]}^{-1}\times {\mathbf{P}}_n\left[\sum _{j=1}^{n_i}{\int }_0^{\tau }{Y}_{ij}(t)\{{\mathbf{X}}_{ij}(t)-\overline{\mathbf{X}}(t)\}{d\epsilon }_{ij0}(t)\right].$$

Since $\mathbf{P}\left[{\sum }_{j=1}^{n_i}{\int }_0^{\tau }{Y}_{ij}(t)\{{\mathbf{X}}_{ij}(t)-\overline{\mathbf{X}}(t)\}{d\epsilon }_{ij0}(t)\right]=0$ and X̄(t) uniformly converges to μ(t) and it belongs to some Donsker class, we have

$$\widehat{\mathit{\beta }}-{\mathit{\beta }}_0={\{\mathbf{\sum }+o_p(1)\}}^{-1}({\mathbf{P}}_n-\mathbf{P})\left[\sum _{j=1}^{n_i}{\int }_0^{\tau }{Y}_{ij}(t)\{{\mathbf{X}}_{ij}(t)-\mathit{\mu }(t)\}{d\epsilon }_{ij0}(t)\right]+o_p(n^{-1/2}).$$ (A.1)

That is, β̂ is an asymptotic linear estimator for β₀ with the influence function

$${\mathbf{S}}_{\mathit{\beta }}({\mathbf{O}}_i)={\mathbf{\sum }}^{-1}\sum _{j=1}^{n_i}{\int }_0^{\tau }{Y}_{ij}(t)\{{\mathbf{X}}_{ij}(t)-\mathit{\mu }(t)\}{d\epsilon }_{ij0}(t),$$

where O_i denotes the observed data from cluster i. Similarly, using the expression of Ĥ, we obtain

$$\widehat{H}(s)-H_0(s)={\int }_0^s\frac{{\mathbf{P}}_n\left\{{\sum }_{j=1}^{n_i}{d\epsilon }_{ij0}(t)\right\}}{E\left\{{\sum }_{j=1}^{n_i}{Y}_{ij}(t)\right\}+o_p(1)}-{\int }_0^s\overline{\mathbf{X}}{(t)}^T(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0)dt.$$

Thus, from (A.1),

$$\widehat{H}(s)-H_0(s)=({\mathbf{P}}_{\mathbf{n}}-\mathbf{P})\left[{\int }_0^s\frac{{\sum }_{j=1}^{n_i}{Y}_{ij}(t){d\epsilon }_{ij0}(t)}{E\left\{{\sum }_{j=1}^{n_i}{Y}_{ij}(t)\right\}}-{\int }_0^s\mathit{\mu }{(t)}^{T}dt{\mathbf{S}}_{\mathit{\beta }}({\mathbf{O}}_i)\right]+o_p(n^{-1/2}),$$ (A.2)

Additionally, (A.2) holds in the metric space l^∞[0, τ]. Equivalently, Ĥ(s) is an asymptotic linear estimator for H₀(s) with influence function

$$S_H({\mathbf{O}}_i;s)={\int }_0^s\frac{{\sum }_{j=1}^{n_i}{d\epsilon }_{ij0}(t)}{E\left\{{\sum }_{j=1}^{n_i}{Y}_{ij}(t)\right\}}-{\int }_0^s\mathit{\mu }{(t)}^{T}dt{\mathbf{S}}_{\mathit{\beta }}({\mathbf{O}}_i).$$

Finally, a similar expansion applies to the left-hand side of (7) and yields

$$\widehat{\theta }-{\theta }_0=({\mathbf{P}}_n-\mathbf{P})S_{\theta }({\mathbf{O}}_i)+o_p(n^{-1/2})$$ (A.3)

for some influence function S_θ. The detail of S_θ is given in Web Appendix.

Proof of Theorem 3

According to the expression of Λ̃(t), we obtain

$$d\stackrel{\sim }{\mathrm{\Lambda }}(t)={d\mathrm{\Lambda }}_0(t)+\frac{1}{n}\sum _{i=1}^n\frac{{\sum }_{j=1}^{n_i}{Y}_{ij}(t){dM}_{ij}(t)}{{\sum }_{j=1}^{n_i}{Y}_{ij}(t)}-\frac{1}{n}\sum _{i=1}^n\frac{{\sum }_{j=1}^{n_i}{Y}_{ij}(t){\mathbf{X}}_{ij}{(t)}^T}{{\sum }_{j=1}^{n_i}{Y}_{ij}(t)}(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0)+\frac{1}{n}\sum _{i=1}^n{\xi }_{i}dt,$$ (A.4)

where dM_ij(t) = dN_ij(t) − dΛ₀(t) − X_ij(t)^T β₀dt − ξ_idt. Clearly, $E\{{\sum }_{j=1}^{n_i}{Y}_{ij}(t){dM}_{ij}(t)/{\sum }_{j=1}^{n_i}{Y}_{ij}(t)\}=0$ and {dM_ij(t) = t ∈ [0, τ]} and {Y_ij(t): t ∈ [0, τ]}are the Glivenko-Cantelli class. Thus, the second term on the right-hand side converges uniformly to zero. Finally, since β̂ converges to β₀ and $n^{-1}{\sum }_{i=1}^n{\xi }_i$ converges to zero, we obtain the uniformly convergence of Λ̃ (t) to Λ₀(t).

The above expansion also implies

$$\sqrt{n}\{\stackrel{\sim }{\mathrm{\Lambda }}(t)-{\mathrm{\Lambda }}_0(t)\}=n^{-1/2}({\mathbf{P}}_n-\mathbf{P})\left[{\int }_0^t\frac{{\sum }_{j=1}^{n_i}{Y}_{ij}(u)\{{dM}_{ij}(u)+{\xi }_{i}du\}}{{\sum }_{j=1}^{n_i}{Y}_{ij}(u)}\right]-\left[{\int }_0^{t}E\left\{\frac{{\sum }_{j=1}^{n_i}{Y}_{ij}(u){\mathbf{X}}_{ij}{(u)}^T}{{\sum }_{j=1}^{n_i}{Y}_{ij}(u)}\right\}du+o_p(1)\right]\sqrt{n}(\widehat{\mathit{\beta }}-{\mathit{\beta }}_0)+o_p(1).$$

Thus, combining with the expansions in (A.1)–(A.3), we immediately have

$$\sqrt{n}\{\widehat{D}(t)-G(t,\widehat{\theta })\}=n^{-1/2}\sum _{i=1}^n{W}_i(t)+o_p(1),$$

where

$$W_i(t)=S_{H,i}(t)-{\int }_0^t\frac{{\sum }_{j=1}^{n_i}{Y}_{ij}(u)\{{dN}_{ij}(u)-{d\mathrm{\Lambda }}_0(u)-{\mathbf{X}}_{ij}{(u)}^T{\mathit{\beta }}_{0}du\}}{{\sum }_{j=1}^{n_i}{Y}_{ij}(u)}+E\left\{{\int }_0^t\frac{{\sum }_{j=1}^{n_i}{Y}_{ij}(u){\mathbf{X}}_{ij}{(u)}^{T}du}{{\sum }_{j=1}^{n_i}{Y}_{ij}(u)}\right\}{\mathbf{S}}_{\mathit{\beta },i}-\frac{\partial }{\partial \theta }G(t;{\theta }_0)S_{\theta ,i}$$

with S_H,i(t), S_β,i and S_{θ, i} being the respective influence functions for Ĥ(t), β̂ and θ̂ from the observations in the ith cluster, as given in the expansions (A.1)–(A.3).