Local complexity of amino acid interactions in a protein core

Abstract

Atomic resolution structures of proteins indicate that the core is typically well packed, suggesting a densely connected network of interactions between amino acid residues. The combinatorial complexity of energetic interactions in such a network could be enormous, a problem that limits our ability to relate structure and function. Here, we report a case study of the complexity of amino acid interactions in a localized region within the core of the GFP, a particularly stable and tightly packed molecule. Mutations at three sites within the chromophore-binding pocket display an overlapping pattern of conformational change and are thermodynamically coupled, seemingly consistent with the dense network model. However, crystallographic and energetic analyses of coupling between mutations paint a different picture; pairs of mutations couple through independent “hotspots” in the region of structural overlap. The data indicate that, even in highly stable proteins, the core contains sufficient plasticity in packing to uncouple high-order energetic interactions of residues, a property that is likely general in proteins.

A characteristic feature of natively folded proteins is a well ordered core consisting of amino acid residues in specific rotamer orientations making well defined packing interactions with neighboring residues. The quality of packing has been reported as uniformly high throughout the core of proteins (1), with mean side chain volumes slightly smaller than those observed in amino acid crystals (2, 3). The efficient packing of residues is often as important as the hydrophobic effect in determining the thermodynamic stability of the folded state (4–8) and may represent a key component of the overall evolutionary pressure guiding sequence variation of a protein fold (9, 10). Also, optimal packing of the core has been used as a design principle in creating artificial proteins, often with improved stability (11, 12).

What is the implication of these observations for the potential complexity of amino acid interactions in proteins? To define this problem, consider all of the ways that the free energy contribution of even one residue for fold stability (or any other thermodynamic property) might arise from the tertiary structure. In the simplest case, this residue might be energetically independent of all other residues; thus, its total free energy contribution is strictly an intrinsic property that involves no pairwise or higher-order interactions with other residues. More realistically, the energetics of the residue might depend on coupled interactions with other residues; in some cases, this might be rationalized as local packing against neighboring residues or through-space electrostatic interactions but may also derive from less intuitive cooperative interactions involving collections of residues that reach to distant sites (13, 14). In the absence of prior knowledge, then, the total thermodynamic value of residue i is given by a combinatorial set of hierarchical structural interactions:

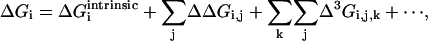[1]

where Δ″G represents the n-way coupling of residues, for instance the three-way coupling of residues i, j, and k.

The extraordinary complexity of energy parsing implied by this relationship shows that proteins could be densely connected networks of residues, where a free energy change introduced at one site (e.g., by ligand binding, covalent modification, or mutation) may parse into many hierarchical levels of interactions (two-way, three-way, etc.) with other residues. How much of this complexity is really significant in proteins? Here, we examine the total hierarchy of interactions for mutations within a local region in the chromophore-binding pocket of GFP, a highly stable molecule that depends on rigidity in the core to deliver its characteristic high quantum yield of fluorescence. The data show that, even in this case, the protein core contains sufficient flexibility in packing to decompose higher-order amino acid interactions, even in local regions. In addition, the results provide a framework for predicting local energetic interactions through structural analysis of proteins.

Materials and Methods

Protein Expression, Purification, and Crystallization. GFP mutants were constructed by using oligonucleotide-directed PCR mutagenesis methods and cloned into the pRSET-B expression vector (Invitrogen). The enhanced GFP (S65T mutant) was taken as the “wild-type” reference. GFP proteins were expressed as N-terminal His-6-tagged fusions in E. coli [BL21(DE3)], and purified through nickel-nitrilotriacetic (Ni-NTA) affinity chromatography. The purified protein was concentrated to 20 mg/ml, and then either flash frozen or used immediately for crystal trials. Crystallization was carried out as described (15) in 22–26% poly(ethylene glycol) (PEG) 4000/50 mM MgCl₂/10 mM 2-mercaptoethanol/50 mM Hepes (pH 8.1–8.5) by mixing 2 μl of well solution with 2 μl of protein solution (12–15 mg/ml protein in 50 mM Hepes, pH 7.5) in hanging drops at room temperature with 750 μl of well solution. Crystals belonged to space group P2₁2₁2₁. Crystals were cryoprotected in stabilizing buffer (crystallization buffer, pH 8.5 plus 2–3% PEG 4000) plus 15% glycerol and flash-frozen in propane. Crystals diffracted at pH 5.5 were serially soaked in solutions of pH 7.5, 7.0, 6.5, 6.0, and 5.5 before being flash frozen.

Analysis of GFP Mutants. The energetic effect of mutations in GFP was measured as the change in the absorbance maximum of the chromophore relative to wild type. Absorbance spectra (scans from 280 to 620 nm) were acquired by using a Lambda 18 UV/visible Spectrophotometer (Perkin–Elmer) at a slit-width of 0.5 nm. Protein concentrations were chosen such that A_max ≈ 0.5. For structures solved at pH 5.5, spectroscopic isosbestic points were confirmed over a range of pH 8.5–5.5. His-6-tagged and cleaved proteins showed identical absorbance spectra.

Data Collection and Structure Determination. Wild-type pH 8.5 and pH 5.5 and Y145C mutant data were collected at our home source with a R-axis IV image plate scanner; T203C pH 8.5 data were collected at National Synchrotron Light Source beamline X4A; and T203C pH 5.5 and Y145C, T203C were collected at Stanford Synchrotron Radiation Laboratory beamline 7-1. Diffraction data were processed and scaled with denzo/scalepack (16), and reduced with the ccp4 package (17). Structures were solved by initial rigid body fitting of the published coordinate file followed by high temperature simulated annealing. The model was built by using o (18), and was iteratively refined in the Crystallography and NMR System software (cns) (19) using positional and B-factor refinement, composite omit maps, solvent modeling, and manual rebuilding in o. A randomly selected set of reflections (5–10%, see Table 1, which is published as supporting information on the PNAS web site) was flagged for statistical cross-validation (20). Final statistics for all structures are given in Table 1. The Ramachandran plot shows excellent geometry and no outliers for all six models.

Structural Displacement and Coupling Parameters. All six refined models were overlaid through least squares minimization of C_α positions in o (18). The quantitative measurement of structure change due to a mutation requires weighting the observed displacement of each atom i in the mutant relative to wild type (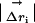) by the experimental errors in determining both the atomic centroids. Thus, Δr_norm,i is a parameter reporting the significance of the structural change

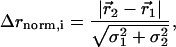where 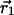and 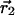represent the centroid positions of atom i in structures 1 and 2, and σ₁ and σ₂ are the associated errors calculated by using the method of Stroud and Fauman (21). This method provides an empirical estimate of the coordinate error for an atom given the refined B factor and the resolution of the data set.

The structural coupling parameter (ΔΔr_norm,i) reports the change in the centroid displacement of an atom i due to one mutation when tried in the background of another mutation (see Fig. 3c), and is calculated from a cycle of four structures. For atom i

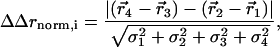where (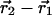) is the centroid displacement due to a mutation in the wild-type background and (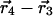) is that in the background of the second mutation. As above, the significance of the structural coupling is the raw difference weighted by the propagated error of atom i in all four structures.

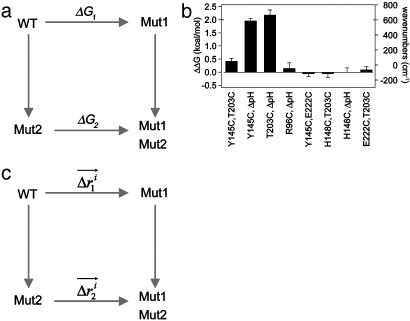
Fig. 3.

Specific two-way thermodynamic interaction of T203C, Y145C, and ΔpH.(a) The double mutant cycle formalism, where the energetic effect of one mutation (m1) is measured in the wild-type background (ΔG₁) and in the background of a second mutation (ΔG₂). The difference in these two (ΔΔG_1,2 = ΔG₁–ΔG₂) is the coupling energy, the degree of thermodynamic interaction between the two mutations. (b) Mutant cycle analysis shows that all three mutations are significantly coupled to each other but are uncoupled from other mutations in the immediate neighborhood. Thus, consistent with the overlap in structural effect, T203C, Y145C, and ΔpH are specifically pairwise coupled. (c) Analogous to the thermodynamic cycle, the structure cycle captures the context dependence of structural change between two mutations. Thus, the displacement of atom i due to one mutation is measured both in the wild-type (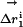) and a second mutant (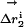) background, and the magnitude of the vector difference (weighted by the propagated positional errors, see methods) gives 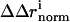, the structural coupling parameter.

Energetic Characterization of the GFP Chromophore-Binding Pocket. GFP is an extremely well packed 11-stranded β-barrel with a fully buried central helix that contains a chromophore (shown in green) generated in an autocatalytic chemical reaction of three residues (Fig. 1a) (15). Tuning of the chromophore absorbance color depends on the net free energy interactions with the surrounding protein (22, 23), and Raman spectroscopic studies show that mutations that alter the absorbance spectrum are directly related to perturbations of the ground state structure of the molecule (24). Thus the GFP absorbance spectrum provides a high-resolution assay for reporting the energetic value of perturbations at sites surrounding the chromophore, and the effects are likely to arise from the crystallographically observable structure.

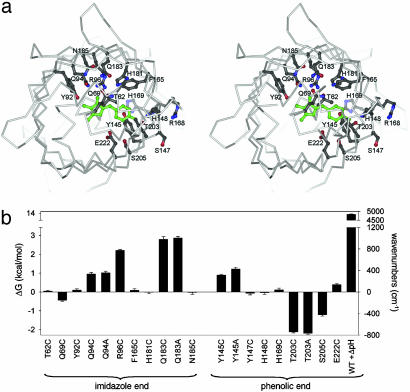
Fig. 1.

Energetic characterization of the GFP chromophore-binding pocket. (a) Stereoview of the binding pocket viewed down the β-barrel axis showing sites included in the mutagenic scan. The p-hydroxybenzylideneimidazolin-one chromophore is shown in green. (b) Mutagenic scan of the chromophore environment including the perturbation of pH shift from 8.5 to 5.5 (ΔpH). The energetic effect of each mutation is measured as change in chromophore absorbance maximum, a property that derives from changes to the ground state structure of GFP (24). Mutation of some sites has no significant energetic effect despite direct interaction with the chromophore (H148C), whereas the largest effect is seen for Q183, which only indirectly contacts the chromophore. This and subsequent figures were prepared by using gl-render (L. Esser, personal communication), povray (34), and raster3d (35).

To characterize the chromophore-binding pocket, we carried out a mutagenic scan of 16 residues within a 9-Å shell around the chromophore (Fig. 1a) and measured changes in spectral tuning (Fig. 1b). In addition to mutagenesis, we included pH change from 8.5 to 5.5 (ΔpH), which induces protonation of the chromophore phenolic oxygen (pK_a = 6.5) and a blue shift in the absorbance maximum. Like point mutagenesis, ΔpH also has its effect on the ground state structure of GFP (24); for simplicity, we refer to this perturbation below as a mutation. These data show that, like at the protein–protein interface (25), hot spots of interaction energy occur within the core of GFP. Some residues that make direct contact with the chromophore, such as H148, show no energetic consequence upon mutation, and yet mutation at positions in the immediate vicinity of H148 (T203C/A, S205C, and Y145C) show substantial energetic effects. More strikingly, position 183, which is further away and only indirectly interacts with the chromophore, shows the largest energetic effect upon mutation.

Structural Effect of Three Single Mutations. We chose three specific mutations (T203C, Y145C, and ΔpH) as a case study for evaluating the total complexity of hierarchical energetic interactions. These mutations all significantly affect chromophore energetics (Fig. 1b) and occur within one shell of packed atoms from each other at or near the phenolic oxygen (Fig. 1a). Atomic resolution structures of four GFP proteins [enhanced GFP at pH 8.5 (26), enhanced EGFP at pH 5.5, and the two point mutants (T203C and Y145C)] were solved under nearly isomorphous conditions by using the structure of wild-type GFP as an initial model for refinement (Table 1, see Materials and Methods). The structures were solved to a resolution of at least 1.6 Å and show a mean C_α deviation of 0.16 Å. The range of final R_free values was 20.1 to 23.1, and all models show excellent geometry (Fig. 7, which is published as supporting information on the PNAS web site).

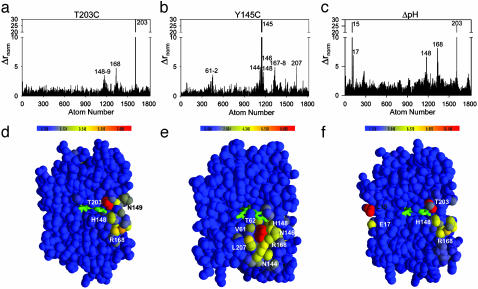
We overlaid all four refined models through least squares minimization of C_α positions and quantitated the structural effect of each mutation by the displacement of each atom in the mutant structures relative to their positions in the wild-type structure (Fig. 2). To account for experimental errors in determining atomic positions, we weighted the observed displacements by the errors of atomic centroids calculated by using the method of Stroud and Fauman (21) (Fig. 8, which is published as supporting information on the PNAS web site, and see Materials and Methods). Point mutation T203C causes very little overall structural change but shows specific displacements of atoms at a few positions in addition to position 203 itself: R168, H148, and N149 (Fig. 2 a and d). Interestingly, these three positions comprise a specific continuous path through the network of packed atoms in the core of GFP connecting position 203 to bulk solvent. The fracture-like propagation of the structural change at position 203 along the path defined by H148 and R168 presumably reflects local mechanical properties of the GFP structure that allow a very anisotropic propagation of the structural effect of the T203C mutation. In contrast, point mutation Y145C induces a nearly isotropic pattern of structure change (Fig. 2 b and e) that overlaps with the pattern observed for T203C at positions 148 and 168. Finally, the global perturbation of pH shift induces two sets of structural changes in GFP that are separated widely in the tertiary structure (Fig. 2 c and f). The first set comprises positions 203, 148, and 168 and nearly fully overlaps with the pattern of structural change seen in T203C, and the second set comprises two residues located on the opposite surface of GFP (15–17).

Fig. 2.

Overlapping specific structural effects of the T203C, Y145C, and ΔpH mutations. Bar graphs (a–c) and colorimetric representations (d–f) of the magnitude of displacement of atoms in the mutant structures T203C (a and d), Y145C (b and e), and ΔpH (c and f) relative to wild type. Δr_norm is the raw atomic displacements weighted by the propagated errors in atomic centroids (see Materials and Methods). (a–c) Atom numbers are in order of PDB file format, and peaks are labeled with the corresponding amino acid position. (d–f) Cross-sections within the core of GFP to display the chromophore region. T203C shows a directional pattern of structural change connecting position 203 with the surface of the β-barrel, whereas Y145C shows an isotropic pattern of change limited to the immediate vicinity that overlaps with the effects of T203C. The global perturbation of ΔpH shows two regions of structural change that are widely separated in the molecule; one of these is nearly the same as for T203C.

Thermodynamic Coupling Among All Pairs of the Three Mutations. The overlapping pattern of structural change for the three mutations is not particularly surprising. The spatial proximity of the mutations and the tight packing of residues in the GFP core would seem to necessitate this outcome, and is consistent with the notion that all three mutations might be energetically coupled to each other. For example, the overlap in the structural response to T203C and ΔpH suggests that the energetic effect of T203C might be different in the background of ΔpH; similarly, the overlap in structural changes suggests that the energetic effect of Y145C might be different in the background of ΔpH, and also might be different in the background of T203C. This context dependence of one mutation in the background of another is the conceptual basis for the thermodynamic mutant cycle, a quantitative formalism for experimentally determining the energetic coupling of mutations. In this method, the energetic effect of one mutation is measured for two conditions: (i) the wild-type background (ΔG₁), and (ii) the background of a mutation at a second site (ΔG₂). The difference in these two energies (ΔΔG_1,2) represents the coupling free energy of the two mutations, the degree to which the energetic effect of mutation 1 is different in the background of mutation 2 (Fig. 3a). If the two mutations are thermodynamically independent, then the energetic effect of mutation 1 is exactly the same in both backgrounds and the coupling energy is zero. If the coupling energy is nonzero, then the two mutations are coupled to an extent measured by the magnitude of ΔΔG_1,2.

It is important to note that ΔΔG_1,2 is a purely thermodynamic parameter and is therefore independent of mechanism; that is, it says nothing directly about how the interaction of mutations 1 and 2 arises from the protein structure. Similarly, just the observation of structural overlap in single mutant effects for mutations 1 and 2 does not itself demonstrate thermodynamic coupling; two mutations might produce structural changes that are entirely independent of each other even though they act on an overlapping set of residues. Nevertheless, previous work (27, 28) provides an empirical rule for making predictions: mutations that show no overlap in their effects are typically thermodynamically independent, and mutations that show overlap often show thermodynamic coupling. Thus, structural overlap in mutational effects does represent a reasonable basis for proposing energetic interaction.

To experimentally test the two-way interactions between the three mutations in GFP, we carried out thermodynamic cycle analysis (29, 30) (Fig. 3 a and b). Consistent with the crystallographic findings, all three perturbations are pairwise coupled to each other, albeit to different degrees (Fig. 3b). These couplings are unlikely to result from subtle global effects of mutagenesis on the GFP protein core because mutations at several other sites in the same vicinity fail to show any significant energetic coupling to the three mutations (Fig. 3b). Thus, consistent with the picture of local structural overlap of the three mutations, we find local thermodynamic coupling of all pairwise combinations of the three mutations.

Structural Mechanism of the Thermodynamic Coupling. What structural mechanism underlies the thermodynamic coupling of these mutations? As a simple approach, consider an analog of the thermodynamic cycle that measures the structural coupling of two mutations (Fig. 3c) (31, 32). Here, the displacement vector for each atom in response to a mutation is measured for two conditions: (i) the wild-type background (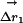), and (ii) the background of a second mutation (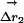). The difference in these two vectors (weighted for errors in atomic positions) is the structural coupling parameter (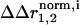), which indicates the degree to which atom i is displaced differently by mutation 1 in the background of mutation 2. Calculated for all atoms, the set of structural coupling values provides a spatial map of the structural interaction of two perturbations, where the two would “feel” each other through the nonadditive response of atoms comprising the underlying coupling mechanism.

An important point is the interpretation of the structural coupling parameter (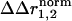) with regard to the thermodynamic coupling energy. The coupling free energy between mutations might arise through changes in any combination of the fundamental forces that bind atoms involved in the coupling mechanism. The distance dependence of the net interaction energy between atoms in any particular case is difficult to predict and is certainly nonlinear. Thus, 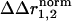cannot be seen as a quantitative representation of the change in interaction energy between atoms. Instead, it simply indicates that sites either do or do not show context dependence in the structural change because of a pair of mutations. In essence, the interpretation of the structural coupling parameter is a binary mapping: a nonzero 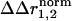represents sites of structural interaction between the mutations, and a 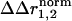of zero indicates lack of any structural interaction at that site.

We applied the structural cycle formalism to study the interaction mechanism of the T203C–ΔpH and Y145C–T203C mutation pairs (Fig. 4). To complete the cycles, we determined the crystal structures of an additional two GFP proteins (T203C at pH 5.5 and the Y145C,T203C double mutant) under nearly identical experimental conditions. The resulting structures show excellent statistics and were refined to 1.58 and 1.60 Å resolution, respectively (Table 1).

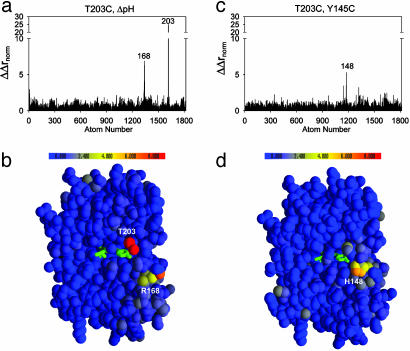
Fig. 4.

Structure cycle analysis shows independent interaction mechanisms for the two-way thermodynamic couplings. Bar graphs (a and c) and colorimetric representations (b and d) of the magnitude of structural coupling (ΔΔr_norm) for each atom in the T203C–ΔpH (a and b) and Y145C–T203C (c and d) cycles. The values report the degree to which each atom feels the effect of one mutation differently when in the background of another mutation and is the structural analog of the double mutant cycle. Despite two-way thermodynamic coupling (Fig. 3) and overlapping structural change (Fig. 2) of the single mutants, the structural cycle analysis predicts that T203C and ΔpH interact through a distinct mechanism from that of the T203C–Y145C pair.

The structural cycles provide three main results. First, the structural coupling is near zero at all sites affected by one mutation but not by the other. For example, sites significantly affected by ΔpH but not by T203C show near additivity of atomic displacements in the cycle (e.g., residues 15 and 17, compare Figs. 2 c and f with 4 a and b). Similarly, many of the sites affected by Y145C but not by T203C show no structural coupling in the Y145C–T203C cycle (compare Figs. 2 a and d with 4 c and d). This result is predictable and consistent with prior work (13, 32); we would not expect a pair of mutations to show coupling at sites where the single mutant effects do not overlap.

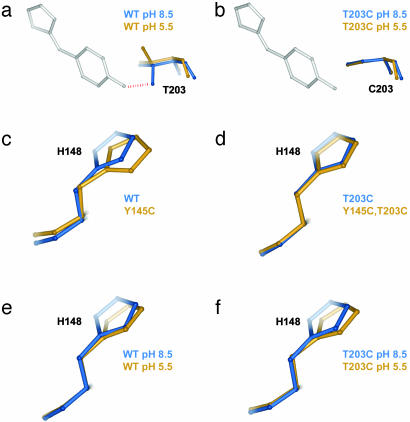
Second, we find significant structural coupling at some sites where the single mutant effects do overlap. Thus, sites 203 and 168 show large nonadditive atomic displacements in the T203C–ΔpH cycle (Fig. 4 a and b), and site 148 shows nonadditivity in the Y145C–T203C cycle (Fig. 4 c and d). As a mechanistically clear and predictable example of structural nonadditivity, Fig. 5 a and b shows the effect of ΔpH at position 203 in a wild-type (Fig. 5a) or in a T203C (Fig. 5b) background. T203 is hydrogen-bonded to the phenolic oxygen of the chromophore at pH 8.5, and protonation of the phenolic oxygen upon pH shift breaks the bond and causes T203 to rotate away by 120° (Fig. 5a, compare blue and gold structures). However, cysteine at 203 is not hydrogen-bonded to the phenolic oxygen at either pH and consequently shows no structural change upon ΔpH (Fig. 5b, compare blue and gold structures). Thus, the structural coupling at position 203 in the T203C–ΔpH cycle simply reflects the fact that either ΔpH or T203C eliminates the hydrogen bond and the double mutant has no further effect than each single mutation taken independently. The origin of the structural coupling at position 148 in the Y145C–T203C cycle (Fig. 5 c and d) is less intuitive but is clearly evident in the context-dependent changes in packing of H148. Overall, these findings confirm the expectation that nonadditive structural responses in a region of overlapping conformational change are associated with the energetic coupling of mutations.

Fig. 5.

Specific examples of the structural cycle analysis. (a and b) The effect of ΔpH at position 203 in the wild-type (a) or T203C (b) mutant background and illustrates a mechanistically clear case of structural nonadditivity (coupling). T203 is hydrogen-bonded to the phenolic oxygen of the chromophore at pH 8.5, and protonation of this site upon pH shift breaks the bond and causes T203 to rotate away by 120°. However, cysteine at 203 is not hydrogen bonded at either pH, and consequently shows no structural change upon ΔpH. Thus, the structural coupling at position 203 reflects the fact that either ΔpH or T203C eliminates the hydrogen bond, and the double mutant has no further effect than that of each mutant taken independently. (c and d) A less predictable example of structural coupling in the Y145C–T203C cycle. H148 is displaced by Y145C in the wild-type background (c) but is not displaced in the T203C background (d); this T203C dependence in the repacking of H148 induced by Y145C is the basis of the observed structural coupling between these two mutations. (e and f) An example of structural additivity in the T203C–ΔpH cycle. H148 is displaced by ΔpH (e), but this displacement is the same in the background of T203C (f); thus, T203C and ΔpH fail to show structural coupling at this site. This result is particularly striking because T203C itself displaces H148 (Fig. 2a).

Finally, the structural cycle analysis reveals a finding that could not have been predicted from the single mutant structures alone. Not all residues in the region of overlap necessarily show structural coupling. For example, position 148 is significantly displaced by both ΔpH and T203C (Fig. 5 e and c, respectively), but ΔpH in the T203C background (Fig. 5f) shows the same displacement of H148 as in the wild-type background. This results in no structural coupling at this site for the T203C–ΔpH cycle (Fig. 4 a and b). Similarly, position 168 is displaced by both Y145C and T203C (Fig. 2 a and b), but shows additive displacement in the Y145C, T203C double mutant (Fig. 4c). These data demonstrate a new finding: the structural mechanism of coupling does not necessarily involve the entire region of overlap between the effects of two mutations. Instead, hotspots of coupling occur within a larger region of structural overlap that represent specific sites of interaction between the mutants. Such localized sites of coupling are reminiscent of hotspots of binding energy at protein–protein interface (25), where the energetic interaction between two proteins is mediated through only a small subset of the buried surface area.

Thermodynamic Independence of the Three-Way Coupling. An unexpected consequence of the hotspots of structural coupling is that, despite overlap in the structural responses of all three mutations (Fig. 2), the T203C–ΔpH and Y145C–T203C interactions are apparently spatially decomposed into independent mechanical processes. T203C and ΔpH interact through sites 203 and 168, whereas Y145C and T203C interact through position 148. The lack of any apparent overlap in the coupling mechanisms makes an interesting prediction: despite energetic importance of all three sites (Fig. 1b) and significant two-way thermodynamic coupling between all three mutations (Fig. 3b), we should expect the three-way coupling of the mutations to be near zero.

To understand the meaning of the three-way coupling of mutations, consider all of the energetic terms that are required to explain the net free energy change of the triple mutant GFP relative to wild-type (ΔG_{T203C,Y145C,ΔpH}). As given by the theory of Horowitz and Fersht (33), the total effect of any triple mutant i, j, k is given by the following hierarchical summation (see Supporting Text, which is published as supporting information on the PNAS web site):

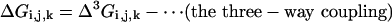[2]

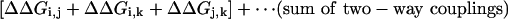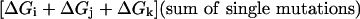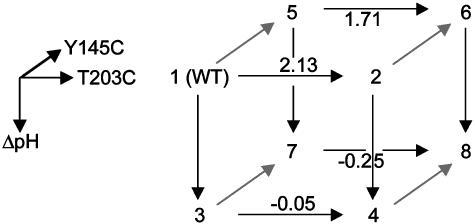
That is, the energetic effect of the triple mutant depends not only on the single mutant effects, but on the sum of all of the constituent pairwise (ΔΔG) and three-way (Δ³G) interaction energies. The two-way coupling energies are experimentally measured by using the double mutant cycle formalism (Fig. 3a). How can we measure the three-way coupling energy? Just as the two-way coupling is the context dependence of a single mutation when tried in the background of another mutation, the three-way coupling is the context dependence of a two-way coupling in the background of a third mutation, for example, the difference in the T203C–ΔpH coupling when tried in the background of Y145C (see Supporting Text and Fig. 9, which is published as supporting information on the PNAS web site). By extension from the graphical representation of the two-way coupling as a thermodynamic box (Fig. 3a), this experiment is represented by a thermodynamic cube (Fig. 6). Each face of the cube is a double mutant cycle with an associated two-way coupling energy, and the energetic difference between two opposing faces is the three-way coupling energy, the degree to which the interaction of two mutations depends on a third.

Fig. 6.

An experimental test of the prediction of three-way independence of T203C, Y145C, and ΔpH. By extension from the definition of the two-way coupling energy (see text), the three-way coupling is the degree to which a given two-way coupling between two mutations depends on a third mutation. A schematic representation of this is the thermodynamic cube, where the front face is the double mutant cycle for T203C–ΔpH, and the back face the same cycle in the background of Y145C. The difference in the two-way coupling energies of the front and back faces gives the three-way coupling energy of the mutants (ΔΔΔG_{T203C,Y145C, ΔpH} = 0.22 ± 0.29 kcal/mol). The cube vertices represent: 1, WT, pH 8.5; 2, T203C, pH 8.5; 3, WT, pH 5.5; 4, T203C, pH 5.5; 5, Y145C, pH 8.5; 6, Y145C, T203C, pH 8.5; 7, Y145C, pH 5.5; 8, Y145C, T203C, pH 5.5. Values shown above arrows are difference energies for the associated pair of mutants in kcal/mol.

We measured the eight GFP proteins that constitute the thermodynamic cube for the T203C–Y145C–ΔpH mutants. The data show that the three-way coupling energy for these mutations is, in fact, near to zero (ΔΔΔG_{T203C,Y145C,ΔpH} = 0.22 ± 0.25 kcal/mol, Fig. 6). This result confirms the prediction from the structural cycle analysis: the lack of any apparent overlap in the coupling mechanism between pairs of the three mutations is correlated with lack of any significant three-way coupling.

Eq. 2 defines a central problem in the rational engineering of proteins through mutagenesis. The number of energy terms required to predict the net effect of a multiple mutant grows dramatically with the number of mutations, and rapidly becomes experimentally intractable. Previous work has provided one practical rule for limiting the size of this problem: single mutants that show no overlap in their structural effects typically produce additive energetic effects when combined (13, 32). However, mutations that occur within 8 Å of each other often show structural overlap (27), and yet such mutations represent the most likely choices for tuning function of an active site. Thus, designing local regions of protein structure requires a more complex algorithm: context-dependent mutagenesis of sites involved in local cooperative interactions, and additive mutagenesis of sites predicted to be independent. The data described here suggest a generalization of the earlier rule that might aid in this process: lack of structural overlap in the effects of mutagenesis at any combinatorial level (e.g., in Δr_norm, the response to single mutagenesis, or in ΔΔr_norm, the structural coupling of mutant pairs) predicts energetic additivity at higher levels. This rule is an empirical one and requires further testing, but its application might permit a new level of control in designing the energetics of local regions of structure through structural analysis of proteins.

Conclusion

The high fluorescence quantum yield of GFP demands an extremely well packed and rigid core to minimize vibrational deactivation of the chromophore. Even in this sort of environment, it appears that the anisotropic mechanics of residue packing can allow for decomposition of local interresidue interactions into distinct mechanisms. It is interesting that no obvious property of either the wild-type or the single mutant structures suggests such mechanical independence; rather, these structures just imply a dense network of overlapping interactions in the local neighborhood. However, the context dependence of one mutation in the background of another clarifies the picture; the coupling mechanism between pairs of mutations reduces to hotspots within a larger region of mutual overlap. The finding of hotspots of coupling demonstrates that specific local amino acid interactions can be maintained within the protein core, and implies that the core contains enough buffering capacity for perturbations to uncouple high-order energetic interactions. A comprehensive mutational study in staphylococcal nuclease (6) showing independence of high-order core mutations suggests that mechanical decomposition of high-order interactions may be a general aspect of proteins.