Changepoint Analysis for Single-Molecule Polarized Total Internal Reflection Fluorescence Microscopy Experiments

Abstract

The experimental study of individual macromolecules has opened a door to determining the details of their mechanochemical operation. Motor enzymes such as the myosin family have been particularly attractive targets for such study, in part because some of them are highly processive and their “product” is spatial motion. But single-molecule resolution comes with its own costs and limitations. Often, the observations rest on single fluorescent dye molecules, which emit a limited number of photons before photobleaching and are subject to complex internal dynamics. Thus, it is important to develop methods that extract the maximum useful information from a finite set of detected photons. We have extended an experimental technique, multiple polarization illumination in total internal reflection fluorescence microscopy (polTIRF), to record the arrival time and polarization state of each individual detected photon. We also extended an analysis technique, previously applied to FRET experiments, that optimally determines times of changes in photon emission rates. Combining these improvements allows us to identify the structural dynamics of a molecular motor (myosin V) with unprecedented detail and temporal resolution.

1. Overview

1.1. The changepoint problem

Many experiments in single-molecule biophysics seek to determine the time course of discrete intramolecular motions (Michalet and Weiss, 2002). For example, we may wish to know when in a mechanochemical cycle does one subunit of an enzyme move spatially relative to another, when does a ligand bind, and so on. One popular method involves Förster resonance energy transfer (FRET; Weiss, 1999). Oversimplifying somewhat, FRET converts the spatial distance between two fluorescent probes attached to a macromolecule (or on two molecules) into an observable signal, a photon emission rate. A second method, and the main application to be discussed in this chapter, is polarized total internal reflection fluorescence microscopy (polTIRF; Beausang et al., 2008; Rosenberg et al., 2005). The method will be discussed in greater detail below, but again oversimplifying, it converts the spatial orientation of a fluorescent probe into a set of distinct photon emission rates. Each rate describes the probe’s average number of emitted photons per time with a particular polarization, given a particular excitatory polarization and intensity.

In each of the situations just described, the experimenter hopes to observe discrete changes of internal state as sudden changes in photon emission rate(s), and to interpret those jumps as specific spatial movements. Ideally, such data will tell us the precise times of the changes, for example, so that kinetic constants may be determined accurately, and also the number of distinct states and the precise spatial distances or orientations in each state. (Different methods based on hidden Markov modeling have been proposed to extract kinetic parameters directly from unbinned single-photon trajectories; Andrec et al., 2003; McKinney et al., 2006). Such methods achieve high time resolution, but unlike ours, they require knowledge of the underlying kinetic scheme.)

Single-molecule fluorescence measurements are limited, however, by shot noise: There are only a finite number of photons available, either because each state is short-lived, or because most fluorophores photobleach (stop fluorescing) after a finite number of excitations. Increasing the photon count via stronger illumination generally hastens the eventual bleach. Slowing the kinetic steps by any of various expedients can distort the natural functioning of the enzyme under study. For all these reasons, we would like to make optimal use of the available photons by employing a good change-point detection scheme.

The “changepoint problem” has a long history in probability theory (Chen and Gupta, 2001). In its abstract form, we consider a time series of observations. We wish to compare the hypotheses: (H0) The observations are independent draws from a single unknown probability distribution, (H1) all the observations up to time τ are independent draws from one unknown distribution, and those made later than τ are independent draws from a different unknown distribution; …(Hp) there are p such sudden transitions. In this general form, the changepoint problem has many applications (e.g., in finance). But it cannot be attacked without specifying our assumptions more completely. For example, as stated, the problem allows us to suppose that every observation is separated from the next by a change-point—not a useful conclusion!

The rest of this overview section gives a concise, self-contained tutorial on changepoint detection. The reader who wants to know what the method can do may wish to examine Figs. 15.1 and 15.2 before proceeding. Succeeding sections give more implementation details (see also Beausang, 2010). A glossary of abbreviations appears at the end.

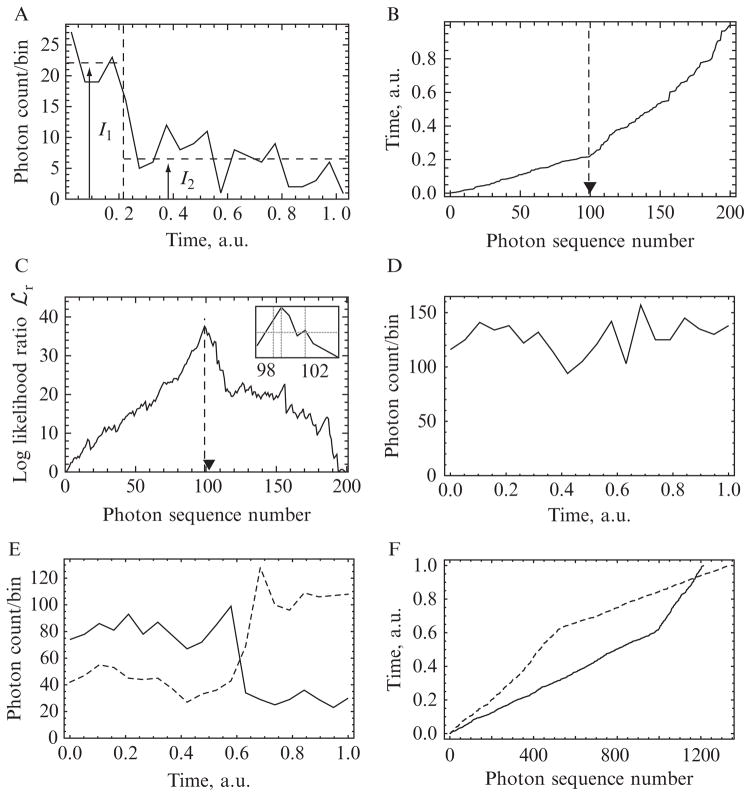
Figure 15.1.

(A–C) Illustration of changepoint detection methods on simulated data with N = 200 photons and a ratio between the high and low rates of χ = 3. (A) The photons are binned into 20 constant-width temporal bins. Examining the graph by eye, we may guess that there is a change in photon rate somewhere around the vertical-dashed line, but neither this change time nor the initial and final rates (I₁ and I₂), nor even the existence of a changepoint, are clear. (B) As described in Section 1.3, the kink in the cumulative distribution of photon arrival times gives a much clearer indication of changepoint time, and the two slopes flanking that point yield the corresponding photon rates. Because these are simulated data, we can compare the actual (triangle) and inferred (dashed line) changepoint times. This chapter describes a quantitative implementation of this simple observation. (C) The peak of the log-likelihood surface occurs at photon sequence number m = 99 (vertical-dotted line), and the 95% confidence intervals at m = 98 and 102 enclose the actual changepoint (inset, vertical lines). (D–F) Illustration on real experimental data. A bifunctional fluorescent dye molecule was attached to one of the two lever arms of a myosin-V molecular motor. The motor bound to an immobilized actin filament and began its mechanochemical cycle in the presence of 10-μm ATP. The dye was excited by polTIRF in each of the several incident polarizations (see Section 2.1), and individual emitted photons were detected after passing through a polarization splitter. (Time-stamped data also arise in FRET measurements.) (D) shows the photon counts in a set of 20-time bins (total of N = 1280 photons recorded). No changepoint is visible to the eye. (E) separates the total counts into the several “flavors,” or tagged subpopulations, of emitted photons. Of these, two have been selected for display as solid and dashed curves. A changepoint is visible, but its time cannot be established to greater accuracy than about two time bins. (F) shows the cumulative distribution described in Section 1.3. Each photon time series displays a sharp kink, and moreover, the two curves’ kinks occur at the same time (vertical position).

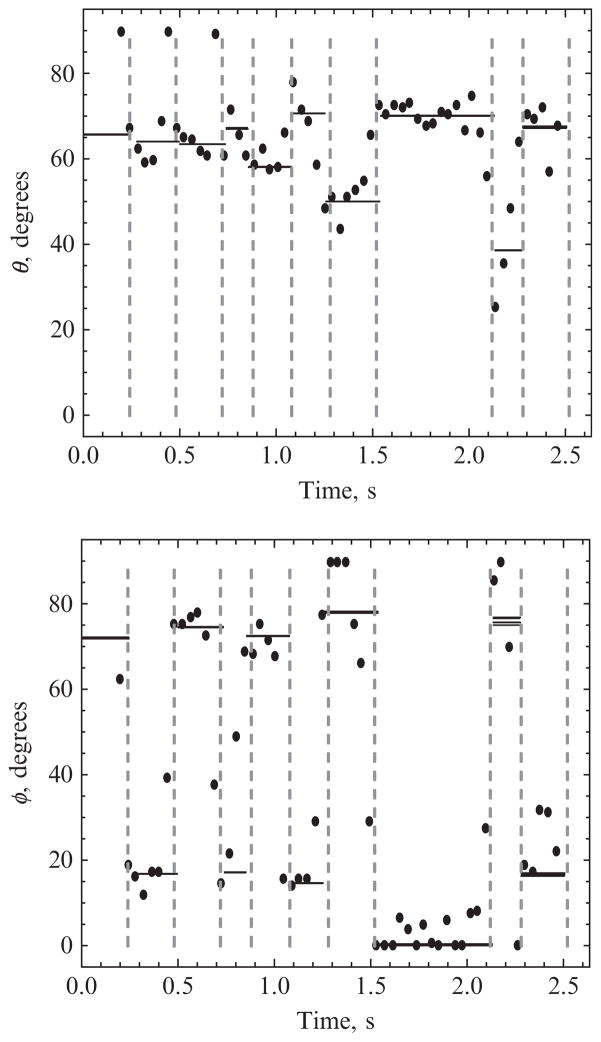
Figure 15.2.

Application of changepoint analysis to experimental data on the motions of the molecular motor myosin V. Dots show polar (θ) and azimuthal (φ) angles of a fluorescent probe attached to one lever arm of the motor inferred from photon rates obtained by the traditional time-binned method. The angles are defined in a system whose polar axis is the optical axis of the microscope. There are many outlier points, in part reflecting transitions that occur in the middle of a time bin. Solid lines show those same angles inferred from all the photons that lie between successive changepoints (dashed lines), indicating a clear alternating stride between well-defined values of φ. For each state, five lines are drawn to indicate the uncertainty in the fit angles, as described in Section 3.4. Generally, these lines are too close to distinguish.

1.2. Traditional approach

For applications to single-molecule biophysics, we can formulate a more specific version of the general changepoint problem: We suppose that, in each quasi-stationary state S^(a), photons are emitted in a Poisson process with some stationary mean rate r^(a). Given a time series of photon arrivals, we then wish to find these rates and the times of the transitions between them.

One way to address the question is to divide time into bins of size Δt large enough that every bin contains many photons. Dividing the count in each bin by Δt gives an estimate of the photon emission rate (intensity). We create a histogram of these estimated rates, identify cut points between its peaks, and declare a changepoint in the data whenever two successive estimates of the rates straddle a cut point. Although it is straightforward, this traditional approach has several weaknesses in single-molecule work. Practically achievable photon rates may not be high, forcing us into a dilemma: We must either take Δt to be large, compromising temporal resolution, or small, giving few photons in each bin. In the former case, most changepoints will lie in the middle of a bin, smearing out the transitions; we may even miss some transitions altogether if a state is too short-lived. In the latter case, ordinary Poisson fluctuations in photon counts become large enough to obliterate some transitions between states with similar rates and conversely can create apparent transitions where none took place.

Figure 15.1 illustrates the issues. The plot in panel (A) shows some simulated data, which could represent the estimated photon emission rate of a single-molecule photobleaching event. Clearly, there is a changepoint, but we cannot manually identify its time to very good accuracy, nor can we identify the rates themselves very well. Section 1.3 gives an improved approach to this same data, and Section 1.4 explains how to convert this observation into a useful statistic.

1.3. Improved approach: Heuristic

Clearly, the dilemma described in Section 1.2 rests with the random character of photon emission; the rates r found in each time bin are just sample average rates. Nevertheless, if we index the photons by sequence number m and plot their arrival times versus m, we should get a bumpy line that eventually shows a well-defined slope 1/r. Changepoints should then appear as kinks in that line. The curve in Fig. 15.1B shows that indeed the very same data used to obtain panel (A) now display a visible kink at a well-defined time. The difference in time resolution between Fig. 15.1A and B arises because in the traditional method, we coarsen our data by binning, whereas in the improved method, every photon’s precise arrival time is retained. Figure 15.1E and F shows the same phenomenon with real experimental data.

One could simply take a time series with many changepoints and visually identify kinks in a graph-like Fig. 15.1B by laying a ruler along straight stretches in the graph. In practice, we would prefer a method that is both more automatic and more objective than that; the rest of this chapter will develop such a method. It may be tempting to modify the visual method by attempting a least-squares fit of Fig. 15.1B to a piecewise linear function, but least-squares rests on assumptions about the statistical character of data that are not met in this context. Section 1.4 and later sections will instead proceed from a more fundamental, maximum-likelihood approach.

As mentioned earlier, we would also like to generalize changepoint analysis to handle situations where several distinct streams of photons are observed, and each macromolecular state a is characterized by the set (r₁, r₂, …, r_np). In our application, each observed photon is tagged by its polarization and by the polarization of the incident radiation that gave rise to it. For example, the data shown in Fig. 15.1E and F include separate traces for two of the subpopula-tions in a particular experiment. (Other photon subpopulations were not displayed because they were not as sensitive to the particular conformational change occurring at this time.) Section 2.2 will pursue this generalization.

Despite the mathematical complexity of the discussion to follow, we wish to emphasize the underlying simplicity of the method: The almost trivial replotting of data in Fig. 15.1B already contains the heart of changepoint detection.

1.4. Simple derivation of changepoint statistic

The single-channel case for detecting changepoints in single-photon counting (SPC) data was developed by Watkins and Yang (2005), who applied it to single-molecule FRET recordings (Watkins and Yang, 2006). This section gives a simple derivation of their key formula.

We can think of successive observations by discretizing time into small slices δt. δt will be sent to zero in the following discussion; it will not enter our final formulas. It is not a time-binning parameter, because we do not lump groups of photons into batches. We then imagine recording (photon)/(no photon) in each slice. This binary random variable is supposed to be distributed as a Bernoulli trial with probability rδt to observe a photon, and (in the limit δt → 0), zero probability to find more than one. If we observe over total time T, we then wish to compare the hypotheses: (H0) Uniform photon emission rate r₀ throughout all T/δt time slices; (H1) Uniform rate r until time τ, then uniform rate r′ thereafter; etc.

Consider first hypothesis (H0) (actually a one-parameter family of hypotheses). Suppose that photons have been observed at times t₁ < … < t_N, all between 0 and T. From this information, we would like to identify the best estimate of the rate r₀. To do so, we calculate and maximize a “log likelihood function” 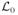(r₀), defined as the logarithm of the probability that the observed photon times would have been observed, had the hypothesis (H0; r₀) been true:

$${\mathcal{L}}_0(r_0)=lnP(t_1,\dots ,t_N\mid r_0)=\sum _{k=1}^{T/\delta t}ln\{\begin{array}{ll}{r}_0\delta t,\hfill & \text{if}\text{a}\text{photon}\text{in}\text{this}\text{slice},\hfill \\ (1-r_0\delta t),\hfill & \text{otherwise}.\hfill \end{array}$$ (15.1)

Taking the limit δt → 0 gives 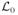(r₀) = N ln(r₀δt) − r₀T. (Exponentiating this formula for 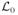, integrating over the allowed range of t’s, and summing over N confirms that the corresponding probability distribution is properly normalized.) Maximizing over the rate r₀ then gives the optimal choice N/T, as could have been expected.

We can now see why the slope of the cumulative photon distribution (Fig. 15.1B and F) tells us a rate, and hence why the heuristic method of Section 1.3 works: The slope in any region not containing a changepoint is just T/N, the reciprocal of the optimal choice just found for the rate r₀.

Turning now to hypothesis (H1), we would like to identify the best estimates of its three parameters r, r′, and τ. For any choice of τ, partition the observed photons into m that arrive prior to τ and m′ = N − m that arrive later than τ. The same steps as before now give

$${\mathcal{L}}_1(r,r^{\prime },\tau )=\mathit{m}lnr+m^{\prime }ln{r}^{\prime }+Nln(\delta t)-r\tau -r^{\prime }(T-\tau ).$$

Maximizing over r and r′ gives r = m/τ, r′ = m′/(T − τ), and so

$${\mathcal{L}}_{1,\mathit{max}}(\tau )=mln(m/\tau )+m^{\prime }ln(m^{\prime }/(T-\tau ))+N(-1+ln\delta t).$$

Our best estimate of the changepoint time is the value of τ that maximizes this quantity (recall that m and m′ are themselves functions of τ).

We can get a more meaningful statistic by computing the ratio of likelihoods for the no- and one-changepoint hypotheses, or equivalently, the difference of log-likelihoods 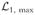(τ) − 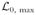, which we will simply call 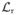(τ):

$${\mathcal{L}}_{\text{r}}(\tau )=mln(m/\tau )+m^{\prime }ln(m^{\prime }/(T-\tau ))-Nln(N/T).$$ (15.2)

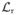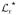The divergent constant ln(δt) has dropped out of this expression. Watkins and Yang obtained Eq. (15.2), following different reasoning from that given here (Eq. (15.4); Watkins and Yang, 2005). Instead of expressing as a function of time, we may equally well regard it as a function of the photon sequence number of the proposed changepoint m, and write . Let denote the absolute maximum of 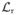overtime (or m).

1.5. Why read this article?

To illustrate the power of this approach, Fig. 15.1C shows the log likelihood ratio function for the same dataset that was used to generate panels (A and B). (A similar plot appears when the method is applied to the experimental data in Fig. 15.1E; not shown.) The graph shows that, at least for changepoints located well away from the starting and ending times, the statistic not only precisely identifies the true changepoint, but also does not identify any other (false) changepoints, provided enough photons have been collected. In fact, the uncertainty in the changepoint, determined from those photons with ≥ 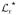− 2, is ±2 photons and encloses the known location of the changepoint (Fig. 15.1C inset). Unlike the traditional approach, no artificial time base due to binning is imposed on the data, and there is no need for user adjustable thresholds that separate the rate trace into supposedly different regions. As a result, different rate regions of the data are determined in a model-independent way; afterward, the photon emission rates in these regions can be used to determine the orientation of each macromolecular state.

Figure 15.2 illustrates the benefit of our improved analysis in the context of polTIRF studies of myosin V; see Section 2.1. In the figure, the dots represent orientations determined by the traditional method by binning the data into 80 ms intervals (Forkey et al., 2005). Although they generally cluster around the results of our method (horizontal lines), the latter is cleaner and eliminates the spurious outlier points that the traditional analysis generates close to changepoints (Section 1.2).

The simple derivation given in Section 1.4 has not yet fully addressed the question of distinguishing hypothesis (H0) from (H1). That is, assuming a single changepoint exists, we found the best estimate of its time, but still have not answered the question of whether in fact any changepoint is present. After all, will always have some maximum; how large a peak is enough to declare a changepoint? Section 3 will discuss this point.

2. Multiple Channels

2.1. Introduction to polTIRF method

Space does not allow a full review of the polTIRF method. For our purposes, however, a simple characterization is sufficient (for details, see Beausang et al., 2008; Forkey et al., 2000, 2003, 2005; Quinlan et al., 2005; Rosenberg et al., 2005).

Most fluorescent molecules absorb and emit light via dipole transitions. Thus, a fluorophore’s dipole moment is a director (headless vector), anchored to a body-fixed frame of reference; overall rotation of the molecule changes the dipole moment’s orientation in space, and hence its ability to be excited by various incident polarizations, and also its propensity to emit photons of various polarizations. Classic early applications to single molecules include Ha et al. (1996,1998) and Sase et al. (1997).

TIRF excites only those fluorophores located within 100 nm or so of a chamber’s boundary by setting up an evanescent wave that penetrates only that far into the chamber. This evanescent wave has a polarization related to that of the propagating wave that created it. Thus, by scanning over several incident beam directions and polarizations (typically 4 or 8), the experimenter sequentially changes the illuminating beam’s character. By means of a timing signal synchronized to the switching optics, each emitted fluorescence photon can be tagged with the illuminating beam polarization that created it. Such SPC techniques have recently begun to enter molecular biophysics (e.g., in Gopich and Szabo, 2009; Hinze and Basché, 2010; Talaga, 2009; Yang and Xie, 2002).

Moreover, by sending the emitted photon beam through a polarization splitter prior to detection, experiments can further subdivide them, for a total of n_p = 8 or 16 polarization channels (photon types), each with its own emission rate. The collection of all these rates, modulo an overall rescaling, can be computed as a function of the fluorophore’s spatial orientation by using Fermi’s Golden Rule. Conversely, if we measure all these rates, we can use a maximum likelihood analysis to identify our best estimate of that orientation (Forkey et al., 2000, 2005).

The above discussion assumed that only one fluorophore is illuminated at a time, and also that the fluorophore is rigidly anchored. In reality, of course, everything in the nanometer world undergoes thermal motion. In fact, a fluorophore anchored to an enzyme may have differing amounts of thermal motion at different steps in the kinetic cycle, revealing changes in the mobility of the probe or of the protein to which it is attached. Thus, the goal of polTIRF is to deduce both the mean of the fluorophore orientation and its variance (“wobble”), as functions of time, from records of photon arrivals (Forkey et al., 2000, 2005).

2.2. Multiple-channel changepoint analysis

The previous section motivated the study of multiple streams of distinct photons. (FRET experiments also involve photon streams with two distinct colors. Xu et al. (2008) developed a correlation analysis for finding simultaneous changepoints in two FRET intensities, different from the one implemented here.)

We thus suppose that each photon is tagged with an index μ running from 1 to n_p. Our experimental data then consist of pairs (t₁, μ₁), …, (t_N, μ_N). Let the total number of photons of type μ be N_μ, so ${\mathrm{\sum }}_{\mu =1}^{n_P}$, N_μ = N.

Hypothesis (H0) now involves a set of n_p photon emission rates {r_0,μ}, and Eq. (15.1) becomes

$${\mathcal{L}}_0(r_{0,\mu })=\sum _{\mu =1}^{n_p}{N}_{\mu }ln\left[(r_{0,\mu }\delta t)-r_{0,\mu }T\right].$$

We optimize over each rate as before to obtain 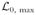. Similarly, generalizing the one-changepoint log likelihood, and subtracting, gives the analog of Eq. (15.2):

$${\mathcal{L}}_r(\tau )=\sum _{\mu =1}^{n_p}[m_{\mu }ln(m_{\mu }/\tau )+{m^{\prime }}_{\mu }ln({m^{\prime }}_{\mu }/(T-\tau ))-N_{\mu }ln(N_{\mu }/T)],$$

where m_μ is the number of photons of type μ detected prior to the proposed changepoint and m′_μ = N_μ − m_μ; thus, Σ_μm_μ = m. As before, we will often regard 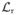as a function of the sequence number m (not time τ) of a proposed changepoint. (Thus, each of the m_μ and m′_μ is a function of m.) Rearranging gives our key formula:

$${\mathcal{L}}_{\text{r}m}=\left[\sum _{\mu =1}^{n_p}(m_{\mu }ln(m_{\mu }/N_{\mu })+{m^{\prime }}_{\mu }ln({m^{\prime }}_{\mu }/N_{\mu }))\right]-[mln(t_m/T)+m^{\prime }ln(1-t_m/T)].$$ (15.3)

The peaks of identify potential changepoints in multiple-channel data.

The two pieces of information recorded in polTIRF experiments can be viewed as separate contributions to Eq. (15.3): The time stamp information reports on the overall emission rate of the fluorophore and is contained in the second term, which depends only on the arrival time of each photon and not its polarization. The polarization information, which consists of a tag μ = 1, 2, …, n_p for each photon, is contained in the first term.

3. Detailed Analysis

An earlier section raised the issue of false positives, which we now explore.

3.1. Threshold for false positives detection

Again, let 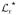denote the absolute maximum of 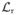overtime (or m). The probability that 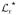is a false positive can be determined from the distribution of 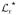values when no changepoint is present. A threshold for false positives can be defined such that for example, 95% of the 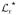are below the threshold and correctly report no change. In data where the presence of a changepoint is unknown, 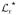that exceed the threshold are taken to be valid changepoints with 95% confidence. Letting α denote the fraction of acceptable false positives, then the desired threshold ρ⁰ is set by requiring that

$$\text{Prob}({\mathcal{L}}_{\text{r}m}>{\rho }_{\alpha }^0\text{for}\text{any}m)=\alpha .$$ (15.4)

Note that the threshold does not depend on the absolute rate of photon emission, but it does depend on the total number of photons in the interval as expected because Eq. (15.2) increases with increasing N.

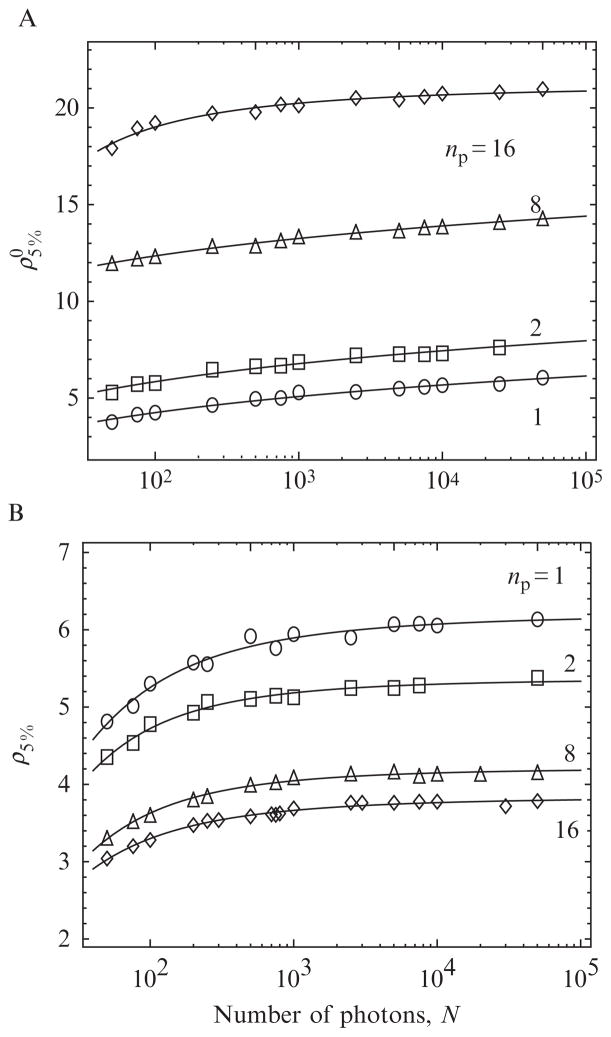
Remarkably, Eq. (15.4) can be computed exactly for the single-channel case by using an algorithm developed by Noé (1972). The threshold is then found by solving Eq. (15.4) for the threshold that yields the desired α. The dependence of the threshold on N is found by repeating the calculations over the range of photon counts that will be encountered experimentally (Owen, 1995; Watkins and Yang, 2005). The threshold is also easy to compute via simulations, which will be necessary in multiple-channel data because Noé’s algorithm only applies to the one-channel case. Thresholds corresponding to α = 0.05 were simulated (see Section 4.1.2) over a wide range of N and fit to a power law function (see Table 15.1) for use in the changepoint algorithm (see n_p = 1 curve in Fig. 15.3A).

Table 15.1.

Fitting parameters used to determine the 5% false-positive threshold ρ_5% for different numbers of polarization channels n_p using the uncorrected (left columns) likelihood ${\rho }_{5\%}^0(N)=A+B{({log}_{10}N)}^C$ and corrected (right columns) log likelihood

np	A	B	C	a	b	c
1	−85.07	87.91	0.0229	6.207	1.481	−3.029
2	−120.0	124.2	0.0182	5.369	1.360	−3.314
8	−50.25	61.09	0.0352	4.212	1.671	−3.377
16	21.22	8.857	−2.004	3.839	1.338	−3.032

The parameters define the interpolating functions ${\rho }_{5\%}^0=A+B{({log}_{10}N)}^C$ and ρ_5% = a/(1 + b(log₁₀ N)^c).

Figure 15.3.

Values of the threshold ρ for 5% false positive rate (error fraction) for the uncorrected (A) and corrected (B) log likelihood function, as a function of the number N of photons in the interval. The correction procedure is discussed in Section 3.2. The curves for n_p > 1 polarization channels are discussed in Section 3.3.

3.2. Correct for nonuniform distribution of false positives

Even though the technique outlined in Section 3.1 successfully determines the number of false positives, the location of these false positives across the interval is highly nonuniform. The probability of detecting a changepoint is ~10× higher in a region near the boundary of the interval (containing ~1–5% of the total photons) than in the center of the interval. This problem has been addressed for single changepoints, and a two-step solution proposed, by Henderson (1990).

Qualitatively, the phenomenon is not unexpected: For changepoints near the edge of the interval, a random fluctuation in the region with a small number of photons is easily fit with a rate that differs from that estimated in the larger region. As a result, changepoints are more likely to be identified near the boundaries of the interval. This bias arises because photons in the middle of the interval can arrive with a relatively wide distribution of times, all of which are centered about t/T ≈ 0.5, whereas photons near the boundaries of the interval have a relatively narrow distribution of times, either close to zero or close to T. Thus, even when we generate photons in a stationary Poisson process, nevertheless the log likelihood ratio 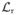is larger on average near the boundaries than in the middle.

In order to correct for this effect, the distribution of at each m is normalized so that it has zero mean and unit standard deviation. This is accomplished by subtracting the mean of the log likelihood ratio, E[ ], and dividing by its standard deviation σ_m at each value of m:

$${\overline{\mathcal{L}}}_{\text{r}m}=\frac{{\mathcal{L}}_{\text{r}m}-E[{\mathcal{L}}_{\text{r}m}]}{{\sigma }_m}.$$ (15.5)

If the initial distributions of at each m were different size Gaussian distributions, then the fraction of false positives would now be uniform across the interval. Actually, however, the are beta-distributed random variables (Henderson, 1990); thus, renormalization alone is not sufficient. An additional weighting function W_m = 0.5 ln (4m(N − m)/N²) is applied to further penalize the likelihoods near the edge of the interval, resulting in the final form of the corrected log likelihood function :

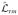$${\widehat{\mathcal{L}}}_{\text{r}m}={\overline{\mathcal{L}}}_{\text{r}m}+W_m=\frac{{\mathcal{L}}_{\text{r}m}-E[{\mathcal{L}}_{\text{r}m}]}{{\sigma }_m}+W_m.$$ (15.6)

For the single-channel case, the E[ ] and σ_m can be evaluated analytically (Henderson, 1990), and thus, the threshold for false positives (using Eq. (15.4) with ρ_α in place of ρ_α⁰) can still be calculated using Noé’s algorithm (Watkins and Yang, 2005). These analytic solutions, however, are not readily extended to multiple channels and so are not repeated here. As will be discussed in Section 4, the E[ ] and σ_m can be obtained from simulations for any number of channels. Determining these correction factors requires numerous simulations over the desired range of photons N and a number of polarization channels n_p (see Section 4.1.1), but they only need to be performed once, tabulated, and then the results referenced by the algorithm.

3.3. False positives, multiple-channel case

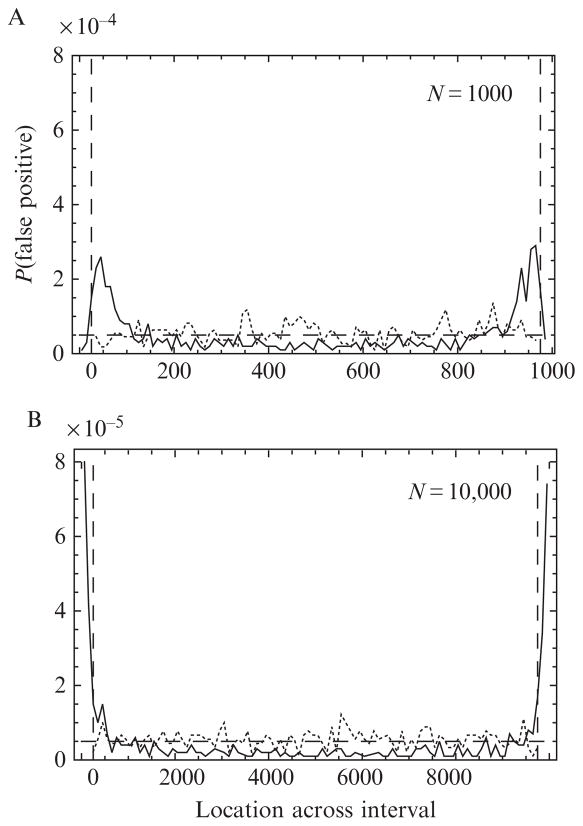
As with the single-channel case, for the multiple-channel case also suffers from a nonuniform distribution of false positives, which is corrected for in the same way as in Section 3.2. This time the simulations start with a fixed overall number of photons N, then partition it randomly into the counts N_μ in each channel, distribute each N_μ randomly within the time interval, evaluate the changepoint likelihood function, and repeat. The resulting correction factors and weighting function are different from the single-channel case and remove most of the bias, except for a small peak very close to the boundary. In order to avoid this residual bias, we estimated the width of the peak and arranged for the MCCP algorithm to accept only those changepoints that occur within the center 95% of the interval. That is, changepoints are neglected if they occur within a buffer region of 0.025 N photons on either end of the interval (see, e.g., Fig. 15.4 vertical-dashed lines for the n_p = 16 channel case).

Figure 15.4.

The solid curve shows the distribution of false positives for n_p = 16 polarization channels across the interval for uncorrected log likelihoods ; it is strongly peaked near the edge of the interval, then decays slowly to a minimum at the center. The distribution becomes increasingly peaked as N is increased from N = 1000 (panel A) to 10,000 (panel B). The fraction of the total probability lying within the first and last 5% of each interval is 30% and 60% (instead of 10%) for N = 1000 and 10,000, respectively. Applying the correction factors (see Eq. (15.6)) to the log likelihood and excluding 2.5% of the photons from near the edges (vertical-dashed lines, see Section 4.1.1) result in a nearly uniform distribution of false positives (dotted curve). For comparison, a uniform distribution with total false positive rate 5% would look like the horizontal-dashed line.

The procedure for locating the peak, finding its confidence interval, and testing for its significance is the same as for the single-channel case, except that a new threshold for false positives must be computed for multiple channels. As mentioned in Section 3.1, the threshold for false positive detection depends on N, but it also depends on the number of polarization channels n_p among which the photons are divided. The new threshold values with the correction factors E[ ] and σ_m, are determined from simulations similar to the single-channel case but with the photons divided among the different polarization channels. The details of the simulations will be discussed in Section 4.1.2, but the thresholds for n_p = 1, 2, 8, and 16 polarization channels and α = 0.05 are shown in Fig. 15.3. We summarized the simulated values with interpolating functions of the form ${\rho }_{5\%}^0=A+B{({log}_{10}N)}^C$ for the uncorrected likelihoods and ρ_5% = a/(1 + b(log₁₀N)^c) for the corrected likelihoods; see Table 15.1 for the values of the best-fit parameters.

3.4. Automated, multiple-channel changepoint detection algorithm

In experimental data (Beausang et al., 2008; Forkey et al., 2003), a processive myosin V molecule is recorded for multiple steps and consequently multiple changes in orientation of the attached fluorophore are contained within the data, not just a single changepoint as has been discussed so far. One way to proceed would be to let q be the number of changepoints and test hypothesis (Hq; τ₁, …, τ_q; r, r′,…) for all possible values of its parameters. This quickly becomes impractical, however, as q grows large.

Fortunately, we can apply our method iteratively to the entire data set (Watkins and Yang, 2005), even though the assumption of constant photon emission rates on either side of any given changepoint is clearly not true. After the changepoints are found in this rough manner, they are optimized one at a time in order to eliminate the influence of neighboring change-points. More precisely:

1. For a single recording, which includes N photons, n_p polarization channels and multiple changepoints, the MCCP algorithm is applied as follows: (a) Calculate for each photon m in the interval, using Eq. (15.3); (b) Apply the correction and weighting factors E[ ], σ_m, and W_m to each value of to obtain the corrected log likelihood function for each photon in the interval 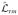; (c) Within the interval 0.025–0.0975N, find the most likely changepoint as the location m^★ of the likelihood peak; (d) Test the candidate changepoint for significance by comparing it with the false-positive threshold $\left({\widehat{\mathcal{L}}}_{\text{r}}^{\ast }>{\rho }_{\alpha }\right)$; (e) If the peak exceeds the threshold, record its location as a changepoint.

2. On the next iteration, only those photons occurring prior to the peak m^★ just found are analyzed, and the location of the largest peak above the threshold is again determined. Similarly, the largest peak in the region between m^★ and the end of the data set is also found. This process is repeated on each subregion of the data, creating a list of candidate changepoints, until no more peaks exceed their respective thresholds.

3. The location of each candidate changepoint is reevaluated over just the range limited by its nearest neighbors. More precisely: (a) Confidence intervals are determined for each changepoint time as those photon sequence numbers with log likelihoods greater than ${\widehat{\mathcal{L}}}_{\text{r}}^{\ast }-2$; (b) Each changepoint time is reevaluated using only the region that starts at the upper confidence limit of the preceding changepoint and ends at the lower confidence limit of the succeeding one. If the changepoint no longer exceeds the significance threshold over this reduced range, then the region is combined with its neighbor and then that neighbor is evaluated. Regions containing fewer than 50 photons are not expected to yield reliable rate information and so are always combined with the neighboring region.

4. After refining the location of each changepoint, the intervals between all adjacent changepoints are tested for any additional changepoints.

5. Steps 2–4 are repeated four times to optimize the location and number of changepoints.

After the changepoints are determined, the photon rates in each interval are used to estimate the maximum likelihood orientation and wobble of the fluorophore, as outlined in Section 2.1. In order to assess the sensitivity of the inferred orientation to the precise location of the changepoint, four additional sets of rates are determined for each interval by using the edges of the confidence intervals as the boundary instead of the changepoint. For example, consider two changepoints at sequence numbers m_i^★ and $m_{i+1}^{\ast }$ with confidence intervals (m_i⁻, m_i⁺), etc. Five sets of orientations are then determined for the ith interval by using the five ranges:

$$(m_i^{\ast },m_{i+1}^{\ast }),(m_i^{-},m_{i+1}^{-}),(m_i^{-},m_{i+1}^{-}),(m_i^{+},m_{i+1}^{-}),(m_i^{+},m_{i+1}^{+}).$$

The five corresponding inferred orientations give us an estimate of the uncertainty of our determination; see Fig. 15.2.

3.5. Critique of multiple-channel changepoint algorithm

The MCCP algorithm makes several simplifying assumptions that will be elaborated here before discussing the simulations.

For single-molecule experiments, the time between photons due to the rate of the fluorophore emission provides an absolute limit on the achievable time resolution. Typical count rates are 20–50 photons/ms.

The statistical model that underlies the multiple-channel log likelihood function (Eq. (15.3)) assumes that photons in each polarization channel are emitted independent of one another and detected simultaneously. In practice, however, polTIRF experiments alternately illuminate the sample so that only one excitation polarization state is active at a time. Artifacts may arise if the molecule moves on time scales comparable to the polarization switching time, but this is not typically the case for biological macromolecules and >10 kHz cycling frequencies.

The threshold for false positives is clearly a crucial parameter, as it determines the validity of a particular changepoint. An advantage of the changepoint analysis is that this threshold is not a user-defined value, but is instead determined by the desired limit α on false positives. The analytic method used to calculate the single-changepoint threshold is not readily applied to multiple photon channels, but we found it was easy to instead find the threshold by using computer simulations. Furthermore, the threshold is a smooth function of the number of photons in the interval (Fig. 15.3), so only a few values of N need to be calculated and the rest can be obtained from an equation fit to the simulations.

In the multiple-channel case, our assumption in Section 3.3 that the photon rates were randomly chosen deserves discussion. For applications to polTIRF experiments, a better assumption might be that the photons are randomly distributed among the channels with an average that is consistent with an isotropic distribution of fluorophores. Because the log likelihood function (Eq. (15.3)) depends on the number of photons in each channel, the false-positive threshold in these two scenarios would not be the same. Distribution of the photons equally in the different channels, however, results in the largest magnitude likelihood (on average), and so, the threshold determined in this way is a conservative estimate of whether or not a false positive occurred. Also, assuming an equal distribution of photons is advantageous because it is independent of the model used to represent the molecule’s fluorescence emission and detection.

The weighting function W, and the 2.5% buffer zone used to remove the remaining bias, are easy to apply to the changepoint analysis with minimal additional computation. The origin of the weighting function appears to be somewhat ad hoc (Henderson, 1990); however, it is effective (Fig. 15.4) and has been used by other groups (Watkins and Yang, 2005). A key feature of the weighting function is that although it suppresses detection of changepoints near the edge of the interval, still it does not preclude them entirely; a legitimate changepoint will be detected if its likelihood is large enough. The additional buffer zone on either end of the interval, however, precludes the detection of changepoints in this small region. Short-duration events that precede or follow a long-duration event may be missed, but in typical experiments, events longer than 10,000 photons are not common, and the resulting dead time equivalent of 250 photons is near the limit of detection in our application. In cases where this trade-off is not desirable, the MCCP algorithm would be useful for identifying the long-duration dwells, which could then be subjected to a local analysis at the two ends to test for additional changepoints.

Estimating the 95% confidence intervals from the log likelihood surface is a common statistical practice (Bevington and Robinson, 2003; Edwards, 1972); however, more rigorous confidence intervals can also be defined (Watkins and Yang, 2005). For example, all photons adjacent to a change-point for which hypothesis (H1) is at least 5% likely to be true would be included in the 95% confidence interval. In the single-channel case, Watkins and Yang (2005) found that the fraction of changepoints that fell within the confidence interval depended on the magnitude of the change-point. Simulations to determine the confidence interval in the multiple-channel case would be more expensive than those used to determine the false positive threshold, because both the magnitude of the changepoint and the number of photons in the interval would need to be varied. Given these limitations, simply estimating the 95% confidence interval from −2 offset on the log likelihood surface (i.e., all photons i with ${\widehat{\mathcal{L}}}_{\text{r}m}\ge {\widehat{\mathcal{L}}}_{\text{r}}^{\ast }-2$) is a practical compromise.

In single-molecule polTIRF experiments, changepoints are expected to occur when the probe changes orientation, but changepoints will also be detected when the total photon rate changes magnitude, similar to the scenario in single-channel changepoint analysis. Typically, genuine reorientations incur little change in the total photon rate, but fluctuations in the total rate do occur. For example, the changepoint algorithm easily detects the step decrease in rate when the single-molecule bleaches to background, as well as the occasional double bleach and blinking events where the fluorophore turns off and then back on again.

4. Simulation Results

Three types of simulations were performed to test the algorithm: (1) No-changepoint simulations tested the null hypothesis (H0) and were used to determine the correction factors E[ ] and σ_m and the threshold for false positives; (2) Single-changepoint simulations assessed the false negative rate of the algorithm over a range of changepoint magnitudes and duration; (3) Double-changepoint simulations of a large transition followed by a short-lived state with a second transition tests the algorithm’s sensitivity to detect substeps within the myosin V cycle. The various photon rates for a simulation are generated either arbitrarily to give intuition on the detection algorithm or by calculating the polarized fluorescent photon rates that correspond to actual fluorophore orientations using a simple model of the probe (Section 2.1).

Our simulations of the MCCP analysis rely on generating a specified number of interphoton arrival times from an exponential distribution. Each photon is randomly assigned to one of the independent polarization channels (usually n_p = 8 or 16, which correspond to the typical number of channels in experimental data) with a probability that is weighted according to its relative rate. For example, if the probe model assigns rate κ to six polarization channels, and rate 2κ to the remaining two, then the photon arrival times are generated with κ_tot = 10κ, and each photon is randomly assigned to one of the six low-rate polarization channels with probability 0.1 and to one of the two high-rate channels with probability 0.2. This two-step process ensures that the total rate is constant and that each of the individual polarization channels has the proper relative rate with exponentially distributed arrival times.

A changepoint is introduced after the mth photon by using one set of weights from 1, …, m and second set of weights from (m + 1), …, N. The MCCP algorithm (Section 3.4) is then applied to the simulated data, and any statistically significant changepoints are recorded. This process is repeated, typically 500–10,000 times depending on the simulation, to minimize statistical fluctuations.

4.1. No-changepoint simulations

The peak log likelihood ${\widehat{\mathcal{L}}}_{\text{r}}^{\ast }$ calculated from Eqs. (15.3) and (15.6) must exceed a threshold to be considered a valid changepoint (with false positive rate α). The threshold is determined from simulations over a range of photons N and polarization channels n_p for α = 0.05.

4.1.1. Correction factors

As discussed in Section 3.2, the distribution of peak log likelihoods simulated under conditions of the null hypothesis (i.e., no changepoint) is not uniform across the interval and results in a bias for detecting false-positive changepoints preferentially near the boundaries of the search inter-val. The distribution of can be empirically determined by repeatedly applying Eq. (15.3) to a constant rate simulation. The mean and standard deviation of 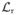at each point across the interval are then used to normalize the likelihood. The process is repeated over a range of N to generate a lookup table for the two correction factors. Values of N not in the lookup table are linearly interpolated between the two nearest values. Determining the correction factors from simulations is computationally expensive, but can be performed on a PC in a few days. Also, it is a one-time cost that can be referenced by the algorithm in a look-up table.

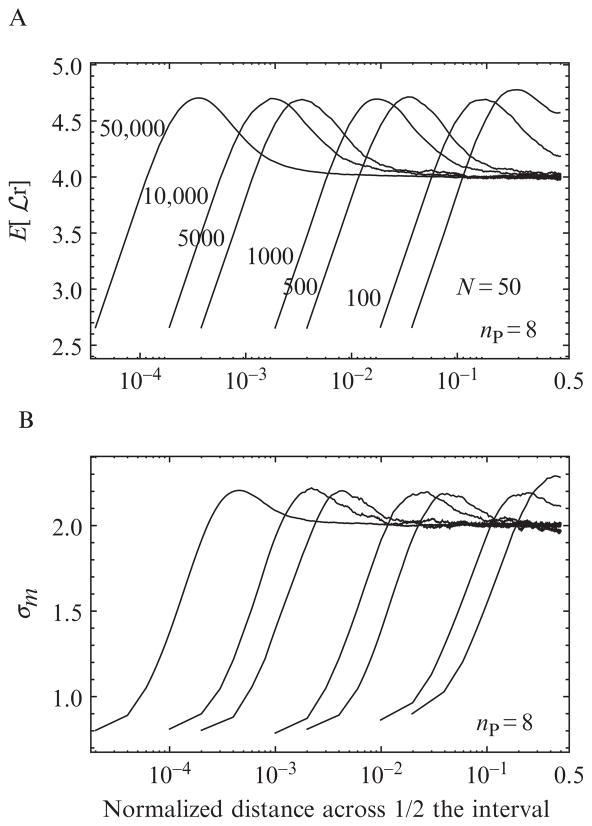
The resulting correction factors E[ ] and σ_m for various N follow similar trends across the interval as N is increased (Fig. 15.5). In order to compare simulations with different numbers of photons on the same graph, the photon index m is normalized by the total number x = m/N and plotted on a logarithmic scale to emphasize the region close to the boundary of the interval. Because the correction factors are symmetric about x = 0.5, the counting statistics are improved twofold by superimposing the results from the two halves of the interval. As the number of polarization channels increases from 8 to 16 (data not shown), the magnitude of both E[ 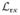] and σ_x increase, as expected since the number of ln terms in Eq. (15.3) doubles. When N is 500, all of the correction factors show a plateau in the center of the interval that increases as the edge of the interval is approached and then falls abruptly immediately at the edge. The increase in both the mean and the standard deviation near the edge of the interval reflects the observed increase in the fraction of false positives. Unlike the correction factors for changepoints with multiple photon channels, the correction factors in the single-channel case (not shown) increase monotonically at the edge of the boundary. The reason that the multiple-channel correction factors experience a sharp decrease immediately at the boundary is that the magnitude of the 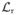depends on the number of terms in Eq. (15.3) that contribute to the sum. If enough photons are present in each region (before and after a changepoint), then every term can contribute to the sum. But, as the algorithm tests points that are closer to the boundary, eventually the number of photons in some of the polarization channels will drop to zero, and the corresponding terms will drop out and lower 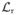proportionally (because 0 ln 0 = 0).

Figure 15.5.

MCCP correction factors for (A) the expected value E[ 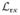] and (B) the standard deviation σ_x of the log likelihood function 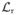(Eq. (15.3)) for N = {50, 100, 500, 1000, 5000, 50,000} and n_p = 8. The horizontal axis x = m/N indicates the position of the mth photon across the interval normalized to the total number of photons. Only half the distribution is shown; the correction factors are symmetric about x = 0.5. These functions are needed to evaluate the correction given in Eq. (15.5).

The final result, including the correction factors, weighting function and buffer, is a uniform distribution of false positives, at least in the range considered here (N = 50–50,000 and n_p = 8) (Fig. 15.4 dotted curves).

4.1.2. False-positive threshold

We found the threshold for false positives from a set of constant rate simulations similar to the ones just described. Instead of recording the first and second moments of 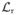, however, the peak log likelihood ${\widehat{\mathcal{L}}}_{\text{r}}^{\ast }$ and its location m^★ is recorded for each of the M simulations. This list of ${\widehat{\mathcal{L}}}_{\text{r}}^{\ast }$ is sorted and the value that separates the largest Mα from the remaining M (1 − α) is the desired threshold. The functional dependence on N is obtained by repeating the calculation over a range. Because actual data can have any value of N, the simulated values of ρ are fit to the interpolating function ρ_α = a/(1 + b(log₁₀N)^c) to determine a, b, and c. Finally, the entire process is repeated for different numbers of polarization channels. The results for n_p = 1, 2, 8, 16 are shown in Fig. 15.3B, and the corresponding values of a, b, and c for each fit are summarized in Table 15.1. All thresholds used here correspond to a 5% false positive rate (α = 0.05).

For comparison, we used the same set of simulations to determine the threshold for the uncorrected log likelihood function 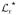(see Fig. 15.3A).

4.2. Single-changepoint simulations

4.2.1. Power to detect arbitrary rate change

A low false positive rate is important for confidence in the results; however, a low fraction of false negatives (i.e., the power of a test) is also crucial in order to detect a majority of the changepoints.

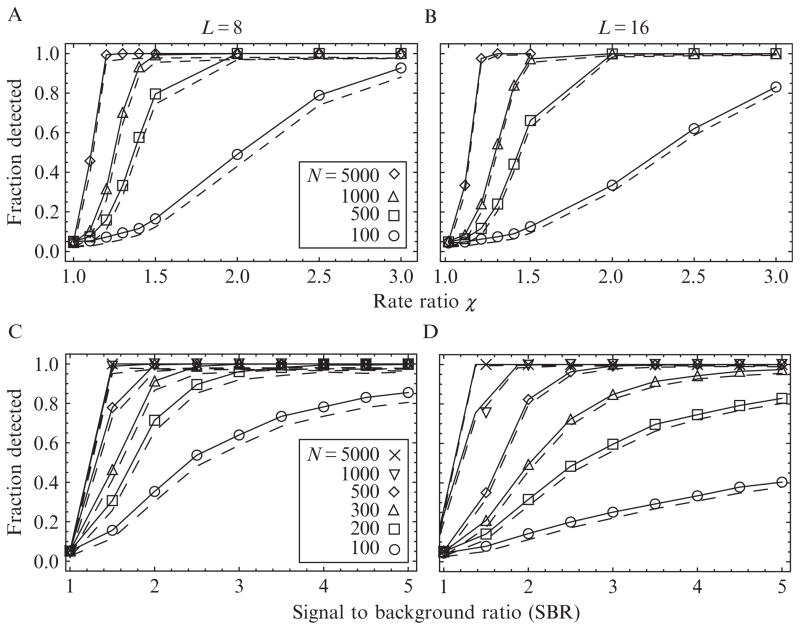
The power of the MCCP algorithm is determined from simulations performed with n_p = 8 and 16 polarization channels for various total photon counts N and rate change magnitudes χ = max(r′/r, r/r′). The photon rates were not based on any assumed orientation of the probe; half of the rates changed from r to χr and the other half change from χr to r, thus ensuring a constant total rate. The simulation placed the changepoints at the midpoint of the interval (N/2) and the MCCP was successful if the ${\widehat{\mathcal{L}}}_{\text{r}}^{\ast }-2$ confidence interval enclosed the true location.

We ran simulations over a range of changepoint magnitudes χ and photon counts N, for n_p = 8 (Fig. 15.6A) and n_p = 16 (Fig. 15.6B). Five thousand simulations for each combination of {N, χ, n_p} were run and the fraction of trials with a changepoint are recorded (solid lines), as well as the fraction of changepoints whose confidence interval includes the true location (dotted lines). As expected, simulations with a large N and χ resulted in a higher fraction of detected changepoints, and larger rate changes required fewer photons to identify the changepoint. At the larger χ and N, nearly 100% of the changepoints are detected. Even though an interval corresponding to the 95% confidence interval was chosen, the actual accuracy of the method exceeded 98% depending on N and χ. The nonzero fraction of detected events at χ = 1 indicates the false positive error rate.

Figure 15.6.

Power of the MCCP algorithm to detect changepoints of different magnitudes, as a function of the number of polarization channels n_p = 8 (A and C) and n_p = 16 (B and D) and the number of photons in the interval. Top row, solid lines, and symbols: The fraction of changepoints detected versus an arbitrary relative photon rate change of χ and various N. Dotted lines: The fraction of changepoints that were detected and assigned a time lying within the ${\widehat{\mathcal{L}}}_{\text{r}}^{\ast }-2$ confidence interval of the true time. The high fraction meeting this condition indicates that these confidence intervals are conservative. Bottom row: The fraction of changepoints detected for an angle change corresponding to the tilting motion of a probe attached to the myosin V lever as it steps (see Table 15.2), as a function of signal-to-background ratios (SBR) for various N.

Increasing the number of polarization channels from 8 to 16 (Fig. 15.6A and C and B and D, respectively) decreases the power of the test slightly due to the increase in the photon counting noise that occurs when N photons are divided into twice as many polarization channels. The sensitivity to additional photon channels is mitigated in the arbitrary rate model used here (Fig. 15.6A vs. B), because all of the rates contribute equally to the change-point. This is not true when the rate change arises from probe reorientations (Fig. 15.6C vs. D), because some of the photon rates respond more strongly to a particular change than others.

4.2.2. Power to detect myosin lever arm change

In order to determine the power of the MCCP in experiments of myosin V stepping, we performed simulations of the probe angle before and after a step using the values in Table 15.2. Instead of an arbitrary rate ratio χ, the simulations were performed by assuming base rates given by a dipole model with specified angles (Table 15.2) plus a base rate representing background fluorescence. We varied the background and present results as a function of the signal-to-background ratio (SBR), defined as (rate of fluorophore + rate of background)/(rate of background). Otherwise, the simulation conditions were similar to those in Section 4.2.1.

Table 15.2.

Orientation and wobble (δ) used in the simulations of myosin V stepping (see Section 2.1)

State	{θ, φ}	{β, α}	δ
Prestep	{96.7, 168.8}	{20, −20}	40
Detached head	–	–	90
Poststep	{18.9, 23.3}	{80, −85}	40

The orientations are represented in polar coordinates, in the microscope (θ, φ) and actin (β, α) frames. That is, β is the polar angle of the probe with respect to the actin filament and α is the azimuthal angle around the filaments, where α = 0 is parallel to the microscope stage and α = 90 is parallel to the optical axis of the microscope. All angles are in degrees.

As in the arbitrary rate case (Section 4.2.1), the power of the algorithm to detect changepoints increases with increasing SBR and the number of photons (Fig. 15.6). The reduction in sensitivity when the number of polarization channels is increased from n_p = 8 (Fig. 15.6C) to 16 (Fig. 15.6D) is larger than in the arbitrary rate case, because some of the additional polarization channels are not sensitive to the angle change yet still “steal” a fraction of the total number of photons from the other channels. Experiments with SBRs of 3 require ~200 and ~400 photons for ~90% detection in the 8 and 16 channel configurations, respectively. If the fluorophore emits photons at rate ~30 ms⁻¹, then the corresponding time resolution in the two cases would be 7–10 ms and 13–25 ms. The shortest-duration detectable events will be tested directly in Section 4.3.

4.3. Two-changepoint detection

Substeps in the myosin V ATPase cycle are predicted to occur in a short period of time immediately before or after a step is taken; that is, a second changepoint adjacent to the large one that accompanies the tilting motion of a step. We ran simulations to determine the sensitivity of the MCCP algorithm to detecting these short-lived states over a range of photon counts in the transient state, N_t = 1 − 1000, and various SBRs.

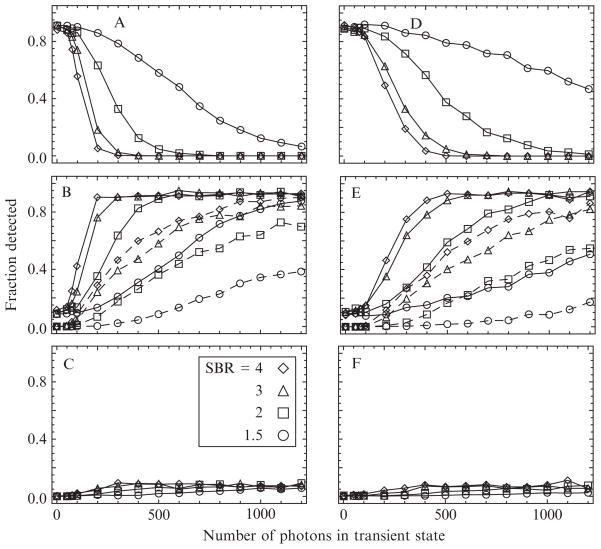
The simulation consists of a long-lived state with a well-defined orientation, followed by a short-lived state with large wobble (no well-defined orientation), and ends in a long-lived state also with a well-defined orientation. Specifically, the angles from Table 15.2 are used to represent a myosin in the (prestep)/(detached head)/(poststep) configurations. The number of photons in the pre- and poststep states is held fixed at 2000 each, and the number of photons in the transient state is varied. Each combination of N_t and SBR is simulated 500 times, and the fraction of trials resulting in single, double, and triple changepoints is recorded for both 8 (Fig. 15.7A–C) and 16 polarization channels (Fig. 15.7D–F).

Figure 15.7.

The power of the MCCP algorithm to detect short-duration (transient) states in the myosin V ATPase cycle, specifically, the short-lived detached state after the motor head releases from actin but before it steps and rebinds, is determined from photon emission rates simulated using the angles in Table 15.2. Simulations with n_p = 8 (left) and n_p = 16 polarization channels (right) indicate one (top), two (middle), or three (bottom) detected changepoints as the number of photons in the transient state is increased from 0 to 1200 for various SBRs. Requiring that the interval be detected with at least 90% accuracy (dashed curves, middle panels) significantly increases the number of photons needed to identify the state reliably (see text).

The simulation technique was outlined in previous sections. To find the changepoints in each trial, the algorithm is applied three times: first to the entire interval of N_t photons, and if the peak log likelihood exceeds the threshold, the regions to the left and right of the peak are interrogated for changepoints in these shorter regions. In the event that three changepoints are detected, the middle one is reevaluated on the interval between the other two and only retained if its peak exceeds the required threshold.

As the number of photons in the transient state increases, the fraction of trials with single changepoints decreases (Fig. 15.7A and D), while the fraction with two changepoints increases to ~90% (Fig. 15.7B and D). The fraction of trials with a spurious third inferred changepoint is relatively constant at ~10%. When there is no transient state, the fraction of trials with single changepoints is ~90%, indicating an ~10% false positive rate.

If the known locations of the simulated changepoints are used to determine the accuracy of the detected changepoints, then fewer of the trials will be considered successes. For example, if the overlap between the detected and the actual interval of the transition is required to be between 90 and 110%, then two to three times more photons in the transition are required to detect the same fraction of events. If a fluorophore emits ~30 photons/ms, then only 300 photons will be recorded during a 10-ms transient state. If the SBR is assumed to be 3, then ~500 photons are required to detect 50% of the events in the 8-channel configuration, and ~700 photons with 16 polarization channels, approximately twice as many as was required in the single-changepoint simulations.

5. Discussion

5.1. Single photon counting in single-molecule biophysics

The main points of our method are summarized in Section 1. Fluorescence experiments that utilize SPC technology can achieve very high time resolution by recording the arrival time of each detected photon. There is no binning of the raw data (i.e., lumping photons into groups); afterward, the experimentalist can choose any bin size for analysis. This chapter has described an alternative approach that never imposes a bin size on the data and uses the photon arrival times directly. Changepoint detection algorithms meet both of these requirements and are particularly powerful because they do not require any user-defined threshold that separates high and low rate states (Watkins and Yang, 2005). All parameters within the changepoint algorithm are statistically defined once a desired false positive error rate is chosen.

The high time resolution polTIRF experiments discussed in Section 2.1 are an example of fluorescence experiments that implement SPC technology. In addition to recording photon arrival times, a polarization tag is also recorded for each detected photon. In these experiments, most change-points do not involve any change of the overall photon rate; instead, we must find the times when the photon rates change relative to one another. Because of this distinction, we developed a new multiple-channel change-point (MCCP) analysis to analyze high time resolution polTIRF data.

The basic idea of the method is to test whether two adjacent regions of the data are better described by two different photon emission rates or by one constant rate. Because three free parameters m, r, r′ will always fit the data better than one r₀, we defined a threshold consistent with a specified false positive rate that requires the two-rate hypothesis to be significantly better than one rate. If that condition is met, the location in the interval with the largest log likelihood above this threshold is identified as a chan-gepoint. All of the changepoints in the data can be determined by applying this test recursively to the intervals between previously determined changepoints.

In recordings with only one channel, the log likelihood simplifies to just the second term of Eq. (15.3) (Watkins and Yang, 2005); changes in the total photon rate can be located within a few photons of the actual change (see Fig. 15.1). Qualitatively, this precision is consistent with the abrupt change in slope when the arrival times are plotted versus the corresponding sequence numbers (Fig. 15.1B).

In recordings with two photon channels, analogous to FRET or to a simplified polarization measurement, the location of the changepoint is often determined predominantly by the first term in Eq. (15.3), because the total photon rate is often approximately constant (see Fig. 15.1D), although the individual photon rates change abruptly (e.g., Fig. 15.1E). Despite the relative coarseness of the polarization information, change-points can still be accurately identified (Fig. 15.1C).

We noted that the uncorrected log likelihood function Eq. (15.3) has the disadvantage that its magnitude is not uniform across the interval and is higher on average near the boundary, even if no changepoint exists. The peaks in the log likelihood function (and thus the changepoints) are therefore biased near the edge of the interval, especially for large numbers of photons (solid line, Fig. 15.4). Analytical corrections for this effect have been derived (Henderson, 1990) for the single-channel case and successfully applied to fluorescence data (Watkins and Yang, 2005). We found analogous correction factors from simulations for the multiple-channel case and used them in the MCCP algorithm. Modifying the likelihood function using the correction factors, a weighting function, and a narrow exclusion region that prohibits changepoints from occurring within the first and last 2.5% of the data, nearly eliminates the bias across a wide range of photons (dotted lineFig. 15.4). Correcting for this effect is particularly relevant for finding substeps in myosin V polTIRF experiments because the intervals of interest are adjacent to a prominent changepoint—the same region that is sensitive to a false positive.

For intervals with a sufficient number of photons N is 500, the shape of the correction factors across the interval follows a pattern as N is increased. Their average values are relatively constant in the center region, peak near the edge, and then drop precipitously at the boundary. The reason for this drop is that the log likelihood (Eq. (15.3)) is proportional to the number of polarization terms; if there are too few photons in a region, then some of the terms drop out and the log likelihood function decreases. This effect is clearly seen when comparing the distribution of correction factors for various number of polarization channels n_p (not shown), where in the single-channel case, there is no decrease at the edge and it becomes more pronounced as the number of channels increases.

Simulated single changepoints with n_p = 8 and 16 polarization channels were accurately identified over a range of photon counts N and SBR (Fig. 15.6). The number of photons required to detect an event was inversely proportional to the size of the transition, that is, large magnitude changepoints events were easier to detect. Simulations that assume that each of the channels participates equally in the changepoint were used to compare the 8 and 16 polarization channel cases (Fig. 15.6A and B). For a given N and SBR, there is a small reduction in the sensitivity when the number of polarization channels is increased, but often this is a useful trade-off because the orientation of the probe is better defined with 16 polarizations.

The accuracy of our method can be determined by comparing the changepoint with its known location. The confidence limits are expected to enclose the known location for 95% of the trials. The actual accuracy depended on the number of photons and SBR, but was often greater than 98% for most of the conditions (dashed lines, Fig. 15.6).

By using the dipole model for the probe to determine the photon rates (Forkey et al., 2005), instead of distributing the photons according to an arbitrary change χ, we assessed the sensitivity of the analysis for experimental data. Because the experiment entails a single molecule of myosin V translocating along actin, we simulated the orientation of the probe before and after the myosin steps (see Table 15.2). The detection of events improves as the number of photons and the SBR increases (Fig. 15.6C and D); however, the sensitivity decreased when the number of polarization channels was increased from 8 to 16. An optimistic value of the SBR in polTIRF experiments is ~3, indicating that ~200 photons are required to detect 95% of the changepoints in the 8-channel case. This number approximately doubles when the number of channels increases to 16. The reason for this is that only a few channels are sensitive to the orientation change; thus, the number of photons contributing to the changepoint can be fewer than expected based on the SBR. For example, a probe that rotates 90° from being aligned along the x-axis to the z-axis would be obvious if the polarizations were aligned along those two directions, but would be invisible to polarizations aligned at 45° to those directions.

Figure 15.2 shows another way to underscore the usefulness of the method: Changepoint analysis lets us identify the widest possible bins for accumulating photon statistics, leading to more reliable estimates of orientations (in polTIRF) or distances (in FRET). In polTIRF, the improvement can be especially significant, because the inferred probe orientation is a highly nonlinear function of the photon rates, and those rates are never exactly known. Suppose that a particular set of photon rates define an orientation uniquely (apart from the unavoidable 180° dipole ambiguity). Nevertheless, in practice, that set of rates may be near enough to a degenerate point that the unavoidable statistical fluctuations in estimating the rates create spurious jumps between two very different inferred orientations. Changepoint analysis addresses this problem by maximizing the number of photons used in each orientation determination, thus minimizing the statistical uncertainty in rate estimates and keeping them away from such degeneracies.

5.2. Vista: Transient state detection

A bigger challenge is to detect a relatively short-lived state immediately adjacent to a large changepoint. Such a pattern is expected during a step of myosin V where the large changepoint corresponds to the tilting of the lever arm before and/or after a step and the small changepoint is the short-lived transient state of the detached head before it rebinds to actin. Our simulations emulated this scenario by modeling three states: (1) a long-lived state (with 2000 photons) corresponding to the prestep head orientation with relatively little wobble since both heads are attached to actin, (2) a variable duration transient state (0–1200 photons) of large probe wobble due to the detached head rapidly diffusing toward the next binding site, and (3) a long-lived state (also with 2000 photons) in the leading head poststep orientation with relatively little wobble.

When there is no such transient state, the algorithm detects 90% of the single changepoints (Fig. 15.7A and D) representing the step, similar to Fig. 15.6C and D. As the number of photons in the transient state increases, the probability to detect it also increases (Fig. 15.7B and E) but plateaus at ~90% due to a relatively constant ~10% probability to detect a spurious third changepoint (Fig. 15.7C and F). For large N, the 3-changepoint cases almost always involves a correct determination of the transient state plus an additional false positive somewhere else in the interval. Detecting the transient state requires more photons in the 16 polarization channel case (Fig. 15.7E) than it does with 8 channels (Fig. 15.7B), similar to the results discussed for single-changepoint detection. For SBR = 3, approximately 750 and 1100 photons are required to detect 80% of the intervals in the 8 and 16 polarization channel cases, respectively. It is important to realize that these simulations give useful estimates for the design of experiments, but the actual sensitivity may be different for different orientations.

Determining the probe orientation and wobble in the interval between changepoints (Section 3.4) can be used to validate whether a particular changepoint is physically relevant or not. In polTIRF experiments, for example, a small change in the overall rate may result in a statistically significant changepoint, but if the corresponding inferred orientation does not also change, then it is not likely to be biologically relevant. The usefulness of this approach, however, is compromised by spurious changes in the orientation that arise from overfitting to photon counting noise. The MCCP algorithm minimizes this problem by ensuring that the maximum number of photons is included in each dwell, but the effect still remains for short-duration dwells.

6. Conclusion

Our conclusions were already summarized in Section 1.5; Figs. 15.1 and 15.2 apply our method to experimental data. We extended a change-point analysis for single-channel fluorescence experiments like FRET (Watkins and Yang, 2005) to make it applicable to multiple-channel data, for example, from polTIRF. Our method dramatically improves the time resolution potential of such experiments and also their accuracy in determining orientation changes in molecular motors.

We tested the method’s accuracy and power to detect changepoints over a range of photon numbers and SBRs. Our simulations indicate that approximately 700 and 1100 photons are required to detect the detached state between myosin V steps in 8- and 16-channel polTIRF configurations. With 8 polarization channels, fewer photons are required to locate the short-lived state; however, 16 channels are required to accurately identify the increase in wobble cone.

A List of Symbols

a

discrete macromolecular state index; S_a: the state indexed by a

α

acceptable fraction of false positives (Section 3.1)

α, β

body-frame angles describing orientation relative to an actin filament

θ, φ

laboratory-frame angles describing orientation of a fluorophore

E[ ], σ_m²

expectation and variance of uncorrected log like-lihood function

i

indexes which of several changepoints is under discussion

κ

simulated photon rate

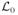(r₀)

log likelihood for no changepoint; 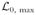: its maximum over r₀

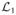(r, r′, τ)

log likelihood for one changepoint; 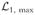(τ): its maximum over r, r′

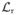(τ) or

log of the likelihood ratio; 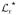: its absolute maxi mum; m★: position of the maximum

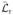and

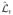
corrected log likelihood ratios (Section 3.2)

m

photon sequence number, from 1 to N; also m, m′: how many of the observed photons came before (resp. after) a proposed changepoint

M

number of simulation runs

μ

index labeling the n_p distinct polarization channels; m_μ, m′_μ: how many of the observed photons of type μ came before/after a proposed changepoint

q

number of proposed changepoints in an interval

r₀

assumed photon rate under the assumption of no changepoint (or r_0,μ in the multiple-rate case)

r, r′

assumed photon rates before and after a changepoint (or r_μ, r_μ′ in the multiple-rate case)

ρ_α⁰ and ρ_α

thresholds to reject false positives for uncorrected and corrected log likelihood ratio

t_m

arrival times of individual photons, in increasing order in the range from 0 to T

τ

proposed value of changepoint time

δt

fictitious time slice, eventually taken → 0; k: index of time slices from 0 to T/δt

Δt

finite bin duration in traditional method

x

photon sequence number as a fraction of the total, = m/N

χ

ratio of photon rates before/after a changepoint

Glossary

FRET

Forster resonance energy transfer

MCCP

Multiple-channel changepoint

polTIRF

Polarized total internal reflection fluorescence microscopy

SBR

Signal to background ratio

SPC

Single photon counting