Accelerating Advanced MRI Reconstructions on GPUs

Abstract

Computational acceleration on graphics processing units (GPUs) can make advanced magnetic resonance imaging (MRI) reconstruction algorithms attractive in clinical settings, thereby improving the quality of MR images across a broad spectrum of applications. This paper describes the acceleration of such an algorithm on NVIDIA’s Quadro FX 5600. The reconstruction of a 3D image with 128³ voxels achieves up to 180 GFLOPS and requires just over one minute on the Quadro, while reconstruction on a quad-core CPU is twenty-one times slower. Furthermore, relative to the true image, the error exhibited by the advanced reconstruction is only 12%, while conventional reconstruction techniques incur error of 42%.

1 Introduction

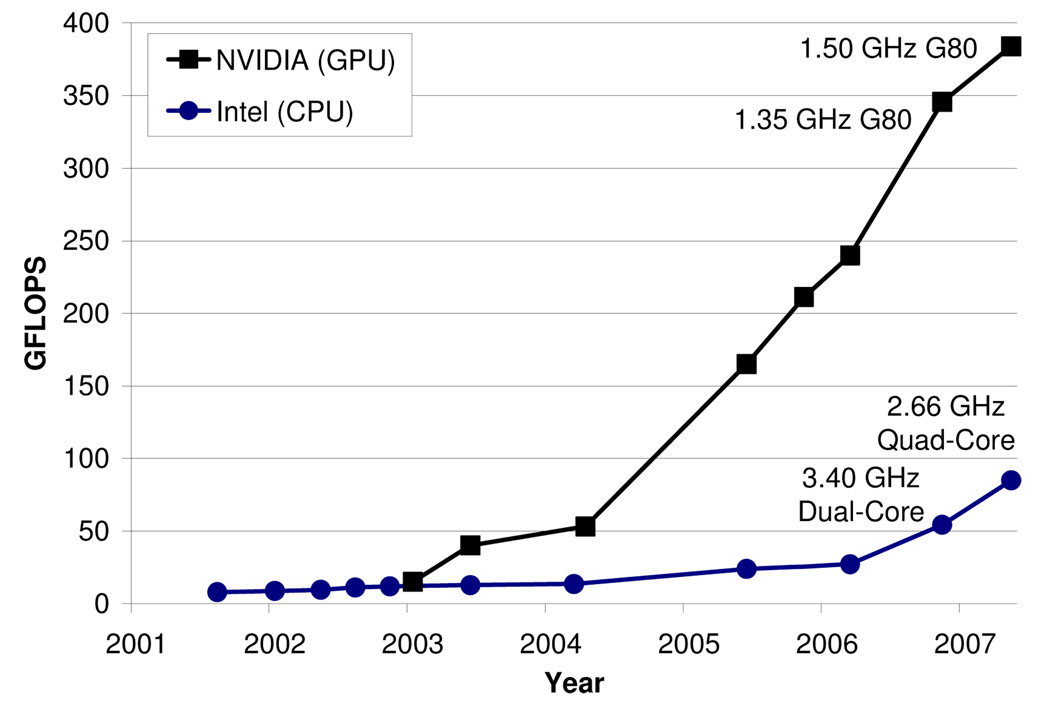
Mainstream microprocessors such as the Intel Pentium and AMD Opteron families have driven rapid performance increases and cost reductions in science and engineering applications for two decades. These commodity micro-processors have delivered GFLOPS to the desktop and hundreds of GFLOPS to cluster servers. This progress, however, slowed in 2003 due to constraints on power consumption. Since that time, accelerators such as graphics processing units (GPUs) have led the advances in computational throughput for science and engineering applications. Figure 1 illustrates this trend.

Fig. 1. Peak throughput of programmable, floating-point, multiply-add operations on GPUs and CPUs.

Adapted with permission from [30] © John Owens et al.

Recent advances in architecture have also increased the GPU’s attractiveness as a platform for science and engineering applications. Prior to 2006, GPUs found very limited use in this domain due to their limited support for both IEEE floating-point standards and arbitrary memory addressing. However, the recently released AMD R580 and NVIDIA G80 GPUs offer strong support for IEEE single-precision floating-point values (with double-precision soon to follow) and permit reads and writes to arbitrary addresses in memory [2,29]. Furthermore, modern GPUs use massive multithreading, fast context switching, and high memory bandwidth to tolerate ever-increasing latencies to main memory by overlapping long-latency loads in stalled threads with useful computation in other threads [25].

Increased programmability has also enhanced the GPU’s suitability for science and engineering applications. For example, the G80 supports the single-program, multiple-data (SPMD) programming model, in which each thread is created from the same program and operates on a distinct data element, but all threads need not follow the same control follow path. As the SPMD programming model has been used on massively parallel supercomputers in the past, it is reasonable to expect that many high-performance applications will port easily to the G80 [25,44]. Furthermore, general-purpose applications targeting the G80 are developed using ANSI C with simple extensions, rather than the cumbersome graphics application programming interfaces (APIs) [37,10] and high-level languages layered on graphics APIs [7,5,43] that have been used in the past.

A wide variety of magnetic resonance imaging (MRI) applications, ranging from quantitative imaging of the brain to dynamic imaging of the beating heart, can benefit greatly from these increases in computational resources and advancements in architecture and programmability. At present, many MRI experiments are specifically designed so that the image can be reconstructed quickly and efficiently on a standard CPU, often by acquiring the scan data on a uniform grid and applying a fast Fourier transform (FFT). However, in many applications the combination of tailored data acquisition and advanced image reconstruction significantly improves image quality. In particular, these techniques can increase signal-to-noise ratio, decrease scan time, and/or reduce imaging artifacts. However, advanced reconstruction algorithms often require several orders of magnitude more computation than conventional reconstruction algorithms. In this paper, we accelerate a reconstruction algorithm that can (1) generate MR images from arbitrary data sampling trajectories, and (2) incorporate prior anatomical knowledge into the reconstruction process, thereby increasing the signal-to-noise ratio while mitigating partial volume artifacts.

For these advanced reconstructions to be viable in clinical settings, dramatic and inexpensive computational acceleration is required. We find that advanced reconstructions from arbitrary scan trajectories are very well suited to acceleration on modern GPUs. In particular, an advanced reconstruction of an image comprising 128³ voxels completes in just over one minute o the G80, while the same reconstruction requires nearly 23 minutes on a quad-core CPU. Furthermore, relative to a conventional reconstruction, the advanced reconstruction reduces the error in the reconstructed image from 42% to 12%. The 21X acceleration achieved on the GPU makes the constrained reconstruction much more appealing in clinical settings.

The remainder of this paper is organized as follows. Section 2 first describes the architecture of the Quadro FX 5600 and its G80 GPU, then discusses the advantages of advanced MRI reconstructions. Section 3 presents the GPU- based implementation of the advanced reconstruction algorithm. Section 4 describes experimental methodology. Section 5 presents results and discusses features of the Quadro that enable the advanced reconstruction to achieve up to 180 GFLOPS in performance. Section 6 discusses related work in GPU-based medical imaging. Section 7 concludes.

2 Background

2.1 The Quadro FX 5600 Graphics Card

The Quadro FX 5600 is a graphics card equipped with a G80 graphics processing unit (GPU). The Quadro has a large set of processor cores that can directly address a global memory. This architecture supports the single-program, multiple-data (SPMD) programming model, which is more general and flexible than the programming models supported by previous generations of GPUs, and which allows developers to easily implement data-parallel algorithms. In this section we discuss NVIDIA’s Compute Unified Device Architecture (CUDA) and the architectural features of the G80 that are most relevant to accelerating MRI reconstructions. Similar descriptions are found in [32,33].The interested reader may refer to [29,27] for additional details.

From the application developer’s perspective, the CUDA programming model consists of ANSI C supported by several keywords and constructs. CUDA treats the GPU as a coprocessor that executes data-parallel kernel functions. The developer supplies a single source program encompassing both host (CPU) and kernel (GPU) code. NVIDIA’s compiler, nvcc, separates the host and kernel codes, which are then compiled by the host compiler and nvcc, respectively. The host code transfers data to and from the GPU’s global memory via API calls, and initiates the kernel code by calling a function.

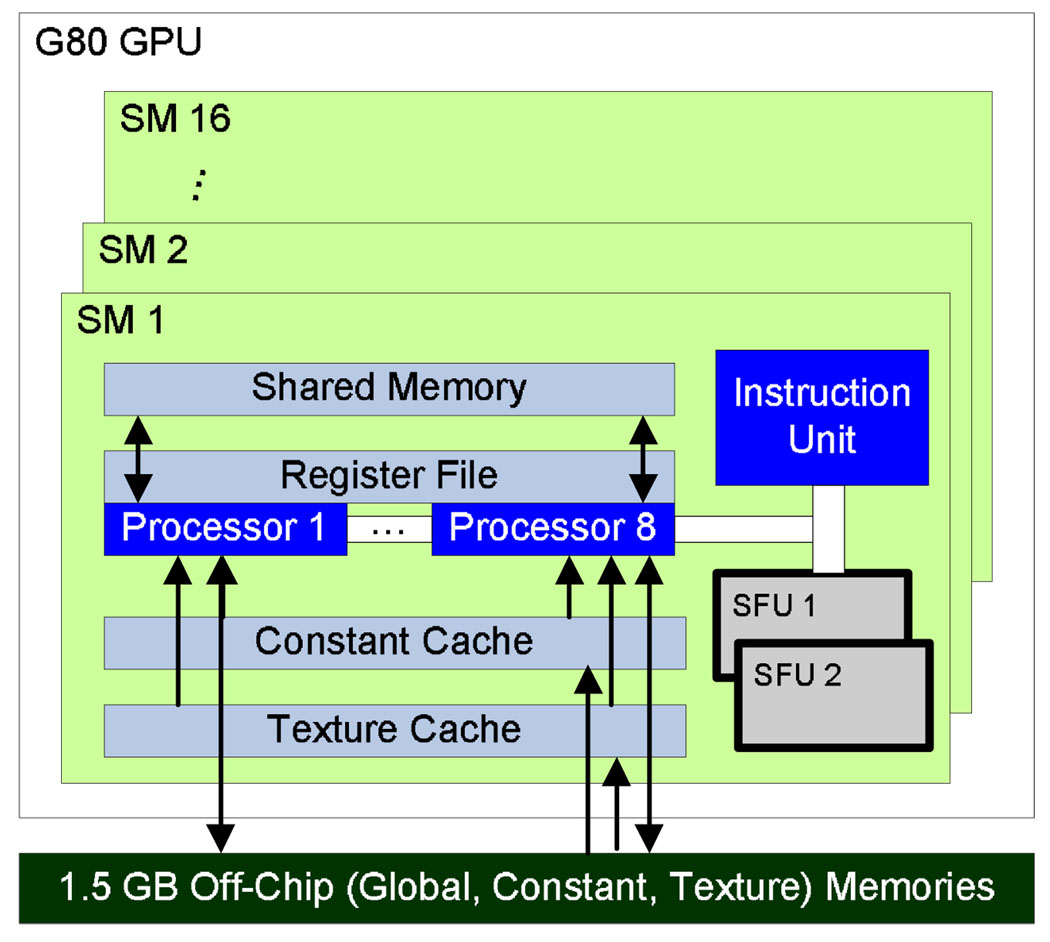
Figure 2 depicts the Quadro’s architecture. The G80 GPU consists of 16 streaming multiprocessors (SMs), each containing eight streaming processors (SPs), or processor cores, running at 1.35 GHz. Each SM has 8,192 registers that are shared among all threads assigned to the SM. The threads on a given SM’s cores execute in SIMD (single-instruction, multiple-data) fashion, with the instruction unit broadcasting the current instruction to the eight cores. Each core has a single arithmetic unit that performs single-precision floating point arithmetic and 32-bit integer operations. Additionally, each SM has two special functional units (SFUs), which perform more complex FP operations such as the trigonometric functions with low latency. Both the arithmetic units and the SFUs are fully pipelined. Thus, each SM can perform 18 FLOPS per clock cycle (one multiply-add operation per SP and one complex operation per SFU), yielding 388.8 GFLOPS (16 SM * 18 FLOP/SM * 1.35 GHz) of peak theoretical performance for the GPU.

Fig. 2.

Architecture of Quadro FX 5600.

The Quadro has 76.8 GB/s of bandwidth to its 1.5 GB, off-chip, global memory. Nevertheless, with computational resources supporting nearly 400 GFLOPS and each multiply-add instruction operating on up to 16 bytes of data, applications can easily saturate that bandwidth. Therefore, as depicted in Figure 2, the G80 has several on-chip memories that can exploit data locality and data sharing to reduce an application’s demands for off-chip memory bandwidth. For example, the Quadro has a 64 KB, off-chip constant memory, and each SM has an 8 KB constant memory cache. Because the cache is single-ported, simultaneous accesses of different addresses yield stalls. However, when multiple threads access the same address during the same cycle, the cache broadcasts that address’s value to those threads with the same latency as a register access. This feature proves quite beneficial for the MRI reconstruction algorithm studied in this paper. In addition to the constant memory cache, each SM has a 16KB shared memory for data that is either written and reused or shared among threads. Finally, for read-only data that is shared by many threads but not necessarily accessed simultaneously by all threads, the off-chip texture memory and the on-chip texture caches exploit 2D data locality to substantially reduce memory latency.

Threads executing on the G80 are organized into a three-level hierarchy. At the highest level, each kernel creates a single grid, which consists of many thread blocks. The maximum number of threads per block is 512. Each thread block is assigned to a single SM for the duration of its execution. Threads in the same block can share data through the shared memory and can perform barrier synchronization by invoking the __syncthreads primitive. Threads are otherwise independent, and synchronization across thread blocks is safely accomplished only by terminating the kernel. Finally, threads within a block are organized into warps of 32 threads. Each warp executes in SIMD fashion, with the SM’s instruction unit broadcasting the same instruction to the eight cores on four consecutive clock cycles.

SMs can interleave warps on an instruction-by-instruction basis to hide the latency of global memory accesses and long-latency arithmetic operations. When one warp stalls, the SM can quickly switch to a ready warp in the same thread block or in some other thread block assigned to the SM. The SM stalls only if there are no warps with all operands available.

2.2 Advanced MRI Reconstruction

Magnetic resonance imaging (MRI) is commonly used by the medical community to safely and non-invasively probe the structure and function of biological tissues from all regions of the body, and images generated using MRI have a profound impact in both clinical and research settings. MR imaging consists of two phases, acquisition (scan) and reconstruction. During the scan phase, the scanner samples data in the k-space domain (i.e., the spatial-frequency domain or Fourier transform domain) along a predefined trajectory. These samples are then transformed into the desired image during the reconstruction phase.

MRI is often limited by high noise levels, significant imaging artifacts, and/or long data acquisition times. In clinical settings, short scan times not only increase scanner throughput but also reduce patient discomfort, which tends to mitigate motion-related artifacts. High image resolution is equally important because it can enable earlier detection of pathology, leading to improved prognoses for patients. However, the goals of short scan time, high resolution, and high signal-to-noise ratio (SNR) often conict; improvements in one metric tend to come at the expense of one or both of the others.

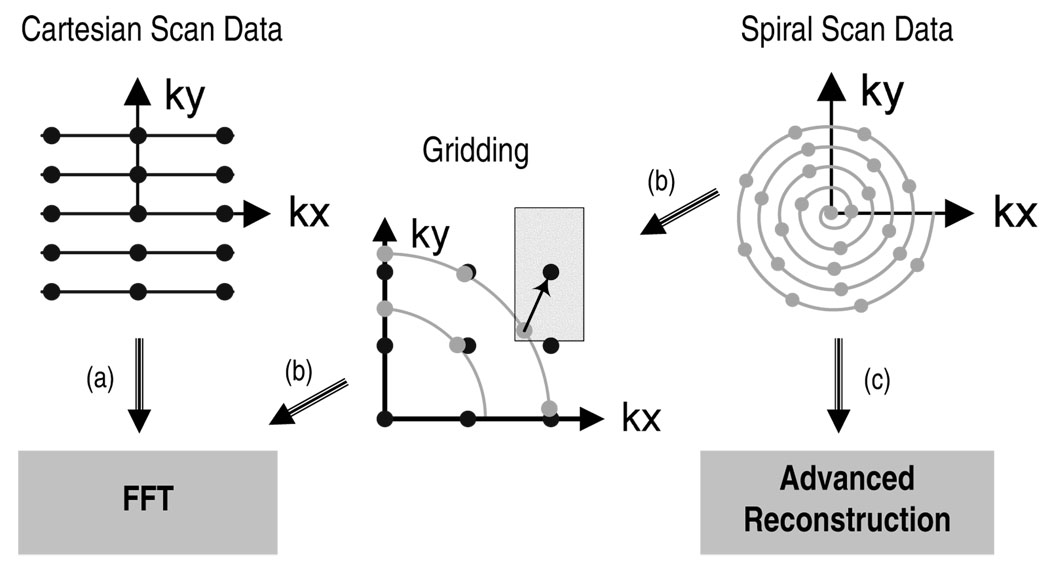
The sampling trajectory used by the MRI scanner can significantly affect the quality of the reconstruction. Figure 3(a) and 3(c) depict a Cartesian scan trajectory and a non-Cartesian (spiral) scan trajectory, respectively. The Cartesian trajectory samples k-space on a uniform grid, which allows image reconstruction to be performed quickly and efficiently by applying a fast Fourier transform (FFT) directly to the acquired data. Although the reconstruction of Cartesian scan data is computationally efficient, non-Cartesian scan trajectories can be preferable because they are often faster and less sensitive to imaging artifacts caused by non-ideal experimental conditions. For these reasons, non-Cartesian trajectories with radial [23] and spiral [1] sampling patterns are becoming increasingly common in MRI.

Fig. 3. MRI reconstruction techniques.

In (a) the scanner samples k-space on a uniform grid and reconstructs the image in one step via the FFT. In (b) the scanner samples k-space on a non-Cartesian (spiral) trajectory, then interpolates the samples onto a uniform grid and reconstructs the image in one step via the FFT. In (c) an advanced reconstruction algorithm is applied directly to the spiral scan data.

Image reconstruction from non-Cartesian scan data presents both challenges and opportunities. In the most common approach, gridding, the samples are first interpolated onto a uniform Cartesian grid and then reconstructed in one step via the FFT (see Figure 3(b)) [20,36]. While gridding is computationally expedient, it satisfies no optimality criterion and cannot leverage prior information such as anatomical constraints. By contrast, statistically optimal image reconstructions can more accurately model imaging physics (e.g., [31,12,42]) and can also incorporate additional prior information. For example, anatomically constrained reconstruction [16] incorporates anatomical information to reduce noise while preserving the resolution of known image features, enabling brief scans to yield high quality images. While such reconstructions have been impractical for large-scale 3D problems due to computational constraints, this paper shows that these reconstructions become viable in clinical settings when accelerated on GPUs. Anatomically constrained reconstruction of non-Cartesian scan data enables brief scans to achieve high SNR, thereby decreasing imaging artifacts and increasing SNR simultaneously. While such advanced reconstructions have been impractical for large-scale problems due to computational constraints, this paper shows that these reconstructions become viable in clinical settings when accelerated on GPUs.

We implemented the anatomically constrained reconstruction algorithm of [16]. This algorithm finds the the solution to the following quasi-Bayesian estimation problem

$$\widehat{\rho }=\arg \underset{\rho }{\text{min}}\underset{\text{data fidelity}}{\underbrace{\parallel \mathbf{\text{F}}\rho -\mathbf{d}{\parallel }_2^2}}+\underset{\text{prior info}}{\underbrace{\parallel \mathbf{\text{W}}\rho {\parallel }_{2\text{'}}^2}}$$ (1)

where ρ̂ is a vector containing voxel values for the reconstructed image, F is a matrix that models the imaging process, d is a vector of data samples, and W is a matrix that can incorporate prior information such as anatomical constraints. In clinical settings, these anatomical constraints are derived from one or more high-resolution, high-SNR scans of the patient, which reveal features such as the location of anatomical structures. The matrix W is derived from these reference images. The first term in the above cost function imposes that data simulated from the reconstructed image should match somewhat closely with the real acquired data; the second term is used to impose prior information regarding the image statistics.

Because Eq. 1 defines a linear least squares problem, the solution is

$$\widehat{\rho }={\left({\mathbf{\text{F}}}^H{\mathbf{\text{F}}+\mathbf{\text{W}}}^H\mathbf{\text{W}}\right)}^{-1}{\mathbf{\text{F}}}^H\mathbf{\text{d}}\text{.}$$ (2)

However, the size of the matrix (F^HF +W^HW) makes direct matrix inversion impractical for high-resolution reconstructions. For the 128³-voxel reconstructions examined in this paper, the inverted matrix contains well over four trillion complex-valued elements (the number of elements in the inverted matrix equals the square of the number of voxels in the reconstructed image). An iterative method for matrix inversion, such as the conjugate gradient (CG) algorithm [19], is therefore preferred.

The conjugate gradient algorithm reconstructs the image by iteratively solving Eq. 2 for ρ̂. During each iteration, the CG algorithm updates the current image estimate ρ to improve the value of the quasi-Bayesian cost function (Eq. 1). The computational effciency of the CG technique is largely determined by the efficiency of matrix-vector multiplication operations involving F^HF andW^HW, as these operations are required during each iteration of the CG algorithm. Fortunately, matrix W often has a sparse structure that permits efficient multiplication by W^HW, and matrix F^HF has a convolutional structure [45,12] that enables efficient matrix multiplication via the FFT.

The advanced reconstruction algorithm described in this paper therefore consists of three primary computations. First, the algorithm computes each element of Q, given by

$$Q({\mathbf{\text{x}}}_n)={\displaystyle \sum _{m=1}^M|}\varphi ({\mathbf{\text{k}}}_m){|}^2{e}^{(i2\pi {\mathbf{\text{k}}}_m\cdot {\mathbf{\text{x}}}_{\text{n}}),}$$ (3)

where Q is the convolution kernel that facilitates multiplication operations involving F^HF and ϕ (·) is the Fourier transform of the voxel basis function.

There are M k-space sampling locations, with k_m denoting the location of the m^th sample. Likewise, there are N voxel coordinates, with x_n denoting the coordinates of the n^th voxel. Because Q depends only on the scan trajectory (not the scan data) and the size of the image, it can be computed before the scan occurs and can be reused during any reconstruction that shares the same scan trajectory and image size.

Second, the algorithm computes the vector F^Hd, defined as

$${\left[{\mathbf{\text{F}}}^H\mathbf{\text{d}}\right]}_n={\displaystyle \sum _{m=1}^M}{\varphi }^{*}({\mathbf{\text{k}}}_m)\mathbf{\text{d}}({\mathbf{\text{k}}}_m)e^{(i2\pi {\mathbf{\text{k}}}_m\cdot {\mathbf{\text{x}}}_n)}.$$ (4)

Although Eq. 3 and Eq. 4 are quite similar, the former necessitates significantly more computation because the Q algorithm oversamples the image space by a factor of two in each dimension. Therefore, during a 3D reconstruction, Eq. 3 is evaluated at 8N values of x_n, while the Eq. 4 is evaluated at only N values of x_n. Finally, the CG solver performs iterative matrix inversion to solve Eq. 2.

The complexity of the advanced reconstruction far exceeds the complexity of a conventional, gridded reconstruction. Given a reconstruction problem of N voxels and M scan data points, the computations of Q and F^Hd have O(MN) complexity, compared to O(N log N) complexity for reconstructions based on gridding and the FFT. For this reason, advanced reconstruction of high resolution, three-dimensional images has been impractical in clinical settings, despite the technique’s clear advantages over conventional reconstructions. Our work demonstrates that these advanced reconstructions can be performed quickly and efficiently on modern GPUs, increasing their viability in clinical settings.

2.3 Example Application: 3D Full-Brain Multi-Echo Acquisition

We illustrate one potential application of this work with real experimental data acquired using a novel acquisition scheme. The new multiparametric 3D structural imaging sequence provides several volumes with varying contrast in a multi-echo acquisition to assist in automatic brain segmentation, and we obtain volumes with T₁-weighting and T₂-weighting simultaneously and in complete registration.

Specifically, a 3D stack of spirals sequence was designed using the method of [14] with a 256 × 256 × 176 matrix size, 1 mm isotropic resolution, 17 spiral shots per slice, and with a TR of 350 ms. The sequence was acquired with multiple echos to obtain a range of different contrasts during a single acquisition. Specifically, we acquired a short echo time (2.2 ms) gradient echo spiral-out acquisition (GRE, T1-weighted), followed by spiral-in/spiral-out acquisitions centered around two spin echo times at 46 ms (SE1) and 92 ms (SE2), respectively. All three images were acquired simultaneously with the same data acquisition trajectories and bandwidth, and therefore are coregistered. Subjects were scanned on a Siemens 3 T Allegra headscanner in accordance with the institutional review board using a single-channel head coil.

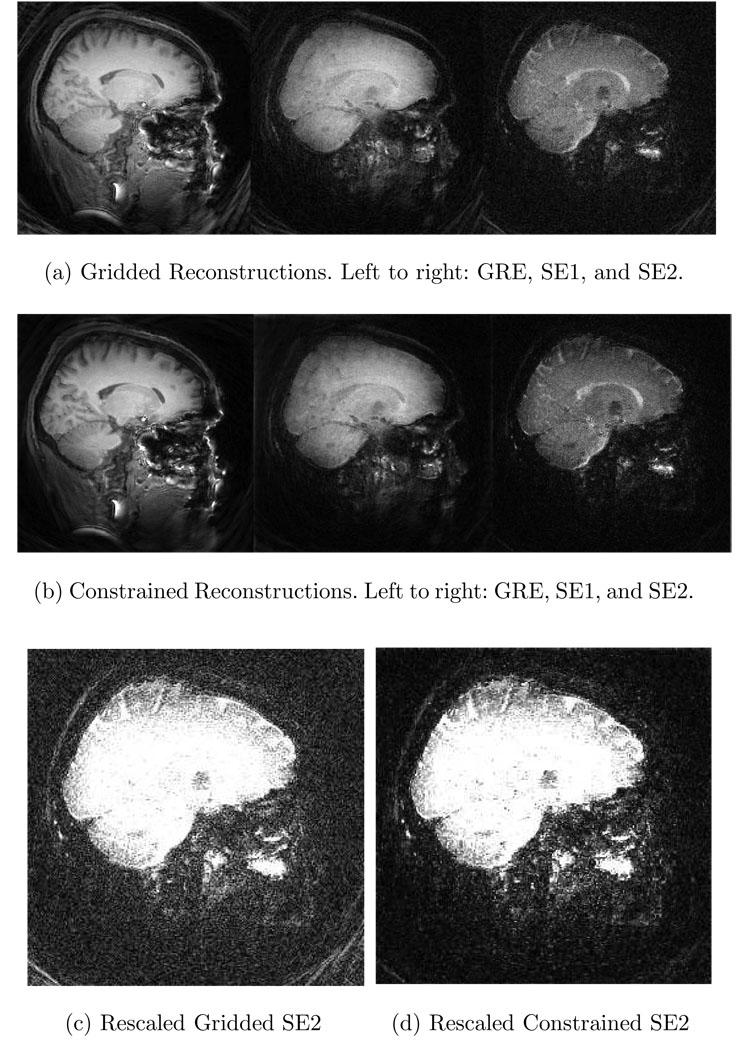
Advanced reconstructions and gridded reconstructions were performed with this data,¹ and the results are shown in Fig. 4. The advanced reconstruction’s noise variance is more than 3 times better than that of the gridded reconstruction. The constraints used in the advanced reconstruction were obtained similarly to the technique described in [17], utilizing the whole image sequence to estimate a shared anatomical structure.

Fig. 4. Application of advanced MRI reconstruction to human brain data.

(a) One slice from the gridding reconstructions from each of the three different images. (b) The corresponding slice from the constrained reconstructions. The SE2 image is shown with a modified colorscale in (c) and (d) to illustrate the significant SNR advantage of the advanced reconstruction. The constrained reconstruction’s noise variance is more than 3 times lower than that of the gridded reconstruction.

3 Advanced MRI Reconstruction

The advanced MRI reconstruction algorithm described in Section 2.2 consists of three steps: computing the data structure Q (which depends only on the scan trajectory), computing the vector F^Hd (which depends on the scan trajectory and the scan data), and finding the image iteratively via a conjugate gradient linear solver. As Figure 5 shows, the algorithms for F^Hd and Q are quite similar.² The most significant difference is that the Q algorithm requires more computation because its outer loop executes 8N iterations, compared to N iterations for F^Hd. Otherwise, Q suffers from the same bottlenecks and benefits from the same code transformations as F^Hd.

Fig. 5. Data-parallel phases of advanced MRI reconstruction.

Panels (a) and (b) show simplified C code for the algorithms that compute Q and F^Hd, respectively. Panel (c) depicts the F^Hd algorithm in CUDA.

Because Q can be computed prior to acquiring an image’s scan data, the critical path for a given reconstruction consists only of computing F^Hd and executing the linear solver. Therefore, the remainder of this section describes the algorithms for F^Hd and the linear solver, focusing on the implementation of the F^Hd algorithm on the GPU. The interested reader may refer to [40] for more detailed discussion of Q.

3.1 F^Hd

As Figure 5(b) shows, the algorithm for F^Hd is an excellent candidate for acceleration on the GPU because it contains substantial data-parallelism. The algorithm first computes the real and imaginary components of mu at each sample point in the trajectory space (k-space), then computes the real and imaginary components of F^Hd at each voxel in the image space. The value of F^Hd at any voxel depends on the values of all sample points, but no elements of F^Hd depend on any other elements of F^Hd. Therefore, all elements of F^Hd can be computed independently and in parallel.

Despite the algorithm’s inherent parallelism, potential performance bottle necks are evident. First, in the loop that computes the elements of F^Hd, the ratio of floating-point operations to memory accesses is at best 3:1 and at worst 1:1. The best case assumes that the sin and cos operations are computed using five-element Taylor series that require 13 and 12 floating-point operations, respectively. The worst case assumes that each trigonometric operation is computed as a single operation in hardware. In either case, the GPU-based implementation of the algorithm must conserve memory bandwidth and tolerate memory latency. Second, the ratio of FP arithmetic to FP trigonometry is only 13:2. Thus, GPU-based implementation must tolerate or avoid stalls due to long-latency sin and cos operations.

The GPU-based implementation of the F^Hd algorithm (see Figure 5(c)) uses the G80’s constant memory caches to eliminate the potential bottleneck posed by memory bandwidth and latency. To overcome the memory bottleneck, the scan data is divided into many tiles, with each tile containing a distinct subset of sample points. For each tile, the host CPU loads the corresponding subset of sample points into constant memory before executing the cmpFhD function. Each thread then computes a partial sum for a single element of F^Hd by iterating over all the sample points in the tile. This optimization significantly increases the ratio of FP operations to global memory accesses.

Likewise, the G80’s special functional units (SFUs) enable the algorithm to avoid the potential bottleneck of long latency trigonometric operations. When the use_fast_math compiler option is invoked, the sin and cos operations are not linked to long-latency library calls, but rather are executed as individual, low-latency instructions on the SFUs. The speed of the SFU comes at the expense of some loss in accuracy when the argument to the sin or cos is very small, but, as we show in Section 5, this optimization does not necessarily decrease the overall accuracy of the algorithm.

3.2 Linear Solver

The final phase of the image reconstruction consists of a linear solver that implements the preconditioned conjugate gradient (PCG) algorithm [9,24]. As described in Section 2, the solver iteratively solves Eq. 2 to find the desired image ρ̂. When the iterations converge or the number of iterations exceeds a threshold, the solver terminates. During each iteration, the solver performs a large FFT and inverse FFT, several BLAS and sparse BLAS operations (including multiplication of sparse matrices and vectors, as well as addition, scaling, and scalar multiplication of vectors), and several other computations (such as summation reduction, shifting, and sampling).

We ported the PCG algorithm from MATLAB to C/CUDA, using NVIDIA’s CUDA CUFFT Library [28] for the FFT and inverse FFT operations, implementing the BLAS and sparse BLAS operations in CUDA, and orchestrating the control flow and data marshaling in C. Complex-valued objects are represented using CUDA’s cufftComplex data type, as required by the CUFFT Library. Sparse matrices are stored in compressed row format [11] to facilitate efficient GPU-based execution of the expression A * x, where A is a sparse matrix and x is a vector. Although we have not rigorously analyzed the performance of the CUDA-based solver, it is roughly 25 times faster than a MATLAB-based version of the same algorithm. We use the CUDA-based solver for all experiments presented in Section 5 and view its performance as acceptable.

4 Methodology

To quantify the effects of the Quadro’s architectural features on the performance and quality of the reconstruction, we implemented seven versions of the algorithm for F^Hd, five of which are depicted in Figure 6. The base version (GPU.Base, see Figure 6(a)) simply executes in data-parallel fashion on the GPU, without using even the simplest optimizations to conserve memory bandwidth or tolerate long latency loads and trigonometric operations. The second version (GPU.RegAlloc, see Figure 6(b)) register allocates the voxel data, thereby conserving some memory bandwidth and reducing the latency of all voxel accesses. GPU.Layout (Figure 6(c)) register allocates the voxel data and changes the layout of the scan data in the Quadro’s global memory so that accesses to the scan data make more effcient use of the memory bandwidth. GPU.ConstMem (Figure 6(d)) register allocates the voxel data and places the scan data in the Quadro’s constant memory so that accesses to the scan data are cached. The fifth version (GPU.FastTrig, see Figure 6(e)) additionally uses the G80’s special functional units to compute fast, approximate versions of the trigonometric operations. The sixth version, GPU.Tune, also uses experimentally-tuned settings for three code transformations: loop unrolling, data tiling (scan points per thread), and number of threads per block. The tuned settings balance allocation of GPU resources to improve hardware utilization and thread efficiency. Finally, GPU.Multi executes the tuned version on multiple Quadros.

Fig. 6.

Versions of the F^Hd algorithm on the GPU.

To obtain a reasonable baseline, we implemented two versions of F^Hd on the CPU. Version CPU.DP uses double-precision for all floating-point values and operations, while version CPU.SP uses single-precision. Both CPU versions are compiled with Intel’s icpc (version 10.1) using flags -O3 -msse3 -axT- vec-report3-fp-model fast=2, which (1) vectorizes the algorithm’s dominant loops using instructions tuned for the Core 2 architecture, and (2) links the trigonometric operations to fast, approximate functions in the math library. Based on experimental tuning with a smaller data set, the inner loops are unrolled by a factor of four and the scan data is tiled to improve locality in the L1 cache.

Each GPU version of F^Hd is compiled using nvcc -O3 (CUDA version 1.1) and executed on a 1.35 GHz Quadro FX 5600. The Quadro card is housed in a system with a 2.4 GHz dual-socket, dual-core Opteron 2216 CPU. Each core has a 1 MB L2 cache. The CPU versions use pthreads to execute on all four cores of 2.66 GHz Core 2 Extreme quad-core CPU, which has peak theoretical capacity of 21.2 GFLOPS per core and a 4 MB L2 cache. The CPU versions perform substantially better on the Core 2 Extreme quad-core than on the dual-socket, dual-core Opteron.

All reconstructions use the GPU version of the linear solver, which executes 60 iterations on the Quadro FX 5600. Two versions of Q were computed on the Core 2 Extreme, one using double-precision and the other using single- precision. The single-precision Q was used for all GPU-based reconstructions and for the reconstruction involving CPU.SP, while the double-precision Q was used only for the reconstruction involving CPU.DP. As the computation of Q is not on the reconstruction’s critical path, we give Q no further consideration.

To facilitate comparison of the advanced reconstruction with a conventional reconstruction, we also evaluated a reconstruction based on gridding and the FFT [20]. Our version of the gridded reconstruction is not optimized for performance, but it is fair to assume that an optimized implementation would execute in several seconds [40].

All reconstructions are performed on sample data obtained from a simulated, three-dimensional, non-Cartesian scan of a phantom image [22]. There are 284,592 sample points in the scan data set, and the image is reconstructed at 128³ resolution, for a total of 2²¹ voxels. In the first set of experiments, the simulated data contains no noise. In the second set of experiments, we added complex white Gaussian noise to the simulated data. When determining the quality of the reconstructed images, the percent error and peak signal-to-noise ratio metrics are used. The percent error is the root-mean-square (RMS) of the voxel error divided by the RMS voxel value in the true image (after the true image has been sampled at 128³ resolution). To permit fair comparison of the gridded and advanced reconstructions, we adjusted the scale of each gridded image to match the scale of the true image before computing the gridded image’s percent error and PSNR.

The data (runtime, GFLOPS, and images) presented in Section 5 were obtained by reconstructing each image once with each of the 11 implementations of the F^Hd algorithm described above. There are two exceptions to this policy. For GPU.Tune and GPU.Multi, the time required to compute F^Hd is so small that run-time variations in performance may become non-negligible. Therefore, for these configurations we computed F^Hd three times and reported the average performance. Also, when performing multiple reconstructions of the same data set back-to-back on the same computer, we do not clear the caches between successive calculations of F^Hd or successive executions of the linear solver. In the case of the F^Hd algorithm, which has a relatively small working set, the runtime increases by roughly 10% when the caches are cold. By contrast, the linear solver, which has a relatively large working set, exhibits a 30% increase in runtime when the caches are cold. However, given that (1) some data in the working sets depend only on the scan trajectory, and (2) clinicians are likely to use the same computer to perform several successive reconstructions on the same patient or with the same scan trajectory, it is difficult to determine the extent to which cold caches are an accurate reflection of clinical conditions. Finally, the reconstruction times reported in Section 5 exclude the time required to create an image from the reconstructed data (roughly one second).

Finally, the advanced reconstruction leverages two optimizations that are not evident elsewhere in our discussion. First, the scan trajectory is symmetric, and the advanced reconstruction uses prior knowledge of that symmetry to mitigate the effects of numerical imprecision on the reconstruction’s accuracy. Second, we manually balanced the resolution and the noise in the advanced reconstruction by performing the reconstruction multiple times while adjusting a regularization parameter. Adjustment of the regularization parameter can be performed prior to acquiring the sample data, given the sampling trajectory, noise levels, and other readily available prior information [15].

5 Evaluation

To be useful in clinical settings, the advanced reconstruction must satisfy two criteria. First, the quality of an image obtained via the advanced reconstruction should significantly exceed the quality of an image obtained via a gridded reconstruction. Second, the reconstruction must complete quickly. After image acquisition, the patient typically remains in the scanner during image reconstruction. The scanner operator then decides whether the image is acceptable or whether it should be acquired again. Any delays therefore increase patient discomfort and decrease scanner throughput. Also, when the administration of a medical treatment depends on the MR images, any delay is at best frustrating and at worst harmful to the patient’s health.

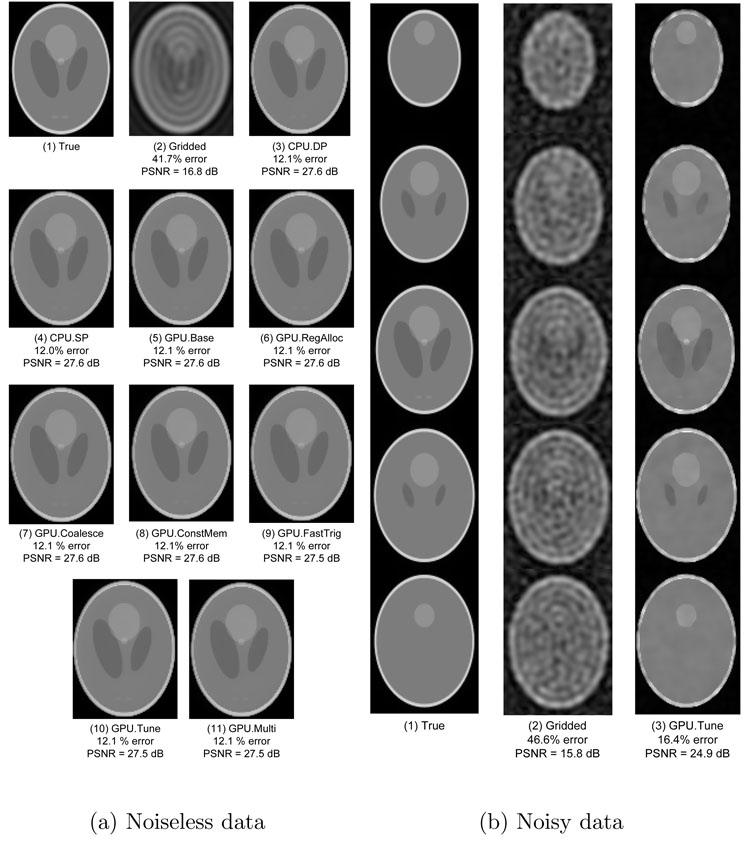
Our experiments indicate that the advanced reconstruction definitely satisfies the first criterion. As Figure 7(a) shows, advanced reconstruction of the noiseless data yields significantly better images than gridded reconstruction. Relative to the true image (Figure 7(a)(1)), the advanced reconstructions (Figure 7(a)(3–11)) exhibit 12% to 13% error and 27 dB to 28 dB PSNR, compared to 42% error and 17 dB PSNR for the gridded reconstruction (Figure 7(a)(2)).There are no significant differences among the images obtained from the advanced reconstruction, despite the use of single-precision floating-point in Figures 7(a)(4–11) and approximate trigonometric operations in Figure 7(a)(3, 4, and 9–11).

Fig. 7. Phantom images.

(a) Noiseless data: One 2D slice of the 3D image. The percent error and PSNR values in each sub-figure caption are calculated over the entire 3D image. (b) Noisy data: Noisy data: Three 2D slices of the 3D image. The percent error and PSNR values in each sub-figure caption are calculated over the entire 3D image.

The images reconstructed from the noisy data (Figure 7(b)) further demonstrate the superiority of the advanced reconstruction. Relative to the true image, the advanced reconstruction exhibits 16% error and 25 dB PSNR, while the error and PSNR for the gridded reconstruction are 47% and 16 dB, respectively. Again, there are no significant differences among the images obtained from the various versions of the advanced reconstruction.

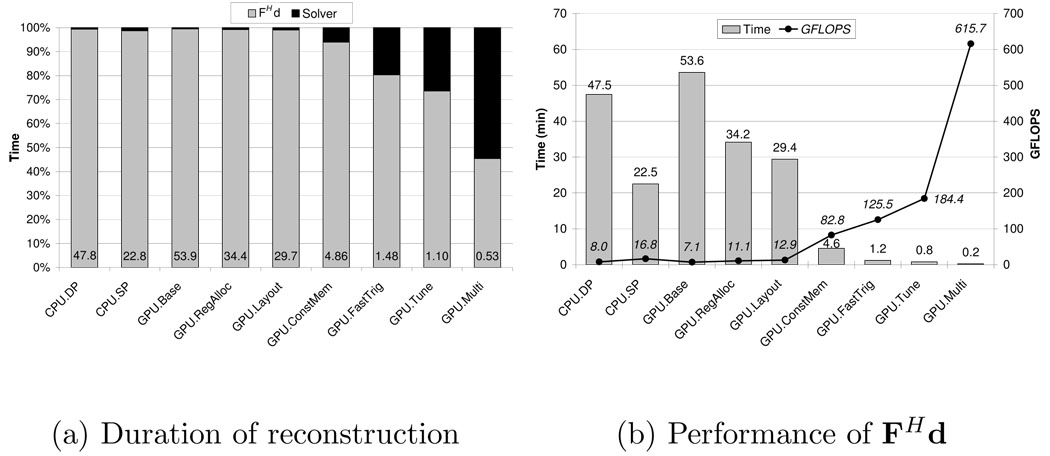
In addition to producing significantly better images than the gridded reconstruction, the GPU-accelerated advanced reconstruction arguably satisfies the second criterion for clinical use: speed. As Figure 8(a) shows, the fastest single-GPU version of the advanced reconstruction completes in 66 seconds. This reconstruction time is clearly much more appealing for clinical applications than the fastest CPU-based reconstruction, which completes in nearly 23 minutes.

Fig. 8. Performance of advanced MRI reconstruction.

(a) The reconstruction time includes the time to compute F^Hd and the time to run 60 iterations of the linear solver. The number at the bottom of each bar is the reconstruction time in minutes. (b) Performance of F^Hd computation. The first six configurations (CPU.DP-GPU.ConstMem) compute the trigonometric functions in software, using approximately 13 and 12 FLOPS for the sin and cos operations, respectively. The remaining configurations compute the trigonometric operations in hardware; therefore, each sin or cos accounts for a single FLOP.

The fastest single-GPU version of the advanced reconstruction computes F^Hd in 49 seconds, compared to 22.5 minutes for the fastest CPU-based reconstruction. The remainder of this section describes how the advanced reconstruction leverages the GPU’s resources to achieve such impressive acceleration when computing F^Hd. We find that the constant memory caches are quite effective in reducing the number of accesses to global memory, while the special functional units provide substantial acceleration for the trigonometric computations in the algorithm’s inner loops. We also find that experimentally-tuned code transformations have a significant impact on the algorithm’s performance. Specifically, the algorithm’s performance increases by 47% when the tiling factor, the number of threads per block, and the loop unrolling factor are experimentally tuned.

5.1 GPU.Base

As Figure 8(b) shows, GPU.Base is significantly slower than CPU.SP, the optimized, single-precision, quad-core implementation of F^Hd. In GPU.Base (see Figure 6(a)), the inner loops are not unrolled. There are 256 threads per block and 256 scan points per tile. Because GPU.Base leverages neither the constant memory nor the shared memory, memory bandwidth and latency are significant performance bottlenecks. With one 4-byte global memory accesses for every three FP operations, and with memory bandwidth of 76.8 GB/s, the upper limit on the kernel’s performance is only 57.6 GFLOPS. Due to other performance bottlenecks, the kernel actually achieves only 7.0 GFLOPS, less than half of the 16.8 GFLOPS achieved by CPU.SP.

5.2 GPU.RegAlloc

Relative to GPU.Base, GPU.RegAlloc (see Figure 6(b)) decreases the time required to compute F^Hd from 53.6 minutes to 34.2 minutes. In short, register allocating the voxel data increases the computation intensity (the ratio of FP operations to off-chip memory accesses) from 3:1 to 5:1. This substantial reduction in required off-chip memory bandwidth translates into increased performance. Eliminating the two stores to global memory during every loop iteration is particularly beneficial.

5.3 GPU.Layout

By changing the layout of the scan data in global memory (see Figure 6(c)), GPU.Layout achieves an additional speedup of 16% over GPU.RegAlloc. The underlying causes of GPU.Layout’s improved performance relative to GPU.RegAlloc are difficult to identify. GPU.Layout does require less overhead to marshal the data into struct-of-arrays format than GPU.RegAlloc requires to marshal the data into array-of-structs format, which may account for a small fraction of the improvement in performance. Furthermore, we speculate that the Quadro’s memory controller may provide some form of buffering that the struct-of-arrays layout leverages more successfully than does the array-of- structs layout. Section 5.4 offers additional insight into the relative merits of these two data layouts.

5.4 GPU.ConstMem

GPU.ConstMem (Figure 6(d)) achieves speedup of 6.4X over GPU.Layout by placing each tile’s scan data in constant memory rather than global memory. GPU.ConstMem therefore benefits from each SM’s 8 KB constant memory cache. At 4.6 minutes and 82.8 GFLOPS, this version of F^Hd is 4.9X faster than the optimized CPU version.

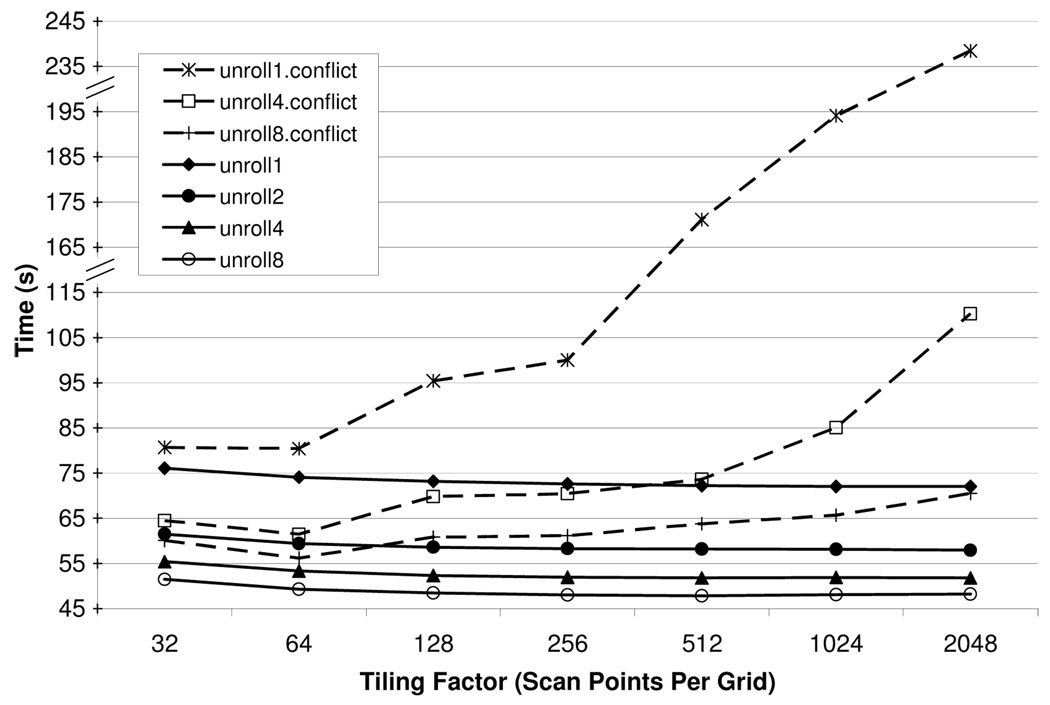
The GPU.ConstMem and GPU.Layout configurations underscore an important trade-off between optimizing latency to off-chip memory and optimizing latency to the constant caches. As discussed above, the array-of-structs data layout in Figure 6(c) improves performance relative to the struct-of-arrays data layout in Figure 6(b). However, as Figure 9 shows, the struct-of-arrays layout yields very bad performance if the scan data is placed in constant memory, presumably because this layout leads to excessive conflicts in the constant cache. In particular, as the tiling factor increases, the time required for these hybrid versions (with scan data in constant memory but with struct-of-arrays layout) to compute F^Hd steadily increases [33]. This phenomenon most likely occurs because elements of nearby scan points (k_x, k_y, etc.) map to the same cache line, so that the warps continually contend for the same cache lines. By contrast, the various versions of GPU.ConstMem actually require less time to compute F^Hd as the tiling factor increases; cache conflicts are clearly much less common.

Fig. 9. Constant cache conflicts.

The three dashed lines represent hybrid versions of GPU.Layout and GPU.ConstMem, such that the scan data is placed in constant memory using the struct-of-arrays layout depicted in Figure 6(c). Each dashed line corresponds to a different loop unrolling factor. Likewise, the four solid lines correspond to versions of GPU.ConstMem with different loop unrolling factors. Con-figurations with loop unrolling factor of 2 are excluded from the hybrid versions because some of those configurations hang for unknown reasons.

We now analyze the off-chip memory accesses on a single SM during the execution of three thread blocks. With 7 global memory accesses per thread, 256 threads per thread block, and 3 thread blocks per SM, there are 5,376 accesses to global memory. Assuming no constant memory cache evictions due to conflicts, there are also 1,280 accesses to constant memory (256 data points per tile, with 5 floating-point values per data element), yielding a total of 6,656 off-chip memory accesses. The number of floating-point computations performed by the 3 thread blocks is 3*256*256*38 = 7,471,104. Thus, the ratio of FP operations to off-chip memory accesses has increased by over two orders of magnitude, from 3:1 to 1100:1. However, GPU.ConstMem still achieves only 82.8 GFLOPS (roughly 20% to 25% of the Quadro’s peak theoretical through-put), which implies the existence of another bottleneck.

5.5 GPU.FastTrig

GPU.FastTrig (Figure 6(e)) achieves acceleration of nearly 4X over GPU.ConstMem by using the special functional units (SFUs) to compute each trigonometric operation as a single operation in hardware. When compiled without the use_fast_math compiler option, the algorithm uses implementations of sin and cos provided by an NVIDIA math library. Assuming that the library computes sin and cos using a five-element Taylor series, the trigonometric operations require 13 and 12 floating-point operations, respectively. By contrast, when compiled with the use_fast_math option, each sin or cos computation executes as a single floating-point operation on an SFU. The SFU achieves low latency at the expense of some accuracy. In our experiments (not shown), the images reconstructed by GPU.FastTrig always had lower or only slightly higher percent error than images reconstructed by GPU.ConstMem. Thus, the SFU’s approximate implementations of sin and cos often have negligible impact on the reconstruction’s accuracy. However, further experimentation is necessary to determine whether there are experimental conditions under which these instructions might decrease the quality of a reconstruction.

5.6 GPU.Tune

While GPU.FastTrig overcomes the potential bottlenecks related to off-chip memory accesses and trigonometric computations, the algorithm still per-forms at only 125.5 GFLOPS, which is roughly one-third of the Quadro’s peak theoretical performance. To determine the impact of experiment-driven code transformations, we conducted an exhaustive search that varied the number of threads per block from 32 to 512 (by increments of 32), the tiling factor from 32 to 2,048 (by powers of 2), and the loop unrolling factor from 1 to 8 (by powers of 2).³ Recent work has demonstrated that this type of experimental tuning can be performed quickly and accurately using static analysis techniques, as long as the code is parameterized correctly [33]. For reference, all previous configurations (GPU.Base - GPU.FastTrig) performed no loop unrolling and set both the number of threads per block and the tiling factor to 256. The exhaustive, experiment-driven search selects 128 threads per block, a tiling factor of 512, and a loop unrolling factor of 8. This configuration increases the algorithm’s performance by 47%, with the runtime decreasing to 49 seconds and the throughput increasing to 184 GFLOPS.

Although the code is now well-optimized and tuned, the achieved throughput is just under 50% of the Quadro’s peak throughput. To understand the remaining constraints on performance, we examined GPU.Tune’s ptx code (the assembly-like code generated by nvcc and consumed by the CUDA runtime). In short, the unrolled loop contains 3 integer instructions at the top and 7 integer instructions at the bottom, with the original loop body replicated 8 times in between. The original loop body consists of five loads (to constant memory) and 14 FP instructions (11 simple arithmetic, 2 trigonometric, and 1 MAD). Thus, the unrolled loop computes 120 FLOPS using 162 instructions (74% efficiency), while the peak theoretical throughput requires 2 FLOPS per instruction (200% efficiency). Clearly, GPU.Tune performs somewhat better than this analysis suggests it would, because 100% efficiency is required to reach 50% of the Quadro’s peak throughput. We assume that the CUDA runtime is responsible for this performance boost. For example, the ptx code uses 3 MUL and 2 ADD instructions to compute the quantity exp in Figure 5(c). As exp is expressed in standard sum-of-products form, 1 MUL and 2 MAD instructions are clearly preferred. This transformation alone would boost GPU.Tune’s efficiency to 82%.

5.7 GPU.Multi

In this final experiment, the voxels are divided into four distinct subsets, with one of four Quadros computing F^Hd for each subset. This optimization decreases the time required to compute F^Hd to 14.5 seconds and increases the throughput to over 600 GFLOPS. The acceleration is slightly sub-linear because the overheads (I/O, data marshaling, etc.) represent a significant fraction the time required to compute F^Hd. With F^Hd’s runtime reduced to just 14.5 seconds, Amdahl’s law is beginning to assert itself.

5.8 Improvements in CUDA 1.1

With CUDA 1.1, the performance of the advanced MRI reconstruction is roughly 20% better than with CUDA 1.0. Enhancements to nvcc’s register allocation policy are partially responsible for the improved performance. As Table 1 shows, GPU.Tune uses 13 registers per thread in CUDA 1.1 (when the loop is unrolled 8 times), compared to 19 registers per thread in CUDA 1.0 (when the loop is unrolled only 5 times). Additional loop unrolling in CUDA 1.0 is counter-productive, as the number of registers per thread steadily increases from 19 to 29 as the loop unrolling factor increases from 5 to 8. Increasing the per-thread register usage causes a corresponding decrease in utilization, because the number of threads that can execute simultaneously is inversely proportional to the number of registers per thread.

Table 1.

CUDA 1.0 vs CUDA 1.1. The Registers column refers to registers per thread.

	FHd				Reconstruction (All times in min:sec)
	CUDA 1.0		CUDA 1.1		CUDA 1.0			CUDA 1.1
Config	Registers	GFLOPS	Registers	GFLOPS	FhD	Solver	Total	FhD	Solver	Total
GPU.Base	14	7.02	18	7.05	53:51	0:25	54:17	53:36	0:17	53:53
GPU.RegAlloc	16	11.07	20	11.07	34:08	0:25	34:33	34:09	0:17	34:27
GPU.Layout	16	13.10	20	12.85	28:51	0:25	29:16	29:25	0:17	29:42
GPU.ConstMem	15	85.82	19	82.79	4:24	0:25	4:50	4:34	0:18	4:52
GPU.FastTrig	13	127.54	13	125.49	1:10	0:25	1:36	1:11	0:17	1:29
GPU.Tune	19	151.45	13	184.40	0:59	0:25	1:25	0:49	0:17	1:06
GPU.Multi	19	502.22	13	615.75	0:18	0:25	0:43	0:15	0:18	0:32

Likewise, enhancements to nvcc’s code generation also contribute to improved performance. In CUDA 1.0, nvcc generates four additional integer instructions each time the inner loop of F^Hd is unrolled. These instructions compute the base address of the next data sample in constant memory. Each load instruction then uses an integer offset to access the desired element of the data sample (e.g., k_x or k_y). By contrast, in CUDA 1.1, the base address of the next data sample is computed once at the top of the unrolled loop, and the integer off-sets are adjusted so that each load accesses the correct data sample. Given that the original loop body contains only 19 ptx instructions, the unnecessary overhead of 4 additional instructions per loop iteration is significant.

6 Related Work

General-purpose computing on graphics processing units (often termed GPGPU or GPU computing) supports a broad range of scientific and engineering applications, including physical simulation, signal and image processing, database management, and data mining [30]. Medical imaging was one of the first GPU computing applications. In 1994 Cabral et al. observed that volume rendering essentially performs a generalized Radon transform, while the filtered backprojection algorithm for computed tomography (CT) reconstruction performs an inverse Radon transform. The CT reconstruction based on filtered backprojection achieved a speedup of two orders of magnitude on the SGI RealityEngine [6].

A wide variety of CT reconstruction algorithms have since been accelerated on graphics processors [25,46,8,26], and the Cell Broadband Engine [4,34]. Filtered backprojection algorithms receive further attention in [25] and [46], while [8] studies the performance of two iterative algorithms for CT reconstruction (the Maximum Likelihood Expectation Maximization and Ordered Subset Expectation Maximization algorithms) on the GPU. In [26] the GPU is used to accelerate Simultaneous Algebraic Reconstruction Technique (SART), an algorithm that increases the quality of image reconstruction relative to the conventional filtered backprojection algorithm under certain conditions. SART, which requires significantly more computation than backprojection, becomes a viable clinical option when executed on the GPU. Finally, [4] and [34] accelerate CT reconstructions based on cone-beam backprojection on the Cell/BE.

By contrast, MRI reconstruction on the GPU has not been studied extensively. Research in this area has focused on accelerating the fast Fourier transform (FFT), which is a key component of many MRI reconstruction algorithms. Speedups on the order of 2x-9x have been reported [41,35,21]. In [38], Sørensen et al. use a GPU to accelerate a gridding algorithm for MRI reconstruction, achieving a substantial speedup over the baseline implementation. GPU-based parallel imaging shows promising results in [18]. Finally, the acceleration of the advanced reconstruction algorithm described in this paper builds on our earlier work with the same algorithm [40,39]. Baskaran et al. have independently observed that the F^Hd algorithm can be efficiently mapped to the GPU using a parallelizing compiler [3].

7 Conclusions and Future Work

In many applications, magnetic resonance imaging is limited by high noise levels, imaging artifacts, and long scan times. Advanced image reconstructions, which can operate on arbitrary scan trajectories and incorporate anatomical constraints, can mitigate these limitations at the expense of substantial computation. The computational resources, architectural features, and programmability of the Quadro FX 5600 reduce the time for an advanced reconstruction of non-uniform MRI scan data from nearly 23 minutes on a quad-core CPU to just over one minute on the Quadro, making the reconstruction practical for many clinical applications.

The single-precision floating-point arithmetic and approximate trigonometric operations that help accelerate the advanced reconstruction may, under certain conditions, degrade the quality of the reconstructed image. While we did not observe this phenomenon during our reconstructions of the 3D phantom image, we view further investigation of the advanced reconstruction algorithm’s sensitivity to numerical approximations as important future work.

Biography