Abstract
One enduring question in evolutionary biology is the extent of archaic admixture in the genomes of present-day populations. In this paper, we present a test for ancient admixture that exploits the asymmetry in the frequencies of the two nonconcordant gene trees in a three-population tree. This test was first applied to detect interbreeding between Neandertals and modern humans. We derive the analytic expectation of a test statistic, called the D statistic, which is sensitive to asymmetry under alternative demographic scenarios. We show that the D statistic is insensitive to some demographic assumptions such as ancestral population sizes and requires only the assumption that the ancestral populations were randomly mating. An important aspect of D statistics is that they can be used to detect archaic admixture even when no archaic sample is available. We explore the effect of sequencing error on the false-positive rate of the test for admixture, and we show how to estimate the proportion of archaic ancestry in the genomes of present-day populations. We also investigate a model of subdivision in ancestral populations that can result in D statistics that indicate recent admixture.
Keywords: admixture, gene genealogies, lineage sorting
Introduction
Detecting ancient admixture and estimating the extent of archaic ancestry in the genomes of present-day populations are of major importance for many aspects of evolutionary biology (Barton 2001). Admixture occurs during secondary contact between previously isolated populations, and it can play an important role in the speciation process (Barton and Hewitt 1985; Barton 2001). Among anthropologists, there is a long-standing debate on the relationships between modern humans and different groups of archaic humans such as Neandertals. A recent analysis of a draft sequence of the Neandertal genome suggested that 1–4% of genomes from people of Eurasian ancestry are derived from Neandertal (Green et al. 2010). However, there is still no consensus on the overall extent of interbreeding between archaic and modern humans (for a review, see Wall and Hammer 2006).
Methods for detecting and estimating archaic admixture often rely on DNA sequence data from extent populations only. One class of such methods relies on the signature that ancient admixture leaves on patterns of linkage disequilibrium (Plagnol and Wall 2006; Wall et al. 2009). Although they have the advantage of not relying on scarce or damaged ancient DNA samples, they make simplifying assumptions about the demographic history of extant populations that are not testable in general (Wall and Hammer 2006). Another class of methods models genetic introgression using spatially explicit simulations. They aim to make predictions about the proportion of introgression in present-day genomes if ancient admixture had occurred. These methods use either forward-in-time computer simulations (Currat and Excoffier 2004) or deterministic modeling (Forhan et al. 2008).
Recently, direct comparisons of DNA sequences between extant and archaic populations have been made possible by the sequencing of ancient DNA samples. In humans, this line of research began with a comparison of mitochondrial DNA between modern humans and Neandertals (Krings et al. 1997; Serre et al. 2004; Green et al. 2008). It was then extended to fragments of Neandertal nuclear DNA (Green et al. 2006; Noonan et al. 2006; Krause et al. 2007; Lalueza-Fox et al. 2007); the full sequence of Neandertals was finally analyzed in Green et al. (2010). Although data from extinct populations are still limited, direct comparison of ancient and modern sequences has the potential to directly determine the proportion of present-day genomes inherited from archaic populations (Wall 2000). Green et al. (2010) developed a formal test for admixture based on the direct comparison of DNA sequences from Neandertals and modern human populations.
Green et al. (2010) defined a new statistic, called the D statistic, to test for admixture between three closely related populations. The expectation of D was derived under a simple model of admixture with constant population size and was used to estimate the proportion of Neandertal ancestry in modern humans (Green et al. 2010, Supplementary Online Material 19). However, Green et al. (2010) noted that their test relies on the assumption that the population ancestral to the sampled populations was randomly mating. In this paper, we extend the results of Green et al. (2010) by deriving the expectation of D under a model where the ancestral populations are not randomly mating. We also study the statistical properties of D. In addition, we explore the effects of sequencing error and ascertainment bias on D, and we show that D can indicate past admixture even when the admixing population is not sampled.
In a first section, we recall the definition of the D statistic and why it is expected to detect admixture in the case of randomly mating ancestral populations. Then we derive the expectation of D under a model of admixture with arbitrarily varying ancestral population sizes, which generalizes the model of admixture proposed in Green et al. (2010). The derivation reveals a strategy to estimate the proportion of archaic introgression in present-day genomes. In a next section, we derive the expectation of D in a model where the ancestral populations are not randomly mating and show that ancient population structure can confound the test for admixture. Then we determine the effect of sequencing error on D, and we study the power of the test for admixture on synthetic data. When D is computed from genotype data, we determine the impact of ascertainment bias on the test for admixture. Although Green et al. (2010) defined D to compare the Neandertal genome with the sequences of modern humans, we show that D statistics can be used to test for admixture when no archaic sample is available. Finally, we apply the test to the Neandertal data published in Green et al. (2010).
Materials and Methods
A Four-Taxon Statistic to Test for Admixture
Assume that we have sequenced one chromosome from two present-day populations and denote by P1 and P2 those populations. Furthermore, assume that we have sampled one chromosome from an archaic population, which we denote as P3, and one chromosome from an outgroup population, denoted O. Suppose that the four sequences were aligned without error. The null hypothesis that we wish to test is a demographic scenario in which P1 and P2 descend from a common ancestral population that diverged from the ancestors of P3 at an earlier time, without any gene flow between P3 and P1 or P2 after they split. The alternative hypothesis is that P3 exchanged genes with P1 or P2 after these two populations diverged.
We first restrict to positions in the genome where we have coverage for P1, P2, P3, and O. We denote the outgroup allele as “A” and restrict our analysis to biallelic sites at which P1 and P2 differ and the alternative allele “B” is seen in P3. At these sites, we have observed two copies of both alleles, making it less likely that the patterns we analyze have arisen because of sequencing error.
For the ordered set {P1, P2, P3, O}, we call the two allelic configurations of interest “ABBA” or “BABA.” The pattern ABBA refers to biallelic sites where P1 has the outgroup allele and P2 and P3 share the derived copy. The pattern BABA corresponds to sites where P1 and P3 share the derived allele and P2 has the outgroup allele. Green et al. (2010) defined a statistic corresponding to the difference in the counts of ABBA and BABA sites across the n base pairs for which we have data of all four samples, normalized by the total number of observations. In this statistic, CABBA(i) and CBABA(i) are indicator variables; they can be 0 or 1 depending on whether an ABBA or a BABA pattern is seen at base i. Green et al. (2010) denoted this statistic by D, and we have
| (1) |
We further denote by S(P1, P2, P3, O) the numerator of D(P1, P2, P3, O).
Under the null hypothesis that P1 and P2 descend from a common ancestral population that diverged at an earlier time from the ancestral population of P3, and if the ancestral population of P1, P2, and P3 was panmictic, then derived alleles in P3 should match derived alleles in P1 and P2 equally often. This is because the patterns ABBA and BABA can only arise from gene trees that are nonconcordant with the population tree of P1, P2, and P3. Under the null hypothesis, the two nonconcordant gene trees should occur with equal frequencies (Tajima 1983; Hudson 1983), and D should equal zero. There are three classes of events that can produce a significant deviation from the null hypothesis. First, P3 exchanged genes with P1 or P2. Then the population ancestral to P1, P2, and P3 may have been structured in such a way that one of the two non-concordant gene trees occurs more often than the other. Alternatively, P1 or P2 could have received genes from an unsampled ghost population that we denote as PG. Note that PG needs to be at least as diverged as P3 from (P1, P2) for D to differ significantly from zero (supplementary fig. S1, Supplementary Material online). Also note that gene flow between P1 and P2, or between P3 and the ancestor of P1 and P2, is not expected to produce a deviation from the null hypothesis.
Although D statistics are primarily designed to be applied on sequence data, they can be readily computed on single nucleotide polymorphism (SNP) data. Assume that n SNPs were genotyped in populations P1, P2, P3, and O. Denote by the observed frequency of SNP i in population Pj (j = 4 denotes population O). We have
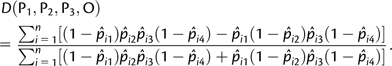 |
(2) |
Thus, computing D on genotype data is straightforward. However, the way SNPs were ascertained can bias estimates of allele frequencies in the different populations (Eberle and Kruglyak 2000; Kuhner et al. 2000; Clark et al. 2005).
A Genealogical Argument for the Expected Frequencies of ABBA and BABA Sites
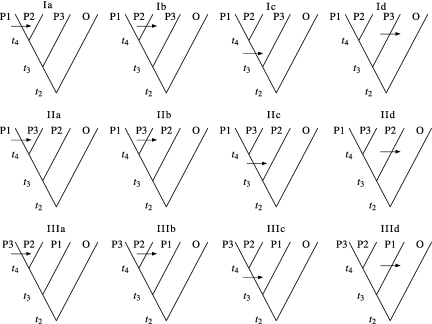
Assume that a single nucleotide substitution occurred on the gene genealogy representing the ancestry of the four samples (P1, P2, P3, and O). There are three possible topologies of the gene genealogy, assuming that O is the outgroup. Each of these topologies has four branches on which a mutation can create a derived allele in P1, P2, and P3. Figure 1 presents the 12 possible configurations for the four samples P1, P2, P3, and O, assuming that O carries the ancestral allele. The pattern BABA (P1 and P3 have the derived nucleotide) is consistent only with tree IIc. The length of the internal branch represents the time during which a mutation can produce the BABA pattern. Similarly, the pattern ABBA (P2 and P3 have the derived nucleotide) is consistent only with tree IIIc, and the length of that internal branch is the time during which mutation can create ABBA. The probability that a randomly chosen site will have either pattern is the probability of the appropriate topology multiplied by the expected branch length multiplied by the mutation rate, μ. Thus, to derive the expected frequencies of patterns ABBA and BABA, we need to compute the probabilities of the corresponding tree topologies and average lengths of the relevant branches under the demographic scenario relating P1, P2, and P3.
FIG. 1.
There are three possible topologies of the gene genealogies, I, II, and III, that can relate samples P1, P2, and P3, and the outgroup O. Assuming that any polymorphisms reflect a single historical mutation, ABBA sites can occur only on a type III gene genealogy due to a mutation that occurs on the branch ancestral to samples P2 and P3 (IIIc), and BABA sites can occur only on a type II gene genealogy due to a mutation on the branch ancestral to samples P1 and P3 (IIc).
In what follows, we derive the expected frequencies of patterns ABBA and BABA under a simple demographic model of ancient admixture. We use this model to show that the test is not confounded by demographic events other than admixture, assuming that the population ancestral to P1, P2, and P3 was panmictic.
Instantaneous Unidirectional Admixture
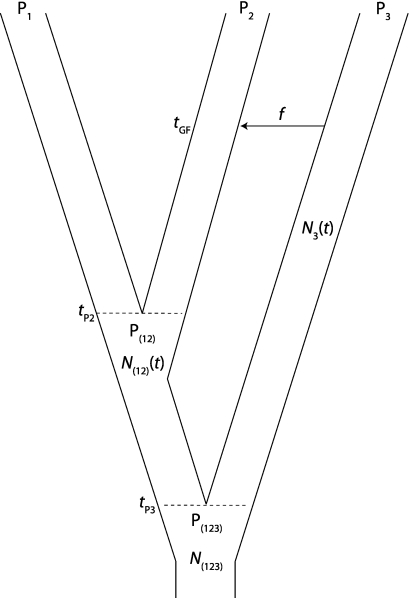
In this model, we assume that there was a single episode of admixture at time tGF in the past (t = 0 being the present) from population P3 to P2 after the separation of populations P1 and P2 (fig. 2). With probability f, the P2 lineage was derived from a lineage from P3. The parameter f represents the fraction of the genomes in P2 that originated from P3. We define the divergence time of P1 and P2 populations as tP2 > tGF. We denote by tP3 > tP2 the divergence time of P3 and the population ancestral to P1 and P2, denoted P(12). At generation t in the past, the effective population size of the P3 population is N3(t); the effective size of P(12) is N(12)(t); and the effective size of the population ancestral to P1, P2, and P3, denoted P(123), is N(123)(t). All the populations are assumed to be unstructured (i.e., they are randomly mating). We denote by IUA the instantaneous unidirectional admixture model.
FIG. 2.
Model of IUA. P1 and P2 split at time tP2. P3 splits from the ancestral population of P1 and P2, denoted P(12), at time tP3. A single episode of admixture takes place from P3 to P2 at time tGF. We denote by f the admixture proportion, which is the proportion of P3 ancestry in P2 individuals at time tGF. We denote by N3(t), N(12)(t), and N(123)(t) the size of populations P3, P(12), and P(123) at generation t in the past. The sizes of populations P1 and P2 do not influence D statistics.
Expected Counts of ABBA and BABA under the Model of Instantaneous Admixture
Under the IUA model, there are three classes of events that can produce the patterns ABBA and BABA. The first class corresponds to the case where the P2 lineage did not originate from P3. It occurs with probability 1 − f. In the second class of events, the P2 lineage traces its ancestry in P3 (probability f), but the P2 and P3 lineages did not coalesce before tP3. The third class corresponds to the case where the P2 lineage originated from P3 (probability f) and the P2 and P3 lineages coalesced before tP3. The first two classes produce patterns ABBA and BABA with equal frequencies. This is because, assuming that P(123) was panmictic, the P3 lineage coalesces first with probability 1/3. The third class of event produces only ABBA because the P2 and P3 lineages coalesced first. The probabilities of ABBA and BABA are derived in Appendix 1 for a model with arbitrary varying population size in P3 and P(12) and constant population size in P(123).
Green et al. (2010) studied the simplified case where population size is constant. When we set N3(t) = N(12)(t) = N(123) = N in Appendix 1, we find, in accordance with Green et al. (2010), that
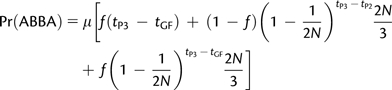 |
(3) |
and
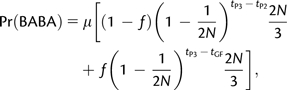 |
(4) |
where μ denotes the per base mutation rate. In this case, the expectation of D reduces to
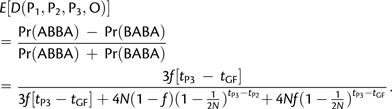 |
(5) |
Note that the test statistic equals 0 when there is no admixture (f = 0). If there is admixture (f > 0), D tends to one when tP3 – tGF becomes large. This is because the P2 and P3 lineages have more time to coalesce as tP3 – tGF increases. Finally, in the case of constant ancestral population size, D tends to 0 when the effective population size becomes large. This is explained by the fact that when N is large, then the probability that the P2 and P3 lineages coalesce in P3 is small.
A Test for Admixture Insensitive to Many Demographic Assumptions
Under the IUA model, equation (A1.5) shows that E[D(P1, P2, P3, O)] = 0 if and only if f = 0 or tGF = tP3, regardless of the population size fluctuations of P1, P2, P3, P(12), and P(123) (as long as population sizes stay finite) and regardless of the times of population divergences and admixture (as long as tGF < tP3). Note that a model with tGF = tP3 is equivalent to a model without admixture (see fig. 2). Thus, under the IUA model assumptions, a significant deviation from 0 of D(P1, P2, P3, O) indicates that P3 exchanged genes with P1 (D(P1, P2, P3, O) < 0) or P2 (D(P1, P2, P3, O) > 0). Although we modeled admixture with an instantaneous episode of gene flow, this conclusion holds for ongoing migration between P3 and P2 or P1.
Sites involved in the computation of D are likely to be in linkage disequilibrium. Therefore, a simple binomial test to assess whether D significantly differs from zero is not appropriate. Instead, the test significance can be assessed using a standard block jackknife procedure (Efron 1981). In this procedure, one removes blocks of adjacent sites one at a time. The size of blocks should be chosen to be larger than the extent of linkage disequilibrium. By computing the variance of the D statistic over the sequences M times leaving each block of the sequence in turn, and then multiplying by M and taking the square root, we can obtain an approximately normally distributed standard error using the theory of the jackknife (Reich et al. 2009).
Constraining the Admixture Proportion
D statistics depend on the demographic parameters in a complex way. As such, they are not good candidates to estimate demographic parameters. However, Appendix 1 shows that the numerator of D, denoted S, is a much simpler function of demographic parameters; for a model with arbitrary varying population sizes, we have
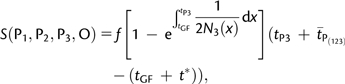 |
(6) |
where is the expected time of coalescence of two lineages in P(123) and t* is the expected time of coalescence of two lineages in P3, given that they coalesced between tGF and tP3. The time is equal to 2N(123) in Appendix 1 where we assumed constant population size in P(123). Assume now that we have sampled a second lineage in P3. Denote by P3,1 and P3,2 the two lineages sampled in P3. It is straightforward to see that S(P1, P3,1, P3,2, O) is equal to S(P1, P2, P3, O) with f = 1 and tGF = 0 because populations P2 and P3 are identical with such parameter values. Therefore,
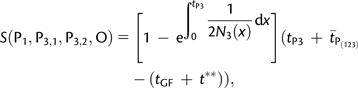 |
(7) |
where t** is the expected time of coalescence of two lineages in P3, given that they coalesced between t = 0 and tP3. Thus, S(P1, P2, P3, O)/S(P1, P3,1, P3,2, O) is an upper bound for f. In the case of constant ancestral population size, we have
| (8) |
If we assume that tGF is small compared with tP3, then one can estimate f by 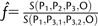 , which is a conservative minimum.
, which is a conservative minimum.
We note here that the strategy to estimate the admixture proportion can be extended to more populations. Assume that a sample from a sister population of P3 is available. Denote by P4 this population and assume that it diverged from P3 before the admixture event (tP4 > tGF, where tP4 is the time of divergence of P3 and P4) (supplementary fig. S2, Supplementary Material online). Then 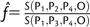 is an unbiased estimate of the admixture proportion independent of population sizes and divergence times.
is an unbiased estimate of the admixture proportion independent of population sizes and divergence times.
Testing for Admixture without Archaic Sample
In practice, it may be very common that no sample from the admixing archaic population is available. On the other hand, it may be fairly easy to sample from other extant populations. Assume that a sample from an outgroup to P1 and P2 is available and denote by P0 this population. Assume that P0 did not exchange genes with P1 or P2. Let tP0 be the time of divergence of P0 and the population ancestral to P1 and P2 (see supplementary fig. S3, Supplementary Material online). We can then derive D(P2, P1, P0, O) following the same methodology as in Appendix 1. In the case where population size is constant and equal to N in all ancestral populations, we have
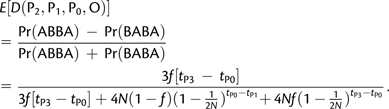 |
(9) |
It is remarkable that equation (9) does not depend on the time of admixture, tGF, which is likely to be unknown. It does depend, however, on the time of divergence of the archaic population, tP3. Using two samples from P0 or P1, one can constrain the admixture proportion by using the same strategy as the one using two samples from P3.
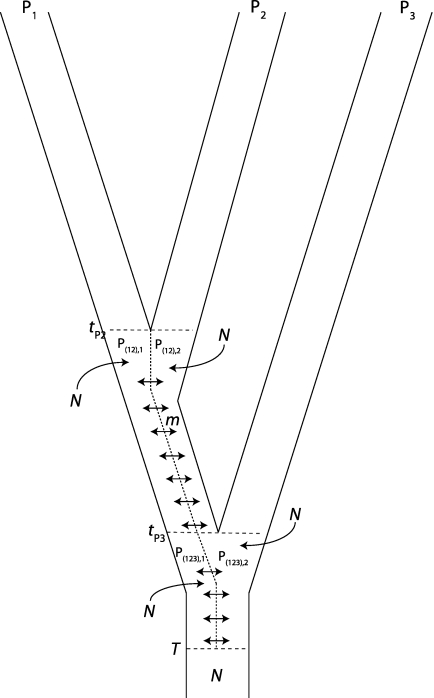
Ancestral Subdivision
Here we derive the expected frequencies of patterns ABBA and BABA under a simple model in which the ancestral population of P1, P2, and P3 is not panmictic. We assume that the ancestral populations P(12) and P(123) were structured in two random mating subpopulations (fig. 3). We denote by P(12),1 and P(12),2 the subpopulations in P(12) and by P(123),1 and P(123),2 in P(123). We assume that subpopulations exchange migrants at symmetrical rate m per generation. At time T in the past, subpopulations merge into one panmictic population. We assume constant population size N in all ancestral populations. A similar model was proposed in Slatkin and Pollack (2008). Slatkin and Pollack (2008) showed that, for large values of T, the nonconcordant gene tree compatible with pattern ABBA occurred with higher frequency than the other nonconcordant gene tree. For small values of m, its frequency is even higher than the frequency of the concordant gene tree. We use AS to denote the ancestral subdivision model.
FIG. 3.
Model of ancient subdivision (AS). P1 and P2 definitively split at time tP2. The ancestral population of P1 and P2 is subdivided in two subpopulations, denoted P(12),1 and P(12),2. The two subpopulations exchange migrants at rate m. P3 splits at time tP3. The subdivision persists in the ancestral population of P(12),1, P(12),2, and P3. We denote by P(123),1 the population ancestral to P(12),1 and by P(123),2 the ancestral population of P(12),2. These two subpopulations exchange migrants at rate m. Subpopulations merge at time T > tP3. All population sizes are constant and equal to N.
Five-State Markov Chain in P(12)
To analyze the ancestry of the P1 and P2 lineages in P(12), we use a Markov chain method similar to the one developed by Slatkin and Pollack (2008). The states of the Markov chain are as follows: state 1, P1 is in P(12),1 and P2 is in P(12),2 (initial state); state 2, P1 is in P(12),2 and P2 is in P(12),1; state 3, P1 and P2 are both in P(12),1; state 4, P1 and P2 are both in P(12),2, and state 5, P1 and P2 coalesced (absorbing state).
To write the transition probabilities, we assume that m is small enough that only one lineage can migrate to another subpopulation per generation. Moreover, coalescent and migration events cannot occur at the same generation. Assuming constant population size N in P(12),1 and P(12),2, the nonzero off-diagonal elements of the transition matrix P(12) are
At time tP3, the distribution of states is π(12)(tP3) = π(12)(tP2)(P(12))tP3 − tP2, where π(12)(tP2) = {1,0,0,0,0}.
Thirteen-State Markov Chain in P(123)
To model the ancestry of P1, P2, and P3 in P(123), we use a 13-state Markov chain with states defined by state 1, P3, P2 | P1; state 2, P1, P3 | P2; state 3, P1, P2 | P3; state 4, P1, P2, P3; state 5, (P2, P3) | P1; state 6, (P1, P3) | P2; state 7, (P1, P2) | P3; state 8, (P2, P3), P1; state 9, (P1, P3), P2; state 10, (P1, P2), P3; state 11, ((P2, P3), P1); state 12, ((P1, P3), P2), and state 13, ((P1, P2), P3). We used the symbol “|” to denote that lineages are in different subpopulations and brackets denote coalescence events. For example, state 6 takes into account the case where P1 and P3 lineages have coalesced, and the resulting ancestral lineage is in a different subpopulation than the P2 lineage.
Again we assume that m is small enough that only one lineage can migrate to another subpopulation per generation and that coalescent and migration events cannot occur at the same generation. Assuming constant population size N in P(123),1 and P(123),2, the nonzero off-diagonal elements of the transition matrix P(123) are
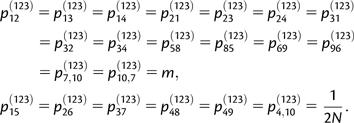 |
At time T, the distribution of states is π(123)(tP3) = π(123)(tP3)(P(123))T − tP3, where π(123)(tP3) = {π1(12),π2(12),π3(12),π4(12),0,0,π5(12),0,0,0,0,0,0}.
Events (coalescence and/or migration) in P(12) only affect the expected value of D by changing the starting probabilities in P(123). Appendix 2 presents the details of all the possible cases leading to ABBA and BABA patterns at time T, where all subpopulations merge into a single random mating population.
The frequencies of patterns ABBA and BABA have no simple analytical expressions under the AS model. However, they can be easily computed numerically for any set of parameter values.
Expected Coalescence Time Conditional on Gene Tree Topology
In this section, we derive the expected coalescence time of P2 and P3, given that they coalesced first, under the IUA and the AS models. This is a quantity of interest because it determines the length of the internal branch of tree topology III (fig. 1), and therefore the frequency of pattern ABBA. We use these derivations to illustrate the confounding effect of ancestral subdivision on the test for admixture.
We denote by τ23(IUA) the expected coalescence time of P2 and P3, given that they coalesced first, under the IUA model with constant ancestral population size. It can be decomposed as the sum of two terms, depending on whether the P2 lineage originated from P3 or not:
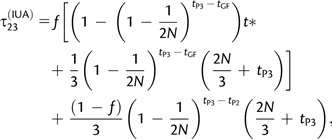 |
(10) |
where t* is the expected time of coalescence of P2 and P3 given that they coalesce between tGF and tP3 (Appendix 1, eq. A1.3).
Then we derive the conditional expected time of coalescence of P2 and P3 under the AS model, denoted τ23(AS). We start by conditioning on whether coalescence occurs before time T:
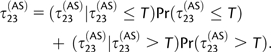 |
(11) |
The first term is equal to the expected time for the Markov chain to first hit state 5, 8, or 11, conditional on this time being lower than T; we compute it using standard Markov chain theory. It can be shown that this conditional time tends to 4N + 1/(2m) when T grows to infinity, which is equal to the expected coalescence time of two individuals in different demes in a two-island model (Slatkin 1991). Because the ancestral population is assumed to be panmictic after time T, the second term of equation (10) is equal to
| (12) |
Although there is no simple analytical expression for τ23(AS), it can be computed numerically for any set of parameter values.
Effect of Sequencing Error on D Statistics
In this section, we study the effect of sequencing error on D. In what follows, we use capital letters to denote the observed count of a pattern and small letters to denote the true counts in the absence of sequencing error. We assume that sequencing error is uniform along the sequence. We denote by e1, e2, e3, and e4 the probability that a base was incorrectly read in population P1, P2, P3, and O, respectively. Let eij be the probability that a site was read with an error in populations Pi and Pj at the same time (j = 4 denotes population O). We neglect terms of higher order. A sequencing error on O will cause the reads for P1, P2, and P3 to be mislabeled. For example, if O was sequenced with an error at a site where the true pattern is “aaaa”, we would read pattern “BBBA.” Thus, for the two patterns of interest, we have
 |
(13) |
and
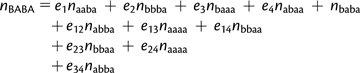 |
(14) |
assuming that error rates are small.
False-Positive Rate in the Presence of Sequencing Error
Here we look at the effect of sequencing error on the false-positive rate of the test for admixture. We assume a null model with no admixture and randomly mating ancestral populations. In this model, the true expected counts verify nabba = nbaba and nabaa = nbaaa. The second equality assumes that the mutation rates in P1 and P2 are equal. Under these assumptions, we have
| (15) |
The effect of sequencing error on D(P1, P2, P3, O) is then
| (16) |
If the sequencing error rates are the same for the four samples, then sequencing error will have no influence on the false-positive rate of the test as long as they are small enough that third-order terms can be ignored.
To illustrate the effect of different sequencing error rates on the false-positive rate of the test, note that in the case where the outgroup divergence time, tO, is large compared with the divergence time of P3, the two dominant patterns will be bbba and aaaa. We considered a case where 98% of sites were aaaa, 0.02% abba and baba, and 1.97% bbba. All other configurations represented 0.01% of sites. We took 109 sites in total. This settings roughly correspond to a population tree where P1 and P2 are modern human populations, P3 is a Neandertal population, and Chimpanzee is the outgroup. Indeed, Green et al. (2010) estimated that the time of divergence of Neandertal and modern humans was less than 440,000 years before present, which is small compared with divergence time of modern humans and chimpanzee.
Under the simplifying assumption that sites are independent, true pattern counts abba and baba follow a binomial distribution with parameters p = 0.5 and n = nabba + nbaba. In this case, the standard deviation (SD) of D is equal to 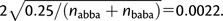 .
.
Synthetic Data Analysis
Power of the Test for Admixture
In order to assess the power of the test for admixture, we simulated data under different demographic scenarios. To simulate counts for ABBA and BABA patterns, we simulated trees using the ms software (Hudson 2002). We then placed a mutation on the tree; the branch it fell on was selected with probability proportional to its length. The descendants of the mutated branch then define which pattern was generated. Under this simulation scheme, the number of independent ms replicates corresponds to the number of unlinked polymorphic sites in the three populations P1, P2, and P3. For all the demographic scenarios described below, we varied this number between 10,000 and 1,000,000.
We simulated counts for ABBA and BABA patterns under the IUA model. The time of divergence of P1 and P2 was set to tP2 = 3,000 generations. P3 diverged from the ancestral population P(123) at time tP3 = 12,000 generations. Admixture occurred at time tGF = 2,500 generations. We considered different cases for the ancestral population sizes: constant size N = 10,000 in all populations; a bottleneck in P3 prior to the admixture event; and a bottleneck in P(12). Both bottlenecks involved a 100-fold reduction in population size and lasted for 1,000 generations. They both started at 3,500 generations in the past. We also considered a case where P1 and P2 exchanged migrants at rate 2Nm = 0.5 between t = 0 and tP2. We varied the admixture proportion f from 0 (no admixture) to 0.1 (10% introgression from P3 into P2).
Because replicates are independent, D is approximately normally distributed, and its SD can be computed from the binomial distribution: 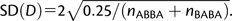 Each simulation class was repeated 1,000 times. We computed the power of the test for admixture as the proportions of the 1,000 repetitions were |D| was larger than twice its standard error. For the simulations without admixture, we expect that roughly 95% of the simulated D statistics will be comprised between plus or minus twice the SD.
Each simulation class was repeated 1,000 times. We computed the power of the test for admixture as the proportions of the 1,000 repetitions were |D| was larger than twice its standard error. For the simulations without admixture, we expect that roughly 95% of the simulated D statistics will be comprised between plus or minus twice the SD.
Effect of Ascertainment Bias
When computed on genotype data, the way SNPs were ascertained can bias D statistics. Typically, an ascertainment scheme consists of two phases. First, SNPs are discovered from the genetic material of a small group of individuals, called the discovery panel. Then the discovered SNPs are typed in a larger sample (Eberle and Kruglyak 2000). The extent to which the ascertainment scheme will bias D statistics depends on many parameters, such as the genetic composition of the discovery panel and its relationship to the larger samples. Ascertainment bias can be corrected when one assumes that the discovery panel is a random sample from the studied population (Nielsen et al. 2004). However, in the context of D statistics, the relationship between the discovery sample and the four typed populations P1, P2, P3, and O can be complex.
To illustrate the effect of a simple ascertainment scheme on D statistics, we simulated genotype data under the IUA model using 100,000 independent replicates of ms (Hudson 2002). The time of divergence of P1 and P2 was set to tP2 = 3,000 generations. P3 diverged from the ancestral population P(123) at time tP3 = 12,000 generations. Admixture occurred at time tGF = 2,500 generations. All population sizes were set equal to N = 10,000. We simulated 100 individuals in P1 and P2 and 1 individual in P3. To simulate ascertainment bias, we subsampled individuals in P1 or P2 and kept only sites that were variable in those individuals. In total, we explored five subsampling scenarios: 1) 2 individuals from P1; 2) 20 individuals from P1; 3) 2 individuals from P2; 4) 20 individuals from P2; and 5) no subsampling (no ascertainment bias). Each of these five subsampling scenarios was repeated for f = 0 (no admixture) and f = 0.05 (5% introgression from P3 into P2).
Application to Neandertal Data
The Neandertal genome was recently sequenced to ∼1× coverage, producing a total of ∼4 billon base pairs (Green et al. 2010). Green et al. (2010) analyzed data from five present-day human males from the CEPH-Human Genome Diversity Project panel (French, Han, Papuan, San, and Yoruba) that were sequenced to ∼5× coverage. For each pair of modern humans P1 and P2, Green et al. (2010) computed D(P1, P2, Neandertal, Chimpanzee). The chimpanzee individual was represented by the reference chimpanzee genome (PanTro2).
Results
Ancient Subdivision Confounds the Test for Admixture
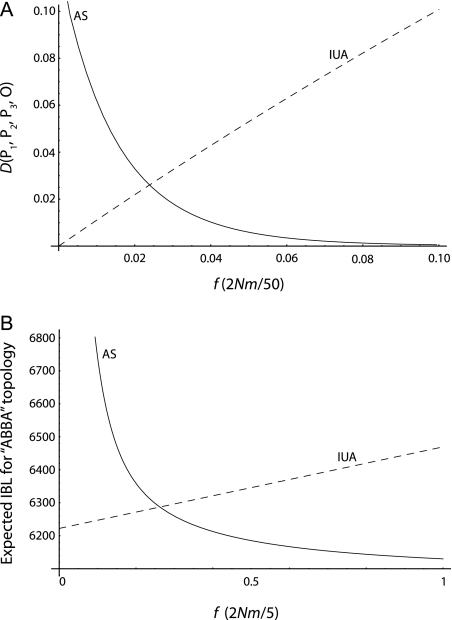
We computed D(P1, P2, P3, O) under the IUA and the AS models (Appendices 1 and 2) for parameter values tGF = 2,500, tP2 = 3,000, tP3 = 12,000, T = 25,000 (times in generations), and a constant ancestral population size equal to N = 10,000. Figure 4A displays D statistics as a function of f (IUA) and 2Nm (AS). We also computed the expected time of coalescence of P2 and P3 given that they coalesced first. Figure 4B displays τ23(IUA) as a function of f and τ23(AS) as a function of 2Nm. We used a computer algebra program to compute numerically quantities under the AS model.
FIG. 4.
D statistics and expected coalescence time of P2 and P3 under the IUA and AS models. We assumed parameter values of tGF = 2,500, tP2 = 3,000, tP3 = 12,000, T = 25,000 (times in generations), and a constant ancestral population size equal to N = 10,000. (A) D(P1, P2, P3, O) as a function of f (IUA) and 2Nm (AS). (B) Expected internal branch length (IBL) for topologies where P2 and P3 coalesced first as a function of f (IUA) and 2Nm (AS). The rescaling for 2Nm on (A) and (B) was chosen so that 2Nm and f vary in the same range.
The D statistic curves intersect, which shows that both the IUA and the AS models can be made to fit data if P3 shares more derived allele with P1 or P2. Therefore, the test for admixture based on D alone will always be confounded by the presence of ancestral subdivision.
More generally, figure 4B shows that the IUA and the AS models predict the same expected coalescence times for some parameter values. Thus, any test for admixture solely based on expected coalescence times between one lineage from different populations will be confounded by nonrandom mating in ancestral populations.
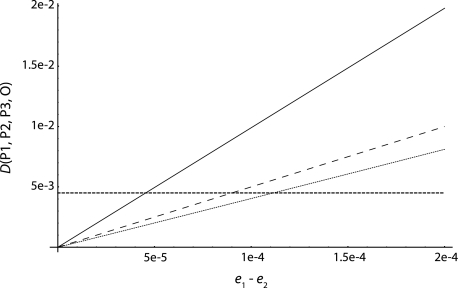
Robustness to Sequencing Error
We assume a background sequencing error of 0.001 in each sample. Figure 5 plots D against e1 − e2, keeping e1 + e2 = 0.002 and e3 = e4 = 0.001. If we assume that the sequencing error rate in two populations is the product of error rates in each of the two populations (i.e., errors are independent in the two populations), then a difference in sequencing error rates e1 − e2 = 0.00011 will cause the test for admixture to produce false-positive results. If we assume that the probability to sequence two populations with an error at the same base is only one order of magnitude lower than the error rate in one population, then differences in error rates of 0.00008 will create false positives. In the worst-case scenario, where sequencing error in two populations is of the same order of magnitude as sequencing error in one populations, then e1 − e2 = 0.000045 is enough to create false positives.
FIG. 5.
D(P1, P2, P3, O) as a function of the sequencing error difference e1 − e2. The dotted curve assumes that the probability to have an error in two populations is equal to the product of sequencing errors in the two populations (eij = ei × ej). The dashed curve corresponds to eij = min(ei, ej)/10, and the solid line assumes eij = min(ei, ej). The horizontal dashed line corresponds to twice the standard error of D, assuming that sites are independent.
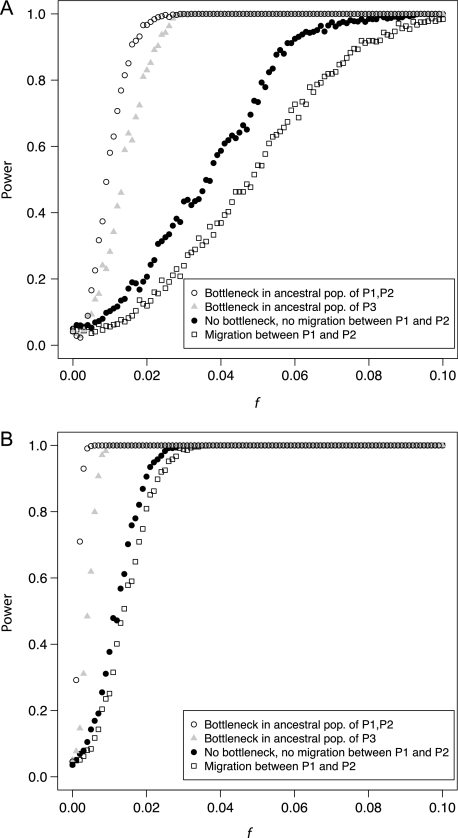
Power of the Test for Admixture
Figure 6 reports the power analysis for the simulations of instantaneous admixture with constant population size, a bottleneck in P3, a bottleneck in P(12), and migration between P1 and P2. Adding a bottleneck in P3 increased the power of the test substantially; this is because, if the P2 lineage originated from P3, the bottleneck increases the probability that the P2 and P3 lineages coalesce before tP3. Adding a bottleneck in P(12) improved the power of the test even more. This is because, in the case where admixture did not happen (eq. A1.1), the probability that the P1 and P2 lineages do not coalesce before tP3 is decreased by the bottleneck. Therefore, this case contributes less to the denominator of D. Migration between P1 and P2 decreased the power of the test for admixture.
FIG. 6.
Power of the test for admixture. We simulated (A) 10,000 unlinked polymorphic sites and (B) 100,000 unlinked polymorphic sites. Dots: no bottleneck and no migration between P1 and P2. Circles: bottleneck in the ancestral population of P1 and P2. Grey triangles: bottleneck in P3. Squares: ongoing migration between P1 and P2 at rate 2Nm = 0.5. All bottlenecks involved a 100-fold reduction in population size and lasted 1,000 generations. They started at 3,500 generations in the past.
For the simulations without admixture (f = 0), figure 6 reports the false-positive rate of the test for admixture at a 5% level. In the case of constant population size, the false-positive rate was 0.050 for 10,000 sites and 0.046 for 100,000 sites. This is an expected result as D is approximately normally distributed for independent sites. Plus or minus twice the SD represents roughly a 95% confidence interval for D. As predicted, adding bottlenecks in the ancestral populations, or migration between P1 and P2, did not significantly affect the false-positive rate of the test.
Robustness to Ascertainment Bias
For data simulated without admixture (f = 0), D(P1, P2, P3, O) did not differ significantly from 0 regardless of the ascertainment scheme used. More precisely, we obtained the following values for D(P1, P2, P3, O) under each scheme: 1) −7.2 × 10−4 (SD = 5.7 × 10−3); 2) 6.2 × 10−4 (SD = 3.4 × 10−3); 3) −2.5 × 10−5 (SD = 5.5 × 10−3); 4) 3.8 × 10−4 (SD = 3.4 × 10−3); and 5) −7.9 × 10−5 (SD = 3.5 × 10−3).
The IUA model with 5% admixture (f = 0.05) predicts D(P1, P2, P3, O) = 0.053 for the demographic parameters we used (eq. A1.5). The simulated data yielded the following values: 1) 0.021 (SD = 4.8 × 10−3); 2) 0.024 (SD = 3.4 × 10−3); 3) 0.037 (SD = 6.0 × 10−3); 4) 0.048 (SD = 3.5 × 10−3); and 5) 0.053 (SD = 3.5 × 10−3).
Therefore, the simple ascertainment scheme we used here did not affect the false-positive rate of the test for admixture. However, it lowered the value of D(P1, P2, P3, O) for scenarios with 5% admixture. We checked that this result was consistent for other admixture proportions (not reported). The difference between the true value and the observed one was larger when the discovery sample was taken in P1.
Application to Neandertal
Testing for Admixture between Neandertals and Modern Humans
Table 1 shows D statistics from Green et al. (2010). D(P1, P2, P3, O) were significantly positive if P1 is an African individual (San or Yoruba) and P2 is a non-African individual (French, Han, or Papuan). When comparing two African individuals (P1 = San and P2 = Yoruba) or two non-African individuals (P1 and P2 = French, Han, or Papuan), D did not differ significantly from 0. Furthermore, D statistics involving one African and one non-African did not differ significantly from one another. Significance was assessed using a standard block jackknife method (Efron 1981). A D value was considered to be significantly different from 0 when its absolute value was greater than three times its standard error. The D statistics are compatible with a scenario where Neandertals admixed with modern humans outside of Africa, before Europeans, East Asians, and Melanesians split (Green et al. 2010).
Table 1.
Neandertals Share More Genetic Variants With Non-Africans than With Africans (Green et al. 2010).
| P1 | P2 | D(P1, P2, N, C), % | |
| African–African | San | Yoruba | −0.1 ± 0.4 |
| African–non-African | San | French | 4.2 ± 0.4 |
| San | Papuan | 3.9 ± 0.5 | |
| San | Han | 5.0 ± 0.5 | |
| Yoruba | French | 4.5 ± 0.4 | |
| Yoruba | Papuan | 4.4 ± 0.6 | |
| Yoruba | Han | 5.3 ± 0.5 | |
| Non-African–non-African | French | Papuan | 0.1 ± 0.5 |
| French | Han | 1.0 ± 0.6 | |
| Papuan | Han | 0.7 ± 0.6 |
We note that Green et al. (2010) used about 7,475,200 biallelic sites for the D statistics analysis (Green et al. 2010, SOM 15). Therefore, we expect the power of the test to be extremely high. Green et al. (2010) also computed D statistics using genotype data from the CEPH-Human Genome Diversity Project panel. D statistics were lower when computed on SNPs than when computed on sequencing data, consistent with the predicted bias of a simple ascertainment scheme. However, it is remarkable that although raw values of D statistics changed, the general conclusion that non-Africans were significantly closer to Neandertals than Africans held.
Estimating the Proportion of Neandertal Ancestry in Non-Africans
Taking advantage of the fact that bones from different Neandertal individuals were available, Green et al. (2010) estimated the proportion of Neandertal ancestry in non-Africans as
where Afr is an African sample (San or Yoruba), OOA is a non-African sample (French, Han, or Papuan), and Nea1 and Nea2 are two Neandertal individuals. The S statistics were averaged over the different possible combinations of African and non-African samples. Using the standard errors of S statistics (estimated by block jackknife), this yielded an estimate of . However, equation (7) shows that this is a conservative minimum. Green et al. (2010) estimated the population divergence time of Neandertals and modern humans to be tN ≈ 270,000 − 440,000 years before present. The time of gene flow has to occur after modern humans went out of Africa, an event that took place an estimated tOOA ≈ 45,000 − 100,000 years before present (Forster and Matsumura 2005). Assuming a constant population size, the bias in the estimator of f is most important when tN − tOOA is small. In the worst-case scenario, the bias is equal to (270,000 − 100,000)/100,000 = 0.063. Therefore, a corrected estimate of f in the case of constant ancestral population size is f* = 1–6%.
The data are also compatible with a scenario of ancestral subdivision. Using tP3 = 12,000 generations, tP2 = 3,000 generations, and a constant population size of N = 10,000, migration rates 1.0 < 2Nm < 2.0 and 15,000 < T < 25,000 generations were compatible with the data. However, we note that the ancestral subdivision has to last for thousands of generations in order for D to be on the order of 5% (supplementary fig. S4, Supplementary Material online). Such subdivision would require that local populations and the geographic barriers that separate them persist for very long times, much longer than seems reasonable for highly mobile and adaptable hominins.
Discussion
Asymmetry in three population gene trees is known to occur in the presence of gene flow (Meng and Kubatko 2009) or ancestral subdivision (Slatkin and Pollack 2008). Here we show that asymmetry can be exploited to design a test for admixture between three closely related populations. The test requires only the assumption that the ancestral population is randomly mating; it is robust to other demographic assumptions such as variations in population size. Moreover, the test is robust to sequencing error if one assumes that the error rate is the same in the sequences analyzed. However, if sequencing error rates differ, then sequencing error can create false positives and that is more likely to be true if sequencing errors are not independent. Finally, we illustrated how to constrain the admixture proportion in a simple model of admixture.
Duration and Direction of Gene Flow
The model of admixture as a one-way instantaneous gene flow event is not intended to be realistic. Instead, instantaneous gene flow is the simplest possible admixture model that enables to derive the D statistic expectation and estimate the admixture proportion. In the more realistic case of ongoing migration, D statistics can be computed numerically using the theory of Markov chains, as illustrated in the ancient structure model.
Introgression is often asymmetrical between hybridizing species (Barton and Hewitt 1985; Orive and Barton 2002). When an expanding population colonizes a new habitat and hybridizes with previous residents, breeding events at the front of expansion can result in the substantial introduction of genes in the expanding population (Currat et al. 2008). As a consequence, detectable ancient admixture is more likely to be found in extant populations when introgression with archaic populations occurred during a range expansion, as is thought to be the case for modern humans and Neandertals (Currat et al. 2008; Green et al. 2010).
However, there are also cases known where detectable introgression occurs from the invasive population to the resident species (Hastings et al. 2005). We note that deriving D statistics when gene flow is bidirectional or in the other direction is not more difficult, and the same methodology can be applied. If there was gene flow from the extant population to the archaic one, then any D statistic involving individuals only from the extant populations would not be affected. This provides a framework to test for the direction of gene flow. Taking advantage that Eurasians are more closely related to some African populations than to others, Green et al. (2010) used a similar argument to rule out substantial gene flow from modern humans to Neandertals.
Effect of Ascertainment Bias
Although D statistics are primarily designed for sequence data, they can be readily applied to genotype data. We showed that the false-positive rate of the test for admixture was not affected by a very simplified ascertainment scheme where we subsampled individuals in either P1 or P2. This is because, in this case, the bias in allele frequencies introduced by the ascertainment compensated itself in patterns ABBA and BABA. However, even this very simple ascertainment scheme lowers the power of the test because the ascertainment biases sampled SNPs toward higher frequencies, increasing the counts of pattern ABBA and BABA to a similar extent, and therefore increasing the denominator of D.
We caution that we used an oversimplified ascertainment scheme. More complex scenarios can introduce bias in an unforeseen way. For example, if the discovery sample is from neither P1 nor P2, then the bias will depend on the genealogical relationships between the population where SNPs were discovered and P1, P2, and P3. However, we note that the main conclusion regarding the test for admixture of Green et al. (2010) held when applied to genotype data. Still, we stress that the test is likely to be more powerful using sequencing data. An investigator wishing to apply the test using genotype data should try to correct allele frequencies for ascertainment bias. Several approaches have been proposed to do so (e.g., Clark et al. 2005).
Effect of Recurrent Mutation
We assumed that each polymorphism was created by a single mutation. If mutations were recurrent, then different copies of the derived allele would arise independently. Hence, many of the gene genealogies in figure 1 that we ignored in computing the expectation of D would have to be accounted for. If the outgroup diverged from the lineage leading to the other populations a long time in the past, as it is the case for modern humans, Neandertals, and chimpanzees, recurrent mutations are likely to occur on the long branch leading to the outgroup. As a consequence, genealogies Ib, IId, and IIIb would create the pattern BABA and genealogies Ia, IIa, and IIId would create the pattern ABBA (see fig. 1). If there is no gene flow from P3 to P1 or P2, and if the mutation rate is the same in the three populations, then Ia = Ib, IId = IIId, and IIIb = IIa (where the equal sign denotes that corresponding trees occur with equal frequencies). Therefore, recurrent mutations are not expected to increase the false-positive rate of the test for Neandertal admixture. In the case where P1, P2, P3, and O are more diverged from each other (e.g., modern humans, chimpanzee, gorilla, and orangutan), recurrent mutations are likely to occur on other branches as well. Recurrent mutations on the terminal branches leading to P1 and P2 could potentially increase the false-positive rate of the test for admixture.
In the presence of gene flow, it is difficult to predict whether recurrent mutation increases or decreases D. The exact result depends on details of the demographic model, but the effect is proportional to the probability that a second mutation occurs and the constant of proportionality is less than one because many of the gene genealogies still have no effect on D. Still, recurrent mutations can affect the power of the test for admixture.
We also note that differing mutation rates in the P1 and P2 populations since their divergence are not expected to bias D. The reason for this is that by restricting to sites where P3 is derived relative to the outgroup O, we are restricting the analysis to mutations that arose prior to divergence of the ancestral populations of P1, P2, and P3.
Effect of Mapping Errors
We assumed that the sequences from P1, P2, P3, and O were aligned to a common sequence without error. Depending on the nature of the sampled populations and the sequencing technology, different alignment strategies may be used. Green et al. (2010) aligned the Neandertal sequence both to the reference human and to the chimpanzee genomes (hg18 and panTro2). Different aligners were used depending on the technology used to sequence the Neandertal and modern humans genomes used in the study. Because of the variety of the alignment strategies, it is difficult to model the effect of mapping error on D statistics in a general framework.
The extent to which D statistics will be affected depends on which sample is more prone to mapping error. Let us assume that all sequences were aligned to the outgroup O. Mapping errors in the P3 sequence are likely to have a negligible effect on the false-positive rate of the test for admixture. This is because mismapping in P3 will equally affect patterns ABBA and BABA. However, alignment error in P3 can affect the power of the test if it artificially increases the counts of patterns ABBA and BABA. Mapping errors in P1 or P2 can have a strong effect on the false-positive rate of the test. Mismapping in P1 will cause P2 and P3 to match each other artificially too often (therefore increasing the count of the ABBA pattern). Thus, it is crucial to test the effect of mapping error in P1 or P2. One possible approach is to stratify the data into categories based on the read coverage in sequences P1 and P2 and to compute D(P1, P2, P3, O) in each category. If mapping is not an issue, then D should remain stable in categories where the coverage is high enough.
Effect of Natural Selection
We implicitly assumed selective neutrality in all our analyses. For natural selection to bias the test for admixture, it must increase the number of derived alleles shared by P3 and P1 or P2. The ABBA and BABA patterns in Green et al. (2010) were distributed genome wide. Therefore, it seems unlikely that the observed D statistics in Green et al. (2010) were biased by natural selection.
However, when the data consist of a few loci, natural selection could potentially bias D statistics by increasing the number of derived alleles in, say, P2. It would result in P2 matching P3 more often than P1, even if there was no admixture. The exact effect of natural selection on D statistics remains a subject of further investigation.
Distinguishing between Gene Flow and AS
We showed that D statistics do not allow us to distinguish between the models of admixture and ancestral subdivision because ancestral subdivision and admixture can produce the same expected coalescence time between two individuals from different populations. However, it is known that ancestral population subdivision results in a higher than expected variance in coalescence times (Wall et al. 2009). Therefore, ancestral subdivision is likely to result in more variation in gene tree depth when using several samples from the extant population. This in turn will affect the site frequency spectrum of the extant population (Harpending et al. 1998). Designing a statistic to distinguish between the two scenarios will require using more than one sample per population.
Concluding Remarks
Inference of ancient admixture is usually limited by the lack of archaic DNA sequence data. Most methods so far have focused on detecting the expected signature of ancient admixture in extant genomes. Here we studied the behavior of a test statistic for ancient admixture based on the direct comparison of DNA sequences of three closely related populations. Our derivation of this test statistic under alternative demographic models showed how to robustly estimate the archaic contribution to extant populations. We demonstrated that our approach can also be applied when no archaic population has been sampled. This paper illustrates the advantage of using one sample per population, which greatly simplifies inference by removing the influence of many demographic assumptions that are not testable in most situations.
Supplementary Material
Supplementary figures S1–S4 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).
Acknowledgments
We thank Anna-Sapfo Malaspinas for helpful discussions that helped improve the manuscript. E.Y.D and M.S were supported by a US National Institute of Health grant (R01-GM40282).
Appendix A. Derivation of D under the Model of Gene Flow
Here we present the detailed derivation of D(P1, P2, P3, O) under the IUA model. For simplicity of notations, we assume that the population size in P(123) is constant and equal to N(123). However, the derivations can be easily extended for arbitrary varying population size in P(123). There are three classes of event that can produce patterns ABBA and BABA.
- The P2 lineage traces its ancestry through the P(12) side of the phylogeny (probability 1−f), and between tP2 and tP3, the P1 and P2 lineages do not coalesce
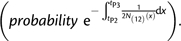
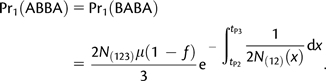
(A1.1) - The P2 lineage traces its ancestry through the P3 side of the phylogeny (probability f), and between tGF and tP3, the two lineages do not coalesce

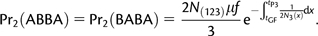
(A1.2) - The P2 lineage traces its ancestry through the P3 side of the phylogeny (probability f), and between tGF and tP3, the two lineages coalesce. This history creates gene genealogies only of type III and results only in ABBA sites (never BABA sites in the absence of recurrent mutation in the same genealogy). The probability that there is a coalescence before tP3 is
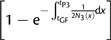 . Once the coalescence occurs, the ancestral lineage cannot coalesce with P1 before tP3. After tP3, the average coalesce time is 2N(123). Therefore, the expected length of the internal branch is , where is the expected coalescence time between P2 and P3, given that the coalescence occurs before tP3. A short analysis shows that
. Once the coalescence occurs, the ancestral lineage cannot coalesce with P1 before tP3. After tP3, the average coalesce time is 2N(123). Therefore, the expected length of the internal branch is , where is the expected coalescence time between P2 and P3, given that the coalescence occurs before tP3. A short analysis shows that
Thus,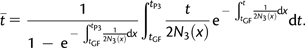
(A1.3)
The overall probability of ABBA and BABA is obtained by adding, and the mutation rate parameter μ cancels. Therefore, Appendix B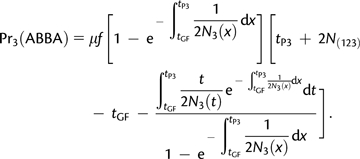
(A1.4)
Here we present the detailed derivation of D(P1, P2, P3, O) under the AS model. At time T, there are six possibilities depending on the states of the Markov chain running in P(123).
Appendix B
No coalescence event occurred
This case corresponds to states 1, 2, 3, and 4 of the Markov chain in P(123). It contributes equally to ABBA and BABA:
| (A2.1) |
2. P1 and P2 lineages coalesced
This case does not contribute to ABBA and BABA.
- 3. P2 and P3 lineages coalesced, but not the P1 lineage
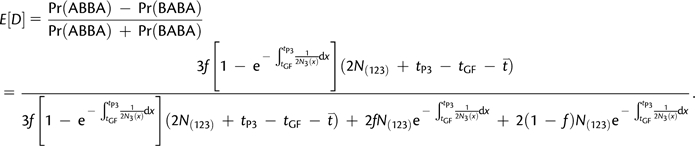
(A1.5)
This case corresponds to states 5 and 8 of the Markov chain in P(123). It does not contribute to BABA. Its contribution to ABBA is
| (A2.2) |
where t23* is the expected time of coalescence of the P2 and P3 lineages given that coalescence occurs between tP3 and T.
4. P3 and P1 lineages coalesced, but not the P2 lineage
This case corresponds to states 6 and 9 of the Markov chain in P(123). It does not contribute to ABBA. Its contribution to BABA is, similarly to case (3),
| (A2.3) |
5. P3 and P2 lineages coalesced first and then with the P1 lineage.
This case corresponds to state 11 of the Markov chain in P(123). It does not contribute to BABA. Its contribution to ABBA is
| (A2.4) |
where t1** is the expected time of coalescence of the P1 lineage, given that coalescence occurs between t23* and T.
6. P3 and P1 lineages coalesced first and then with the P2 lineage.
This case corresponds to state 12 of the Markov chain in P(123). It does not contribute to ABBA. Similarly to case (5), its contribution to BABA is
| (A2.5) |
where t2** is the expected time of coalescence of the P2 lineage, given that coalescence occurs between t13* and T.
The conditional expected coalescence times, t23*, t13*, t1**, and t2** are computed using standard Markov chain theory as the expected times of first hit of corresponding states given that the hit occurred before time T. We have
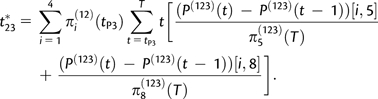 |
(A2.6) |
The other conditional expected coalescence times are computed similarly. There is no simple analytic expression for D.
References
- Barton N. The role of hybridization in evolution. Mol Ecol. 2001;10:551–568. doi: 10.1046/j.1365-294x.2001.01216.x. [DOI] [PubMed] [Google Scholar]
- Barton N, Hewitt G. Analysis of hybrid zones. Annu Rev Ecol Syst. 1985;16:113–148. [Google Scholar]
- Clark AG, Hubisz MJ, Bustamante CD, Williamson SH, Nielsen R. Ascertainment bias in studies of human genome-wide polymorphism. Genome Res. 2005;15(11):1496–1502. doi: 10.1101/gr.4107905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Currat M, Excoffier L. Modern humans did not admix with Neanderthals during their range expansion into Europe. PLoS Biol. 2004;2(12):e421. doi: 10.1371/journal.pbio.0020421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Currat M, Ruedi M, Petit RJ, Excoffier L. The hidden side of invasions: massive introgression by local genes. Evolution. 2008;62(8):1908–1920. doi: 10.1111/j.1558-5646.2008.00413.x. [DOI] [PubMed] [Google Scholar]
- Eberle M, Kruglyak L. An analysis of strategies for discovery of single-nucleotide polymorphisms. Genet Epidemiol. 2000;19(Suppl 1):S29–S35. doi: 10.1002/1098-2272(2000)19:1+<::AID-GEPI5>3.0.CO;2-P. [DOI] [PubMed] [Google Scholar]
- Efron B. Nonparametric estimates of standard error: the jackknife, the bootstrap and other methods. Biometrika. 1981;68(3):589–599. [Google Scholar]
- Forhan G, Martiel J, Blum M. A deterministic model of admixture and genetic introgression: the case of Neanderthal and Cro-Magnon. Math Biosci. 2008;216:71–76. doi: 10.1016/j.mbs.2008.08.004. [DOI] [PubMed] [Google Scholar]
- Forster P, Matsumura S. Evolution—did early humans go north or south? Science. 2005;308(5724):965–966. doi: 10.1126/science.1113261. [DOI] [PubMed] [Google Scholar]
- Green RE, Krause J, Briggs AW, et al. A draft sequence of the Neandertal genome. Science. (56 co-authors). 2010;328(5979):710–722. doi: 10.1126/science.1188021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green RE, Krause J, Ptak SE, et al. Analysis of one million base pairs of Neanderthal DNA. Nature. (11 co-authors). 2006;444(7117):330–336. doi: 10.1038/nature05336. [DOI] [PubMed] [Google Scholar]
- Green RE, Malaspinas AS, Krause J, et al. A complete Neandertal mitochondrial genome sequence determined by high-throughput sequencing. Cell. (25 co-authors). 2008;134(3):416–426. doi: 10.1016/j.cell.2008.06.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harpending HC, Batzer MA, Gurven M, Jorde LB, Rogers AR, Sherry ST. Genetic traces of ancient demography. Proc Natl Acad Sci U S A. 1998;95(4):1961–1967. doi: 10.1073/pnas.95.4.1961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastings A, Cuddington K, Davies K. The spatial spread of invasions: new developments in theory and evidence. Ecol Lett. 2005;8(1):91–101. [Google Scholar]
- Hudson RR. Testing the constant-rate neutral allele model with protein-sequence data. Evolution. 1983;37(1):203–217. doi: 10.1111/j.1558-5646.1983.tb05528.x. [DOI] [PubMed] [Google Scholar]
- Hudson RR. Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics. 2002;18(2):337–338. doi: 10.1093/bioinformatics/18.2.337. [DOI] [PubMed] [Google Scholar]
- Krause J, Lalueza-Fox C, Orlando L, et al. The derived FOXP2 variant of modern humans was shared with Neandertals. Curr Biol. (13 co-authors). 2007;17(21):1908–1912. doi: 10.1016/j.cub.2007.10.008. [DOI] [PubMed] [Google Scholar]
- Krings M, Stone A, Schmitz RW, Krainitzki H, Stoneking M, Pääbo S. Neandertal DNA sequences and the origin of modern humans. Cell. 1997;90(1):19–30. doi: 10.1016/s0092-8674(00)80310-4. [DOI] [PubMed] [Google Scholar]
- Kuhner MK, Beerli P, Yamato J, Felsenstein J. Usefulness of single nucleotide polymorphism data for estimating population parameters. Genetics. 2000;156(1):439–447. doi: 10.1093/genetics/156.1.439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lalueza-Fox C, Rompler H, Caramelli D, et al. A melanocortin 1 receptor allele suggests varying pigmentation among Neanderthals. Science. (17 co-authors). 2007;318(5855):1453–1455. doi: 10.1126/science.1147417. [DOI] [PubMed] [Google Scholar]
- Meng C, Kubatko LS. Detecting hybrid speciation in the presence of incomplete lineage sorting using gene tree incongruence: a model. Theor Popul Biol. 2009;75(1):35–45. doi: 10.1016/j.tpb.2008.10.004. [DOI] [PubMed] [Google Scholar]
- Nielsen R, Hubisz M, Clark A. Reconstituting the frequency spectrum of ascertained single-nucleotide polymorphism data. Genetics. 2004;168(4):2373–2382. doi: 10.1534/genetics.104.031039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noonan JP, Coop G, Kudaravalli S, et al. Sequencing and analysis of Neanderthal genomic DNA. Science. (11 co-authors). 2006;314(5802):1113–1118. doi: 10.1126/science.1131412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orive ME, Barton NH. Associations between cytoplasmic and nuclear loci in hybridizing populations. Genetics. 2002;162(3):1469–1485. doi: 10.1093/genetics/162.3.1469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plagnol V, Wall JD. Possible ancestral structure in human populations. PLoS Genet. 2006;2(7):e105. doi: 10.1371/journal.pgen.0020105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reich D, Thangaraj K, Patterson N, Price AL, Singh L. Reconstructing Indian population history. Nature. 2009;461(7263):489–494. doi: 10.1038/nature08365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serre D, et al. No evidence of Neandertal mtDNA contribution to early modern humans. PLoS Biol. 2004;2(3):E57. doi: 10.1371/journal.pbio.0020057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slatkin M. Inbreeding coefficients and coalescence times. Genet Res. 1991;58(2):167–175. doi: 10.1017/s0016672300029827. [DOI] [PubMed] [Google Scholar]
- Slatkin M, Pollack JL. Subdivision in an ancestral species creates asymmetry in gene trees. Mol Biol Evol. 2008;25(10):2241–2246. doi: 10.1093/molbev/msn172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tajima F. Evolutionary relationship of DNA sequences in finite populations. Genetics. 1983;105:437–460. doi: 10.1093/genetics/105.2.437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wall JD. Detecting ancient admixture in humans using sequence polymorphism data. Genetics. 2000;154(3):1271–1279. doi: 10.1093/genetics/154.3.1271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wall JD, Hammer MF. Archaic admixture in the human genome. Curr Opin Genet Dev. 2006;16(6):606–610. doi: 10.1016/j.gde.2006.09.006. [DOI] [PubMed] [Google Scholar]
- Wall JD, Lohmueller KE, Plagnol V. Detecting ancient admixture and estimating demographic parameters in multiple human populations. Mol Biol Evol. 2009;26(8):1823–1827. doi: 10.1093/molbev/msp096. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.