Genetic Variation in Native Americans, Inferred from Latino SNP and Resequencing Data

Abstract

Analyses of genetic polymorphism data have the potential to be highly informative about the demographic history of Native American populations, but due to a combination of historical and political factors, there are essentially no autosomal sequence polymorphism data from any Native American group. However, there are many resequencing studies involving Latinos, whose genomes contain segments inherited from their Native American ancestors. In this study, we introduce a new method for estimating local ancestry across the genomes of admixed individuals and show how this method, along with dense genotyping and targeted resequencing, can be used to assay genetic variation in ancestral Native American groups. We analyze roughly 6 Mb of resequencing data from 22 Mexican Americans to provide the first large-scale view of sequence level variation in Native Americans. We observe low levels of diversity and high levels of linkage disequilibrium in the Native American–derived sequences, consistent with a recent severe population bottleneck associated with the initial peopling of the Americas. Using two different computational approaches, one novel, we estimate that this bottleneck occurred roughly 12.5 Kya; when uncertainty in the estimation process is taken into account, our results are consistent with archeological estimates for the colonization of the Americas.

Introduction

Evolutionary geneticists have long used genetic polymorphism data to make inferences about human demographic history, utilizing restriction site polymorphism surveys (e.g., Cann et al. 1987), microsatellite data (e.g., Rosenberg et al. 2002), single nucleotide polymorphism (SNP) data (e.g., Conrad et al. 2006; International HapMap Consortium 2007), and resequencing data (e.g., Vigilant et al. 1991; Harding et al. 1997; Kaessmann et al. 1999). Resequencing studies, where all sampled individuals are fully sequenced across the target regions, are more informative than SNP or microsatellite-based studies because they provide an unbiased and complete snapshot of both rare and common variants in the study sample. With recent advances in molecular sequencing technology, we now have resequencing data from more than 1,000 genetic regions spanning more than 20 Mb of sequence (e.g., Reich et al. 2001; Crawford et al. 2004; Livingston et al. 2004; Voight et al. 2005; ENCODE Project Consortium 2007; Wall et al. 2008). Although Old World continental groups (i.e., Europeans, Asians, and Africans) are well sampled in these studies, populations indigenous to the Americas are generally not included. In fact, although large-scale SNP (Jakobsson et al. 2008; Li et al. 2008) and microsatellite (Wang et al. 2007) studies have been performed with Native American samples, the amount of autosomal resequencing data generated (from Native American samples) is almost negligible (see, e.g., Hey 2005), and the insights gained from the analyses of Native American resequencing data have been limited. In this paper, we address this knowledge gap by collecting and analyzing genetic data from admixed “Latinos,” who have partial Native American ancestry.

Latinos (also called Hispanics) are considered an ethnic group with a shared cultural heritage spread out over most of the Americas, without regard to race or ancestry. Latinos encompass a mix of European, Native American, and African ancestries, and the relative contributions of these three ancestral continental groups can vary substantially between self-identified Latino subgroups (e.g., between Mexican Americans and Puerto Ricans) and among individuals within the same subgroup (e.g., Salari et al. 2005; Choudhry et al. 2006; Bryc et al. 2010). For example, the estimated proportion of European ancestry in a sample of 181 Mexican controls varied from ∼0% to ∼100% (Choudhry et al. 2006). This heterogeneity is a problem both for evolutionary studies and for genetic association studies in Latinos unless genetic ancestry can be measured and accounted for.

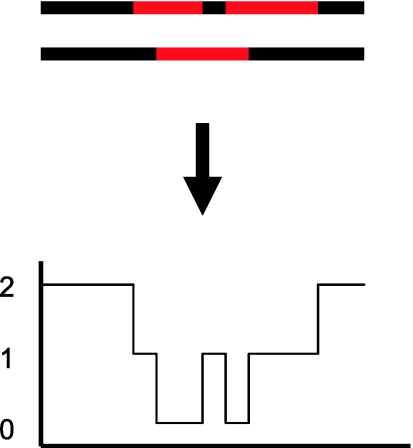
Recently, several methods have been developed to estimate local genetic ancestry in admixed individuals from dense genotype data (e.g., Falush et al. 2003; Tang et al. 2006; Sankararaman et al. 2008; Price et al. 2009; Bryc et al. 2010). Specifically, at each position in the genome, these methods estimate how many copies (0, 1, or 2) were inherited from prespecified ancestral populations (see fig. 1). If the mixing between ancestral populations is recent (e.g., within the last 500 years), then the size of chromosomal “chunks” inherited from one of the ancestral populations is still relatively large (e.g., several megabases long on average) and the methods tend to work reasonably well.

FIG. 1.

Schematic showing a pair of chromosomes from an admixed individual with ancestry from different continental populations (shown in black and red). Local ancestry can be inferred by estimating the number of copies inherited from each ancestral population at each location across the genome.

In this paper, we integrate the estimation of local ancestry in admixed individuals with targeted resequencing to obtain sequences directly inherited from the ancestral populations. Specifically, we first use dense genotype data (e.g., from commercially available SNP chips) to estimate continent of origin across the genomes of admixed Mexican American individuals. Then, we analyze resequencing data from parts of the admixed genomes inferred to have been inherited from Native American ancestors. The result is a data set of diploid sequences, all of which were inherited from Native American ancestors within the past 500 years. We focused our study on 22 Mexican Americans from Los Angeles that are part of the NIGMS Human Variation Collection; these individuals have already been sequenced at several hundred genes as part of the ongoing NIEHS SNPs project (Livingston et al. 2004). In total, we analyze roughly 6 Mb of sequence data from 244 genes, roughly 100 times more Native American resequencing data than currently exist in the public domain. We use this data set to address a longstanding question about the demographic history of Native American populations—the timing of the initial founding of the Americas over the Bering land bridge. We use two different computational methods for estimating demographic parameters: a composite likelihood approach that has previously been used to analyze subsets of the NIEHS SNPs data (Plagnol and Wall 2006; Wall et al. 2009) and a novel summary likelihood method that is roughly an order of magnitude faster than the other approach. Although these data are not ideal for demographic inference due to the potential effects of direct or linked selection on patterns of genetic variation, we are analyzing the largest publicly available resequencing data set from Latino individuals, and the NIEHS SNP project data allow us to make a direct comparison with patterns of genetic variation in other ethnic groups.

Materials and Methods

Genotyping

Twenty-two samples from the NIGMS human variation panel of Mexican Americans (Coriell Catalog ID HD100MEX) were genotyped using Affymetrix 6.0 arrays. Genotype calls were made using the birdseed v2 algorithm using default parameters. An additional 40 Latino samples genotyped for a separate project were temporarily included to improve the performance of the base-calling algorithm but removed prior to all other analyses. A list of the sample ID's used is given in supplementary table S2 (Supplementary Material online).

Estimating Local Ancestry

We assume there were two ancestral populations, corresponding to Europeans and Native Americans and utilize a sliding-window composite likelihood approach. At each location across the genome, there are four possible ancestral configurations, corresponding to European versus Native American assignment for the maternal and paternal alleles. One configuration corresponds to the inheritance of two European alleles, another to the inheritance of two Native American alleles, and the remaining two configurations correspond to the inheritance of one European and one Native American allele. In sliding windows of 2 cm, we calculated the likelihood of each ancestral configuration (for each individual separately), assuming

• i) no change in ancestral configuration across the window

• ii) each SNP is independent

• iii) allele frequencies in the ancestral populations can be estimated from publicly available genotype data from European Americans (International HapMap Consortium 2007) and Native Americans (Mesoamerican samples from Mao et al. 2007).

We then tabulated the ancestral configuration with the maximum (composite) likelihood for each window and used majority rule over all windows containing a particular marker to make each ancestry call. For step iii, we implemented the quality control filters suggested by Mao et al. (2007), excluding SNPs with >20% missing data or Hardy–Weinberg equilibrium (HWE) test P values <0.05.

For each sequenced gene in the NIEHS SNP database, we then calculated the ancestral configuration for each of the 22 Mexican American sequences, excluding those where the inferred configuration changes from one end of the gene to the other. To exclude individuals with potential African ancestry, we tabulated for each gene a list of all polymorphisms present in the Yoruba + African American samples but absent in the European + East Asian samples. These “African-specific” SNPs can be used to identify individuals with African ancestry at a particular gene. Specifically, we added up the frequencies of the African-specific SNPs to obtain a rough estimate of the total number of African-specific alleles expected in a sequence with African ancestry—if an African-specific allele is at frequency k, then a randomly sampled African sequence would have a probability of k of having the allele. If there are multiple African-specific SNPs with frequencies k₁, … k_j, then the expected number of African-specific alleles in a random haploid sequence is k₁ + … + k_j. For each Latino individual, we excluded the (diploid) sequence at a particular gene if the number of African-specific alleles was greater than 50% of the expectation (for a haploid sequence) calculated above (i.e., closer to the expectation of an individual with one African sequence than to those with no African sequences).

A complete list of the loci used, and the ancestral assignments for each locus, is given in supplementary table S3 (Supplementary Material online). Despite the potential problems of the independence across SNPs assumption, the method performs quite well on simulated data sets—substantially better than Structure (Falush et al. 2003) or LAMP (Sankararaman et al. 2008) and comparable to Hapmix (see table 1).

Table 1.

Comparison of Different Methods for Estimating Local Ancestry.

Method	δ	Marker-specific accuracy (%)
Our method (unphased data)	0.2	91.0
	0.05	92.3
Our method (phased data)	0.2	93.4
	0.05	94.5
Hapmix	0.2	96.1
	0.05	98.0
LAMP	0.2	84.1
Structure	0.4	72.0

We used only those SNPs with ancestral allele frequencies that differed by at least δ in the two ancestral populations. We calculated the average accuracy of the marker-specific ancestry calls for each method. Note that different methods make different assumptions about phased versus unphased data. See text for further details.

Estimating Local Ancestry with Phase-Known Data

The method described above assumes that phase is unknown in both the ancestral and admixed genotypes. To facilitate comparisons with Hapmix (Price et al. 2009), we also implemented a version of our ancestry estimation algorithm that assumes that phase is known in the admixed individuals’ genotypes. In this alternate implementation, we estimate the local ancestry of each chromosome using the same sliding-window composite likelihood approach but with only two possible ancestral states, corresponding to ancestry from each of the two ancestral populations. Diploid ancestry calls are obtained by a post hoc “adding” of the ancestry calls from each of an individual’s pair of chromosomes.

Comparison Across Methods

We used a standard coalescent simulator (Hudson 2002) to generate five small chromosomes’ worth of sequence data appropriate for multiple continental populations (ms command line: ms 1600 1 –t 2500. –r 30000. 10000000 –I 2 800 800 0. –ej .06 1 2). These simulated data sets had SNP densities comparable to extant genotyping arrays such as the Affymetrix 6.0, and levels of population differentiation similar to what is found between Europeans and Native Americans. We then used the following algorithm to simulate a chromosome with y% inherited from the first population and instantaneous admixture x generations ago:

1. Choose a random ancestral chromosome (y% probability from the first population, 100 − y% probability from the second population)

2. Copy this ancestral chromosome for an exponentially distributed distance with mean 100/x centimorgans

3. Switch to a different ancestral chromosome, chosen as in step 1

4. Repeat steps 2 and 3 until the end of the chromosome is reached

We generated 400 admixed chromosomes with x = 10 and y = 25 and 50 (200 for each value of y) and randomly paired chromosomes with the same y value to form diploid “individuals.” We then used 50 (diploid) individuals from each of the ancestral populations to estimate ancestral allele frequencies and used each of the four methods to estimate local ancestry across the remaining individuals. For each SNP, the methods estimated the number of copies (i.e., 0, 1, or 2) inherited from population 1. Due to the slow speed and model assumptions of Structure, we further thinned the data (δ, the difference in allele frequency in the two ancestral populations, was required to be ≥0.4) to only include the most informative SNPs. We tabulated the proportion of ancestry calls that were correct across each method.

We also performed a similar comparison using actual genotype data from Chromosome 2 (from Affymetrix 6.0 arrays) from 88 Native Americans and 112 Europeans (Shriver M, unpublished data). We phased the data using BEAGLE (Browning SR and Browning BL 2007), constructed “admixed” individuals using the same algorithm as above, and estimated the accuracy of local ancestry calls using Hapmix (Price et al. 2009) and our composite likelihood method. Our results were similar to the accuracies estimated from simulated data (table 1). For δ = 0.2, Hapmix and our haplotype-based approach had accuracies of 96% and 94%, respectively, whereas our genotype-based approach had an accuracy of 91%.

Population Genetic Analyses

We downloaded all loci using sample population panel 2 from the NIEHS SNPs Web site (http://egp.gs.washington.edu) in November 2009. A total of 244 genes were accessed (supplementary table S3, Supplementary Material online), and we utilized all biallelic polymorphisms (both SNPs and short indels) for our analyses. θ_W (Watterson 1975) and π (Tajima 1983) were calculated across each locus, adjusting for different sample sizes and missing data. ρ (Hudson 2001) and F_ST (Hudson et al. 1992) were estimated for each gene with more than ten polymorphisms and averaged across loci. One hundred and sixty-three of the 244 loci had six or more individuals with two Native American–inferred sequences. To construct the 163 loci data set, we sampled the six with the lowest individual number as labeled in supplementary table S2 (Supplementary Material online). In addition, we included six Europeans (Coriell ID's NA11882, NA11994, NA11995, NA12815, NA12891, and NA12892), six East Asians (Coriell ID's NA18526, NA18545, NA18562, NA18566, NA18609, and NA18621), and six West Africans (Coriell ID's NA18502, NA18504, NA18870, NA19153, NA19201, and NA19223) to ensure equal sampling from each continental region.

Estimation of Demographic Parameters

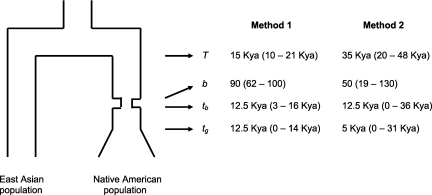
We used two different likelihood-based approaches for estimating demographic parameters from the Native American–inferred sequences. The first method uses a composite likelihood method used before in other contexts (Plagnol and Wall 2006; Wall et al. 2009). We started with a simple demographic model (fig. 2) roughly appropriate for the history of the East Asian and Native American samples: a panmictic ancestral population splits at time T into two daughter populations. One daughter population experiences a 1,000-year long population bottleneck, leading to a b-fold reduction in population size, ending at time t_b. Then, at time t_g (≤t_b), that population experiences exponential growth, leading to a 100-fold increase in population size at the present.

FIG. 2.

Diagram of the demographic model used, with estimates and 95% confidence intervals (in parentheses) for T, the time when the two populations split; t_g, the time of onset of population growth,; t_b, the time since the end of the population bottleneck; and b, the strength of the bottleneck. Parameter estimates, along with approximate 95% confidence intervals in parentheses, are given to the right of the figure. Method 1 is the composite likelihood method described in Plagnol and Wall (2006), and method 2 is a summary likelihood method described in the Materials and Methods.

To estimate the model parameters, we summarized the data using several summary statistics and then calculated the (composite) likelihood of the summarized data on a grid of parameter values. The composite likelihood was estimated using modifications of the ancestral recombination graph (ARG) simulator ms (Hudson 2002). See Plagnol and Wall (2006) for further details.

Summary statistics were divided into two categories. The first category of summary statistics divided SNPs at a locus into four categories: private SNPs in population 1, private SNPs in population 2, shared SNPs with minor allele frequency (MAF) in the total sample ≤0.1, and shared SNPs with MAF >0.1. We label these summaries s₁, s₂, s₃, and s₄, respectively. For each branch of the ARG, all mutations on this branch will belong to a single category, so we can estimate probabilities f₁, f₂, f₃, f₄ that a particular SNP will fall into one of the four categories defined above. Our likelihoods here condition on the total number of SNPs s (= s₁ + s₂ + s₃ + s₄) at a locus. Conditional on the ARG and s, the distribution of (s₁, s₂, s₃, s₄) is multinomial and can be estimated explicitly by averaging over the computed probabilities for each simulated ARG. The second category included Tajima’s (1989) D from each population, Fu and Li’s (1993) D* in population 2, and F_ST (Hudson et al. 1992) between the two populations. Both D and D* are measures of the frequency spectrum, whereas F_ST measures the level of divergence between populations. For each parameter combination, we estimated the joint likelihood of these statistics by fitting the data to a multivariate normal distribution. Coalescent simulations were used to estimate the vector of means and the covariance matrix.

Even though these two sets of summary statistics are correlated, we cannot estimate their joint distribution. So, we estimated a composite likelihood approximation by assuming that the two categories of summary statistics are independent. We calculated composite likelihoods separately for each locus and then multiplied them together to obtain the overall (composite) likelihood of the data. We calculated point estimates for each parameter value, as well as approximate 95% confidence intervals, with a log-likelihood cutoff of 2.8 estimated from simulations (results not shown).

We also implemented a much quicker summary likelihood approach for estimating demographic parameters. We utilized the same demographic model as before (fig. 2) and used common summary statistics θ_W (Watterson 1975), D (Tajima 1989), F_ST (Hudson et al. 1992), and $\widehat{\rho }$ (Hudson 2001) to estimate the four model parameters. Specifically, we ran coalescent simulations (Hudson 2002) and a rejection sampling algorithm to estimate the likelihood of obtaining the observed mean values (across loci) of θ_W, D, F_ST, and $\widehat{\rho }$, as a function of the model parameters Θ = {T, b, t_b, t_g}. We then obtained a composite likelihood by assuming that the summary statistics used are independent of each other.

We assumed an average generation time of 25 years. For each parameter combination Θ = {T, b, t_b, t_g}, we ran 32,600 coalescent simulations, comprising 200 simulations with the same number of base pairs sequenced and total distance (from one end of the sequence to the other) for each of the 163 actual loci. We considered increments of 2.5 thousand years for T, t_b, and t_g and increments of 5–10 for b (5 if b ≤ 70, 10 otherwise). θ and ρ per base pair (for each simulation) were drawn from gamma distributions with parameters (8, 14700) and (0.5, 1850), respectively. These distributions, though ad hoc, reproduce the observed means and variances of θ_W, D, and $\widehat{\rho }$ in the East Asian sample. We then calculated θ_W, D, F_ST, and $\widehat{\rho }$ for each simulation, repeatedly subsampled 163 simulated loci and estimated Pr (|sample mean − actual mean | < 0.01 × actual mean | Θ) for each summary. Note that b, t_b, and t_g depend exclusively on θ_W, D, and $\widehat{\rho }$, respectively, in the Native American (simulated or real) data. This simplifies some of the calculations.

For individual parameters, we used profile likelihood curves to calculate approximate 95% confidence intervals. Final calculations for the maximum likelihood estimate and confidence intervals were obtained using five times more simulations than described above for particular combinations of Θ.

Results and Discussion

First, we genotyped the 22 samples using the Affymetrix 6.0 platform. We then used this genotype data to estimate the continent of origin along the chromosomes of each genome in our sample. We assumed there were two ancestral populations, corresponding to Europeans and Native Americans and estimated allele frequencies in the ancestral populations from publicly available genotype data (International HapMap Consortium 2007; Mao et al. 2007). For each marker, we used a composite likelihood approach (see Materials and Methods) to estimate the most likely ancestral configuration (i.e., two European alleles, one European, and one Native American alleles or two Native American alleles). This approach runs quickly (several minutes to estimate local ancestry across the whole genome of an admixed individual on a standard desktop computer), and simulations suggest that it is substantially more accurate for estimating local ancestry than two commonly used programs that accept unphased data, Structure (Falush et al. 2003) and LAMP (Sankararaman et al. 2008). If phase is known, the accuracy of our composite likelihood method is slightly worse than that of Hapmix (Price et al. 2009) (e.g., 93.4% for our method vs. 96.1% for Hapmix with δ = 0.2; cf. table 1). Because genotypic phase is generally not experimentally determined, the results across methods are not directly comparable. Structure, LAMP, and the genotype version of our method use unphased genotype data from the ancestral and admixed populations, whereas the Hapmix runs used phased data from the ancestral populations and unphased data from the admixed population, and the haplotype version of our method uses phased data from the admixed population and unphased data from the ancestral populations.

For the remainder of our analyses, we stayed away from using local ancestry programs that require phased data (i.e., Hapmix and our haplotype-based local ancestry estimation) to avoid compounding ancestry estimation error with phasing error. For each of 244 genes sequenced as part of the NIEHS SNPs project, we tabulated the estimated continental ancestry of each diploid sequence, excluding all sequences with evidence of African ancestry or with ambiguous ancestral assignments (see Materials and Methods). We then analyzed subsets of the data consisting of sequences with the same ancestral configuration.

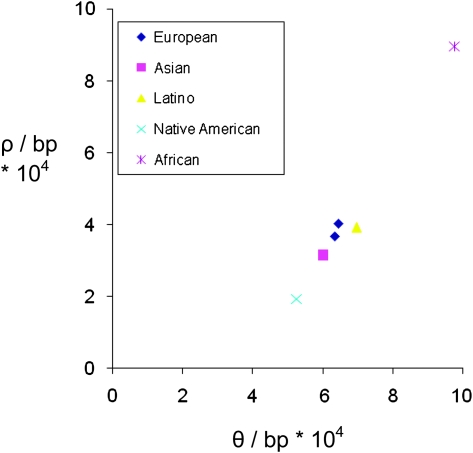
To test the accuracy of our ancestry inference, we compared patterns of genetic variation in European individuals and Mexican American individuals inferred to have two European-derived sequences. The two sets of samples show similar levels of genetic variation (Watterson 1975; Tajima 1983) and linkage disequilibrium (LD) (Hudson 2001) (fig. 3). In addition, there were no systematic differences in allele frequencies (mean F_ST = 0.001) between the two sets of samples, consistent with observed levels of population structure in different European populations (e.g., Novembre et al. 2008). From these and other observations, we conclude that the European-inferred sequences really were derived from European ancestors within the last several hundred years.

FIG. 3.

Plot of diversity θ (= 4Nμ, where N is the effective population size and μ is the mutation rate per base pair per generation) versus estimated recombination rate ρ (= 4Nr, where r is the recombination rate per base pair per generation) for individuals with different continental ancestries. The two blue diamonds refer to a European sample and a Mexican American sample with two European-derived sequences.

Next, we examined the relative numbers of individuals assigned to each of the three possible ancestral configurations for each gene. If mating were random with respect to genetic ancestry, the relative proportions are expected to be in HWE. Instead, we observe a significant deficit (16% less than expected) of individuals with mixed continental ancestry (i.e., one European and one Native American alleles). This could be a result of assortative mating with a trait that correlates with ancestry estimates, such as physical appearance or socioeconomic status, or a sign of ongoing immigration from a source population with a different average genetic ancestry from the current Latino population in Los Angeles. To explore the two potential explanations further, we estimated local ancestry in 23 pairs of Mexican American parents from HapMap phase 3 trio data. We found a significant correlation (P < 0.05) between the estimated Native American ancestry of the father and the estimated Native American ancestry of the mother (supplementary fig. S1, Supplementary Material online), suggesting that assortative mating is a significant factor in our observed deficit of individuals with mixed continental ancestry.

We then compared levels of genetic variation and LD in the NIEHS SNPs database for ethnic groups defined either by self-identity or our inference method (fig. 3). As with previous studies of human sequence variation (e.g., Voight et al. 2005; Wall et al. 2008), we find that sub-Saharan Africans have substantially more variation and less LD than do non-African populations. Additionally, for non-admixed populations, we observe a trend of decreasing diversity and increasing LD with increasing distance away from Africa, consistent with the serial bottleneck model of recent human evolution (Ramachandran et al. 2005).

To control for any possible biases associated with sample size, we reanalyzed a subset of our data consisting of six (inferred) Native American individuals, six East Asian individuals, six European individuals, and six West African individuals from 163 of the 244 loci. (The remaining loci had fewer than six individuals with both gene copies inferred to be of Native American ancestry.) We observed the same trends as before with increasing LD and decreasing diversity for the European, Asian, and Native American sequences, respectively. Interestingly, all four population samples show comparable numbers of polymorphisms shared across multiple continental regions, and the differences in overall levels of diversity are mostly explained by differences in the number of private alleles in each continental sample (see supplementary table S1, Supplementary Material online).

We then used two different likelihood-based methods on the 163 locus data set to estimate historical demographic parameters for the inferred Native American sequences (fig. 2). Previous archeological and linguistic studies suggest that humans first entered the Americas across the Bering land bridge and then migrated southwards to North and South America (e.g., Greenberg et al. 1986; Goebel 1999). It is likely that there was a significant population bottleneck associated with the initial founding of the Americas, though the timing of this bottleneck is disputed (e.g., Nichols 1990; Nettle 1999; Fiedel 2000; Hey 2005). Our main interest is in using the patterns of genetic variation to estimate the timing and strength of this bottleneck. Both methods estimate that the bottleneck ended roughly 12.5 Kya (t_b, fig. 2), roughly consistent with the age (∼14 Kya) of the oldest undisputed New World archaeological site at Monte Verde, Chile (Meltzer 1997; Fiedel 2000). The estimated 95% confidence intervals for t_b are 3–16 and 0–36 Kya for the two methods (see fig. 2 and Materials and Methods). The former suggests that an early occupation of the Americas (>30 Kya, cf. Nichols 1990) is unlikely.

In general, the first method (cf., Plagnol and Wall 2006 and Materials and Methods) has tighter confidence intervals and estimates a stronger bottleneck and a more recent split time than the second method does. We speculate that the difficulties in precisely estimating parameter values (in both methods) are due to the small sample sizes from each population or to heterogeneity within the Native American–inferred sequences (i.e., population structure within the Native American ancestors of our Latino samples). The demographic model considered is obviously a simplification of the truth, and additional studies with more Latino samples will be needed to obtain more precise parameter estimates or to address more complex questions, such as the number of different major migrations from North Asia into the Americas or the degree of structure within populations from the Americas.

Supplementary Material

Supplementary tables S1–S3 and supplementary figure S1 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).