In situ nano-compression testing of irradiated copper

Abstract

Increasing demand for energy and reduction of CO₂ emissions has revived interest in nuclear energy. Designing materials for radiation environments necessitates fundamental understanding of how radiation-induced defects alter mechanical properties. Ion beams create radiation damage efficiently without material activation, but their limited penetration depth requires small-scale testing. However, strength measurements of nano-scale irradiated specimens have not been previously performed. Here we show that yield strengths approaching macroscopic values are measured from irradiated ~400 nm diameter copper specimens. Quantitative in situ nano-compression testing in a transmission electron microscope reveals that the strength of larger samples is controlled by dislocation-irradiation defect interactions, yielding size-independent strengths. Below ~400 nm, size-dependent strength results from dislocation source limitation. This transition length-scale should be universal, but depend on material and irradiation conditions. We conclude that for irradiated copper, and presumably related materials, nano-scale in situ testing can determine bulk-like yield strengths and simultaneously identify deformation mechanisms.

While conventional light water reactors undergo lifetime extension programs¹, new and advanced fusion and fission reactors are also being considered. Among the main limiting factors for both concepts are the materials available to engineers designing the plants. Radiation environments pose a challenge for materials scientists in terms of choosing and developing suitable materials for long term applications². In order to design better materials, it is crucial to understand the way radiation-induced defects alter the mechanical properties on a fundamental level^3,4. Therefore, a quantitative study of the deformation mechanisms in irradiated materials is a key requirement for the realization of new advanced reactor concepts.

As opposed to neutron irradiation, ion beam irradiation can create radiation damage in a short time and without the hazards caused by material activation. A significant amount of work has been performed to relate ion beam radiation damage to neutron radiation damage^5,6, where it has been shown that the resulting defect structures are comparable⁶. Still, a major limitation of ion beam irradiation lies in the limited beam penetration depth. Therefore, micromechanical testing concepts capable of locally probing small volumes are essential to assess the properties of ion beam irradiated materials. While nanoindentation has proven to be very useful over the past decades^4,7-10, recently developed miniaturized uniaxial tests with a defined gauge section ease the evaluation of mechanical data on a nanometer scale and allow a straightforward determination of the whole flow curve^9,11-13. Moreover, using in situ techniques, the deformation mechanisms can be identified simultaneously^14-18.

In order to understand and predict the property changes in structural materials under radiation, there have been significant efforts in both computational^19-23 and experimental^22,23 studies in recent years. Molecular dynamics (MD) and dislocation dynamics (DD) modeling provide detailed observations of the atomistic and dislocation processes. Typically, such approaches apply higher strain rates than what is used experimentally, and are presently limited in the achievable length and time scales^19-21. However, by considering representative model setups (e.g. sufficiently large specimen in DD, periodic boundary conditions in MD), bulk-like responses can be derived from such computational studies and related to experiments.

To obtain experimental observations of radiation damage associated deformation mechanisms, conventional in situ transmission electron microscopy (TEM) straining experiments of irradiated or quenched material have been performed and were able to deliver detailed observations of dislocation mechanisms, confirming and challenging the computational studies at the same time^22,23. Although conventional TEM straining experiments allow for careful mechanistic analysis, they deliver only qualitative results correlating the mechanical response to the created defects. While details differ, these studies show that vacancies remaining from collision cascades condense into stacking-fault tetrahedra (SFTs) and dislocation loops in fcc metals at ambient temperatures, where the fraction of SFTs versus dislocation loops depends on the material and stacking fault energy. A number of studies^22-24 suggests that during plastic deformation, these defects can be partially removed by interaction with a single dislocation or by shearing due to the passage of multiple dislocations. This can serve as an explanation for the occurrence of defect free channels in macroscopically deformed irradiated materials. Notably, different mechanisms have been reported at higher temperatures or for significantly larger SFTs originating from quenching²³.

Through the recent development of improved nano-mechanical testing methods^11,25-27, the possibility now exists to close the gap between computational and experimental studies in a quantitative manner¹². It is, however, well established that such miniaturized tests exhibit intrinsic size effects on sample strength^{4,11,12,27,28}, complicating the extraction of bulk properties from such kind of experiments. Besides downscaling of the sample dimensions, direct in situ observations of the deformation mechanisms are crucial for understanding the response of irradiated materials on a fundamental level. Here we report the first quantitative in situ observation of the deformation behavior of proton irradiated material, which allows for a direct relation to bulk material strengths and predictions from computational models.

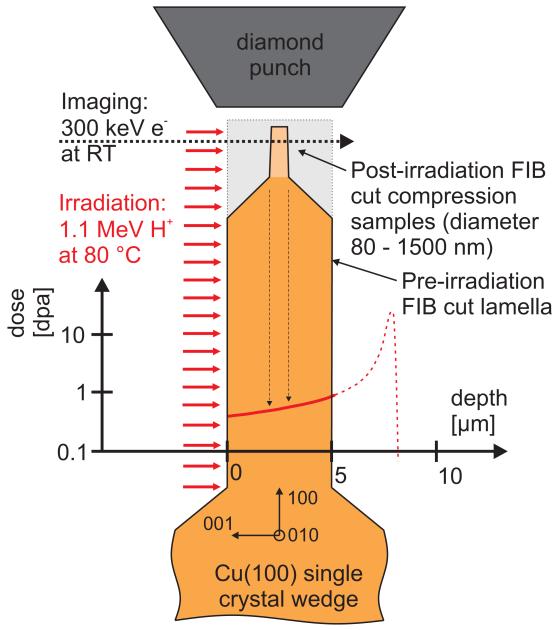
A (100) oriented copper single crystal was irradiated to a dose of 0.8 displacements per atom (dpa) using a 1.1 MeV proton beam at near ambient temperature (see Fig. 1). We subsequently machined nano-compression samples with a focused ion beam (FIB) and performed quantitative in situ tests in a TEM in order to understand the influence of irradiation defects on the material properties. Through this first-of a-kind experiment, we have established the transition from a size-affected yield strength to one controlled by the radiation defects, enabling the determination of bulk-like yield strengths from nano-scale samples.

Figure 1. Schematic of experimental procedure.

A 5 μm thick lamella was FIB cut into a (100) copper single crystal and subsequently irradiated at 80 °C using 1.1 MeV protons, resulting in the indicated logarithmic dose profile (red line) for the lamella. Subsequently, pillars with diameters ranging from 80 nm – 1500 nm were FIB machined into the lamella. From their position, the sample dose is estimated to be 0.8 dpa. These specimens were finally loaded in compression in situ in a TEM operated at 300 keV using a nanoindenter equipped with a flat conductive diamond tip.

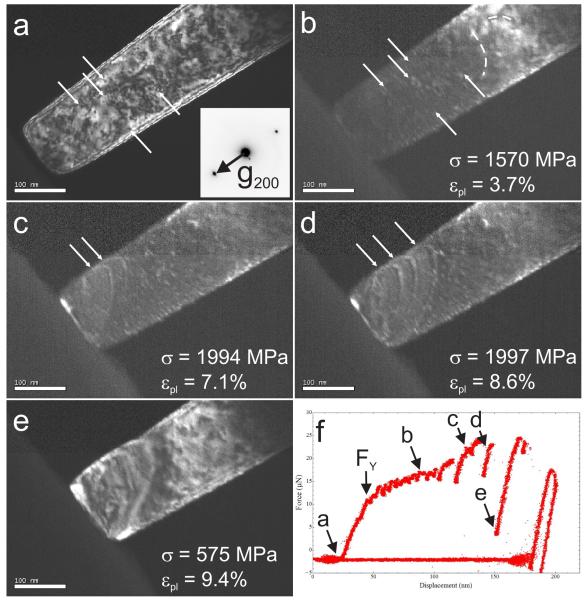
Still images extracted from a video recorded during in situ TEM compression testing of an irradiated (100) copper pillar 118 nm in diameter are shown in Fig. 2 along with the recorded load – displacement data. The full video is provided as Supporting Video 1. Before contact with the flat diamond punch, the pillar (Fig. 2a) shows a characteristic high density of small irradiation defects. It was reported that 90% of the radiation-induced defects in copper at 20-100°C are 0.5 nm – 2.5 nm SFTs with the maximum frequency at ~2 nm, the balance being dislocation loops²⁹, consistent with our observations in this study (see later discussion regarding Figs. 4 and 5). After yield, plasticity and hardening are to a large extent governed by the bowing and escape of short dislocation segments, an example of which is shown in Fig. 2b. This resembles a pinning – de-pinning motion of short dislocations between the radiation-induced obstacles. Note that several defects are still visible within the pillar, as exemplarily indicated by arrows. In Figs. 2c and 2d dislocations extend across the sample cross sectional area, resulting in pronounced load drops unseen before in Fig. 2f. Further deformation is localized to a single slip plane characteristic of a spiral dislocation source¹⁵, leading to the formation of a large slip step (Fig. 2e). Studying the deformation behavior for sample sizes ranging from 80 nm – 1500 nm, we consistently observed this localized slip, which was not the case for unirradiated Cu²⁸, where even for the smallest specimens slip preceded on multiple and adjacent planes, see Supplementary Figure 1.

Figure 2. Dark field still images extracted from an in situ TEM compression test of a (100) oriented 118 nm diameter copper pillar irradiated to 0.8 dpa (a-e) and the measured load – displacement data (f).

(a) Before contact to the diamond punch, the pillar contains a high density of defects. (b) After yield, deformation and hardening are governed by the bowing and exit of short dislocations, evidenced by gentle load drops in (f). In (c) and (d) dislocations emitted from a spiral dislocation source extend across a slip plane and lead to significant load drops in (f). (e) The slip produced by this dislocation source operation leads to the formation of a large slip step, to which further deformation is confined.

The increase in load in Fig. 2f between F_Y, corresponding to a yield stress of σ_Y = 1103 MPa, and the point where the spiral dislocation source starts to operate in Fig. 2c (σ = 1994 MPa), is presumably not due to any kind of classical strain hardening. Rather the physical significance of the load displacement curve would seem to be that there are a series of yielding events, starting with a single dislocation source that is shut down because the emitted dislocations get pinned by obstacles in the sample²⁸, requiring activation of further slip events with sequentially higher loads²⁸, until the long segment spiral sources begins to operate in a continuous fashion, producing the observed slip step. Interestingly, the stress in Figs. 2c and 2d is essentially unchanged. Moreover, one would expect differences in the average free mean path of moving dislocations in the two different regimes, being shorter in the first hardening stage and larger during operation of the dislocation spiral source. However, due to limits in temporal resolution as outlined in the supporting online material (SOM), quantification of this mean free path was not attempted.

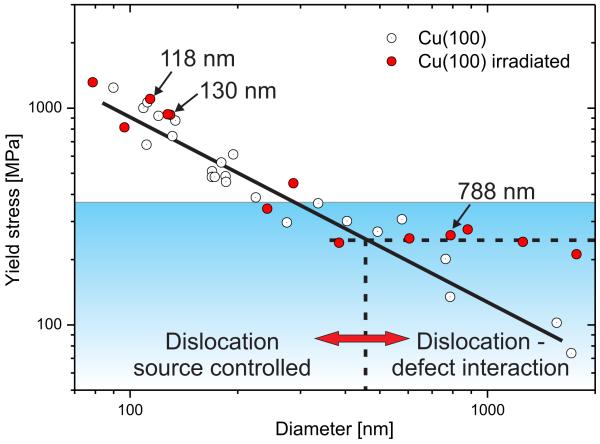
The size-dependent yield strengths determined from the in situ compression tests are shown in comparison to unirradiated copper²⁸, both fabricated from the identical macroscopic single crystal, in Fig. 3. Yield in this study is understood as the first group of dislocations sweeping across the sample, more details are provided in the Methods chapter, the SOM or Ref. 28. While the non-irradiated material (open circles) exhibits a size-dependent strength over the entire investigated size range¹², the irradiated samples (red circles) follow this trend only for specimen diameters up to ~400 nm. Above this, the measured yield strengths are in the range of 220 MPa – 280 MPa, well within the scatter typically observed in these dimensions¹¹ and seemingly independent of size. The dashed horizontal line in Fig. 3 is added to guide the eye.

Figure 3. Size-dependent yield stress for (100) oriented irradiated and unirradiated copper nano-compression samples.

While the unirradiated material (open circles)²⁸ exhibits a size-dependent yield strength over the whole size range, the irradiated material (red symbols) transitions to a size-independent yield stress for sample diameters larger ~400 nm. The shaded area depicts the regime of maximum obstacle strength found for dislocation – SFT interactions in copper using MD and DD computations¹⁹. The specimens shown in Figs. 2, 4 and 5 are indicated.

To evaluate what determines this fundamental length scale, we have considered the effect of the most likely internal structural element in the irradiated samples for the current conditions – small SFTs^29,30. The blue shaded regime in Fig. 3 marks the range of maximum obstacle strength of 4.7 nm large SFTs in copper for 70 nm-long dislocation segments of multiple character and orientation as determined by Marian et al. from MD and DD computations¹⁹. The same authors demonstrated that the SFT size has no actual influence on strength, rather the SFT area intersected by the dislocation glide plane is the important geometric parameter.

Fig. 4 shows a dark field TEM image of a deformed 130 nm diameter irradiated pillar, indicated in Fig. 3. There was some initial deformation at the sample top, but most of the plasticity localized by formation of a large slip step near the specimen middle. It should be mentioned that the slipped part appears thicker, as it is not imaged in projection, but inclined to the transmitted beam. More deformed samples of different sizes showing the same strong localized deformation are shown in the Supplementary Figure 1a-d, compared to the much wider sheared regions in unirradiated samples in Supplementary Figure 1e-g and Ref. 28. As SFTs are several atomic planes high, dislocations might leave their slip plane by cross-slip or obstacle interaction and still encounter the same SFTs, keeping the situation essentially unaltered. Such cross-slip during operation of spiral sources was observed in Ref. 13 and can explain the rather wide sheared regions of unirradiated pillars (Supplementary Figure 1e-g and Ref. 22).

Figure 4. Dark field image of a deformed irradiated (100) copper specimen with 130 nm diameter.

Plasticity is limited to some deformation at the top and a large slip step in the sample mid. Several long dislocation segments are present on this slip plane. Moreover, fewer defects are visible in the sheared region compared to undeformed areas (an undeformed area is outlined).

The deformed areas in Fig. 4 contain long dislocation segments and are largely devoid of irradiation defects, thereby resembling the defect free channels observed macroscopically, while numerous defects are visible in the undeformed sample parts^29,30. Evaluation of the defect density in the undeformed sample part (boxed area in Fig. 4) by counting all defects excluding long dislocation lines in the known volume yields an average three-dimensional spacing of 19.4 nm ±2 nm and an obstacle spacing on the glide plane of 68 nm ±30 nm. For details please refer to the SOM. The defect density of 1.4·10²³ m⁻³ (including FIB induced defects) in the deformed specimen is lower compared to typically ~1·10²⁴ m⁻³ irradiation defects in proton irradiated bulk material³⁰. This is understandable, as the defect density determined from Fig. 4 reflects a lower limit, the smallest SFTs present in the sample were possibly not resolved in TEM. A detailed evaluation on possible influences on the cluster density is provided in the SOM and will be discussed later in the text.

To identify with certain the nature of the observed defects, a TEM lamella was prepared from a 788 nm thick sample after deformation using FIB lift-out and subsequent low energy Ar⁺ ion milling at 500 eV to remove preparation artifacts. For details refer to the SOM. A low magnification image of the pillar surrounded by the protective Pt coating is shown in Fig. 5a. The high resolution image recorded in the marked area well within the pillar material is depicted in Fig. 5b, showing ~2 – 3 nm large SFTs exhibiting the typical triangular contrast in (110) projection.

Figure 5. Post deformation irradiation defect characterization using high resolution TEM.

(a) Low magnification TEM image of a deformed 788 nm diameter copper pillar after FIB lift out and subsequent Ar⁺ low energy ion milling at 500 eV. (b) Atomic resolution image taken from the area indicated in (a) showing ~2 – 3 nm large SFTs imaged along the (110) projection.

It is well known that the smallest internal structural element can provide a characteristic length-scale determining the strength of a material³¹. For miniaturized single crystal samples a size effect is observed where the yield strength inversely relates to the sample size¹¹, except when the material is defect free (from grown in defects as well as FIB defects) and deforms at the theoretical strength⁴. Moreover, in complex materials there is not a single length scale. The overall yield/flow stress is governed by the superposition of contributions from different features, such as dispersed obstacles of various types and strengths, dislocations and grain boundaries. Therefore, when testing a miniaturized sample containing densely spaced obstacles, the effect of sample size can become a secondary consideration. This was recently demonstrated for a Ni-based oxide-dispersion strengthened alloy, where no sample-size effect was observed for samples ranging from 200 nm to 4 μm³². In the present case, there is a transition in the relation between yield strength and sample size. Above ~400 nm the strength of the irradiated samples deviates from the unirradiated material and becomes size-independent. Notably, the deformation behavior stays essentially unaltered and differs from the unirradiated material.

This can be explained by rationalizing that the defects in this study behave similar to the oxide particles used by B. Girault et al.³², but the SFTs have a more limited strength¹⁹, indicated in Fig. 3. Moreover, during plastic deformation the SFTs are partially removed by passing dislocations^19,22,23. Therefore, a transition from the size-independent yield strength to a size-affected strength can be expected for two possible reasons: (i) The stresses to activate fewer and smaller dislocation sources will eventually become higher than the obstacle strength of the irradiation defects. (ii) With a reduction of the sample volume, it might not contain enough defects to be considered a representative volume element. However, given the upper bound observed average obstacle spacing on the glide plane of 68 nm ±30 nm and required slip distances of more than 100 nm even for the smallest samples, we do not believe this latter explanation can be supported.

Taking the established cluster density of ~1·10²⁴ m⁻³ for proton irradiated bulk material³⁰ results in an obstacle spacing of 20 nm – 44.7 nm. From the measured stresses in the bulk-like regime, the dislocation source size of a spiral dislocation source¹⁵, can be evaluated after Rao et al.³³, amounting to 50 nm – 70 nm. This source size is closely related to the shortest distance between the pinning point and the sample surface, as this is the critical configuration to overcome during operation. Interestingly, this length is in agreement with the evaluated obstacle spacing per slip plane from our experiments. This is in contrast to the smaller samples in the size-dependent regime, shown for example in Fig. 2 and Fig. 4, where the dislocation source size at yield is evaluated to be just ~8 nm and ~11 nm, respectively, which is well below the obstacle spacing.

Essentially, larger dislocation sources are operated by lower stresses in the absence of defects. But if presented with smaller spacing’s, the defects control the onset of plasticity. Smaller sources require high stresses, so they are relatively unaffected by the presence of the defects. Therefore, in the size-dependent regime the critical step is the activation of a spiral dislocation source that is much smaller than the obstacle spacing. In the size-independent regime, the dislocation sources are larger than the obstacle spacing, rendering the passing of the SFTs by moving dislocations the critical step. The concept that the evaluated dislocation source size in the size-independent regime fits the low experimental defect density indicates that the dislocation source sizes evolve during the experiment¹⁵, and that large SFTs might act as pinning points. A detailed assessment of this observation requires data on different obstacle spacings, which is currently under research. Details on the above quoted values can be found in the SOM.

The fact that Girault et al.³² did not see a transition from their size-independent bulk strength to a size-dependent behavior is interesting and seems on the first view contradictory to the present results. However, the authors stated that the oxide particle spacing was well below 100 nm, while their smallest sample was still 200 nm in diameter. In that case the limiting factor for the dislocation source size is still the oxide particle spacing, not the pillar dimension, in agreement with the present results. From Fig. 3 in Ref. 32 one would expect to see a transition below ~150 nm.

The notion that the experimentally observed size-independent yield strength lies well within the simulation results in Fig. 3 is not very surprising, as the range of maximum obstacle strengths imposed by 4.7 nm large SFTs to a passing dislocation was taken from the computations¹⁹. In an averaged ensemble such as the current experiments, overcoming the strongest obstacle on the slip plane should be the critical step. The size of the simulated SFTs was larger than in the experiments, thereby giving higher maximum obstacle strengths of ~360 MPa, compared to 220 MPa – 280 MPa in our experiments.

Much more exciting is the question how these values relate to bulk properties. Studies on ‘real’ neutron irradiated polycrystalline bulk copper report a yield strength of 310 MPa³⁴. Under the assumption that the damage produced by the different irradiation conditions is similar (as detailed in the SOM), the data should be comparable. Taking into account the Hall-Petch strengthening of the neutron irradiated polycrystalline material from Ref. 34 (see SOM), the intrinsic strength of irradiated single crystal copper would be ~273 MPa, which is in accordance with the present results (Fig. 3) and estimates using the dispersed barrier hardening model.

While in the current case the results for nanoscale testing relate reasonably well to bulk properties, it should be pointed out that this is a rather simple model material. As outlined before, in advanced structural materials several different length scales come into play, rendering the bridging from nanoscale tests to bulk properties far more complicated. Moreover, the homogenization occurring in bulk materials does not take place in nanoscale tests, where scatter occurs due to the inherently stochastic nature of yielding in small volumes, particularly where the obstacle spacing on the slip plane is on the order of the specimen dimension.

In summary, we showed that in single crystal (100) oriented copper irradiated to 0.8 dpa the strength is affected by the interaction between moving dislocations and radiation-induced defects, and size-independent yield strengths are measured for samples as small as only ~400 nm. For even smaller specimens, the yield strength of the nano-pillars becomes affected by the sample size, as the stress required to operate ever-smaller dislocation sources overcomes the obstacle strength posed by the radiation-induced defects. It is worth pointing out that this transition length scale is not a general feature, but depends on the defect characteristics and therefore on the material, irradiation dose and temperature. The sample deformation was observed to be strongly localized over the whole tested size range from 80 nm – 1500 nm due to the requirement of forming a large enough dislocation source in a volume containing densely spaced irradiation defects. These results bear important implications for the application of small scale testing in nuclear environments as well as for the design of MEMS components to be used in an irradiation environment.

Methods

Material irradiation

3 mm × 3 mm wedges were prepared from single crystal copper with a (100) orientation (MaTecK GmbH, Juelich, Germany), using mechanical and electrochemical polishing. The subsequent experimental procedure is shown in Fig. 1: A 5 μm thick and 200 μm long lamella was machined out of the single crystal wedge using an FIB microscope (FEI Strata 235; FEI, Hillsboro, OR, USA) operated with Ga⁺ ions at 30 keV. The wedge was then irradiated with a 1.1 MeV proton beam, having a Bragg peak at 7 μm depth³⁵. Therefore, the proton beam passes through the FIB lamella, as seen from the logarithmic dose profile in Fig. 1, thereby avoiding hydrogen implantation in the relevant region of the specimen and having a relatively flat damage profile throughout the entire pillar. The irradiation setup was described in detail in Ref. 36 and the dose profile shown in Fig. 1 was calculated with the experimental beam current averaging of 17 μA·cm⁻² using the SRIM code³⁵. The irradiation temperature continuously monitored on the sample holder was 80 °C. The actual sample temperature might be higher, which would affect the defect annihilation and result in a lower defect density. Still, as copper is an excellent thermal conductor and the ion stopping region is not within the lamella, we do not expect a significantly different temperature.

Sample fabrication

After irradiation of the lamella, nanopillars with diameters ranging from 80 nm – 1500 nm and heights at least five times the diameter were fabricated by cutting annular trenches with the FIB. Final milling currents were 10 pA and the samples had an inevitable axial taper of ≤2.5°. The high aspect ratios of 5:1 were chosen to minimize for lateral boundary constraints and to avoid apparent hardening, especially after the formation of large slip offsets²⁸. From the dose profile and the pillar positions, the resultant dose for the nano-compression samples is estimated to be 0.8 ±0.01 dpa for the smaller samples and 0.8 ±0.09 dpa for the largest pillars. Additional damage emerges from the FIB fabrication process. This generates small dislocation loops and implantation of Ga in the surface area¹⁴. This surface FIB damage has a distinct influence on the mechanical properties of a defect free material⁴. However, given the large number of proton irradiation defects in the whole volume of our material and the pronounced difference to the unirradiated material, it is considered of minor concern in the present case.

Sample testing

Sample testing was performed in situ in a TEM (JEOL 3010, Tokyo, Japan) working at 300 keV using a Hysitron Picoindenter (Hysitron, Minneapolis, MN, USA) equipped with a flat conductive diamond tip and operating in displacement controlled mode with a nominal displacement rate of ~1 nm·s⁻¹, resulting in strain rates of ~10⁻³ s⁻¹. Videos were recorded with a charge-coupled device (CCD) camera (Gatan Orius SC200D; Gatan, Pleasanton, CA, USA) at 30 frames per second. There is a slight difference in image contrast (seen in the low intensity Fig. 2c and 2d) between the upper third of the image and the lower part. This emerges because the CCD image readout uses two channels to increase the frame rate, and there is a slight difference between the two dark currents.

Data evaluation

The recorded load – displacement data is combined with the in situ video to properly evaluate yield stresses, calculated from the load right before the first load drop and the measured contact diameter (assuming a circular pillar cross-section) at this point. Proper axial alignment was ensured by comparing the loading and unloading slopes for each test, as misalignment results in a pronounced reduction of the loading slope. Further details on sample fabrication, experimental conditions and data evaluation are provided in Ref. 28.

Evaluation of the spiral dislocation source size to relate stress, σ, to source size, L, follows Rao et al.³³:

$$\sigma =\frac{k\cdot G\cdot b}{mL}\cdot ln\left(\frac{L}{b}\right),$$ (1)

with k = 0.09 for a mixed type dislocation, shear modulus G = 47 GPa, Burgers vector b = 0.256 nm, and Schmid factor m = 0.408. To calculate critical resolved shear stresses (CRSS) for single crystal or polycrystalline data, the normal stress has to be divided by 2.45 (the inverse Schmid factor) and 3.1 (the Taylor factor), respectively. For more details please refer to the SOM.