Initial Dynamics of Cell Spreading Are Governed by Dissipation in the Actin Cortex

Abstract

The initial stages of spreading of a suspended cell onto a substrate under the effect of (specific or nonspecific) adhesion exhibit a universal behavior, which is cell-type independent. We show that this behavior is governed only by cell-scale phenomena. This can be understood if the main retarding force that opposes cell adhesion is of mechanical origin, that is, dissipation occurring during the spreading. By comparing several naive models that generate different patterns of dissipation, we show by numerical simulation that only dissipation due to the deformation of the actin cortex is compatible with the experimental observations. This viscous-like dissipation corresponds to the energetic cost of rearranging the cytoskeleton, and is the trace of all dissipative events occurring in the cell cortex during the early spreading, such as the binding and unbinding of cross-linkers and molecular friction.

Introduction

Complex systems are characterized by the emergence of elaborate behaviors from the interplay of simple components. This is undoubtedly a striking feature of live cells in general, and the mechanical behavior of live cells is, among other behaviors, definitely complex and seemingly unpredictable from the properties of the cell components. Understanding such a system involves of course, as a first step, to isolate these components and describe their individual properties, before understanding their role in the whole machinery of the cell. This has been, and is to remain, the main route toward a global understanding of cell dynamics.

Here however, we offer a different stance, which may be used to shortcut the need of understanding the function of the actomyosin cortex in some situations. Indeed, rather than focusing on the definite role of one of the features of the actomyosin cortex, we show that during early cell spreading, its effect as a bulk can be accounted for by a simple dissipative model. It is found that in this situation, a force of dissipative nature opposes the deformation of the cortex. This does not tell the origin of this observed dissipation: it must partly arise from classical molecular friction, but also from the energy dissipated in breaking cross-links between filaments, and work done against molecular motors pulling. Thus, the gain is not a better understanding of the function of the actomyosin cortex, but insight into the role it plays as a whole in a process of physiological relevance. This role is passive and thus very limited in the case of early spreading—which is why a simple model can describe it—but understanding and quantifying this could allow, in cases where the cortex plays an active role, to compare its energetic balance with a well-defined ground state behavior, namely this passive behavior.

Early cell spreading has recently retained the attention of biophysical investigations, following the seminal work by Dubin-Thaler et al. (1), Giannone et al. (2), Döbereiner et al. (3), and further investigation by Cuvelier et al. (4). In these studies, cells initially suspended in the medium are allowed to settle and spread on a glass coverslip. The authors track the area of cell membrane that is closely aligned with a glass substrate, typically within a few hundred nanometers. Note that within this area, some parts of the membrane are in closer contact with the substrate. In (5–7) the authors distinguish between the flattened area, which we name here aligned area, and the molecular contact area, which is the area within a few tens of nanometers of the substrate. The dynamics of the aligned area and those of the molecular contact area are likely to obey different rules.

Because alignment with a substrate exposes the suspended cell to an abrupt change of its mechanical environment, the dynamics that result from this change can provide the biophysicist with a valuable insight into the mechanical balance within the cell. Of course, the observed dynamics is the result of both a mechanical response to a change of conditions and an active response of the cell. A major question to address is how to determine which of these dominates during the time of observation. After a few minutes of spreading, Dubin-Thaler et al. (1) clearly demonstrate the domination of active processes, generating local, transient extension periods (dubbed STEPs). However, before this regime appears, Döbereiner et al. (3) and Cuvelier et al. (4) evidence a spreading regime where the area of cell membrane aligned with the substrate grows linearly in time, independently of the cell type and adhesion type (4). This phase is dubbed phase 1, or P₁. This regime is followed by an abrupt transition to another, slower spreading regime, phase P₂, which in turn is followed by the initiation of active processes (STEPs, phase P₃).

Although it is clearly demonstrated that P₂ is strongly dependent on actin polymerization and myosin motors activity, P₁ is mostly independent of these (see cytochalasin-D, latrunculin A, and ML-7 drug treatments in (2)). Cuvelier et al. (4) show that during P₁, the cell area in close vicinity to the substrate grows in time as a power-law, with an exponent close to one and which is independent of cell type and adhesion type (specific or nonspecific), although the prefactor to this power-law varies. The fact that the initial P₁ regime is a (linear) power-law must proceed from a balance of leading-order processes that govern the dynamics (e.g., energy inputs and dissipation). Indeed, when a power-law solution exists for a dynamical system, the exponent of this power-law is only dependent on the nature of the leading-order terms and not on the numerical value of parameters—while the prefactor is dependent on both. This exponent thus offers a discriminating test for predictive models with a large robustness with respect to numerical parameters chosen, as the dominance of the corresponding terms only has an effect on the predicted exponent.

The transition between P₁ and P₂ is quite abrupt, lasting a fraction of a decade, whereas P₁ can be observed for nearly two decades in time. Cuvelier et al. (4) hint that this behavior may be of purely physical origin, and that regime switch is triggered by geometrical change. However, they do not validate this hypothesis through experimental means, and assume that the transition occurs when cells reach a flattened shape where the lower, substrate-bound part of the actomyosin cortex and its upper part are brought close to one another.

The experimental part of this work aims mainly at testing the hypothesis that the abrupt termination of the linear growth regime P₁ is triggered by geometrical causes, and determining the shape of the cell at that instant. If it is of geometrical origin, the regime change must occur when the spreading cell reaches a given shape, regardless of its size and of the size of the aligned area. Thus, the extent of spreading at this transition has to scale like the size of the cell itself, which is what we observe. These observations are obtained by tracking the area of the cell in close vicinity to the substrate, but excluding thin dynamical structures such as microvilli and lamellipodia, which do not account for a global deformation of the cell.

This being established, we deduce that, during an early stage of spreading that includes the linear growth regime and the regime change, the dominating effect is the mechanical response of the cell, rather than its active response to the presence of the substrate. We then turn to modeling to determine which of the cell compartments has the most importance in this mechanical response. Simulations demonstrate that the dissipative response of a compartment corresponding to the cell actomyosin cortex leads to a spreading profile that matches the experimental spreading profile, while other mechanical models can be ruled out.

Materials and Methods

Cell culture

T24 cell line (bladder carcinoma) was obtained from ATTC (Rockville, MD), and was cultured in RPMI 1640 supplemented with 10% fetal bovine serum and antibiotics. Cultures were kept at 37°C in a 5% CO₂ humidified atmosphere. For studying the spreading of cells by total internal reflection fluorescence (TIRF), we have used a stable T24 transfectant cell line expressing green fluorescent protein (GFP) (8).

Microscopy techniques

TIRF microscopy images of spreading cells were collected using an EMCCD camera (Evolve 512, Roper Scientific, Ottobrunn, Germany) on a Zeiss Aviovert200M inverted microscope (Carl Zeiss, Jena, Germany) using a 100×/1.46 Plan-Apochromat objective and a 488 nm argon laser line. The image acquisition was performed using MetaMorph v.7.5.6 software (Universal Imaging, Marlow, UK)).

T24 cells were imaged in time-lapse sequences at a continuous rate of one frame every 5 s with 150 ms exposure for each channel for the overall period of 30 min. Cells were maintained at 37°C in a humidified atmosphere containing 5% CO₂, and deposited in the two-well chambered coverglass (Lab-Tek, Nalge Nunc International, Rochester, NY) coated with a 10 μg/ml fibronectin solution, and placed into the on-stage cell incubator (XL3, PeCon, Erbach, Germany).

For confocal microscopy, T24 cells transfected with actin-GFP were left to adhere 15 min on coverglass precoated with 5 μg/ml fibronectin, and rapidly fixed for 10 min with 4% paraformaldehyde. After three washes with phosphate buffered saline, nuclei were labeled with Hoescht 33342, and cells were observed on a Zeiss confocal microscope LSM 710. Measurements were made thanks to the software Volocity (PerkinElmer, Waltham, MA).

Image analysis

Images were treated with ImageJ software (National Institutes of Health, Bethesda, MD). Characteristic cell section area A₀ is determined manually in the transmission images taken before any adhesive patch appears in TIRF microscopy. Cells are still spherical at that time, and transmission images give a circular shape, see Fig. 1 a. Thresholding was used to determine areas of significant fluorescence. For each cell spreading event, two different threshold levels were defined: one corresponding to intense fluorescence and defining a central, stable area of cell alignment with the substrate, and a lower threshold that defines a larger area of cell alignment, which includes a dynamic peripheral area (Fig. 1 b). Both of these thresholds were fixed to a constant for the full duration of each spreading experiment. The ImageJ particle analysis feature is employed to measure the area of the thresholded area, which we named aligned area.

Figure 1.

(a) Experimental tracking of a T24 cell spreading on a fibronectin-coated substrate. At $t=0$, a transmission image is acquired, which allows determining A₀. For $t>0$, TIRF signal is acquired every 5 s, imaging the portion of the cell close to the substrate. White contours delineate the high fluorescence zone, excluding lower fluorescence peripheral zones (arrow heads). (b) TIRF evidence of transient protrusions of the lower fluorescence zones: TIRF images from $t=109$ s to $t=159$ s. The horizontal white line corresponds to the section shown on the kymograph (c). Inner contours delineate the high fluorescence zone as in a, outer contours delineate the lower fluorescence zone. (c) Kymograph of the lower fluorescence zones along a section of the cell. The central, high fluorescence zone is shown in black. The outer contour of the lower fluorescence zone is very dynamic and subject to sudden bursts of growth and retraction (arrow heads), visible on (a) at the relevant instant. The central, high fluorescence zone grows in a quasi-monotonic way, with a nearly constant growth rate until $t\approx 225$ s. (d) Dynamics of the high and lower fluorescence zones: movements of the barycenter of, respectively, the high fluorescence zone (black) and the lower fluorescence zone (gray) between two snapshots (5 s apart). The movements of the peripheral lower fluorescence zone have a threefold larger amplitude than the central high fluorescence zone. This corresponds to the existence of sudden bursts of growth and retraction of the peripheral zone that offset its barycenter.

Experimental Results

TIRF imaging distinguishes thin, dynamic peripheral structures from cell body

We dynamically monitor the spreading of T24 cells on a flat substrate coated with fibronectin. TIRF microscopy allows us to image the patch of cell area located at $0.2\mu \text{m}$ or less from the substrate (Fig. 1 a, Movie S1 in the Supporting Material). Image analysis allows us to discriminate between areas of high and lower fluorescence (Fig. 1 b). Because the whole of the cytoplasm is marked with GFP, this fluorescence intensity is proportional to the volume occupancy of the cell in the vicinity of the coverslip. The high fluorescence area forms a convex, central region, which grows steadily and smoothly throughout the early spreading stage (black central region in the kymograph on (Fig. 1 c). The lower fluorescence areas are localized at the periphery of the cell. They are highly dynamic compared to the central region. They experience sudden, localized growth bursts before receding (arrow heads in Fig. 1 a).

Cell body aligned area grows linearly before a geometrical transition to slower growth

Next, we focus on the high-intensity fluorescent area. This patch, which we name cell body aligned area, is found to grow radially (see Fig. 1 a). Its area $A\left(t\right)$ grows monotonically in time, Fig. 2 a, and it is found that this growth is close to linear in its initial part: for the range $A<0.6A_0$, linear regression by ${\left(t/{\tau }^{\prime }\right)}^{\alpha }$ yields exponents α around an average $\mu \left(\alpha \right)=1.02$ and SD $\sigma \left(\alpha \right)=0.17$ ($n=11$, see Fig. 2 c). The spreading coefficient ${\tau }^{\prime }$, however, is highly variable from one cell to another. This is as reported for a number of other cell lines in (4), despite the fact that α corresponds to the cell body aligned area here while exponents in (4) refer to the whole cell. These exponents also correspond to one of the two possible spreading rates of the whole cell during P₁ found in (3).

Figure 2.

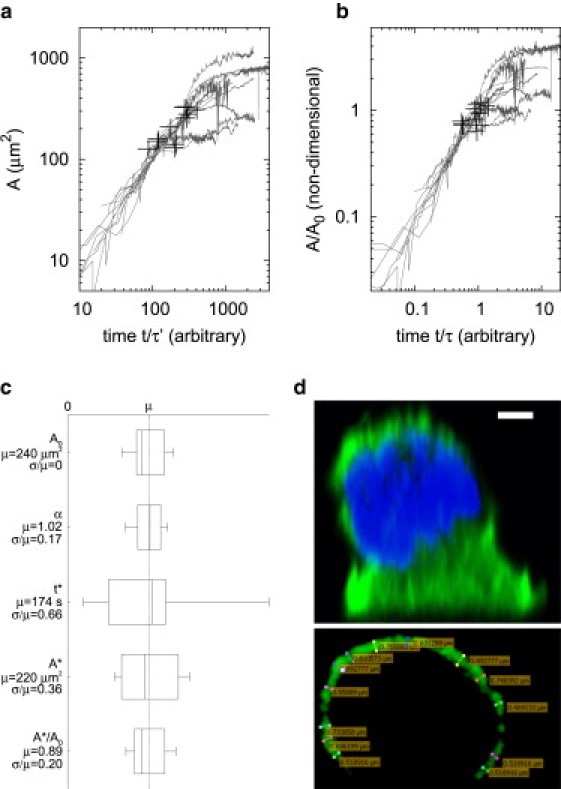
(a) Aligned cell body area $A\left(t\right)$ and (b), reduced cell body aligned area $A\left(t\right)/A_0$ T24 cells ($n=11$) as a function of time, rescaled by a cell-dependent spreading coefficients ${\tau }^{\prime }$ in a and τ in b calculated by linear regression. The curves are seen to collapse initially for both a and b. Crosses indicate the points $\left(t^{\ast }/{\tau }^{\prime },A^{\ast }\right)$ in a and $\left(t^{\ast }/\tau ,+A^{\ast }/A_0\right)$ in b for each cell, where spreading ceases to be a linear function of time according to least square error. (c) Box plots of A₀, α, $t^{\ast }$, $A^{\ast }$ and $a^{\ast }=A^{\ast }/A_0$ showing the sample minimum, lower quartile, median, higher quartile, and sample maximum relative to their mean value μ of $n=11$ cells. Mean μ and coefficient of variation $\sigma /\mu$ are indicated in each case. (d) Top, shape of a spreading T24 cell in $\left(x,z\right)$ plane for $A\left(t\right)/A_0=1.03\gtrsim a^{\ast }$ observed by confocal microscopy: Green, actin-GFP; blue, nucleus labeled with Hoescht 33342. Scale bar, 3 μm. Bottom, $\left(x,y\right)$ slice of actin-GFP of the same cell, showing the actin cortex thickness.

This linear growth is followed by a slower growth after a transition. We define $t^{\ast }$ and $A^{\ast }=A\left(t^{\ast }\right)$ as the time and current aligned area at this transition (see also supplementary note in the Supporting Material, Determination of the transition between linear and slow spreading regimes). To check whether this transition happens at a determined shape of the spreading cell, knowledge of the cell volume is needed. This is achieved by acquiring a transmission microscopy image of the cell just after contact with the substrate has initiated (Fig. 1 a). At this time, the cell still has the spherical shape that cells assume when in suspension, which makes the section area A₀ of the circular transmission image proportional to its volume to the exponent $2/3$. This section area A₀ can hence be used to scale the aligned area $A\left(t\right)$: the ratio $A\left(t\right)/A_0$ corresponds to a given shape of the spreading cell. In our experiments, the section area A₀ varies between $161\mu {\text{m}}^2$ and $313\mu {\text{m}}^2$, with a coefficient of variation of 0.21 (that is, the ratio of the SD to the mean). Linear regression allows the collapse of the initial spreading of cells for $A\lesssim 100\mu m^2$ on a curve $A\left(t\right)\propto t/{\tau }^{\prime }$ where ${\tau }^{\prime }$ varies from one cell to another (Fig. 2 a). However, the transition time $t^{\ast }$ appears to be highly variable from cell to cell (coefficient of variation, 0.66, see Fig. 2 c). The transition area $A^{\ast }$ is also variable from one experiment to the other (cross symbols, Fig. 2 a), coefficient of variation, 0.36 (Fig. 2 c). Next, we plot the spread area reduced by the characteristic size of each cell $A\left(t\right)/A_0$, where A₀ is observed for each cell before it spreads (Fig. 2 b). These curves are seen to depart from linear spreading at a much better defined critical reduced area, equal to $a^{\ast }=A^{\ast }/A_0\simeq 0.81$ (cross symbols, Fig. 2 b). Indeed, the coefficient of variation of $a^{\ast }$ is only 0.20 (Fig. 2 c). Thus, $A^{\ast }$ varies in proportion with A₀, which means that the transition area scales with the size of the spreading cell. This supports the fact that the transition between the linear spreading regime, for $A\left(t\right)<A^{\ast }$, and the slower spreading, for $A\left(t\right)>A^{\ast }$, happens at a given shape of the cell, characterized by a constant critical value of $a^{\ast }\simeq 0.81$ for every cell. A confocal image in Fig. 2 d shows the shape for $A\left(t\right)/A_0\simeq 1$.

This validates the assumption that geometry triggers the transition, rather than elapsed time or absolute dimension of the aligned patch. Thus, it makes sense to apply the scaling theory, considering that phenomena are invariant when all spatial dimensions are normalized by the typical size of the suspended cell considered, $A\left(t\right)/A_0$. Because the growth profile before and after time $t^{\ast }$ obeys power-laws with seemingly universal exponents, complete collapse of aligned area profiles onto a master curve can be obtained by further rescaling times with a characteristic time τ, which will take a different value for each cell. This characteristic time may depend on a host of parameters, and can only be interpreted in the light of a particular model.

On the other hand, because characteristic spatial scales of molecular processes are the same independently of the size of the cell, we infer that these phenomena do not govern a cell-size-dependent process, and thus only phenomena occurring at the cell scale are relevant in this study.

Transition occurs for $A^{\ast }/A_0=a^{\ast }\simeq 0.81$ (median value), which means that the aligned area is smaller than the area of the equatorial section of the cell when it is spherical. The approximative shape of the cell is thus the one of a truncated sphere, on which smaller-scale dynamic structures such as microvilli or thin lamellipodia (not included in $A^{\ast }$) are superimposed, see Fig. 2 d. For a spread area $A/A_0\simeq 0.81$, the deformation undergone by the cell is thus small (compared to a fully spread cell), and does not necessarily imply structural changes in its cytoskeleton. This means that a purely mechanical process can still be the leading-order phenomenon setting the spreading rate even after transition. To test this hypothesis, the next sections are devoted to the definition of biomimetic continuum models of cells, and to determining the spreading rate that such objects would have in the same conditions as cells in experiments, finally retaining only models that exhibit the sequence of power-laws observed for cells with the correct transition shape.

Numerical Results

Numerical simulations of three simple models are performed, and the corresponding spreading time profiles are obtained. In all models, the dynamics are set by a balance between the adhesion energy gain when spreading on the substrate and dissipation due to deformation. The difference between models lays in the geometric pattern of dissipation.

In the first model, the relation between deformation and dissipation (that is, viscosity), is taken to be homogeneous within the object. This corresponds to the physical case of a highly viscous drop. The second model object has a peripheral region (cortex) that is much harder to deform than its interior. Finally, we simulate homogeneous drops with an inextensible membrane, to check whether the fact that the cytoskeleton is bound to the outer cell membrane can significantly modify the dynamics. The dynamics resulting for each of these models is compared to the one observed for cells.

Viscous drops

A spherical drop is suspended in a fluid at distance d₁ from a solid substrate. Drop and suspending fluids are viscous, incompressible, and the initial condition is quiescence. The only driving force in this model is adhesion force between drop interface and substrate, interfacial tension is neglected (see the Supporting Material, Modeling and numerical technique). This corresponds to the Stokes equations applied in the whole computational domain, with viscosities μ_d and μ_s for the drop and suspending fluid, respectively. The adhesion force is modeled as a generic potential, which is long-range attractive and short-range repulsive. This potential is parameterized by an adhesion strength w. Changing the value of w only modifies the characteristic time of the flow, without affecting the dynamics themselves: e.g., if one observes dynamics going as a power-law $C{t}^{\alpha }$ for some choice of w, a different value $w^{\prime }$ will yield a power-law $C^{\prime }{t}^{\alpha }$, with $C^{\prime }=C{w}^{\prime }/w$ and α unchanged. The same holds if μ_d and μ_s are changed while the viscosity ratio ${\mu }_d/{\mu }_s$ is kept constant. Thus, the only parameter that affects the dynamics is this viscosity ratio ${\mu }_d/{\mu }_s$. We perform direct numerical simulations of these equations using finite elements (see the Supporting Material).

Contact can be established through two different mechanisms. First, the drop can settle undeformed until its south pole is below $z=d_0$. This is the scenario for high-viscosity drops. Second, the globally immobile drop can deform locally at its south pole until contact is established. This is the high-viscosity suspending fluid scenario. At intermediate viscosity contrasts, both mechanisms compete (see Fig. 3, a–c).

Figure 3.

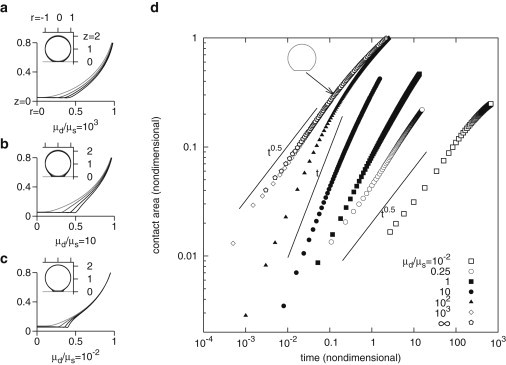
Initial drop spreading obeys power-laws that depend on viscosity contrast. (a–c) Shape evolution for different viscosity contrasts ${\mu }_d/{\mu }_s$, in $\left(r,z\right)$ coordinates. Insets, global view (negative values of r are drawn by symmetry), main plots, close-up next to substrate. Gray levels correspond to regularly spaced time intervals, from light to dark. (a), for ${\mu }_d/{\mu }_s={10}^3$ the drop deformation is minimized, this is also the case for higher viscosity contrasts and corresponds to a spreading profile $A\propto t^{0.5}$. Identical evolution is obtained for any ratio ${\mu }_d/{\mu }_s\ge 500$. (b), for ${\mu }_d/{\mu }_s=10$ the drop deforms to allow efficient drainage of the medium, this corresponds to a spreading profile $A\propto t$. Identical evolution is obtained for any ratio $2\le {\mu }_d/{\mu }_s\le 20$. (c), for ${\mu }_d/{\mu }_s={10}^{-2}$ the drag on the drop is very high and spreading occurs through local deformations only, the top part of the drop is nearly immobile (inset). Identical evolution is obtained for any ratio ${\mu }_d/{\mu }_s\le 0.5$. (d) Growth of aligned area of drops is shown as a function of time for different viscosity contrasts. Power-law initial spreading rates are clearly identified, behaving as t or $t^{0.5}$ depending on the viscosity contrast. For area $A\gtrsim A_{drop}^{\ast }=0.3A_0$, the rate is lower. Inset shows the shape of a viscous drop in the void (viscosity contrast infinite) for $A_{drop}^{\ast }=0.3A_0$ (arrow).

Further spreading depends on the viscosity ratio in the same manner. In Fig. 3 d, we plot the extent of (the logarithm of) aligned area versus (logarithm of) time elapsed from contact time. The overall spreading speed depends of course on the viscosity contrast. If the drop viscosity is defined as the reference viscosity, decreasing the suspending fluid viscosity (thus increasing the viscosity contrast) speeds up the process (from right to left in Fig. 3 d). More interestingly, the profile of each spreading curve is a power-law (phase P₁) followed by a slower spreading regime (phase P₂), which does not seem to be a power-law. For large $A/A_0$, the system would eventually reach a spherical cap geometry and obey the classical law of capillary spreading (9), however we have neglected the surface energy between the drop and the suspending fluid, which means that the simulations are not relevant anymore when A is greater than A₀. The exponent of the P₁ power-law is found to be different depending on the range of viscosity contrast. For ${\mu }_d/{\mu }_s\le 1/4$, we find that $A\propto t^{0.5}$, then for $10\le {\mu }_s/{\mu }_d\le 50$, we have $A\propto t$, and finally when ${\mu }_d/{\mu }_s\ge 1000$, the power-law is again $A\propto t^{0.5}$. This nontrivial dependence of the spreading rate of the drop can clearly be explained by comparing the energy dissipated instantaneously in the drop and outside of the drop, which can be calculated in the simulation. We find that highly viscous suspending fluid is slow to drain from the lubrication film in the aligned zone and sets the low viscosity contrast dynamics. Very viscous drops are hard to deform, setting another dynamical equilibrium. At intermediate contrasts, dissipation is shared between the two fluids, see Fig. S4. The resulting shape evolution is the same for any choice of the viscosity contrast within one of the three ranges mentioned. These three dynamics are shown in Fig. 3, a–c.

After this first stage of spreading P₁, a transition is always found to a slower spreading regime P₂. For high contrasts, this occurs for a reduced aligned area $A\left(t\right)/A_0=a^{\ast }=A^{\ast }/A_0$ of the order $a^{\ast }\simeq 0.3$, somewhat earlier for low contrasts (${\mu }_d/{\mu }_s\lesssim 10$). The regime in P₂ does not seem to follow a power-law. The variations in the initial spreading rate are seen to depend on viscosity contrast over more than four decades. Deriving this dependence analytically does not seem straightforward (10), and our numerical results clearly differ from the law $A\sim t^2$ derived from an order of magnitude analysis in (4).

Viscosity contrast between cell and culture medium is estimated in the range of 10⁴–10⁶ (e.g., (11)). Thus, simulations show that in these conditions, the rate of spreading of a drop is $A\sim t^{1/2}$ during the P₁ phase, and not linear as in experiments with cells. This simple model is inconsistent with the experiments and other features of the cell need to be taken into account; this is the topic of the following sections.

Composite drops

The spatial arrangement of long polymeric filaments in cells is well known and described (12), thus a first refinement to the crude drop model of the cell is to introduce spatial variations of viscosity. The densest part of the cell (and hence most viscous) is the nucleus, however due to geometry it has little relevance in the initial stages of spreading. A second region of interest, namely the actin cortex, is at the periphery of the cell, where a dense network of actin filaments grows. This is likely to affect the spreading profile, because the peripheral regions are the ones where shear is higher. As proposed by Cuvelier et al. (4), we introduce a composite drop model to account for this heterogeneity, where viscosity is initially distributed in a concentric manner, see Fig. 4 a. The cortex thickness is taken to be from 1% to 7.5% of the cell diameter, which corresponds to thicknesses from ∼0.2 to 1.3 μm for the typical cell size in our experiments. The model in this case is identical to the case of viscous drops, except for this initial distribution of viscosities, which is shown to be conserved by the spreading dynamics. Numerical simulations are performed with different values of the viscosity in the interior part of the composite drop, ranging from a viscosity equal to the one of the cortex down to the one of the outer medium. It is found that, as soon as the interior viscosity is one order of magnitude smaller than the cortex viscosity, and for all choices of the cortex thickness, the spreading profile is invariant with respect to this parameter (up to a time constant). In the sequel, we thus use an interior viscosity equal to the one of the outer medium. This distribution of viscosity modifies the distribution of dissipation, and it is verified in simulations that energy dissipation is mainly occurring in the cortex. However, it also modifies the deformation itself, because the relatively easy deformable interior allows for bending of the cortical shell, which appears to be less dissipative than shearing it, see Fig. 4, b and c.

Figure 4.

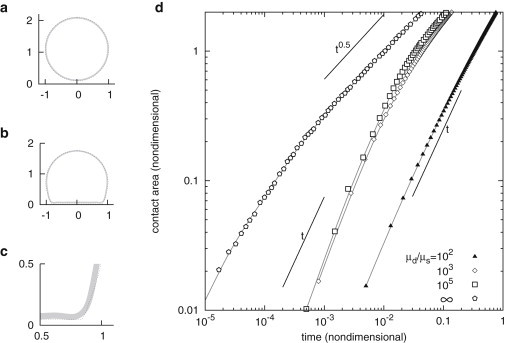
Composite drop spreading on a substrate. (a–c) Geometry of composite drop in $\left(r,z\right)$ coordinates (negative values of r are drawn by symmetry). The gray zone has viscosity${\mu }_d$, white have viscosity ${\mu }_s$. Dotted line shows the shape of a homogeneous drop. Identical evolution is obtained for any ratio ${\mu }_d/{\mu }_s\ge {10}^3$, including infinite ratio. (a) Initial geometry at $t=0$. (b) Geometry as $A=0.8A_0$. The composite drop can bend its cortex, while the homogeneous drop cannot. (c) Close-up of the contact zone in b. (d) Growth of aligned area of composite drops as a function of time for different viscosity contrasts. For a contrast of 100, a linear growth is observed. At higher contrasts, a transition to a square-root growth regime is observed for aligned area A above a threshold that weakly depends on viscosity contrast, going from $0.6A_0$ at ${\mu }_d/{\mu }_s=4\cdot {10}^3$ to $0.3A_0$ at ${\mu }_d/{\mu }_s={10}^3$. For a composite drop with infinite viscosity contrast, transition occurs early at $A\simeq 0.1A_0$.

Simulations show that this strongly affects the rate of spreading (see Fig. 4 d). For a viscosity contrast of 100, the aligned area growth is very close to linear over the whole relevant range of spread areas ($A/A_0\lesssim 1$), although the rate of spreading of a drop at the same viscosity contrast decreases from $A/A_0\simeq 0.2$. For higher viscosity ratios, aligned area growth is initially linear and then decreases to a distinctive square-root growth. Although this happens early in spreading for an infinite viscosity contrast ($A^{\ast }/A_0=a^{\ast }\simeq 0.1$, regardless of cortex thickness), the transition is taking place at $A^{\ast }/A_0=a^{\ast }\simeq 0.8$ for viscosity contrasts in the range of 10³–10⁵ and cortex thickness 2.5% of cell diameter. The transition $a^{\ast }$ increases with cortex thickness, and the choice of 2.5% of cell diameter, corresponding to 0.45 μm for T24 cells, matches the transition in the experiments. This is close to the average cortex thickness observed in Fig. 2 d. Other parameters do not noticeably affect this transition.

Although this behavior is qualitatively identical to the one predicted by the order of magnitude analysis in (4), the localization of dissipation calculated in simulations does not correspond to the assumptions formulated in the order of magnitude analysis. The shape at which the transition occurs is also very different from the flattened cell shape that justifies it in (4).

We were not able to perform reliable multiphasic numerical simulations for higher viscosity contrasts. However, 10⁵ is a good estimate of the actual viscosity contrast between cell cortex and medium, and spreading profiles being identical for contrasts between 10³ and 10⁵, it can be assumed that there is little change for viscosity contrasts one or two orders of magnitude higher. We hypothesize that the sequence of linear and slower regimes is conserved as the viscosity contrast increases, and that only the transition $a^{\ast }$ varies by slowly decreasing from 0.8 to 0.1 for infinite contrasts. For all the range of relevant viscosity contrasts, the spreading of composite drops is thus very similar to the one observed experimentally for cells.

Vesicles

Another mechanical feature of cells that may affect their spreading rate is their outer plasma membrane. Shear localization can also arise because of such a membrane, and this section investigates whether the spreading profiles obtained with composite drops are also found with drops surrounded by an inextensible membrane.

Drops surrounded by a lipid bilayer membrane are called vesicles and can be fabricated artificially, and could be used for an experimental investigation of cell spreading. However, it is technically difficult to reach high viscosity contrasts between the inner fluid and the suspending medium, which would be necessary for comparison with the present numerical results. The mechanical model governing these vesicles is the same as for viscous drops, with the addition of a constraint imposing that the membrane area is conserved everywhere locally. This is imposed numerically in simulations using a Lagrange multiplier, called the membrane tension (tension assumes the same role in enforcing area-conservation as pressure in enforcing volume-conservation for incompressible fluids, see the Supporting Material).

It has been said that suspended cells assume a spherical shape, yet incompressible spherical objects with an inextensible membrane are not deformable. Some excess area must be provided to allow spreading, and is initially present at the membrane periphery before spreading (13). If one assumes an initial spherical shape with a pattern of wrinkles superimposed (Fig. 5 a), a membrane-bound drop of viscosity 100 times the one of the suspending fluid will initially spread because excess area in the wrinkles allow for deformation, until it reaches the shape of a truncated sphere (Fig. S3). This corresponds to the maximum spreading, where all excess area is employed and the object is rigid with respect to further spreading.

Figure 5.

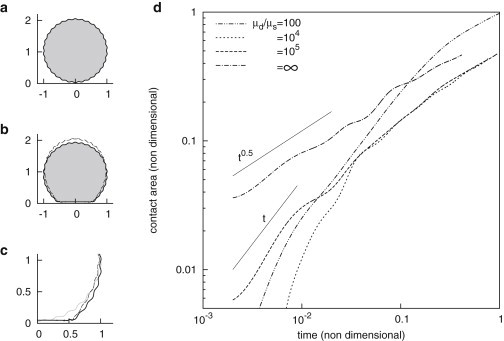
Vesicles spreading on a substrate. (a) Initial geometry of composite drop in $\left(r,z\right)$ coordinates (negative values of r are drawn by symmetry). The gray zone has viscosity ${\mu }_d$, white have viscosity ${\mu }_s$, and the solid line represents the inextensible membrane. (b) Solid line, geometry of a spreading vesicle with infinite viscosity contrast, dashed line, of a vesicle of viscosity contrast ${\mu }_d/{\mu }_s={10}^5$. To allow spreading, the membrane wrinkles are depleted everywhere for infinite viscosity contrast, only close to the substrate for finite viscosity contrast. Compare shape of vesicle at infinite viscosity contrast with Fig. 3a, at finite viscosity contrast with Fig. 3b. (c) Close-up of (b), with initial geometry overlaid in gray. Note the depletion of the wrinkles. (d) Growth of aligned area as a function of time for different viscosity contrasts. For contrasts up to 10⁵, an initial P₁ phase with $A\propto t$ is noted, followed by a slower P₂ regime $A\propto t^{1/2}$. Transition reduced area $a^{\ast }$ falls from 0.6 for ${\mu }_d/{\mu }_s=100$ to 0.08 for ${\mu }_d/{\mu }_s={10}^5$. For infinite contrast, the $A\propto t$ regime is not observed at all.

In Fig. 5 c, one sees that at viscosity contrast 100, vesicle spreading features the successive phases P₁ and P₂ with transition $A^{\ast }\simeq 0.7A_0$ (double dot-dashed curve in Fig. 5 c, also Fig. S3). However, when viscosity contrast increases, the transition between these regimes occurs earlier for $A^{\ast }\le 0.1A_0$, which differs with cell experiments. At infinite viscosity contrasts, one obtains a square-root spreading profile.

Discussion

Spreading cells form two distinct compartments

Thresholding the fluorescence intensity allows discriminating between a central region where a dense part of the cytoplasm is aligned with the substrate, and a peripheral region where transient, much less dense structures evolve with a fast dynamics (Fig. 1). Thus, there exist two distinct compartments during cell spreading. Compared to experimental observations by Giannone et al. (2) and Fardin et al. (14), we can identify the dynamic peripheral area with the thin lamellipodium that is observed at the cell periphery during spreading. Compared to the central, high fluorescence area, these thin structures are highly dynamic. These structures were characterized as being cell protrusions dependent on actin polymerization (2). The central, high fluorescence zone is much more steady both in shape and position of its barycenter (Fig. 1, b and d), and has a steadily growing area (Fig. 2 a).

These compartments can be distinguished for the whole of phase P₁ and somewhat into phase P₂. At the center is the cell body, which accounts for the large majority of cell volume and whose initial shape is spherical when the cell is suspended. This body deforms steadily to accommodate the flat substrate, and the part of its surface area aligned with the substrate grows smoothly. At the periphery, thin structures protrude transiently and retract (Movie S1).

Cell-scale phenomena govern initial spreading of the cell body

Comparison of growth profiles of the cell body aligned area for cells of a different size demonstrates the scale invariance of this process with respect to cell size (Fig. 2, b and c). Spreading during phase P₁ obeys a power-law

$$\frac{A\left(t\right)}{A_0}={\left(\frac{t}{\tau }\right)}^{\alpha }\text{for}t<t^{\ast },$$ (1)

where A₀ characterizes the size of the cell (it is the section area when the cell has a spherical shape), and the other parameters are fitted for each cell from measurements. Cuvelier et al. (4) found that $\alpha =1$ for two different cell lines, independent of the type of cell adhesion. This is also found here with yet another cell line, $\alpha =1.02\pm 0.17$ ($n=11$, see Fig. 2 c). The spreading coefficient τ is very variable from one cell to the other and not correlated with A₀. The time $t^{\ast }$ and spread area $A^{\ast }=A\left(t^{\ast }\right)$ up to which Eq. 1 holds is also highly variable from one cell to another, however, the scaled transition area $A^{\ast }/A_0=a^{\ast }$ depends only weakly on the cell considered, $a^{\ast }=0.89\pm 0.18$ ($n=11$). The reduced area $A\left(t\right)/A_0$ is representative of the shape of the cell at a particular time. Thus, a conserved transition in terms of $A^{\ast }/A_0$ implies that transition from P₁ to P₂ occurs for a definite geometrical shape, regardless of cell size. The direct conclusion is that the relevant scale at which the leading forces act is the scale of the whole cell, rather than a molecular scale. Indeed, a transition triggered by events at the molecular scale would be independent of the cell size (and would happen after a certain time $t^{\ast }$ or displacement characterized by the absolute value of $A^{\ast }$).

This observation thus confirms the hypothesis by Cuvelier et al. (4) that binder dynamics is not setting the rate of initial cell spreading, as was already hinted by the robustness of spreading laws with respect to the type of adhesion (specific or nonspecific (4)), which is expected to modify the rate of spreading (15). Cuvelier (16) also stresses that the required binder diffusion rate would have to be several orders of magnitude higher than the one on lipid membranes to explain the growth rate of the adhered patch.

Spreading of cell body compartment is mostly driven by adhesion and opposed by resistance to deformation

The robustness of the spreading rate characteristic exponent α and of the transition shape $a^{\ast }$ suggest that mechanical causes prevail over active cell deformation, as far as the cell body is concerned, as compared to the thin, dynamic protrusions that have been demonstrated to be actively generated by the cell (14,17). The fact that the transition happens when the cell shape is very far from flattened, see Fig. 2 d, and that this transition is quickly gone through (within tens of seconds), further support the hypothesis that the whole of phase P₁, and the transition to phase P₂, are not actively driven by the cell, as this would require instant reaction to an hypothetic shape detection. This does not have to mean that the cell body behaves like dead matter when spreading, but that the living activity (such as motor pulling) is not directed toward or against spreading, but remains distributed independently of the spreading event during these early stages, which last no more than a few minutes.

Thus, the energy that is being used for spreading is not the cell chemical energy, but the adhesion energy that is gained by closely aligning with the substrate. The possible retarding force of mechanical origin opposing the adhesion force and setting the balance is the resistance to deformation. If the cell does not actively reshape its cytoskeleton in response to the adhesion force, the cytoskeleton has to be deformed to conform locally to the plane geometry of the substrate. At the timescale of spreading, of the order of 100 s, the elastic resistance to deformation is largely dominated by dissipation (18). This dissipation includes of course molecular friction (viscosity), but also other effects more specific to living cells, such as the necessity of breaking cross-links, and work done against molecular motors. At the cell scale however, these events retain the trace of energy dissipation per unit deformation, and thus express in units of viscosity. Thus, the spreading of the cell body can be compared with models that feature an adhesive driving force and a bulk dissipation of viscous type, as is the case in the three different models investigated in this paper.

Parameter dependence of the simulations

Numerical simulations show that the initial spreading of a viscous object on a substrate under the action of a generic adhesion force exhibit a great wealth of behaviors, depending on the distribution of viscosity. In all numerical simulations, it was found that the spreading profile assumed initially a power-law behavior, of the type $A\left(t\right)/A_0\simeq {\left(t/\tau \right)}^{\alpha }$ for $A\left(t\right)/A_0<a^{\ast }$ (phase P₁), and then a slower spreading $A\left(t\right)/A_0\propto t^{\beta }$ with $\beta <\alpha$ (phase P₂). The constant τ was strongly dependent on both the model (drop, composite drop, or vesicle) and the parameters (viscosities and adhesion parameter), however the exponents α and β, as well as the reduced transition area $a^{\ast }$, were found to be very robust with respect to these, and depend only on the order of magnitude of the viscosity contrast (Fig. 6 a). This means that the values chosen for the models only need to be in the broad range of their equivalent for actual cells for the models to give relevant α, β, and $a^{\ast }$.

Figure 6.

Composite drops reproduce the time profile of spreading observed in experiments on living cells, whereas drops and vesicles exhibit slower spreading for physiological viscosity contrasts. (a) Power-law exponent of initial spreading depends on viscosity contrast over more than five decades; composite drops are closest to experimental results. Exponent of the best-fit power law of aligned area growth of drops, composite drops, vesicles, and composite vesicles with area reservoirs as a function of the viscosity contrast. A critical viscosity contrast separates approximately linear regimes from approximately square-root regimes, and differs depending on the model. In the range of viscosity contrast relevant to live cells, only composite drops robustly exhibit a close to linear spreading profile. (b) Comparison of growth regimes in experiments and numerical simulations with relevant viscosity contrast. Experimental curves are reproduced from Fig. 2b. Viscosity contrast: drop, infinite, composite drop, and vesicle, 10⁵.

The value of α is always between 1/2 and 1 (Fig. 6 a). When the viscosity contrast between the object and the suspending fluid is either very small or very large, α tends to 1/2 regardless of the distribution of viscosity in the object. When the contrast between the viscosity μ_d of the object and the one of the suspending fluid μ_s is in some intermediate range, α is close to 1 and β to 1/2. This intermediate range is different for each model, and is largest for composite drops. We find that this model only is consistent with cell observations, because it is the only one that exhibits a rate $\alpha =1$ for viscosity contrasts of the order of 10⁴–10⁶, which is what is expected for actual cells in medium.

Within the model objects studied here, the composite drop model is the only one allowing reproduction of the experimental cell spreading profiles. This model reproduces the linear exponent of the stage P₁ of spreading, and also the transition shape from stage P₁ to stage P₂, measured by the ratio $a^{\ast }=A^{\ast }/A_0$ (Fig. 6 b).

To fit the data, only one parameter needs to be adjusted, namely the characteristic time $T=R_0{\mu }_0/w$. Values of μ₀ and w compatible with the experimental results fall in the range of cell viscosities and adhesion energy found in the literature, but do not provide additional accuracy in evaluating these values in the absence of an independent measurement of either of them. On the other hand, the match with experimental data is robust in the sense that results depend only on this physical parameter, and there is no other adjustable parameter of first order influence.

Dissipation in the actin cortex governs the dynamics of spreading

We show that the rate at which the body of the cell aligns with the flat substrate is determined by mechanical phenomena during phase P₁ of cell spreading up to the transition to the slower phase P₂. In addition, among mechanical models featuring the leading order characteristics of animal cells, the composite drop model is the only one that robustly features the spreading profile during these phases. This allows us to offer an explanation for the mechanism setting the cell body spreading dynamics by comparison with those at play in this model.

In the composite drop model, the spreading rate is governed by the rate of dissipation of energy gained through adhesion. This dissipation occurs nearly exclusively in the high-viscosity cortex of the composite drop (Fig. S5), and is proportional to the product of a viscosity coefficient and the total amount of shear incurred during the deformation of the cortex to accommodate the flat substrate.

In living cells as well, energy is necessary to deform the initially spherical cell cortex and accommodate the flat substrate. In addition to mere intermolecular friction, the flattening of the basal part of the cell body requires remodeling of the dense actin cytoskeleton. This remodeling occurs notably through the unbinding (and subsequent rebinding) of actin cross-linking molecules (19). As long as the cell is not actively spreading at this early stage, adhesion provides the energy source for this.

Comparison with the numerical simulations suggests that this is the leading order energy transfer that sets the rate of spreading of the cell body. This allows us to conceive the following scenario for early cell spreading. First is a sedimentation stage in which the suspended, spherical cell slowly settles undeformed toward the substrate. Occasional transient protrusions develop at the cell surface, powered by actin polymerization and probably myosin, however these concern only a very small fraction of cell mass. The protrusions located at the bottom part of the cell surface encounter the substrate, and transiently develop along it; they may develop forces sufficient to bring the cell into contact with the substrate (countering the fluid drag from the medium) but not deform the cell. Through these forces and gravity, the south pole of the cell is brought into contact with the substrate (first bright patch in TIRF visualization, Fig. 1 a at $t=18$ s). Active cell protrusions continue at the periphery (arrows in Fig. 1 a) while the adhesion energy gained by aligning the base of the cell body with the fibronectin-coated substrate provides the energy necessary for rearranging the actin cortex in this new configuration (phase P₁). As the cell attains the approximate shape of a half sphere, the rate of spreading using this modality decreases sharply, as shown in numerical simulation and as phase P₂ begins. In this subsequent phase, it is likely that active force generation and decision making through signaling cascades gradually take over purely mechanical force imbalances and govern the dynamics of spreading and, eventually, arrest or migration.