Universal fractal scaling of self-organized networks

Abstract

There is an abundance of literature on complex networks describing a variety of relationships among units in social, biological, and technological systems. Such networks, consisting of interconnected nodes, are often self-organized, naturally emerging without any overarching designs on topological structure yet enabling efficient interactions among nodes. Here we show that the number of nodes and the density of connections in such self-organized networks exhibit a power law relationship. We examined the size and connection density of 47 self-organizing networks of various biological, social, and technological origins, and found that the size-density relationship follows a fractal relationship spanning over 6 orders of magnitude. This finding indicates that there is an optimal connection density in self-organized networks following fractal scaling regardless of their sizes.

1. Introduction

There has been considerable interest in the organization of complex networks since the descriptions of small-world [1] and scale-free [2] networks at the end of the 1990s. Of particular interest are naturally occurring complex networks based on self-organizing principles [2]. In particular, self-organized processes have been shown to exhibit some scale-free and fractal behaviors [2, 3]. Barabási and colleagues demonstrated that scale-free degree distributions in many self-organized networks [2, 4–6], which has sparked a great debate [7–9] on the actual existence of scale-free behavior in naturally occurring networks. Although the degree distributions of many networks were initially considered to follow power law distributions [9–13], severe truncation has often been observed [14]. Nevertheless, it is intriguing that self-organized networks can exhibit scale-free degree distributions, and this has led scientists to the search for universality within self-organized systems.

The literature on network organization encompasses a broad range of disciplines and disparate types of networks. The literature boasts networks that range from email communications to protein interactions to word frequencies in texts. The number of nodes and the density of connections in these networks span multiple orders of magnitude, complicating comparisons of metrics extracted from various studies. One common characteristic, however, is that the majority of them are self-organized–from social to technological to biological networks, the interactions between the nodes were not predetermined by a top-down blueprint design. Despite this lack of top-down design, some self-organized networks exhibit interesting characteristics associated with the connection density and the network size. For example, utility networks from different countries in Europe tend to have similar average degrees although these networks tremendously differ in size [15, 16]. Another interesting observation is that the density of connections in social networks seems to decay non-linearly as the size of the network increases [17]. These observations suggest that there may be an underlying relationship between the size (the number of nodes, N) and the connection density (the ratio of the number of existing edges to the number of all possible connections, d) in these network. Although these findings are based on particular types of networks, it is possible that this relationship is universal to all types of self-organized networks. Thus, in this work, we examined any universal relationship between network size and connection density, as well as the average node degree, across various types of systems.

2. Methods and Materials

Network parameters from 47 unique networks were collected from the literature or publicly available databases. Table 1 lists N and d, as well as the average node degree K and the total number of edges m from these networks. Although d and/or K have been reported in some of these networks, these metrics are recalculated based on N and m for consistency. Namely, we use the formulae d = 2m/N(N − 1) and K = 2m/N. Although some of the networks are directed networks, we use the formulae for undirected networks in order to focus on the density of connections regardless of their directions. Note that, from these formulae, the relationship between K and d can be expressed as d = K/(N − 1). If N is sufficiently large, d ≃ K/N.

Table 1.

Networks considered in the size-density relationship analysis. Parameters culled from the literature are network size (N) and the number of edges (m). The network density (d) and the mean degree (K) are calculated based on N and m. Networks marked with ‡ contain directed connections. All other networks contain undirected connections. Note that the functional cortical connectivity network was generated by applying a threshold to a correlation matrix, yielding a network that had the edge density of approximately 10%.

Network classes	Networks	N	m	d	K	References
Biological	C. Elegans metabolic	453	2033	1.986×10−2	9.0	[18]
	C. Elegans neural	277	1918	5.018×10−2	13.8	[19, 20]
	E. Coli reaction	315	8915	0.180	56.6	[19, 21]
	E. Coli substrate	282	1036	2.615×10−2	7.3	[19, 21]
	Freshwater food web ‡	92	997	0.238	21.7	[22, 23]
	Functional cortical connectivity	90	405	0.101	9.0	[19, 24]
	Macaque cortex	95	1522	0.341	32.0	[19, 20]
	Marine food web ‡	135	598	6.611×10−2	8.9	[22, 25]
	Metabolic network	765	3686	1.261×10−2	9.6	[4, 22]
	Neural network ‡	307	2359	5.022×10−2	15.4	[22]
	Yeast protein interactions	2115	2240	1.002×10−3	2.1	[22, 26]
Information	Altavista ‡	2.035×108	2.130×109	1.028×10−7	20.9	[22]
	Book purchases	105	441	8.077×10−2	8.4	[19]
	Citation ‡	783339	6.716×106	2.189×10−5	17.1	[22]
	Rogets thesaurus ‡	1022	5103	9.781×10−3	10.0	[27]
	Word adjacency	112	425	6.837×10−2	7.6	[19, 28]
	Word co-occurrence	460902	1.70×107	1.601×10−4	73.8	[22]
	WWW nd.edu ‡	325729	1.470×106	2.770×10−5	9.0	[29]
Social	Biology co-authorship	1.520×106	1.180×107	1.021×10−5	15.5	[22, 30]
	Company directors	7673	55392	1.882×10−3	14.4	[22, 31]
	Dolphins	62	159	8.408×10−2	5.1	[19, 32]
	Email URV	1133	5452	8.502×10−3	9.6	[33]
	Email messages ‡	59912	86300	4.809×10−5	2.9	[22, 34]
	Email address book ‡	16881	57029	4.003×10−4	6.8	[22, 35]
	Film actors	449913	2.552×107	2.521×10−4	113.4	[22]
	Football	115	613	9.352×10−2	10.7	[36]
	German directors	4185	30438	3.477×10−3	14.5	[19, 37]
	Jazz	198	2742	0.141	27.7	[38]
	Karate	34	78	0.139	4.6	[39]
	Math co-authorship	253339	496489	1.547×10−5	3.9	[22, 40]
	Newspaper article co-occurrence	459	1422	1.353×10−2	6.2	[19, 41]
	Physics co-authorship	52909	245300	1.753×10−4	9.3	[22, 30]
	Student relationships	573	477	2.911×10−3	1.7	[22, 42]
	Telephone calls ‡	4.7×107	8.0×107	7.243×10−8	3.4	[22]
	UK directors	8850	39741	1.015×10−3	9.0	[19, 37]
	US directors	11057	74414	1.217×10−3	13.5	[19, 37]
Technological	Electronic circuits	24097	53248	1.834×10−4	4.4	[22, 43]
	Internet (1998)	10697	31992	5.592×10−4	6.0	[11, 22]
	Internet (2006)	22963	48436	1.837×10−4	4.2	[44]
	Peer-to-peer network	880	1296	3.351×10−3	2.9	[22, 45]
	Power grid (EU)	2783	3762	9.718×10−4	2.7	[16]
	Power grid (US)	4941	6594	5.403×10−4	2.7	[1, 22]
	Software classes ‡	1377	2213	2.336×10−3	3.2	[22, 46]
	Software packages ‡	1439	1723	1.665×10−3	2.4	[22, 47]
	Train routes	587	19603	0.114	66.8	[22, 48]
	Trans-European gas network	24010	25554	8.866×10−5	2.1	[15]
	US airlines	332	2126	3.869×10−2	12.8	[49]

In this data set, the relationship between N and d was examined. In particular, d was expressed as an exponent function of N (i.e., d ∝ N^−γ) and the exponent describing the power-law relationship γ was determined. Moreover, the relationship between N and K was also examined in a similar manner. If the observations by [15, 16] extends to other types of networks, K should remain approximately constant over the range of N.

3. Results

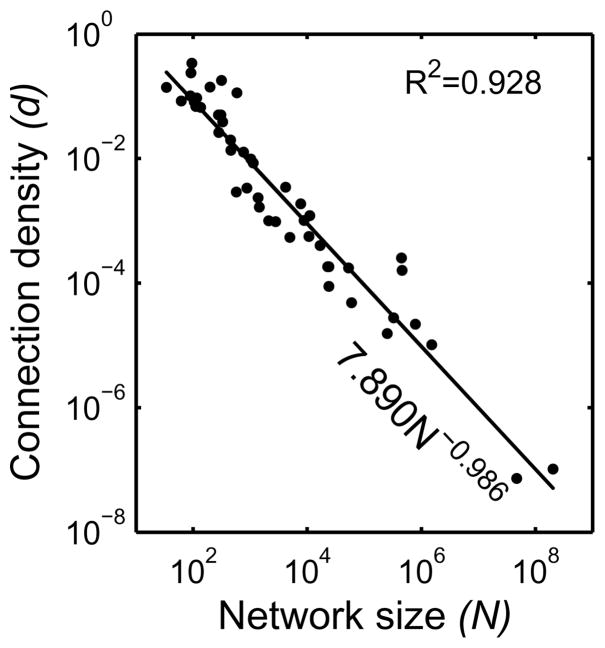
When the network size N and the connection density d are plotted on a log-log plot (Figure 1), there is an obvious linear relationship between the variables. The fit to the data (d = 7.890N^−0.986) reveals a power law relationship between the size and density of the networks. The scaling exponent approaches negative one (−1), indicating that the relationship is fractal in nature with 1/f properties. Despite the wide variety of networks, there is a pronounced power law relationship between the size and the density covering more than 6 orders of magnitude. The fit to the data is very strong (R² = 0.928 on log₁₀ transformed data), and there is no indication of truncation at the very large network sizes. It can be seen from Figure 1 that there are two extraordinarily large networks included in the analysis. These networks demonstrate that there is no truncation of the relationship at the extreme values. Even when these networks are removed, the correlation remains very strong (R² = 0.893) and the exponent is −0.978. Thus, these two points are not unduly influencing the analysis.

Figure 1.

Log-log plot of the relationship between the number of nodes in a network (network size, N) and the density of connections (d). Each point represents a different network based on the previous literature. The fit shows a power-law relationship that spans more than 6 orders of magnitude with an exponent of -0.986 consistent with a scale-free fractal behavior.

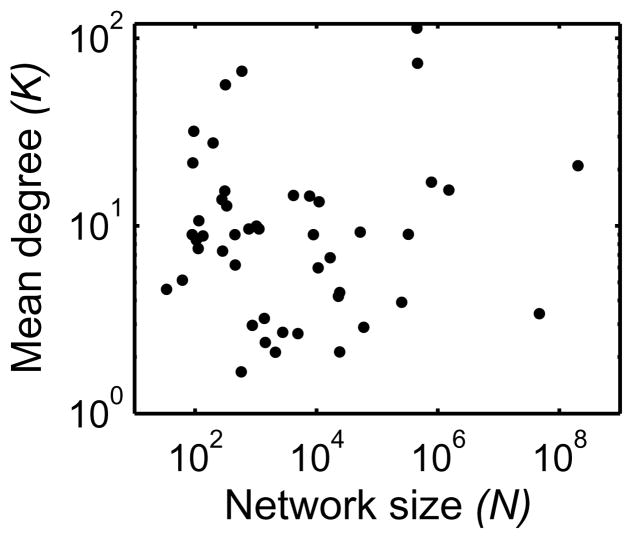
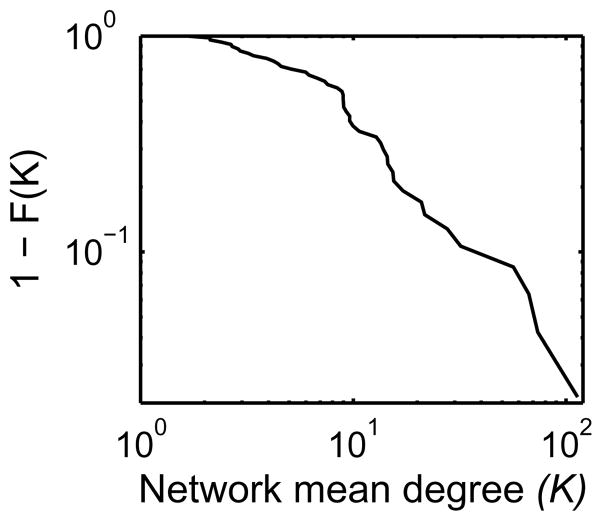
When N is sufficiently large, a consequence of a power-law relationship d ∝ N⁻¹ is that K does not depend on N. This stems from the relationship d ≃ K/N, which can be rewritten as K ≃ dN = cN⁻¹N = c where c is a constant. Since our observation above indicates a power-law relationship between d and N with the exponent approximately −1, the scatter plot of K and N does not indicate any association between them (see Figure 2). In other words, a large network size in terms of N is not necessarily associated with large K. It is interesting to note, in Figure 2, that there seems to be a small number of networks with unusually large K compared to the other networks. This is likely a consequence of the mean degree K having a long-tail distribution, as seen in its cumulative distribution plot in Figure 3. In this type of distributions, outliers such as K > 50 are likely to occur while the vast majority of K is reasonably small and similar. These outliers seem to occur over the range of N, indicating that such outliers occur randomly without any systematic dependance on N.

Figure 2.

A scatter plot of the mean degree K of various networks plotted against their network size N. Surprisingly, K does not change systematically over 6 orders of magnitude of N.

Figure 3.

The complementary cumulative distribution (1 − F(K)) of the mean degree K. The distribution exhibits a profile of a long-tail distribution despite the limited number of observations (47 networks).

4. Discussion

The findings reported here demonstrate a universal relationship in self-organized networks such that the network size dictates the density. The fractal behavior observed is of particular interest because it indicates that self-organized networks are critically organized. The number of connections within each network is scaled to the size of the network, and this universal behavior likely represents an optimal organization that ensures maximal capacity at a minimal cost. Furthermore, the critical organization would indicate that a density reduction would decrease the communication capabilities of the system. Interestingly, this relationship maintains the mean degree K approximately constant across different network sizes. A similar finding has been reported on the mean degree of the gas and power networks from European countries despite the large disparity in the network size [15, 16]. Our findings further generalizes the constant mean degree K in a variety of network types. It should be noted that the relationship d ∝ N⁻¹ is not expected from the relationship d ≃ K/N alone, as K could also depend on N rather than being constant. To the best of our knowledge, this work is the first to demonstrate the power-law relationship between d and N, and consequently K being almost constant over 6 orders of magnitude of N.

The relationship d ∝ N⁻¹ is not surprising if one considers the emergence of a giant component in an Erdős-Rényi (ER)-type random graph. In an ER random graph, a giant component, or a large cluster of nodes comprising a large proportion of a network, emerges if the connection density d is above the percolation threshold p_c = 1/N [50, 51]. At d = p_c, the corresponding value of K is unity, but the observed K’s in real networks are always larger than unity as seen in Table 1. There are some possible explanations for this. First, most of the networks listed in Table 1 are not formed in the same way as an ER random graph, but in much different mechanisms resulting in long-tail degree distributions [2, 14]. In such networks, the phase transition for formation of a giant component occurs at a different threshold than that of the ER random graphs [52]. Secondly, the actual connection density d in the observed networks may be elevated compared to the percolation threshold p_c, resulting in K being larger than unity. This may be because the networks in Table 1 may only represent the giant component of a much larger network which includes many small isolated clusters. In other words, only a portion of the network that happened to form a connected cluster is observed, and the connection density in such a cluster may be slightly elevated compared to pc just because all the nodes are connected to that cluster.

It is true that one could artificially generate networks that do not exhibit the size-density relationship found above. In fact, the literature contains such artificially generated networks that do not lie near our plotted line. However, such artificially created networks probably do not have real world relevance. We show here the scale-free relationship between network size and connection density in real networks from such diverse origins, supporting the notion of a universal law for network organization.

While replication of these findings from additional networks will be important, there are a number of practical implications of these findings. First, the construction of networks is inherently limited by the sampling procedure used to identify nodes and links. If a self-organized network is found to disobey this relationship, one should seriously consider that there was a bias in the sampling of the network structure. Second, when building artificial networks to be compared to naturally occurring systems, the size-density relationship should roughly follow the 1/f relationship. For example, in studies of functional brain networks, cross-correlation matrices of nodal time series are often thresholded to identify links between nodes [53]. The optimal threshold to be applied is not known, and the typical solution is to utilize multiple thresholds [54] producing networks with various densities. Based on the findings presented here, an optimal threshold can be easily determined, resulting in a network following the 1/f size-density relationship. Finally, engineered networks for practical applications may realize an optimal cost-benefit trade-off by ensuring that the density of connections is appropriate for the network size.

5. Conclusion

We show an important, apparently universal feature of self-organized networks: fractal scaling of size and density of connections. This fractal scaling is independent of network types, as the analysis spanned a wide gamut of networks, including biological, information, social, and technological. Thus, it appears that there is an underlying principle to organizing these self-emergent networks, a principle that probably ensures optimal network functioning.

Research Highlights.

• Network size and connection density exhibit a power-law relationship

• Fractal scaling size-density relationship spans over 6 orders of magnitude

• Average degree does not depend on network size in self-organized networks