Abstract
Positron emission tomography (PET) systems are best described by a linear shift-varying model. However, image reconstruction often assumes simplified shift-invariant models to the detriment of image quality and quantitative accuracy. We investigated a shift-varying model of the geometrical system response based on an analytical formulation. The model was incorporated within a list-mode, fully 3-D iterative reconstruction process in which the system response coefficients are calculated online on a graphics processing unit (GPU). The implementation requires less than 512 Mb of GPU memory and can process two million events per minute (forward and back projection).
For small detector volume elements, the analytical model compared well to reference calculations. Images reconstructed with the shift-varying model achieved higher quality and quantitative accuracy than those that used a simpler shift-invariant model. For an 8 mm sphere in a warm background, the contrast recovery was 95.8% for the shift-varying model vs. 85.9% for the shift-invariant model. In addition, the spatial resolution was more uniform across the field-of-view: for an array of 1.75 mm hot spheres in air, the variation in reconstructed sphere size was 0.5 mm RMS for the shift-invariant model, compared to 0.07 mm RMS for the shift-varying model.
Keywords: Positron Emission Tomography, Image Reconstruction, System Response Modeling, Point-Spread Function, Graphics Processing Units, List-Mode, OSEM
1. Introduction
The measurements in positron emission tomography (PET) involve complex physical processes and, as a result, the system response is shift-varying. One of the main reasons for the shift-varying nature of the system response is the parallax effect, which is a confounding issue in PET (Sureau et al. 2008, Levin 2008). Crystals in PET are long and narrow and they are oriented facing the center of the FOV. When a photon is emitted near the center of the system, it only sees the narrow dimension of the crystals. However, a photon emitted close to the edge of the FOV sees the full length of the crystal. For this reason, a reconstructed point source appears smaller if placed at the center of a PET scanner than near the edge of the field-of-view (FOV).
The bore of conventional PET system is designed to be much larger than the typical patient to ensure that the spatial resolution remains roughly constant throughout the useful FOV. This constraint inadvertently drives the cost of the system up since more crystal material is needed, and it also results in a decrease of the solid angle coverage and a subsequent degradation of the photon sensitivity. Small-animal PET scanners, on the other hand, have a small bore for high photon sensitivity and, therefore, are subject to parallax errors. A few groups have built systems that combine multiple layers of short detectors for increasing the photon sensitivity while keeping the parallax errors low (Wang et al. 2006, Spanoudaki et al. 2007). In a small-animal system we are developing, 5 mm-thick slabs of Cadmium-Zinc-Telluride (CZT) are arranged in a 8 × 8 × 8 cm3 box geometry (Gu et al. 2011, Pratx & Levin 2009). The detector volume element (a.k.a. “detector voxel”) is defined as the minimum volume that the cross-strip CZT detector can localize individual photon interactions, which for our detectors is 1 × 5 × 1 mm3. In this design, the cathode electrode pitch determines the photon interaction depth resolution, which is 5 mm. Yet, this level of depth-of-interaction precision is not sufficient to completely remove all parallax errors, because the system response is highly correlated with the LOR orientation–even at the center of the FOV, and some LORs are very oblique with respect to the detector voxel (up to 80 deg angle). Yet, a box geometry offers high packing fraction, resulting in high photon sensitivity and, thus, higher attainable spatial resolution and signal-to-noise ratio (SNR). (Habte et al. 2007).
Algorithmic corrections can compensate for spatially-varying response, provided the SNR is adequate. The use of an accurate spatially-varying model of the system response within image reconstruction can mitigate non-uniform system resolution blur. The system response can be either measured, simulated or calculated analytically.
In the case of a measured system response, a radioactive point-source is robotically stepped through the scanner FOV (Panin et al. 2006). The point-spread function (PSF) of the system is measured by acquiring a long scan for every point-source position. This process requires several weeks of acquisition as well as large memory storage. Measuring the PSF is labor-intensive and, as a result, Monte-Carlo simulations are often performed instead (Herraiz et al. 2006, Rafecas et al. 2004). The PSF at a given location is available by simulating a point-source of activity at that location.
Analytical models can also be used to compute the detector response function (Rahmim et al. 2008, Strul et al. 2003, Selivanov et al. 2000, Yamaya et al. 2005, Yamaya et al. 2008). The spatial resolution in PET is the convolution of multiple factors (Levin & Hoffman 1999), and therefore there does not exist a perfect analytical model that includes everything. However, it is possible to approximate dominant effects with an analytical model.
For the box-shaped PET system studied in this work, we have assumed that the geometrical response of the detectors dominates over all the other blurring processes. The justification for this approximation is as follows: First, positron range can be factored out of the system matrix. Then, owing to the small diameter of the bore of our system (80 mm), photon acolinearity is a small blurring effect (~0.2 mm) (Levin & Hoffman 1999). Last, because the system under consideration allows individual interactions to be read out independently, the resolution-degrading effect of inter-crystal scatter is significantly reduced before image reconstruction (Pratx & Levin 2009). The detector response blurring, on the other hand, is on the order of W cos θ + T sin θ, where W stands for the effective detector voxel width (1 mm for the system studied), T for the thickness of the detector voxel along the radial direction (5 mm) and θ is the photon incidence angle (Sorenson & Phelps 1980).
Regardless of how the system response is obtained, its most general and accurate representation is a kernel parameterized by three coordinates in image space and four coordinates in projection space (Alessio et al. 2006). For practical implementation, the system response model is often simplified. For instance, it can be separated into a generic projection operator and a sinogram blurring kernel (Qi et al. 1998, Alessio et al. 2006), provided that the measurements are processed in sinogram format and not in list-mode. Alternatively, it can be modelled by an image-based blurring kernel followed by a generic projection operator (Rapisarda et al. 2010). When the system response is modeled as a kernel varying both in image domain and in projection domain, symmetries and near-symmetries can be exploited to simplify implementation (Herraiz et al. 2006, Panin et al. 2006).
The work presented in this paper includes five novel contributions. One main novelty is that our physical detector response model is computed on the fly, within fully 3-D reconstruction. Although other research groups have also published online implementations (Pratx et al. 2009, Rahmim et al. 2005), this new method is considerably more innovative because of the high complexity of the model, which is the product of a 4-D transaxial kernel that depends on two image-domain and two projection-domain parameters, and a shift-invariant axial kernel. Computing the model online requires little memory, and the geometry of the PET system can be modified without having to recompute the system matrix.
Secondly, a novel computationally-tractable approximation of an existing analytical model (Lecomte et al. 1984) is proposed for PET systems that have small detection voxels. The main advantage of the new formulation is that it does not require a convolution but only a polynomial evaluation.
Thirdly, because the kernel is applied within projection operations, the method is fully compatible with the list-mode reconstruction format. Because of applications such as TOF PET, dynamic PET and ultra-high resolution, list-mode processing is increasingly popular, and there is a need for compatible model-based image reconstruction methods.
Fourthly, the entire reconstruction-including the online calculation of the system response model–is performed on a graphics processing unit (GPU) which reduces processing time.
Fifthly and last, we demonstrate that resolution recovery is achieved all the way to the edge of the field-of-view (FOV), even for a box-shaped geometry. This is because the system response model is accurate for almost any positions of the LOR endpoints, even for very oblique LORs (> 80deg).
2. System Response Model
2.1. Mathematical Model for PET
Mathematically, a raw PET dataset consists of a non-negative integer vector m ∈ ℕP, which represents the number of prompt coincidence events recorded for all P LORs in the system. A random vector Y is used to describe the stochastic distribution of these measurements. The components Yi are independent and follow a Poisson distribution with mean yi
| (1) |
The mean number of prompt coincidence events y on each LOR is well described by a discrete-continuous, linear spatially-varying model that relates the discrete vector of measurements m to the continuous tracer spatial distribution f(r), a 3-D function of the spatial variable r. The contribution from a point of unit strength located at r to LOR i is represented by a kernel hi(r) (Levin et al. 2003). Ignoring scattered and random coincidences and attenuation, the expected measurement yi on LOR i can be expressed as
| (2) |
where Ω is the support of the tracer spatial distribution. Assuming a discrete representation u of the tracer distribution, (2) can be expressed as
| (3) |
where A is the system matrix. The rows of the system matrix are discrete representations of the integration kernel hi(r).
2.2. Coincident Detector Response Function
In a cylindrical ring system, the response of a pair of detector voxels is symmetrical. We have extended a framework based on coincident detector response functions (CDRF, also referred to as coincident aperture function (Lecomte et al. 1984)) to include non-ring geometries, such as box or dual-panel geometries. In addition, our design is suitable for system designs that have several layers of detector voxels to measure the depth of interaction (Zhang et al. 2007, Rafecas et al. 2004). Last, we have further simplified the geometrical model by assuming a piecewise linear representation for the intrinsic detector response function (IDRF).
For any given LOR i and location r in the FOV, the CDRF is obtained by summing the response of the detector voxel pair to a pencil beam of oppositely-directed photons over the range of all admissible angles φ (red area in figure 1). Two rectangular detector voxels, rotated by an angle θA and θB, respectively, with respect to the LOR axis (horizontal dashed line), can record coincidences for positron annihilations that occur in their convex hull (area shaded in light yellow). Positrons that annihilate outside that area do not contribute to the CDRF because of the coincidence criterion. When an annihilation occurs at a location r, two anti-colinear photons are emitted at an angle φ with respect to the LOR axis (red line in figure 1). The probability that photon A, incident onto the detector with an angle θ = θA + φ and an offset x, interacts with detector voxel A is given by the IDRF gθ(x). In practice, an approximation is used (Lecomte et al. 1984). Only a small range of photon angles φ will result in coincidences (area shaded in light red), especially when the inter-detector distance sA + sB is much larger than the detector voxel size. Therefore, φ is assumed to be much smaller than θA for the purpose of computing the IDRF. This is equivalent to assuming that the detector voxel is irradiated by a beam of parallel photons. This assumption simplifies the calculations greatly since x ↦ gθ(x) has a compact analytical expression, while θ ↦ gθ(x) does not. An approximation of the CDRF can then be calculated by using
Figure 1.
Geometry used for calculating the CDRF. The two detector voxels (blue) can be oriented arbitrarily with respect to each other. The integration is performed over the angle φ within the integration cone (light red). The CDRF is calculated at a location r in the convex hull of the detector voxels (light yellow), offset by q with respect to the LOR axis (dashed line), at a distance sA and sB from each detector.
| (4) |
where sA and sB are the distances indicated in figure 1. Using the small-angle (SA) approximation for tan φ, (4) can be further simplified to yield the model used in (Lecomte et al. 1984), which is a scaled convolution:
| (5) |
where x = q + sA φ is the new integration variable, [I, J] is the integration domain and ε = sB/sA is the ratio of the distances to each detector voxel.
This formulation differs slightly from (Lecomte et al. 1984). In particular, it can be used for ε > 1 and, as a result, it is suitable for non-ring systems where the detector voxels are not arranged symmetrically.
The SA approximation is valid provided that the distance between the two detectors is at least three times greater than the crystal size. For a ring geometry, this condition is always satisfied. For a box geometry with extended FOV, the SA formulation does not yield the exact CDRF near the corners of the box, a limitation of little consequence for small-animal imaging since activity is seldom present in the corners of the FOV.
2.3. Intrinsic Detector Response Function
The IDRF can be calculated by considering the photon linear attenuation in the detector material. Neglecting scatter in the detectors, a photon produces a detectable signal if it interacts with the detector and it is not attenuated by any material along its trajectory. For the calculation of the IDRF, neighboring detectors are considered as attenuating material. For an array of detector voxels, such as the one depicted on figure 2, the probability gθ(x) that a photon of initial energy E0 = 511 keV interacts with the highlighted detector voxel, and does not interact with other detectors on its trajectory, is given by the exponential attenuation law
Figure 2.
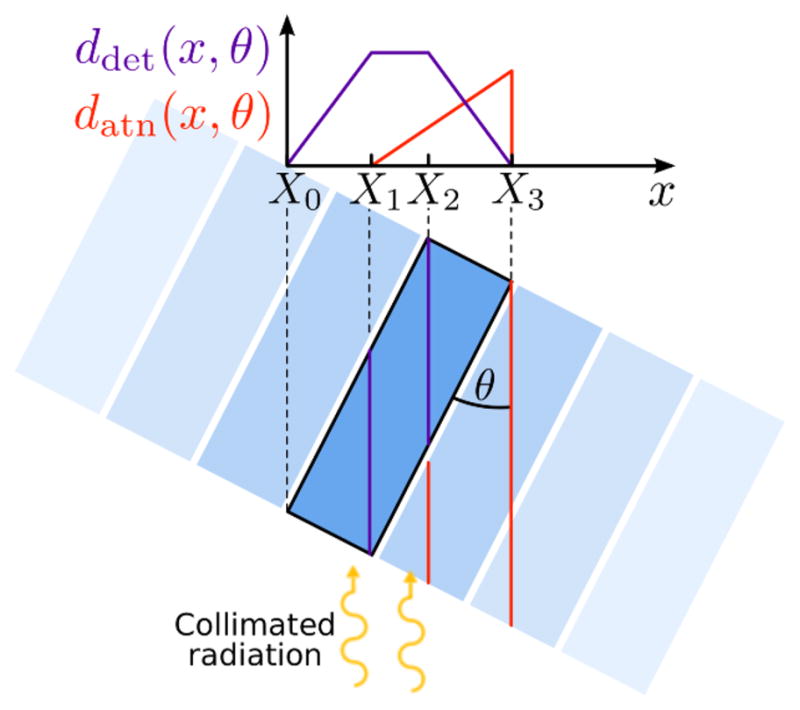
Representation of the detection length ddet(x, θ) and the attenuation length datn (x, θ) as a function of the offset x and the incident angle θ for a set of array of adjacent detector voxels. The two functions are piecewise linear and can be evaluated with minimal computation.
| (6) |
where ddet(x, θ) and datn (x, θ) are the length of the beam path traversing the detector voxel of interest, and attenuating material, respectively (figure 2). In the following, these two quantities will be called detection length and attenuation length, respectively. The linear attenuation coefficient μ includes both Compton and photoelectric attenuation at 511 keV.
The IDRF for a rectangular detector voxel is a piecewise exponential function. The in-plane width and thickness of the detector voxel are denoted by W and T, respectively, and its orientation with respect to the incoming photons beam is represented by the angle θ. The four interval boundaries (or knots) for the piecewise exponential IDRF are denoted by (Xl, Yl) where Yl = = gθ(Xl) and l = 0, …, 3. The X coordinate of the knots can be computed following
| (7) |
Let us assume that the knots are sorted such that X0 < X1 < X2 < X3. The knots are located symmetrically around zero: X0 = −X3 and X1 = −X2 (figure 2).
The detector voxel efficiency depends on both the detection and attenuation lengths. The detection length ddet(x, θ) is zero outside the outer knots X0 and X3. Between X0 and X1, ddet(x, θ) increases linearly. It also decreases linearly down to zero between X2 and X3 (figure 2). The detection length reaches a maximum between X1 and X2, and is equal to min { } on this interval.
In a standard detector array, neighboring detectors can attenuate the photon beam. To derive the IDRF, the amount of detector material that the photon traverses before interacting was derived assuming no curvature in the lateral dimension of the detector array. This assumption is always fully satisfied for a box geometry. For a ring geometry with no inter-detector gaps, given the short range of photons in detector material (≤ 5 mm), this assumption is quite accurate since the curvature on the detectors can be neglected over such small distances. Following this assumption, the attenuation length datn (x, θ) is zero for the two knots that correspond to the front of the detector voxel (X0 and X1 in figure 2), and it increases linearly until its peak value , which it attains either at X0 or X3–depending on the incident angle θ.
For layered detectors that measure photon depth-of-interaction, the inner layers attenuate the photon beam seen by the outer layers. Mechanical structures required to hold the detectors together, support readout electronics, or provide heat dissipation in the detectors can result in additional attenuation. However, this spatially-uniform attenuation does not need to be modelled within the forward and back-projections, and is instead automatically corrected during detector normalization.
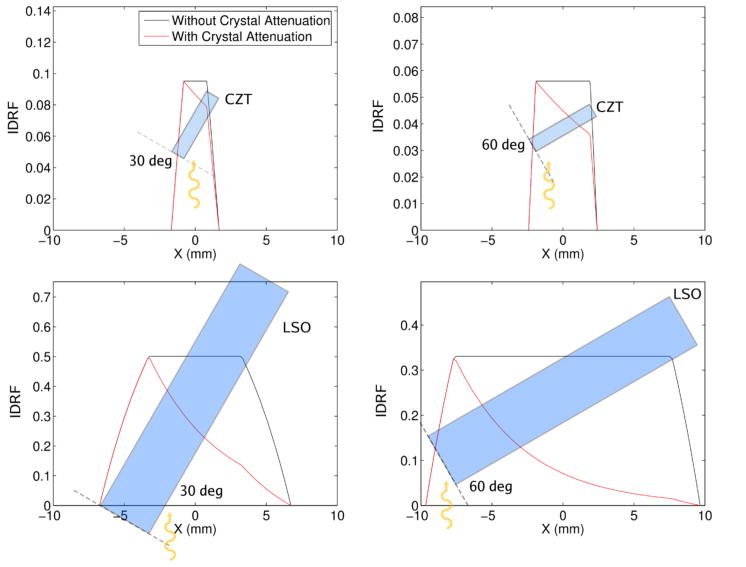
Figure 3 compares the IDRF for a 1 × 5 × 1 mm3 detector voxel, used in the high-resolution CZT system under development at Stanford, and for a 4 × 20 × 4 mm3 LSO crystal element used in the Siemens Biograph PET system. In addition to being smaller, the CZT detector voxel has a lower linear attenuation coefficient than LSO: At 511 keV, μCZT =0.5 cm−1 compared to μLSO =0.869 cm−1. As a result, the exponential behavior of the IDRF can be reasonably approximated by a linear function for small CZT detector voxels. This approximation, called the small detector voxel (SDV) approximation, is accurate within 2.5% (RMS) provided that the detector voxel thickness and attenuation coefficient satisfy μT ≤ 0.5 cosθmax, where θmax is the largest angle between a detector voxel and a LOR. For the CZT PET system considered in this study, the SDV approximation is accurate for θ ≤ 60 deg.
Figure 3.
Comparison of the IDRF for a 1 × 5 × 1 mm3 CZT detector voxels and a 4 × 20 × 4 mm3 LSO crystal. Two different incident angles are shown (30 and 60 deg). The IDRF is shown with (red) and without (black) attenuation from surrounding detector voxels. For the small CZT detector voxel, the IDRF is well approximated by a piecewise linear function.
Linearizing the IDRF has the advantage of facilitating the computation of the CDRF by the scaled convolution method (5). Furthermore, due to symmetries, the linearized IDRF can be represented by only four floating-points numbers (X0, X1, Y1, and Y2) which reduces the storage requirements.
2.4. Fast Calculation of the CDRF
In general, convolutions are computed either numerically or analytically. An analytical expression was derived for the CDRF based on the the SDV approximation. This approach requires little computation and memory, thus enabling the CDRF coefficients to be computed fast, when needed, within the reconstruction.
Let us consider a pair of detector voxels, denoted A and B, and a point r where the CDRF is to be evaluated. For each detector voxel, the IDRF is approximated by a linear function over each interval [ ] where l ∈ {0, 1, 2} and d ∈ {A, B} identifies the detector voxel. We can further express the IDRF as the sum of three linear functions
| (8) |
where
| (9) |
and and are the coefficients of the linear function.
Using these notations, the CDRF can be decomposed into the sum of nine elementary convolutions
| (10) |
where
can be further expressed as
| (11) |
with integration bounds Il,m and Jl,m computed using
| (12) |
and
| (13) |
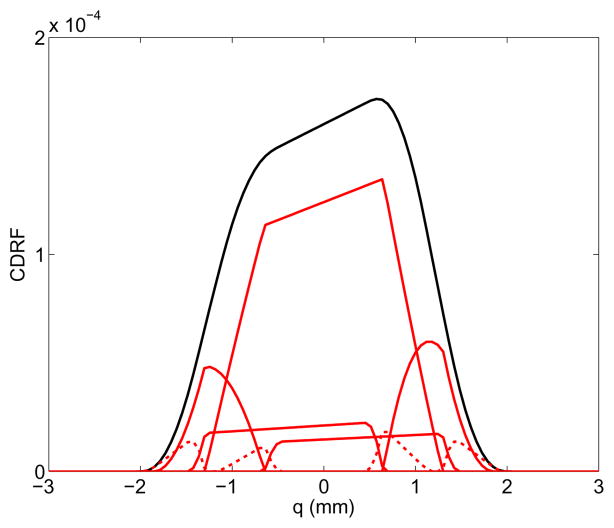
Figure 4 shows a section through the CDRF of a sample LOR, as well as its decomposition into nine elementary convolutions Kl,m(q). All the components of the CDRF do not contribute equally. In particular, a fast approximation (not implemented in this paper) can be achieved by neglecting the kernels that have the smallest contribution to the overall CDRF, i.e. K1,1(q), K3,3(q), K1,3(q), and K3,1(q), represented by a dashed line in figure 4.
Figure 4.
The CDRF (black) can be accurately decomposed into the sum of nine functions (red) that are calculated analytically using 11. Four of the kernels (dashed lines) only contribute marginally to the CDRF.
The SDV approach, by favoring arithmetic calculation over memory access, has high arithmetic intensity. Furthermore, only eight floating point values need to be stored for each LOR (four for each of the two IDRFs). Therefore, this approach is efficient on GPUs because these processors devote far more transistors to arithmetic operations than to memory caching.
3. Evaluation
3.1. GPU Implementation
The approach presented in the previous section was applied to generate an accurate system matrix, on a GPU, within the reconstruction. Because it relies on GPU computation rather than memory access, it provides a fast alternative to storing the full detector response model. In addition, it is advantageous in cases where the PET system geometry is different for every scan (for example a dual-panel breast cancer PET system with variable detector separation).
The model based on the analytical CDRF was implemented for a small-animal PET system with small CZT detector voxels (Pratx & Levin 2009). Owing to the large number of LORs in that system (more than 10 billion), reconstruction was performed in list-mode using a fully 3-D ordered-subsets expectation-maximization (OSEM) algorithm. The system matrix coefficients were calculated on the fly. In order to accelerate the computation, we used the GPU to perform the line projections and the kernel evaluation.
The GPU implementation relies on an existing line projection library (Pratx et al. 2009). In this library, the voxels contained inside a cylinder of radius η, centered on the LOR axis and called the tube of response (TOR), participate in the forward and back-projections. For each voxel inside the cylinder, a GPU function is called to calculate the projection kernel value. In this work, the procedure outlined in section 2.4 is called for each voxel in the TOR.
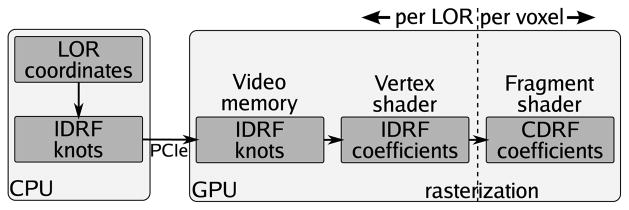
The calculation of the CDRF is split into three stages (figure 5). The first stage, performed on the CPU, consists in calculating a piecewise linear approximation of both IDRFs for all the LORs in the current subset. Each IDRF, stored using only four floating-point coefficients (X0, X1, Y1 and Y2), is copied to a 2-D texture in the GPU video memory. In the second stage, which takes place in the GPU parallel vertex shaders, the IDRFs are reformulated according to (9), and the linear coefficients and are calculated for every LOR. These coefficients are streamed to the fragment shaders, where, as a the third stage, the projection kernel is evaluated for every voxel within the TOR following (10).
Figure 5.
Schematics of the computation architecture used for calculating the CDRF. The complete process is divided into three stages, one running on the CPU, one in the vertex shaders and one in the fragment shaders.
3.2. CDRF Accuracy
Three ways of computing the CDRF were compared. The first method, based on numerical integration (NI), generated coincidence events by randomly sampling the detector voxels using a uniform distribution. Each randomly-generated coincidence event was weighted by its probability of occurrence, computed based on photon linear attenuation. An estimate of the CDRF was obtained by combining many simulated coincidence events according to their respective probability weights. The second method, based on the SA approximation, sampled the exact IDRFs using 200 samples, based on (6), and performed a numerical convolution according to the SA approximation (5). The third method combined the SA and SDV approximations to calculate the CDRF analytically, according to (10).
3.3. CDRF-Based Reconstruction
The Monte-Carlo package GRAY (Olcott et al. 2006) was used to simulate the acquisition of two phantoms with the CZT-based PET system. To keep the simulation as realistic as possible, the output from GRAY was used to position each photon event. Due to the low photo-fraction of the CZT material, incoming photon events often interact multiple times in the detectors. Such photon events were positioned at the estimated location of the first interaction and binned to the nearest 1 × 5 × 1 mm3 bin (Pratx & Levin 2009). Consistent with measurements (Levin 2008), we modeled the energy resolution by adding Gaussian noise with , where E is the energy of the single interaction in keV.
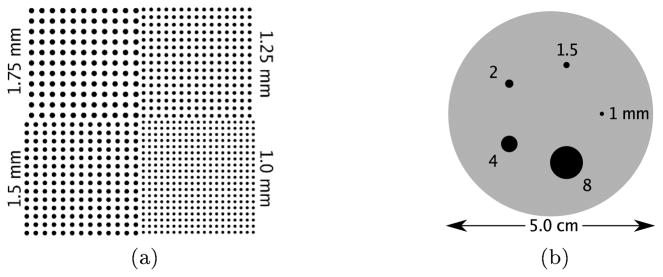
The sphere phantom [figure 6(a)] was used to research the effects of accurate system modeling on image resolution. The phantom was composed of four quadrants of spheres in air, all in the central axial plane, placed all the way to the edge of the 8 × 8 × 8 cm3 transaxial FOV. The spheres were 1, 1.25, 1.5, and 1.75 mm in diameter. Their centers were placed twice their diameters apart. The phantom had a total of 29.6 MBq (800 μCi) and five seconds of acquisition were simulated, yielding 27.2 million coincident events.
Figure 6.
Depiction of phantoms used for measuring the effect of shift-varying system response models. (a) The sphere phantom consists of four sphere patterns, placed in the central plane of the CZT system. (b) The contrast phantom consists of a 2.5 cm-radius, 6 cm-long cylinder filled with a warm solution of activity, in which are placed five hot spheres, the activity in which is ten times more concentrated than the background.
The contrast phantom [figure 6(b)] was used to assess the quantitative contrast recovery (CR). The phantom was composed of a 2.5 cm-radius, 6 cm-long cylinder, filled with a warm solution of activity, in which five hot spheres were placed. The spheres were centered on the central axial plane and their diameters were 1, 1.5, 2, 4, and 8 mm. The activity was ten times more concentrated in the hot spheres than in the warm background. The phantom also had a total of 29.6 MBq (800 μCi) and five seconds of acquisition were simulated, yielding 14.6 million coincident events.
Both phantoms were reconstructed with the same list-mode OSEM algorithm, using an image voxel size of 0.5 mm. Coincidence events acquired from the sphere phantom and contrast phantom were partitioned in 10 and two subsets, respectively. Within the reconstruction, the projection kernel was either a shift-invariant 1 mm-FWHM Gaussian kernel, or a shift-varying model based on the analytical CDRF. The shift-invariant Gaussian model was parameterized by the distance from the voxel to the LOR. To compute the transaxial component of the shift-varying model, the 3-D coordinates of the voxel and detectors were projected onto a 2-D transaxial plane. A 1 mm shift-invariant Gaussian kernel was used in the axial direction.
Geometric variations in the system’s photon sensitivity and photon attenuation over different LORs are included in the computation of the sensitivity map. Geometric photon detection efficiency was measured by simulating a normalization phantom, consisting of a uniformly radioactive cube of water occupying the entire FOV with 800 μCi of total activity. The sensitivity map, computed by backprojecting all LORs with a weighting factor, requires a daunting effort for a system with more than 33 billion LORs. Instead, a smaller set of 100 million LORs, chosen in a Monte-Carlo fashion, were backprojected to form the sensitivity image (Qi 2006).
Image analysis was performed on the reconstructed images to evaluate the performance of the image reconstruction. For the sphere phantom, the reconstructed sphere FWHM was measured by fitting a sum of Gaussians to 1-D profiles through the reconstructed image. The 1 mm spheres were considered too small relative to the voxel size for a reliable measure of their FWHM, and were not included in this analysis.
For the contrast phantom, the CR was measured in the reconstructed image as a function of iteration number. The mean reconstructed activity was measured in the hot spheres using spherical regions-of-interest (ROIs). These 3-D ROIs were drawn in a fully automated manner using the known physical position and diameter of the spheres: Voxels included in a ROI were those whose center was less one radius away from the sphere center. The background activity was evaluated by averaging the reconstructed intensity in two 22 mm-high, 26.5 mm-diameter cylindrical ROIs, placed 5 mm away from the central axial plane. The noise was approximated by the spatial standard deviation in the background ROI, normalized by the mean background intensity.
4. Results
4.1. Coincident Detector Response Function
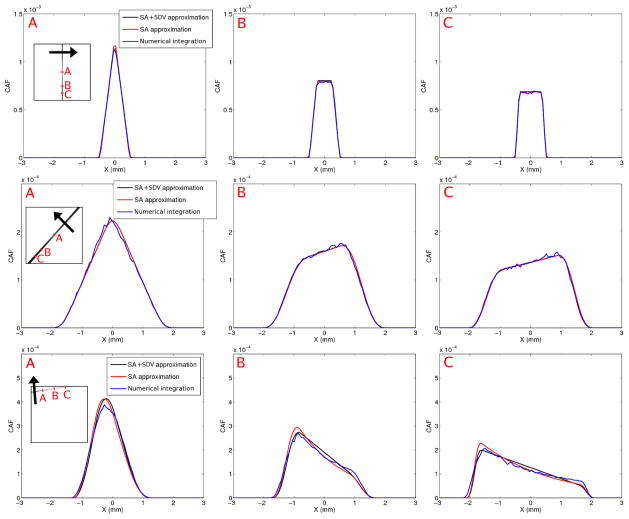
For a LOR normal to the detector voxel (figure 7, first row), the detector response is a trapezoid except at the center where it is a triangle. The three methods for computing the CDRF are in good agreement. The NI approach is indeed more noisy since it relies on the simulation of a limited number of discrete events. Normal LORs, not being subject to parallax errors, provide the highest resolution in the system. For these LORs, the FWHM of the CDRF at the center is equal to half of the detector voxel size (0.5 mm).
Figure 7.
CDRF for three LORs, shown along profiles taken perpendicular to the LOR axis, in the direction of the back arrow. Top row: Normal LOR connecting two 1 × 5 × 1 mm3 CZT detector voxels. The profiles through the CDRF at three locations (noted A, B and C in inset) are shown for three CDRF calculation methods: Numerical integration (NI), small-angle approximation (SA) and a combination of the SA and small detector voxel approximation (SA+SDV). Middle row: CDRF for a 45 deg oblique LOR going through the center of the FOV, with both detector voxels oriented vertically. Bottom row: CDRF for a very oblique LOR. The leftmost detector voxel, oriented horizontally, forms a 9 deg angle with the LOR while the rightmost detector voxel, oriented vertically, forms an 81 deg angle with the LOR.
In the standard ring geometry, the resolution is optimal at the center of the system because all the LORs that pass through that point are normal to the detector voxels. In a box-shaped geometry, there is no such “sweet spot”. Hence, LORs with degraded resolution traverse the center of the system. As an example, for a 45 deg angle LOR (figure 7, second row), the blurring kernel FWHM is equal to 1.8 mm at the LOR center, more than three times the value for a normal LOR. For a 45 deg LOR, both the SA and the SA+SDV approximations provide accurate CDRF models compared to the reference NI method. Due to detector penetration, the coincident response is asymmetric.
For a very oblique LOR, which forms a 9 deg angle with the leftmost detector and an 81 deg angle with the rightmost one (figure 7, third row), spatial resolution is good in the proximity of the leftmost detector (profile A), but it degrades quickly when approaching the rightmost detector (profiles B and C). In addition, the quality of both analytical models is inferior for short and very oblique LORs. For such LORs, the SA approximation deviates from the true distribution because the angle φ (see figure 1) can no longer be assumed to be small. The additional SDV approximation results in further deviation: due to the very oblique angle of the LOR, the IDRF is not well approximated by a piece wise linear function.
4.2. Spatial Resolution
The image of the sphere resolution phantom reconstructed using a shift-invariant model has non-uniform resolution due to parallax errors [figure 8(a)]. Radial blurring is noticeable at the edge of the FOV due to the larger effective detector voxel area seen by oblique LORs. In contrast, the image reconstructed using a shift-varying model based on the analytical CDRF shows fewer signs of resolution degradation near the edge of the FOV [figure 8(b)].
Figure 8.
Sphere phantom, reconstructed on the GPU with five iterations of list-mode 3D-OSEM with 10 subsets and (a) a shift-invariant Gaussian kernel or (b) an accurate model of the system response based on the analytical CDRF.
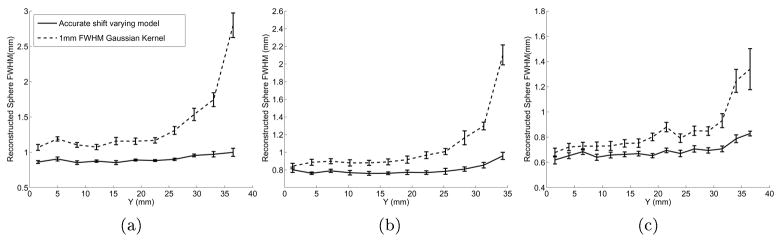
This is further confirmed by measuring the reconstructed sphere FWHM along horizontal profiles as a function of sphere position (figure 9). All the reconstructed spheres (1.75, 1.5 and 1.25 mm) are significantly smaller when an accurate shift-varying model is used. In addition, the spatial resolution is uniform throughout the entire FOV, as evidenced by the uniform reconstructed sphere FWHM.
Figure 9.
Reconstructed sphere size (FWHM in mm) as a function of sphere position, for two projection models, measured by fitting a Gaussian mixture with offset to 1D profiles though the reconstructed images (figure 8). (a) 1.75 mm spheres; (b) 1.5 mm spheres; and (c) 1.25 mm spheres.
4.3. Contrast Recovery
Figure 10 shows the reconstructed contrast phantom after reconstruction with a shift-invariant Gaussian kernel and the system response model based on the CDRF. In both cases, reconstruction was performed by running 50 iterations of list-mode OSEM with two subsets, using 0.5 mm voxels. The image reconstructed with the shift-varying model shows less pixel-to-pixel variability, both in the background and in the lesions. Contrast is also noticeably higher.
Figure 10.
Contrast phantom, reconstructed with 50 iterations of list-mode 3D-OSEM with two subsets, using (a) a shift-invariant Gaussian kernel and (b) a shift-varying model based on the CDRF.
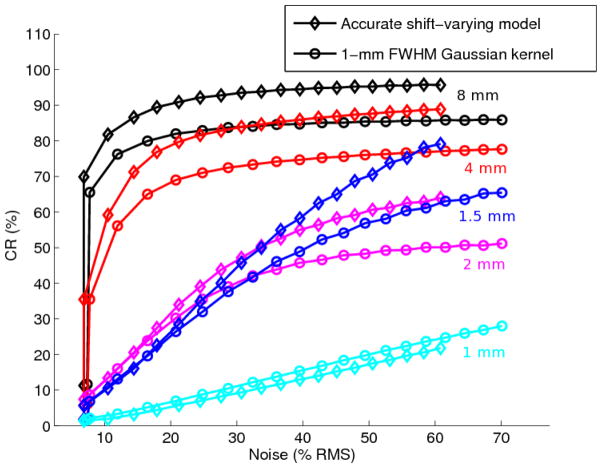
Figure 11 compares the contrast–noise trade-off for reconstructing the contrast phantom with list-mode OSEM, using shift-varying and shift-invariant kernels. Because high-frequency components are only recovered in the late iterations, premature termination of the OSEM iterations was used as implicit regularization to produce the trade-off curve. For all five spheres, the use of a more accurate model improves the trade-off between contrast and noise. More specifically, at any given iteration number, the CR is higher and the noise is lower for the shift-varying reconstruction, except for the 1 mm sphere which could not be resolved with either method. For the 8 mm sphere, close to full CR is observed (95.7% at convergence). In addition, the background variability is lower for the shift-varying reconstruction (figure 11).
Figure 11.
Contrast recovery (CR) plotted as a function of noise for varying iteration numbers (datapoints) and sphere sizes. The curves are shown for the five sphere sizes (black: 8mm, red: 4 mm, magenta: 2 mm, blue: 1.5 mm, and cyan: 1 mm) and for two types of reconstruction: accurate projection model (diamond) or shift-invariant Gaussian model (circle).
4.4. Processing Time
The reconstruction time was measured for the simple Gaussian shift-invariant and accurate shift-varying model in table 1. Both measurements were made for the hot sphere phantom dataset, using a GeForce 285 GTX (NVIDIA, Santa Clara, CA). The image size was 160 × 160 × 160. Consistent with (Pratx et al. 2009), the Gaussian kernel width was 1 mm, much narrower than the average width of the shift-varying kernel based on the CDRF. Hence, the TOR cut-off parameter η was set to 3.5 voxels–eight times the standard deviation of the Gaussian kernel–for the shift-invariant projections, and to 5.5 voxels for the shift-varying projections–larger than the maximum CDRF kernel width. As a result, the reconstruction with accurate, shift-varying model was ten times slower than the simpler method based on the shift-invariant Gaussian kernel (table 1).
Table 1.
Reconstruction time
| Projection model | Recon. time |
|---|---|
| Shift-invariant Gaussian kernel (Pratx et al. 2009) | 3.0 |
| Shift-varying kernel (CDRF) | 29.9 |
seconds per million events processed (forward and back -projection)
If no subject-specific attenuation correction is used, the same sensitivity image can be used for multiple reconstructions. In our experiments, attenuation correction was applied, and the sensitivity image was computed prior to reconstruction by backprojecting 100 million LORs, which took 25 and 2.5 min for the shift-varying and shift-invariant implementations, respectively.
It should be noted that the results reported in table 1 for the shift-invariant kernel are better than those reported in (Pratx et al. 2009), since the value reported in this section was obtained on a newer computer equipped with a more powerful GPU.
5. Discussion
The benefits of using a more accurate, shift-varying model are clear and have already been demonstrated elsewhere (Rahmim et al. 2008, Strul et al. 2003, Selivanov et al. 2000, Herraiz et al. 2006, Alessio et al. 2006, Alessio et al. 2010, Yamaya et al. 2005). For the CZT system we are developing, we have shown that a system response model based solely on the detector response brings four main improvements. First, the reconstructed spatial resolution is more uniform across the FOV (figure 8 and figure 9). By incorporating accurate shift-varying information in the system matrix, the spatially-variant blur present in the projections does not propagate to the reconstructed image. In particular, uniform spatial resolution is achieved all the way to the edge of the FOV, which suggests that four or more mice can be scanned concurrently in an 8 cm FOV system, such as the CZT system under construction, or, alternatively, the bore of the PET system can be made smaller for high photon sensitivity, even perhaps touching the animal.
Secondly, the smaller measured size of the spheres reconstructed with a shift-varying model suggests that the spatial resolution is globally higher (figure 9) and hence being recovered. Thirdly, the reconstructed images are more quantitatively accurate, as evidenced by the better CR (figure 11), thanks to more accurate models of the photon detection process, and reduced partial volume effects (PVE). For instance, for the 8 mm diameter sphere, which is large enough not to be affected by PVE, the CR after 20 iterations is 95.8% for the shift-varying model vs. 85.9% for the shift-invariant Gaussian projection. Fourthly, the noise is globally lower at a fixed contrast or iteration number (figure 11) because using a more accurate system matrix in the reconstruction reduces the amount of inconsistency between the different measurements.
Due to PVE, lower CR is generally achieved for smaller spheres (figure 11), with one exception: the 1.5 mm-diameter sphere showed higher CR than the 2 mm one. CR should be interpreted with care for lesions of different size: for small ROIs, voxel quantization at the ROI boundary can substantially affect the computed CR. The ROIs for the 1.5 and 2 mm spheres were comprised of 12 and 36 voxels, respectively. Furthermore, locally-correlated statistical noise can also affect the contrast of small ROIs. However, differences observed between shift-varying and invariant reconstructions are less affected by such biases because they are measured for the same ROI and the same statistical realization.
Because the ML estimate is non-linear, the reconstructed sphere size (figure 9) should be analyzed with care and should not be interpreted in terms of modulation transfer function. It is however an interesting figure of merit to study since it defines the ability of the reconstruction algorithm to distinguish small lesions that are close to each other. It should be further noted that the smaller size of the reconstructed spheres compared to their original diameter is an expected phenomenon: The FWHM of a perfect sphere blurred with a Gaussian kernel can be either smaller or larger than the original sphere diameter. We have empirically observed that the reconstructed sphere FWHM is a non-monotonical convex function of the blurring kernel FWHM (Pratx 2010). Hence, smaller reconstructed spheres might indicate either higher or lower spatial resolution. In practice, the relationship is monotonical provided that the blurring kernels are wide enough. For the 1.75 mm spheres used in this study, this condition requires the system blur to be greater than 0.5 mm (Pratx 2010).
The total reconstruction time is ten times larger when the shift-varying model is used (table 1). This is due to two factors: an increase in the number of voxels processed, and an increase in the computation required to evaluate the shift-varying kernel. For the shift-invariant Gaussian kernel, 7×7 voxels participate within each slice, compared to 11 × 11 voxels for the broad tube used for modeling the CDRF. In addition, each participating voxel requires the evaluation of nine different kernel functions that are added together. Overall, list-mode reconstruction with shift-varying system response model has much higher computational requirements than similar methods based on sinograms. In sinogram mode, cross-talk between different LORs can be modeled efficiently by a simple convolution, whereas, in list mode, it has to be modeled in image domain, using a broad TOR for each LOR.
The system response model can be implemented in many different ways. In this work, we have chosen not to store any information but rather to compute the coefficients of the system matrix on the fly. As a consequence, this approach is useful when the PET geometry needs to be adjusted to the patient morphology. It is also a scalable technique which uses a constant amount of computing resources, independent of the number of LORs in the system.
A shift-varying model can also be stored in memory, however there exists a tradeoff between the accuracy of the representation and the amount of memory used. Our approach, based on linearizing the IDRF, is accurate for the majority of the LORs (figure 7) and uses little memory. In addition, the computation of the kernel on the GPU is partially hidden by the latency of reading the voxel values from GPU memory.
The model presented in this work is based on a scaled convolution that only depends on the in-plane dimensions, i.e. it assumes that both detectors lie in the same axial plane. Unlike 2-D PET systems, in which all LORs are co-planar, modern PET systems acquire additional oblique LORs to improve the photon sensitivity. A complete system response model would include the ring difference as a parameter, resulting in a non-separable 6-D function, which would entail a considerable increase in computation. In an effort to make fully 3-D image reconstruction computationally tractable, our system response model ignores the ring difference; furthermore, it assumes that blur along the axial direction can be described by a separable shift-invariant Gaussian kernel. Hence, in place of a non-separable 6-D kernel, we model the system response as the product of a non-separable 4-D kernel by a 1-D Gaussian kernel. Reducing the dimensionality of the system response model is common for achieving practical reconstruction times in 3-D PET (Qi et al. 1998, Alessio et al. 2006, Herraiz et al. 2006, Alessio et al. 2010).
6. Conclusion
A method for modeling and calculating an approximate model of the detector response was developed for an ultra-high resolution CZT PET system with small detector voxels. We showed that such a model could be calculated on-the-fly and incorporated within GPU-based list-mode iterative reconstruction. Doing so resulted in superior image quality, quantitative accuracy and resolution uniformity compared to standard reconstruction based on a shift-invariant model. The framework is flexible and can be readily applied to a wide array of PET systems that use small detector voxels (for which the piecewise linear approximation holds), with or without depth-of-interaction capabilities.
Acknowledgments
This work was supported in part by the National Institutes of Health (NIH) under Grants R01-CA119056, R01-CA120474, and R01-CA119056-S1 (ARRA), and by a fellowship from the Stanford Bio-X program.
References
- Alessio A, Kinahan P, Lewellen T. Modeling and incorporation of system response functions in 3-D whole body PET. IEEE Trans Med Imag. 2006;25(7):828–837. doi: 10.1109/tmi.2006.873222. [DOI] [PubMed] [Google Scholar]
- Alessio A, Stearns C, Tong S, Ross S, Kohlmyer S, Ganin A, Kinahan P. Application and evaluation of a measured spatially variant system model for PET image reconstruction. IEEE Trans Med Imag. 2010;29(3):938–949. doi: 10.1109/TMI.2010.2040188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu Y, Matteson JL, Skelton RT, Deal AC, Stephan EA, Duttweiler F, Gasaway TM, Levin CS. Study of a high-resolution, 3D positioning cadmium zinc telluride detector for PET. Phys Med Biol. 2011;56(6):1563–1584. doi: 10.1088/0031-9155/56/6/004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Habte F, Foudray AMK, Olcott PD, Levin CS. Effects of system geometry and other physical factors on photon sensitivity of high-resolution positron emission tomography. Phys Med Bio. 2007;52:3753–3772. doi: 10.1088/0031-9155/52/13/007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herraiz JL, Espana S, Vaquero JJ, Desco M, Udias JM. FIRST: Fast iterative reconstruction software for (PET) tomography. Phys Med Bio. 2006;51:4547–4565. doi: 10.1088/0031-9155/51/18/007. [DOI] [PubMed] [Google Scholar]
- Lecomte R, Schmitt D, Lamoureux G. Geometry study of a high resolution PET detection system using small detectors. IEEE Trans Nucl Sci. 1984;31(1):556–561. [Google Scholar]
- Levin CS. New imaging technologies to enhance the molecular sensitivity of positron emission tomography. Proceedings of the IEEE. 2008;96(3):439–467. [Google Scholar]
- Levin CS, Foudray AMK, Olcott PD, Habte F. Investigation of position sensitive avalanche photodiodes for a new high resolution pet detector design. IEEE Nucl Sci Symp Conf Rec. 2003;4:2262–2266. [Google Scholar]
- Levin CS, Hoffman EJ. Calculation of positron range and its effect on the fundamental limit of positron emission tomography system spatial resolution. Phys Med Bio. 1999;44(3):781–799. doi: 10.1088/0031-9155/44/3/019. [DOI] [PubMed] [Google Scholar]
- Olcott P, Buss S, Levin C, Pratx G, Sramek C. GRAY: High energy photon ray tracer for PET applications. IEEE Nuclear Science Symposium Conference Record. 2006:2011–2015. [Google Scholar]
- Panin VY, Kehren F, Michel C, Casey ME. Fully 3D PET reconstruction with system matrix derived from point source measurements. IEEE Trans Med Imag. 2006;25(7):907–921. doi: 10.1109/tmi.2006.876171. [DOI] [PubMed] [Google Scholar]
- Pratx G. PhD thesis. Stanford University; 2010. Image Reconstruction in High-Resolution PET: GPU-accelerated strategies for improving image quality and accuracy. [Google Scholar]
- Pratx G, Chinn G, Olcott P, Levin C. Accurate and shift-varying line projections for iterative reconstruction using the GPU. IEEE Trans Med Imag. 2009;28(3):415–422. doi: 10.1109/TMI.2008.2006518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pratx G, Levin CS. Bayesian reconstruction of photon interaction sequences for high-resolution pet detectors. Phys Med Bio. 2009;54:5073–5094. doi: 10.1088/0031-9155/54/17/001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qi J. Calculation of the sensitivity image in list-mode reconstruction for PET. IEEE Trans Med Imag. 2006;53:2746–2751. doi: 10.1109/TMI.2004.829333. [DOI] [PubMed] [Google Scholar]
- Qi J, Leahy RM, Cherry SR, Chatziioannou A, Farquhar TH. High-resolution 3D bayesian image reconstruction using the microPET small-animal scanner. Phys Med Bio. 1998;43:1001–1013. doi: 10.1088/0031-9155/43/4/027. [DOI] [PubMed] [Google Scholar]
- Rafecas M, Mosler B, Dietz M, Pogl M, Stamatakis A, McElroy D, Ziegler S. Use of a Monte Carlo-based probability matrix for 3-D iterative reconstruction of MADPET-II data. IEEE Trans Nucl Sci. 2004;51(5):2597–2605. [Google Scholar]
- Rahmim A, Cheng JC, Blinder S, Camborde ML, Sossi V. Statistical dynamic image reconstruction in state-of-the-art high-resolution PET. Phys Med Bio. 2005;50:4887–4912. doi: 10.1088/0031-9155/50/20/010. [DOI] [PubMed] [Google Scholar]
- Rahmim A, Tang J, Lodge MA, Lashkari S, Ay MR, Lautamaki R, Tsui BMW, Bengel FM. Analytic system matrix resolution modeling in PET: an application to Rb-82 cardiac imaging. Phys Med Bio. 2008;53(21):5947–5965. doi: 10.1088/0031-9155/53/21/004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rapisarda E, Bettinardi V, Thielemans K, Gilardi MC. Image-based point spread function implementation in a fully 3d osem reconstruction algorithm for pet. Phys Med Biol. 2010;55(14):4131. doi: 10.1088/0031-9155/55/14/012. [DOI] [PubMed] [Google Scholar]
- Selivanov V, Picard Y, Cadorette J, Rodrigue S, Lecomte R. Detector response models for statistical iterative image reconstruction in high resolution PET. IEEE Trans Nucl Sci. 2000;47(3):1168–1175. [Google Scholar]
- Sorenson JA, Phelps ME. Physics in nuclear medicine. Grune & Stratton; New York: 1980. [Google Scholar]
- Spanoudaki V, Torres-Espallardo I, Rafecas M, Ziegler S. Performance evaluation of MADPET-II, a small animal dual layer LSO-APD PET scanner with individual detector read out and depth of interaction information. J Nucl Med Meeting Abstracts. 2007;48:39P. [Google Scholar]
- Strul D, Slates RB, Dahlbom M, Cherry SR, Marsden PK. An improved analytical detector response function model for multilayer small-diameter PET scanners. Phys Med Bio. 2003;48(8):979–994. doi: 10.1088/0031-9155/48/8/302. [DOI] [PubMed] [Google Scholar]
- Sureau FC, Reader AJ, Comtat C, Leroy C, Ribeiro MJ, Buvat I, Trebossen R. Impact of image-space resolution modeling for studies with the high-resolution research tomograph. J Nucl Med. 2008;49(6):1000–1008. doi: 10.2967/jnumed.107.045351. [DOI] [PubMed] [Google Scholar]
- Wang Y, Seidel J, Tsui BMW, Vaquero JJ, Pomper MG. Performance evaluation of the GE healthcare eXplore Vista dual-ring small-animal PET scanner. J Nucl Med. 2006;47:1891–1900. [PubMed] [Google Scholar]
- Yamaya T, Hagiwara N, Obi T, Yamaguchi M, Ohyama N, Kitamura K, Hasegawa T, Haneishi H, Yoshida E, Inadama N, Murayama H. Transaxial system models for JPET-D4 image reconstruction. Phys Med Biol. 2005;50(22):5339–5355. doi: 10.1088/0031-9155/50/22/009. [DOI] [PubMed] [Google Scholar]
- Yamaya T, Yoshida E, Obi T, Ito H, Yoshikawa K, Murayama H. First human brain imaging by the JPET-D4 prototype with a pre-computed system matrix. IEEE Trans Nucl Sci. 2008;55(5):2482–2492. [Google Scholar]
- Zhang J, Foudray A, Olcott P, Farrell R, Shah K, Levin C. Performance characterization of a novel thin position-sensitive avalanche photodiode for 1 mm resolution positron emission tomography. IEEE Trans Nucl Sci. 2007;54(3):415–421. [Google Scholar]