Wall Shear Stress-Based Model for Adhesive Dynamics of Red Blood Cells in Malaria

Abstract

Red blood cells (RBCs) infected by the Plasmodium falciparum (Pf-RBCs) parasite lose their membrane deformability and they also exhibit enhanced cytoadherence to vascular endothelium and other healthy and infected RBCs. The combined effect may lead to severe disruptions of normal blood circulation due to capillary occlusions. Here we extend the adhesion model to investigate the adhesive dynamics of Pf-RBCs as a function of wall shear stress (WSS) and other parameters using a three-dimensional, multiscale RBC model. Several types of adhesive behavior are identified, including firm adhesion, flipping dynamics, and slow slipping along the wall. In particular, the flipping dynamics of Pf-RBCs observed in experiments appears to be due to the increased stiffness of infected cells and the presence of the solid parasite inside the RBC, which may cause an irregular adhesion behavior. Specifically, a transition from crawling dynamics to flipping behavior occurs at a Young's modulus approximately three times larger than that of healthy RBCs. The simulated dynamics of Pf-RBCs is in excellent quantitative agreement with available microfluidic experiments if the force exerted on the receptors and ligands by an existing bond is modeled as a nonlinear function of WSS.

Introduction

In malaria, red blood cells (RBCs) become hosts of Plasmodium parasites. P. falciparum (Pf) is considered to be one of the most dangerous forms of the disease, with several million deaths per year worldwide. Pf-parasitized cells (Pf-RBCs) are subject to a gradual membrane stiffening (1–4) during the stages of intraerythrocytic parasite development (ring → trophozoite → schizont), and the RBC membrane can stiffen by up to a factor of 10 in comparison with healthy RBCs. This may significantly affect normal blood flow and lead to capillary occlusions (2,5). Moreover, at the final stage of intraerythrocytic parasite development (the schizont stage), the formed parasitic vacuoles may force a RBC to attain a near-spherical shape, further impairing its ability to deform. An additional change in the RBC properties, which may dramatically alter blood flow, is cytoadherence of Pf-RBCs to vascular endothelium and to other RBCs at later stages (6–8).

Even though infected RBCs are virtually invisible to the immune system, freely circulating Pf-RBCs can be destroyed in the spleen (9). Pf parasites expose adhesive proteins on the RBC membrane surface to mediate adhesion to the endothelium. This allows the parasites to survive for several days, i.e., long enough to ensure successful intracell development. Although this mechanism facilitates further progression of malaria, it may also severely disrupt normal blood flow. Adherence of infected RBCs is believed to be the main cause of bleeding complications in cerebral malaria due to blockages of small vessels in the brain (10).

RBC adherence can occur in any individual suffering from malaria. However, whereas some people are subject to severe forms of malaria, others may show only slight symptoms with relatively high parasitemia levels. This is likely due to differences in the adhesive properties of infected RBCs among individuals. In vitro experiments (11–13) on cytoadherence of Pf-RBCs in flow chambers revealed strikingly different adhesive dynamics for distinct coatings of the flow chamber walls. The adhesive dynamics of Pf-RBCs on purified ICAM-1 is characterized by stable and persistent flipping (rolling) behavior for a wide range of wall shear stress (WSS) values (13). In contrast, the dynamics of infected RBCs on grown mammalian CHO cells shows firm adhesion with a potential sudden detachment for the same range of WSS values, even though they express the same type of ligands (13). The basis of such behavioral dissimilarity is attributed to a different flow microenvironment; however, it is not well understood.

In this work, we conducted numerical simulations to examine the complex interactions that occur between the exposed proteins of Pf parasites and ligands on a coated surface. We used a previously developed RBC model (14,15) in combination with adhesive interactions to simulate the adhesive dynamics of Pf-RBCs. We studied the adhesive behavior of Pf-RBCs for a range of model parameters (including WSS) because, to the best of our knowledge, no data on specific bond properties are available. The flipping behavior of infected RBCs appears to be due to increased cell stiffness and the presence of a rigid parasite inside the cells, whereas healthy RBCs under similar modeled adhesion conditions yield crawling dynamics. Such modeling may yield limited insights into the molecular interactions of Pf-RBC adhesion (e.g., binding kinetics and single-bond properties); however, it allows us to describe and quantify the complex relations among the cells' mechanical properties, adhesive interactions, and flow conditions, and to identify their effect on the adhesive dynamics of RBCs in malaria. We compare out results with those obtained by experiment (13) whenever possible, and discuss the physical insights obtained.

Materials and Methods

We modeled the Pf-RBCs and their external/internal fluids using the dissipative particle dynamics (DPD) method (16). DPD is a particle-based method for mesoscopic simulations, such that each DPD particle corresponds to a lump of atoms or molecules. A detailed description of the DPD method can be found elsewhere (16,17).

RBC membrane

The RBC membrane is constructed by N_v = 500 DPD particles $\left\{{\mathbf{x}}_{i=1\dots N_v}\right\}$, which correspond to a two-dimensional triangulated network on the RBC surface (15,18). The network has a fixed connectivity with the energy as follows:

$$V\left(\left\{{\text{x}}_{\mathit{i}}\right\}\right)={\mathit{V}}_{\mathit{s}}+{\mathit{V}}_{\mathit{b}}+{\mathit{V}}_{\mathit{a}+\mathit{v}}$$ (1)

where V_s is the spring's potential energy, V_b is the bending energy, and V_a+v corresponds to the area and volume conservation constraints. The V_s contribution provides membrane elasticity similar to that found in a spectrin network of RBC membrane. A dashpot is attached to each spring, and therefore the spring forces are a combination of conservative elastic forces and dissipative forces that provide a network viscous response similar to RBC membrane viscosity. The bending energy mimics the bending resistance of the RBC membrane, whereas the area and volume conservation constraints mimic the area incompressibility of the lipid bilayer and incompressibility of a cytosol, respectively.

Linear analysis for a regular hexagonal network allows us to uniquely relate the model parameters and the network macroscopic properties (see Fedosov et al. (14,15) for details). Thus, in practice, the given macroscopic RBC properties serve as an input for calculating the necessary mesoscopic model parameters without any manual adjustment. We also employ a stress-free model (14,15) that eliminates existing artifacts of irregular triangulation. This is obtained by computational annealing, such that each spring assumes its own equilibrium spring length adjusted to be the edge length after triangulation.

Both internal and external fluids are simulated by a collection of free DPD particles and are separated by the RBC membrane through bounce-back reflections of these particles at a membrane surface. Moreover, a dissipative force between the fluid particles and membrane vertices is set properly to account for the no-slip boundary conditions at the membrane surface. In addition, a single simulation is run with specular reflection at the cell membrane to verify that the simulation results are independent of the selected reflection rule. More details on the RBC model and boundary conditions can be found in the Supporting Material.

Adhesion model

Adhesion of Pf-RBCs to coated surfaces is mediated by the interactions between receptors and ligands, which are the adhesion sites distributed on a cell and a surface, respectively. Adhesive interactions are modeled with a stochastic bond formation/dissociation model, which is an extension of the well-known adhesive dynamics model developed by Hammer and Apte (1). The bonds are modeled as linear springs, with the spring parameter k_s modeled as a linear or a nonlinear function of WSS. In addition, the bonds' formation rate k_on and dissociation rate k_off depend on the separation distance between the Pf-RBC receptors and ligands. The receptor and ligand densities in simulations may differ from those observed in experiments (13). Note that the receptor-ligand interactions in simulations correspond to effective adhesive interactions of Pf-RBCs with the wall. They do not correspond to actual molecular bonds, and may represent a number of existing molecular interactions. To model adhesive dynamics in simulations, we proceed by 1), checking for potential dissociation of existing bonds with probability 1 – exp(– k_offΔt), where Δt is the time step; 2), testing unbound ligands for potential bond formation with probability 1 – exp(– k_onΔt); and 3), applying the forces of all existing bonds. More details on the adhesive dynamics and model parameters can be found in the Supporting Material.

Results and Discussion

Cytoadhesive dynamics depends on a number of factors, such as the density of and interactions between the available receptors and ligands (e.g., bond formation/dissociation rates and bond strength), cell properties (e.g., cell shape, elasticity, and bending rigidity), and flow conditions (e.g., shear rate and shear stress). We examined the effect of some of these conditions on infected RBCs in malaria. In particular, Pf-RBCs showed a flipping rather than a rolling behavior, which we attribute to an increased cell stiffness in comparison with healthy RBCs. We compare our results with those obtained by experiment whenever possible.

Simulation setup and physical parameters

We modeled a Pf-RBC using the stress-free membrane model (14,15) with the following properties: N_v = 500, RBC diameter D₀ = 7.82 × 10⁻⁶ m, membrane Young's modulus Y₀ = 16.8 × 10⁻⁵ N/m, and bending rigidity k_c = 3.7 × 10⁻¹⁹ J. These RBC properties are termed the “default RBC properties” below, and they correspond to the schizont stage of intracell parasite development with a Young's modulus approximately 10 times larger than that of healthy RBCs.

The three-dimensional simulations were performed in a microchannel with the lower wall functionalized and the upper wall not functionalized. The domain dimensions were set to 40 × 30 × 20 μm. We generated shear flow by moving the upper wall (y = 30 μm) with velocity V_x while keeping the lower wall stationary. The WSS was defined as V_xη/H, where η is the fluid viscosity and H = 30 μm. An infected RBC had N_r = 500 receptors, and ligands were distributed on the lower wall according to the square lattice with lattice constant d = 0.5 μm. Initially, a Pf-RBC was placed at a distance of 100 nm from the lower wall. Before flow was initiated, each simulation was run for 0.5 s in equilibrium (V_x = 0) to allow for initial binding of the cell. The shear flow was then started and the RBC dynamics was monitored for ∼30 s. A complete list of the model and physical parameters used in the simulations can be found in the Supporting Material.

Dynamics of infected RBCs and comparison with experiments

We studied the adhesive dynamics of Pf-RBCs in shear flow for various WSS values. We compared the simulated RBC dynamics with that found in experiments (13) for two cases of wall coatings: with purified ICAM-1 and with mammalian CHO cells. Fig. 1 shows several successive snapshots of a cell rolling on the wall for the default setup. The dynamics of the Pf-RBC is characterized by flipping behavior initiated first by the cell peeling off the wall due to the force of the hydrodynamic flow after flat RBC adhesion (the first snapshot in Fig. 1). After the majority of the initial cell contact area with the wall is peeled off, an RBC flips over on its other side, facilitated by the remaining small contact area with the wall. During these steps, Pf-RBCs undergo strong membrane deformations as illustrated in Fig. 1. A similar behavior was previously observed in experiments with Pf-RBCs (13), which showed flipping (rolling) along a wall coated with purified ICAM-1. In agreement with the simulations, RBCs in the experiments also showed strong membrane deformations characterized by local membrane buckling.

Figure 1.

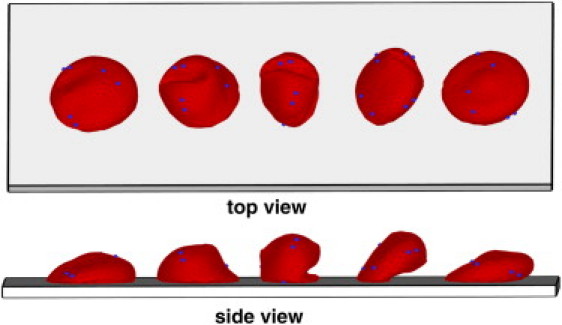
Top and side views of successive snapshots of a single flipping of an infected RBC for the default case. Coordinates along the wall for different snapshots are shifted to separate them for visual clarity. Blue particles are added as tracers during postprocessing to illustrate the membrane dynamics.

Fig. 2 presents the corresponding displacement along the x coordinate (a) and instantaneous RBC velocity (b). An infected RBC rolls in a relatively stable motion that resembles a staircase. The segments of smaller displacements correspond to the stage of a flat RBC adhesion followed by its slow peeling off the wall (see Fig. 1), whereas the fragments of larger displacements represent the stage of RBC fast flipping described above. The RBC velocity, in agreement with the displacement, shows high peaks or fast cell motion during the time segments with larger displacements. The average cell velocity is ∼5.8 μm/s. Fig. 3 shows RBC displacements along the z cross-flow coordinate (a) and instantaneous contact area (b) for the default simulation parameters. The displacement across the wall shows a jerky motion of an infected RBC within several microns. This is due to a discrete number of bonds and their random rupture or dissociation. Thus, if there is a nonuniform distribution of bonds over the contact area at some instance of time, a Pf-RBC may be pulled to one side. In addition, the hydrodynamic force on the RBC may be nonzero in the z direction because the cell is not symmetric due to the local deformations shown in Fig. 1. The RBC contact area in Fig. 3 b is correlated with its displacement and velocity in Fig. 2. Minima in the contact area coincide with maxima in the RBC velocity corresponding to the stage of fast cell flipping from one side to the other. The cell contact area remains within the range of 10–50 μm², and the average value is equal to 38.6 μm².

Figure 2.

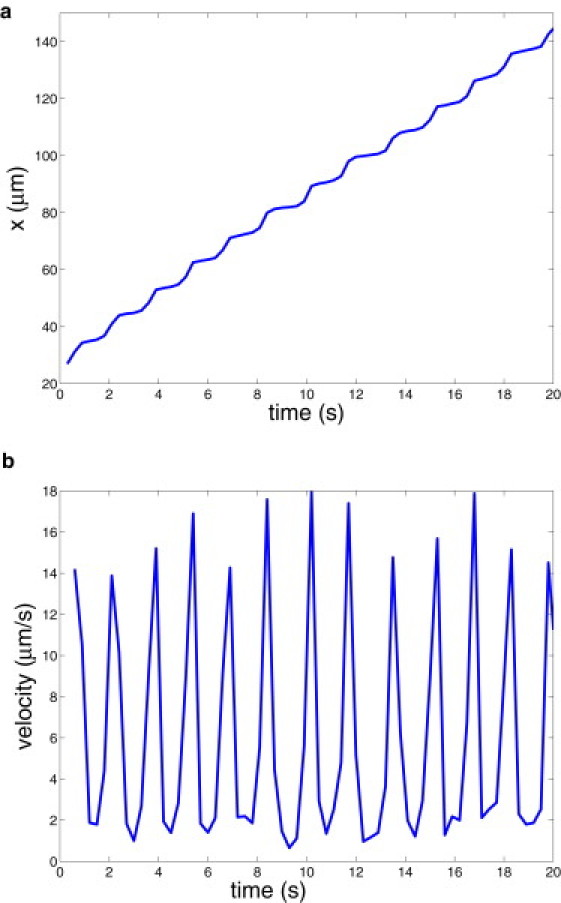
Pf-RBC displacement (a) and velocity (b) along the wall for the default case.

Figure 3.

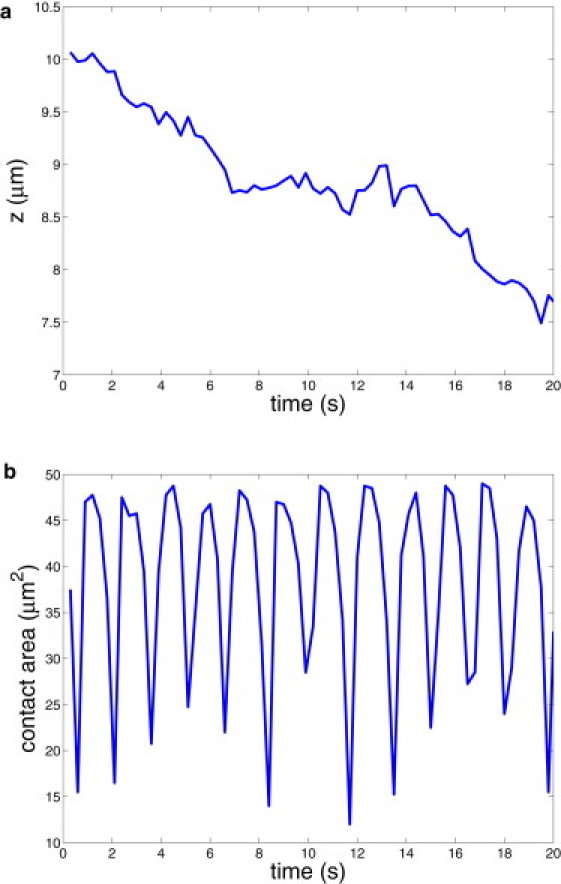
RBC displacement across the wall (a) and the cell contact area (b) for the default setup.

To investigate the dependence of RBC adhesive dynamics on WSS, we change the velocity of the upper plate. Note that the shear rate is altered at the same time. However, the WSS appears to be a key parameter governing RBC adhesive dynamics, since adhered RBCs are driven by fluid stresses and roll along the wall with a much smaller velocity than that of the shear flow.

Several initial simulations with a varying WSS and other parameters fixed revealed that a Pf-RBC may exhibit firm adhesion at a WSS lower than ∼0.317 Pa for the default case, and can completely detach from the wall at higher WSS. At low WSS, the adhesion forces are strong enough to counteract the stress exerted on the cell by the flow, resulting in the cell sticking firmly to the lower wall. In contrast, at high WSS values, the existing bonds do not provide sufficiently strong adhesive interactions, and the RBCs detach from the wall. RBC visualizations showed that the detachment at high WSS occurs during the relatively fast motion of RBC flipping, since the contact area at that step corresponds to its minimum. However, in experiments (13), the Pf-RBCs, which moved on a surface coated with the purified ICAM-1, showed persistent and stable rolling over long observation times and for a wide range of WSS values between 0.2 Pa and 2 Pa. This suggests that there must be a mechanism for the shear-enhanced adhesion that stabilizes the rolling of infected RBCs at high WSS. For example, Pf-RBC adhesive dynamics may be regulated by catch bonds, which are known to have a force-dependent strength. Similar behavior with respect to WSS is observed in leukocyte rolling adhesion, which can be actively regulated depending on the flow conditions and biochemical constituents present (19,20).

To incorporate shear-enhanced adhesion into the model, which can stabilize RBC binding at high WSS, we introduce adaptivity of the bond spring parameter (k_s). As the first approximation, we assume a linear dependence of k_s on the WSS, such that k_s is increased or decreased proportionally to an increase or decrease in the WSS. Fig. 4 presents the average rolling velocity of a Pf-RBC in comparison with experiments of cell rolling on a surface coated with purified ICAM-1 (13). The simulated average velocities for the linear case show a near-linear dependence on the WSS and are in good agreement with experiments. An observed discrepancy at the highest simulated WSS suggests that a further strengthening of cell-wall bond interactions may be required. However, the simulated value remains between the 10th and 90th percentiles found in experiments. The dependence of the RBC rolling velocity on WSS found in experiments is clearly nonlinear. Therefore, the assumption of linear dependence of k_s on the WSS is likely to be an oversimplification. The simulation results marked “nonlinear” in Fig. 4 adopt a nonlinear dependence of k_s on the WSS (see the Supporting Material for details), and show excellent agreement with experiments.

Figure 4.

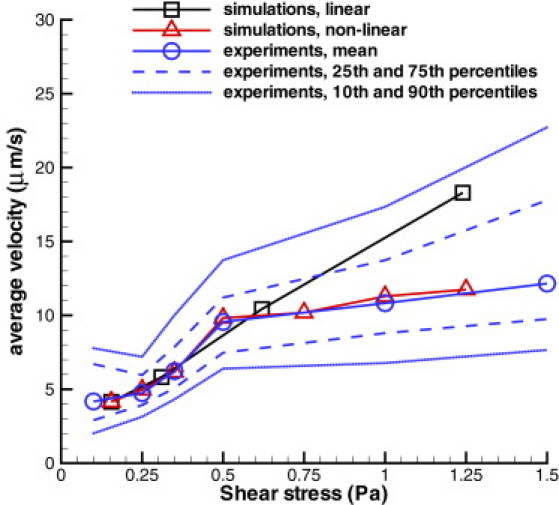
Average rolling velocity of infected RBCs depending on the WSS in comparison with the experiments of cell rolling on purified ICAM-1 (13). Experimental data include mean values and curves that correspond to the 10th, 25th, 75th, and 90th percentiles.

In addition, there may be a change in bond association and dissociation kinetics with WSS that would be able to aid in the rolling stabilization of infected RBCs at high shear rates. Our simulations suggest that the adhesive dynamics of Pf-RBCs is not very sensitive to a moderate change (below 30–40%) in k_on⁰ and k_off⁰; however, the cell dynamics may be strongly affected if these parameters are changed considerably. Moreover, the experimental data show a much larger scatter in the average RBC velocity for different cells than was observed in the simulations (not shown). This is likely related to nonuniform distributions of receptors on the RBC membrane and ligands on the wall. In the simulations, the distributions of both receptors and ligands are fixed and nearly homogeneous, with approximately the same area occupied by each receptor or each ligand. A scatter in behavior among distinct RBCs in the simulations is solely related to the stochastic nature of the adhesive model. However, in experiments, irregular distributions of receptors and ligands are likely to significantly contribute to a scatter in RBC adhesive dynamics.

Finally, numerical errors may contribute to the scatter in the behavior of different Pf-RBCs in the simulations. Here, the error analysis is complicated by the time dependency of the Pf-RBC dynamics. To estimate the order of the error for the average rolling velocity and contact area, we ran five additional, statistically independent simulations for the default setup. The standard deviation of the simulated average quantities is <5% of the corresponding mean values. A relatively low error value is consistent with the very stable flipping dynamics of Pf-RBC shown in Fig. 2. Even though the sample we used to estimate numerical errors is quite small, it is fair enough to say that the errors for the average velocity and contact area remain within 10–15%.

Antia et al. (13) also examined the adhesive dynamics of Pf-RBCs on a surface functionalized with grown mammalian CHO cells. Most of the infected RBCs showed persistent firm adhesion with infrequent complete detachment. It is believed that both ICAM-1 and CHO cells express the same type of ligands, and therefore the difference in Pf-RBC adhesive dynamics was attributed to the flow microenvironment. In contrast, firm adhesion in the simulations appeared to always be stable, with no detachment occurring within the simulated time of ∼30 s. Careful inspection of the experimental video of the Pf-RBC adhesive dynamics on mammalian CHO cells revealed that the adhered Pf-RBCs displayed very slow slipping along the surface before they suddenly detached. To reconcile the differences in the adhesive dynamics observed in the simulations and experiments, we hypothesize that this sudden complete detachment from the wall is caused by RBC slipping into a wall region with a limited number of ligands available for binding. This hypothesis provides a plausible explanation for such behavior in Pf-RBCs, which was tested in simulations (see the Supporting Material for details). At this time, we know of no other change in the physical parameters of cell adhesion that would be able to reproduce this dynamics.

Dependence of RBC adhesive dynamics on membrane properties

In this section, we describe the adhesive dynamics of Pf-RBCs in shear flow for different membrane properties, including the bending rigidity and Young's modulus. By increasing the membrane bending rigidity five times with respect to the default case, we find that the membrane surface is much smoother than that in Fig. 1 (see Fig. S2). Fig. 5 shows the average rolling velocity (a) and the average contact area (b) with respect to the membrane bending rigidity normalized by its default value k_c = 3.7 × 10⁻¹⁹ J. RBCs with lower bending rigidity roll with lower velocity along the wall than those with higher bending resistance. Fig. 5 b shows that more-compliant RBCs form a larger contact area with the solid surface, resulting in a larger number of bonds connecting cell receptors with the wall ligands. Hence, softer cells experience stronger binding interactions with the wall, which slows down their rolling motion. Note that for normalized bending rigidities larger than ∼7–8, the RBC rolling velocity and contact area seem to level off to constant values. This indicates that the RBC adhesive dynamics becomes independent of the membrane bending rigidity when the RBC is sufficiently stiff.

Figure 5.

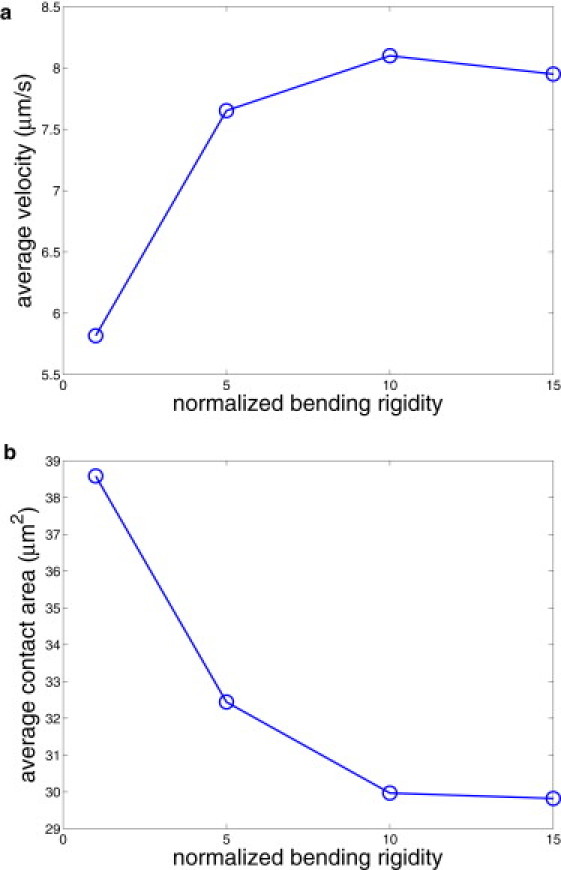
Average RBC rolling velocity (a) and average contact area (b) for different membrane bending rigidities normalized by 3.7 × 10⁻¹⁹ J.

We further considered the effect of the membrane Young's modulus on the RBC adhesive dynamics. The Young's modulus of Pf-RBCs increases during intracell parasite development. The default case of RBC adhesive dynamics presented above corresponds to the last stage of parasite development (the schizont stage) with the Young's modulus ∼10 times larger than that of a healthy RBC. However, adhesion of a Pf-RBC also occurs at the trophozoite stage of parasite development, which precedes the schizont stage and is characterized by a fivefold increase in the membrane Young's modulus compared with that of healthy RBCs. Therefore, the Young's modulus in simulations is varied from its value for healthy RBCs (Y₀ = 18.9 × 10⁻⁶ N/m) to that of the schizont stage (Y₀ = 16.8 × 10⁻⁵ N/m).

Fig. 6 presents successive snapshots of a rolling RBC with the same membrane properties as a healthy RBC. The plotted sequence of RBC snapshots shows that the cell crawls on the wall, in contrast to the flipping dynamics found in the case of a high Young's modulus. The physics of this transition has the same basis as the tumbling-to-tank-treading transition in shear flow. Before an RBC can undergo a tank-treading motion in shear flow, a certain energy barrier must be exceeded. Hence, RBC tumbling in shear flow is observed when the shear forces exerted by the flow are not strong enough to overcome the tank-treading energy barrier, which depends roughly linearly on the membrane Young's modulus. By analogy, an adherent RBC crawls along the wall in a tank-treading-like motion when the tank-treading energy barrier is exceeded by near-wall shear forces as shown in Fig. 6. However, a sufficient increase in the membrane Young's modulus hinders RBC tank-treading, which forces the cell to peel off the surface with a consequent flipping from one side to the other. Thus, the flipping dynamics of Pf-RBCs is mediated by the increased membrane stiffness. In addition, it can be affected by the presence of a rigid parasite inside the cell, which will be discussed in the next section.

Figure 6.

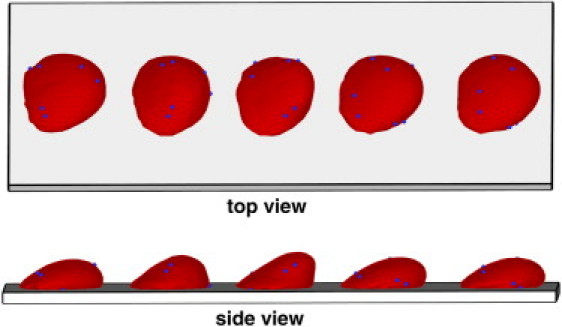
Top and side views of several snapshots of a rolling RBC with Young's modulus Y₀ = 18.9 × 10⁻⁶ N/m. Coordinates along the wall for different snapshots are shifted to separate them for visual clarity. Blue particles are added as tracers during postprocessing to show the membrane dynamics.

Fig. 7 shows the average rolling velocity (a) and the average contact area (b) with respect to the membrane Young's modulus normalized by its value for healthy RBCs. Stiffer RBCs roll with faster velocity because their contact area is smaller than that of softer RBCs, resulting in weaker adhesive interactions with the wall. A similar conclusion was drawn from simulations of leukocyte adhesive dynamics for varying membrane stiffness (21,22). Note that the transition from crawling dynamics to flipping behavior occurs at a Young's modulus approximately three times larger than that of healthy RBCs. This confirms that Pf-RBCs at the trophozoite stage of parasite development are subject to flipping dynamics.

Figure 7.

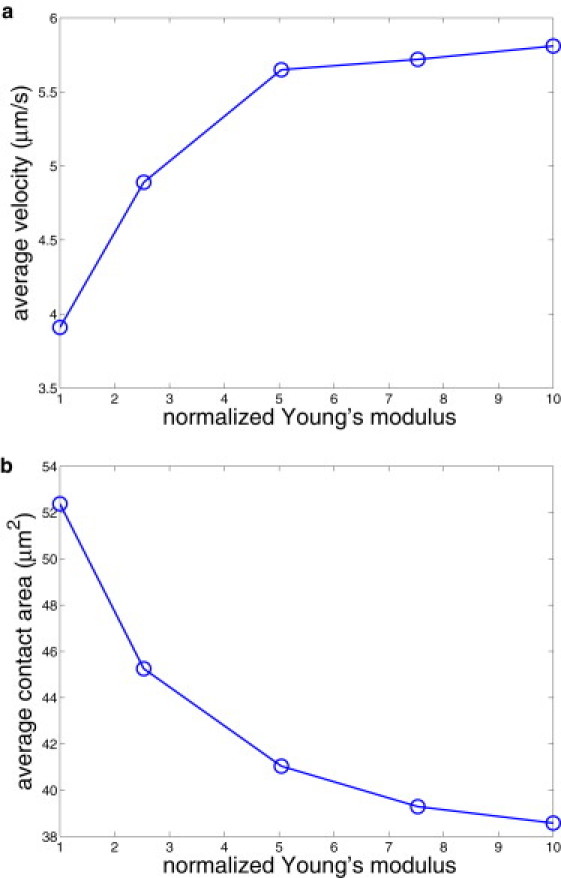
Average rolling velocity (a) and average contact area (b) for different Young's moduli normalized by the value Y = 18.9 × 10⁻⁶ N/m.

Influence of rigid parasite on adhesive dynamics

Up to this point, the Pf-RBCs were modeled as thin, stiff membranes filled with a Newtonian fluid. Under realistic conditions, Pf-RBCs contain a rigid parasite undergoing growth. Recent experiments (4) suggest that the volume of cytosol may be reduced threefold in the later stages of intracell parasite development in comparison with that of healthy RBCs, indicating that the parasite can take up a considerable volume inside an RBC. A sufficiently large parasite can provide a rigid backbone inside an RBC that may strongly affect RBC adhesive dynamics and contribute to the flipping behavior described above.

The parasite is modeled by a collection of DPD particles uniformly distributed within the cylindrical volume with a radius of 3.3 μm and a height of 0.2 μm. This set of particles is placed inside the modeled RBC and is constrained to undergo rigid motion. To prevent the parasite body from crossing the RBC membrane, we introduce Lennard-Jones interactions between the parasite body particles and membrane vertices (see the Supporting Material for details). However, the parasite swims freely in the RBC cytosol. The number of DPD particles that represents the RBC cytosol is reduced according to the volume occupied by the parasite body. The simulation parameters for the membrane and adhesive interactions are the same as for the default setup.

Fig. 8 presents successive snapshots of a rolling RBC with a rigid parasite inside the cell. The plot confirms that the parasite body serves as a rigid backbone that contributes to RBC flipping dynamics. The RBC membrane displays local buckling due to its low bending rigidity, which is consistent with the RBC visualizations in Fig. 1. However, the RBC does not experience such a severe flexural deformation while the cell peels off the wall, as observed in Fig. 1. Here, the parasite body constrains the RBC membrane by supplying a rigid support, which forces the RBC to flip without substantial bending.

Figure 8.

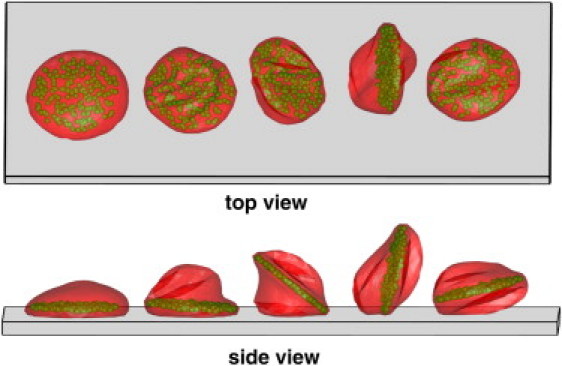
Top and side views of several snapshots of a rolling RBC with a parasite body inside the cell drawn in green. Coordinates along the wall for different snapshots are shifted to separate them for visual clarity. The RBC membrane is partially transparent (see Movie S1).

Fig. 9 shows the corresponding RBC displacement (a) and instantaneous velocity (b). The RBC displacement and velocity display a more erratic pattern than those shown in Fig. 2. For example, the curves in Fig. 9 indicate that there are several time segments in which the Pf-RBC shows firm adhesion for several seconds. Furthermore, firm adhesion may be followed by several fast flips of the RBC along the surface, characterized by two closely located peaks of velocity around the time of 20 s. Visualizations of the cell dynamics also revealed that the smaller peaks in cell velocity in Fig. 9 b correspond to a tank-treading-like motion facilitated by the parasite body. This occurs as a result of the parasite being freely suspended in the RBC cytosol. A proper positioning of the parasite body inside the RBC may result in a stress on the front part of the membrane forcing the RBC into a crawling-like motion.

Figure 9.

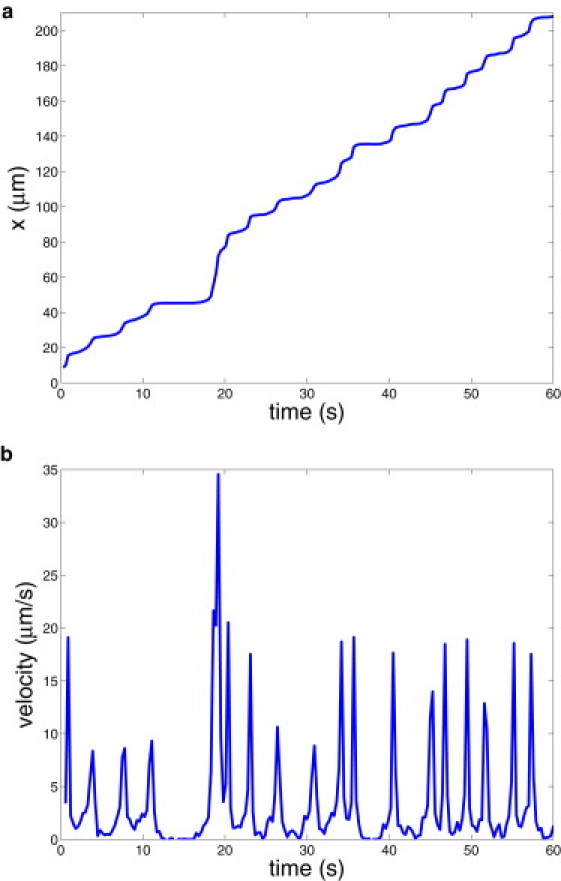
Infected RBC displacement (a) and velocity (b) along the wall for the case of explicit modeling of the rigid parasite body inside the cell.

The presence of a rigid body inside an RBC significantly affects the RBC adhesive dynamics, resulting in more-erratic behavior compared with the adhesive dynamics of Pf-RBCs with no parasites. We considered a thin disk to represent the parasite body; however, a different geometric form (e.g. a sphere) or size of the parasite may have a different effect on RBC adhesive dynamics. Therefore, an experimental characterization of the parasite geometry for different stages of parasite development would be of great interest. In addition, the modeled parasite body was freely suspended in the RBC cytosol, whereas under realistic conditions the parasite would likely have some attachments to the membrane, since it exposes adhesive proteins on the membrane surface to mediate binding to the wall. These unresolved issues require further experimental and numerical investigations.

Adhesion of Pf-RBCs in microchannel flow

A flow of an RBC suspension is simulated in a rectangular microchannel with the dimensions 100 × 30 × 50 μm; only the lower wall is covered with ICAM-1. This geometry is similar to the flow chamber employed in experiments (13). The RBC suspension is characterized by a hematocrit of H_t = 0.1 and a parasitemia level of 10%, where the infected cells correspond to the schizont stage of intra-RBC parasite development. Ligand sites are placed on a square lattice on the lower wall in the y direction with a lattice constant d = 0.5 μm. The flow is driven by a uniform constant force applied to all particles to mimic the pressure gradient. The simulated flow is nearly symmetric, with the maximum velocity of ∼150 μm/s at the center. The maximum shear rate measured at the lower wall is equal to 27 s^–1, which is close to the value used previously for the default case. This yields a maximum WSS of ∼0.26 Pa. In addition, RBCs are subject to the buoyant force (similar to the gravity force), which results in a faster contact between RBCs and the lower wall and facilitates a faster binding of Pf-RBCs to the wall to overcome the difficulty of a limited total time during which the simulations can be advanced. The total physical time in simulations is limited to ∼1 min because of the computational expense, whereas the corresponding flow in experiments (13) was observed over a period of 10–20 min.

After several seconds, some Pf-RBCs may closely approach the lower wall, where cell binding can occur. Fig. 10 presents snapshots of three examples of binding of Pf-RBCs to the wall. Panel A shows RBC binding when the cell is oriented nearly perpendicular to the wall. The RBC continues rolling along the wall for several seconds with a relatively small contact area. In panel B, RBC binding starts with the formation of a small contact area. Subsequently, the fluid flow forces the cell to flip from one side to the other, resulting in a binding with a large contact area. Panel C illustrates Pf-RBC binding to the wall, where a large contact area is instantly formed. Fig. 11 shows the corresponding displacements and instantaneous velocities for the three cases. In panel A, the RBC initially binds to the wall and then continues rolling on its side for several seconds, as confirmed by its displacement and velocity plots. Eventually, the infected RBC forms a larger contact area with the wall, as displayed by a substantial drop in its velocity at t = 14 s in Fig. 11 A, because rolling on the side is not stable and is expected to be a transient behavior. Afterward, the RBC exhibits flipping dynamics similar to that discussed above. In contrast, the adhesive dynamics of an infected RBC in panel B shows a rapid, strong binding with the wall, followed by several seconds of cell arrest. At t = 9 s, the RBC flips from one side to the other, and then a repeated period of firm adhesion is observed. The z coordinate of the RBC initial binding site is equal to ∼45 μm, which is close to the channel corner. The local shear rate at z = 45 μm is equal to ∼18 s^–1, in comparison with the maximum wall shear rate of 27 s^–1, resulting in a substantial decrease of local shear stresses on the RBC exerted by the flow. The local shear stresses are likely too small to enforce persistent flipping dynamics, and hence relatively long periods of firm adhesion are observed. The RBC adhesive dynamics in panel C confirms this idea. The infected RBC shows a consistent flipping dynamics, as shown in Fig. 11 C. However, its position in the z coordinate is close to the middle of the microchannel, where the WSS attains its maximum. The average rolling velocity after adhesion is equal to 6.1 μm/s. Note that all of the Pf-RBCs that bound with the wall remained bound for the rest of the simulation time. Similar observations were reported in studies (13) of Pf-RBCs rolling on ICAM-1 in a flow chamber.

Figure 10.

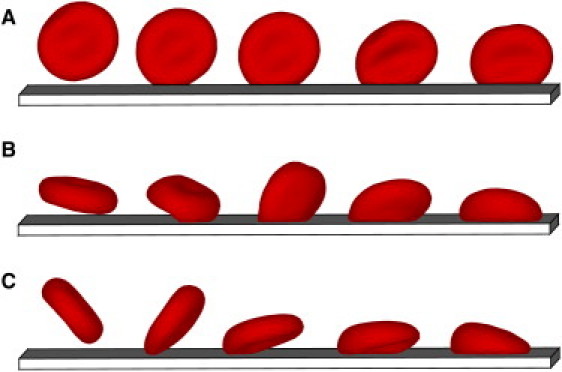
Snapshots of RBC binding to the lower wall of a microchannel. (A) Pf-RBC binding with a small contact area. (B and C) Binding with a large contact area. Coordinates along the wall for different snapshots are shifted to separate them for visual clarity (see Movie S2).

Figure 11.

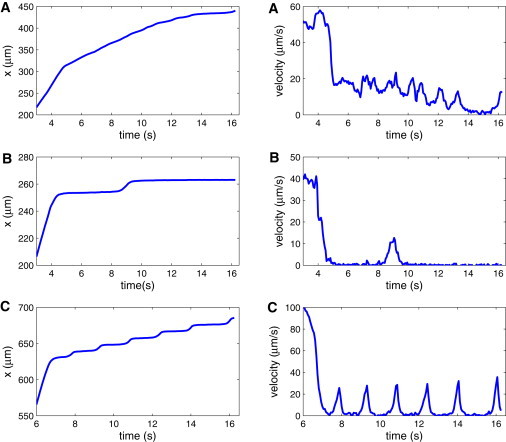
Pf-RBC displacements and instantaneous velocities for the three examples shown in Fig. 10.

The simulation results regarding the adhesive dynamics of Pf-RBCs in the microchannel illustrate the complexity of cell behavior. The adhesive dynamics strongly depends on local microflow conditions due to varying shear stresses. The initial binding of infected RBCs may show great variability in cell transient dynamics; however, a strong binding with the wall is eventually formed, yielding predictable flipping behavior or firm adhesion. In addition, freely flowing RBCs may collide with adhered cells and affect their adhesive dynamics.

Conclusions

We simulated the adhesive dynamics of Pf-RBCs by using an extension of the stochastic bond formation/dissociation model to include nonlinear WSS dependence. Pf-RBCs adhering to vascular endothelium in a flow exhibit flipping dynamics. RBC flipping is characterized by the cell peeling off the wall due to forces exerted by the hydrodynamic flow and subsequently flipping from one side to the other. This behavior appears to be due to an increased membrane stiffness of Pf-RBCs. Healthy RBCs under the same conditions of adhesive interactions crawl along the wall in a tank-treading motion. When the Young's modulus of the membrane is ∼3-fold larger than that of healthy RBCs, a transition to flipping dynamics is observed because the tank-treading motion is hindered by a proportional increase in the tank-treading energy barrier. In addition, the adhesive dynamics of Pf-RBCs depends on the membrane bending rigidity. More-compliant RBCs show stronger membrane deformations during adhesion. They also are able to form a larger contact area with the wall, which slows down their rolling velocity in comparison with RBCs with higher membrane bending rigidity.

The simulated adhesive dynamics of infected RBCs is in agreement with experiments of Pf-RBCs rolling on ICAM-1, in which flipping dynamics was observed for a wide range of WSS values. Adhesive dynamics on mammalian CHO cells found in experiments shows prolonged firm adhesion of Pf-RBCs with a slight slipping along the wall and rare detachments. The firm adhesion was found to be exceptionally stable in simulations, with no RBC detachments observed. Thus, our simulations suggest that this behavior is likely caused by an irregular distribution of ligands on the wall. Firmly adhered RBCs may slip into a region with a small number of ligands available for binding, which would cause their detachment from the wall. In addition, several simulations were performed with explicit modeling of a rigid parasite inside infected RBCs. The presence of a rigid body strongly affects the simulated adhesive dynamics characterized by more-irregular RBC flipping with short periods of intermittent firm adhesion. The adhesive dynamics of Pf-RBCs in a rectangular microchannel is further complicated by variations in local WSS and the presence of other healthy and infected RBCs in the flow.