Using the structure of inhibitory networks to unravel mechanisms of spatiotemporal patterning

Summary

Neuronal networks exhibit a rich dynamical repertoire, a consequence of both the intrinsic properties of neurons and the structure of the network. It has been hypothesized that inhibitory interneurons corral principal neurons into transiently synchronous ensembles that encode sensory information and sub–serve behavior. How does the structure of the inhibitory network facilitate such spatiotemporal patterning? We established a relationship between an important structural property of a network, its colorings, and the dynamics it constrains. Using a model of the insect antennal lobe we show that our description allows the explicit identification of the groups of inhibitory interneurons that switch, during odor stimulation, between activity and quiescence in a coordinated manner determined by features of the network structure. This description optimally matches the perspective of the downstream neurons looking for synchrony in ensembles of pre–synaptic cells and allows a low–dimensional description of seemingly complex high–dimensional network activity.

Introduction

Coordinated spiking of neuronal populations underlies the perception of sensory stimuli (Gray and Singer, 1989), the planning of movement (Bouyer et al., 1987), and the acquisition of new memories (Cheng and Frank, 2008). A number of studies have shown that such patterning, to a large extent, depends on the temporal and the spatial distribution of inhibition (Buzsáki and Chrobak, 1995). For example, in hippocampal networks, GABAergic interneurons form the hubs of a network that selectively synchronizes sub–populations of pyramidal cells (Bonifazi et al., 2009). The back and forth interaction between inhibitory granule cells and excitatory mitral cells in the mouse olfactory bulb leads to synchronous spiking in mitral cells (Schoppa, 2006). Synchrony extends across mitral cells that are electrically uncoupled and affiliated with different glomeruli. Feedback inhibition mediated by local interneurons synchronizes cortical pyramidal cells in the gamma frequency band underlying cognitive processing and provides a mechanism for the temporal binding of sensory stimuli (Joliot et al., 1994; Llinas and Ribary, 1993; Singer and Gray, 1995). In vertebrates (Grillner, 2003) and invertebrates (Marder and Bucher, 2007), coordinated movement is achieved by interneuron networks that work in concert to generate appropriate phases of spiking in motor neurons.

The antennal lobe (AL), the insect equivalent of the olfactory bulb in mammals, provides an ideal system where the effects of inhibitory networks can be examined. Local inhibitory interneurons (LNs) extend extensive connections to each other and excitatory projection neurons (PNs) in the AL (Leitch and Laurent, 1996). Odor driven activity of PNs in the AL evolves over multiple spatial and temporal scales (Laurent, 2002). The collective spiking activity of PNs generates an oscillatory local field potential (LFP) (Laurent and Davidowitz, 1994b). The composition of synchronized groups of PNs contributing to the LFP oscillation changes on a cycle–by–cycle basis (Laurent and Davidowitz, 1994b; Laurent et al., 1996; Wehr and Laurent, 1996). Projection neurons receive input from local inhibitory interneurons (LNs). Blocking fast LN-mediated inhibition by the application of the GABA–activated chloride channel blocker, picrotoxin, leads to the desynchronization of PNs and consequently abolishes the oscillatory output of the AL (Ito et al., 2009; MacLeod and Laurent, 1996; Stopfer et al., 1997; Tanaka et al., 2009). Since dynamic changes in collective PN activity during odor stimulation far exceed changes in input to the network they must be attributed to the network interactions within the AL (Raman et al., 2010). Previously, we proposed that competitive inhibitory interactions between LNs generate alternately spiking groups of neurons. These groups entrain different populations of PNs, shaping their spike timings and generating a spatiotemporal representation of an odor (Bazhenov et al., 2001b). The basic cause of transient synchrony in PNs, recovery from concerted inhibition, is well understood in insect (MacLeod and Laurent, 1996; Stopfer et al., 1997) (Bazhenov et al., 2001b) and mammalian (Schoppa, 2006) olfactory circuits. However, a clear relationship between the global structure of the inhibitory network and the collective dynamics of PNs and LNs is not known.

An understanding of structure–dynamics relationships in a network is often challenging because of the formidable dimensionality of the system and the inherent non–linear properties of neurons and synapses that constitute the network. Recent approaches have been restricted to two broad classes (Boccaletti et al., 2006). The first class examines complex dynamics, albeit in relatively simple networks. These networks (often consisting of a few (<10) neurons) (Shilnikov et al., 2008) are designed to resemble the characteristic building blocks of networks known as motifs that recur with considerable frequency in neuro–anatomical data sets (Milo et al., 2002; Sporns et al., 2004; Sporns and Kötter, 2004) . Another commonly studied example of the same class is a large network with simple connectivity (all–to–all, or nearest neighbor) that can also demonstrate a rich repertoire of dynamical patterns (Assisi et al., 2005). A second class of studies examines simple dynamics in networks with arbitrarily complex topologies (Arenas et al., 2008). These studies have been largely limited to the analysis of the stability of completely synchronized states (Pecora and Carroll, 1998) and have been applied to a variety of systems (see (Boccaletti et al., 2006) for a review).

Our approach is a novel departure from these two classes. Here we establish a relationship between a structural property of the network, its colorings, and the dynamics it constrains. Further we show that the description of network dynamics based on its coloring comes with a fortuitous benefit. It helps us define a low–dimensional space in which the seemingly high–dimensional dynamics of networks of excitatory and inhibitory neurons reliably forms a series of orthogonally propagating waves, a predictable and simple pattern where synchronous ensembles of excitatory projecting cells are successively recruited.

Results

Dynamics of inhibitory networks

A ‘coloring’ of a network (or graph) is an assignment of colors to the nodes of the graph so that nodes (such as neurons) that are directly connected to each other are assigned different colors (see supplementary material for a detailed example). Graph coloring problems first emerged as interesting mathematical curiosities (Biggs et al., 1986; Kubale, 2004), but have since been applied to resolving scheduling conflicts, reinterpret the Sudoku puzzle (Herzberg and Murty, 2007) and, most prominently, to coloring maps (see (Appel and Haken, 1977a) for a proof of the famous four–color theorem; (Appel and Haken, 1977b) and (Biggs et al., 1986) describe the colorful history). We found that antagonistic interactions in a network of inhibitory neurons can be usefully related to its coloring. To illustrate, consider the simplest possible inhibitory network, one consisting of two reciprocally connected inhibitory interneurons. Since these neurons are directly connected to each other, by definition, we must assign a different color to each neuron. A general property of such a network is that neurons inhibiting each other via fast GABAergic synapses tend to spike asynchronously. This simple network may burst in rhythmic alternation (see Figure 1a) (Shpiro et al., 2007), or act as a flip– flop (Kleinfeld et al., 1990; Lu et al., 2006) (see (Vreeswijk et al., 1994) for exceptions to the desynchronizing effects of inhibition). Antagonistic interactions explain why only one neuron remains active at any given time. But how does switching take place?

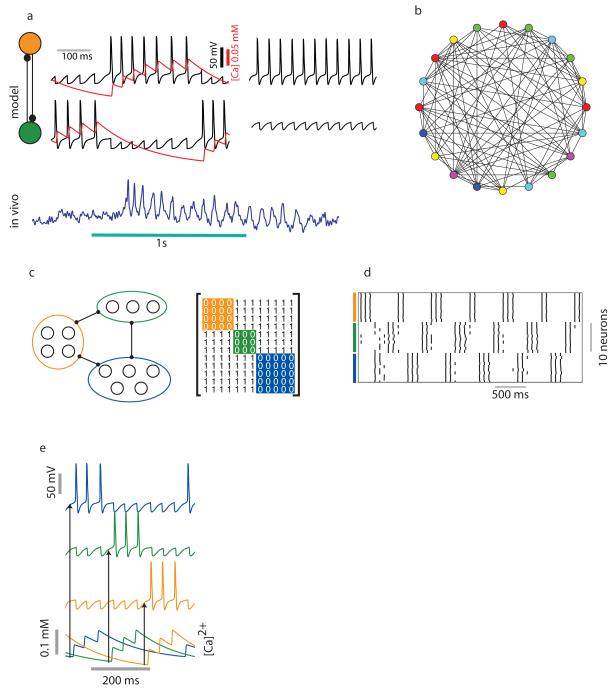
Figure 1.

Clustering in inhibitory networks as a function of graph coloring. a) A reciprocally connected pair of inhibitory neurons is an example of a graph with chromatic number two. Left traces: An alternating pattern of bursts is generated in response to a constant external stimulus to both neurons. A Ca²⁺ dependent K current (shown in red) causes spike frequency adaptation. Right traces: In the absence of a Ca²⁺ dependent K current only one neuron produces spikes and the other is quiescent. Blue trace at the bottom: spike frequency adaptation in a local inhibitory interneuron recorded in vivo from locust antennal lobe.

b) A coloring generated for a random network of 20 neurons with connection probability 0.5. c) A graph with chromatic number 3 and its corresponding adjacency matrix. d) Raster plot showing the activity of a network of 30 neurons with chromatic number three. Ten neurons are associated with each color. e) The role of Ca²⁺ concentration on the timing of LN bursts. The bottom traces show the Ca²⁺ concentration in three LNs (top three traces) associated with three different colors. The neuron with the lowest concentration of Ca²⁺ tends to spike first.

In addition to the fast time scale of spiking (~10’s of milliseconds), responses of inhibitory interneurons in the locust antennal lobe can vary on a slow time scale (~100 ms) over which spiking frequency gradually declined. As the example in Figure 1a shows, once below a threshold frequency, the quiescent neuron was released from inhibition and generated a burst of spikes that, in turn, silenced the other neuron of the pair. In the absence of spike frequency adaptation, one of the neurons remained in an active state while the other was constantly inhibited (Fig. 1a, right). This slow time scale resulted from a hyperpolarizing Ca²⁺ dependent potassium current (red trace) that was activated by Ca²⁺ spikes in the inhibitory neuron (see Supplementary material) (Bazhenov et al., 2001b). Spike frequency adaptation is common in different classes of spiking interneurons (McCormick, 2004) and may be achieved through a variety of mechanisms (Benda and Herz, 2003) .

In this two–neuron network, neurons associated with different colors tend to spike in alternating bursts. In larger, more realistic networks, we hypothesize that neurons associated with the same color will not directly compete and, assuming they receive similar external inputs, will tend to burst together. A simple strategy to verify this hypothesis would be to generate a random network, characterize it’s coloring, and compare the coloring with the dynamics. However, this strategy is impractical for two reasons. First, one would like to query the dynamics of the network after systematically varying its coloring–based properties like the number of neurons associated with a particular color or the number of colors. It is not clear how to achieve this with a random network (Figure 1b). A second difficulty is to generate all possible colorings of the network as the size of the network grows. Thus, we chose instead to construct a set of networks that each posses properties of interest. For example, to construct a network with three colors, we generated three groups of nodes and connected every pair belonging to different groups. No within-group connections were implemented. The resulting adjacency matrix consisted of diagonal blocks of zeros with all other elements set to unity (Figure 1c). Our simulations of activity in this network showed that neurons associated with the same color tended to fire in synchronous bursts. The period between bursts in one group were occupied by similar bursting patterns generated by neurons associated with other colors (figure 1d). This simple model showed the coloring of the network was closely related to the dynamics of its constituent neurons. The temporal sequence of these bursts can be determined by a number of factors. Asymmetries in the intrinsic properties of individual LNs and directed connections between neurons can ensure that specific sequences of spiking are stabilized. In addition to changes in the intrinsic and synaptic parameters, a neuron’s Ca²⁺ concentration can also influence the ordering of LN bursts (Ahn et al., 2010). The larger the Ca²⁺ level in a cell, the less likely it is to generate a spike in the next cycle, because of the negative impact of Ca²⁺ dependent K currents. In figure 1e note that the ordering of bursts in a three color network can be predicted by the level of Ca²⁺.

Network geometry also influenced other attributes of individual bursts. In a network with chromatic number two (a minimum of two colors was required to color the network), the burst duration of neurons associated with a color depended on the number of neurons in the group. Asymmetries in the network’s structure were manifest as asymmetries in burst duration: larger groups dominated the dynamics (Figure 2a). The average duration of a burst was a nonlinear function of the number of neurons associated with the group and showed a sharp transition as the group size grew (Figure 2b). For a given network, as the number of separate groups increased, the number of neurons associated with each color decreased and thus exerted diminished inhibitory influence upon other groups. And as this influence diminished, strict coloring–based dynamics tended to break down (Figure 2c, compare top and bottom panels). We quantified this loss of structure as the amount of overlap in activity between different groups (Figure 2d). For a selected network with 100 inhibitory cells, this overlap showed an abrupt transition when the number of colors increased from four to five. We simulated a larger network consisting of 200 neurons to see if this transition was determined by the size of the network. A similar abrupt increase in variability was also evident in this larger network. Increasing the time constant of recovery from adaptation, however, shifted the transition point to the right (not shown). This transition was also seen in the distribution of burst lengths across all groups (Figure 2e). For a chromatic number below four, the burst length for all groups was very narrowly distributed. When the number of colors exceeded four, the standard deviation of the distribution increased abruptly (Figure 2e). This suggests that below a threshold level of inhibition, neurons showed very low within–group variability. In addition, the simple periodic sequences observed in networks with few colors were replaced by more complex sequences of activity when the number of colors increased. However, even for networks with high chromatic numbers (~8–10) (Bottom panel of Figure 2c), the influence of graph coloring continued to be evident in the network’s dynamics.

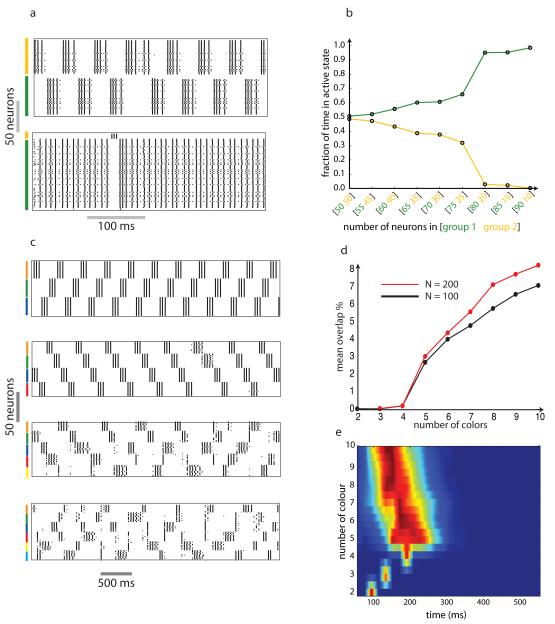
Figure 2.

Dynamical properties of networks based on graph coloring. a-b) Influence of the number of neurons associated with a particular color in a network with chromatic number 2. In symmetrical networks (each group has the same number of neurons) both groups spend equal time in the active state (top panel of (a) and the point [50 50] in (b)). As the asymmetry in network structure increases, the larger group increasingly dominates ((b) and bottom panel of (a)). c-e) Influence of the number of colors. As the number of colors increased the switching pattern became more noisy (compare top and bottom panels of (c)). d) Mean overlap time for networks consisting of 100 or 200 neurons. The percentage of time during which multiple groups are simultaneously active increases with chromatic number. e) Burst length distribution as a function of chromatic number. The width of the distribution increased abruptly when the chromatic number of the graph exceeded 4.

Dynamical consequences of multiple colorings

The example inhibitory networks shown thus far possess a unique coloring (Fig. 3a); in such a network neurons associated with a particular color can spike synchronously only with those neurons that share the same color. However, in the antennal lobe individual projection neurons, and therefore, by necessity, inhibitory interneurons, may switch allegiance between different synchronously spiking groups (Wehr and Laurent, 1996). Similar dynamic changes in the composition of synchronous groups of neurons have also been observed in other systems (Riehle et al., 1997) . Networks that possess a unique coloring do not permit such dynamics. To circumvent this difficulty we constructed networks with multiple colorings. For example, the graph in Figure 3b possesses chromatic number three. One of the four nodes is not connected to either the red or the blue node. Therefore, two colorings, one where this group is colored red and the other where it is colored blue, are permissible colorings of the graph. A dynamical consequence of this ‘structural ambiguity’ is shown in Figure 3c. The group that may be colored either red or blue is able to switch allegiance to spike synchronously with both the red and the blue group while remaining silent when the green group of neurons is activated. Based on our formalism, complex dynamics observed in vivo in the insect antennal lobe (Laurent et al., 1996) and other neuronal networks can thus be attributed to its structure – a network with multiple colorings permits transient synchrony in overlapping groups of neurons.

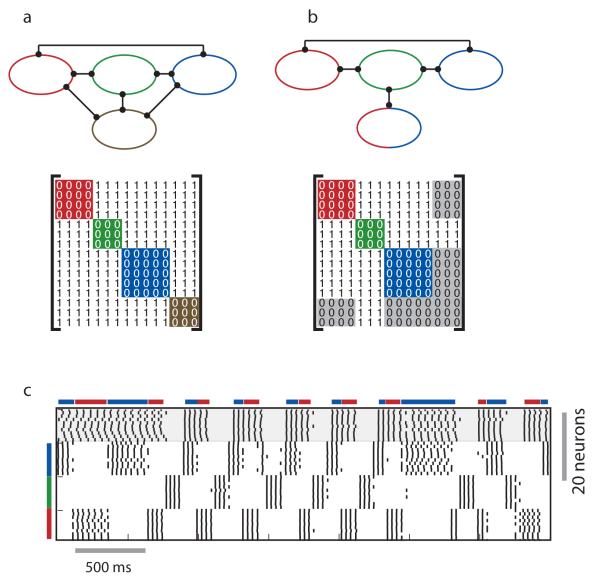
Figure 3.

Networks can have unique or multiple colorings. a) A network with a chromatic number 4 and a single coloring; b) A network with a chromatic number 3 and 2 different colorings. The neuron that may be colored either red or blue is shown with both colors. Bottom panels: adjacency matrices corresponding to the networks above. c) The dynamics of a network of 40 neurons with connectivity like the network in (b). The bars on the side of the panel correspond to the red, green and blue groups of 10 neurons. Note that the neuron colored red or blue switches allegiance between the red and the blue groups. The bars on top of the panel indicate the intervals of time when this group of neurons synchronizes with the red or the blue groups.

Excitation does not disrupt coloring-based dynamics

The coloring of a purely inhibitory network provides a strong constraint on its dynamics. However, many biological networks, including the olfactory system, include populations of excitatory neurons as well. To explore the consequences of implementing excitatory neurons, we constructed a network containing excitatory and inhibitory neurons with random connections between them (connection probability = 0.5) (Bazhenov et al., 2001b) (Figure 4a). This network was previously proposed as a model of locust antennal lobe dynamics (Assisi et al., 2007; Bazhenov et al., 2001a; Bazhenov et al., 2001b; Bazhenov et al., 2005).

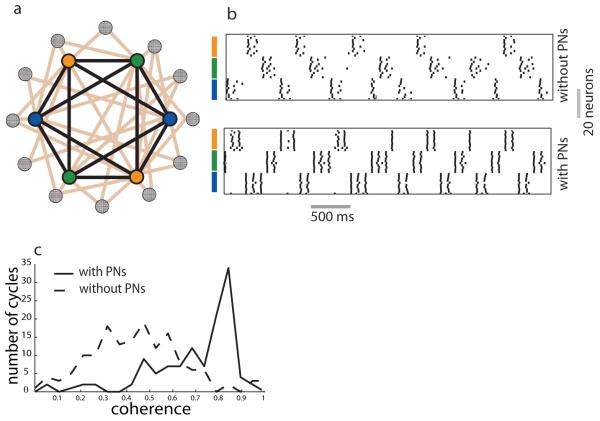
Figure 4.

Excitation preserves coloring–based dynamics.a) Schematic of the antennal lobe network. Nodes with solid colors: groups of inhibitory interneurons associated with a particular color. Projection neurons (shown as checkered circles) are randomly connected to and receive connections from the inhibitory sub– network. b) Raster plot showing the dynamics of the inhibitory sub–network when excitatory neurons were present (bottom panel) or absent (top panel). c) The distribution of a measure of spike coherence over cycles of the local field potential oscillation, the mean coherence of spikes within a cycle increased when excitatory connections were added. The coherence (R) of spikes within each cycle of the oscillatory local field potential R_j =(∑Cosθ_i )² +(∑Sinθ_i )² was calculated for each cycle j. The distribution was generated from all values of R_j. Excitation enhanced coloring–based dynamics of the inhibitory network.

We found that the coloring–based dynamics were not compromised by the addition of excitatory neurons (Figure 4b), but were rather strengthened. The spike coherence within individual cycles of the oscillatory field potential (mean activity) increased significantly when excitation was added (Figure 4c).

The mechanism of synchronization of PNs and LNs can be understood by considering a single reciprocally connected pair. When reciprocally coupled, the LNs and PNs oscillate in anti–phase. A Na⁺ spike generated by a PN elicits an EPSP in the LN which in turn generates a spike that delays the onset of a subsequent PN spike. The frequency of the resulting oscillations is controlled by the duration and the amplitude of the IPSP (see (Bazhenov et al., 2001b) figure 2). When a single LN projects to many postsynaptic PNs, it equally delays and synchronizes spikes in those PNs. This mechanism, a classic example of feedback inhibition (Bazhenov and Stopfer, 2010) is also referred to as PING (Pyramidal Interneuronal Network Gamma) (Borgers et al., 2005; Borgers and Kopell, 2003, 2005) and implicated as a prominent mechanism in the generation of cortical and hippocampal gamma oscillations.

Properties of follower neurons define an ordering of the network nodes

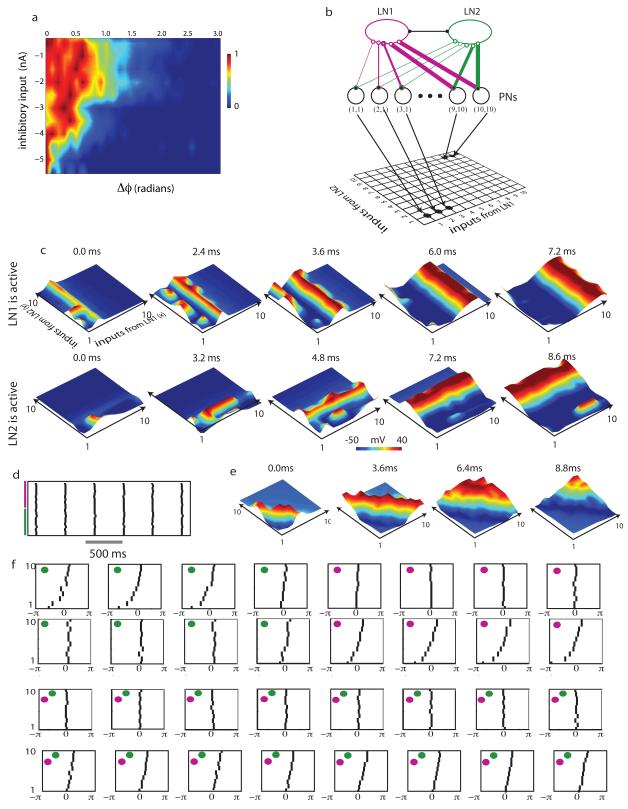
The distance between neuronal network nodes has often been defined as the shortest synaptic path length between them. This measure of distance is particularly relevant to networks of excitatory neurons that act as threshold units that generate a spike whenever a pre–determined number of pre–synaptic neurons fire a spike. A path in such network (a physical chain of neurons connected with excitatory synapses) therefore often translates into a temporal sequence of spikes (Abeles et al., 1993; Diesmann et al., 1999). Neurons located in close proximity (in a metric defined by the number of synapses separating them) would commonly spike within a short temporal interval providing common drive to their postsynaptic targets. However, in networks consisting of excitatory and inhibitory units, each capable of acting over multiple time scales and interacting nonlinearly, this measure of distance may not provide a complete account of the network’s possible dynamical states. Feedback inhibition from a single inhibitory neuron can induce complex patterns of spiking (Ermentrout, 1992). Sequences of spikes need not result from physically connected synaptic paths in the network. Is there another ‘hidden metric’ that underlies the observable network (Boguñá et al., 2009); a measure of distance between nodes that takes account of relevant biological variables? An answer to this question comes from understanding how neurons that follow the AL network in the olfactory processing hierarchy read their pre–synaptic input. Kenyon cells (KC) of the mushroom body (MB) receive convergent input from excitatory PNs of the AL and are known to be sensitive to the synchrony of pre–synaptic input (Perez-Orive et al., 2004; Perez-Orive et al., 2002). Only when a population of pre–synaptic excitatory PNs fire in synchrony does it provide sufficient input to activate a post–synaptic KC. Similar properties have been also been described in the thalamocortical system and the hippocampal formation (Pouille and Scanziani, 2001). Therefore we sought to construct a space in which synchronously active PNs could be readily identified. To do this, we considered how inhibition affects the responses of excitatory PNs. Greater inhibitory input was always accompanied by increased synchrony in the firing of PNs (Figure 5a) (Bazhenov et al., 2001b). In addition, PNs that received similar inhibitory input tended to spike together in a highly correlated manner. Therefore, a space that places PNs receiving similar inhibitory input close together would be a useful candidate for defining the network’s inter–nodal distances. In what follows, we demonstrate how knowledge of the coloring of the inhibitory sub–network can be effectively employed to achieve this goal.

Figure 5.

Coloring based reordering generates low–dimensional dynamics. a) Distribution of spikes within each cycle of the oscillatory local field potential as a function of pre–synaptic inhibitory input. For each interval of pre–synaptic inhibitory input (0.5nA intervals) neurons that produce spikes within a particular cycle were picked and the deviation of spike phase from the mean was calculated. The spread of the distribution narrowed as the inhibitory input increased (from top to bottom). b) Projection neurons were ordered in a two–dimensional space depending on the number of inputs each received from a particular group of inhibitory neurons. c) Projection neuron spikes form traveling waves in the reconstructed space. Top panel shows the activity when LN1 is active and the middle panel shows the activity when LN2 is active. d) Raster plot of LN activity when interactions between LN1 and LN2 were removed. e) The pattern of wave propagation by PNs in the network with no lateral inhibition between LNs. f) Spike raster showing the activity of a subset of neurons as a function of the phase of the oscillatory LFP. Different panels in each row correspond to different cycles of the oscillation. The color of the filled circle indicates which of the two groups of neurons (LN1 or LN2) was active during that particular cycle. Top two rows – intact LN1-LN2 inhibition. The top row of panels shows the activity of a group of neurons that receive exactly seven inputs from LN1. The second row shows a group of neurons that receive seven inputs from LN2. Bottom two rows - LN1 and LN2 are disconnected. The third row shows the activity of a group of neurons that are arranged along the diagonal of the grid. Each neuron along this diagonal receives a sum of five inputs from the groups LN1 and LN2. The fourth row shows the same group of neurons as in second row but with no LN1-LN2 inhibition.

To illustrate the construction of this space we used an inhibitory sub–network with two colors. These groups (LN1 and LN2) generated alternating patterns of activity as described above. We located each PN within a two–dimensional plane with x and y coordinates corresponding to the number of inputs it received from the group LN1 (magenta) and LN2 (green) respectively (Figure 5b). The Euclidean distance between PNs in this plane is a measure of the similarity of inhibitory input each received. Neurons placed along any line parallel to the y–axis received the same amount of inhibitory input from the group LN1; the exact amount of this inhibition depended on how close these neurons were to the y-axis. When LN1 was active (LN2 silent), projection neurons placed close to the y–axis received only weak inhibitory input (since most of their input come from LN2) and tended to fire randomly during each cycle of the oscillatory LFP (see spiking activity close to the y–axis in the top group of panels in Figure 5c). Further away from the y–axis, the inhibitory input from LN1 increased, as did the coherence of spiking in groups of PNs. Inhibition had the effect of delaying the onset of the PN spikes; the duration of this delay was dictated by the amount of inhibition. Therefore, in this space, neurons further away from the y–axis spiked later and in greater synchrony than those close to the y–axis.

In our reconfigured space, this differential timing led to the appearance of a wave propagating along the x–axis. When LN1 became quiescent and LN2 was activated, a wave propagating in the orthogonal direction was generated. Extending these results to a network with N colors, the reconstructed space will be N – dimensional with (N-1) – dimensional wave–fronts propagating along orthogonal directions. This seemingly low–dimensional dynamics became apparent only as a consequence of the coloring based reordering of projection neurons, one that may be used to derive a reduced set of mode equations that reproduces the dynamics of the network (Assisi et al., 2005).

Earlier studies have demonstrated that the participation of PNs in a synchronized ensemble during odor stimulation is usually transient, lasting a few cycles of the oscillatory ensemble response. The space based on the coloring of the inhibitory network provides an ideal representation to examine transient synchrony in PNs. We hypothesized that transient synchrony of groups of PNs is a consequence of the topography of competitive interactions in the LN sub–network. According to this hypothesis eliminating inhibitory connections between LNs should remove LN clustering and eliminate transient PN synchronization. Therefore, to study the specific effects of network topology on transient synchrony we eliminated all connections between LN1 and LN2 and simulated the network keeping all other parameters identical to the simulations shown in Figure 5c. In the absence of competition between LN1 and LN2, both groups of neurons spiked synchronously in response to an external input (Fig. 5d). Widespread excitatory inputs from randomly selected PNs tended to further synchronize the LN populations and reduced the variability of spikes within a cycle. The inhibitory input to individual PNs did not vary over different cycles since both LN1 and LN2 generated spikes at the same time. A PN located at the point (x,y) in the reconfigured space received x + y inhibitory spikes during each cycle. PNs located along diagonal lines (corresponding to x + y= constant) received the same amount of inhibitory input during each cycle and tended to spike synchronously. As in the earlier example PNs receiving greater inhibitory input generated spikes at later phases of the cycle. This differential input led to the appearance of a propagating wave of activity in the reconfigured space. However, unlike in the case where LN–LN interactions were intact, here we found that the waves traveled along the diagonal (figure 5e)). Most importantly, each cycle of ensemble activity generated an identical wave of activity and each PN remained either synchronized or not in every cycle leaving no possibility for transient PN synchronization.

To emphasize the difference between the two cases and to test whether that LN–LN interactions indeed generate transient synchrony in PNs in a manner consistent with previous experimental results we picked subsets of transiently synchronous PNs and observed the dynamics across the course of 8 cycles of the LFP oscillation. The top two groups of panels in figure 5d show the dynamics of a subset of PNs when LN1–LN2 connections were intact. The bottom two groups of panels shows the dynamics of the same subset of PNs when LN1–LN2 connections were removed. We picked two different subsets of neurons. In the topmost panel PNs that received exactly seven inputs from LN1 were selected. These PNs were synchronized only when the group LN1 was activated (last four cycles). When LN2 was activated (first four cycles) the phase at which these neurons spiked was distributed across the oscillatory cycle. In the next group of panels (second row) we picked neurons that received exactly seven inputs from LN2 and fired in synchrony only when LN2 was active (first four cycles). This population desynchronized during subsequent cycles. In contrast, when LN1–LN2 connections were removed (Fig. 5f, bottom two rows), each group of PNs was either synchronized (3d row) or not (4th row) across all cycles of the oscillatory LFP. A comparison with recordings made in vivo from the locust AL (Laurent et al., 1996) suggest that this form of constant synchrony is not observed in a majority of PNs suggesting that the topography of LN–LN interactions plays a crucial role in transient synchrony in the AL.

These traveling waves of activity are evident only in the abstract space defined by the coloring of the inhibitory network. Our incomplete knowledge of the detailed connectivity of the locust’s LN sub–network and limitations on size of the sets of simultaneously recorded neurons preclude the possibility of directly observing these waves in recordings made in vivo from the locust AL. However, knowledge of the existence of these relatively low–dimensional patterns of activity provides a general way to understand how information propagates from the AL to their followers, the KCs of the mushroom body. KCs are sensitive to coincidence in pre–synaptic input (Perez-Orive et al., 2004; Perez-Orive et al., 2002). If KCs receive identical synchronized input from PNs during every cycle of the oscillation, the same set of KCs will be activated repeatedly over the duration of the odor presentation. However, experimental recordings show that KCs generate very few spikes (~2-3) during the odor presentation. The absence of LN–LN interactions would therefore compromise the temporal sparseness of the odor representation by KCs.

Application to realistic networks of neurons

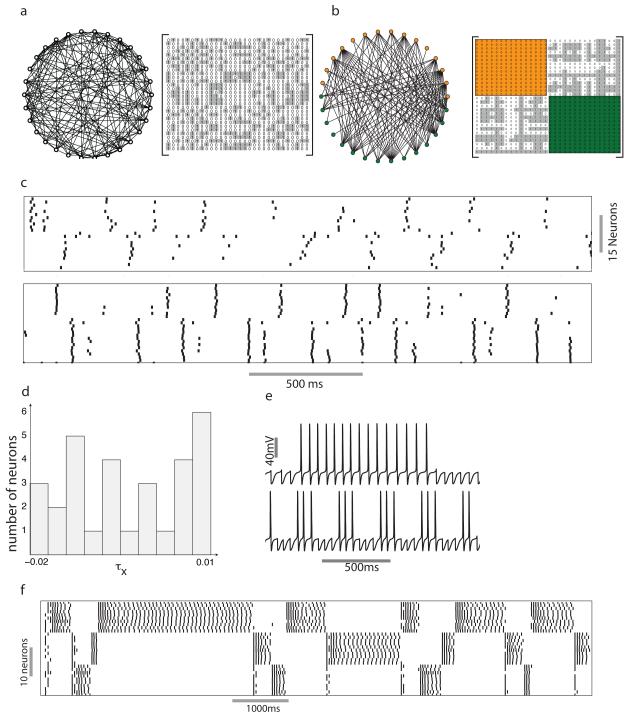
A number of algorithms to color random graphs exist. However, except under special circumstances, these algorithms do not guarantee that the coloring will always be minimal or that all possible colorings of the network will be obtained in a reasonable length of time (Kubale, 2004). Given the complexity of the graph coloring problem, using random graphs as our starting point would have been impractical. Hence we chose to construct graphs in which neurons associated with a particular color were connected to all neurons associated with other colors. How well do these constructed networks emulate the dynamics of realistic random networks? In the networks constructed thus far, each neuron received an equal number of connections as all other neurons that were affiliated with the same color. In realistic random networks this assumption is not true in general. Variability in input across LNs can cause the dynamics of the network to deviate from the dynamics predicted by the networks we simulated. To test the effect of perturbations to the network structure we simulated a network consisting of two groups of fifteen neurons that were reciprocally connected to each other (figure 6a). Neurons in each group extended one to fourteen connections to neurons belonging to the other group. This is the widest possible variability in connections that can be achieved in this network while ensuring that no neuron is isolated from the network. In addition a network constructed in this manner is also guaranteed to possess a chromatic number two. First, we reordered the rows and columns of the adjacency matrix of the network such that neurons affiliated with the same color were grouped together (Figure 6b). As in previous examples, the adjacency matrix of the random network consisted of diagonal blocks of zeros. However, all elements of the off–diagonal blocks are not uniformly one. Does this variability in the number of connections per neuron alter the coloring–based dynamics of the network? We found that, while variability in the network connectivity perturbed the network dynamics, the coloring structure still clearly defined the neuron responses (Figure 6c, top panel).

Figure 6.

Coloring–based dynamics in realistic neural networks. a) A random bipartite graph. Individual neurons receive between 1 and 14 inputs from LNs belonging to a different color and the corresponding adjacency matrix. b) The neurons were grouped into two groups based on the color. Adjacency matrix of the network shows off–diagonal blocks with ones (shaded gray) and zeros. c) Raster plot showing the response of the network to input in the absence (top panel) and the presence (bottom panel) of random excitatory input from PNs. d) Distribution of the parameter τ_x that perturbs the time scale of the Ca²⁺ dependent potassium current. e) Dynamics of inhibitory LNs as a function of τ_x. The top trace shows the response of a neuron belonging to a reciprocally inhibitory pair with τ_x = 0.01. The bottom trace shows the response of a neuron with τ_x = 0.02. f) Dynamics of a group of 30 LNs that form a three–color network. The value of τ_x for each LN in the network was picked from the distributions shown in (d).

Furthermore, we could reduce the effect of these perturbations by incorporating connections between excitatory PNs and the inhibitory LNs (Figure 6c, bottom panel) that would mimic a typical biological network like the insect antennal lobe consisting of interacting excitatory and inhibitory neurons. The back and forth interaction between excitation and inhibition tends to promote synchrony in both sets of neurons. Each group of LNs spiked in alternation thus respecting the coloring of the network as a constraint. (Borgers and Kopell, 2003) have also demonstrated that increasing the strength of excitatory to inhibitory neurons tends to mitigate the influence of heterogeneity due to random connectivity. This synchronization mechanism has been demonstrated in the olfactory bulb of rats where the interaction between mitral cells and granule cells results in the emergence of rapid synchrony in the network (Schoppa, 2006) (but see (Galan et al., 2006)).

In previous simulations we had introduced small variations in the excitability of individual neurons to ensure that the solutions would be robust to parameter noise. We also added a small amplitude noise term (approximately 10% of the amplitude of the DC input to each neuron) (see supplementary material for details). The role of the coloring of the network on the dynamics remained robustly evident in spite of these variations. However we kept a key parameter, the time scale of adaptation, constant across all neurons. Adaptation allows the LNs to switch from a spiking to a quiescent state (figure 1). The time scale of adaptation affects the duration that a neuron spends in each state. In a realistic network the time scale of adaptation may be distributed across the population of LNs. We sought to determine if such variation can compromise the coloring–based dynamics of the inhibitory sub–network. We simulated the dynamics of the network with broad variability consistent with the time scale of the Ca²⁺ dependent potassium current. A parameter τ_x was added to the time scale τ_m of the Ca²⁺ dependent potassium current (see equation for m in the section Ca²⁺ dependent potassium current I_KCa in supplementary material). Its value τ_x was picked from a uniform random distribution with values extending from −0.02 to 0.01 (figure 6d). The range of this distribution was adjusted to generate a large variation in the oscillatory switching frequency of two reciprocally coupled LNs. Switching between the active and quiescent state was slow τ_x = 0.01 and increased dramatically for τ_x = −0.02 (Fig. 6e). We found that a wide variation in the Ca²⁺ dependent potassium current leads to non-uniformity in the duration of LN spike bursts across the duration of the odor presentation. However, despite this realistic variability, the dynamics of the LNs continues to follow the coloring of the network (Fig. 6f).

Discussion

Transient synchrony and inhibition

In this study we demonstrated that inhibition mediated by a local interneuron population may generate transiently synchronous spiking in evolving populations of excitatory neurons and constructed a space in which this transient synchrony could be easily identified. In agreement with our previous studies (Bazhenov et al., 2001a; Bazhenov et al., 2001b) our model predicts that during odor stimulation the sequence of transitions between synchronized and desynchronized states (with respect to the oscillatory mean activity) of the excitatory neurons in the insect AL should match the sequence of alternations between active and quiescent states in the inhibitory sub–network that shapes the timing of spikes in excitatory cells. In this new study we further established a link between a structural characteristic of every inhibitory network, its colorings, and the resulting collective dynamics of that network and, as a result, the information flow through this system. We showed that (1) lateral inhibition between local interneurons is required to transiently synchronize projection neurons in the antennal lobe; (2) graph coloring provides a useful description of competitive lateral inhibition between inhibitory interneurons that (3) also allows a low-dimensional description of the complex AL network dynamics in a manner consistent with the perspective of follower neurons. Our approach allowed us to rank excitatory neurons not by their distance in physical space but by the strength of inhibition they receive thus providing a natural way to group together the neurons that act together (fire in synchrony) – a necessary condition to activate postsynaptic neurons based on coincidence detection type of information coding.

The neurons receiving strongest inhibitory input also spike with largest delay; therefore, in the reconfigured space, this differential timing led to the appearance of waves of activity propagating in directions defined by dynamics of inhibitory interneurons. In the absence of this reordering, the dynamics of PNs would appear as randomly occurring patterns of activity correlated with the dynamics of LNs. The traveling wave–like dynamics only observed in the reconfigured space represents a dramatic reduction in the dimensionality of the description. This simplified description of the network’s behavior provides a foundation for generating more tractable models of spatiotemporal patterning in the coupled networks of excitatory and inhibitory neurons.

Locust AL dynamics

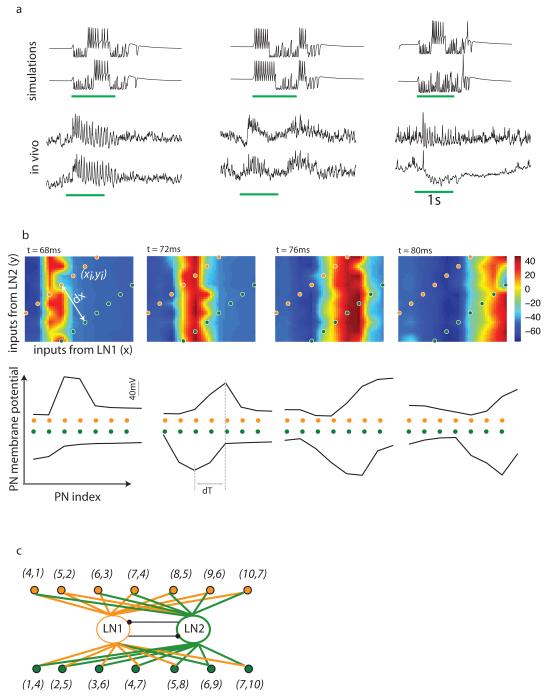
In the locust AL, a typical PN displays a rather simple pattern of transitions between synchronized and desynchronized states while responding to an odor (Laurent and Davidowitz, 1994b; Laurent et al., 1996). This pattern of synchrony must be driven by contiguous bursts of spikes in inhibitory interneurons alternating with silence. Such activity is in fact typical of inhibitory interneuron firing patterns during odor stimulation. Recordings made in vivo from the locust antennal lobe demonstrate that inhibitory interneurons tend to show rather simple activity patterns consisting of a single burst of activity during a particular odor presentation. Many inhibitory interneurons display tonic activation over the entire duration of odor stimulation in contrast to others that remain hyperpolarized (figure 7a, bottom). Such patterns of activity are well described by our model (figure 7a, top). In this example, for the network with non–unique coloring, one group of LN neurons remained active during the entire duration of stimulation while the two other groups of neurons switched between active and silent states.

Figure 7.

a) Example traces of local inhibitory interneuron activity from model simulations (top two traces) and in vivo intra–cellular recordings from locust local interneurons (bottom two traces). In the left and central panel, traces show responses of a single LN to multiple presentations of the same odor. In the rightmost panel, the two traces show the responses of different neurons to the same odor. The green lines below the traces show the duration over which the stimulus was presented.

b-c) Coloring based model of a segmental swimming pattern generator. Two groups of neurons along off–diagonal lines in the plot (b, top panels) were picked. The perpendicular distance between them is marked dx. Waves of activity generated by the network (b, top panels) were seen in these sub–groups of neurons (b, bottom panels). The time difference between the peaks of the traveling waves is marked dT. The sub–network that generates traveling waves along these lines of neurons is shown in (c). Each neuron is marked by two coordinates (x_i,y_i). The x–coordinate shows the number of inhibitory inputs received by a given PN from the group LN1. The y–coordinate shows the number of inhibitory inputs received from the group LN2.

Why do LNs in the antennal lobe exhibit only a subset of the broad repertoire of patterns that the networks simulated here are capable of generating? The formalism we developed in our manuscript points us toward several possibilities. These dynamical patterns are likely to result from an intrinsic asymmetry within the antennal lobe sub–network that gets activated in response to a specific odor. If only a subset of neurons receives strong activation during specific odor stimulation, these neurons will dominate the response. Asymmetries in coupling strength can also result in the predominance of one group that would prevent switching between groups to occur. In addition, if the number of colors is large a trajectory may never recur during odor stimulation. Hence the same LN may not generate multiple bursts of spikes.

We have shown that fast GABAergic inhibition mediated by GABA_A receptors transiently synchronizes PN activity over a few cycles of the ensemble oscillatory response. A second important form of inhibition found in the AL is mediated by slow GABA_B receptors acts over a time scale in the range of hundreds of milliseconds (Wilson and Laurent, 2005). Experiments (MacLeod and Laurent, 1996) and models (Bazhenov et al., 2001a) have demonstrated that this type of interaction leads to lengthy epochs of time where individual PNs are hyperpolarized and do not spike at all. Picrotoxin applied to the AL spares patterning caused by slow inhibition while abolishing oscillatory synchronization on a fast time scale. The time scales separating the two forms of inhibition differ by approximately an order of magnitude. To explore how network structure leads to transient synchrony, a key dynamical variable involved in fine discrimination in the olfactory system (Stopfer et al., 1997), we focus here on fast inhibition while minimizing the effects of slow inhibition in the model.

The repertoire of patterns generated by the inhibitory sub–network in the locust antennal lobe forms a subset of the full range of patterns that can be generated by the networks simulated here. Feedforward architecture and coincidence detection mechanisms like those illustrated here are not unique to the insect olfactory system. Pre–synaptic synchrony allows feedforward thalamic input caused by sensory stimulation in various modalities to be faithfully transmitted to the cortex in spite of the inability of individual thalamocortical projections to drive cortical activity (Bruno and Sakmann, 2006). Similarities in structure have also occasioned comparisons between the function of the olfactory bulb and the thalamus (Kay and Sherman, 2007). In the mammalian spinal cord it has been shown that genetically silencing certain groups of neurons can have profound behavioral consequences (Gosgnach et al., 2006; Lanuza et al., 2004; Zhang et al., 2008). For example, silencing excitatory V3a interneurons compromises the rhythmicity and stability of locomotor outputs (Zhang et al., 2008). The coherence of spiking activity in our model network was also similarly compromised by the removal of excitatory interactions.

The sequence of bursts generated by the networks constructed here qualitatively resemble the kind of dynamics seen in networks that exhibit a form of competition termed winnerless competition (WLC) (Rabinovich et al., 2001). These patterns of activity have been hypothesized to be heteroclinic orbits that connect saddle fixed points or saddle limit cycles in the system’s state space (Rabinovich, 2006). The stability of these sequences and the capacity of the network to generate sequential patterns have been analyzed in detail. However, the relationship between the structure of the network and the resulting patterns of activation are not yet known. (Ahn et al., 2010) derive a computationally efficient and analytically tractable discrete time dynamical system that accurately replicates the dynamics of more complex Hodgkin–Huxley type neuronal network. The discrete time model predicts which group of neurons will spike next given that a specific group of neurons spiked during a previous epoch. The constraints imposed on the model include the Ca²⁺ concentration in the cells, the ionic conductances, neuronal thresholds, and the number of inputs each neuron receives from a group that spiked in a preceding epoch. Our approach is complementary to that of (Ahn et al., 2010).We use a global descriptor of the network structure (its colorings) to deduce the set of all possible solutions of the system (a solution is valid only if it respects the coloring of the network). Additional constraints such as the directed connections between neurons, asymmetries in intrinsic parameters, and Ca²⁺ concentration in the cell (Ahn et al., 2010) can make specific solutions stable.

Constructing networks that generate pre–specified temporal relationships among components

In this study we used the insect olfactory system to derive a structure–dynamics relationship in neuronal networks. This relationship can be tested in other well–charted networks such as central pattern generators (Marder and Calabrese, 1996). In the stomatogastric ganglion, where reciprocal inhibition is ubiquitous and implicated in generating periodic patterns (Getting, 1989; Marder and Calabrese, 1996), alternating bursts are produced by a number of different mechanisms. The pyloric rhythm of the crustacean stomatogastric ganglion is generated by a combination of intrinsic bursting and post–inhibitory rebound in the same circuit producing a rhythmic pattern of alternation that is consistent with the coloring of the underlying network (see Figure 4a and 4b in (Marder and Bucher, 2007). The AB neuron entrains the PD neuron via gap junction coupling. These neurons together inhibit the other neurons in the network. The alternating tri–phasic pattern is generated by groups of neurons that are associated with different colors). The output from central pattern generators drives motor neurons that synapse onto muscles to generate rhythmic patterns of movement. The temporal ordering of different components of the system is crucial to the generation of appropriate movement. Using an inhibitory network as a nucleus we can generate spiking in excitatory neurons that obeys specific temporal relationships.

In Figure 7 we illustrate the construction of a segmental swimming pattern generator using a sub–network extracted from the network defined in Figure 5. We chose two groups of inhibitory interneurons (identified as LN1 and LN2 in Figure 7c) that were reciprocally coupled to each other. The resulting dynamics of the inhibitory network produced an alternating pattern of bursts that provided input to a set of PNs. The number of inputs that each PN received from a particular group is marked (x,y) where x is the number of inputs from group LN1 and y the number of inputs from group LN2. Our goal was to choose two sets of PNs each of which could generate a traveling wave, one following the other with a time difference dT. The dynamics of this sub–network could emulate the swimming pattern in an organism like the lamprey that swims forward as a wave of muscular activity courses along two sides of its length (Wallen and Williams, 1984). Inhibitory input from LNs tends to delay the onset of the following PN spike. The extent of the delay in the PN spikes increased with increasing values of inhibition. A traveling wave could, therefore, be generated by choosing PNs that received increasing number of inputs from either one of the inhibitory neuron groups, LN1 or LN2, and arranging them linearly (see Figure 7b). When the inhibitory group LN1 was active a wave of excitatory activity propagated parallel to the y–axis (top panels of figure 7b). The peak of this wave intersected with the lines of neurons marked by the filled circles and generated traveling waves of activity in each of these two groups (Figure 7b, bottom panels) (see Supplementary Information, movie S1). The time delay between these two waves (marked dT in Figure 7b, bottom panel) increased with increasing the perpendicular distance (marked dx in Figure 7b, top panel) between the two groups of excitatory neurons. Thus, by extracting these groups of excitatory neurons and adjusting the distance between them (dx) we could generate a pair of traveling waves with a desired delay (dT) between them. The leading and the following wave could be switched by switching the active inhibitory group from LN1 to LN2. This can be achieved by the autonomous dynamics of the inhibitory network or by applying an external perturbation. Other phase relationships between neurons can be obtained by choosing appropriate groups of PNs from the two–dimensional ordering of excitatory neurons shown in Figure 5 and Figure 7b (top panels). More complex phase relationships can be generated by using a larger number of colors and multiple colorings of the network. This simple example illustrates that knowing the coloring structure of the inhibitory network, we can predict the dynamics of the excitatory principal cells despite the complex and seemingly random synaptic structure between excitatory and inhibitory neurons.

Conclusion

The ultimate goal of exploring sensory network dynamics is to understand the spatio–temporal activity of excitatory principal neurons since this activity is what typically drives the responses of neurons at downstream levels of processing. In many circuits where information processing is based on the detection of coincidence between spikes (for example, between insect the AL and MB), a property important for understanding information flow is synchrony between excitatory neurons. In this study we showed a relationship between the connectivity structure of the inhibitory sub–network and synchronization properties of excitatory neurons. Further, we used the coloring of the inhibitory sub–network as a tool to construct a space in which the distance between excitatory neurons is defined not by the length of the synaptic path connecting those neurons but by the similarity of the inhibitory input they receive. This description optimally matches the perspective of the downstream neurons looking for synchrony in ensembles of pre–synaptic cells and, therefore, allows a low–dimensional description of seemingly complex high–dimensional network activity.

Methods

Network model

Individual projection neurons and local neurons were modeled by a single compartment that included voltage and Ca²⁺ dependent currents described by Hodgkin–Huxley kinetics (Hodgkin and Huxley, 1990). Since the biophysical make-up of insects’ olfactory neurons has not yet been completely characterized, we used parameters drawn from well-described cell types while following two guiding principles: (1) minimize the number of currents and their complexity in each cell type; (2) generate realistic (though simplified) firing profiles. Our LN model includes a transient Ca²⁺ current (Laurent et al., 1993), a calcium-dependent potassium current (Sloper and Powell, 1979), a fast potassium current (Traub and Miles, 1991) and a potassium leak current thus producing profiles devoid of Na⁺ action potentials but capable of Ca²⁺-dependent active responses, as observed experimentally (Laurent and Davidowitz, 1994a). Our PN model includes a fast sodium current (Traub and Miles, 1991), a fast potassium current (Traub and Miles, 1991), a transient K⁺ A-current (Huguenard et al., 1991) and a potassium leak current I_KL. Equations for all intrinsic currents in locust LNs and PNs can be found in (Bazhenov et al., 2001a; Bazhenov et al., 2001b).

In the model, isolated projection neurons displayed overshooting Na⁺ spikes at a fixed frequency throughout DC stimulation. Local neurons, in contrast, fired low amplitude Ca²⁺ spikes and displayed spike frequency adaptation caused by Ca²⁺–dependent potassium currents. Fast GABA (local neuron–projection neuron and local neuron–local neuron connections) and nicotinic cholinergic synaptic currents (projection neuron–local neuron connections) were modeled by first order activation schemes. The equations for all intrinsic and synaptic currents are given in the Supplementary Information and based on (Bazhenov et al., 2001a; Bazhenov et al., 2001b).

In figure 1– figure 3 we simulated isolated networks of LNs. The population of LNs and the specific connectivity are shown in the respective figures. In the following figures we simulated networks including both excitatory PNs and inhibitory LNs. Drawing from the basic anatomy of the insect AL, the PNs received inputs from LNs and projected random connections back to LNs. The AL model simulated in figure 5 included 20 LNs and 100 PNs.

Local neuron–projection neuron connections were determined such that each projection neuron occupied a position on the grid in Figure 5. We tested the network with a larger population of local neurons and projection neurons with random connectivity to obtain the same result (propagating waves of activity in the two–dimensional plane). With random connections the population of projection neurons simulated did not cover all points on the two–dimensional grid. However, the waves of activity could be clearly seen in spite of gaps in the grid of projection neurons. We also simulated a network with chromatic number three and were able to generate two–dimensional wave–fronts that propagated along orthogonal directions.

Electrophysiology

Intracellular recordings (Figure 1 and Figure 7) were made from local neurons in adult locusts (Schistocerca Americana) obtained from a crowded colony. Animals were immobilized and stabilized with wax with one antenna was secured. The brain was exposed, desheathed and superfused with locust saline as previously described (Laurent and Davidowitz, 1994b). Intracellular electrodes were sharp glass micropipettes (O.D = 1.0mm, Warner Instruments, 80-230 MΩ, Sutter P97 horizontal puller, Sutter Instruments) were filled with 0.5 M potassium acetate and 5% neurobiotin (Vector Laboratories). Data were digitally acquired (5 kHz sampling rate, LabView software and PCI-6602 DAQ and PCI- MIO-16E-4 hardware, National Instruments), stored on a PC hard drive and analyzed off- line using MATLAB (The MathWorks Inc.). Odors puffs were dilute grass volatiles delivered as described in (Brown et al., 2005)

Highlights.

• Activity of AL neurons is shaped by spatiotemporal patterns of inhibition.

• The coloring, a structural attribute, of the LN network constrains its dynamics.

• Coloring–based ordering of PNs identifies neurons firing in synchrony.

• This description of AL dynamics matches the encoding properties of KCs.