Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2011 Jul 18;108(31):12675-12680. doi: 10.1073/pnas.1104030108

Processive phosphorylation of ERK MAP kinase in mammalian cells

Kazuhiro Aoki a,b,1,2, Masashi Yamada c,1, Katsuyuki Kunida c, Shuhei Yasuda a, Michiyuki Matsuda a,c
PMCID: PMC3150946  PMID: 21768338

Abstract

The mitogen-activated protein (MAP) kinase pathway is comprised of a three-tiered kinase cascade. The distributive kinetic mechanism of two-site MAP kinase phosphorylation inherently generates a nonlinear switch-like response. However, a linear graded response of MAP kinase has also been observed in mammalian cells, and its molecular mechanism remains unclear. To dissect these input-output behaviors, we quantitatively measured the kinetic parameters involved in the MEK (MAPK/ERK kinase)-ERK MAP kinase signaling module in HeLa cells. Using a numerical analysis based on experimentally determined parameters, we predicted in silico and validated in vivo that ERK is processively phosphorylated in HeLa cells. Finally, we identified molecular crowding as a critical factor that converts distributive phosphorylation into processive phosphorylation. We proposed the term quasi-processive phosphorylation to describe this mode of ERK phosphorylation that is operated under the physiological condition of molecular crowding. The generality of this phenomenon may provide a new paradigm for a diverse set of biochemical reactions including multiple posttranslational modifications.

Keywords: simulation, phos-tag, crowder, quantitative parameter, EGF

Mitogen-activated protein (MAP) kinase cascades are evolutionarily conserved signaling pathways that are involved in the control of physiological and pathological cellular processes including cell proliferation, survival, differentiation, apoptosis, and tumorigenesis (1–4). Each MAP kinase pathway contains a three-tiered kinase cascade consisting of a MAP kinase kinase kinase, a MAP kinase kinase, and the MAP kinase, which are sequentially activated in this order. MAP kinases, which are activated by dual phosphorylation of conserved threonine and tyrosine residues within the activation loop, phosphorylate their targets on serine or threonine residues (1, 3, 5). Five distinct groups of MAP kinases have been characterized in mammals. Among the five groups, the most studied is the Raf/MEK/ERK MAP kinase cascade (hereafter called the ERK MAP kinase cascade), which is activated by mitogenic ligands such as growth factors, cytokines, and phorbol esters.

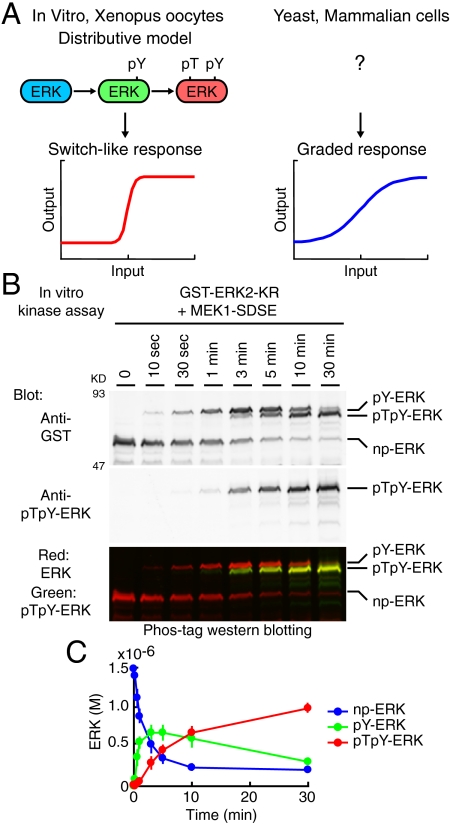
Ferrell and coworkers found that in Xenopus oocytes the ERK MAP kinase pathway responds to increasing levels of progesterone in an all-or-none or “switch-like” manner, in which individual cells in the population exhibit either “on” or “off” status (6, 7). This property of ERK MAP kinase system befits to determine all-or-none irreversible responses including cell-cycle progression, neuronal differentiation, and T cell selection (6–10). The switch-like responses can arise from both positive feedback via protein synthesis and dual phosphorylation steps of the MAP kinase, which is called the “distributive phosphorylation model” (11–15) (Fig. 1A). The distributive model of ERK phosphorylation results in an increase in the cooperativity of this system, and consequently contributes to a switch-like input-output response.

Fig. 1.

Fig. 1.

Open in a new tab

ERK phosphorylation in vitro. (A) Schematic representation of the input-output response of ERK MAP kinase. The distributive phosphorylation model leads to switch-like response. On the other hand, no model is currently validated for the graded response of ERK, which is observed in mammalian cells and yeast. (B) His-tagged MEK1-SDSE and GST-ERK2-KR were incubated with ATP for the indicated periods, followed by Phos-tag Western blotting analysis. All phospho-isoforms of ERK were detected by anti-GST rabbit antibody (upper) and IRDye680-conjugated anti-rabbit IgG antibody as a secondary antibody. The positions of the phospho-isoforms of ERK are indicated at right (SI Appendix: Fig. S4). pTpY-ERK was simultaneously detected by anti-pTpY-ERK mouse antibody (middle) and IRDye800-conjugated anti-mouse IgG antibody as a secondary antibody. The lower image is the merged image (Red: ERK, Green: pTpY-ERK). (C) The phospho-isoforms of ERK were quantified and plotted with SD (n = 3).

In different cellular contexts, however, the ERK MAP kinase cascade exhibits “graded” response, in which all cells in the population uniformly gain their signal output proportionally in response to the level of input stimulus. This input-output response is observed in the pheromone-stimulated Saccharomyces cerevisiae (16–18) and growth factor stimulated-HeLa cells and fibroblasts (19, 20). These graded responses can suit the physiological property of signaling, including the reversibility and the activation by different inputs with a wide range of threshold doses (18). However, MAP kinase cascades should inherently induce the switch-like response behavior due to the three-tiered enzyme cascade. To answer this question, it has been theoretically proposed that scaffold proteins might convert the switch-like response into the graded response (21). Here, the scaffold protein holds MAP kinase kinase and MAP kinase, thereby inducing dual phosphorylation at a single collision, which is called the “processive phosphorylation model” (11, 21–25). However, it is not known whether the scaffold proteins in mammals contribute to the processive phosphorylation of MAP kinase (10). Hence, the mechanism by which MAP kinase activity adopts a graded response remains unclear in mammalian cells.

In this study, we demonstrate that ERK is phosphorylated in a processive manner by employing quantitative simulation model of the ERK MAP kinase cascade. Furthermore, a condition that mimics physiological molecular crowding has been shown to convert the mode of ERK phosphorylation from distributive to processive. Under this condition, MEK and ERK do not form a stable complex as proposed in the processive phosphorylation model. Therefore, we propose that ERK is phosphorylated in a “quasi-processive” manner under the physiological condition of molecular crowding.

Results

Kinetic Parameters That Determine the Dynamics of the MEK-ERK Signaling Module.

Our goal is to comprehend the systems behavior of the MEK-ERK signaling module. To this end, we attempted to determine most, if not all, of the kinetic parameters required for the kinetic simulation model, using HeLa cells as a model system. The model requires four classes of parameters: protein concentrations, association/dissociation rates, nuclear import/export rates, and phosphorylation/dephosphorylation rates. We experimentally determined approximately 30 parameters (SI Appendix: Fig. S1–7 and Tables S1 and S2). Notably, this study focused on the phosphorylation kinetics of the MEK-ERK module in the early phase of the signaling event. Thus, we neglected the role of ERK-induced gene expression of negative regulators such as dual specificity phosphatases, which shape the dynamics of intracellular signaling starting from 30 min after ligand addition (26).

In Vitro Phosphorylation Rates of ERK Measured by Phos-Tag Gel Electrophoresis.

All parameters used in this study are determined in living HeLa cells except for the phosphorylation rates of ERK, which was determined as follows. MEK activates ERK by phosphorylating two critical amino acid residues within the activation loop, threonine and tyrosine; therefore, we quantified four phospho-isoforms of ERK, nonphosphorylated ERK (np-ERK), tyrosine monophosphorylated ERK (pY-ERK), threonine monophosphorylated ERK (pT-ERK), and bis-phosphorylated ERK (pTpY-ERK) by Phos-tag Western blotting (27). Phos-tag is a phosphorylated amino acid chelator. Because the electrophoretic mobility of phosphorylated proteins is significantly reduced in separation gels containing Phos-tag, the fractions of nonphosphorylated and phosphorylated proteins can be visualized quantitatively. Notably, the effect of Phos-tag on the electrophoretic mobility varies among phospho-proteins, demanding a preliminary experiment of the identification of each phospho-protein by immunoblotting with specific antibodies (SI Appendix: Fig. S4). We found that the order of electrophoretic mobility in the Phos-tag gel was, from the slowest to fastest, pY-ERK, pTpY-ERK, pT-ERK, and np-ERK. This order was also confirmed with phosphatase inhibitors. Treatment with the phospho-tyrosine phosphatase inhibitor bpV, and the phospho-serine/threonine-phosphatase inhibitor Calyculin A, increased the intensity of the pY-ERK and pT-ERK bands, respectively (SI Appendix: Fig. S6).

The rates of ERK phosphorylation by MEK were first determined in vitro using a kinase-dead mutant of ERK2 (ERK2-KR) and constitutively active mutant of MEK1 (MEK1-SDSE). As previously demonstrated (11), pY-ERK was initially accumulated, followed by pTpY-ERK (Fig. 1 B and C). pT-ERK could not be detected under this condition. Importantly, the amount of the intermediate product, pY-ERK, exceeded that of the enzyme, MEK1-SDSE (3.0 × 10-7 M in Fig. 1C), indicating that ERK was phosphorylated by a manner consistent with the distributive phosphorylation model in vitro (11). In this way, we obtained the first and second reaction rates with linear assumption (kcat/Km) of 3.9 × 104 [/M/ sec ] and 2.1 × 104 [/M/ sec ], respectively (SI Appendix: Fig. S5 and Table S2). The reason why pT-ERK was not detected may be because the first step of the reactions from np-ERK to pT-ERK is markedly slower than the second step from pT-ERK to pTpY-ERK in vitro. Therefore, the phosphorylation reaction rate (kcat/Km) from pT-ERK to pTpY-ERK was examined in vitro using pT-ERK as a substrate, and was found to be 2.0 × 104 [/M/ sec ] (SI Appendix: Table S2). Thus, pT-ERK production from np-ERK could be ignored at least in the phosphorylation reactions (SI Appendix: Fig. S5G).

Validation of the Distributive Phosphorylation Model.

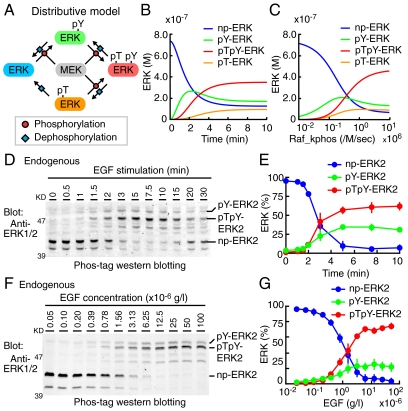
Based on these parameters determined experimentally (SI Appendix: Tables S1 and S2), we built a distributive phosphorylation model of the MEK-ERK signaling module (Fig. 2A, SI Appendix: Fig. S8A), and numerically solved the ERK phosphorylation (Fig. 2 B and C). The input signal, i.e., the turnover rate of MEK phosphorylation by cRaf, was initially set to 1.0 × 106 [/M/ sec ] to reproduce the experimental data, and was varied with a broad range (SI Appendix: Fig. S9). Upon stimulation in silico, pY-ERK was steeply increased, followed by a gradual increase in pTpY-ERK and pT-ERK (Fig. 2B). pY-ERK was predominant over pTpY-ERK in low input strength, and vice versa for high input strength at 10 min after stimulation (Fig. 2C). These data were consistent with the distributive phosphorylation model demonstrated in vitro (Fig. 1) and in Xenopus oocytes (6, 11).

Fig. 2.

Fig. 2.

Open in a new tab

Numerical and experimental analyses of the distributive phosphorylation model. (A) Schematic representation of the distributive model (see SI Appendix: Fig. S8A in detail). (B and C) Results of numerical simulations are represented based on experimentally determined parameters (SI Appendix: Tables S1 and S2). (B) Concentrations of np-ERK (blue), pY-ERK (green), pTpY-ERK (red), and pT-ERK (orange) are plotted against time. The kcat/Km value of cRaf kinase for MEK phosphorylation (Raf_kphos) is 1.0 × 106 [/M/ sec ]. (C) Concentrations of the phospho-isoforms of ERK are plotted against the Raf_kphos value at time = 10 (min). (D and E) After serum starvation, HeLa cells were stimulated with 1.0 × 10-5 g/L EGF at the indicated time period. (D) Cell lysates were separated by SDS-polyacrylamide gel containing Phos-tag and probed with an anti-ERK antibody. (E) The amounts of np-ERK2 (blue), pY-ERK2 (green), and pTpY-ERK2 (red) are plotted against time after EGF stimulation with SD (n = 3). (F and G) After serum starvation, HeLa cells were stimulated with the indicated concentration of EGF for 7.5 min. (F) Cell lysates were analyzed by Phos-tag Western blot analysis as in (D). (G) The amounts of np-ERK2 (blue), pY-ERK2 (green), and pTpY-ERK2 (red) are plotted as a function of the EGF concentration with SD (n = 5).

We next examined whether the phosphorylation of ERK2 in HeLa cells follows the distributive model. Against the prediction in silico, the increase in pY-ERK2 did not precede to, but rather accompanied the increase in pTpY-ERK2 upon EGF stimulation (Fig. 2 D and E). Furthermore, pY-ERK2 increased in a dose-dependent manner as the EGF input increased (Fig. 2 F and G), but did not increase in a bell-shaped manner as predicted in silico (Fig. 2C). Of note, we could not detect the endogenous pT-ERK2 quantitatively due to the low abundance and to the signals of comigrating pY-ERK1.

Prediction of a Processive Phosphorylation Model In Silico.

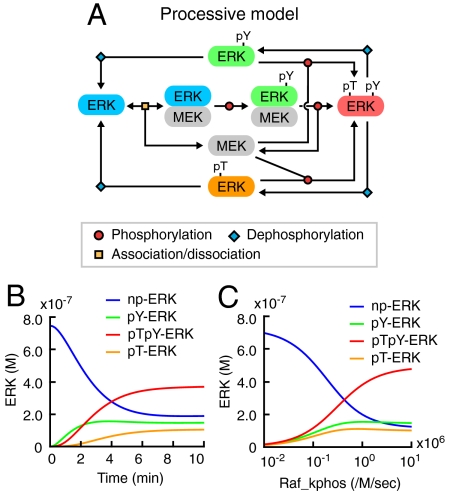
Because we determined all parameters in the cells except for the phosphorylation reaction rates, which were obtained in vitro, we speculated that the discrepancy between the experimental and in silico data of the MEK-induced ERK phosphorylation might have arisen from parameters related to the phosphorylation rates of ERK. Hence, we built a processive model by changing one reaction pathway of the distributive model (Fig. 3A, SI Appendix: Fig. S8B, Tables S1 and S2). Here, activated MEK does not dissociate from pY-ERK but processively phosphorylates threonine of pY-ERK to generate pTpY-ERK. Therefore, this model contains two species of pY-ERK, i.e., pY-ERK in complex with MEK and pY-ERK generated by the dephosphorylation of pTpY-ERK.

Fig. 3.

Fig. 3.

Open in a new tab

Computational simulation of the processive phosphorylation model. (A) Schematic representation of the processive model (see SI Appendix: Fig. S8B in detail). (B) Results of numerical simulations are represented based on experimentally determined parameters (SI Appendix: Tables S1 and S2). Time series of np-ERK (blue), pY-ERK (green), pTpY-ERK (red), and pT-ERK (orange) concentrations are plotted at Raf_kphos value = 1.0 × 106 [/M/ sec ]. (C) Concentrations of the phospho-isoforms of ERK are plotted as a function of Raf_kphos value at time = 10 (min).

With this processive model, the experimental observation (Fig. 2 D–G) was reproduced successfully (Fig. 3 B and C, SI Appendix: Fig. S9). Namely, the increase in pY-ERK paralleled the increase in pTpY-ERK both in the time course analysis and the input-output response analysis. These results implied that ERK is processively phosphorylated by MEK.

Experimental Validation of the Processive Model 1: pY-ERK Dynamics.

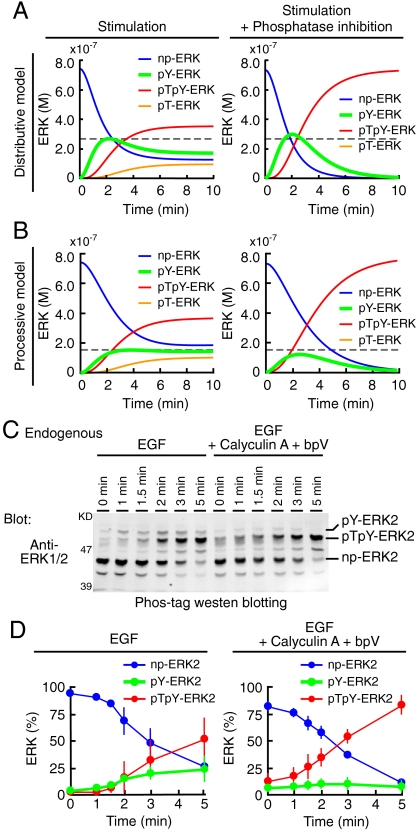
By employing computer-assisted kinetic simulation, we designed an experimental condition that distinguishes between the distributive model and the processive model. When cells are stimulated in the presence of phosphatase inhibitors, pY-ERK will be increased in the distributive model (Fig. 4A, green lines, and SI Appendix: Fig. S10A) and decreased in the processive model (Fig. 4B, green lines, and SI Appendix: Fig. S10B). This difference is because pY-ERK is generated primarily as the intermediate phosphorylation product in the distributive model, whereas in the processive model pY-ERK is produced by the dephosphorylation of pTpY-ERK. For the execution of the designed experiment, HeLa cells were stimulated with EGF in the absence or presence of inhibitors for tyrosine- and serine/threonine-phosphatase, bpV, and Calyculin A, respectively. As expected in the processive model, phosphatase inhibitors substantially reduced the accumulation of pY-ERK, arguing for the processive phosphorylation model (Fig. 4 C and D).

Fig. 4.

Fig. 4.

Open in a new tab

Validation of the processive model by pY-ERK dynamics. (A and B) Numerical simulations were performed based on the distributive model (A) and the processive model (B) in the absence (left column) or presence (right column) of the inhibition of all phosphatase reactions. Time series of np-ERK (blue), pY-ERK (green), pTpY-ERK (red), and pT-ERK (orange) concentrations are plotted at Raf_kphos value = 1.0 × 106 [/M/ sec ]. Maximal levels of pY-ERK without inhibition are indicated by gray dashed lines. (C and D) After serum starvation, HeLa cells were treated with mock or 1.0 × 10-7 M Calyculin A and 1.0 × 10-4 M bpV for 2 min, followed by 1.0 × 10-5 g/L EGF for the indicated time period. (C) Cell lysates were separated by electrophoresis in SDS-polyacrylamide gels containing Phos-tag and probed with an anti-ERK antibody. (D) Time series of np-ERK2 (blue), pY-ERK2 (green), and pTpY-ERK2 (red) concentrations without (left) or with (right) phosphatase inhibitors are plotted after EGF stimulation with SD (n = 4).

Experimental Validation of the Processive Model 2: Input-Output Response.

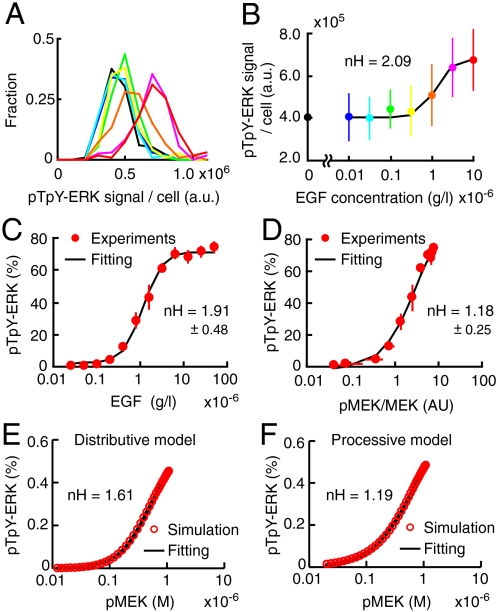
Previous studies supported the distributive phosphorylation model primarily because it explains the nonlinear switch-like response of MAP kinase upon stimulation. Therefore, to understand the contribution of the MEK-ERK signaling module to the switch-like response of ERK to EGF, we examined the input-output behavior of ERK phosphorylation in our experimental conditions. We quantified the amount of pTpY-ERK1/2 in individual cells by immuno-staining with anti-pTpY-ERK1/2 antibody. As reported previously in HeLa cells and fibroblasts stimulated with EGF and TPA, respectively (19, 20), this approach could provide quantitative relationship between the input signal and output response (Fig. 5 A and B). The Hill coefficient obtained by this method was 2.09 (Fig. 5B). Next, we confirmed this observation by Western blotting, which also demonstrated a mild nonlinear cooperativity, having 1.91 Hill coefficient (Fig. 5C). However, when we examined the correlation of the fraction of active MEK with the fraction of pTpY-ERK, we observed almost linear input-output response of ERK, having 1.18 Hill coefficient (Fig. 5D). Importantly, this Hill coefficient value determined experimentally was nearly identical to the Hill coefficient calculated at 1.19 by the processive model (Fig. 5F), but significantly smaller than the Hill coefficient calculated at 1.61 by the distributive model (Fig. 5E). Notably, the Hill coefficients might be slightly overestimated because they were calculated at the time point before reaching plateau. Nevertheless, these results strongly supported the processive model, which should exhibit linear input-output response.

Fig. 5.

Fig. 5.

Open in a new tab

Validation of the processive model by input-output response. (A and B) Serum-starved HeLa cells were stimulated with the different concentration of EGF (blue, 0.01; cyan, 0.03; green, 0.1; yellow, 0.3; orange, 1.0; pink, 3.0; and red, 10( × 10-6 [g/L])) or 2.0 × 10-5 M U0126 (black) for 5 min, and then stained with anti-pTpY-ERK1/2 antibody. (A) Fluorescent signals in each cell are represented in a histogram, demonstrating unimodal distributions (n > 90 cells). (B) The average fluorescent intensities are plotted as a function of EGF concentration with SD. Hill coefficient value, nH, was obtained by curve fitting with standard Hill equation (black line). (C) The average of fraction of pTpY-ERK are plotted as a function of EGF concentration with SD (n = 5). This data is same as shown in Fig. 2G (red line). (D) The average of fraction of pTpY-ERK was plotted as a function of ratio value of phosphorylated MEK1/2 to total MEK1/2 with SD (n = 5). (E and F) The pTpY-ERK concentration at time = 10 (min) after stimulation in distributive (E) and processive (F) model are plotted as a function of phosphorylated MEK concentration.

Numerical Validation of the Processive Model.

To examine which of the distributive and processive models is the plausible mechanism to account for the observed data (Fig. 2E and Fig. 4D), we calculated residual sum of squares (RSS) values, Akaike information criterion (AIC) values, and Hill coefficients for both models after parameter fitting (28) (SI Appendix: Fig. S11). This in silico validation was performed under three conditions of different numbers of variables. Condition 1: all phosphorylation rates were multiplied by a common constant value, which was optimized to fit the experimental data. Condition 2: the phosphorylation rates were individually fitted to the experimental data. Condition 3: in addition to the phosphorylation rates, the dephosphorylation rates were also fitted individually to the experimental data. In all conditions, experimentally determined parameters were used as the initial values for the fitting. In Conditions 1 and 2, the processive model was more plausible than the distributive model because the AIC of the former model was smaller than the AIC of the latter model. Although both distributive and processive models exhibited the lowest RSS in Condition 3, the AIC values were higher than those in the other conditions, which indicated overfitting in Condition 3. Importantly, the Hill coefficients calculated by the processive model were closer to the experimental value than the Hill coefficients calculated by the distributive model (Fig. 5F). Taken together, these analyses strongly argued that ERK is processively phosphorylated by MEK in HeLa cells.

Molecular Crowding as a Determinant for Processive Phosphorylation.

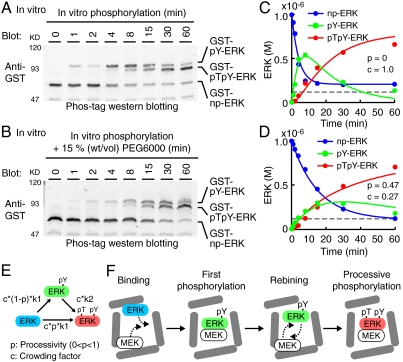
What kind of factor(s) is a critical determinant for changing the distributive nature of ERK phosphorylation into the processive one in the cells? A critical difference between the environment in vitro and that within cells is the effect of molecular crowding (29, 30). To evaluate the effect of molecular crowding, we examined whether or not ERK is phosphorylated in a processive manner in diluted cytoplasmic cell extract. Similarly to the results of in vitro ERK phosphorylation, ERK is phosphorylated in a distributive manner in the cytoplasmic extract, which was manifested by the initial accumulation of pY-ERK (SI Appendix: Fig. S12). Conversely, we mimicked the physiological molecular crowding by adding 15% (wt/vol) polyethylene glycol (PEG) to in vitro kinase reaction solution as a crowder (31) (Fig. 6 A and B). The addition of PEG reduced the production rate of pY-ERK without changing the net production rate of pTpY-ERK, indicating an increase in the “processivity” of ERK phosphorylation (Fig. 6 C and D). Lastly, we built a partial processive model by combining the distributive and processive models and fitted it to the experimental data (Fig. 6E). For this purpose, we introduced two additional parameters: Processivity, p, as the probability of pTpY-ERK production in the processive manner, and crowding factor, c, as the effect of the crowder or viscosity on the net reaction rates. By the fitting we found that the presence of 15% PEG increased in the processivity of ERK phosphorylation of 47%, and decreased the reaction rates to 27% by viscosity (Fig. 6 C and D). Of note, the amount of pY-ERK at the zenith exceeded the net amount of MEK (Fig. 6D, dashed line), indicating that pY-ERK was not accumulated due to the sequestration by MEK binding. Thus, the molecular crowding within the cells could convert the distributive phosphorylation in vitro to the processive phosphorylation as seen in the cells.

Fig. 6.

Fig. 6.

Open in a new tab

Effect of molecular crowding on processive phosphorylation. (A and B) ERK was phosphorylated by MEK in the absence (A) or presence (B) of 15% (w/v) polyethylene glycol (PEG) in vitro and were subjected to Phos-tag Western blotting analysis. (C and D) The concentrations of phospho-isoforms of ERK in (A and B) are plotted as dots against time. Concentration of constitutively active mutant of MEK (1.0 × 10-7 M) used in these experiments is indicated by gray dashed lines. The same experiments were repeated four times with reproducible results, and representative results are shown. Lines represent the concentration of phospho-isoforms of ERK obtained by fitting the processive model in (E) with the experimental data. The fitted parameters of processivity (p) and crowding factor (c) are represented. (E) Schematic representation of processive phosphorylation. p and c indicate processivity (0 < p < 1) and crowding factor, respectively. (F) Schematic view of quasi-processive model under the condition of molecular crowding.

Discussion

In this study, we have demonstrated that the amino acid residues in the activation loop of ERK, threonine, and tyrosine, are processively phosphorylated in HeLa cells, and have identified molecular crowding as one possible factor in determining whether the mode of phosphorylation will be distributive or processive. The term “processive phosphorylation” is used to describe reactions in which the substrate-enzyme complex is stable during the first and second phosphorylation reactions, which is not the case for the phosphorylation of ERK (Fig. 6D). We therefore proposed the term “quasi-processive phosphorylation” to describe two sequential phosphorylation reactions that are controlled by molecular crowding (Fig. 6F). In this model, MEK first phosphorylates ERK at the tyrosine residue and dissociates from the product, pY-ERK. Under the physiological conditions within cells, the diffusions of both MEK and pY-ERK are considerably restricted by the molecular crowding effect; therefore, MEK rebinds to and phosphorylates pY-ERK with high probability. Consequently, MEK phosphorylates ERK in a processive manner. Another MAP kinase, p38, also exhibited typical hallmarks of the processive phosphorylation (SI Appendix: Fig. S13), indicating the generality of the quasi-processive phosphorylation of MAP kinase within cells. In contrast to the phosphorylation step, this quasi-processive phosphorylation model could not be applicable to the dephosphorylation step of pTpY-ERK, because the premise of quasi-processive phosphorylation is sequential reactions operated by the identical enzyme. The dephosphorylation reactions of phospho-threonine and phospho-tyrosine were mediated probably by different classes of phosphatase at least in our experimental conditions (SI Appendix: Fig. S6).

The quasi-processive phosphorylation is critically different from the previously proposed processive phosphorylation model, in which scaffold proteins anchor MEK and ERK in order to cause sequential phosphorylation reactions by a single collision (21). The scaffold proteins are known to regulate assembly of two or more components of signaling pathways in many signaling cascades (21–25). As far as we have examined, however, none of the scaffold proteins for MEK and ERK contributed significantly to cause the processivity of ERK phosphorylation (SI Appendix: Fig. S14), consistent with the previous study on KSR (10). Therefore, at this moment, we failed to obtain any evidence that scaffold proteins cause processive phosphorylation in mammalian cells. Importantly, Takahashi and Pryciak have concluded that sole expression of Ste5 scaffold did not induce linear response of MAP kinase phosphorylation in yeast, and instead the recruitment of the scaffold to the plasma membrane resulted in linear response of MAP kinase phosphorylation (18). This model seems to fit very well with our findings, in that the effect of Ste5 could be due to molecular crowding or confinement, rather than scaffolding per se. Recently, Takahashi et al., demonstrated by particle simulation that rapid rebinding of enzyme molecules to the substrate after modification of the first site can turn a distributive model into a processive model (32). Their simulation model has predicted that molecular crowding will make enzyme-substrate rebindings more likely due to subdiffusion, strongly providing the theoretical basis of our findings.

It has been suggested that the high cooperativity of Xenopus oocytes in reaction to progesterone stimulation is at least partly accomplished by the distributive phosphorylation of ERK (6, 7). Some degree of molecular crowding probably exists in Xenopus oocytes, indicating an important point of disagreement between these previous studies and our present findings. However, it should be noted that the phosphorylation dynamics of ERK phospho-isoforms has only been investigated in vitro, and has never been investigated experimentally in Xenopus oocytes or cells. Therefore, it is possible that ERK is processively phosphorylated in Xenopus oocytes as in HeLa cells. There may exist nonlinear reactions in the signaling pathway upstream of MEK, e.g., receptor activation or Mos activation, in Xenopus oocytes. Actually, the input-output relationship between EGF concentration and pTpY-ERK demonstrated higher cooperativity; namely, the Hill coefficient was almost two (Fig. 5 A–C). In contrast, the Hill coefficient for active MEK and pTpY-ERK phosphorylation was approximately one, implying the presence of a nonlinear reaction(s) in the signaling cascade upstream of MEK. Consistent with this assumption, it has been reported that EGFR phosphorylation responded in a highly amplified and switch-like manner by coupling EGFR activation and PTP inhibition (33).

As has been described in this study, the discrepancy between the data acquired from the cells and the data predicted by the kinetic simulation model led us to the finding that ERK is processively phosphorylated within cells. Therefore, our results underscore the importance of simulation models based on experimentally determined kinetic parameters. Another important message from this study is that, in some cases, the physiological condition of molecular crowding significantly affected the mode of phosphorylation. Recent proteomic data demonstrates that proteins in a eukaryotic cell harbor multiple phosphorylation sites, each of which regulates different functions of their proteins (24). Therefore, molecular crowding, which is ubiquitous in biological systems, introduces additional complexity in their regulation. Thus, the finding that molecular crowding changes the mode of successive reactions to a processive type provides a new paradigm for a diverse set of biochemical reactions.

Materials and Methods

Plasmids, Cells, Reagents, and Antibodies.

The plasmids used here were constructed according to the standard methods. Cells, reagents, and antibodies are detailed in SI Appendix.

Purification of Recombinant Proteins, Cytoplasm Extract, and In Vitro Kinase Assay.

Details of purification of recombinant proteins, cytoplasmic extract and in vitro kinase assay are provided in SI Appendix.

Phos-Tag Polyacrylamide Gel Electrophoresis.

Phos-tag polyacrylamide gel electrophoresis was performed essentially as described previously (27). For Phos-tag Western blottings of ERK and p38, 5.0 × 10-5 and 1.5 × 10-4 M Phos-tag and 1.0 × 10-4 and 3.0 × 10-4 M MnCl2 were added to conventional SDS-polyacrylamide separation gels according to the manufacturer’s protocol, respectively. Proteins were detected by using an Odyssey Infrared Imaging System (LI-COR).

Imaging.

Live cell imaging was performed essentially as described (34).

Kinetic Modeling and Numerical Simulation.

Numerical simulation and parameter search were implemented by MATLAB software with ode23 and fminsearch function, respectively. The details are described in SI Appendix.

Immunostaining.

Details of pTpY-ERK immunostaining are provided in SI Appendix.

Data Analysis.

For the determination of kinetic parameters, curve fitting were performed by the solver function of Microsoft excel (Microsoft).

Supplementary Material

Supporting Information
supp_108_31_12675__index.html (824B, html)

Acknowledgments.

We thank M. White, B. Neel, A. Miyawaki, T. Akagi, F. Ishikawa, and J. Miyazaki for the plasmids. A. Nishiyama-Abe, R. Sakai, Y. Kasakawa, and N. Nonaka are also to be thanked for their technical assistance. We are grateful to the members of the Matsuda Laboratory for their helpful discussions. K.A. and M.M. were supported by Research Program of Innovative Cell Biology by Innovative Technology (Cell Innovation) from the Ministry of Education, Culture, Sports, and Science, Japan. K.A. was supported by the JST PRESTO program. M.Y. and K.K. were supported by the Global Center of Excellence (COE) Program “Center for Frontier Medicine” initiated by the Ministry of Education, Culture, Sports, Science, and Technology, Japan.

Footnotes

The authors declare no conflict of interest.

This article is a PNAS Direct Submission.

This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1104030108/-/DCSupplemental.

References

  • 1.Qi M, Elion EA. MAP kinase pathways. JCell Sci. 2005;118:3569–3572. doi: 10.1242/jcs.02470. [DOI] [PubMed] [Google Scholar]
  • 2.Chang L, Karin M. Mammalian MAP kinase signalling cascades. Nature. 2001;410:37–40. doi: 10.1038/35065000. [DOI] [PubMed] [Google Scholar]
  • 3.Chen Z, et al. MAP kinases. ChemRev. 2001;101:2449–2476. doi: 10.1021/cr000241p. [DOI] [PubMed] [Google Scholar]
  • 4.Nishida E, Gotoh Y. The MAP kinase cascade is essential for diverse signal transduction pathways. Trends Biochem Sci. 1993;18:128–131. doi: 10.1016/0968-0004(93)90019-j. [DOI] [PubMed] [Google Scholar]
  • 5.Songyang Z, et al. A structural basis for substrate specificities of protein Ser/Thr kinases: primary sequence preference of casein kinases I and II, NIMA, phosphorylase kinase, calmodulin-dependent kinase II, CDK5, and Erk1. Mol Cell Biol. 1996;16:6486–6493. doi: 10.1128/mcb.16.11.6486. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Ferrell JE, Jr, Machleder EM. The biochemical basis of an all-or-none cell fate switch in Xenopus oocytes. Science. 1998;280:895–898. doi: 10.1126/science.280.5365.895. [DOI] [PubMed] [Google Scholar]
  • 7.Xiong W, Ferrell JE., Jr A positive-feedback-based bistable ‘memory module’ that governs a cell fate decision. Nature. 2003;426:460–465. doi: 10.1038/nature02089. [DOI] [PubMed] [Google Scholar]
  • 8.Santos SD, Verveer PJ, Bastiaens PI. Growth factor-induced MAPK network topology shapes Erk response determining PC-12 cell fate. Nat Cell Biol. 2007;9:324–330. doi: 10.1038/ncb1543. [DOI] [PubMed] [Google Scholar]
  • 9.Daniels MA, et al. Thymic selection threshold defined by compartmentalization of Ras/MAPK signalling. Nature. 2006;444:724–729. doi: 10.1038/nature05269. [DOI] [PubMed] [Google Scholar]
  • 10.Lin J, Harding A, Giurisato E, Shaw AS. KSR1 modulates the sensitivity of mitogen-activated protein kinase pathway activation in T cells without altering fundamental system outputs. Mol Cell Biol. 2009;29:2082–2091. doi: 10.1128/MCB.01634-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Ferrell JE, Jr, Bhatt RR. Mechanistic studies of the dual phosphorylation of mitogen-activated protein kinase. J Biol Chem. 1997;272:19008–19016. doi: 10.1074/jbc.272.30.19008. [DOI] [PubMed] [Google Scholar]
  • 12.Huang CY, Ferrell JE., Jr Ultrasensitivity in the mitogen-activated protein kinase cascade. Proc Natl Acad Sci USA. 1996;93:10078–10083. doi: 10.1073/pnas.93.19.10078. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Markevich NI, Hoek JB, Kholodenko BN. Signaling switches and bistability arising from multisite phosphorylation in protein kinase cascades. J Cell Biol. 2004;164:353–359. doi: 10.1083/jcb.200308060. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Haystead TA, Dent P, Wu J, Haystead CM, Sturgill TW. Ordered phosphorylation of p42mapk by MAP kinase kinase. FEBS Lett. 1992;306:17–22. doi: 10.1016/0014-5793(92)80828-5. [DOI] [PubMed] [Google Scholar]
  • 15.Burack WR, Sturgill TW. The activating dual phosphorylation of MAPK by MEK is nonprocessive. Biochemistry (Mosc) 1997;36:5929–5933. doi: 10.1021/bi970535d. [DOI] [PubMed] [Google Scholar]
  • 16.Colman-Lerner A, et al. Regulated cell-to-cell variation in a cell-fate decision system. Nature. 2005;437:699–706. doi: 10.1038/nature03998. [DOI] [PubMed] [Google Scholar]
  • 17.Poritz MA, Malmstrom S, Kim MK, Rossmeissl PJ, Kamb A. Graded mode of transcriptional induction in yeast pheromone signalling revealed by single-cell analysis. Yeast. 2001;18:1331–1338. doi: 10.1002/yea.777. [DOI] [PubMed] [Google Scholar]
  • 18.Takahashi S, Pryciak PM. Membrane localization of scaffold proteins promotes graded signaling in the yeast MAP kinase cascade. Curr Biol. 2008;18:1184–1191. doi: 10.1016/j.cub.2008.07.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Mackeigan JP, Murphy LO, Dimitri CA, Blenis J. Graded mitogen-activated protein kinase activity precedes switch-like c-Fos induction in mammalian cells. Mol Cell Biol. 2005;25:4676–4682. doi: 10.1128/MCB.25.11.4676-4682.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Whitehurst A, Cobb MH, White MA. Stimulus-coupled spatial restriction of extracellular signal-regulated kinase 1/2 activity contributes to the specificity of signal-response pathways. Mol Cell Biol. 2004;24:10145–10150. doi: 10.1128/MCB.24.23.10145-10150.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Levchenko A, Bruck J, Sternberg PW. Scaffold proteins may biphasically affect the levels of mitogen-activated protein kinase signaling and reduce its threshold properties. Proc Natl Acad Sci USA. 2000;97:5818–5823. doi: 10.1073/pnas.97.11.5818. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Burack WR, Shaw AS. Signal transduction: hanging on a scaffold. Curr Opin Cell Biol. 2000;12:211–216. doi: 10.1016/s0955-0674(99)00078-2. [DOI] [PubMed] [Google Scholar]
  • 23.Kolch W. Coordinating ERK/MAPK signalling through scaffolds and inhibitors. Nat Rev Mol Cell Biol. 2005;6:827–837. doi: 10.1038/nrm1743. [DOI] [PubMed] [Google Scholar]
  • 24.Patwardhan P, Miller WT. Processive phosphorylation: mechanism and biological importance. Cellular Signalling. 2007;19:2218–2226. doi: 10.1016/j.cellsig.2007.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Shaw AS, Filbert EL. Scaffold proteins and immune-cell signalling. Nat Rev Immunol. 2009;9:47–56. doi: 10.1038/nri2473. [DOI] [PubMed] [Google Scholar]
  • 26.Amit I, et al. A module of negative feedback regulators defines growth factor signaling. Nat Genet. 2007;39:503–512. doi: 10.1038/ng1987. [DOI] [PubMed] [Google Scholar]
  • 27.Kinoshita E, Kinoshita-Kikuta E, Takiyama K, Koike T. Phosphate-binding tag, a new tool to visualize phosphorylated proteins. Mol Cell Proteomics. 2006;5:749–757. doi: 10.1074/mcp.T500024-MCP200. [DOI] [PubMed] [Google Scholar]
  • 28.Schilling M, et al. Theoretical and experimental analysis links isoform-specific ERK signalling to cell fate decisions. Mol Syst Biol. 2009;5:334-1–18. doi: 10.1038/msb.2009.91. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Ellis RJ. Macromolecular crowding: an important but neglected aspect of the intracellular environment. Curr Opin Struct Biol. 2001;11:114–119. doi: 10.1016/s0959-440x(00)00172-x. [DOI] [PubMed] [Google Scholar]
  • 30.Minton AP. How can biochemical reactions within cells differ from those in test tubes? J Cell Sci. 2006;119:2863–2869. doi: 10.1242/jcs.03063. [DOI] [PubMed] [Google Scholar]
  • 31.Shtilerman MD, Ding TT, Lansbury PT., Jr Molecular crowding accelerates fibrillization of alpha-synuclein: could an increase in the cytoplasmic protein concentration induce Parkinson’s disease? Biochemistry (Mosc) 2002;41:3855–3860. doi: 10.1021/bi0120906. [DOI] [PubMed] [Google Scholar]
  • 32.Takahashi K, Tanase-Nicola S, ten Wolde PR. Spatio-temporal correlations can drastically change the response of a MAPK pathway. Proc Natl Acad Sci USA. 2010;107:2473–2478. doi: 10.1073/pnas.0906885107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Reynolds AR, Tischer C, Verveer PJ, Rocks O, Bastiaens PI. EGFR activation coupled to inhibition of tyrosine phosphatases causes lateral signal propagation. Nat Cell Biol. 2003;5:447–453. doi: 10.1038/ncb981. [DOI] [PubMed] [Google Scholar]
  • 34.Fujioka A, et al. Dynamics of the Ras/ERK MAPK cascade as monitored by fluorescent probes. J Biol Chem. 2006;281:8917–8926. doi: 10.1074/jbc.M509344200. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
supp_108_31_12675__index.html (824B, html)
1104030108_Appendix.pdf (1.3MB, pdf)

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES