The role of macromolecular crowding in the evolution of lens crystallins with high molecular refractive index

Abstract

Crystallins are present in the lens at extremely high concentrations in order to provide transparency and generate a high refractive power of the lens. The crystallin families prevalent in the highest density lens tissues are γ crystallins in vertebrates and S crystallins in cephalopods. In parallel evolution, both have evolved molecular refractive index increments 5 – 10 % above those of most proteins. Although this is a small increase, it is statistically very significant and can be achieved only by very unusual amino acid compositions. In contrast, such a molecular adaptation to aid in the refractive function of the lens did not occur in crystallins that are preferentially located in lower density lens tissues, such as vertebrate α crystallin and taxon specific crystallins. In the current work, we apply a model of non-interacting hard spheres to examine the thermodynamic contributions of volume exclusion at lenticular protein concentrations. We show that the small concentration decrease afforded by the higher molecular refractive index increment of crystallins can amplify nonlinearly to produce order of magnitude differences in chemical activities, and lead to reduced osmotic pressure and the reduced propensity for protein aggregation. Quantitatively, this amplification sets in only at protein concentrations as high as those found in hard lenses or the nucleus of soft lenses, in good correspondence to the observed crystalline properties in different tissues and different species. This suggests that volume exclusion effects provide the evolutionary driving force for the unusual refractive properties and the unusual amino acid compositions of γ crystallins and S crystallins.

Introduction

The cytoplasm of lens fiber cells consist almost entirely of crystallins, which contribute more than 90% of the fiber cell dry weight [1]. They are present at high concentrations so as to generate a high tissue refractive index that allows the lens to focus the light on the retina. Concentrations of 240 mg/ml have been estimated for the cortex of the lens [2], and much higher concentrations of up to 400 – 600 mg/ml and higher [3,4] were estimated for the nucleus of the lens of different animal species. This concentration gradient, in conjunction with a gradient in the distribution of crystallin types [3], supports a spatial refractive index gradient in the lens, which reduces spherical aberration [5].

In vertebrates, the major crystallins are α−, β−, and γ−crystallins. Although α-crystallin is overall the most abundant crystallin in mammals, it is preferentially excluded from the denser nucleus of the lens, where the predominant or even exclusive species are γ crystallins [6,7,8]. γ crystallins are also the predominant crystallin species in fish, which, due to the lack of corneal refractive power in water, have lenses with significantly higher refractive index [5]. While specific γ crystallin functions remain unclear [9,10,11], they are thought to be particularly adapted to highest density packing [12,13]. This is consistent with the observation that most birds, with their soft, low-density lenses, have no γ crystalline [14]. In addition to the major crystalllins, the lenses of some species contain taxon-specific crystallins, which have arisen by co-opting proteins from non-lens tissue for expression at high concentration in the lens [15,16]. Often they are metabolic enzymes, but there is no conceivable enzymatic role justifying their high concentration in the lens, and in many cases they lost their enzymatic function after gene duplication [15,16]. An example is δ-crystallin, a taxon-specific crystallin prevalent in most birds and some reptiles derived from arginosuccinate lyase [14]. The role of the taxon-specific crystallins in the lens remains largely unclear, although some molecules have the potential to sequester UV absorbing chromophores [15], such as gecko ι-crystallin, which is derived from a chromophore binding protein CRBP and is thought to aid in UV protection in this species [17].

Besides the high refractive index, an equally important requirement for the lens is that it be transparent. Transparency is likewise conferred by a very high concentration of soluble protein, by suppressing long-range concentration fluctuations that would cause scattering of light and lens opacity [18,19,20]. Further, to avoid scattering, fiber cells lack organelles and have no nucleus, with the consequence that there is no protein turn-over [1]. This poses extraordinary stability requirements on the crystallins, both with regard to the solubility at high concentrations and with regard to the longevity of the proteins which must last for the lifetime of the individual. Protein aggregation, crystallization, and liquid-liquid phase transitions are some of the mechanisms of cataract formation [21,22], which seems almost inevitable for senescent lenses in humans and represents the leading cause of blindness worldwide [23].

Crystallin molecules have adopted several strategies to cope with this difficulty. α-crystallin is a member of the small heat-shock protein superfamily. It has chaperone activity, binding to misfolded proteins and preventing their aggregation [24,25,26,27]. β-, and γ-crystallins belong to a superfamily characterized structurally by the Greek key motif, which confers high thermodynamic and kinetic stability [28,29,30,31]. Further, they also exhibit surface charges that create inter-particle potentials (repulsive for α- and β-crystallin, and attractive for γ-crystallin) leading to reduced aggregation and increased solubility [32,33].

Pierscionek et al. have shown that bovine γ-crystallin also has an unusually high refractive index increment [34], which is thought to help increase the tissue refractive index. More recently, an increased molecular refractive index increment was speculated to be the purpose of the extremely high fraction of sulfur-containing residues in γ-crystallins of aquatic species [35]. As a reference for a more detailed comparison, we have recently determined the distribution of refractive indices of all known proteins in humans and several other species [36]. The distribution is remarkably narrow, consistent with the paradigm that all proteins have virtually the same refractive index increment [37]. This shows that the bovine γ-crystallin value of 0.203 ml/g is indeed very significantly above the average of (0.190±0.003) ml/g. In a separate communication, we describe the computational sequence analysis of evolutionarily related protein sequences from the βγ crystallin family, which identified the most extreme γ-crystallins to be γM-crystallins from lenses of aquatic vertebrates, with refractive index increments as high as 0.209 ml/g (Zhao et al., submitted). In contrast, non-lens members of the βγ crystallin family have average refractive indices. The study showed that the high refractive index increment is a result of specific evolution of lens γ-crystallins towards highly unusual amino acid compositions that are strongly enriched in high refractive index amino acids, including aromatic and sulfur-containing amino acids, and at the same time depleted of amino acids with low refractive index, including proline, alanine, serine, and leucine. (This naturally explains the observation that fish γ-crystallins may contain up to 15% methionine [38,39], and very little or no alanine.) Furthermore, we found that the same trait has developed, in an example of convergent evolution, in the S-crystallins in the eyes of cephalopods (Zhao et al., submitted), which are structurally completely unrelated proteins and belong to the family of glutathione-S-tranferases [40] (non-lens members of which, again, have only average refractive index increments). In contrast, taxon specific crystallins, which exist only as minor crystallin species or in soft lenses, were found to have only average refractive index increments, similar to those of α crystallins (Zhao et al., submitted).

This poses the question how such a small increase in the refractive index increment of the major crystallins, typically only in the order of 5 – 8 %, can confer such a consistent evolutionary advantage, and why this selection takes only place for the highest density lenses. In the current communication, we examine this question from a thermodynamic perspective.

At concentrations of 500 mg/ml, the average distance between spherical proteins is only approximately half their radius. Thus, it is obvious that volume exclusion and macromolecular crowding will be a key factor in their thermodynamic properties. It is well-established that macromolecular crowding can promote protein complex formation and polymerization (for reviews, see [41,42,43,44]). For example, the bacterial cell division protein FtsZ exhibits strongly enhanced filamentation and displays ring formation in crowded media [45,46,47]. Crowding was also observed to favor the assembly of actin [48] and tubulin [49]. Similarly, macromolecular crowding has been recognized as an important factor contributing to protein assembly diseases, and was found to determine the rate of formation of amyloid fibrils [50,51,52,53]. Perhaps the quantitatively best-studied case of crowding-induced protein polymerization is the polymerization of hemoglobin S (HbS) giving rise to sickle cell disease [54,55,56]. At a concentration of ~ 340 mg/ml, the major constituent of the cytosol of the red cell is hemoglobin, which in sickle cell disease will spontaneously form polymers when deoxygenated. In this process, the crowded environment in the red cell plays a pivotal role, and the thermodynamic observables are quantitatively well captured by non-ideal two-phase hard-sphere model [55,57,58,59].

In the present work, we use the same framework to demonstrate that a highly non-linear enhancement of crystallin aggregation as a function of crystallin concentration is to be expected at concentrations prevalent in the nucleus of high refractive index lenses, but not in the lens cortex or in soft lenses. We show that even a very small change in crystallin concentration can substantially relieve the chemical potential and osmotic pressure.

Methods

Tissue refractive index and molecular refractive increments

For calculating the effect of a molecular refractive index increment (dn/dc)_L on the lens refractive index n_L

$$n_L=n_0+{(\frac{dn}{dc})}_{L}c$$ (Eq. 1)

We will compare this with the hypothetical concentration c* required to achieve the same lens refractive index at a standard refractive index increment (dn/dc)₀, relative to which the crystallin refractive index is elevated by the fraction f :

$$n_L=n_0+{(\frac{dn}{dc})}_{L}c=n_0+{(\frac{dn}{dc})}_0(1+f)c=n_0+{(\frac{dn}{dc})}_0{c}^{*}$$ (Eq. 2)

, i.e. concentrations elevated by the factor c* = (1+f)c.

Thermodynamic model for crowded solutions

Since crystallins concentrations are very high, it is essential to capture the salient features of crowded, non-ideal solutions. For simplicity we model the protein as an effective hard sphere solely with excluded volume interactions. The chemical potential is given as

$$\mu ={\mu }_0+RT\text{ln}(a)$$ (Eq. 3)

, where a is the chemical activity (or ‘effective concentration’), and a = γc with the chemical activity coefficient γ. (The symbol γ customarily for this thermodynamic quantity of an activity coefficient in the equations is not to be confused with the name γ of the family of crystallin.) Several equations of state have been developed for hard sphere fluids. They differ slightly in their physical foundation, and were found to also differ in their predictions above packing fractions of 0.5 [60,61].

First, we consider a virial expansion for hard spheres, which leads to the power series for γ n the concentration c :

$$\text{ln}\gamma ={\displaystyle \sum _{i=1}^{\infty }{B}_{i+1}{c}^i}$$ (Eq. 4)

The coefficients B₂ to B₇ arising from the volume exclusion effects with an effective hard sphere inter-particle potential were reported as: B₂ = 8 v, B₃ = 15 v², B₄ = 24.48 v³, B₅ = 35.30 v⁴, B₆ = 47.7 v⁵, B₇ = 65.9 v⁶, where v is the molar volume of the equivalent spheres [61,62]. For the osmotic pressure Π as a function of concentration, the relationship

$$c\frac{\partial \text{ln}\gamma }{\partial c}=\frac{1}{RT}\frac{\partial \Pi }{\partial c}-1$$ (Eq. 5)

(with R denoting the gas constant and T the temperature) leads from Eq. 4 to a power series for Π(c) with coefficients

$$\Pi (c)=RT(c+4\nu c^2+10{\nu }^2{c}^3+18.36{\nu }^3{c}^4+28.24{\nu }^4{c}^5+39.5{\nu }^5{c}^6+56.4{\nu }^6{c}^7+\dots )$$ (Eq. 6)

as reported in [61,62].

As a refinement on Eq. 4 and 6 at higher concentrations, the next higher order term was estimated by Ree & Hover as additional term B₈ ~ 103 v⁷ in the power-series of ln γ, and a term 90v⁷c⁸ in the corresponding expression for the osmotic pressure Π(c) [62]. Another extension of the virial expansion has been hypothesized by Minton [61] based on the observation that B_n ≈ 0.171B₂B_n−1 for n = 6 and 7 (which we note also leads to the approximated value of B₈ to within 11%) :

$$\text{ln}\gamma (c)=B_{2}c+B_3{c}^2+B_4{c}^3+B_5{c}^4\times {(1-0.171B_{2}c)}^{-1}$$ (Eq. 7)

This expression has the virtue of converging to the correct hexagonal packing limit for spheres [61].

Alternatively, from scaled particle theory (SPT), the chemical potential of a particle in a fluid can be calculated as the work required for creating sufficient empty volume in solution to accommodate that particle [63]. This provides an alternative theoretical framework to predict the activity coefficient as a function of concentration, leading to

$$\text{ln}{\gamma }_{\mathit{\text{SPT}}}=-\text{ln}(1-\varphi )+7\frac{\varphi }{1-\varphi }+\frac{15}{2}{(\frac{\varphi }{1-\varphi })}^2+3{(\frac{\varphi }{1-\varphi })}^3$$ (Eq. 8)

where ϕ= vc is the volume fraction occupied by the hard spheres [61]. Integration according to Eq. 5 leads to the osmotic pressure

$${\Pi }_{\mathit{\text{SPT}}}(c)=\text{RT}c\frac{({\varphi }^2+\varphi +1)}{{(1-\varphi )}^3}$$ (Eq. 9)

in the approximation of SPT [63,64]. More detailed corrections to the SPT for higher have been reported and vetted against molecular dynamics simulations [64]. However, since the non-spherical shape of crystallin as well as inter-particle interactions will increasingly influence the exact chemical potential at very high densities, more detailed theoretical hard-sphere models were not attempted (see discussion). Likewise, corrections for the explicit consideration of the contributions of water molecules to the excluded volume proposed by Berg [65] were not applied.

The goal of the present work is to examine the effects of small concentration differences on the thermodynamic parameters. With regard to the chemical activity, we can express the relative increase da/a caused by a relative concentration increase dc/c as an amplification factor α

$$\alpha =\frac{da/a}{dc/c}=1+c\frac{d\text{ln}\gamma }{dc}=\frac{1}{RT}\frac{\partial \mathrm{\Pi }}{\partial c}$$ (Eq. 10)

, which we find to be identical to the concentration derivative of the osmotic pressure. In the virial expansion and SPT, it is

$${\alpha }_V=1+\sum _{i=1}^{\infty }i{B}_{i+1}{c}^i$$ (Eq. 11a)

$${\alpha }_{SPT}=\frac{{(2\varphi +1)}^2}{{(1-\varphi )}^4}$$ (Eq. 11b)

, respectively. From these expressions, we can discern that the amplification factor shows a stronger concentration-dependent increase than ln γ.

The influence of non-ideality on the thermodynamics of the process of polymerization (aggregation or crystallization) of crystallin may be described by

$$\Delta G=\Delta G^0+RT\text{ln}(a_P)-RT\text{ln}(a_S)$$ (Eq. 12)

where ΔG and ΔG⁰ are the free energy of crystallin entering from the solution phase into the polymer phase under ideal and non-ideal conditions, respectively, and µ_P = RT ln(a_P) and µ_S = RT ln(a_S) are the chemical potentials of crystallin a polymer and the solution phase, respectively [66]. In the ‘crystal approximation’ – a model applied previously to the polymerization of sickle hemoglobin in red cells – the chemical activity of the protein in the polymer phase is thought to be governed by the protein contacts and vibrations in the crystal and independent of solution concentration [55,59,66]. This leads to the concentration-dependence of the free energy change ΔG^sol for polymerization as a function of solution concentration

$$\Delta G^{sol}=-RT\text{ln}(c\gamma )$$ (Eq. 13)

which can be evaluated with the help of Eq. 4, Eq. 7, or Eq. 8, respectively.

For the evaluation of above expressions towards the relative changes with concentration of chemical activity and osmotic pressure, the occupied volume fraction ϕ = vc is required. It can be expressed through weight concentration and partial-specific volume. We assumed the proteins to be spherical, with a partial specific volume of 0.73 ml/g and be hydrated with 0.1 g/g water per protein. This reflects the fact that γ crystallins have a Greek key fold, which renders these molecules very compact, and that they are thought to have relatively little hydration. The molecular weights of γ crystallins in different species range from 11.8 kDa to 26.8 kDa, with the majority between 20 – 22 kDa. For example, for a 21.8 kDa protein, our model corresponds to a sphere with radius of 1.93 nm and volume of 30.0 nm³, which may be compared with, for example, the 21.8 kDa human γB crystallin of the structure 2JDF [67], that would fit in a rectangular box of 4.6 × 2.3 × 3.2 nm³, has a Stokes radius of 2.35 nm (calculated with the finite element program BEST [68]) and a solvent-excluded volume of 41.5 nm³. However, interaction potentials between molecules other than hard sphere repulsion can lead to effective hard-sphere models where the hard-sphere radius is modulated by the interaction [69]. Thus, the model with the parameters used is aimed at a conservative and qualitative estimate for the effects of concentration differences at high concentrations.

Results

With crystallin molecules that have a higher refractive index increment, the same lens refractive index can be achieved with a lower concentration of crystallin molecules. To find the selective advantage of high dn/dc crystallins we can therefore look at the cost associated with generating a highly concentrated protein solution, and the energetic cost of keeping the molecules soluble such that they do not form aggregates that would scatter light.

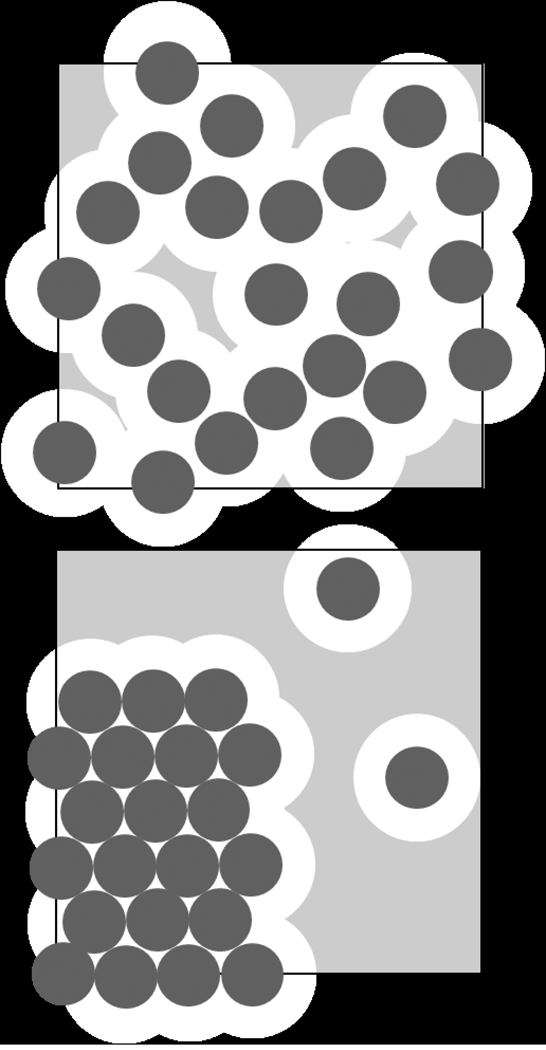
The driving force for chemical reactions is the difference between the chemical potential of the reactant and product species. The contribution of crowding to the chemical potential of a macromolecule can be imagined as the work required for creating sufficient space in solution to accommodate that macromolecule [41,63]. Clearly, this is increasingly more costly in more concentrated protein solutions where steric volume exclusion dominates the macromolecular interactions over electrostatic or other more specific attractive or repulsive interaction potentials. The cartoon in Figure 1 illustrates this point, simplifying macromolecules to be hard spheres (drawn as circles). Since no two spheres can occupy the same space at the same time, the distance between their centers cannot be closer than one diameter. From the total volume v_tot, this leaves only the light grey space as the accessible volume v_A for possible locations where one more sphere could be inserted. In a solution of hard spheres where volume exclusion is the sole macromolecular interaction, the activity coefficient is equal to the inverse of the fraction of this accessible space, γ = v_tot/v_A [41,63,70]. This determines the contribution to the chemical potential μ arising from non-ideality, which is RTln(γ). As indicated in the bottom panel, the transfer of the macromolecules into an ordered (polymeric or crystalline) state causes a reduction in the excluded volume, i.e., an increase in the accessible space and therefore a reduction of the chemical potential of the soluble macromolecules.

Figure 1.

Cartoon illustrating the effect of volume exclusion at high concentrations on the chemical activity. Let us consider a total solution volume v_tot indicated by the square, and molecules indicated as dark spheres. Additional spheres could be inserted only with the center located in the grey shaded area depicting the accessible volume v_A, in order to avoid overlap. For molecules interacting exclusively as hard spheres, scaled particle theory predicts the chemical activity coefficient γ to be the inverse of the accessible volume fraction (1/γ = v_A/v_tot) [41]. The contribution to the chemical potential arising from non-ideality is RTlog(γ). Top: If all molecules are moving freely in solution, the accessible volume is smallest, and the chemical potential highest, since the excluded volume is higher than the occupied volume. Bottom: If some of the molecules are in an aggregate phase, the accessible volume is much larger, and the remaining soluble proteins have lower chemical potential.

It is useful to regard the chemical activity a as an ‘effective concentration’ in non-ideal solutions, in a sense that the mass action laws that hold in dilute solutions between species concentrations still hold in non-ideal solutions if species’ concentrations are replaced by species’ activities [41]. In the geometric concept, since the chemical activity is a = γ×c, it is the reduction in accessible volume by a factor γ that causes a proportional increase in the ‘effective concentration’.

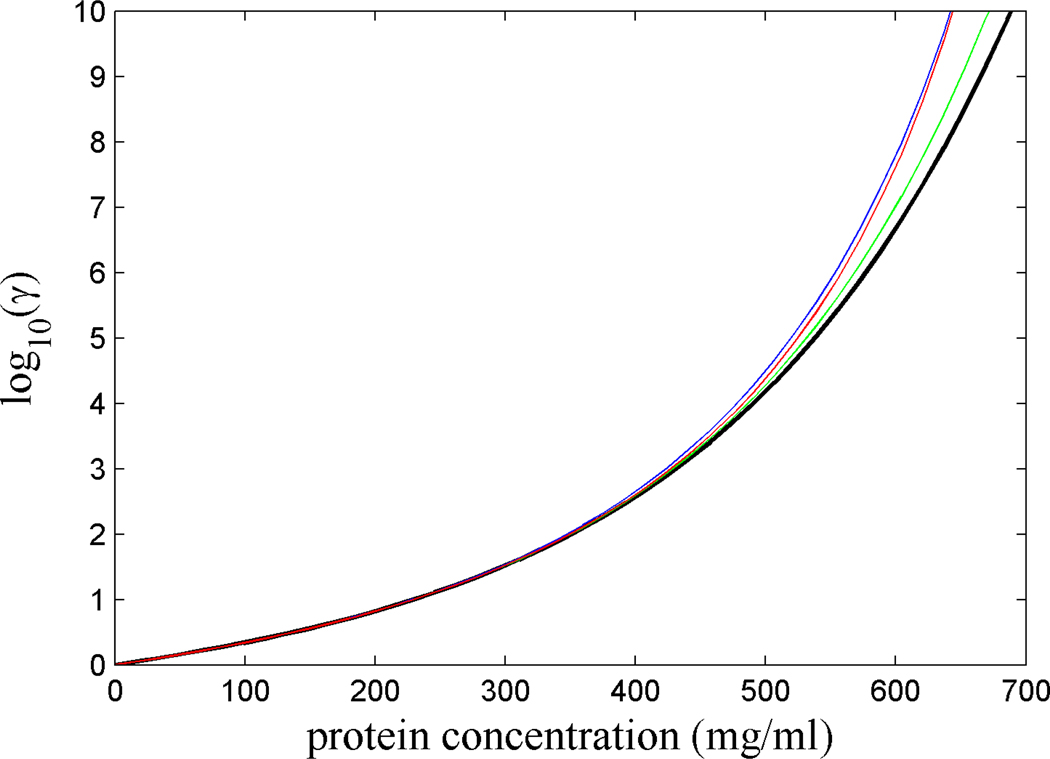
For estimating the chemical activity coefficient as a function of concentration, for simplicity, we chose a model that describes the crystallin as rigid hard spheres without ‘specific’ near-field or long-range interactions. From Figure 2, it can be discerned that the activity coefficient increases steeply with increasing concentration, comprising many decades. As previously noted by Boublik [60] and Minton [61], above 400 – 500 mg/ml the equations of state for hard sphere fluids from the various theoretical frameworks show increasing differences. The 7-term virial expansion exhibits the lowest prediction (black line), slightly increased by the 8^th term (green line). SPT (blue) yields values quite similar to the extension of the virial expansion byMinton (red), which correctly yields a singularity at the close packing limit where v_A approaches zero. We note that, for fundamental reasons, qualitatively such a divergence of γ(c) to infinity will hold true also for more realistic inter-particle potentials that do not vanish at distances greater than the sphere diameter, as well as for potentials between particles of non-spherical shape. However, the meaningful prediction of the chemical potentials near the approach of the singularity at the packing limit seems virtually impossible, and was not attempted.

Figure 2.

Chemical activity of crystallin solutions as a function of concentration predicted by virial expansion with 7 terms (black), including an approximate 8^th term (green), in the form Eq. 8 (red), and by scaled particle theory (blue). The molar volume of the equivalent spheres calculated on the basis of a molecular weight of 20 kDa, a partial-specific volume of 0.73 ml/g, and 0.1 g/g hydration.

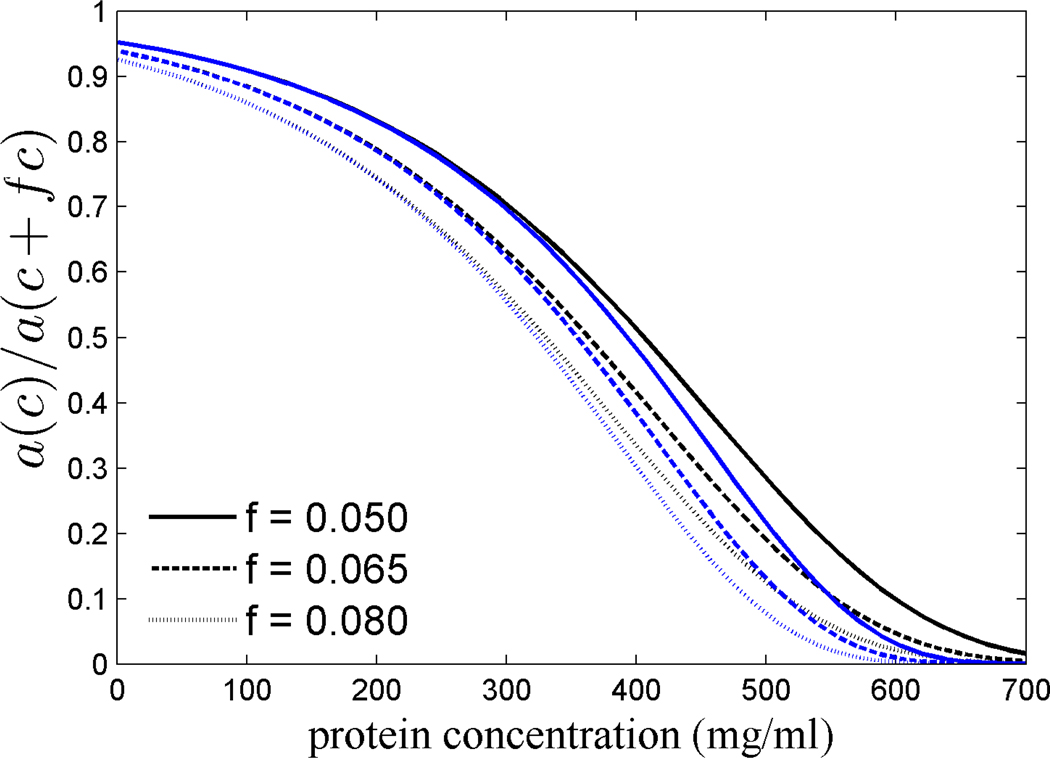
Based on the estimated activity coefficients, we can determine the relative decrease in the chemical activity a (‘effective concentration’) afforded by a small reduction of the actual concentration, expressed as ratio a(c)/a(c+fc) (Figure 3). If c is the lenticular concentration of crystallins that have a refractive index increment (dn/dc)_L that is higher by a fraction f, then c*=c+fc would be the concentration required in order to achieve the same lens refractive index with proteins of average refractive index increment (dn/dc)₀ (Eq. 2). From the sequence-based computational prediction of crystallin dn/dc values, the factor f will be approximately in the range of 0.05 to 0.08 for different γ crystallins and S crystallins. As a measure for the variance of the different predictions, we will consider in the following the 7-term virial expansion and SPT.

Figure 3.

Ratio of the chemical activity (or ‘effective concentration’) at a concentration c to that at a higher concentration c+fc that would be required for achieving the same lens refractive index with crystallins with a refractive index increment that is lower by a fraction f, where f is 5% (solid lines), 6.5 % (short dashed line), and 8% (dotted line). Data shown are calculated on the basis of 7-term virial expansion (black) and scaled particle theory (blue).

As can be discerned from Figure 3, the relative decrease in the chemical activity is not constant, but instead is highly concentration dependent in a non-linear manner. At very low concentrations, γ is close to unity and therefore a(c)/a(c+fc) is 1/(1+f). At 300 mg/ml total protein concentration, a 5% reduction in concentration reduces the chemical activity by 1.44-fold. In contrast, at 600 mg/ml total protein concentration, a 5% reduction in concentration reduces the chemical activity by at least 11-fold based on the 7-term virial expansion, or more than 30-fold based on the predictions of SPT. Higher refractive indices yield substantially stronger reductions of the ‘effective concentration’, as will higher lenticular protein concentrations.

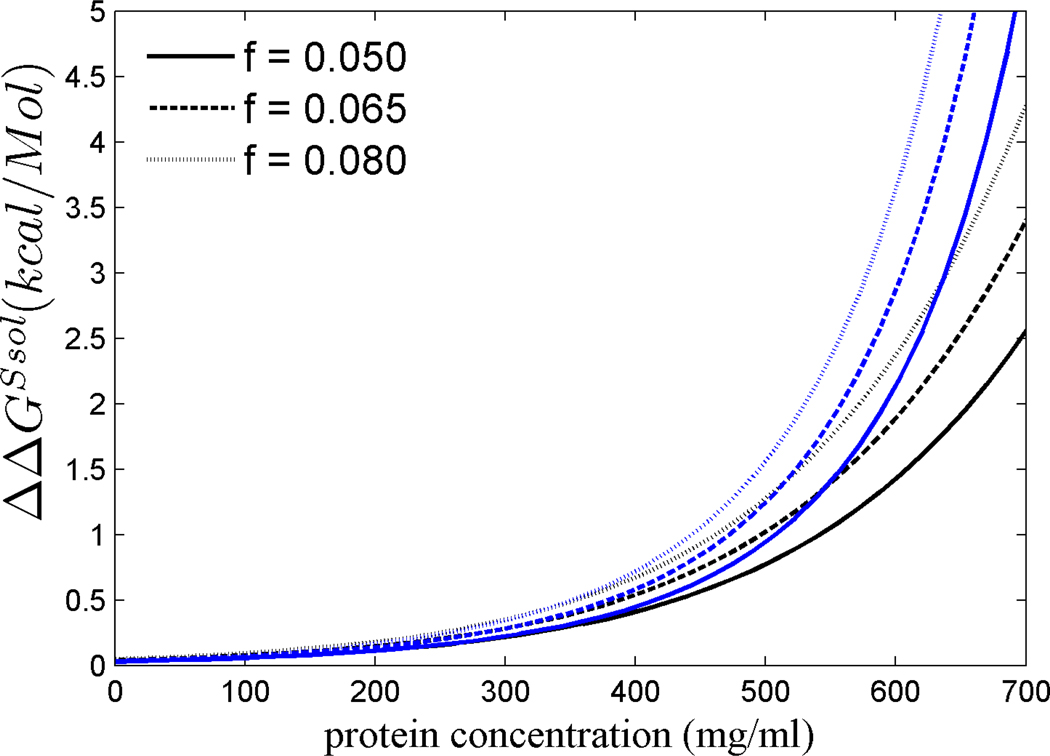
Next, we estimated the contribution of the solution chemical potential to the free energy for transfer of a crystallin molecule from solution into the polymer (or crystallin) phase, ΔG^sol(c), at a concentration c, ΔG^sol(c) (Eq. 13), relative to that at an elevated concentration, ΔG^sol(c+fc), which would be required if the dn/dc of the crystallins were only average. Figure 4 plots the difference ΔΔG^sol = ΔG^sol(c) - ΔG^sol(c+fc) for different fractions f from 5% to 8 %, again for both scaled particle theory and virial expansion. From the positive sign it can be discerned that the increased refractive index of crystallins allows for a stabilization of the soluble state, i.e. for a lower free energy gain for polymerization. At a concentration of up to 400 mg/ml, the magnitude of this stabilization is only on the order of 0.5 kcal/Mol or less. However, a much stronger stabilization is predicted in all models at higher concentrations: for example, ΔΔG^sol amounts to 2 – 3 kcal/Mol for f = 6.5% at a concentration of 600 mg/ml, steeply increasing with higher concentration.

Figure 4.

Difference between the free energy for the transfer of a molecule from solution into the polymer phase at concentration c and at concentration c+fc: ΔΔG^sol = ΔG^sol(c) - ΔG^sol(c+fc). Data shown are calculated on the basis of 7-term virial expansion (black) and scaled particle theory (blue).

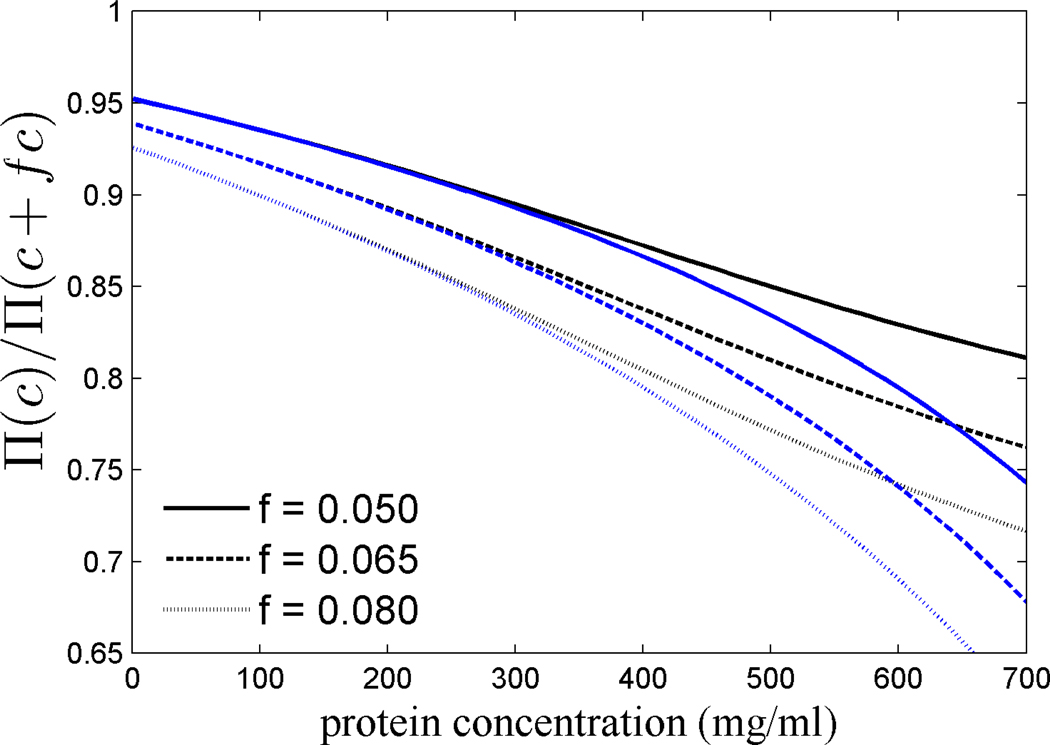
Finally, we calculated the osmostic pressure as a function of concentration from Eqs. 6 and 9, and determined the ratio Π(c)/ Π(c+fc), i.e. the savings in the osmotic pressure afforded by an increase in the molecular refractive index increment (Figure 5). While under ideal conditions, a reduction in concentration produces just a proportional reduction in osmotic pressure, under non-ideal conditions this reduction is enhanced. For example, at 600 mg/ml the 8% increase in dn/dc of some γM crystallins of fish would afford an 25–30% reduction in osmotic pressure.

Figure 5.

Relative decrease in the osmotic pressure Π(c)/Π(c+fc) afforded by a factor 1/(1+f) lower concentration, for different values of f, calculated on the basis of 7-term virial expansion (black) and, for comparison, with scaled particle theory (blue).

Discussion

In the present work, we have used a model of crystallin as non-interacting hard spheres. This is certainly a significant simplification, which neglects the detailed shape of the proteins [13,71], their interactions [32,33,72,73], the co-existence of different crystallin species [33,74] [20], all of which have been well studied and should play important roles in modulating the effects of high protein concentrations. In general, the more detailed thermodynamic description of highly concentrated protein solutions such as found in the fiber cell cytoplasm is a field of active research. Furthermore, it is unknown what the critical concentrations are in vivo for aggregation, phase transitions, crystallization or other pathways to the creation of larger particles that lead to turbidity. Given the strongly age-dependent incidence of cataract, this also appears not to be constant but decreasing with time, probably due to age-dependent protein modifications that, in turn, change their solubility and interactions. These factors make it impossible to realistically model the effect of slightly increased concentrations that would be required for solutions of equal refractive index made from lower refractive index increment molecules.

Therefore, the goal of the model in the present paper was limited to identify the consequences of molecular volume exclusion, and to show semi-quantitatively how this obligatory aspect of highly concentrated solutions can serve as a mechanism to strongly amplify the effect of small concentration differences. To this extent, the salient features of volume exclusion are captured well with the hard sphere model, which we have applied here with conservative assumptions on molecular size, neglegting different types of electrostatic interactions between different crystallin types [3,75]. That small concentration differences can amplify in crowded solutions to large biological effects was previously observed, and shown to be a mechanism for cellular volume regulation [76,77,78].

It should be noted that, despite the pragmatic nature in the reduction of details, effective hard-sphere models have often been very useful in describing protein solutions [79]. For example, the chemical activity of hemoglobin measured up to 400 mg/ml and higher concentrations is well described by a hard sphere model [66,80], and the two-phase hard sphere model has been very successful in describing the experimentally observed crowding and non-ideality effects in the polymerization of sickle hemoglobin [55,57,58,59]. In the case of crystallin, a model of non-attracting hard spheres was found to fit well the concentration-dependence of the x-ray forward scattering amplitude obtained from cytoplasmic crystalline preparations up to concentrations of 510 mg/ml [19]. The predictions of the hard sphere model are consistent with the concentration-dependence of the apparent self-association constants of bovine γ crystallin measured in NMR studies of the rotational correlation times, which were found to be approximately 10-fold higher at 350 mg/ml versus 80 mg/ml [2], in good agreement with the prediction of a 16-fold increase of the chemical activity over this range of hard spheres in Figure 2.

The hard sphere model of excluded volume allows us to distinguish qualitative differences in the effect that a small change in the molecular refractive index of crystallins might have, dependent on overall lenticular crystallin concentrations.

The concentration range of 200 – 300 mg/ml and below includes soft lenses such as that from turkey [14] and the cortex of mammalian lenses [2,81]. Although non-ideality is a significant factor that will affect chemical equilibria, there is not a very strong amplification of small changes of concentrations into changes of ‘effective concentration’, within the range of possible protein refractive index increments (Figure 3). Likewise, in this concentration range there is not a large energetic penalty for keeping the molecules soluble at slightly higher concentrations (Figure 3). This can explain why no improvement of the refractive index increment of taxon-specific crystallins, such as the avian δ-crystallin, over the average protein dn/dc has taken place. Similarly, this might be why α-crystallin, which is preferentially located in the cortex, has only an insignificantly elevated dn/dc.

A different picture emerges in the concentration range prevalent in the nucleus of lenses from human and other diurnal mammals. In human, the crystallin concentration was estimated to be ~ 440 mg/ml, based on the results from Raman microspectroscopy [82], in agreement with a peak refractive index of 1.42 [83]. In rabbit, nuclear concentrations of ~500 mg/ml were measured [82], and slightly higher values can be estimated from the observed water content in the nucleus of calf lenses [81]. In this concentration range, due to the large fraction of excluded volume, small differences in protein concentration are nonlinearly amplified into large differences in the ‘effective concentrations’. From the simple hard-sphere model, the adaptation of human γ crystallins from the average protein refractive index increment of 0.190 ml/g to the value of 0.200 ml/g would lead to a 15% lower osmotic pressure (Figure 5), an order of magnitude lower ‘effective concentrations’ (Figure 3), and an energetic contribution from excluded volume of ~ 1 kcal/Mol promoting the soluble state (Figure 4).

We may compare this energy with the experimental binding or crystallization energies reported in the literature. An association constant for indefinite isodesmic self-association of 134 M⁻¹ at 20°C, corresponding to a free energy of binding of ~ -3 kcal/Mol, was reported by Siezen & Owen [84] from measurements of bovine γ crystallin preparations at concentrations not exceeding 67 mg/ml. A detailed study of the energies of transfer of protein and water molecules from the solution into the crystal phase was carried out by Berland and colleagues [85]. From experimental measurement of the liquidus lines (solid-liquid phase boundaries) of different bovine γ crystallins, and a theoretical analysis aimed at concentrations up to volume fractions of 0.2, transfer energies of ~ 8kT were determined, corresponding to ~ 5 kcal/Mol. More recently, a theoretical study of the phase separation of binary eye lens protein mixtures found significant changes in the phase separation behavior from changes of only 0.2 kT in the interaction between the two proteins [75], suggesting there may be a delicate energetic balance keeping lens crystallins soluble. In comparison, it seems that the possible savings in the energetic driving force from solution crowding of ~ 1 kcal/Mol by high dn/dc crystallins are in the range that would have a significant impact. Thus, even though the decrease in actual concentration possible through high dn/dc molecules seems small, it may well allow crystallins to remain soluble, at least for a longer time during the life-span of the individual.

Even higher protein concentrations are prevalent in hard lenses, such as those found in nocturnal and aquatic animals [11]. For example, measurements for the highest protein concentrations in lenses of rats have resulted in estimates ranging from 600 mg/ml (measured biochemically [4]) to 875 mg/ml (based on a measured refractive index of 1.508 [86]). From the refractive index in the core of the cephalopod eye lens of 1.485, we can estimate the protein concentration to be ~760 mg/ml [87]. In rainbow trout, a refractive index of ~1.54 was measured in the lens nucleus [88], suggesting that protein concentrations in fish lenses can exceed 1,000 mg/ml [29], possibly in a gelled state [20].

The theory applied in the present work does not allow the thermodynamic description of this concentration range. However, though the various equations of state differ in their predictions (Figure 1), all agree on increasing slopes of ln(γ(c)) at higher concentrations. In fact, it can be seen from Eq. 11 that the parameter describing the sensitivity to concentration changes α grows more rapidly with concentration than ln γ. This is plausible when simply considering that increasing volume exclusion at higher concentrations has to take place, causing divergence of the chemical potential and a singularity at the close packing limit. Correspondingly, the values of ΔΔG^sol (Figure 4) and a(c)/a(c+fc) (Figure 3) extrapolate to very large and very small values, respectively. Therefore, we believe that the reduction in concentration afforded by high dn/dc molecules will have an even more dramatic effect in the hard lenses of aquatic species than at the more moderate concentrations in the nucleus of terrestrial diurnal mammals.

As a consequence, high crystallin refractive index increments should confer a significant evolutionary advantage. This corresponds well to the observation of the highest crystallin dn/dc values in fish γM crystallins. As will be described in a separate communication, γM crystallins exhibit the most unusual amino acid compositions, with low fractions of amino acids with low dn/dc (such as alanine, which in some fish γM crystallins are completely absent (Zhao et al., submitted )), and high fractions of amino acids with high dn/dc (such as methionine, which provides up to 15% of all amino acids in some fish γM crystallins [38]). Similarly unusual amino acid compositions are observed in S crystallins of squid [40] (Zhao et al., submitted ). We propose that the independent evolution of such unusual amino acid compositions in vertebrate γ crystallins and cephalopod S crystallins is a direct consequence of the universal thermodynamic consequences of volume exclusion.