High regularity of Z-DNA revealed by ultra high-resolution crystal structure at 0.55 Å

Abstract

The crystal structure of a Z-DNA hexamer duplex d(CGCGCG)₂ determined at ultra high resolution of 0.55 Å and refined without restraints, displays a high degree of regularity and rigidity in its stereochemistry, in contrast to the more flexible B-DNA duplexes. The estimations of standard uncertainties of all individually refined parameters, obtained by full-matrix least-squares optimization, are comparable with values that are typical for small-molecule crystallography. The Z-DNA model generated with ultra high-resolution diffraction data can be used to revise the stereochemical restraints applied in lower resolution refinements. Detailed comparisons of the stereochemical library values with the present accurate Z-DNA parameters, shows in general a good agreement, but also reveals significant discrepancies in the description of guanine-sugar valence angles and in the geometry of the phosphate groups.

INTRODUCTION

Among various crystal forms of DNA, oligomers of the left-handed Z-DNA have the potential to diffract X-rays to the highest resolution, a fact that was already exploited in the 1970s in the laboratory of Alexander Rich (1). Indeed, a number of atomic-resolution crystal structures of the d(CGCGCG)₂ hexamer duplex cocrystallized with various polyamines and ions are available in the Protein Data Bank (PDB) (2) and Nucleic Acid Data Bank (NDB) (3), or described in the literature without deposition of atomic models in public databases. The basic information about these structures is presented in Table 1. The most studied crystal form of the hexamer duplex, d(CGCGCG)₂, is orthorhombic, space group P2₁2₁2₁, with cell dimensions of ∼18 × 31 × 44 Å. Although almost all of those structures were refined against diffraction data reaching atomic resolution of ∼1.0 Å, only one model (1ICK) was refined with anisotropic atomic displacement parameters (ADPs) (4). Moreover, fewer than half of the PDB coordinate depositions are accompanied by the corresponding structure factors. This concerns also the ultra high-resolution (0.60 Å) structure 1I0T, published in 2001 (5), which was refined to a surprisingly high R_factor of 16.0%. In the present study, we have measured X-ray diffraction data extending to 0.55 Å resolution for a d(CGCGCG)₂ crystal, and describe its high-quality structural model (R = 7.77%). The structure has been refined in the full-matrix anisotropic mode with total absence of stereochemical restraints for DNA, essentially analogous to the practice of small-molecule crystallography. In this way, not only very accurate, unbiased values of atomic coordinates and displacement parameters are obtained, but they are also accompanied by reliable estimates of their standard uncertainties. In consequence, we are able to present a detailed analysis of very fine features of the Z-DNA stereochemistry, not available in the current literature.

Table 1.

Structures of d(CGCGCG)₂ available in the PDB and NDB (code in italics)

Data Base Code	Resolution (Å)	R (%)	i/aa	SFb	Crystal form	a (Å)	b (Å)	c (Å)	Amine	Metal ions	Reference
2DCG	0.90	14.0	i	n	A	17.87	31.55	44.58	Spermine	Mg2+	(1)
1DCG	1.00	17.5	i	n	A	18.01	31.03	44.80	–	Mg2+	(33)
ZDF013c	1.00	19.5	i	n	A	17.45	31.63	45.56	–	–	(34)
292D	1.00	16.1	i	n	A	17.94	31.23	44.55	Polyamine	Mg2+, Na+	(35)
293D	1.00	19.1	i	n	A	17.93	31.23	44.64	Spermidine	Mg2+, Na+	(36)
336D	1.00	19.0	i	n	A	17.98	31.51	44.38	Thermospermine	Mg2+	(37)
1ICK	0.95	8.6	a	y	A	17.87	31.55	44.58	Spermine	Mg2+	(4)
1DJ6	1.00	16.9	i	y	A	17.93	31.36	44.62	Polyamine	Mg2+	(38)
2ELG	1.00	23.2	i	y	A	17.85	30.99	44.02	Spermidine	Mg2+, Na+	(39)
2IE1	1.60	19.0	i	y	A	17.64	30.38	43.63	Polyamine	–	(40)
3P4J	0.55	7.77	a	y	A	17.88	31.42	43.90	Spermine	–	This work
1D48	1.00	18.5	i	n	B	18.41	30.77	43.15	Spermine	–	(14)
131D	1.00	18.0	i	n	B	18.27	30.69	42.46	Spermine	Na+	(41)
1I0T	0.60	16.0	i	n	B	18.32	30.68	42.49	Spermine	–	(5)
1V9G	1.80Nd	22.2	i	y	B	18.46	30.76	43.18	Spermine(D)e	–	(42)
1WOE	1.50Nd	17.6	i	y	B	18.46	30.76	43.18	Spermine	–	(42)

^aModel refined isotropically (i) or anisotropically (a).

^bStructure factors available (y) or not available (n) in the database.

^cData taken from Nucleic Acid Database (all other data are from PDB).

^dRefined against neutron data.

^eN-deuterated.

It should be noted that the crystal structure presented here has a nearly record-breaking resolution in the PDB, being only second to the structure of crambin (1EJG) determined at 0.54 Å (6). In the area of nucleic acids, it is currently the highest resolution model.

MATERIALS AND METHODS

Crystallization and diffraction data

A 1.5 mM water solution of the d(CGCGCG)₂ hexamer DNA was annealed at 65°C for 12 min. Crystals were grown using the hanging-drop vapor-diffusion method at room temperature by mixing 3 µl of the DNA solution and 3 µl of precipitating solution containing 10% (v/v) 2-methyl-2,4-pentanediol (MPD), 12 mM sperminium tetrachloride, 80 mM NaCl and 40 mM sodium cacodylate buffer, pH 7.0. The drops were equilibrated against 1.0 ml of 35% (v/v) MPD. Single crystals appeared within one week.

X-ray diffraction data for a single crystal measuring 0.3 × 0.4 × 0.4 mm were collected using synchrotron radiation [advanced photon source (APS), Northeastern collaborative access team (NE-CAT) beam line 24ID-C] with a wavelength of 0.5904 Å and an Area Detector Systems Corp. detector ADSC Q315. The crystal was fished out from the crystallization drop in a rayon loop and vitrified at 100 K in a stream of nitrogen gas. The diffraction data were collected in three passes with different effective exposures, corresponding to low (1.24 Å), medium (1.04 Å) and high (0.55 Å) resolution, in order to adequately measure both the strongest and weakest reflections. The low resolution data set was recorded first and consisted of 90 images with 2° oscillation at 500 mm crystal-to-detector distance. The medium resolution dataset consisted of 120 images recorded with 1.5° oscillation at 400 mm crystal-to-detector distance. The high resolution data set recorded in the third pass contained 180 images of 1° with 125 mm crystal-to-detector distance. The detector was lifted by 100 mm from its central position to capture the high resolution reflections at high angles. Indexing and integration of all images was performed in DENZO and scaling in SCALEPACK, both from the HKL2000 program package (7). Table 2 summarizes the statistics of the final data set.

Table 2.

Statistics of the diffraction data and structure refinement

Data collection
Beamline	24ID-C (NE-CAT)
Temperature (K)	100
Wavelength (Å)	0.5904
Space group	P212121
a (Å)	17.88
b (Å)	31.42
c (Å)	43.90
Resolution limit (Å)	30–0.55 (0.57–0.55)
Reflections measured	328 759 (14 043)
Reflections unique	130 650 (6382)
Multiplicity	2.5 (1.7)
Completeness native (%)	96.6 (80.6)
Completeness anomalous (%)	84.5 (53.0)
Rmerge (%)	5.7 (27.6)
Average I/σ(I)	16.7 (2.7)
Wilson B-factor (Å2)	2.5
Refinement
Resolution (Å)	30–0.55
No. of parameters	3740
wR2 (%)	20.19
Rfactor, Fo>4σ(Fo) (%)	6.77
Reflections, Fo>4σ(Fo)	112 143
Rfactor, all reflections (%)	7.77
All reflections	130 650
RfreeFo>4σ(Fo) (%)	7.47
Free reflections, Fo>4σ(Fo)	1470
Rfree, all reflections (%)	8.47
All free reflections	1724
Asymmetric unit contents
DNA nucleotides	12a
DNA atoms	240
Average B-factor of DNA atoms (Å2)	2.69
Spermine atomic sitesb	22
Average B-factor of spermine atoms (Å2)	9.80
Fully occupied water sites	22
Alternative pairs of water sites	13
Partially occupied water sites	93
Total occupancy of all water sites	78.6
Average B-factor of all water sites (Å2)	8.48
PDB code	3P4J

Values corresponding to the highest resolution range are given in parentheses.

^aBoth Z-DNA strands lack the 5′-terminal phosphate groups at Cyt1 and Cyt7.

^bSpermine atoms between C7 and N14 are split into two alternative sites with occupancies of 0.56/0.44

Refinement

The refinement started with the Z-DNA model 1ICK stripped of all water and ligand molecules. The initial isotropic and later anisotropic refinement with SHELXL (8), which minimized the function ∑w(F_o²−F_c²)², was performed with resolution gradually extended from 1.5 to 0.55 Å. Every 10 cycles of CGLS (conjugate-gradient least-squares) minimization, the model was checked visually using COOT (9). During the manual inspection sessions, one spermine molecule was modeled and water molecules selected in difference Fourier maps were added. No metal ions were detected in the structure. The water molecules were classified as 22 fully occupied sites, as 13 pairs of close sites with a combined occupancy of 1.0, and as 93 individual partially occupied sites. The total sum of the occupancies of all water molecules is 78.6. Stereochemical restraints (10) were applied only to a partially disordered fragment of the spermine molecule, whereas all non-hydrogen atoms of the Z-DNA were refined freely without any restraints. The SHELXL ISOR, SIMU and DELU restraints of the ADP parameters were applied only to the disordered non-H atoms of spermine and water molecules. Hydrogen atoms were introduced at their expected positions and refined isotropically as ‘riding’ on their parent atoms. There was no attempt to introduce the hydrogen atoms of water molecules. The ratio of the number of reflections to the number of refined parameters in the final refinement was 130 650/3740 ≈ 35. Throughout the refinement, about 1500 randomly selected reflections were used for R_free factor (11) calculations.

At the final stages of the refinement, the algorithm was changed to full-matrix least-squares (SHELXL L.S. command), which provided estimations of standard uncertainties of all individual refined parameters and of all derived geometrical parameters. The residues in the two oligonucleotide chains are labeled 5′-Cyt1·Gua2·Cyt3·Gua4·Cyt5·Gua6-3′ and 5′-Cyt7·Gua8·Cyt9·Gua10·Cyt11·Gua12-3′, and the base pairing is Cyt1-Gua12, Gua2-Cyt11, … Gua6-Cyt7.

Although the anomalous scattering effect at the short wavelength used for data collection is rather small, the collective contribution of the 10 phosphorus atoms with f''(P) = 0.065, estimated by CROSSEC (12), and the strong handedness of their substructure lead to an anomalous effect that can be detected with very accurate data. In particular, the Flack parameter refined in the SHELXL program (x = 0.17 ± 0.02) gave a weak but significant indication of the correctness of the model chirality. For this reason, the final refinement was carried out with unmerged Friedel pairs. This refinement was accepted as final and the resulting atomic parameters and structure factors have been deposited in the PDB with the ID code 3P4J.

Figures presenting the model and electron density were prepared with PyMOL (13).

RESULTS AND DISCUSSION

The final model

The molecule of Z-DNA is generally similar to other models of d(CGCGCG)₂ present in the PDB (Supplementary Table S1), although a detailed comparison reveals that there are two groups of structures in the PDB, which, despite similar dimensions of the P2₁2₁2₁ unit cell, are not isomorphous and display a somewhat different mode of crystal packing, as pointed out earlier (14), where the terms ‘pure spermine form’ and ‘mixed magnesium/spermine form’ were used. However, inspection of Table 1 shows that the occurrence of the particular crystal form is not fully correlated with the presence of spermine or metal ions. The root-mean-square (r.m.s.) deviations calculated for all 240 non-hydrogen atoms of the Z-DNA molecule between the present model and some representative structures selected from the PDB, are presented in Table 3 (and in Supplementary Table S1) and the differences between the two non-isomorphous forms are illustrated in Figure 1.

Table 3.

R.m.s.d. of bond lengths (Å) and angles (°) from the mean values of their individual types calculated for all bonds and angles within the whole structural moieties

Moiety	Range of uncertainties	No. of cases	This work	1D48	1DCG	2DCG	1I0T	1ICK
Bonds
Cytidine	0.0017–0.0035	54	0.0033	0.0077	0.0157	0.0194	0.0137	0.0120
Guanosine	0.0018–0.0034	78	0.0038	0.0096	0.0163	0.0193	0.0139	0.0119
Sugar	0.0017–0.0035	128	0.0070	0.0252	0.0380	0.0318	0.0137	0.0159
Phosphate	0.0015–0.0028	40	0.0064	0.0306	0.0469	0.0262	0.0200	0.0108
Angles
Cytidine	0.10–0.19	72	0.41	1.01	1.55	1.54	1.17	0.90
Guanosine	0.10–0.19	114	0.38	0.74	1.20	1.38	1.07	0.79
Sugar	0.09–0.18	144	1.24	2.26	2.62	2.48	1.38	1.63
Phosphate	0.06–0.16	60	2.18	2.79	4.99	2.46	2.28	2.25

The second column gives the range of uncertainties of bond lengths (or angles) estimated from the full-matrix refinement of the current structure

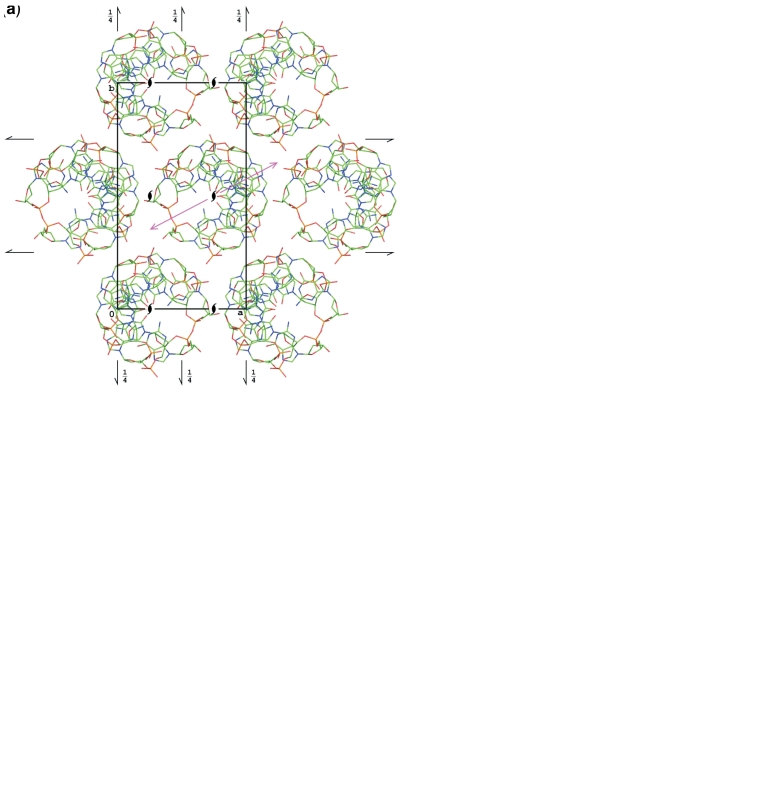
Figure 1.

Packing of the Z-DNA molecules in the current structure and in other structures marked A in Table 1 (a and b), and in the structures marked B (c and d). In (a) and (c) the structures are projected down the crystal a-axis, coincident with the helix axis. In (b) and (d), the structures are projected along the helix 2-fold axes (marked as magenta arrows in a and c), lying in the b and c plane.

In all the structures, the d(CGCGCG)₂ duplex is located at the 2₁ screw axis parallel to the z-direction, so that it forms an infinite helix throughout the entire crystal. The c cell dimension of ∼44 Å corresponds to 12 stacking repeats with an average distance of ∼3.6 Å. The a cell parameter corresponds to the diameter of the Z-DNA double helix and, indeed, the crystal contains layers of parallel helices in the a, c-plane, with the helical axes translated by the cell repeat distance of about 18 Å. The adjacent, symmetry-equivalent layers, related by the other two screw axes, are in effect translated by one-half of the cell edge in the a and b directions, forming a pattern, which in a projection along c has a pseudo hexagonal appearance. This is the consequence of the ratio of the cell parameters, b/a ≈ 31/18 ≈ 1.72 ≈ √3.

The difference between the two non-isomorphous groups of the d(CGCGCG)₂ structures lies in the orientation of the duplex around the 2₁ axis and in its translation along the c-axis. In the first group (the current model and all structures marked A in Table 1) the approximate local two-fold axis of the duplex (perpendicular to the helical axis) forms an angle of about 25° with the [100] direction, whereas in the second group (B) this angle is about 38°. In group A, the center of the duplex is at z = 0.63, whereas in group B it is at z = 0.43. As a consequence of the different shift along the c-axis, the interaction between the layer of helices at y = 0.5 and the neighboring layers at y = 0 and y = 1 is different in the two groups of structures, as illustrated in Figure 1. For all comparisons (and illustrations), the models from the PDB were transformed by crystallographic symmetry and, if necessary, by a suitable shift of the origin, to create the most similar patterns of molecules.

Several crystal structures of d(CGCGCG)₂ contain spermine [NH₂-(CH₂)₃-NH-(CH₂)₄-NH-(CH₂)₃-NH₂], but its mode of binding is different in the two crystal forms. In the current structure, as well as in other type A crystals (2DCG, 1ICK), its terminal N1 atom forms hydrogen bonds with two phosphate groups of two neighboring DNA duplexes (atoms OP1_6 and OP2_9), N5 is H-bonded to OP2_5, N10 (partially disordered in the current structure) is H-bonded to the N7_8 atom of a guanine base, and N14 is in the neighborhood of the O6_4 atom of a cytosine base. In the B-type crystals (1D48, 2I0T) the N1 atom of spermine forms two H-bonds with two neighboring Z-DNA duplexes (atoms OP1_3 and OP1_12), N5 H-ponds to OP2_11, N10 forms an H-bond with N7_8 and N14 forms an H-bond with O6_10.

In some other structures (1DJ6, 2ELG, 2IE1, 292D, 293D, 336D), the polyamine moieties are modeled with highly improbable conformations or have unconvincing electron density, and consequently those models have been omitted from further structural comparisons.

There are no detectable metal ions in the current structure, although the presence of partially occupied sites of counter-ions other than spermine, e.g. Na⁺ ions from the precipitant solution, cannot be excluded.

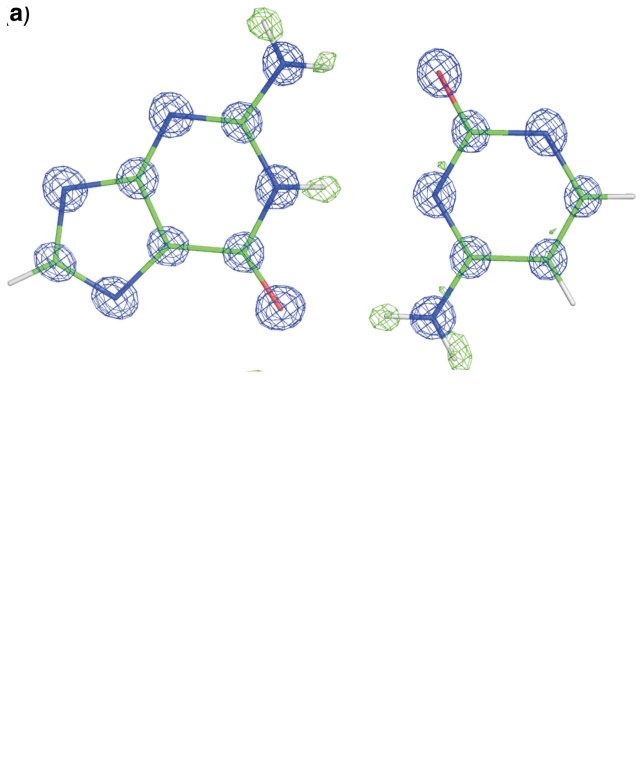
The Watson–Crick pair Cyt3-Gua10 is illustrated in Figure 2 with the (F_obs, α_calc) map and the corresponding difference electron density map, calculated before the inclusion of hydrogen atoms, at two contour levels. Due to the very high resolution of the data, not only the positions of the hydrogen atoms are revealed clearly, but also indications of densities related to bonding electrons are visible well above the map noise level. The high ratio of observations to individual atoms makes it possible to carry out a deformation density study of the DNA model. A multipole refinement of such a model is in progress.

Figure 2.

The Watson–Crick pair Cyt3-Gua10 with the corresponding F_obs map (blue, at 3σ contour level) and a difference F_o−F_c map calculated without contribution of hydrogen atoms (green) and displayed at two contour levels, (a) 3.5σ and (b) 2σ. The lower contour level reveals electron density of valence electrons at the centers of covalent bonds.

Accuracy of the 0.55 Å structure and its geometrical features

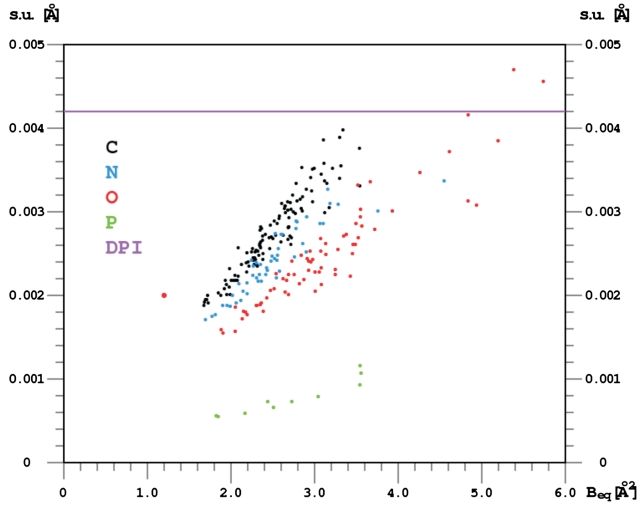
Although in general terms, the refined molecule is close to the other models of d(CGCGCG)₂ deposited in the PDB, there is a significant difference in the achieved accuracy of the refined parameters of the present structure. With data extending to the unprecedented resolution of 0.55 Å and the final R_factor below 8%, the standard uncertainties (s.u. or σ) of fully occupied atomic positions approach values typical for small organic crystal structures, as illustrated in Figure 3. It is apparent that they are inversely proportional to the atomic number of the refined atoms and correlated with their ADP's. The recommended estimator of the global accuracy of atomic positions in macromolecular crystallography is the Cruickshank's diffraction-component precision index (15), DPI = 3^1/2 × (N_i/n_obs)^1/2 × C^-1/3 × R_free × d_min (N_i, number of fully occupied atomic sites; n_obs, number of independent data; C, fractional completeness of the data to the maximum resolution of d_min). It gives 0.0042 Å as the average accuracy of the atomic positions in the present structure. This value is intermediate between the individual error estimates (calculated by the inversion of the least-squares matrix) for well defined atoms (0.002–0.004 Å, except for phosphorus atoms, where it is about 0.001 Å, Figure 3), and for partially occupied, disordered water molecules.

Figure 3.

Uncertainties (s.u.) of the Z-DNA atomic coordinates obtained from the full-matrix least-squares refinement, plotted against their B_eq ADP values. B_eq is calculated as 1/3 of the trace of the anisotropic ADP tensor, expressed in B units. The overall diffraction-component precision index [DPI, Cruickshank, (15)] is shown as a horizontal line.

A comparison of bond lengths and angles in the current structure and in some other ones reveals that the individual residues of Z-DNA tend to have much more regular geometry than suggested by the previous studies. Table 3 (and, in more detail, Supplementary Table S2) shows that the values of bond lengths and angles within analogous structural moieties (i.e. within 6 cytosine, 6 guanine, 12 sugar and 10 phosphodiester units) have very narrow spread around the mean values. In other words, the bonds and angles between the same atoms in different residues have very similar values, much less scattered than in any of the other available models of Z-DNA. In the current structure, the r.m.s.d. values for bond lengths within the cytosine and guanine units (0.0033 and 0.0038 Å, respectively) are in keeping with the accuracy of their values estimated from the full-matrix refinement (s.u. in the range 0.0017–0.0035 Å). For the deoxyribose units, the r.m.s.d. value of the bond lengths is larger (0.0064 Å) than the least-squares s.u. values (0.0017–0.0035 Å), reflecting a higher flexibility of the sugar rings and their different conformation and pucker in different residues, as shown in Table 4. The r.m.s.d. values for the P–O bond lengths (0.0064 Å) are also larger than their s.u. values (0.0015–0.0028 Å), again highlighting the fact that different residues of the Z-DNA have different backbone conformation.

Table 4.

Sugar and phosphate backbone torsion angles

Angle name	Angle definition	Cyt1	Cyt3	Cyt5	Cyt7	Cyt9	Cyt11	Gua2	Gua4	Gua6	Gua8	Gua10	Gua12
α	O3′-P-O5′-C3′		−148.1	167.9		−142.6	148.9	60.2	68.7	75.2	61.1	65.2	78.5
β	P-O5′-C5′-C4′		−121.3	167.1		132.1	−122.8	−169.3	−170.2	−179.4	−172.6	−179.5	−176.3
γ	O5′-C5′-C4′-C3′	53.3	54.5	44.1	54.2	56.3	54.9	178.2	−179.5	−176.4	176.8	179.8	−175.2
δ	C5′-C4′-C3′-O3′	142.7	148.2	142.9	148.4	146.7	141.2	90.6	92.4	147.5	92.9	98.5	152.8
ε	C4′-C 3′-O3′-P	−92.8	−98.4	−94.5	−88.0	−91.6	−96.8	−120.2	−177.9		−111.1	−117.3
ζ	C3′-O3′-P-O5	78.0	71.8	73.5	73.5	74.0	67.3	−68.9	65.6		−77.5	−69.2
χ	O4′-C1′-N1/9-C2/4	−152.3	−154.4	−143.6	−145.1	−155.3	−156.0	59.2	55.8	77.2	67.3	62.1	77.7
ν0	C4′-O4′-C1′-C2′	−25.1	−25.5	−22.7	−20.1	−21.3	−24.7	−6.5	−4.1	−19.4	−8.0	−0.1	−19.7
ν1	O4′-C1′-C2′-C3′	35.4	38.4	33.3	33.6	34.4	35.0	−13.6	−13.6	33.1	−11.4	−15.3	36.1
ν2	C1′-C2′-C3′-C4′	−31.7	−36.2	−30.8	−33.8	−33.7	−31.7	26.7	24.7	−33.4	24.8	23.5	−37.8
ν3	C2′-C3′-C4′-O4′	18.1	22.6	18.4	23.2	22.1	18.2	−31.2	−27.7	22.9	−29.9	−23.9	27.7
ν4	C3′-C4′-O4′-C1′	4.3	1.8	2.5	−2.1	−0.7	4.1	24.0	20.2	−2.4	24.0	15.3	−5.1
Saenger type		ZI	ZI	Z′	ZI	ZI	ZI	ZI	ZII	Z′	ZI	ZI	Z′
Pseudorotation parameters:
P		154.9	159.2	157.5	165.0	162.6	155.3	29.9	26.5	165.5	33.2	18.2	169.0
τm		36.0	39.7	34.2	35.9	36.3	35.7	31.5	28.2	35.3	30.2	25.2	39.5
Sugar pucker		C2′-endo	C2′-endo	C2′-endo	C2′-endo	C2′-endo	C2′-endo	C3′-endo	C3′-endo	C2′-endo	C3′-endo	C3′-endo	C2′-endo
Sundaralingam notation		(2T1)	(2E)	(2T1)	(2E)	(2E)	(2T1)	(3T4)	(3T4)	(2T3)	(43T)	(3E)	(2T3)
Deviation from ideal:
C2′-endo		−7.1	−2.8	−4.5	3.0	0.6	−6.7			3.5			7.0
C3′-endo								11.9	8.5		15.2	0.2
Comment		High pucker	Very high pucker		High pucker	High pucker	High pucker		Low pucker	High pucker		Very low pucker	Very high pucker

The standard uncertainties of these angles are <0.2°. The furanose pseudorotation amplitude (τ_m) and phase angle (P) as well as their deviations from the ideal (cyclopentane) model have been calculated by the method of Jaskolski (43). These deviations are in the range 0.5–0.8° for P and 0.3–0.5° for τ_m. All numerical values in the table are in degrees. The Z-DNA classification according to Saenger (17) is given as ‘Saenger type’. Sugar pucker in Sundaralingam notation (44) is given in parentheses.

A similar trend is visible in the behavior of bond angles, although their variation is considerably larger than the estimated uncertainties of their refined values. For example, within the Cyt and Gua bases, the s.u. values are in the range 0.10–0.19° while the r.m.s.d. values are 0.41 and 0.38°, respectively. The angular variation is larger in the sugars and even larger in the phosphate moieties. The 12 deoxyribose rings differ in their conformation, which influences the bond angles to a higher degree than the bond distances.

In the canonical alternating purine/pyrimidine Z-DNA structure, all pyrimidine nucleotides have C2′-endo puckered deoxyribose, anti glycosidic bond and gauche⁺ side-chain conformation. In contrast, the purine nucleotides are C3′-endo, syn and trans. In the present structure, all the cytidine units have the expected C2′-endo pucker. Interestingly, the C3′-endo guanosine conformation is observed only for the four inner nucleotides, whereas the 3′-terminal sugars have C2′-endo pucker. In addition, their torsion angles differ among the analogous residues (Table 4). The glycosidic angles χ, which describe the orientation of the nucleobase relative to the sugar ring, indicate the expected conformations. However, while the spread of the pyrimidine χ values is not very large (from −155.9° to −143.6°), the spread for the purines is much larger (55.6–77.7°), with the two 3′-terminal guanosines being again outliers (χ of about 80° versus ∼60° for the remaining Gua units). The side-chain torsion angle γ (O5′-C5′-C4′-C3′) has the expected gauche⁺ conformation in the Cyt units (44.0–56.2°) and the trans conformation in the Gua units (−176.3 to 176.8°). In this case, the spread within the pyrimidine nucleotides is larger but this is due to a single outlier (Cyt5, 44.0°).

It has been noted before (16,17) that the length of the glycosidic bond is very sensitive to both electronic and conformational factors. In the present nucleosides the syn glycosidic bonds in the purines are clearly longer [mean value 1.467(1) Å] than in the pyrimidines [1.449(2) Å], which are anti. Although the spread of the distances [1.441(3)–1.455(3) Å] in the Gua nucleosides, which take both the C3′-endo and C2′-endo form, is somewhat larger than in the Cyt nucleosides [1.462(3)–1.470(2) Å], which are uniformly C2′-endo, there seems to be no correlation between the glycosidic bond length and the torsion angle χ around this bond or the phase angle of pseudorotation of the deoxyribose ring.

Evaluation of stereochemical restraints

Since the structure has been refined without geometrical restraints, it is possible, and indeed quite illuminating, to compare the experimental stereochemical characteristics of the final model with the target library values (18). In general, the values of the freely refined bond lengths and angles agree well with the restraint library entries. The only significant discrepancy of about 3° is observed for the direction of the glycosidic bond at the guanosine N9 atom. As shown in Supplementary Table S2, in all Z-DNA structures the angles C4-N9-C1′ are in the range 128.9–130.0° while the library value is 126.5(13)°. Similarly, the angles C8-N9-C1′ are limited to 123.8–125.3°, whereas the library value is 127.0(13)°. This exceptional aspect of the N9 atom geometry can be linked to the unusual syn orientation of the purine nucleobase around the glycosidic bond. The stereochemical restraint library should be modified to include this aspect of Z-DNA stereochemistry, or the syn conformation of the glycosidic bond in general.

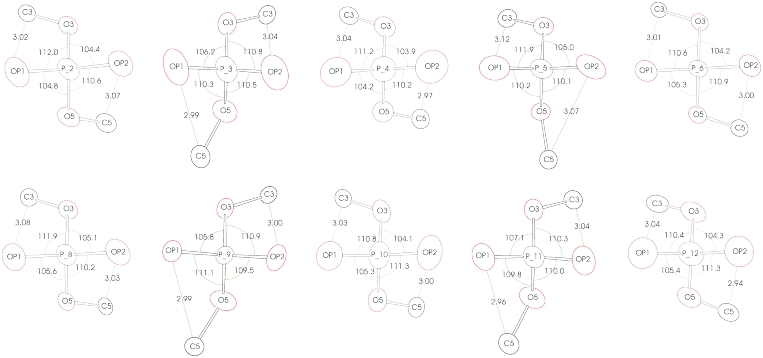
The phosphate groups display a particularly pronounced variation of the bond angles. A closer inspection reveals that their geometry is highly correlated with the conformation of the Z-DNA backbone. Figure 4 illustrates that as a result of the repulsive interaction between the OP1 and OP2 oxygen atoms and the C3′ or C5′ atoms of the neighboring sugar units, the phosphorus atoms acquire a degree of chirality and, in consequence, some theoretically equivalent O-P-O angles differ by up to 7°. The library restraints (presented in Supplementary Table S1) correspond to a more symmetric arrangement of the oxygen atoms, with the two planes, defined by O3′-P-O5′ and OP1-P-OP2, intersecting at 90°, whereas in the current structure they are up to 5° away from being strictly perpendicular.

Figure 4.

Conformation of the phosphodiester groups. The bond angles around the phosphorus atoms are given in degrees and selected distances are shown in Å. The atoms are represented by their anisotropic thermal ellipsoids drawn at the 50% probability level.

The observed variation of theoretically equivalent bond angles is evidently related to the conformational context and suggests that the restraint targets applied in refinement of structures at lower than atomic resolution should differ depending on the stereochemistry of the refined fragment. A similar action has recently been proposed for the refinement of proteins (19,20), where e.g. certain bond angles are significantly different in α-helices and in β-sheets. In nucleic acid structures, differentiation of restraints may be dictated by the significant variation of the backbone conformation, sugar pucker and other characteristics of individual nucleotides in Z-, A- and B-DNA.

Water structure and hydration of Z-DNA

All water sites were refined without positional restraints, but weak ISOR restraints were applied to their anisotropic ADPs to prevent inflated anisotropy. With respect to the occupancy parameters, those water molecules for which they refined to values close to unity (22 sites) had their occupancies fixed at 1.0; those close pairs of sites for which the sum of their refined occupancies converged close to unity (13 pairs) have their total occupancy constrained to 1.0; the remaining 93 sites had their occupancies refined freely to fractional values.

The majority of the water sites are therefore only partially occupied and often situated in close vicinity of each other at alternative, disordered locations. However, despite this relatively high level of disorder, those water molecules that are hydrogen-bonded to the Z-DNA molecule display a marked degree of regularity. Most of the polar groups (containing N or O atoms) of the Z-DNA are engaged in hydrogen bonds with solvent water molecules. The exceptions are the ring N3 atoms of the guanosine residues, which, owing to the unusual syn conformation of the purines in Z-DNA, are effectively shielded from solvent by their sugar fragments (C3′-H for the C3′-endo sugars of Gua2, Gua4, Gua8 and Gua10, or C2′-H for the C′-endo sugars of Gua6 and Gua12), located about 3.1–3.3 Å away. Also the O4′ atoms of the cytidine units are not engaged in any hydrogen bonds, as they are all pointing towards the neighboring six-membered guanine rings and are therefore shielded by those rings from access by water molecules. The guanosine sugar O4′ atoms are located on the outside of the duplex but most of them are shielded by the neighboring Z-DNA molecules in the crystal packing so that only two of them (Gua4 and Gua6) form H-bonds with water molecules.

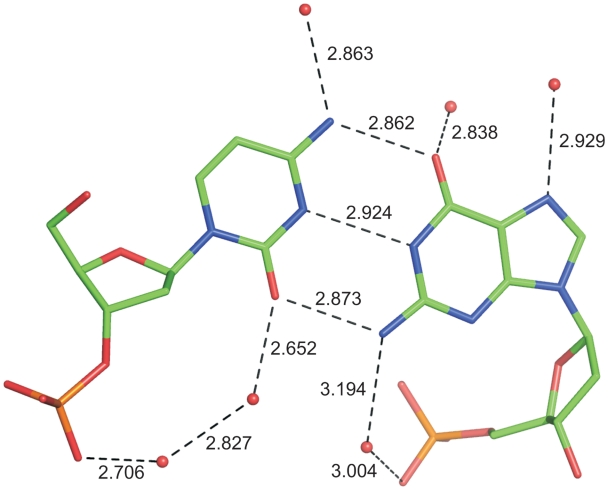
All O and N atoms involved in base pairing in the ‘outer’ hydrogen bonds, facing the major groove, are also engaged in interactions with solvent water molecules in a way illustrated in Figure 5. Typically, the O2 atoms of cytosine and O6 atoms of guanine form H-bonds with water molecules with O…O distances of approximately 2.7–2.85 Å, whereas the H-bonds involving the exoamino groups N4 (cytosine) and N2 (guanine) have donor…acceptor distances of 2.9–3.2 Å. All guanine N7 atoms are also engaged in H-bonds with water molecules. The N and O atoms of the bases located inside the helix are linked to the phosphate oxygen atoms OP2 via a chain of H-bonds involving one or two water molecules. However, many water molecules that interact with polar groups of the Z-DNA at the inner or outer side of the double helix have fractional occupancies and split positions, indicating that the hydrogen-bonding network of the solvating water may be realized in multiple ways.

Figure 5.

The Cyt9-Gua4 pair of nucleosides with all hydrogen bonds involving these residues. The hydrogen bond distances are given in Å. Other residues have a similar system of hydrogen bonds. Water molecules are represented by red spheres.

In fact, modeling of the solvent region is not fully satisfactory even at the resolution of 0.55 Å, and there are still features in the final difference Fourier map (within −0.9 to 1.0 e Å⁻³) which could be only unconvincingly modeled with a large number of water sites of low occupancies. Such a highly subjective procedure would not be warranted by any acceptable validation criteria and hence the final model of solvent molecules should be treated as a compromise. This situation is also typical for the refinement of protein crystal structures at atomic resolution (21), where modeling of partially occupied water and small-ligand sites (as well as of some solvent-exposed amino acid side chains) presents the most difficult challenge towards the end of the model-polishing stage.

Among the phosphate oxygen atoms, all OP1 and OP2 atoms are engaged in (usually multiple) H-bonds with water molecules. Again, most of these water sites are partially occupied. The OP1 atom of Gua2 forms a direct H-bond with the O3′ atom of Gua12 from the neighboring molecule (plus one H-bond with a water molecule). Among the ester O atoms connecting the phosphorus atoms with the sugars units, most of the O3′ atoms (except Gua4) are H-bonded to water molecules, but only four O5′ atoms (from residues 2, 4, 6 and 7) form such H-bonds, whereas the rest are not solvated directly.

The total sum of occupancies of all water sites in the asymmetric unit is 78.6. At such a high resolution, and relatively densely packed macromolecular crystal structure, it is tempting to address the issue of what fraction of all water molecules in the asymmetric unit have been modeled in the atomic coordinate set. For proteins, the calculation is relatively straightforward and is based on the concept of Matthews volume (22) and the specific density of dry protein material, which is roughly constant, 1.35 g cm⁻³, although differences of opinion exist even on this relatively well-established subject (23–25). For the aggregated Z-DNA structure including the spermine component in the present crystal, the Matthews volume is 1.58 ų.Da⁻¹. Assuming that DNA has specific density of ∼1.7 g cm⁻³, as observed for single crystals of nucleoside phosphates (26), the predicted volume fraction of the solvent region is 0.40, which corresponds to 83 fully occupied water sites in the asymmetric unit. This is fairly close to the number of water molecules included in the model, and one might wonder if in this situation the modeling of bulk solvent scattering (for example, using the Babinet parametrization implemented in the SWAT option of SHELXL) is physically justified. We have addressed this question by introducing the SWAT instruction in the structure refinement, and conclude that refinement with bulk-solvent correction does not lead to a significant improvement of the results (R_free change from 7.47% to 7.46%).

In the structures crystallized in the presence of Mg²⁺ (1DCG, 2DCG, 1ICK), this ion is octahedrally coordinated by the N7 atom of guanine Gua6 and five water molecules. In the present structure, this position is filled with a water molecule, whose site occupancy refined to 0.25. It is surrounded irregularly by several other water sites with fractional occupancies.

Electrostatic neutrality of the crystal structure requires the presence of additional six units of positive charge in the crystallographic asymmetric unit. Those positively charged entities are most likely ammonium or metal cations. Unfortunately, even a very careful analysis of the solvent region did not lead to the identification of these cationic species. Chemical entities such as H₂O, H₃O⁺, NH₄⁺, Mg²⁺ or Na⁺ (all of which could be present in the crystal structure) are isoelectronic and therefore difficult to differentiate by X-ray diffraction. On the other hand, the very high resolution of this X-ray diffraction experiment should already allow proper identification of these species because the corresponding atomic scattering factors are sufficiently different at high diffraction angles. Additionally, interactomic interactions and coordination geometry should also help (for instance, a tetrahedral system of H-bonds to four acceptors would favor NH₄⁺ over H₂O; an octahedral pattern of six neighbors would favor a metal cation over H₂O/NH₄⁺ and shorter distances would indicate Mg²⁺; etc.). We have analyzed the solvent region of the crystal with these stereochemical rules in mind but have been unable to unambiguously identify any metal cationic sites. It is probable that some of the (numerous) partial water sites within the significantly disordered solvent region may be filled by or shared with partially occupied metal ions. However, even with the outstanding resolution and quality of the present diffraction data, detection of such nuances is not feasible. It is also possible that some of the water sites may be occupied by ammonium or hydronium cations but we have been unable to make the distinction either. It must be, therefore, concluded that even at this level of accuracy of crystal structure determination the issue of electrostatic neutrality cannot be satisfactorily resolved.

CONCLUSIONS

The very high resolution of the X-ray diffraction data permitted a refinement of the model of d(CGCGCG)₂ Z-DNA with unprecedented accuracy, yielding average uncertainties of the atomic positions in the range of 0.002–0.004 Å, i.e. comparable to the situation achievable for small organic crystal structures. The analysis of the model stereochemistry revealed a high degree of regularity of its structure, with the bond lengths and angles of each analogous residue being practically identical within the margin of the high positional accuracy. The freely refined geometry parameters in general agree well with the commonly used restraint target values but in some cases they clearly suggest that an adjustment of the targets would be necessary.

It has been noted in protein crystal structures that increase of resolution is typically correlated with a roughly proportional increase of the number of residues, or their fragments, that can be confidently modeled in dual (or even multiple) conformations (27–29). This is due to the fact that only sufficiently high resolution of the diffraction data allows separate modeling of alternative conformations that are too close together to be distinguished by lower resolution data. However, this simplistic rule of thumb does not seem to apply to the current structure, where there is no disorder observed in the DNA part. The only significant degree of disorder is seen in the polyamine component of the crystal structure and in the solvent region. In the Z-DNA molecule, high degree of stability and excellent definition in electron density maps is observed not only for the base pairs, which are located in the core of the molecule, but also for the potentially more flexible peripheral backbone elements, including the sugar moieties.

In the present structure, the Z-DNA molecule is highly rigid and ordered, in a way contradicting the ‘flexible DNA’ model, illustrated, for example, by the atomic-resolution structures of B-DNA, where an appreciable degree of flexibility and disorder is seen (30–32). One might speculate that the stereochemistry of the DNA components is really compatible with right-handed helicity, where certain ranges of stereochemical parameters are accessible. The less common Z-DNA form, on the other hand, has more restricted ranges of parameter values, so that when it does form, it must assume these values with very little deviation. The rigidity of the Z-DNA molecule can be also linked with its compact structure, reflected in its small diameter (18 Å versus 20 Å in B-DNA), which leads to a tighter packing of the phosphates and bases against the sugars.

ACCESSION NUMBER

PDB: 3P4J.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Intramural Research Program of NIH, National Cancer Institute, Center for Cancer Research, and with Federal funds from the National Cancer Institute, National Institutes of Health (Contract HHSN2612008000001E, partial). Polish Ministry of Science and Higher Education (grant no. N N204 005136 to M.K.); National Center for Research Resources at the National Institutes of Health, NE-CAT beam line (award RR-15301); U.S. Department of Energy, Office of Basic Energy Sciences, Advanced Photon Source (Contract No. W-31-109-Eng-38). Funding for open access charge: Budget of the National Cancer Institute.

Conflict of interest statement. None declared.