S66: A Well-balanced Database of Benchmark Interaction Energies Relevant to Biomolecular Structures

Abstract

With numerous new quantum chemistry methods being developed in recent years and the promise of even more new methods to be developed in the near future, it is clearly critical that highly accurate, well-balanced, reference data for many different atomic and molecular properties be available for the parametrization and validation of these methods. One area of research that is of particular importance in many areas of chemistry, biology, and material science is the study of noncovalent interactions. Because these interactions are often strongly influenced by correlation effects, it is necessary to use computationally expensive high-order wave function methods to describe them accurately. Here, we present a large new database of interaction energies calculated using an accurate CCSD(T)/CBS scheme. Data are presented for 66 molecular complexes, at their reference equilibrium geometries and at 8 points systematically exploring their dissociation curves; in total, the database contains 594 points: 66 at equilibrium geometries, and 528 in dissociation curves. The data set is designed to cover the most common types of noncovalent interactions in biomolecules, while keeping a balanced representation of dispersion and electrostatic contributions. The data set is therefore well suited for testing and development of methods applicable to bioorganic systems. In addition to the benchmark CCSD(T) results, we also provide decompositions of the interaction energies by means of DFT-SAPT calculations. The data set was used to test several correlated QM methods, including those parametrized specifically for noncovalent interactions. Among these, the SCS-MI-CCSD method outperforms all other tested methods, with a root-mean-square error of 0.08 kcal/mol for the S66 data set.

Introduction

In the past decade, we have seen a great acceleration in the development of new quantum chemical methods, resulting in dozens of new computational techniques that potentially improve the accuracy of results and/or computational efficiency.¹⁻³ Among these methods, many contain at least one empirical parameter fitted to reference data. As the value of all scientific models must ultimately be determined by comparison with experimental observations, it would be ideal if the empirical models were based on experimental data. Unfortunately, in many cases, the computed quantity cannot be isolated in an experiment, and direct comparison is thus not possible.(4) In such cases, it is necessary to establish a set of very accurate, well-characterized computational data that can be used to parametrize and validate empirical models. These benchmark data also serve as a valuable tool for the assessment of the accuracy of nonempirical, but more approximate, methods.

One area of intensive development of computational methods in the past decade is in the proper treatment of noncovalent interactions. As these types of interactions occur throughout nature, designing accurate, computationally efficient, quantum chemical techniques that give accurate interaction energies and geometries for intermolecular interactions is critical in the treatment of a vast number of systems relevant in areas of chemistry, biodisciplines, and material science.

As it has become increasingly clear in the past several years that there are many possibilities for developing new computational methods that give improved accuracy at lower computational costs, it has also become clear that there should exist standard databases of high-quality data against which new methods can be parametrized and validated. Many such databases have recently been developed for several different molecular properties, including heats of formation, ionization potentials, electron affinities, and intermolecular interaction energies. The existence of reliable data for the latter of these properties has historically been very limited because of the large computational expense associated with the calculation of accurate interaction energies for all but the smallest molecular complexes. Only recently has it become possible to compute interaction energies for medium-sized complexes (up to approximately 40 atoms) with accuracy that is sufficient for benchmark data. There are two main reasons that it has now become possible to get these types of data. The first of these is the development of new computer hardware (including computer parallelization) that allows for much more efficient computations on molecules and molecular clusters. The second reason is the development of a hybrid estimated CCSD(T)/CBS method, which requires only computation of the extrapolated MP2/CBS result as well as the CCSD(T) interaction energy with a small/medium basis set.⁵⁻⁸ This method is the most computationally inexpensive technique that has been shown to give accurate interaction energies for many different types of molecular complexes.

Our main goal in this work is to create a well-balanced database of benchmark interaction energies for noncovalent interactions relevant to biological chemistry. Noncovalent interactions are extremely important in biomolecules, as they play large roles in determining their structure and dynamics, and are also responsible for recognition processes in biological systems. Thus, the development of new computational tools that accurately describe noncovalent interactions within biomolecules in an efficient way is crucial if significant advances are to be made in computational biophysical chemistry. The development of such methods, which generally contain several empirical parameters, critically depends on the availability of high-quality reference data.

There are several interaction energy databases that have been developed in the past 5–10 years, each with distinct strengths and weaknesses.⁹⁻¹⁶ The most important of these databases are the ones that use the estimated CCSD(T)/CBS method, or other similar (CCSD(T)-based) methods for the reference values. Below we will describe some of the most notable of these data sets.

The S22 reference set,(9) which was developed in this laboratory in 2006, has become the most popular interaction energy database and has been used extensively in the parametrization and validation of many different computational techniques (more in discussion below). At the time of its creation, this database represented the state-of-the-art in terms of the level of accuracy that could be attained for relatively large complexes (the largest complex contains 30 atoms). The interaction energies in this test set were computed using the estimated CCSD(T)/CBS procedure, which had recently been developed.

Despite the fact that S22 is extremely useful and has served as a model in the development of newer databases, there are some problems associated with this data set. Although the interaction energies published in the original S22 paper were very accurate relative to the standard methods of the time, it has been shown that, using more modern computers, it is possible to improve the accuracies of these values by using larger basis sets. Thus, S22 interaction energies were recalculated by Sherrill and co-workers(17) and by Szalewicz and co-workers(18) using larger basis sets consistently for all of the complexes. Another potential problem with the S22 set is that it is heavily weighted toward nucleic acid-like structures, containing many base pair-like (cyclic) hydrogen bonds and many examples of stacked aromatic (especially heterocyclic aromatic) species. There are several interaction motifs that are strongly under-represented, such as single hydrogen bonds and aromatic–aliphatic dispersion interactions, or practically missing, such as aliphatic–aliphatic dispersion interactions.

Several years after the development of S22, dissociation curves of the 22 complexes were calculated by Merz and co-workers(19) and in this laboratory.(10) In our approach, the resulting data set (named S22 × 5) contains five examples of each of the S22 complexes, with relative displacements of 0.9, 1.0 (ie the equilibrium geometry), 1.2, 1.5, and 2.0. In this study, DFT-SAPT analyses were employed, principally to determine the relative contributions of electrostatic and dispersion terms to the total interaction energy of each complex.

Recently, Grimme and co-workers published the GMTKN30 (General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions) data set, which might actually be classified as a superdatabase containing 30 distinct data sets collected from the literature.^11,12 As indicated by the title, the GMTKN30 set contains data sets for several different molecular properties, including barrier heights, reaction energies, and properties for noncovalent interactions. Among the 30 data sets, there are 10 that deal explicitly with noncovalent interactions, with five interaction energy databases (containing a total of 89 complexes) and five databases of relative energies for molecules containing intramolecular noncovalent interactions (58 molecules). It should be noted that S22 is one of the five interaction energy data sets contained within the GMTKN30 database.

Zhao and Truhlar have also developed a superdatabase of atomic and molecular properties that is divided into six categories: thermochemistry, barrier heights, electronic spectroscopy, transition metal reaction energies, structural data, and noncovalent interactions.(3) The noncovalent interaction category (NCIE53) contains eight separate subsets with a total of 53 complexes.²⁰⁻²² As in the case of the GMTKN30 database, the S22 set is contained within the NCIE53 set. The additional subsets contain hydrogen bonds, charge-transfer complexes, dipole interactions, weak (dispersion dominated) interactions, and π–π stacking complexes. The NCIE53 database can be said to be better balanced than the S22 set, mainly because of its inclusion of single hydrogen-bonding complexes, dipole interactions, and charge transfer complexes. In terms of dispersion-dominated interactions, this data set, like the S22, heavily favors aromatic complexes. This is true because the weak interactions subset contains mainly noble gas dimers, which have extremely low interaction energies (often less than 0.1 kcal/mol); thus, the S22 dispersion complexes dominate this category.

In an ambitious project, Friesner and co-workers constructed an extremely large database of interaction energies containing 2027 complexes.(15) This set was constructed by collecting almost all of the interaction energy data that had been produced at (at least) the estimated CCSD(T)/CBS level at the time (December 2010). Also included within this test set are several potential energy curves for various complexes. This collection is, of course, very valuable, as it represents the largest single repository of interaction energy data. There are, however, several reasons that this database is not well suited to certain applications. Because of the data set’s enormous size, it is not practical to routinely use it for the parametrization of new methods; this is especially true when the method is computationally demanding. Another issue is that the database is not very well balanced in terms of inclusion of different interaction motifs. For example, among the 2027 complexes contained in the set, 1892 of them include at least one aromatic molecule (93.3%, 59.8% contain benzene), while there are only 66 examples of aliphatic–aliphatic interactions (3.3%). Finally, the data collected from various sources were calculated using different setups; this may have a non-negligible impact on the quality of the data found in the set. Most importantly, deficiencies in the size of the basis set might lead to inconsistencies of the order of magnitude of the accuracy of the methods parametrized on these data.

Here, we present a database of accurate interaction energies for 66 molecular complexes, which we refer to as the S66 database, computed at the estimated CCSD(T)/CBS level of theory. The complexes contained within the database represent a wide distribution of interaction motifs, including electrostatic dominated (hydrogen bonding), dispersion dominated, as well as mixed (electrostatic/dispersion) interactions. Several variations of each interaction type are also taken into account; for example, both single and double (cyclic) hydrogen bonds are included. Among the dispersion dominated interactions, examples of aromatic–aromatic (stacking), aromatic–aliphatic, and aliphatic–aliphatic interactions are incorporated into the set. We include molecules containing only carbon, oxygen, nitrogen, and hydrogen, as these are the most commonly encountered elements in biochemistry. One valuable property of this database is that it is easily expandable and the addition of complexes containing additional elements should be straightforward.

We include not only accurate interaction energies at the potential energy minima, but also a set of 8 points along the dissociation curve, referred to as the S66 × 8 data set. The accurate description of the entire potential energy surface is of great importance for any method that is applied to calculations on nonequilibrium geometries, or that is used for geometry minimizations, vibration analyses, or molecular dynamics simulations. The former is especially important in the case of large systems where a given moiety may interact with a great number of other chemical groups, with the number of interactions quickly increasing as a function of distance.

Description of the S66 Data Set

S66 Data Set Construction

Our goal is to design a new, larger, data set that covers noncovalent interactions in bioorganic molecules in a balanced way. The data set consists of 66 complexes formed by combining 14 monomers in various configurations. The monomers were chosen so that they represent the motifs and functional groups most commonly found in biomolecules (see Table 1). The smaller molecules considered are generally carriers of the functional group of interest (i.e., methanol, methylamine, etc.), while the larger ones are actual biomolecular building blocks (uracil, N-methylacetamide as a peptide bond model). A more detailed list of the interactions obtained by combining these is given below; the complexes are depicted in Figure S1 in the Supporting Information. The size of the data set was chosen so that various types of interactions are well represented, yet it is small enough to make more demanding calculations on it practical. Only complexes with interactions stronger than approximately 1.5 kcal/mol were included in the set to minimize the number of systems that contribute negligibly to the statistical analysis of the errors (when an absolute error measure is used). Also, duplicate entries for the same interaction (i.e., hydrogen-bond donor/acceptor group combination) were removed from the set, usually keeping the smaller complex.

Table 1. Monomers Used To Construct the Complexes in the S66 Data Set.

molecule	model for
acetic acid	cyclic hydrogen bonds with OH donor, electrostatic interactions
acetamide	cyclic hydrogen bonds with NH donor, electrostatic interactions
benzene	π–π and X−π interactions – aromatic
cyclopentane	aliphatic dispersion – cyclic hydrocarbons
ethene	π–π and X−π interactions – nonaromatic
ethyne	π–π and X−π interactions of triple bond
neopentane	aliphatic dispersion – branched hydrocarbons
n-pentane	aliphatic dispersion – linear hydrocarbons
methylamine	hydrogen bonding – NH group
methanol	hydrogen bonding – OH group
N-methylacetamide	peptide bond model, carbonyl hydrogen bonds
pyridine	π–π and X−π interactions in heterocycles
uracil	π–π and X−π interactions, base pairing
water	hydrogen bonds and other interactions with water

In this work, we do not consider charged species, for which interaction energies calculated in small gas-phase models are not directly applicable to real system in the condensed phase. Also, such interactions are an order of magnitude stronger than the ones in neutral complexes, which would distort the even distribution of interaction energies desired in the data set. Moreover, most computational methods can describe ionic interactions well. This topic may be addressed by a separate data set.

One of the main goals of this work is to produce a interaction energy data set that is very well balanced. Toward that end, it is our goal to include roughly equal amounts of electrostatic-rich, dispersion-rich, and mixed (electrostatic/dispersion) interactions in the set. The S66 set is divided into three categories: hydrogen bonding (23 complexes), dispersion-dominated (23), and “other” (20). This classification is somewhat arbitrary but is consistent with previous works in the field. In addition, we provide interaction energy decompositions from DFT-SAPT calculations that allow quantifying the ratio between electrostatics and dispersion when more accurate characterization of an interaction is desired. Each interaction is assigned a category, SAPT-electrostatic (23 complexes), SAPT-dispersion (27), or SAPT-mixed (16), based on the relative contributions of electrostatic and dispersion forces. The heuristic categorization and the actual calculations are in good agreement.

In the first group, there are 23 hydrogen-bonded complexes. The single hydrogen bonds cover all possible combinations of donors and acceptors in the water molecule, hydroxyl group, amine group, and carbonyl group, plus some other hydrogen bonds possible within our set of monomers. Our selection of complexes therefore allows detailed examination of how a given method performs for different types of hydrogen bonds. Five cyclic hydrogen bonds, represented by both small models (acetic acid and acetamide) and the uracil dimer, are included to cover hydrogen bonding in nucleic acid base pairs. This category contains only strong X–H···Y (X = O,N; Y = O,N) hydrogen bonds; there are several electrostatic interactions that can also be classified as hydrogen bonds, such as in ethyne···water, included in the “others” category.

The group of dispersion-dominated complexes (23 systems) is built from two types of monomers with different properties: planar, often aromatic molecules and aliphatic hydrocarbons, which results in three possible interaction classes: π–π stacking (10 systems), aliphatic–aliphatic (5 systems), and π–aliphatic (8 systems) interactions. These interactions are often described differently by approximate computational methods; it is therefore very important to include all of them in the data set. The aliphatic hydrocarbons are represented by three different isomers of pentane to cover linear, branched, and cyclic hydrocarbon chains.

The last group, named “others”, contains 20 complexes that do not fit to the two categories above. Generally, an interaction in this category contains a combination of dispersion and electrostatics. This group includes X–H···π (X = C,O,N) interactions, T-shaped aromatic ring complexes, nonspecific interactions of polar molecules, and others.

Data Set Properties

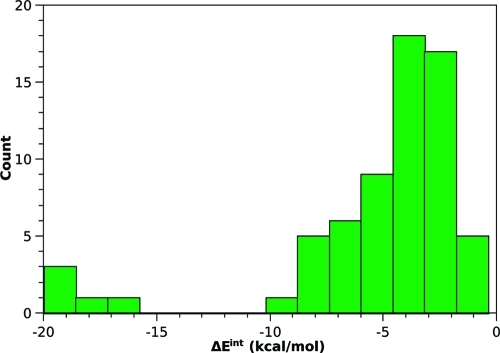
In a well-designed data set, the interaction energy should be equally distributed among all of the systems. The histogram of interaction energies in the S66 data set is shown in Figure 1. The majority of complexes have interaction energies that are around −4 kcal/mol, approximately following a normal distribution. The only outlying points are the double hydrogen bonds with interaction energies between −15 and −20 kcal/mol; these cannot be eliminated because we want to include this type of interaction in the set.

Figure 1.

Distribution of interaction energies in the 66 complexes of the S66 data set.

All of the groups of complexes should ideally have equal interaction energy sums if the data set is used to parametrize or test methods that should describe all types of interaction equally. This is hard to achieve in a set of this size when we also would like to include all of the most important interactions. In S66, the sum of interaction energies in hydrogen-bonded complexes (−205 kcal/mol) is more than twice as large as that in dispersion-dominated (−80 kcal/mol) or “other” (−70 kcal/mol) complexes. Although the hydrogen bonds dominate in such a summation, there are other arguments to consider: In the group “other”, dispersion still makes a very important contribution, and it cannot be neglected even in the H-bonded complexes. Overall, the DFT-SAPT decomposition shows that the dispersion to electrostatics ratio for the entire set is 0.86:1, which is not far from being an even representation of both interaction types. Therefore, we consider the S66 to be well balanced for general use. In cases where more control over the separate components is needed, the desired weighting can be applied.

S66 × 8 Data Set

In addition to equilibrium geometries, we also provide data for eight points along the dissociation curve of each complex. The resulting set, named S66 × 8, contains 528 points. The displaced complexes are created by scaling the intermolecular distance in the optimized structure; details are given in the Methods. Using eight points for each complex enables an accurate reconstruction of the dissociation curve by interpolation. The sampling of the region around equilibrium was improved to allow accurate determination of the minimum of the dissociation curve. This information is very important for parametrization of new methods where fitting to the extended set should lead to better reproduction of the geometries of noncovalent complexes. The possibility to interpolate the optimal distance accurately allows for assessment of the performance of a method based on comparison of equilibrium intermolecular distances with benchmark data, the minimum at the CCSD(T)/CBS level obtained from the S66 × 8 set. The interaction energies in this set are all calculated at the CCSD(T)/CBS level.

The S66 and S66 × 8 data sets do not overlap exactly, but the S66 geometries are always close to one of the S66 × 8 points. Therefore, they should be used separately, S66 × 8 to explore the entire dissociation curve and S66 when a more accurate description of the minima is needed.

Comparison to the S22 Data Set

In the past 6 years, the S22 database(9) developed in our laboratory has been widely adopted as a standard data set used to test and develop methods focused on noncovalent interactions. Other databases of benchmark data covering interaction energies often include the S22 set, as described above. Therefore, a detailed comparison of the S22 and S66 data sets clearly highlights all of the issues S66 attempts to correct, and this comparison also partially applies to other data sets based on S22.

• (1) The S66 set contains 3 times more complexes than S22. This becomes important when one focuses on some particular type of interaction, for example, hydrogen bonds. In such a case, the S22 set does not contain enough complexes of a given type for reliable statistical processing of the data.
• (2) The S22 set is focused mainly on interactions of nucleic acid bases and does not include other types of interactions with comparable weights. Regarding hydrogen bonds, most of the complexes, and an even larger fraction of the total H-bonding energy, feature double hydrogen bonds that are stronger than the single ones. This has been improved by extending the set by four more complexes, forming the S26 set.(23) In dispersion-dominated complexes, the S22 set contains only stacked aromatic molecules, with the only exception being the methane dimer, for which the magnitude of the interaction energy is very small, making its contribution to the entire set negligible. This is, in our opinion, the most important drawback of the S22 set, because many methods parametrized on S22, or performing well on it, fail to describe dispersion interactions between aliphatic hydrocarbon groups (see the discussion of the results below). This has been noted previously but has not been solved systematically.(24)
• (3) In contrast to S22, the same basis sets are used for benchmark calculations on all of the complexes in the S66 data set, regardless of the size of the system. Although more accurate calculations are possible for the smaller complexes, our approach eliminates possible method-dependent errors.
• (4) The same applies to the geometries; all complexes in the S66 data set were optimized using the same protocol. With the intermolecular distance interpolated from CCSD(T)/CBS calculations, the geometries of the larger complexes should be more accurate than the ones used previously.
• (5) The DFT-SAPT interaction energy decomposition provided for the S66 data set allows unbiased categorization of the nature of the interactions and more detailed analysis of the results, that is, correlating the errors in a tested method with a numerical descriptor of the nature of the interaction. This decomposition is available for the S22 set, but it has been published only very recently.(25)
• (6) The S66 × 8 data set provides a better description of the dissociation curve than our extension of the S22 data set, the S22 × 5 set.(10) Better sampling around the minimum allows accurate interpolation of the potential energy surface.

Planned Extensions

Despite the size of the data set, we do not consider it complete. Now, it covers the most common interactions in biomolecules containing only H, C, N, and O elements. We are working on extension of the data set to other elements and functional groups often present in bioorganic systems. The same methodology is being applied so that the new data will be perfectly compatible with the S66 set. These extensions are another important reason for our choice of a reference method that can routinely be applied to a large number of systems. Another extension we are working on is a better coverage of the potential energy surface of the S66 complexes. In addition to the dissociation curves presented in the S66 data set, we will also sample other intermolecular degrees of freedom.

Methods

Interaction Energy Calculations

Interaction energies for all of the complexes considered here were computed using fixed monomer geometries, meaning that deformation energies of monomers are not included. The structures of the monomers were taken directly from the dimer optimizations (described below), and no further geometry optimizations were performed on them. The counterpoise correction was employed in all interaction energy calculations to minimize the effects of the basis set superposition error (BSSE).

Basis Sets

Dunning’s correlation-consistent series of basis sets(26) with diffuse functions(27) are used throughout this study. The use of diffuse functions is crucial for the accurate description of noncovalent interactions. In the following text, we use an abbreviated form aXZ (X = D,T,Q) instead of the full names (aug-cc-pVXZ). The cc-pVTZ basis set (abbreviated TZ) is used in specific cases discussed below.

CCSD(T)/CBS

To calculate interaction energies in the S66 and S66 × 8 data sets (66 and 528 entries, respectively), we had to choose a method that balances accuracy and available computational resources. We use the method of estimating the CCSD(T)/CBS limit described in refs (5−8). The Hartree–Fock, MP2, and ΔCCSD(T) = CCSD(T) – MP2 terms are calculated separately in suitable basis sets, and the total energy is composed as follows:

The HF energy converges with the basis set faster than the correlation energy, and one calculation using a large basis set is adequate.(28) Here, we use the aQZ basis set. The MP2 correlation energy is extrapolated to the CBS limit using Helgaker’s formula(29) from the aTZ and aQZ basis sets. We have tested other extrapolation schemes,^30,31 but none produced smaller errors when interaction energies were compared to accurate CBS limit estimates in a set of small complexes. Therefore, we conservatively choose the Helgaker scheme, which is robust and free of empirical parameters. The most important part of the CCSD(T)/CBS scheme is the choice of basis set for the CCSD(T) calculation, for which we are much more limited by the steep scaling of the calculation with system size. In contrast to some other works that use customized basis sets, we wanted to use a standard basis so that our protocol can be easily reproduced. In the series of correlation-consistent basis sets, the largest basis sets suitable for these calculations are TZ and aDZ; the latter has a lower maximum quantum number, but includes diffuse functions. We tested both basis sets against more accurate calculations on a set of small complexes, and aDZ performed noticeably better. It has been previously noted that aDZ is the smallest basis set that can be used for the ΔCCSD(T) correction that gives errors of less than 0.1 kcal/mol.^32,33 For these reasons, we have chosen to use this basis throughout this work.

Geometries

We have followed a multistep protocol to prepare high-quality geometries for complexes of this size.

• (1) Complex preparation: For complexes for which the minimum geometry was not known beforehand, we performed a search along the most important degrees of freedom at the SCC-DFTB-D(34) level to identify possible conformations. If multiple minima close in energy were found, we applied the following steps to all of them until we were able to select the one with the lowest energy using a method with accuracy better than the energy difference between them.
• (2) Preliminary optimization of the geometry has been performed using density functional theory with an empirical dispersion correction(35) (DFT-D), using the TPSS functional(36) and the TZVP basis set(37) along with a dispersion correction optimized for this combination of functional and basis set. No symmetry was assumed in any calculation, and the starting structures were perturbed randomly to remove any possible symmetry. This procedure is used to avoid possible optimization to a saddle point instead of a minimum.
• (3) Final optimization of the complexes was carried out at the counterpoise-corrected MP2/TZ level. The resolution of the identity (RI-MP2 method) was used to accelerate the calculations. This setup has been shown to yield geometries close to those obtained at the coupled clusters level.^24,38 Tight optimization limits (energy change 3 × 10^–4 kcal/mol (5 × 10^–7 au), max. gradient component 0.06 kcal/mol/Å (5 × 10^–5 au), root-mean-square(RMS) gradient 0.03 kcal/mol/Å (2.5 × 10^–5 au)) were used to ensure good convergence, even in the intermolecular degrees of freedom. Such an optimization requires well converged energy calculations, so an SCF convergence threshold of 10^–9 au was used.
• (4) From these geometries, the S66 × 8 set was prepared by scaling the closest intermolecular distance in the complex along an intermolecular axis. The definition of the axis is different for different types of complexes. For hydrogen bonds, it is defined by the hydrogen and the acceptor atom. For cyclic hydrogen bonds, the average of both hydrogen bonds is used. For most other complexes, the centers of mass of the monomers are used, with some exceptions in, for example, T-shaped complexes, where only some atoms have been arbitrarily chosen as the centers to conserve the original arrangement in the displaced geometries. Details on the displacement coordinate are provided in the Supporting Information, Table S3. One of the monomers is moved along the axis so that the minimum distance between them is 0.9, 0.95, 1.05, 1.1, 1.25, 1.5, and 2.0 times the equilibrium value. These seven extensions, along with the MP2 equilibrium geometry, form the S66 × 8 data set.
• (5) Once the CCSD(T)/CBS interaction energies for the S66 × 8 set were calculated, we used the first five points of each dissociation curve (factors of 0.9–1.1 multiplying the equilibrium distance) to obtain a new minimum in the distance coordinate at the coupled clusters level. The selected points were interpolated with a fourth-order polynomial, and the position of the minimum of this function was used to construct a new geometry. These geometries form the S66 data set.

DFT-SAPT

The DFT-SAPT³⁹⁻⁴² interaction energy decomposition has been performed with the aDZ basis set to make calculations on larger complexes practical. It is known that the dispersion is slightly underestimated in this setup. We have shown that this can be addressed by scaling of the dispersion component;(43) in this work, we apply the scaling factor of 1.193 recommended for this basis set (all DFT-SAPT dispersion energies listed in this Article are already scaled). Such a scaling has been shown to improve the results consistently; the accuracy that can be reached is sufficient for our analysis, which accompanies more accurate CCSD(T)/CBS calculations. The PBE0AC functional recommended by the authors of the method was used for the DFT-SAPT calculations;(44) the calculations of the monomers have been performed in the basis set of the dimer. The shift needed to correct the asymptotic behavior of the functional was calculated as the difference between the HOMO energy of each monomer and the true ionization potential obtained from the calculation of its neutral and ionized form, using the same functional and basis set. Density fitting was used to speed up these calculations.(45)

The interactions of each of the complexes in the S66 set were characterized as being electrostatics dominated, dispersion dominated, or mixed (electrostatic/dispersion). The complexes with dispersion/electrostatics ratios lower than 0.59 are categorized as electrostatic, those with D/E ratios higher than 1.7 (1/0.59) are categorized as dispersion bound, and complexes with D/E ratios between 0.59 and 1.7 are categorized as mixed. The threshold of 0.59 generates groups that agree well with empirical categorization.

Other Methods Tested in This Study

We have used the newly obtained benchmark data to analyze the performance of several advanced wave function methods that are supposed to closely reproduce CCSD(T)/CBS data. The complete basis set limit for these methods has been calculated analogously as in the CCSD(T)/CBS scheme by combining the MP2/CBS term extrapolated from aTZ and aQZ basis set and the higher order correction calculated in aDZ basis set. In addition to plain MP2, MP3, and CCSD calculations, we have focused on correlated WFT methods that use empirical parameters, MP2.5(46) SCS-MP2,(47) SCS-MI-MP2,(48) SCS-CCSD,(49) SCS-MI-CCSD,(50) dispersion-weighted MP2(51) (DW-MP2), and nonempirically corrected MP2C.^52,53 All of the spin-component-scaled results have been derived from the calculations already performed to obtain the benchmark data. MP2 with a time-dependent DFT based dispersion correction (MP2C) represents another approach to improve the performance of the relatively efficient MP2 method.

In the spin component scaled methods, we used the following scaling coefficients for the other-spin (singlet) and same-spin (triplet) terms: The SCS-MP2 method uses c_os = 6/5 and c_ss = 1/3 regardless of the basis set used. The SCS-MI-MP2 was optimized to reproduce interaction energies in the S22 set. We use coefficients published for extrapolation from the TZ to QZ basis sets(48) (c_os = 0.4, c_ss = 1.29). We extrapolate from the equivalent, but augmented, basis sets; the difference in the CBS value is negligible. The SCS-CCSD method (c_os = 1.27, c_ss = 1.13) was developed using the QZ basis set, while we use extrapolation to the CBS limit; we expect the parameters to be transferable because the quadruple-ζ basis should not be far from the CBS limit. The SCS-MI-CCSD coefficients (c_os = 1.11, c_ss = 1.28) were optimized on the S22 data set, which uses different basis sets for complexes of varying size; here, the transferability of the parameters is an open question.

The DW-MP2 method was originally based on explicitly correlated MP2 (MP2-F12) calculations; this approach improves the convergence of the MP2 energy with basis set size and allows the use of a smaller basis set (aDZ). In this work, we have replaced it with the extrapolated MP2 results as another means to approach the complete basis set limit. Therefore, minor differences in our DW-MP2 results can be expected as compared to ref (51).

Computational Details

All DFT and RI-MP2 optimizations have been carried out in Turbomole 6.2.(54) Interaction energies at the MP2, MP3, MP2C, CCSD, and CCSD(T) levels and DFT-SAPT interaction energy decompositions have been calculated using the MOLPRO program(55) in versions 2009 and 2010. A threshold for SCF convergence of at least 10^–8 au was used for all of the calculations. Density fitting was used for the MP2 calculations used to obtain the MP2/CBS correlation energy term. For the SCC-DFTB-D calculations, the DFTB+ program(56) was used.

Error Analysis

The performance of the studied methods, with respect to the benchmark calculations, can be described by multiple statistical tools. For the S66 data set, we provide multiple error measures that often carry different information. We consider the root-mean-square error (RMSE) as the most important one, because it reflects the overall quality of the tested method well and is widely used in the field. It is also the variable optimized in parametrization of a method using the least-squares algorithm. Additionally, we list the mean unsigned error, the average (signed) error, which indicates the systematic component of the error, and the largest (maximum unsigned) error, expressed as a percentage, representing the worst case scenario.

We also provide the error separately for different groups of complexes of the data set. Because the average interaction energy in these groups differs, an error in the units of energy does not allow comparison between these groups. Therefore, we use relative errors, calculated as an RMSE divided by the average interaction energy in the group, expressed as percentages.

Results and Discussion

Geometries

Construction of the S66 × 8 set allowed us to interpolate the CCSD(T)/CBS energies around the MP2 minimum to obtain an accurate estimate of the equilibrium distance at the CCSD(T)/CBS level (see Methods for description of the procedure).

Comparing the energy predicted by the interpolation with the actual calculation on the new geometry can be used to assess the quality of the fit. Even the largest difference in the set is only 0.002 kcal/mol (0.05% of the interaction energy), which indicates that our polynomial fit accurately represents the potential energy surface and that the obtained geometry can be safely considered a minimum in this coordinate.

Comparison of the MP2 and CCSD(T) minima, in terms of distance and CCSD(T)/CBS interaction energies, allows us to measure the quality of the (counterpoise corrected) MP2/TZ geometries. The relative difference in geometries, measured as the change of the closest distance, is on average 0.03 Å. In the worst case, for the stacked benzene dimer, it is 0.11 Å or 3% of the distance.

Of course, the changes in geometry affect the interaction energies. Because the intermolecular potentials are rather flat, such small changes in geometry translate into comparably small improvements in the interaction energies. Over the entire set, we measured an RMSE of 0.020, and a maximum of 0.086 kcal/mol (3% of E_int). This is comparable to the estimated accuracy of the method used for the interaction energy calculation; therefore, the MP2 optimization can be safely used in cases when we are interested only in the interaction energy at higher levels. These results confirm previous studies that recommend the TZ basis set for MP2 optimizations.(38)

The interaction remains attractive even in the geometries with shortest distance (displacement factor 0.9). In all but the π–π stacked systems, the interaction remains very strong; on average, it amounts to 83% of the interaction energy in equilibrium. In the stacked complexes, the repulsion is steeper due to the large contact area and short equilibrium distance, and the interaction energy becomes as low as 10% of the equilibrium value.

Benchmark Calculations

The final CCSD(T)/CBS interaction energies are provided in Table 2. To estimate the accuracy of our benchmark data, we compare the scheme used in the S66 data set with more accurate estimates of CCSD(T)/CBS. This has been done on a set of ten small complexes introduced in our previous work.(43) For these, we extrapolated the CCSD(T) correlation energy to the complete basis set limit from calculations using the aTZ and aQZ basis sets. Table S4 in the Supporting Information gives the results of the comparison of the current benchmark technique with the extrapolated CCSD(T)/CBS(aTZ→aQZ) method. For this small test set, the S66 benchmark method gives an average error value of 1.2% with the largest error being 2.5%. These results indicate that the errors associated with the current benchmark method should be reasonably small; for the S66 test set, we expect that the errors should generally be below 3%.

Table 2. List of the Benchmark CCSD(T)/CBS Interaction Energies (in kcal/mol), the Dispersion/Electrostatics Ratio from the DFT-SAPT Decomposition, and the Interaction Type (E, Electrostatics-Dominated; D, Dispersion-Dominated; and M, Mixed) Based on It for the S66 Data Set.

	hydrogen bonds	ΔE	disp/elec	category
1	water···water	–4.92	0.29	E
2	water···MeOH	–5.59	0.35	E
3	water···MeNH2	–6.91	0.30	E
4	water···peptide	–8.10	0.37	E
5	MeOH···MeOH	–5.76	0.40	E
6	MeOH···MeNH2	–7.55	0.38	E
7	MeOH···peptide	–8.23	0.42	E
8	MeOH···water	–5.01	0.34	E
9	MeNH2···MeOH	–3.06	0.71	M
10	MeNH2···MeNH2	–4.16	0.71	M
11	MeNH2···peptide	–5.42	0.79	M
12	MeNH2···water	–7.27	0.33	E
13	peptide···MeOH	–6.19	0.56	E
14	peptide···MeNH2	–7.45	0.50	E
15	peptide···peptide	–8.63	0.56	E
16	peptide···water	–5.12	0.42	E
17	uracil···uracil (BP)	–17.18	0.35	E
18	water···pyridine	–6.86	0.34	E
19	MeOH···pyridine	–7.41	0.40	E
20	AcOH···AcOH	–19.09	0.30	E
21	AcNH2···AcNH2	–16.26	0.32	E
22	AcOH···uracil	–19.49	0.31	E
23	AcNH2···uracil	–19.19	0.31	E

	dispersion	ΔE	disp/elec	category
24	benzene···benzene (π–π)	–2.82	3.83	D
25	pyridine···pyridine (π–π)	–3.90	2.41	D
26	uracil···uracil (π–π)	–9.83	1.35	M
27	benzene···pyridine (π–π)	–3.44	2.86	D
28	benzene···uracil (π–π)	–5.71	2.16	D
29	pyridine···uracil (π–π)	–6.82	1.75	M
30	benzene···ethene	–1.43	4.57	D
31	uracil···ethene	–3.38	1.86	D
32	uracil···ethyne	–3.74	1.33	M
33	pyridine···ethene	–1.87	3.00	D
34	pentane···pentane	–3.78	4.46	D
35	neopentane···pentane	–2.61	5.42	D
36	neopentane···neopentane	–1.78	4.28	D
37	cyclopentane···neopentane	–2.40	4.33	D
38	cyclopentane···cyclopentane	–3.00	3.98	D
39	benzene···cyclopentane	–3.58	3.10	D
40	benzene···neopentane	–2.90	3.17	D
41	uracil···pentane	–4.85	3.44	D
42	uracil···cyclopentane	–4.14	3.72	D
43	uracil···neopentane	–3.71	2.80	D
44	ethene···pentane	–2.01	4.46	D
45	ethyne···pentane	–1.75	3.11	D
46	peptide···pentane	–4.26	3.32	D

	others	ΔE	disp/elec	category
47	benzene···benzene (TS)	–2.88	2.60	D
48	pyridine···pyridine (TS)	–3.54	1.83	D
49	benzene···pyridine (TS)	–3.33	2.13	D
50	benzene···ethyne (CH···π)	–2.87	1.60	M
51	ethyne···ethyne (TS)	–1.52	0.79	M
52	benzene···AcOH (OH···π)	–4.71	1.25	M
53	benzene···AcNH2 (NH···π)	–4.36	0.98	M
54	benzene···w ater (OH···π)	–3.28	1.08	M
55	benzene···MeOH (OH···π)	–4.19	1.54	M
56	benzene···MeNH2 (NH···π)	–3.23	2.07	D
57	benzene···peptide (NH···π)	–5.28	1.74	M
58	pyridine···pyridine (CH···N)	–4.15	0.88	M
59	ethyne···water (CH···O)	–2.85	0.40	E
60	ethyne···AcOH (OH···π)	–4.87	0.54	E
61	pentane···AcOH	–2.91	3.60	D
62	pentane···AcNH2	–3.53	3.09	D
63	benzene···AcOH	–3.80	1.97	D
64	peptide···ethene	–3.00	1.70	M
65	pyridine···ethyne	–3.99	0.46	E
66	MeNH2···pyridine	–3.97	1.21	M

We are aware of the fact that the errors present in our benchmark data are close to the errors of some of the studied methods to which they are compared. However, in the comparison of similar methods, using the same extrapolation scheme and basis sets, the major part of the error coming from the contributions shared by both methods is canceled. For example, the CCSD(T)/CBS approach is consistent with all of the CCSD-based methods where the MP2 and ΔCCSD terms are the same and the protocol differs only in omitting the triples.

DFT-SAPT

Table 2 gives the DFT-SAPT dispersion/electrostatic ratios and the SAPT-electrostatic/dispersion/mixed (SAPT-E/D/M) category for all of the complexes in the S66 set.

It can be seen in this table that among the interactions in the hydrogen-bonding category, 20 are clasified as SAPT-electrostatic, while three are classified as SAPT-mixed. The complexes containing cyclic hydrogen bonds or water exhibit the smallest D/E ratios. The range of D/E ratios for single H-bonds involving NH₂ or NH donors is 0.33–0.79, while the corresponding ratios for single H-bonds involving OH donors are 0.29–0.42. The three SAPT-mixed complexes in this group, MeNH₂···MeOH, MeNH₂···MeNH₂, and MeNH₂···peptide, represent three of the four complexes that have MeNH₂ as the hydrogen-bond donor. Here, the hydrogen bond itself is weaker, while the secondary (dispersion) interactions in the systems are not negligible.

The D/E values for the interactions in the dispersion category are in the range from 1.33 to 5.42. Within this group, there are 20 SAPT-dispersion interactions and three SAPT-mixed interactions, which are for the uracil···ethyne, uracil···uracil, and pyridine···uracil complexes. Generally the interactions that are most electrostatic in nature are π–π interactions involving the two heterocyclic aromatic molecules (uracil and pyridine). This trend stands to reason as the uracil and pyridine heteroatoms give these molecules large charge separations. As would be expected, the aliphatic–aliphatic interactions exhibit the least amount of electrostatic character.

There are three SAPT-electrostatic, 10 SAPT-mixed, and seven SAPT-dispersion complexes within the mixed category. Here, it can be seen that interactions involving ethyne are generally electrostatic in nature, with three of these, ethyne···water, ethyne···AcOH, and pyridine···ethyne, being categorized as SAPT-electrostatic.

Methods Tested

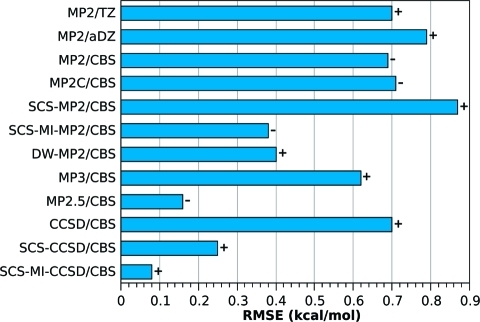
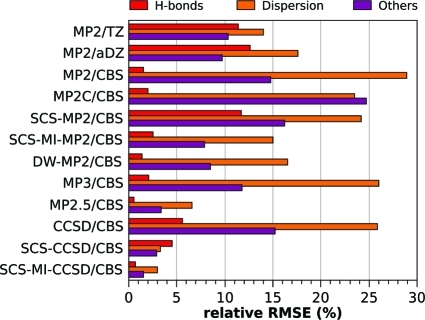
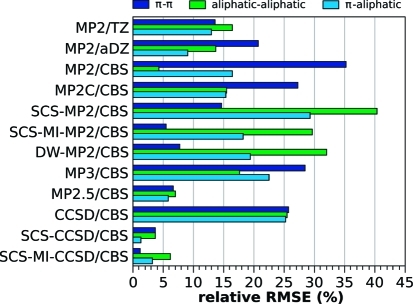
Selected error measures of the tested methods for the S66 test set are listed in Table 3 and plotted in Figure 2. Relative errors for different interaction categories are plotted in Figure 3; the dispersion category is further divided to π–π, aliphatic–aliphatic, and π–aliphatic interactions, for which the relative errors are plotted in Figure 4. The full listing of the errors for these groups is provided in Table S1 in the Supporting Information. The performance of the individual methods is discussed in the following text.

Table 3. Errors of the Studied Methods with Respect to the Benchmark CCSD(T)/CBS Calculations on the S66 Data Set^a.

method	RMSE, kcal/mol	MUE, kcal/mol	AVG, kcal/mol	MAX %
MP2/TZ	0.70	0.56	0.43	29
MP2/aDZ	0.79	0.58	0.31	32
MP2/CBS	0.69	0.45	–0.44	40
MP2C/CBS	0.71	0.47	–0.01	174
SCS-MP2/CBS	0.87	0.74	0.73	79
SCS-MI-MP2/CBS	0.38	0.28	0.21	54
DW-MP2/CBS	0.40	0.27	0.09	58
MP3/CBS	0.62	0.45	0.44	64
MP2.5/CBS	0.16	0.12	0.00	16
CCSD/CBS	0.70	0.62	0.62	73
SCS-CCSD/CBS	0.25	0.15	0.12	6
SCS-MI-CCSD/CBS	0.08	0.06	–0.04	6

^aThe errors are reported as RMSE, mean unsigned error (MUE), average signed error (AVG), and largest error in the set relative to the interaction energy (MAX).

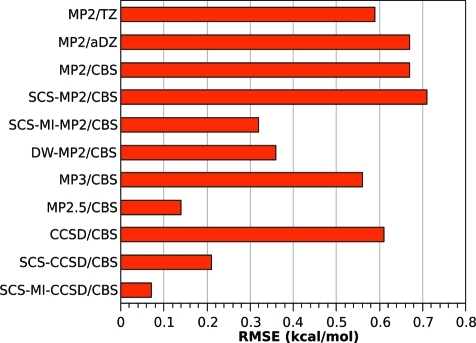
Figure 2.

The RMSE (kcal/mol) with respect to the CCSD(T)/CBS benchmark. The symbol next to the bar is the sign of the average error. Plus indicates that the method underestimates the strength of the binding over the whole data set; minus indicates systematic overbinding.

Figure 3.

Relative errors (%) for the three groups of complexes: hydrogen bonds, dispersion-dominated, and others. The error is calculated as a RMSE relative to average interaction energy in the group so that the errors can be compared between the groups.

Figure 4.

Relative errors (%) for the three types of dispersion-dominated complexes: π–π, aliphatic–aliphatic, and π–aliphatic interactions. The error is calculated as a RMSE relative to average interaction energy in the group so that the errors can be compared between the groups.

1. MP2

The MP2 method has long served as the workhorse in calculations on molecular complexes. This method is generally regarded as yielding qualitatively, or semiquantitatively, accurate results (when used with the counterpoise correction), with the quality of its interaction energy values depending strongly on the basis set with which it is used. In a previous study in this laboratory, we have shown that MP2 generally yields its best results when it is paired with either the aDZ or the TZ basis.(57) Here, we investigate the performance of this method with the aDZ and TZ bases, as well as at the CBS limit.

It can be seen in Figure 2 that similar errors are produced by the MP2/aDZ (0.79 kcal/mol), MP2/CBS (0.69 kcal/mol), and MP2/TZ (0.70 kcal/mol) methods. These errors are rather high, as compared to those of many of the other methods considered here. However, it should be kept in mind that MP2/aDZ and MP2/TZ are the least computationally expensive methods included in the study and have much better scaling properties than any method that includes any higher order terms (especially when density fitting is used).

Inspection of Figure 3 reveals that, despite the fact that MP2 produces similar overall errors with TZ, aDZ, and at the CBS limit, MP2/TZ gives the most balanced description of the various interaction categories, giving its largest relative error for the dispersion category (14%). MP2/CBS gives extremely accurate results for hydrogen bonding complexes (2%), while producing very large errors for interactions in the dispersion category (29%).

2. SCS-MP2 and SCS-MI-MP2

The SCS-MP2 method makes use of a separate scaling of the singlet and triplet MP2 correlation and was originally developed for reaction energies. The SCS-MI-MP2 method uses the same scaling scheme, but was parametrized for improved performance in the description of noncovalent interactions (using the S22 data set).

Results for SCS-MP2/CBS and SCS-MI-MP2/CBS are depicted in Figure 2. Not surprisingly, SCS-MP2/CBS gives errors that are relatively high (RMSE 0.87 kcal/mol), as the method is not parametrized for intermolecular interactions. SCS-MI-MP2/CBS, on the other hand, yields an RMSE value of 0.38 kcal/mol, which represents a significant improvement over the unscaled MP2 method (for any of the basis sets tested here). Comparing SCS-MI-MP2/CBS to MP2/TZ (the best MP2 performer), it can be seen in Figure 3 that the scaled MP2 method gives improved results for hydrogen bonds and interactions in the “other” category, with especially large improvements for the hydrogen bonds (11% vs 3%). Dispersion interactions are slightly better described by MP2/TZ (14% vs 15%).

3. MP3 and MP2.5

The most computationally expensive part of the MP2.5 method (as utilized here) is the MP3/aDZ calculation, meaning that this technique is only more computationally intensive than the MP2-based methods. MP3 is known to strongly underestimate dispersion interactions, as opposed to MP2/CBS, which is known to overbind dispersion bound complexes. The basis for the MP2.5 method, which is constructed as an average of MP2 and MP3, is a mutual cancellation of these errors.

As might be expected, MP3/CBS yields relatively high RMSEs (0.62 kcal/mol). On the other hand, MP2.5/CBS yields surprisingly accurate results for this data set, considering its relatively low cost, and the fact that it does not (technically) contain any empirical parameters. Figure 2 reveals that the only method producing RMSEs lower than MP2.5 (0.16 kcal/mol) is SCS-MI-CCSD/CBS (0.08 kcal/mol). Considering the data presented in Figure 3, it can be seen that MP2.5 gives a well-balanced description of the three interaction categories, producing relative errors of no more than 7% for any particular interaction type. The lowest errors occur for hydrogen bonds (1%), while the largest errors occur for the dispersion complexes (7%). MP2.5 gives a very well-balanced description of the dispersion-bound complexes, with errors between 6% and 7% for all three dispersion subcategories.

4. CCSD, SCS-CCSD, and SCS-MI-CCSD

Like SCS-MP2, SCS-CCSD was parametrized to improve CCSD’s description of reaction energies. It has also been noted that this method gives improved results for noncovalent interactions. As in the case of SCS-MP2, SCS-CCSD has also been parametrized (against the S22 set) to give improved results for molecular complexes; with the new parameters the method is designated SCS-MI-CCSD. This reparameterization leads to significant improvement of the accuracy from RMSE of 0.25 kcal/mol in SCS-CCSD/CBS to 0.08 kcal/mol in SCS-MI-CCSD/CBS.

It can be seen in Figure 2 that the RMSEs produced by both SCS-CCSD/CBS and SCS-MI-CCSD/CBS are much lower than that of CCSD/CBS (0.70 kcal/mol). To highlight the accuracy that can be obtained with each of these techniques, it will be noted that the maximum relative error produced by each of these methods is 6%. Figure 3 shows that both SCS-CCSD/CBS and SCS-MI-CCSD/CBS produce very small errors for all interaction categories. The SCS-MI-CCSD technique gives particularly low errors for all interaction categories, producing its largest relative RMSE for the dispersion category (3%). Both SCS-CCSD and SCS-MI-CCSD produce small relative errors for the dispersion subcategories, with SCS-CCSD giving its largest error for the π–π and aliphatic–aliphatic categories (4%) and SCS-MI-CCSD giving its largest error for the aliphatic–aliphatic category (6%).

The SCS-MI-CCSD/CBS is the most accurate method from the studied set. The error with which it reproduces the CCSD(T)/CBS benchmark is smaller than the estimated accuracy of the benchmark calculations. The method is also very robust, as indicated by the narrow range between maximum and minimum error. Therefore, it can be recommended as an alternative to CCSD(T) calculations for larger systems or for any purpose where the ultimate accuracy is not required.

5. Dispersion Weighted MP2

The DW-MP2 method, which utilizes a (system dependent) weighted average of MP2/CBS and SCS-MP2/CBS results to compute interaction energies, yields results that are improved with respect to its parent methods, both in terms of overall errors (RMSE 0.40 kcal/mol) and in terms of errors for the three interaction categories. This is somewhat surprising; given the relatively poor performance of SCS-MP2 for dispersion bound complexes, it would be expected that DW-MP2 should give low errors for hydrogen-bonding complexes (as does MP2/CBS) and higher errors for dispersion bound complexes (as does SCS-MP2/CBS). However, it should be noted that the signs of the errors given by MP2/CBS and SCS-MP2 for dispersion bound complexes are generally opposite in sign; that is, MP2/CBS tends to overbind, while SCS-MP2/CBS tends to underbind. Thus, any interaction energy constructed as a linear combination of results from these two methods will exhibit some inherent error cancellation, which is likely responsible for this method’s relatively low errors.

6. MP2C

The MP2C method, which incorporates a TD-DFT description of dispersion, yields an RMSE (0.71 kcal/mol) that is comparable to those of MP2/CBS (0.69 kcal/mol) and MP2/TZ (0.70 kcal/mol). This technique gives very low errors for hydrogen-bonding complexes (2%) but rather high errors for both the dispersion (24%) and the “other” (25%) categories. This is somewhat surprising because, from the theoretical point of view, the MP2C offers a well justified improvement over MP2 itself. On the other hand, it is still only a second-order perturbation treatment, which cannot describe higher order contributions.

DFT-SAPT Decomposition as a Tool for Method Assessment

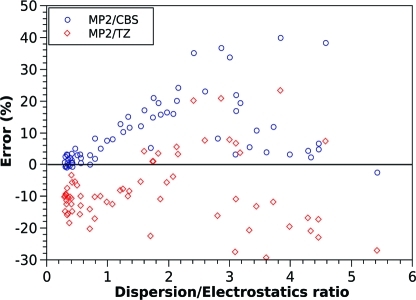
The availability of DFT-SAPT electrostatic and dispersion data for all of the S66 complexes allows for the assessment of various methods in terms of the errors they produce for varying dispersion/electrostatic ratios. As an example, we have prepared a plot depicting the (percentagewise) errors as a function of the dispersion/electrostatic ratio for the MP2/CBS and MP2/TZ methods (Figure 5). The results shown here are in good agreement with the known properties of these two methods. MP2/CBS gives a very good description of electrostatically driven interactions while overbinding substantially for dispersion-bound complexes. MP2/TZ, on the other hand, underestimates electrostatically driven interactions and generally gives a better overall description of dispersion dominated and mixed interactions (although the errors are still significant), yielding errors that indicate no specific tendency to overbind or underbind. The type of plot shown for MP2/CBS and MP2/TZ can be used for the assessment and development of new methods and as a tool for better determining their strengths and weaknesses.

Figure 5.

Errors of selected methods plotted against the ratio of dispersion to electrostatic term from the DFT-SAPT decomposition.

Tests on S66 × 8 Set

Figure 6 shows the RMSEs produced by the tested methods for the S66 × 8 data set. The MP2C method was not applied to these sets because the improvement as compared to MP2 itself is expected to be small, while the computational demands are much larger. It will be noted here that errors for the S66 × 8 data set are generally smaller than those for the S66 set, which is attributable to the fact that interaction energies for structures far from their equilibrium geometries are generally very small, and the corresponding errors for these structures will also tend to be small.

Figure 6.

The RMSE (kcal/mol) in the S66 × 8 (dissociation curves of the 66 complexes).

It can be seen in Figures 2 and 6 that, in terms of the relative performance of each of the tested methods, the same general trends are followed for the S66 and S66 × 8 data sets. Table S2 (Supporting Information) gives the S66 × 8 RMSEs for each of the tested methods along with a description of the errors that occur at long intermolecular separations (displacement factors 1.1–2.0) and short intermolecular separations (factor of 0.9). Here, it can be seen that the relative errors at the shorter intermolecular distances are always about 2–3 times larger than those at the longer separations. This is not a surprising result, as it would be expected that larger errors occur in regions where the potential energy curves are the steepest.

Conclusions

Here, we have presented a database of interaction energies for 66 intermolecular complexes, each in 9 distinct geometric configurations. The data set was constructed to include a balanced set of commonly encountered interaction motifs involved in biomolecular structures containing C, O, N, and H. This data set was designed to be expandable, meaning that complexes containing additional binding motifs, or additional elements, can easily be added. Reference data were obtained at a high level of theory using the CCSD(T)/CBS scheme consistently for all 594 points. Importantly, the reference method and basis sets used for each of the complexes are identical to avoid the introduction of additional random error.

Data Availability

Geometries of the complexes in S66 and S66 × 8 data sets, the benchmark CCSD(T)/CBS interaction energies, and results of all of the methods tested here are available through the BEGDB Web site(58) (www.begdb.com) for download and interactive browsing.

Geometries

The geometries of the complexes in the S66 data set have been carefully optimized, and the intermolecular distance is the minimum at the CCSD(T)/CBS level. This is an important advantage over previous data sets where geometries of all but very small complexes had been optimized at only the MP2 level. Accurate equilibrium geometries are a valuable tool for parametrization of new methods that should yield not only accurate energies, but also equilibrium geometries, and potential energy surfaces in general.

S66 × 8 Geometries

The S66 × 8 data set contains eight points on the dissociation curves of each of the S66 systems (528 in total). For a given complex, the region around the equilibrium distance is sampled preferentially, which allows for accurate interpolation of the true minimum of the curve.

S66 Benchmark Results

The S66 data set contains 66 CCSD(T)/CBS interaction energies obtained using aTZ and aQZ basis sets for the extrapolation of MP2 correlation energy and aDZ for the ΔCCSD(T) term. These values have been calculated on refined geometries where the intermolecular distance is a true minimum at this computational level.

S66 × 8 Benchmark Results

For the 528 nonequilibrium geometries contained in these sets, we provide CCSD(T)/CBS interaction energies obtained using the same setup.

Tested Methods

The enormous computational expense associated with the CCSD(T) method, even with a relatively small basis set such as aDZ, makes it necessary to seek less costly methods that can produce comparable results. Of the 12 wave function-based methods tested in this work, there are three that stand out, in terms of their performance on the S66 and S66 × 8 sets, as producing particularly low errors at a given computational cost point; these are SCS-MI-CCSD/CBS, MP2.5/CBS, and SCS-MI-MP2/CBS. Both of the SCS-MI- (MP2 and CCSD) methods yield errors that are substantially lower than their parent methods, with SCS-MI-CCSD/CBS giving errors that are extremely low for both data sets (RMSE 0.08 kcal/mol in the S66 set). MP2.5/CBS produces errors that are only slightly higher than those of SCS-MI-CCSD/CBS (0.16 kcal/mol), at a much lower computational cost.

Supporting Information Available

A detailed error analysis of the tested methods (Tables S1 and S2), pictures of all of the complexes in the S66 set (Figure S1), definition of the displacement coordinates used to construct the S66 × 8 set (Table S3), and results of benchmark CCSD(T) calculations on model complexes used to assess the accuracy of the methodology applied to S66 and S66 × 8 data sets (Table S4). This material is available free of charge via the Internet at http://pubs.acs.org.

This article was published ASAP on July 19, 2011. Changes have been made to entries 35, 36, 37, and 38 in Table 2. The correct version was published on July 26, 2011.