Three-Dimensional Polymer Constructs Exhibiting a Tunable Negative Poisson’s Ratio

Abstract

Young’s modulus and Poisson’s ratio of a porous polymeric construct (scaffold) quantitatively describe how it supports and transmits external stresses to its surroundings. While Young’s modulus is always non-negative and highly tunable in magnitude, Poisson’s ratio can, indeed, take on negative values despite the fact that it is non-negative for virtually every naturally occurring and artificial material. In some applications, a construct having a tunable negative Poisson’s ratio (an auxetic construct) may be more suitable for supporting the external forces imposed upon it by its environment. Here, three-dimensional polyethylene glycol scaffolds with tunable negative Poisson’s ratios are fabricated. Digital micromirror device projection printing (DMD-PP) is used to print single-layer constructs composed of cellular structures (pores) with special geometries, arrangements, and deformation mechanisms. The presence of the unit-cellular structures tunes the magnitude and polarity (positive or negative) of Poisson’s ratio. Multilayer constructs are fabricated with DMD-PP by stacking the single-layer constructs with alternating layers of vertical connecting posts. The Poisson’s ratios of the single- and multilayer constructs are determined from strain experiments, which show (1) that the Poisson’s ratios of the constructs are accurately predicted by analytical deformation models and (2) that no slipping occurrs between layers in the multilayer constructs and the addition of new layers does not affect Poisson’s ratio.

1. Introduction

The elastic behavior of a porous construct can be described by its Young’s modulus (stiffness) and Poisson’s ratio, which depend on its porosity, the intrinsic properties of the material making up the rib structures, and any anisotropic behavior due to the presence of pores.^[1] For porous solids in which stress and strain are linearly proportional, knowledge of Young’s modulus and Poisson’s ratio are sufficient at completely describing the elastic signature of the solid. Moreover, optimizing these elastic properties requires control over pore structure, which can be quite difficult to achieve.

Yield strength and stiffness are of vital importance in determining whether a porous construct demonstrates satisfactory mechanical integrity, and demonstrate a power-law relationship with regards to the degree of the construct’s porosity.^[2] While stiffness characterizes a construct’s elastic behavior in the loading direction, Poisson’s ratio describes the degree to which a material contracts (expands) transversally when axially strained. The Poisson’s ratio (see the Supporting Information, Equation 1) of virtually every naturally-occurring and artificial material or porous construct (porous scaffolding material) is non-negative, i.e., it contracts in the transverse direction upon expanding in the axial direction and vice versa. When Poisson’s ratio is negative, expansion occurs in both the axial and transverse directions simultaneously. This unusual phenomenon has been show to occur in crystalline α-cristobalite SiO₂,^[3,4] other crystalline materials,^[5,6] with hinged crystal structures,^[7,8] carbon allotropes,^[9] foams,^[10–12] microporous polymers and laminates,^[13–16] and other extreme states of matter^[17,18] (see ref. [19,20]). However, to date, nothing has been reported on the fabrication of three-dimensional polymeric constructs exhibiting a tunable negative Poisson’s ratio.

In some applications, e.g., in tissue engineering, porous constructs or scaffolds having a negative Poisson’s ratio may be more suitable for emulating the behavior of native tissues and accommodating and transmitting forces to the host tissue site.^[3,21–27] The elastic properties of a scaffold are critical to its efficacy in regenerating tissue and reducing inflammatory responses and must be matched with the elastic properties of the native tissue it is aimed at replacing. Moreover, a biological construct should also be sufficiently robust to accommodate the forces applied by cells and other outboard mechanical loads imposed during wound healing, blood flow, patient activity (e.g., walking), etc.^[2]

One example of a tissue that demonstrates a negative Poisson’s ratio is the arterial endothelium. The arterial endothelium is subjected to both wall shear stresses and a cyclic circumferential strain due to pulsatile blood flow. Accordingly, it was observed that the sub-endothelial axially aligned fiber layer of bovine carotid arteries thickens in response to a circumferential strain; such an observation indicates negative Poisson’s behavior.^[22] A scaffold made out of an auxetic material (an auxetic scaffold) would expand and contract in tandem with the strains resulting from the cyclical pressures from pulsatile blood flow. Thus, an auxetic scaffold that exhibits concurrent axial and transverse expansion (contraction) would likely better integrate with native tissues and better promote clinical tissue regeneration. Other examples where auxetic constructs could be useful are in myocardial tissue engineering (as an auxetic cardiac patch), skin and fat tissue engineering, and in wound management (e.g., auxetic medical sutures).

It has been shown that man-made auxetic (negative Poisson’s) polymers can be constructed by patterning non-auxetic polymers with an artificial lattice of rib-containing unit-cells (pores), which tune Poisson’s ratio by their shape and deformation mechanisms.^{[10,12,14,28–32]} Materials of this sort have been coined, cellular or hinged materials, owing to the fact that their constitutive pore structure can have a sizable effect on their mechanical behavior. Several unit-cell models have been proposed, each having well-defined strain-dependent Poisson’s ratios (Poisson’s function) described analytically.^{[10,19,33,34]} In the past, auxetic polyurethane foams have been formed by annealing the foams in a compressed state, which naturally causes a re-organization in their cellular microstructure;^[10,28] however, the annealing process renders little practical control over the cellular microstructure comprising the foams, making it very difficult to premeditatedly modulate the strain-dependent behavior of Poisson’s ratio. Moreover, to our knowledge, no auxetic unit-cell model has been deliberately and precisely implemented in useful elastic materials, especially materials of utility in biological applications. In applications like tissue engineering, one must have the capability to precisely tune the magnitude and polarity (positive or negative) of Poisson’s ratio in three-dimensional constructs to match the properties of the specific tissue that is regenerated. In addition, the command over the Poisson’s ratio of tissue constructs must be attainable in biologically relevant materials with pore arrangements that satisfy the restrictions that the pores must be open to the environment and completely interconnected.

Here, we fabricated three-dimensional constructs in polyethylene glycol (PEG) that exhibit determinate (predictable) in-plane negative Poisson’s ratios. Auxetic behavior was achieved by patterning specially arranged and shaped unit-cellular (pore) structures with a digital micromirror device projection printing (DMD-PP) system (see the Supporting Information, Figure S1).^[35–37] Unit-cell geometries and spatial-arrangements were designed from existing analytical models that predict strain-dependent negative Poisson’s behavior. We chose to use an acrylated-PEG hydrogel as we have reported its use in porous tissue scaffolds seeded with bone marrow-derived progenitor cells and have shown that it can encapsulate timed-release biomolecules that stimulate tissue growth.^[35–37] Harnessing the capabilities of DMD-PP micro-stereolithography, we are the first to report the fabrication of three-dimensional polymer scaffolds having negative strain-dependent in-plane Poisson’s ratios, which (1) are tunable by varying pore (unit-cell) structure and (2) can be easily described (and predicted) by analytical models.

2. Results and Discussion

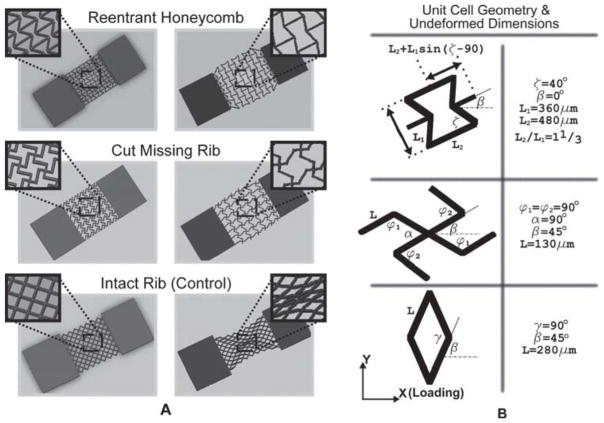
Figure 1A shows the simulated deformation of single-layer PEG constructs composed of arrays of constitutive unit-cells with the: 1) re-entrant honeycomb, 2) cut missing-rib, and 3) intact-rib architectures. The simulations show the elastic deformation of the constructs resulting from the application of a tensile “pulling” axial load. The reentrant and cut missing-rib designs were adapted from models reported in the literature and are auxetic.^[1,38–40] The intact-rib model is not auxetic (positive Poisson’s ratio) and was used as a control in our tests of Poisson’s ratio. The material walls of each model are denoted as ribs and have a rectangular cross-section approximately 40 micrometers in width and 100 micrometers in depth. The arrangement of the ribs defines unit-cell shape and encloses pores with well-defined geometries, which we desire in a biomaterial tissue construct. Figure 1B highlights the geometry and relevant dimensions of each unit-cell type. Rectangular slabs of material were incorporated at the ends of each porous sheet to ensure the mechanical integrity of the sheet for handling during strain testing.

Figure 1.

A) Stress-strain simulations of single-layer PEG constructs composed of unit-cells with reentrant honeycomb,^[1,34,40] cut missing-rib,^[38,39] and intact-rib architectures.^[39] The reentrant and missing-rib architectures exhibit negative Poisson’s (auxetic) behavior. The intact-rib is not auxetic and was used as a control in tests for Poisson’s ratio. B) Unit-cell geometry and relevant dimensional parameters. The walls of the unit-cells (denoted as ribs) are approximately 40 micrometers wide and 100 micrometers deep.

In the unit-cell models of Figure 1, the position and arrangement of the ribs relative to one another engender a negative and magnified strain-dependent Poisson’s ratio by virtue of a combination of rib bending (flexure), stretching, and hinging (angular deformations).^[1,30,33,40] The degree to which each mode of deformation contributes to the elastic properties of a cellular meshwork depends on unit-cell geometry and the material properties of the ribs. Poisson’s ratio is usually strain-dependent for cellular materials, but unit-cell shape and orientation relative to the direction of loading (angle β for each unit cell in Figure 1B) also play a critical role in the magnitude and polarity of Poisson’s ratio. The way the constitutive unit-cell of a cellular material responds to shear loads is known as the off-axis elastic response of the unit cell.^[39] Accordingly, we note that the in-plane Poisson’s ratio is directional (anisotropic) if it varies in magnitude or polarity with the direction of loading. It is also imperative to note that, as long as the in-plane deformations of the construct remain elastic, Poisson’s ratio is controlled solely by the structure of the pores and not the intrinsic properties of the material making up the ribs.^[33] Thus, the Poisson’s ratio of the constructs is both scale independent and independent of the choice of rib material for strains in the elastic regime.

The reentrant structure (Figure 1) is formed by changing the four side angles (angle ζ) between the vertices (ribs) in a six-sided honeycomb (hexagon), with some additional modifications.^[33,40] Two rib lengths, L₁ and L₂, constrain the dimensions of the unit cell, including angle ζ (the value of angle ζ is set by the rib-length ratio and is not arbitrarily set), and the ratio of the two rib lengths has a sizable influence on Poisson’s ratio. The reentrant mesh demonstrates a high degree of anisotropy, with uniform in-plane expansion (compression) demonstrated only when normal stresses are applied (σ_x, σ_y) with respect to the orientation shown in Figure 1 (β = 0°). The reentrant structure yields to shear stresses imposed by “diagonal” loads, leading to states of strain that are not auxetic.^[34] The in-plane off-axis properties of the reentrant unit cell are well-documented.^[34] Varying angle ζ alters the magnitude of Poisson’s ratio, and gives Poisson’s ratio its strain-dependent response.

The missing-rib model (Figure 1) is formed by removing select ribs from the intact model, so that the intact form then has “missing” ribs.^[39] Like the reentrant mesh, the missing-rib mesh demonstrates auxetic behavior that varies with changes in unit-cell dimensions, particularly angles α and β (Figure 1B); however, unlike the reentrant model, the off-axis properties of the missing-rib unit-cell are not well documented. Changes in the central angles, α and β, play a critical role in imposing the strain-dependent response of the missing-rib unit-cell.

The intact-rib meshwork (Figure 1) has a positive Poisson’s ratio regardless of the direction of loading. Similar to the missing-rib model, the off-axis response of the intact-rib unit-cell is not well documented. The strain-dependent nature of the Poisson’s ratio for the intact unit-cell is predominately caused by changes in angle γ resulting from increasing values of axial strain.

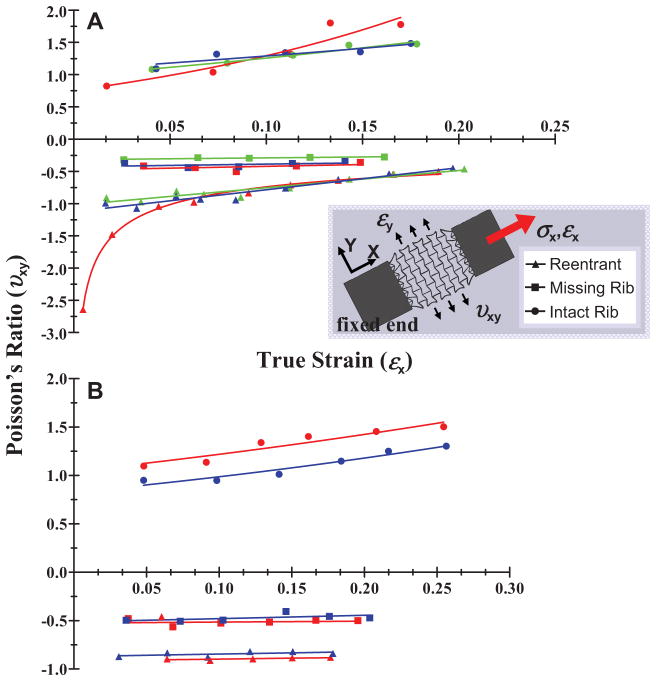
Single-layer PEG constructs were patterned with the unit-cell lattices depicted in Figure 1; the constructs are shown in the SEM images of Figures 2A–C. Strain tests were conducted to determine the Poisson’s ratios of the single-layer constructs as a function of true (instantaneous) axial strain (see the Supporting Information, Equation 2). Testing was implemented by fixing one end of the scaffolds while applying an axial tensile load at the other end. Poisson’s ratios were approximated by measuring the axial and transverse deformations of the overall scaffold meshworks. In Figure 3A a plot of Poisson’s ratios of the single-layer constructs for values of true strain (ε = δL/L where ε is true strain, L is length, and δL is incremental change in length) is shown from 0 to approximately 0.2 for each unit-cell type. See also the Supporting Information (Discussion 1 and Equations 1 and 2) for a description on how Poisson’s ratio and true strain were determined in producing Figure 3. Poisson’s ratio (υ_xy) was calculated by υ_xy = − ε_y/ε_x, where x is the loading direction and y is the lateral (transverse) direction. Three experiments, denoted by color in the plots, were conducted for each unit-cell type; each experiment was performed with a different sample. Figure 4A illustrates the mechanical responses of the single-layer constructs resulting from the application of the axial tensile load. The side-by-side optical images show the constructs in their undeformed and strained states, and were taken from one of the three tests performed for each unit-cell. The insets depict deformations in the individual pores (unit-cells). Movies in the Supporting Information show the elastic behavior of the single-layer constructs with the reentrant (Movie 1), missing-rib (Movie 2), and intact-rib (Movie 3) meshworks.

Figure 2.

Scanning electron microscopy images of cellular polymer scaffolds constructed from polyethylene glycol (PEG) with tunable negative Poisson’s ratios. The constructs were fabricated using a digital micromirror device micro-stereolithography system.^[35,44] A–C) Single-layer PEG constructs; D–F) double-layer PEG constructs; G–I) triple-layer reentrant PEG construct. Blocks of PEG were connected to the ends of the constructs to provide mechanical stability in handling and strain testing. Single-layer constructs are composed of a lattice of specially-arranged unit-cells having well-defined geometries resembling the reentrant (A, D, G–I), missing-rib (B, D), and intact-rib architectures (C, F). Constructs with the reentrant and missing-rib unit-cells exhibit a negative Poisson’s ratio while those with the intact-rib structure have a positive Poisson’s ratio; the strain-dependent behavior of the Poisson’s ratios are well-described by analytical models. Multi-layer constructs (double- and triple-layer) were assembled by connecting single-layer constructs with alternating layers of vertical posts. The ribs making up the unit-cells enclose pores having a well-defined shape, and the multi-layer constructs have pore arrangements that are accessible to the environment and demonstrate 100% interconnectivity as desired in a biomaterial tissue construct.^[2]

Figure 3.

Measured Poisson’s ratio as a function of true strain for the (A) single-layer and (B) double-layer constructs composed of the reentrant, missing-rib, and intact-rib unit-cell geometries. Three strain-dependent experiments were performed for each type of single-layer construct and two strain-dependent experiments were performed for each double-layer construct; each strain test was conducted with a different construct. Separate experiments are denoted by color in the plots.

Figure 4.

Optical images of the expansion (contraction) of the (A) single-layer and (B) double-layer PEG scaffolds in response to an applied axial strain. The side-by-side images show the scaffolds in their (left) undeformed and (right) deformed strain states. The insets show deformation in the individual unit-cells (and the pores enclosed by the ribs).

As shown in Figure 3A, the Poisson’s ratios of the single-layer reentrant and missing-rib constructs were negative while the intact-rib construct (used as a control) was not-auxetic for the values of true strain that were tested (0–0.2). Because PEG is not auxetic, our results show that pore geometry (or unit-cell shape) induced auxetic behavior as predicted by analytical models and our deformation simulations (Figure 1).

The experimental Poisson’s ratios for the single-layer reentrant construct decreased linearly (in magnitude) from approximately −1 to approximately −0.5 for increasing values of true axial strain from 0–0.2 (Figure 3A). This corresponds to a linear rate of change in Poisson’s ratio (magnitude) of approximately −3 (Δυ_xy/Δε_x) for ζ ≥ 40° (note: Δ denotes change, i.e., the difference between the final and undeformed or initial values).

According to the simple hinging model reported by Gibson and Ashby,^[1] axial strain causes solely a change in angle ζ while the magnitude of the negative Poisson’s ratio depends upon both ζ and the ratio L₂/L₁, where the rib-length ratio is assumed to stay constant (see the Supporting Information, Equation 3). Accordingly, if you examine the optical images for the reentrant sheet in Figure 4A, it is evident that there is, indeed, predominately hinging of angle ζ with little flexure or change in rib length. For L₂/L₁ = 1.33 (our structures as denoted in Figure 1B), which gave an undeformed angle ζ of approximately 40°, the hinging model yields a theoretical Poisson’s ratio of approximately −1 at zero strain that linearly decreases (magnitude) to about −0.7 for axial strains of 0–0.2 and (see the Supporting Information, Equation 3 and Figure S2). This corresponds to a linear change in Poisson’s ratio (in magnitude) at a rate of approximately −2 (Δυ_xy/Δε_x) for ζ ≥ 40°. Moreover, from Equation 4 in the Supporting Information, axial strains between 0–0.2 theoretically cause angle ζ to increase from 40° to approximately 52° (changes in angle ζ were not measured experimentally). Thus, our experimental values (−1 to −0.5) are very similar to those predicted by the analytical model (−1 to −0.7) for axial strains of 0–0.2.

In one of the reentrant experiments, we extrapolated a Poisson’s ratio of approximately −2.6 for a small axial strain (less than 0.05), though we found a logarithmic increase in Poisson’s ratio to nearly −1 after just a slight increase in axial strain (Figure 3A, red reentrant markers). According to the hinging model, the magnitude of the negative Poisson’s ratio does, indeed, decline in a logarithmic fashion as ζ gets smaller for about ζ ≥ 40°; however, based on the fact that the undeformed ζ in our samples was approximately 40° and the nominal axial strains applied to each sample were the same, it is likely that this particular sample had some inherent mechanical discrepancies introduced by the DMD-PP fabrication process. In could have also been possible that the scaffold was slightly compressed due to the way the sample was introduced into our strain measurement system. Nevertheless, our data for the single-layer reentrant construct agrees quite well with the simple hinging model.

The single-layer missing-rib structure demonstrated Poisson’s ratios of about −0.3 to −0.5 (Figure 3A), which showed that Poisson’s ratio stayed relatively constant for the range of axial strains tested in our experiments. Our results agree closely with the model reported by Gaspar et al.,^[38] who expanded the original missing-rib model developed by Smith et al. (see the Supporting Information, Equation 5).^[39] Both models neglect rib stretching and bending (flexure), though each model has subtle differences. The Gaspar missing-rib model (Supporting Information, Equation 6) was derived from engineering strain considerations and assumed hinging of the central angle α (Figure 1B, missing-rib model), i.e., |Δα| ≥ 0 (and Δα*/Δβ ≥ 0 where α*= 180 − α) in addition to the hinging proposed in the Smith model. The Smith model assumes unit-cell unfolding with hinging of joint angles φ₁, φ₂, and b (Figure 1B) and only rotational deformation around the central node so that Δα = 0 (and Δα*/Δβ = 0). If you examine the optical images for the missing-rib sheet (Figure 4A), it is evident that there are, indeed, predominately changes in φ₁and φ₂ as proposed in the Smith model, with little central node hinging. For the dimensions of our missing-rib structure (Figure 1B), the Smith model predicts a υ_xy = −1, overshooting Poisson’s ratio by two-fold in magnitude, while the Gaspar model predicts a linearly increasing (although nearly constant) Poisson’s ratio from −0.4 to −0.5 for axial strains of 0–0.2 for Δα*/Δβ = 0.5 (see the Supporting Information, Equation 6 and Figure S2). Using Equation 7 in the Supporting Information, angle β was calculated to have theoretically increased from 40° to approximately 55° for axial strains between 0–0.2 (changes in angle β were not measured experimentally). Because our data matches up well with the Gaspar model, one would assume that there is some change in angle α resulting from central node hinging, and would have amounted to about one-half the change in angle β.

The single-layer intact-rib constructs demonstrated experimental Poisson’s ratios which varied from slightly below 0.8 to over 1.8 in an exponential fashion according to υ_xy ∝ e^kε_x where k is the relative growth rate, and was an average of k = +3 in our experiments (Figure 3A) for axial strains from approximately 0–0.2^[41]. The Smith intact-rib model^[39] yielded similar results with a k ≈ 5 for γ of 86° and β = 45° (the single-layer constructs had γ = 90° and β = 45° as shown in Figure 1B), resulting in an exponential increase in Poisson’s ratio from approximately 1–2.5 for the same range of axial strains as tested in our experiments (see the Supporting Information, Equation 8 and Figure S2). The Smith model assumes that deformation is caused solely by the hinging of angle γ with little to no rib stretching or flexure. The optical images for the intact-rib sheet (Figure 4A) appear to confirm the model as they show mostly hinging of angle γ, causing the square pore shape to become oblong. For axial strains of 0–0.2, the Smith intact-rib model yields a decrease in angle γ from 90° to approximately 65° (changes in angle γ were not measured experimentally; Supporting Information, Equation 9). Although our experimental values for Poisson’s ratio data (0.8–1.8) grew at a slower rate than predicted by the missing-rib model, the model still appears to be a good approximation of the behavior of the single-layer constructs.

In comparing the single-layer data among the three strain tests performed for each unit-cell geometry, Poisson’s ratios appeared to be quite consistent (Figure 3A). Some variability existed, as expected, likely because of the fact that each experiment was performed with a different sample. Small, yet unavoidable, differences in the samples were likely introduced during DMD-PP fabrication, which would have imposed some differences in elasticity. It is also possible that the constructs experienced some minor pre-loading and straining when they were secured in our strain testing system, which could have affected the Poisson’s ratio values at small strains. However, it is clear that geometry and spatial arrangement of the pores (unit-cell) controlled the polarity and magnitude of the Poisson’s ratio of the overall meshworks, and that the strain-dependent behavior was predicted well by stress-strain analytical models. Thus, the single-layer sheets demonstrated negative Poisson’s ratios that were both determinate and tunable by virtue of their well-defined cellular meshworks. Further discussions of the analytical models can be found in the Supporting Information, Discussion 2.

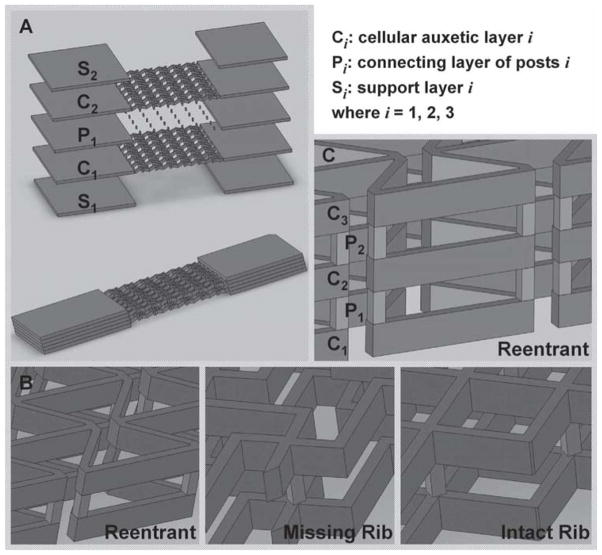
Based on the lattice meshworks of our single-layer constructs, we fabricated three-dimensional PEG scaffolds (Figure 5A, B) by stacking two single-layer sheets (C₁ and C₂) with a layer of vertical posts (P₁). The double-layer constructs were fabricated in a layer-by-layer manner using a series of virtual photomasks in DMD-PP; each layer was approximately 100 micrometers thick and the rib structures were approximately 40 micrometers in width. Figure 2D–F show SEM images of the double-layer PEG constructs fabricated with DMD-PP. The superimposed layers were aligned precisely on top of one another, though you can clearly see the separate layers in the magnified angle views shown in the SEM insets. As with the single-layer constructs, each layer of the multi-layer constructs had rectangular blocks that provided for mechanical support for handling and strain testing. The double-layer scaffolds have an internal pore architecture that is open to the environment and completely interconnected as desired in a tissue construct. Movies in the Supporting Information show the elastic behavior of the double-layer constructs having the reentrant (Movie 4), missing-rib (Movie 5), and intact-rib (Movie 6) meshworks.

Figure 5.

A) Schematic image of the double-layer auxetic scaffolds assembled by stacking single-layer cellular constructs with a connecting layer of vertical posts; B) magnified views of the double-layer stacks; C) magnified view of a triple-layer stack containing constructs with the reentrant pore structure. The design approach shown in (A) was used to make the triple-layer structure.

Strain experiments were conducted on the double-layer constructs to determine if the addition of multiple layers would alter the Poisson’s ratios relative to the single-layer constructs. Figure 3B shows the strain-dependent Poisson’s ratios for the double-layer constructs for axial strains of approximately 0–0.2; two experiments, denoted by color, were performed for each type of construct. Figure 4B shows optical images of the double-layer constructs in their undeformed and deformed states; the insets show the deformations in the individual pores. The double-layer reentrant and missing-rib constructs continued to exhibit auxetic behavior while the intact-rib construct persisted to show a positive Poisson’s ratio.

The reentrant scaffold exhibited a relatively constant Poisson’s ratio of approximately −0.8 to −0.9 for strains up to slightly less than 0.20 (Figure 3B). In one of the double-layer reentrant experiments, we found a Poisson’s ratio of −0.5 for an axial strain of 0.05 (red data markers for the reentrant unit-cell, Figure 3B); however, for a slight increase in axial strain (<0.005 increase in ε_x), the Poisson’s ratio increased (magnitude) from −0.5 to −0.9 and then remained relatively stable for increasing axial strains. Comparing the optical images of Figure 4 between the single- and double-layer reentrant constructs, the deformation of the individual pores (insets) appears very similar, in terms of the deformation mechanisms where mostly hinging of angle ζ occurs. Moreover, both auxetic layers, C₁ and C₂ (Figures 5A, B), appeared to deform equally and in tandem without slipping as evident in the optical photos (Figure 4B). There was a small discrepancy in the Poisson’s ratios between the single- and double-layer reentrant constructs as the single-layer constructs had a Poisson’s ratio that started at approximately −1 and linearly decreased to about −0.5, while the double-layer constructs demonstrated a Poisson’s ratio of almost a constant −0.9 (Figure 3). It is possible that adding the second layer may have caused this discrepancy, but it still appears that adding an additional layer did not alter the strain-dependent Poisson’s ratio to a large degree.

The double-layer missing-rib scaffold exhibited a Poisson’s ratio of approximately a constant −0.5 in both strain tests (Figure 3B). Comparing deformations in the individual pores between the single-layer and double-layer missing-rib constructs (Figure 4), the additional layer had very little impact on the deformation mechanisms of the unit-cell (still mostly hinging of φ₁ and φ₂).

Poisson’s ratios for the two intact-rib experiments varied in magnitude slightly, varying from 0.9 to 1.3 in one experiment and 1.1 to 1.5 in the other, both for axial strains between 0 and 0.25 (Figure 3B). In both strain tests of the intact rib, the Poisson’s ratio increased exponentially with an average relative growth (k) of approximately +2 (υ_xy ∝ e^kε_x), which was very similar to the single-layer intact-rib constructs. As was the case for the double-layer reentrant scaffold, the optical images show that the individual pores (Figure 4B) in the vertically aligned cellular layers appeared to deform equally and in tandem.

Comparing the two strain tests performed for each type of double-layer scaffold, Poisson’s ratio showed some variability likely due to the fact that a different scaffold was used in each test (Figure 3B); this was the case for the single-layer constructs as well. Additionally, despite some small disparities between the Poisson’s ratios of the single- and double-layer constructs, the addition of the second cellular layer appeared to have little influence on Poisson’s ratio. This rather congruous behavior suggests that the same three-dimensional configuration (Figure 5A, B) could be used to make an auxetic scaffold with more than two layers. Applying the design approach of Figure 5A, we used DMD-PP to build a triple-layer reentrant scaffold (Figure 5C). Three separate auxetic layers (C₁, C₂, C₃) were connected by alternating layers of vertical posts (P₁, P₂). Figure 2G-I shows SEM images of the triple-layer reentrant construct. Similar to the double-layer scaffolds, the vertical alignment of the cellular layers is quite precise, making it very difficult to make out the multiple layers from a top view of the scaffold; however, you can clearly distinguish the layers from the magnified angular perspectives (Figure 2H, I).

3. Conclusions

We constructed single-layer and double-layer PEG scaffolds, which exhibited tunable in-plane negative Poisson’s ratios. The single-layer constructs were designed from analytical models found in the literature, and were found to have Poisson’s ratios that were consistent with the models. The double-layer scaffolds were fabricated by assembling single-layer constructs in a layer-by-layer fashion and contained pores that were accessible to the environment and completely interconnected as desired in a polymer tissue scaffold. The double-layer scaffolds exhibited strain-dependent Poisson’s ratios that were very similar to those of the single-layer constructs, which suggests that adding additional layers to a scaffold does not markedly affect the tunability of the Poisson’s ratio. Finally, we used our multi-layer scaffold design scheme to fabricate a triple-layer reentrant scaffold with precise vertical alignment, which shows that our design methodology can be used to make a biomaterial construct with multiple layers.

4. Experimental Section

Preparation of Photocurable Monomer

Poly (ethylene glycol) diacrylate (PEGDA, mol. wt. = 700), acrylic acid (AA), and 2,2,6,6-tetramethylpiperidine 1-oxyl (TEMPO, free-radical quencher) were obtained from Sigma–Aldrich. Photoinitiator Irgacure 2959 and TINUVIN 234 UV-dye were obtained from Ciba Chemistry. TINUVIN 234 is a UV-absorbing agent, which was used to reduce the curing depth of the monomers and adjust the thickness of the microstructures in the DMD-based layer-by-layer fabrication process. TEMPO, on the other hand, enhances the contrast of the UV-curing process and optimizes feature resolution at the projection plane. Irgacure 2959 [1% (w/v)], TINUVIN 234 [0.15% (w/v)], and TEMPO [0.01% (w/v)] were added to the PEGDA monomer and mixed thoroughly.

Digital Micro-Mirror Array Device Projection Printing (DMD-PP)

Figure S1 of the Supporting Information shows a schematic of the DMD-based system used to fabricate the auxetic polymer scaffolds. Two-dimensional (2D) graphics models of the scaffold layers were designed in computer-aided drafting (CAD) software (AutoCAD LT 2006; Autodesk, Inc., San Raphael, CA, USA). CAD models in the drawing interchange format (DXF file extension, outputted from AutoCAD) were converted into standard bitmap format (BMP file extension) and exported to LabVIEW software (National Instruments, Austin, TX, USA), which was used to control the DMD system. The bitmap graphics files were used as virtual photomasks during the DMD layer-by-layer photocuring process.

A servo-stage was positioned 100 μm below a transparent quartz plate (quartz microscope slide), leaving a 100 μm gap between the plate and the stage. Photocurable prepolymer (10 μL) was injected into the gap with a syringe pump. The gap-spacing controlled the thickness of the photo-polymerized layer of PEG. Light emitted from the UV source was passed through a projection lens down to the projection plane, which was coplanar with the bottom side of the quartz substrate (UV source not shown in Supporting Information, Figure S1). The light was spatially modulated at the projection plane by a digital micro-mirror (DM) array controlled by the virtual software masks. Prepolymer was exposed with a 50 mW/cm² dose of UV-light for 11 sec to solidify select locations of the PEG.

After an individual layer was patterned, the stage was translated downwards 300 μm, pulling the solidified micropatterned sheet of PEG off the quartz substrate so that it only remained attached to the servo-stage. The release process was aided by coating the substrate with a silane (tridecafluoro-1,1,2,2-tetrahydrooctyl-1 trichlorosilane) (United Chemical Technologies, Inc., Bristol, PA, USA), which gave the surface a low surface energy (or high contact angle).^[42,43] After a layer was fabricated, uncured polymer was washed away with deionized water. To create a second layer, the stage was translated slightly upwards until the top of the previously formed structure was approximately 100 μm below the quartz substrate, leaving another 100 μm gap. Once again, fresh prepolymer was pumped into the 100 μm gap, and the polymer was selectively cured using another software mask. The steps were repeated using a combination of software masks until a three-dimensional multilayer scaffold was constructed.

Stress-Strain Finite Element Simulations

AutoCAD LT was used to design the 2D scaffold layers with the desired unit-cell structures. The unit-cell structures were designed from analytical models proposed in the literature. The 2D models were imported into Solidworks (Solidworks 2009, Dassault Systèmes SolidWorks Corp., Concord, MA, USA) and extruded to form 3D models of the single-layer sheets. The 3D models were utilized to simulate the elastic stress-strain (deformation) behavior of the single-layer PEG constructs using finite element analysis (also conducted with Solidworks; Figure 1A), taking into account the material properties of the PEG. The simulations allowed us to determine if the unit-cell structures would, theoretically, yield auxetic behavior as desired. The simulations were performed in the same way in which the strain experiments were conducted, i.e., where one of the rectangular side-blocks was fixed (see Figure 1), while an axial tensile stress was applied to the other rectangular block causing the scaffold to strain. 3D simulations were conducted for each unit-cell type (reentrant, missing-rib, and intact-rib unit-cells).

Strain Testing for the Determination of Poisson’s Ratios

The PEG constructs were loaded into a homemade strain measurement system by fixing one of their ends (at the rectangular blocks, see Figure 1 and Figure 5) on an immovable stage while fixing their other end on a movable single-axis (axial direction) nano-positioning stage. The stage was connected to a motorized servo-actuator (CMA-25CCCL Closed-Loop DC Servo-actuator, Newport Corp., Irvine, CA, USA) that was capable of providing motion in 200-nm incremental steps. The actuator was driven and controlled by an axis-motion controller (ESP300 Axis Motion Controller and Driver, Newport Corp., Irvine, CA, USA) that provided stable and precise movement along with a programmable Lab View interface (LabView^™, National Instruments, Austin, TX, USA). A “pulling” axial tensile stress was applied to the end of the PEG constructs, attached to the movable stage, by the motion of the actuator while the other end of the PEG constructs, which were fixed to the immovable stage, remained still. The axial stresses exerted on the constructs ultimately caused them to strain in the axial direction. In-plane movement of the construct in the axial and transverse directions was observed with a color CCD camera system with magnifying optics (CV-S3200P CCD camera, JAI Inc., San Jose, CA, USA; magnifying camera optics, Edmund Industrial Optics, Barrington, NJ, USA).

Still images were recorded with the CCD camera for precise levels of travel of the actuator stage. Axial and transverse strains were estimated by measuring the displacement in the axial and transverse directions, respectively. Digitizer software (GetData Graph Digitizer 2.24, http://www.getdata-graph-digitizer.com) was used to digitize the optical images so that the displacements could be accurately determined based on the undeformed in-plane dimensions of the constructs. Digitized SEM images were used to determine the undeformed dimensions. Movies 1–6 in the Supporting Information show the deformation behavior of the single-layer (Movies 1–3) and double-layer (Movies 4–6) PEG constructs. Movie 1 and 4 shows the axial and transverse expansions of the single- and double-layer reentrant constructs; Movie 2 and 5 shows the axial and transverse expansion of the single- and double-layer missing-rib constructs; Movie 3 and 6 shows the deformation of the single- and double-layer intact-rib construct (used as controls), which demonstrate axial expansion but transverse compression due to a positive Poisson’s ratio.

Scanning Electron Microscopy (SEM)

Samples were coated with a thin 10-nm layer of platinum/palladium by sputter coating (208HR High-Resolution Sputter Coater, Cressington Scientific Instruments, Watford, England). SEM images were acquired with a Zeiss SUPRA 40 VP (variable pressure) Field-emission Scanning Electron Microscope at 30 kV (Zeiss SUPRA 40 VP FESEM, Carl Zeiss SMT Inc., Peabody, MA, USA).

Calculation of Poisson’s Ratios

Details of the Poisson’s ratio calculations can be found in Supporting Information, Discussion 1.

Unit-Cell Analytical Models

Further details of the analytical cellular models can be found in Supporting Information, Discussion 2. Figure 2 of the Supporting Information shows Poisson’s ratio as a function of true strain as given by the analytical models.