Abstract
Summary: StochKit2 is the first major upgrade of the popular StochKit stochastic simulation software package. StochKit2 provides highly efficient implementations of several variants of Gillespie's stochastic simulation algorithm (SSA), and tau-leaping with automatic step size selection. StochKit2 features include automatic selection of the optimal SSA method based on model properties, event handling, and automatic parallelism on multicore architectures. The underlying structure of the code has been completely updated to provide a flexible framework for extending its functionality.
Availability: StochKit2 runs on Linux/Unix, Mac OS X and Windows. It is freely available under GPL version 3 and can be downloaded from http://sourceforge.net/projects/stochkit/.
Contact: petzold@engineering.ucsb.edu
1 INTRODUCTION
Traditional deterministic representations of biochemical systems are useful when the interacting chemical species are present in high concentrations. However, many processes in systems biology are driven by reactions between chemicals with small copy numbers. These processes are inherently stochastic and often display behavior that cannot be captured by deterministic models.
Gillespie's stochastic simulation algorithm (SSA) provides a method for generating trajectories that capture the stochastic behavior of biochemical models (Gillespie, 1977). The SSA begins with a model of N chemical species {S1, S2,…,SN} with associated discrete populations {x1, x2,…,xN}. These species interact via M reaction channels {R1, R2,…,RM}. Reaction Ri is characterized by a stoichiometric vector denoted vi and a propensity function denoted ai. The stoichiometric vector describes the change in population that occurs when reaction Ri fires. The propensity function describes the probability that reaction Ri will occur in the next infinitesimal time interval dt. With a few simplifying assumptions, including spatial homogeneity, the evolution of the system can be represented as a Markov jump process that is described by the chemical master equation (CME).
The CME is generally too complex to solve directly. The SSA is a Monte Carlo method that proceeds by simulating every reaction event in the system to generate exact trajectories of the CME. Generally, an ensemble of trajectories is run to obtain an estimate of the probability distribution. Since Gillespie's pioneering work, there have been numerous advances in efficient exact SSA variants as well as approximate methods that sacrifice exactness in exchange for increased computational efficiency (e.g. Cao et al., 2004, 2006; Gillespie, 2001; Slepoy et al., 2008).
The StochKit2 software package allows practicing systems biologists to perform stochastic simulations of biochemical models. The simulation algorithms automatically detect and utilize multicore architectures for efficiency and perform consistency checks for reliability. The code has been built upon a carefully designed simulation framework to be easily extensible.
2 FEATURES AND IMPLEMENTATION
In this section we present a brief overview of the key features of StochKit2. For more information, a detailed user's manual is provided with the StochKit2 distribution.
2.1 Simulation algorithms
StochKit2 provides implementations of several (exact) SSA algorithms, including the direct method (Gillespie, 1977), optimized direct method (Cao et al., 2004) and composition-rejection method (Slepoy et al., 2008). These methods all generate exact samples (trajectories) from the chemical master equation but use modified underlying formulations of the SSA and data structures to achieve different performance and scaling properties. The direct method, which uses simple data structures, tends to be best for relatively small models. For very large models, the composition-rejection method of Slepoy et al. (2008) is most efficient because the constant scaling (with respect to the number of reaction channels) outweighs the overhead of maintaining the more complicated data structures. For all this complexity, the StochKit2 user interface is simple: ‘ssa’. When a user runs the SSA method, the software immediately analyzes the model and simulation options and chooses the appropriate algorithm automatically.
StochKit2 also provides an interface for running stochastic simulations using an adaptive, explicit tau-leaping method (Cao et al., 2006; Gillespie, 2001). The tau-leaping method sacrifices exactness in exchange for taking larger time steps. The algorithm adaptively selects the step size based on an error tolerance and reverts to the SSA method when tau-leaping is not advantageous. Again, the user interface is simple: ‘tau_leaping’. However, advanced users have the flexibility to set the error tolerance and the conditions under which the method reverts to the SSA.
2.2 Model representation
StochKit2 uses a simple XML-based format for its model specification files. For example, a reaction such as
| (1) |
is represented using ‘<Reactant>’ (S1 and S2) and ‘<Product>’ (S3) tags. The stoichiometric vector for a reaction is the difference between the Product and Reactant vectors. For an elementary reaction such as (1), the rate constant c determines the propensity function (a=cx1 x2) and is stored in the <Rate> tag. However, StochKit2 also allows users the flexibility to define arbitrary functions (e.g. Michaelis–Menten rates) as propensities using mathematical functions, state variables and parameters. The model files are editable in any standard text editor and several example model files are provided with the StochKit2 distribution. For models already represented in the Systems Biology Markup Language (SBML; Hucka et al., 2003), an SBML to StochKit2 model conversion function is provided.
2.3 Event handling
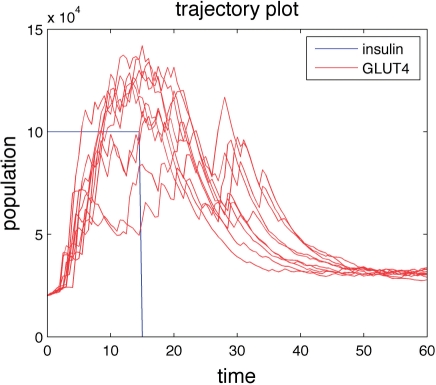
Another new feature in StochKit2 is a version of the SSA direct method with built-in support for event handling. Events are discrete changes in the system state or parameter values that occur when a condition is satisfied. These events' ‘triggers’ can be time-based or state-based and are typically used to mimic biological processes or to recreate experimental conditions. For example, Kwei et al. (2009) used a time-based trigger event to remove insulin from an insulin-signaling model when the simulation time reached 15 min, to match an experimental protocol (see Fig. 1).
Fig. 1.
Plot of 10 trajectories of a stochastic insulin-signaling model based on Kwei et al. (2009). Constant insulin input (blue) stimulates glucose transporter, GLUT4 (red). At t=15, insulin is removed from the system using the event handling capabilities in StochKit2.
2.4 Output options and visualization tools
By default, StochKit2 computes the mean and variance of all chemical species in the simulated model. The user can choose to save output at any number of uniformly spaced time intervals. In addition to statistics, StochKit2 can also store individual trajectories and histogram data. Means, variances and trajectories data are stored as ASCII text files to be easily readable by standard visualization software.
2.4.1 Visualization tools
StochKit2 provides several plotting and analysis tools for visualizing simulation data. These tools are provided as MATLAB/Octave compatible functions. For each simulation output data type, there is an associated plotting function (e.g. plotStats, plotTrajectories, plotHistograms). In addition, there is a histogram distance function that computes Euclidean and Manhattan distances between two histograms and graphs them on the same axes using transparent colors to show the overlap in the distributions.
3 CONCLUSION
StochKit2 is an efficient and extensible software package for discrete stochastic simulation of biochemical systems. It provides implementations of several exact and approximate SSA variants, including an implementation of the SSA that handles events. It runs on Windows, Mac OS X, and Linux/Unix and is free for non-commercial use. StochKit2 is available for download at http://sourceforge.net/projects/stochkit/.
Funding: National Institute of Biomedical Imaging and Bioengineering (Grant No. R01EB007511); Institute for Collaborative Biotechnologies from the US Army Research Office (Grant No. DFR3A-8-447850-23002); DOE Contract No. DE-FG02-04ER25621; NSF Contract No. IGERT DG02-21715 and DMS-1001012; National Science Foundation Graduate Research Fellowships (to K.S. and R.K.L).
Conflict of Interest: none declared.
REFERENCES
- Cao Y., et al. Efficient formulation of the stochastic simulation algorithm for chemically reacting systems. J. Chem. Phys. 2004;121:4059–4067. doi: 10.1063/1.1778376. [DOI] [PubMed] [Google Scholar]
- Cao Y., et al. Efficient step size selection for the tau-leaping simulation method. J. Chem. Phys. 2006;124:044109. doi: 10.1063/1.2159468. [DOI] [PubMed] [Google Scholar]
- Gillespie D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977;81:2340–2361. [Google Scholar]
- Gillespie D.T. Approximate accelerated stochastic simulation of chemically reacting systems. J. Chem. Phys. 2001;115:1716–1733. [Google Scholar]
- Hucka M., et al. The Systems Biology Markup Language (SBML): a medium for representation and exchange of biochemical network models. Bioinformatics. 2003;19:524–531. doi: 10.1093/bioinformatics/btg015. [DOI] [PubMed] [Google Scholar]
- Kwei E., et al. Proceedings of the 2009 FOSBE Conference. Colorado, USA: Denver; 2009. Model-based therapeutic target discrimination using stochastic simulation and robustness analysis in an insulin signaling pathway. [Google Scholar]
- Slepoy A., et al. A constant-time kinetic Monte Carlo algorithm for simulations of large biochemical reaction networks. J. Chem. Phys. 2008;128:205101. doi: 10.1063/1.2919546. [DOI] [PubMed] [Google Scholar]