DECOD: fast and accurate discriminative DNA motif finding

Abstract

Motivation: Motif discovery is now routinely used in high-throughput studies including large-scale sequencing and proteomics. These datasets present new challenges. The first is speed. Many motif discovery methods do not scale well to large datasets. Another issue is identifying discriminative rather than generative motifs. Such discriminative motifs are important for identifying co-factors and for explaining changes in behavior between different conditions.

Results: To address these issues we developed a method for DECOnvolved Discriminative motif discovery (DECOD). DECOD uses a k-mer count table and so its running time is independent of the size of the input set. By deconvolving the k-mers DECOD considers context information without using the sequences directly. DECOD outperforms previous methods both in speed and in accuracy when using simulated and real biological benchmark data. We performed new binding experiments for p53 mutants and used DECOD to identify p53 co-factors, suggesting new mechanisms for p53 activation.

Availability: The source code and binaries for DECOD are available at http://www.sb.cs.cmu.edu/DECOD

Contact: zivbj@cs.cmu.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

DNA motif discovery has been a central problem in computational biology for almost two decades. Many methods based on word enumeration or probabilistic models including position weight matrices (PWMs) and Hidden Markov models (HMMs) have been developed for this task (Das and Dai, 2007). Word enumeration-based methods are usually only able to find short motifs and tend to fail when the motif includes weak positions (Das and Dai, 2007). Most probabilistic methods involve iteratively scanning the input sequences to identify potential motifs and then updating the motifs to improve the likelihood of the model until convergence (Bailey and Elkan, 1994; Frith et al., 2004; Roth et al., 1998; Sinha and Tompa, 2003). In such methods motifs are usually defined as subsequences, which are present at a much higher rate than expected when compared with a background model (D'Haeseleer, 2006).

The use of motif discovery methods has dramatically increased over the last few years due to the rise in sequencing capacity and the advancement of other high-throughput methods. These methods are routinely used to identify and predict transcription factor binding sites (Hu et al., 2010), protein phosphorylation sites (Schwartz and Church, 2010), microRNAs targets (Linhart et al., 2008) and alternative splicing locations (Suyama et al., 2010). However, these high-throughput methods have also led to new requirements from motif search algorithms. The first is speed. Many studies now routinely search for motifs in very large sets of input sequences. For example, several ChIP-Seq experiments identify thousands of targets for specific mammalian transcription factors (Robertson et al., 2007; Yu et al., 2009). The second requirement is for identifying discriminative motifs (Sinha, 2003). Unlike traditional motif searches that are performed against a general background model, in discriminative motif search one looks for motifs that are present at a high rate in a positive set compared to a negative set. These sets can be genes that are up- or downregulated at a specific time point or condition (Ernst et al., 2007), proteins that are initially co-localized but later diverge, genes that are bound in one condition by a TF but not in another, etc. These and other studies, including cross species analysis and methods for modeling gene regulation, require discriminative motif discovery methods that can scale to large datasets.

Several discriminative motif-finding methods have been developed so far. DIPS (Sinha, 2006) uses a probabilistic score to quantify the difference in the number of occurrences of a PWM between two sets of sequences and uses heuristic hill climbing to search the sequences for motifs that maximizes this score. ALSE (Leung and Chin, 2006) uses a target function based on the hypergeometric distribution. This function searches for a PWM using an EM-like heuristic and then evaluates the likelihood that the PWM it identified represents a real motif. DEME (Redhead and Bailey, 2007) performs a combination of global and local search to find a PWM that maximizes the conditional log likelihood of the sequence labels given the sequences and models parameters. Seeder (Fauteux et al., 2008) is a word-based enumerative method. It first generates seeds by finding significantly enriched words in the positive set based on a word-specific background probability distribution, and then iteratively extends these seeds to form a new PWM and updates the seeds until convergence. CMF (Mason et al., 2010) is also a word-based method that starts by finding enriched words in the positive set based on a z-score, and then iteratively updates the motif model and rescans the sequences to update the seeds and avoid false positives until convergence. See Supplementary Material for detailed descriptions.

While the above methods can successfully identify discriminative motifs, they usually do not scale well for large sequence datasets since they are based on repeated analysis of the positive and negative sequences. For example, DIPS (Sinha, 2006) was only suggested to be run on tens of sequences with length around 1000bp, and even so its run time is very long (several hours). The running time of DEME (Redhead and Bailey, 2007) depends quadratically on the size of the positive sequences, making it prohibitive for most motif discovery tasks. Other methods are also slow when dealing with large datasets as we show in Section 3.

DME (Smith et al., 2005) attempts to address the speed issue by enumerating over a discrete space of pre-defined matrices representing possible motifs. It then uses a log likelihood ratio as a target function to score the overrepresentation of a motif matrix in one set of sequences versus another. However, while DME is indeed very fast, it is based on a pre-defined set of matrices and is thus often restricted in terms of the set of motifs it can identify. In addition, DME ignores the context information encoded as part of the sequences, which may lead to a shifted PWM that does not accurately represent the real motif.

In this article, we present a new method that addresses both the speed and accuracy issues for discriminative motif finding. Our method, deconvolved discriminative motif finder (DECOD), only uses k-mer counts and so does not depend on the size of the input set. To compensate for the errors introduced from ignoring the dependence between the consecutive and overlapping k-mers in the sequences that they are from (the context of a k-mer), we use a deconvolution method that accounts for the higher rates of k-mers containing subsets of the true motif. We applied the method to simulated and biological benchmark data and compared it with previous methods. As we show, our method enables motif discovery in cases that could not have been studied before due to the size of the input, and it outperformed other methods in terms of both accuracy and running time. We used our method to study various post-translational modification of the human transcription factor p53. We performed new ChIP-chip experiments and identified different sets of binding targets for the p53 mutants. Using our new motif discovery algorithm we were able to identify a number of potential co-factors of p53 and study the way in which they interact with p53.

2 METHODS

2.1 DECOnvolved Discriminative motif discovery method

Similar to other methods (Fauteux et al., 2008; Leung and Chin, 2006; Redhead and Bailey, 2007; Smith et al., 2005; Sinha, 2006), DECOD starts with a user-specified motif length k. Given k, we extract all k-mers from the positive and negative sequences (Fig. 1). Following this step the entire analysis is only performed on the k-mer counts table. Since the size of this table is independent of the number and length of the input sequences, DECOD scales very well to large datasets.

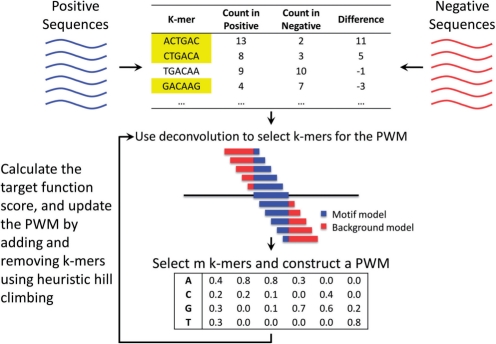
Fig. 1.

Overview of DECOD. We extract counts of all k-mers in the positive and negative sequences (top) and store them in a k-mer count table. Next, we search for a discriminative PWM that matches many k-mers on the positive set while only matching a few on the negative set. The PWM is constructed using a site set containing a small number of k-mers (highlighted in yellow). To determine which k-mers to include in the site set we use a deconvolution based target function (middle) which overcomes the lack of context information for the k-mers. Once appropriate k-mers are identified we revise the PWM (bottom) and the process is repeated until no further improvement to the target function can be achieved.

We assume a generative mixture model for k-mer distributions: Each k-mer is either generated by the motif model represented by a PWM, or by the background model (similar to a zeroth-order HMM). Following (Sinha, 2006), DECOD searches for a PWM that maximizes a discriminative target function: the difference in the expected number of times that the motif model is used to generate the positive and negative sequences (Fig. 1, top). The PWM is constructed from a subset of the k-mers which are selected based on the k-mer count table (termed ‘the site set’ (Sinha, 2006), highlighted k–mers in Figure 1). While using only the k-mer counts provides significant speed benefits with large input datasets, such representation ignores important context information for each k-mer within a sequence. This may result in selecting shifted versions of the same k-mers that lead to a convolved (and inaccurate) PWM (Fig. 1, middle). To correct for this we use a deconvolution method that accounts for the higher rates of k-mers that contain a subset of the true motif in the positive set. In an iterative process we continuously improve our PWM by adding and removing k-mers from the site set using heuristic hill climbing search methods until convergence. Once the algorithm converges we remove instances of the identified PWM from the k-mer count table, and then search for a second PWM and so forth. We next discuss each of these steps in details.

2.1.1 The mixture model for k-mers

DECOD uses the following mixture model that includes a motif component Z and a background component B to model the k-mer distribution M:

(1)

Here, Z and B are the probability distributions over the k-mers (i.e. non-negative vectors of dimension 4^k whose entries sum to 1) generated by the motif and background models respectively and p is the probability of motif occurrence. The mixture model M can also be considered as a zeroth order HMM that generates k-mers as follows: (i) choose a hidden state h from {z, b} with state probabilities p and 1−p respectively; (ii) if h=‘z’, emit a k-mer according to the distribution Z; if h=‘b’, emit a k-mer according to the distribution B.

2.1.2 The motif component Z and deconvolution

The simplest way to model Z by a PWM θ is to define each element Z_a to be

(2)

in which a=a₁…a_k is a k-mer, θ_i,ai is the entry for the letter a_i in the i's column of θ and we use θ^a as a shorthand notation for Pr(a|θ). We call such Z simple motif component.

However, our method for extracting overlapping k-mers, while greatly speeding up computational time for large input datasets, ignores the context of the k-mers. Thus, several k-mers that do not fully match the motif may still overlap parts of it and thus may be overrepresented in the data. To overcome this, note that each k-mer in its context can be generated by 2k−1 combinations of the motif component and the background component (Fig. 1). Thus instead of the simple PWM mixture component, we define the following convolved motif component:

(3)

where Z₀ is the k-mer frequencies obtained from the PWM θ, and Z_j the k-mer frequencies from a PWM obtained by taking the first j columns of θ (or the last j columns if j<0), and adding k−j columns of background as a prefix (or suffix if j<0). Note that using the convolved motif component, the mixture model becomes

(4)

2.1.3 Discriminative PWM search

We are given a set of positive sequences S₊ and a set of negative sequences S₋ as input. Normalized k-mer counts are extracted and denoted by X for the positive set and Y for the negative set, and together they form the input for DECOD. Assuming that X was generated by the mixture model, the expected number of times that the motif component Z was used in the zeroth-order HMM is

(5)

in which Z_a=Pr(a|θ) is the probability of observing a under the motif model, B_a=Pr(a|B) is the probability of observing a under the background model, and X_a is the count of a in the positive sequences. A similar expression can be written for Y.

Following (Sinha, 2006), given X, Y as input, we aim to maximize the expected difference

(6)

in which Z and B represent the estimated distributions on k-mers as discussed above. The background B is estimated from the base frequencies of the input sequences using a simple zeroth-order model. Below we will regard B as a PWM as well, with all columns equal.

Assuming a simple motif component Z, let θ denote the PWM for Z. Then the discriminative score can be written as

(7)

For a convolved motif component Z, a similar formula can be derived. For PWMs A, B of length k, let 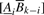denote the PWM obtained by concatenating the last i columns from A with the first k−i columns from B. Then the discriminative score for the convolved motif component is:

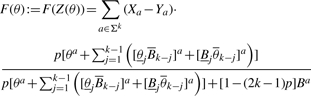(8)

As before, our aim is to find a PWM θ that maximizes the above function, and we adopt a discretized heuristic hill climbing approach very similar to DIPS (Sinha, 2006) to search for this PWM (Methods in Supplementary Material). After a PWM is found, we remove the signals of that PWM from the k-mer count table and start searching for a second one if desired. See Methods in Supplementary Material for details.

In practice when the two input datasets are not equal in size and have different base frequencies, we replace the counts X_a and Y_a above with the frequencies of the k-mer a in the two sets, and we use different Bs estimated from the two sets respectively, and calculate w(X; Z) and w(Y; Z) separately. Also for the probability of motif occurrence p, we show that similar to DIPS (Sinha, 2006), our method is not sensitive to the choice of this parameter (Results in Supplementary Materials), and we set it to be once per positive sequence.

2.1.4 Speeding up the calculation and search

While the run time of DECOD is independent of the input dataset size, it does depend on the motif width k. Calculating the exact target functions in (8) includes summation over all possible k-mers, and thus the running time increases exponentially with k. To speed up the calculation of the target function we developed a speedup version of DECOD. In this version we first calculate the frequencies of all k-mers in the positive and negative sets, and then the summation in Equation (8) is calculated only over those k-mers exhibiting large differences between the positive and negative sets. In addition, we perform two rounds of search in each iteration. The first round is crude search in which we only use the partial derivatives of (8) to estimate the change resulting from adding or removing a k-mer from the motif without doing exact calculation of the target function. After obtaining a set of m k-mers leading to a motif θ we expand this set by including all other k-mers that are similar to θ. See Methods in Supplementary Materials for complete details.

2.2 ChIP-chip experiment of p53 mutant binding

We designed a p53-focused array as previously described in (Shaked et al., 2008), which contains 540 p53-PET sites, 62 additional previously described p53 target regions and 846 randomly chosen promoter regions. For the experiments discussed in this article, H1299 tet-off inducible cell lines were created as previously described in (Chen et al., 1996). Levels of p53 for the different mutants were similar to each other as determined by Western analysis (Supplementary Figure S1). Chromatin immunoprecipitation (ChIP)-on-chip analysis was performed (Lee et al., 2006) using 10 μg anti-p53 antibody DO-1 (Santa Cruz). Approximately 5×10⁷ cells were used. The experiment was performed in duplicate, and the average binding ratio for each spot was calculated. The significance of the enrichment observed in each spot was determined by calculating the deviation of each ratio from the mean of the random promoters control spots (Z score). Only ~ 1% of the random promoters obtained Z of >2.5; thus, this cutoff is equivalent to an FDR of 0.01. We have also performed gene-specific validations that confirmed the array results (data not shown), using a ChIP assay subjecting the non-amplified immunoprecipitation and input fractions to 36 cycles of semiquantitative PCR. See Methods in Supplementary Materials for complete details. The data from the ChIP-chip experiment has been deposited in ArrayExpress (accession number E-MEXP-3027).

3 RESULTS

3.1 Discriminative motif finding on simulated data

We first tested the performance of DECOD by comparing it to several other discriminative motif finding methods including DME (v2 beta 2008.08.30, Smith et al., 2005), DIPS (v1.1, Sinha, 2006), ALSE (v1.07, Leung and Chin, 2006), DEME (v1.0, Redhead and Bailey, 2007), Seeder (v0.01, Fauteux et al., 2008) and CMF (Mason et al., 2010) using simulated data. For each simulated study, 100 datasets were generated and results were averaged. In each dataset, two groups of positive and negative sequences of length 400bp each were first generated with equal probabilities for A, C, G and T, respectively. Then, in the positive set, palindrome motif(s) of various strength [as represented by the information content of each column (column IC), see Methods in Supplementary Materials] were planted at randomly chosen positions. For all cases, the accuracy was measured by the average Kullback–Leibler (K-L) divergence per column (AKLD) between the recovered motif and the known planted motif (Smith et al., 2005) (Methods in Supplementary Materials). The lower the AKLD, the closer the recovered motif is to the planted motif. In addition, for DECOD, both the exact and speedup calculations were compared (referred to as ‘DECOD-exact’ and ‘DECOD-speedup’ hereafter, see Section 2). For DIPS, we considered running for 5 iterations and 20 iterations (referred to as ‘DIPS-5iters’ and ‘DIPS-20iters’ hereafter).

3.1.1 Single unimodal motif, small input size

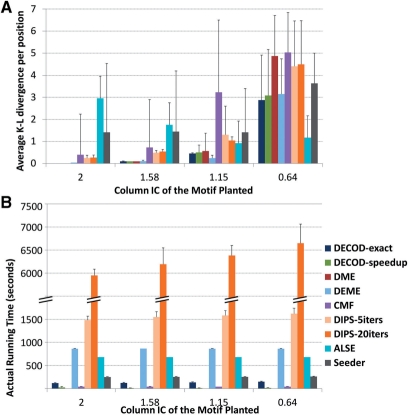
We first planted one palindrome motif of width 6 into each positive sequence. Each position of the motif had one dominating nucleotide (thereby unimodal), with column IC ranging from 2 bits to 0.64 bits (Methods in Supplementary Materials). One hundred positive and negative sequences were generated respectively for each dataset and we compared the ability of each method to recover the planted motifs. When the planted motif was strong with a column IC≥1.58, most methods including DECOD-exact, DECOD-speedup, DME, DEME, DIPS-5iters, DIPS-20iters and CMF (to a lesser extent with larger variance) were able to accurately recover the planted motif (average AKLD ≤1, Figure 2A). However, when the column IC was reduced to 1.15, using CMF, DIPS-5iters and DIPS-20iters led to an AKLD higher than 1, while DECOD-exact, DECOD-speedup, DME and DEME still performed well and were also stable (AKLD < 0.6 with small variance, Figure 2A). When the column IC was further reduced to 0.64, the planted motif instances became too noisy with few instances preserving the dominating positions of the motif, and with the small number of sequences available, virtually all methods except ALSE failed (AKLD > 2, Figure 2A). However, among all the tested methods, ALSE and Seeder performed poorly when the planted motif was strong. For Seeder, its weak performance for the strong-planted motifs may have been related to the motif length. The seed width for Seeder as input should be shorter than the motif width, but in this case the two were set to be equal since the minimum possible seed width for Seeder was 6. For ALSE, the apparent decreasing AKLD with weaker motif was because ALSE reported matrices in which the distribution at each column is diluted (e.g. [0.5 0.167 0.167 0.167] instead of [1 0 0 0]). In terms of running time, DEME and DIPS required a long time to run (~ 15 min for DEME, ~ 25 min for DIPS-5iters and >1.5 h for DIPS-20iters, Figure 2B). In contrast, DECOD (particularly the speedup version) and DME were the fastest taking <1 min.

Fig. 2.

Performance comparison on the simulated data planting one motif in each of the 100 positive sequences. (A) Average accuracy as measured by AKLD (B) Actual running time. The error bars represent standard deviation based on results from 100 datasets.

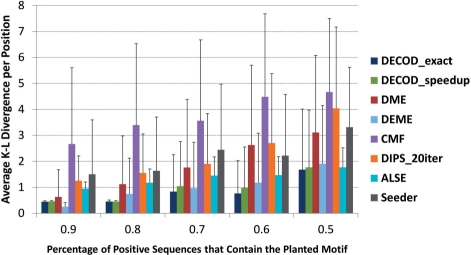
To further mimic real cases in which the motif of interest does not necessarily exist in all positive sequences, we generated simulated datasets in which only some of the 100 positive sequences (percentage denoted as q, varying from 50% to 90%) contained the planted motif (with an column IC of 1.15). In all the ranges of q tested, DECOD-exact, DECOD-speedup and DEME outperformed the other methods, including DME, in terms of the accuracy of the recovered motif (Fig. 3). Note that the running time for DEME was more than 15 times longer than DECOD (Fig. 2B). When q was high (>=0.8), both DECOD-exact and DECOD-speedup had a small variance suggesting that their performance was relatively stable. In contrast, DME had a much larger variance, indicating that it failed on a lot more of the 100 simulated datasets than DECOD (Fig. 3). We also tested DECOD by planting a longer motif of width 8. As with the shorter motif, DECOD-speedup was able to accurately recover the PWM as well as the locations of the planted motifs (Supplementary Figures S4 and S5 and Results in Supplementary Materials).

Fig. 3.

Performance comparison of accuracy as measured by AKLD on the simulated dataset in which the motif is only planted in some (x-axis) of the 100 positive sequences.

3.1.2 Single unimodal motif, large input size

To investigate how well each method scales with the size of the input data, we next increased the number of sequences for each dataset to 1 000, and we still planted one motif with varying column IC in each positive sequence. With this large input dataset size, DIPS failed to run, the running time for DEME and Seeder became prohibitively long (>6 h), and the running time for ALSE increased to more than 1.5 h. We thus excluded them from the analysis and only compared DECOD-exact, DECOD-speedup, DME and CMF. All four methods were able to precisely recover the planted motif and the AKLDs were very similar for all the methods, although the AKLDs increased with lower column IC of the planted motif as expected (Supplementary Fig. S2A). In terms of running time, DECOD-speedup and DME were the fastest (<1 min), followed by DECOD-exact (~ 2 min) and CMF (~ 6 min, Supplementary Figure S2B).

3.1.3 Single bimodal motif

We next tested a more difficult case where some positions (ranging from one to all six) in the planted motif are bimodal (column IC 0.53, see Methods in Supplementary Materials). Such cases, in which a motif contains a few weak positions, are very common in practice. As the number of bimodal positions increased, the recovered motifs by all methods tended to diverge further from the planted motif (Supplementary Fig. S3). However, the AKLDs of the motifs recovered by both DECOD-exact and DECOD-speedup were in most cases comparable to DME and both were better than CMF.

3.1.4 More than one motif per sequence

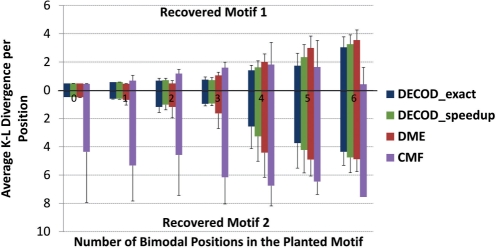
In real data, genes are often combinatorially regulated by multiple TFs. To test the ability of our method to recover more than one motif from a dataset and compare with the other methods, we next planted two different motifs in each positive sequence in a simulated dataset containing 1000 sequences each. The planted motifs had 0–6 bimodal positions (column IC 0.53) and the other positions were unimodal (column IC 1.15) (see Methods in Supplementary Materials). Both DECOD-exact and DECOD-speedup were able to correctly recover the two planted motifs (AKLD<1) and outperformed DME, especially when the number of bimodal positions were >3 (Fig. 4 and Methods in Supplementary Materials). Interestingly, CMF was able to correctly recover one of the two motifs in most cases and always failed to recover the other (Fig. 4, downward bars representing the recovered motif with larger AKLD, see Methods in Supplementary Materials).

Fig. 4.

Performance comparison of accuracy as measured by AKLD on the simulated dataset in which two motifs were planted in each of the 1000 positive sequences. Each method was set to report 2 motifs. Upward, the AKLD of the recovered motif closer to the two known motifs. Downward, the AKLD of the other recovered motif to the corresponding known motif.

3.2 Performance comparison on recovering motifs from biological benchmark datasets

We next applied DECOD to identify transcription factor binding sites (TFBSs) in real biological datasets. For this purpose, we first used a benchmark dataset in Saccharomyces cerevisiae (Harbison et al., 2004) and compared DECOD's results with the other methods. For each of the 65 TFs reported in (Harbison et al., 2004), the probe sequences bound by the TF were used as the positive set (Methods in Supplementary Materials). Note that not all bound sequences contained the motif for the corresponding TF. Negative datasets were constructed for each TF by using the probes most unlikely to be bound (Methods in Supplementary Materials). We then run each method to search for one motif of the known width for each dataset, and we matched the motifs discovered against a database containing all the motifs for those TFs reported in (Harbison et al., 2004) using STAMP (Mahony and Benos, 2007). A discovered motif is considered to be correct if the true TF is within the top 5 matches returned by STAMP. We did not include DIPS in our comparison due to its prohibitive running time. For our method, we only used the speedup version since many motifs are longer than 8.

Out of all the 65 motifs, DECOD was able to recover 28, compared to 31 for DME and 34 for DEME (none of the other methods correctly recovered more than 34 motifs, Table 1 and Supplementary Table S2). However, the motifs for these 65 TFs are not equally reliable. An enrichment score for each motif was calculated in (Harbison et al., 2004) to measure the relative enrichment of the motif in the bound probes compared with all intergenic sequences in yeast. Motifs with a higher enrichment score occur more densely in the bound probes and are therefore more reliable. Of the 21 motifs with an enrichment score ≥25, DECOD was able to recover 15, similar to the number recovered by DEME (also 15) and higher than the number recovered by DME (13) (Table 1). It should be noted that many of the motifs correctly recovered by DECOD are longer than 10 (Supplementary Table S2), and that the running time for DECOD is always much faster than DEME. Therefore, DECOD performs well in recovering yeast motifs from this dataset especially for highly reliable motifs.

Table 1.

Comparison of discriminative motif finding methods on the yeast dataset

TF	DECOD	DME	DEME	CMF	Seeder	ALSE	Width	Enrichment
ABF1	+	+	+	+	+		13	99
CBF1	+	+	+	+		+	7	99
FHL1	+	+	+	+	+		10	99
RAP1	+	+	+	+			10	79.92
REB1	+	+	+	+	+		7	77.93
UME6	+	+	+	+	+		8	72.32
RPN4							9	72.02
GCN4	+	+	+	+	+		7	64.62
YAP7							8	62.65
MCM1		+	+				11	55.28
NRG1				+			7	45.42
MBP1	+	+	+	+	+		7	40
SKN7						+	9	38.79
CIN5	+		+	+			8	38.36
SUM1	+	+	+		+		10	36.47
SWI6	+	+	+	+	+		7	33.62
HSF1	+						13	32.96
SWI4	+	+	+	+	+		7	31.96
TYE7	+	+	+	+	+	+	8	30.56
SFP1							9	26.64
FKH2	+		+	+	+		7	26.62
Total (Top)	15	13	15	14	11	3
Total (All)	28	31	34	24	17	9

+: Correctly recover the known motif.

Total (Top): the total number of the top 21 motifs with enrichment score ≥25 correctly recovered by each method.

Total (All): the total number of all motifs correctly recovered by each method (see Results in Supplementary Materials for details).

We also tested the performance of DECOD on another biological benchmark dataset that contains known TFBS in higher organisms including fly, mouse and human (Tompa et al., 2005). As we show in Supplementary Figure S6, for this data DECOD was superior to DME and DEME in terms of the sensitivity and positive prediction value at the nucleotide level. See Results in Supplementary Materials for detailed discussion.

3.3 Motif discovery from p53 mutant binding targets

We next looked at the tumor suppressor p53 in human, a TF which plays a major role in cancer by binding numerous targets (Wei et al., 2006). P53 is regulated by many posttranslational modifications, primarily at the amino and carboxyl terminal regions (Riley et al., 2008). In particular multiple lysines within the C-terminal domain (CTD) have been reported to undergo numerous modifications including acetylation, methylation, ubiquitination, and SUMOylation (Kruse and Gu, 2009). The functions of the acetylation of these lysines have remained elusive. To study the role of the acetylation of these CTD lysines in p53 binding, we performed ChIP-on-chip experiments comparing three H1299 cell lines expressing p53 variants expressed from a tetracycline-regulatable promoter (tet-off) in which the levels of p53 protein can be regulated by varying the amount of tetracycline in the culture medium (Section 2). The levels of p53 were calibrated so that equivalent amounts of p53 were expressed in each of the following three cell lines containing: (i) wild-type p53 (WT p53); (ii) mutant p53 in which the six lysine residues in the C-terminus were mutated to arginine (6KR p53), which conserve charge but disallow any lysine modification; and (iii) mutant p53 in which the same six lysines were mutated to glutamine (6KQ p53) which is thought in some cases to mimic acetylation (Karni-Schmidt et al., 2007) (Methods in Supplementary Materials). To determine their relative affinity for p53 target sites, we used a p53 custom array containing promoters for 600 of p53's targets binding sites.

We found that WT p53 bound to 330 targets, 6KR p53 bound to 255 targets and 6KQ p53 bound to only 150 targets. Interestingly, the 6KQ targets were included in the 6KR targets, which in turn were included in the WT targets. Thus, each of the p53 forms bound a smaller subset of related targets (Fig. 5A). Since all genes on the array contain a strong p53 binding motif, motif discovery on one target set would lead to the same motif. Thus we used DECOD to search for discriminative motifs that are enriched in one set of these targets versus another. The bound sequences identified in the ChIP-chip experiment in each pairwise comparison of the wild-type p53 and two mutant p53 (6KR and 6KQ) were repeat masked and then used for this analysis. Since the experiment is not strand-specific, both strands were included in the input sequences. We used STAMP (Mahony and Benos, 2007) to match the motifs we recover with known transcription factor binding sites in the TRANSFAC 11.3 database (Matys et al., 2006).

Fig. 5.

Results on the p53 dataset. (A) Number of targets and inclusion patterns for the three p53 forms we tested. (B–D) Discriminative motifs identified by DECOD for the p53 binding datasets. Left: Motifs found by DECOD. Right: matched motifs in TRANSFAC using STAMP (Mahony and Benos, 2007) (E-values provided by STAMP). (B) The SOX4 motif found in the comparison of the WT p53 targets against the 6KR p53 targets. (C) The IRF-1 motif found in the comparison of the 6KR p53 targets against 6KQ p53 targets. (D) The p53 motif found in the comparison of the 6KQ p53 targets against the control sequences.

DECOD identified several such discriminative motifs in pairwise comparisons between these sets (Fig. 5B–D and Supplementary Material). The motifs identified provide new insights regarding co-factors of p53 and the post-translational modification that it undergoes. For example, when comparing targets of WT p53 that are not targets of 6KR p53 to targets of 6KR p53, DECOD identified a motif closely matching the PWM for Sox4 (Fig. 5B, E-value = 6.35e-8). Sox4 participates in a wide range of cellular processes particularly in cancer (Rhodes et al., 2004), and recently it was reported to physically interact with p53 and regulate p53 stability at the protein level (Pan et al., 2009). Both the DNA-binding domain (DBD) and the C-terminal domain (CTD) of p53 were shown to be involved in forming the interaction with Sox4 (Pan et al., 2009). Since the Sox4 motif was only found to be enriched in comparing the WT p53 targets against 6KR p53 (in which the CTD was mutated) but not in the other comparisons, our result confirms this finding and also suggests that the CTD lysines might be important in maintaining the conformation of the binding site between the p53 and Sox4 proteins. Another example is the motif closely matching the PWM for interferon regulatory factor 1 (IRF-1) when comparing the 6KR p53 against the 6KQ p53 targets (Fig. 5C, E-value = 2.75e-7). IRF-1 acts synergistically with p53 at the p21 promoter and is coordinately upregulated with p53 during DNA damage response (Pamment et al., 2002). On the p21 promoter IRF-1 and p53 interact through the p300 acetyl transferase, and this interaction is important for the acetylation of p53 (Dornan et al., 2004). If p300 is indeed necessary for IRF-1 – p53 interaction, we expect it to be lost after p53 is fully acetylated. Indeed, we found that IRF-1 binding sites are depleted from promoters of the acetylation mimicking mutation (6KQ) raising the possibility that p53 needs the interaction with the IRF-1 protein to control a subset of its targets. Finally, in comparing the 6KQ targets against a control set, DECOD was able to recover the motif corresponding to the PWM for p53 (Fig. 5D, E-value = 1.09e-11). Note that the p53 motif was not found in either of the previous comparisons due to the discriminative nature of the method, which is what we desired since all the three sets of targets contains the motif. The other methods could not recover the Sox4 or the p53 motif when run on this dataset (Supplementary Table S3 and Results in Supplementary Materials).

4 DISCUSSION

We presented DECOD, a novel method for discriminative motif finding in DNA sequences. DECOD uses a deconvolution method which allows it to have a run time independent of the input data size while still taking into account context information.

While DECOD's run time is independent of the input data size, calculating the exact target function (DECOD-exact) increases exponentially with the motif length k. We presented a solution for speeding up the calculation by only using the most informative k-mers (DECOD-speedup), and showed that it yields motifs that are almost as accurate as those obtained using DECOD-exact while the running time is greatly reduced. As we discuss in Results in Supplementary Materials, DECOD is robust to several input parameters including the choice of the probability of motif occurrence.

When tested on simulated data, for which the correct motif is known, DECOD outperforms all other methods when searching for complicated motifs with bimodal position and when looking for combinatorial regulation. It is also much faster than most other methods making it applicable to large sequencing datasets. On real biological benchmark datasets (both yeast and higher eukaryotes), we showed that DECOD was comparable, or better, than other discriminative motif finding methods with the possible exception of DEME for the yeast data. However, as mentioned above, DEME is very slow and so may not be a useful method when studying large datasets. Using DECOD we were also able to identify motifs that are differentially enriched in different p53 mutants which allowed us to identify co-factors of this important TF. Additional experiments are crucial for deciphering the exact interactions between p53 and these other factors, and our bioinformatics analysis using DECOD paves the way for future experiments. We have also tested DECOD using large-scale ChIP-Seq dataset for 5 TFs. For all five DECOD was able to identify the correct motif indicating that it works well on high-throughput datasets as well. See Results in Supplementary Materials and Supplementary Table S4 for details.

While DECOD was successful in our analysis, it also has limitations. Since DECOD depends on k-mer counts, it does not work well on motifs with large gaps in the middle, since the signals for the k-mers corresponding to the occurrences of such motifs will be more uniform due to the gaps. In future we hope to further extend DECOD to deal with such cases. Moreover, we also hope to further improve DECOD by developing ways to automatically determine the length of the motif to be searched for, which can be important when presented with new dataset in which the motif is completely unknown.

Funding: National Institute of Health (1RO1 GM085022, in part); National Science Foundation CAREER award (0448453, to Z.B.J., in part). Israeli Cancer Research Foundation; Israeli Cancer Association; Weinkselbaum Family foundation (to I.S., in part).

Conflict of Interest: none declared.