Response rescaling in bacterial chemotaxis

Abstract

Sensory systems rescale their response sensitivity upon adaptation according to simple strategies that recur in processes as diverse as single-cell signaling, neural network responses, and whole-organism perception. Here, we study response rescaling in Escherichia coli chemotaxis, where adaptation dynamically tunes the cells’ motile response during searches for nutrients. Using in vivo fluorescence resonance energy transfer (FRET) measurements on immobilized cells, we demonstrate that the design of this prokaryotic signaling network follows the fold-change detection (FCD) strategy, responding faithfully to the shape of the input profile irrespective of its absolute intensity. Using a microfluidics-based assay for free swimming cells, we confirm intensity-independent gradient responses at the behavioral level. By theoretical analysis, we identify a set of sufficient conditions for FCD in E. coli chemotaxis, which leads to the prediction that the adaptation timescale is invariant with respect to the background input level. Additional FRET experiments confirm that the adaptation timescale is invariant over an ∼10,000-fold range of background concentrations. These observations in a highly optimized bacterial system support the concept that FCD represents a robust sensing strategy for spatial searches. To our knowledge, these experiments provide a unique demonstration of FCD in any biological sensory system.

Maximizing the information content of perceived signals is a nontrivial problem for biological systems, as it requires adaptive tuning of sensory responses to match the statistics of input signals (1). Remarkably, strategies for inferring the likely distribution of inputs from recent experience appear to be “hard coded” in many adaptive sensory systems, leading to well-defined relationships between the current response sensitivity and recent background inputs (2). The most prevalent of such relationships is Weber's law, which prescribes that the magnitude of the immediate sensory response, Δr, following a small step change in input, Δs, is proportional to the ratio of the step size to the background input level, s₀; i.e., 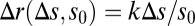, where k is a constant (3). The underlying sensing strategy exploits a scenario commonplace in nature, where both the uninformative background intensity, s₀, and informative deviations from it, Δs, are proportionately scaled by a common source of signal power that fluctuates slowly in time—for example, sunlight that sets the brightness of images at different times of day (4). Weber's law ensures that the response, Δr, remains invariant when both the stimulus, Δs, and the background, s₀, are rescaled by the same factor γ; i.e., Δr(Δs, s₀) = Δr(γΔs, γs₀). This relation obviates the need to optimize the stimulus-response relation at every level of signal power.

Recently, a response rescaling strategy that applies to a broader class of input stimuli, called fold-change detection (FCD), has been described on the basis of indirect evidence in a number of eukaryotic cell sensory systems (5–7). FCD is conceptually similar to Weber's law—it yields invariant responses under proportionate scaling of the stimulus with the background—but it applies to the entire time series of the response, Δr(t), to a stimulus time series, Δs(t), not only to the instantaneous response following a step stimulus. In addition, FCD is not limited to small-amplitude stimuli, but applies also to time-varying stimuli of arbitrary amplitude and waveform. Thus, the FCD strategy prescribes scale-invariant responses to the complete input time series, Δr(Δs(t), s₀; t) = Δr(γΔs(t), γs₀; t), and as such imposes more stringent design constraints on sensory systems than does Weber's law (8). In the aforementioned eukaryotic systems (5–7), FCD has been suggested to buffer cell-to-cell differences in the basal expression level of signaling proteins. In addition, it has been hypothesized that FCD is a desirable property for sensory systems guiding spatial searches by motile organisms (8). However, whether and how any biological signaling network implements the FCD strategy remain unknown.

Here, we study response rescaling in the signaling network of Escherichia coli chemotaxis, which guides this bacterium's search for nutrients and is arguably the simplest sensory network known to exhibit adaptation over a broad dynamic range. Pioneering work by Adler and colleagues in the 1970s (9), as well as more recent work (10), has demonstrated logarithmic sensing behavior reminiscent of Weber's law in E. coli's chemosensory system, which senses chemoeffector gradients as the bacterium samples its environment by swimming. Gradient sensing is achieved through temporal comparisons (11) mediated by fast and slow molecular processes (12). On a rapid timescale, chemoeffector binding to transmembrane receptors produces an excitatory response, by modifying the activity of an intracellular signal that is relayed to the flagellar motor. On a slower timescale, enzyme-mediated covalent modification of the receptors restores pathway activity toward the prestimulus level, while also rescaling the sensitivity of receptors to ligand molecules (13).

The manner in which E. coli rescales its fast chemoreceptor response has been characterized in some detail by fluorescence resonance energy transfer (FRET) measurements of intracellular signaling. Using small-step stimulation by chemoeffectors, the response sensitivity was found to remain high at a nearly constant level over a broad range of background concentrations (14), confirming that Weber's law holds at the level of the rapid chemoreceptor response. However, biologically relevant inputs often vary slowly over time, because the high diffusivity (D ∼ 10⁻⁹ m²/s) of small-molecule chemoeffectors leads to smooth concentration profiles in typical environments. To test whether E. coli demonstrates FCD in rescaling its chemotactic response to such smoothly varying inputs, we combine here FRET experiments encompassing both timescales of intracellular signaling and microfluidics-based assays of migration behavior. These experiments demonstrate that the dynamic output of the chemotaxis pathway activity is invariant under proportionate scaling of a time-varying stimulus with the background over a broad dynamic range. Thus, the E. coli chemotaxis system demonstrates FCD, as recently predicted on theoretical grounds (8). By analyzing a theoretical model of E. coli chemotaxis (15), we find that FCD imposes more stringent constraints on the design of the signaling system than does Weber's law and identify a set of sufficient conditions for FCD in terms of the molecular parameters of the system.

Results

FCD and Its Dynamic Range in E. coli Chemotactic Signaling.

The output response of the chemotaxis system can be characterized by a single variable, a(t), that corresponds to the activity of a central kinase, CheA, controlled by clustered chemoreceptors. CheA activity determines the concentration of the phosphorylated response regulator protein CheY, which in turn controls cell swimming behavior (12, 16). A FRET pair, consisting of CheY and its phosphatase, CheZ, fused to yellow and cyan fluorescent proteins (YFP and CFP), respectively (17), provides a real-time readout proportional to a(t) for timescales greater than the relaxation time of the CheY phosphorylation cycle. In addition to enabling studies on receptor sensitivity (14, 18, 19), this FRET system has been combined with time-varying stimuli to measure the in vivo kinetics of the adaptation enzymes CheR and CheB (20), which provide negative feedback through covalent receptor modification (reversible methylation at multiple sites) and determine the slower timescale of the adaptation response, τ_m.

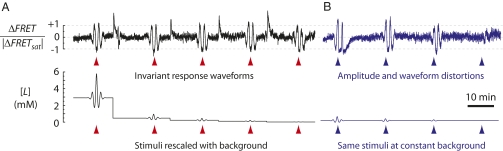
To study how the temporal response of chemotactic signaling depends upon the background level, we conducted FRET experiments in which bacteria, adapted to a background concentration [L]₀ of the nonmetabolizable attractant α-methylaspartate (MeAsp), were subjected to a time-varying stimulus Δ[L](t). The stimulus was applied by modulating the input in time, as [L](t) = [L]₀ + Δ[L](t), using a fluid mixing apparatus (SI Text). Fig. 1A shows results from an experiment in which the stimuli, Δ[L]_i(t), differed in amplitude but the inputs, [L]_i(t), had otherwise identical waveforms; i.e., [L]_i(t) ≡ [L]_0,iλ(t), where [L]_0,i is the ith background concentration. The dimensionless waveform λ(t) was held constant between all stimuli in this experiment, so that the stimulus-to-background ratio, Δ[L]_i(t)/[L]_0,i = (λ(t) – 1), was invariant. For this scenario, we found that the response time series, ΔFRET(t), was very similar over a broad range of background concentrations ([L]₀ = 0.018–2.9 mM). In contrast, in the experiment in Fig. 1B the sequence of stimuli, Δ[L]_i(t), was the same as that of the last four stimuli in the experiment in Fig. 1A but the background level was held constant at [L]₀ = 0.23 mM. In this case, the FRET response to each stimulus in the sequence differed in both amplitude and waveform. Thus, the response to time-varying stimuli is not determined by the absolute difference from the background, [L](t) − [L]₀, but rather by the fold change over the background, [L](t)/[L]₀, indicating that chemotactic signaling in E. coli exhibits FCD.

Fig. 1.

E. coli chemotaxis displays FCD. (Upper) FRET response, ΔFRET, normalized by the magnitude of the response to saturating stimuli (|ΔFRET_sat|), of cells exposed to time-varying concentrations of MeAsp (Lower). (A) Response to five stimuli, Δ[L]_i(t), of identical waveforms and amplitudes scaled by the same factor as the background concentrations [L]_0,i = (2.9, 0.48, 0.23, 0.11, 0.018) mM. (B) The last four stimuli [i = (2, 3, 4, 5)] were repeated while the background was kept constant (0.23 mM). (The first stimulus, at i = 1, could not be applied at this background because [L]₀ + Δ[L]₁(t) would reach negative values at [L]_0,1 = 2.9 mM.)

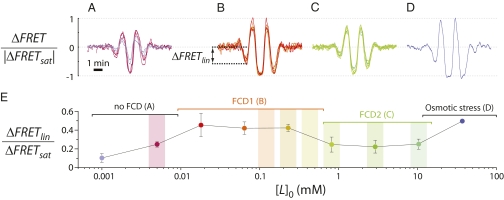
To probe the dynamic range over which FCD holds, we compared the temporal response profiles at different background concentrations in experiments of the type shown in Fig. 1A. One can use any function for λ(t) to test for FCD, which, by definition, holds for arbitrary input waveforms. We chose an oscillatory waveform with a frequency, ν = 0.01 Hz, close to the characteristic frequency of the system's adaptation kinetics, v_m ∼ 0.006 Hz (at 22 °C) (20), with a Gaussian amplitude modulation (see SI Text for the exact expression) to probe both the low-amplitude regime, where the stimulus-response relation is expected to be linear (i.e., ΔFRET ∝ Δ[L]), and the high-amplitude regime, where the stimulus-response relation saturates (i.e., ΔFRET → ΔFRET_sat). Fig. 2 shows the FRET response time series over an ∼30,000-fold range of background concentrations. We identified four concentration regimes. For [L]₀ < 0.018 mM (Fig. 2A), the response amplitude increased with the background concentration. We detected two adjacent but distinct regimes where FCD holds locally: at intermediate ([L]₀ = 0.018–0.23 mM; Fig. 2B) and high ([L]₀ = 0.82–10.3 mM; Fig. 2C) background concentrations, responses were invariant in both amplitude and waveform. We hereafter refer to these regimes as FCD1 and FCD2, respectively, and to the low concentration regime, where the response amplitude depended on the background level (Fig. 2A), as the “no FCD” regime. At very high concentrations (>10.3 mM; Fig. 2D), osmotic stress perturbs the chemoreceptors (21) and this regime is not considered further.

Fig. 2.

Dynamic range of FCD. (A–D) FRET response to a stimulus waveform (Fig. 4B, blue curve) for different background concentrations: (A) [L]₀ = 0.001 and 0.005 mM; (B) [L]₀ = 0.018, 0.064, and 0.23 mM; (C) [L]₀ = 0.82, 2.9, and 10.3 mM; (D) [L]₀ = 36.9 mM. Two replicates for each concentration are shown. (E) Response amplitude, ΔFRET_lin, for the same cases, computed as the peak in the linear response regime (see B). Vertical bars indicate the concentration ranges used in microfluidic gradient experiments (Fig. 3).

The two FCD regimes differ in the response magnitude, most notably in the low-amplitude regime of the response, where ΔFRET << ΔFRET_sat (Fig. 2 B and C and SI Text). Therefore, we characterized the amplitude of the first negative peak, ΔFRET_lin (Fig. 2B), which was always much smaller than ΔFRET_sat and thus provides a good approximation of the response within the linear regime of the stimulus-response relation. ΔFRET_lin depends only weakly on background concentration (Fig. 2E), with a <2-fold difference over an ∼2,000-fold concentration interval ([L]₀ = 0.005–10.3 mM). Interestingly, this dependence of amplitude on background concentration closely resembles the previously reported (14) step-response sensitivity of chemoreceptors [defined as (Δa/a₀)/(Δ[L]/[L]₀), where a₀ is the steady-state kinase output], suggesting that the dependence arises within the fast timescale chemoreceptor response.

FCD Extends to Chemotactic Responses of Swimming Cells in Spatial Gradients.

If the chemotaxis signaling response is invariant under rescaling of temporal gradients by the same factor as the background level, a swimming E. coli cell might do equally well at climbing different spatial gradients when these are similarly rescaled. A single bacterium's trajectory is difficult to follow experimentally over extended times. However, the spatial distribution of an ensemble of cells is readily imaged over long periods. If FCD holds on the behavioral level, the spatial distribution of the population is predicted to evolve identically in different chemoeffector gradients, as long as bacteria are preadapted to concentrations scaled by the same factor as the fold change in the gradients’ magnitude.

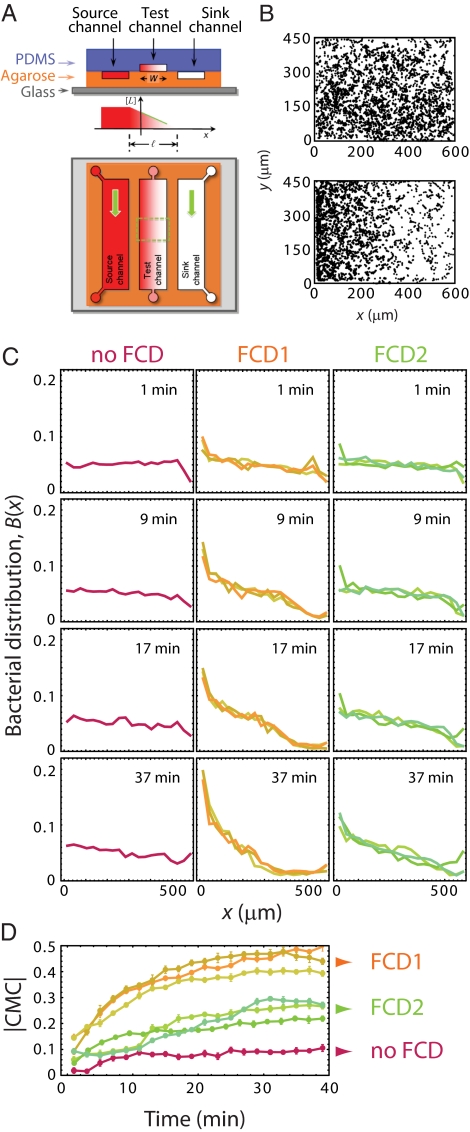
To test this prediction, we studied the migration of swimming cells in spatial gradients of MeAsp, established in a microfluidic system (Fig. 3A) of a type described before (10, 22, 23). The device, consisting of polydimethylsiloxane (PDMS) and agarose, creates and maintains a steady linear MeAsp gradient (SI Text). Bacteria are introduced into a “test channel” of width W = 600 μm, patterned in the PDMS layer, which has one face open to the underlying agarose layer. A linear gradient is preestablished within the agarose by flowing buffer with different MeAsp concentrations in the two flanking channels, higher in the “source channel” and lower in the “sink channel” (Fig. 3A). A gradient mirroring that of the underlying agarose layer rapidly develops within the test channel, because of its small depth. We followed the migration of cell populations in the test channel by video microscopy. Typical images of cell trajectories demonstrate that bacteria are initially uniformly distributed (Fig. 3B, Upper), but subsequently accumulate on the side closest to the source channel (Fig. 3B, Lower). Analysis of sequences of images yielded the bacterial distribution, B(x), along the gradient.

Fig. 3.

FCD demonstrated for swimming cells. (A) Schematic of the microfluidic device used to create a steady linear MeAsp gradient, of magnitude ∇[L] (see text). (B) Spatial distribution of cells at the start of an experiment (Upper) and 19 min after establishment of a ∇[L] = 0.15 mM/mm gradient along –x (Lower), demonstrating chemotaxis. (C) Time evolution of the bacterial distribution in gradients of differing magnitude, but identical fold change. In each experiment, bacteria were preadapted to a concentration [L]_m such that ∇[L]/[L]_m was kept fixed (2/3 mm⁻¹). The values of [L]_m (0.005, 0.12, 0.23, 0.43, 0.81, 2.9, and 10.3 mM) are also indicated in Fig. 2E. (D) Time series of the absolute value of the chemotactic migration coefficient (|CMC|; see text).

We tested seven different gradients, each time rescaling the steepness of the gradient by the same factor as the mean concentration, [L]_m (shaded bars in Fig. 2E). Fig. 3C shows the temporal evolution of the spatial distributions of bacteria, B(x). The Fig. 3C, Left corresponds to [L]_m = 0.005 mM, within the no-FCD regime. As expected from the low amplitude of the FRET response in this range (Fig. 2E), the chemotactic accumulation was weak. For [L]_m within each FCD regime (Fig. 3C, Center and Right) the entire temporal evolution of B(x) was invariant, despite the ∼12-fold variation in [L]_m among experiments. The accumulation was stronger within the FCD1 regime than within the FCD2 regime, consistent with the difference in sensitivity measured by FRET (Fig. 2E).

The invariance of the distributions is demonstrated more quantitatively in Fig. 3D, where we plot the time series of a dimensionless number of merit, the chemotactic migration coefficient (CMC) (24). The latter is defined as 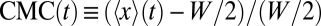, where W is the width of the test channel and 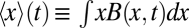is the population-averaged spatial coordinate of the bacteria, x (along the chemoeffector gradient), measuring the mean displacement of the population from the center of the channel. The CMC(t) time series are nearly identical for gradients within each FCD regime (Fig. 3D). Taken together with the FRET data, these results demonstrate that within each concentration regime where intracellular signaling responses are invariant, the chemotactic performance in spatial gradients is also invariant. Thus, the FCD property extends from intracellular signaling to the behavior of swimming cells.

Mechanistic Requirements for Response Rescaling.

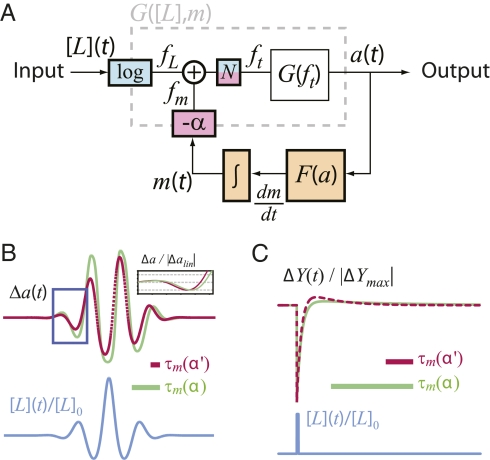
To gain insight into the mechanistic requirements for FCD, we analyzed a coarse-grained model of the chemotaxis network that has successfully explained a large body of quantitative experiments on chemotactic signaling (15). This model was recently shown to satisfy the general mathematical requirements for FCD, but those conditions alone do not fully constrain the possible molecular mechanisms (8). Here we identify specific relationships between molecular parameters that lead to FCD-type response rescaling predicted to yield observable consequences. From a functional perspective, this model can be described as a negative feedback loop (Fig. 4A) in which the ligand concentration, [L](t), is the input, the receptor-kinase activity, a(t), is the output, and the average receptor methylation level, m(t), is the feedback signal. The relationships between these variables are mediated by two transfer functions: F(a), representing enzyme-driven methylation kinetics, and G([L], m), representing cooperative kinase activation by chemoreceptors. The dependence of G([L], m) on ligand concentration and methylation level is through a free-energy difference, f_t([L], m), between active and inactive states of the receptor–kinase complex, described by an allosteric two-state model of the Monod–Wyman–Changeux (MWC) type (25) (see SI Text for a full description of the model).

Fig. 4.

Requirements for FCD response rescaling. (A) Block diagram of the integral feedback network of E. coli chemotaxis. The receptor–kinase transfer function G([L], m) constantly compares the ligand input [L](t) with the methylation-feedback signal m(t). Through another transfer function F(a), the output a(t) exerts control on the rate of change of m(t), yielding an integral-form feedback, which guarantees exact adaptation given appropriate conditions on F(a) (see text). (B and C) Waveform distortions for sinusoidal (B) and impulse (C) stimuli, [L](t)/[L]₀ (blue curves), for a hypothetical threefold change in the response timescale, τ_m(α), upon adaptation from one input level (green curves) to another (magenta curves). (B, Inset) Small-amplitude portion of the response (blue boxed region in B), with each response normalized by its amplitude. Note that the phase shift in the response in B and shape change in the impulse response in C are due to the difference in τ_m.

This model was previously used to explain Weber's-law-type response rescaling for step stimuli (15), which yielded a set of sufficient conditions on mechanistic parameters of this model. We find here (SI Text) that requiring FCD imposes an additional constraint on the design of the chemotaxis network, beyond those necessary for Weber's law, yielding the following as sufficient conditions for FCD:

• i) Exact adaptation: The steady-state output, a₀, is constant.

• ii) Logarithmic coupling of ligand input, [L], to the free energy, f_t: ∂f_t/∂ln[L] = constant.

• iii) Linear coupling of methylation feedback, m, to the free energy, f_t: ∂f_t/∂m = constant.

All three of these constancy conditions must hold under changes in [L]₀. Exact adaptation (condition i; orange in Fig. 4A) requires that the dynamics of the kinase activity, a(t), have a unique globally stable fixed point. This requirement is fulfilled by the integral feedback architecture of this pathway (26), provided that the transfer function, F(a), is determined uniquely by the kinase activity, a, and crosses zero only once with a negative slope (15). The remaining two conditions are constraints on the total free energy, which can be decomposed as 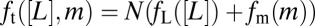, where f_L([L]) represents the contribution from ligand binding, f_m(m) represents that from methylation, and N is the size of the cooperative receptor cluster (SI Text). Logarithmic input coupling (condition ii; blue in Fig. 4A) means that the ligand effect on the total free energy, f_t, is proportional to the logarithm of ligand concentration. In MWC-type allosteric models, the assumption that both ligand binding and the active ↔ inactive transitions are thermally driven means that the ligand effect on activity depends on the distinct dissociation constants for the active and inactive states, K_A and K_I, respectively, through the relation 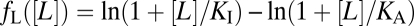. So condition ii is satisfied for MWC models when the ligand concentration is in the range K_A << [L] << K_I (where f_L([L]) ∼ ln[L]), given that the receptor cluster size, N, is also constant. Linear feedback coupling (condition iii; pink in Fig. 3A) signifies that the methylation effect on the total free energy, f_t, is directly proportional to the current methylation level, m.

Of these three conditions for FCD, conditions i and ii are sufficient for Weber's law for step stimuli (15). Thus, the only additional requirement for FCD is condition iii, that the slope of the methylation-dependent free energy must be a constant or, in other words, that f_m(m) must be a linear function of m. Such a linear dependence was discovered in recent FRET experiments using step stimuli (20), where the function 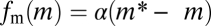yielded good fits to the data with α ∼ 2 and m* ∼ 0.5. The requirement for a constant α can be understood intuitively by examining the dynamics of this model, which predicts (15) that the characteristic timescale, τ_m, of chemotactic adaptation [defined as the relaxation time for the decay of the response, Δa(t), after a small step change in input; SI Text] is inversely proportional to α: 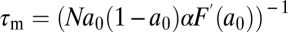. Thus, changes in α are expected to lead to distortions in the output waveform. In Fig. 4 B and C we illustrate the consequences of breaking this condition by numerical integration of a model that satisfies conditions i and ii, but not condition iii (SI Text). For both smoothly varying stimuli (Fig. 4B) and impulsive stimuli (Fig. 4C), the response, Δa(t), to the same input waveform, λ(t) (= [L](t)/[L]₀), differs for two distinct feedback coupling coefficients α and α′ [as could result from a nonlinear f_m(m) when adapted to two different background concentrations]. Thus, conditions i and ii are not sufficient for FCD, even though this system will demonstrate response rescaling to step stimuli according to Weber's law.

Chemotactic Adaptation Timescale Is Invariant over a Broad Concentration Range.

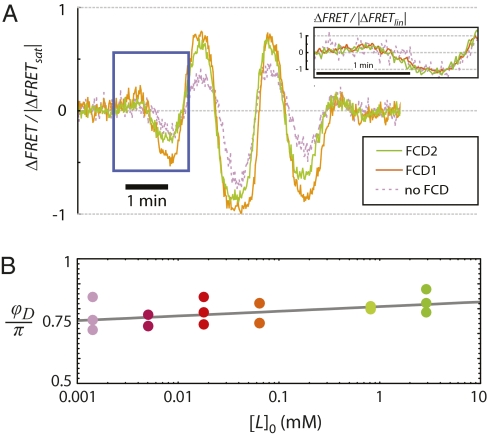
Our analysis of the requirements for FCD implies that the adaptation timescale, τ_m, is constant within each of the two FCD regimes identified in the FRET data (Fig. 2). However, this observation does not rule out the possibility that τ_m depends on the background concentration over a broader range than each FCD regime. We reasoned that appreciable changes in τ_m would be observable as distortions in the output waveforms because this timescale directly determines the characteristic cutoff frequency, 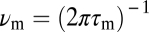, for the linear signal filtering performed by the chemotaxis pathway (15, 20). Therefore, we compared the output waveforms between the two FCD regimes, as well as the no FCD regime, by superimposing the FRET response time series (Fig. 2), averaged within each of the three regimes (Fig. 5A). The linear filtering analysis applies only for the small-amplitude regime of output, so inferring properties of τ_m from output waveform comparisons is valid only for the initial interval before saturation. When normalized by |ΔFRET_lin|, responses within this interval (boxed region in Fig. 5A) from all three regimes collapse onto a single output waveform (Fig. 5A, Inset). Because large changes in τ_m would result in distortions of the output waveform, this collapse suggests the adaptation timescale, τ_m, is essentially invariant over the entire ∼10,000-fold range of background concentrations spanned by these three regimes (Fig. 4B, Inset).

Fig. 5.

Invariance of the adaptation timescale over an ∼10,000-fold range. (A) Overlaid view of output waveforms for the different background concentrations tested, separately averaged within the “FCD1”, “FCD2”, and “no FCD” regimes. The boxed region indicates the linear regime of the response. (Inset) The linear-regime response is invariant when rescaled by |ΔFRET_lin| (Fig. 2B). (B) Phase delays, ϕ_D, for responses to exponential sinusoids with ν = 0.006 Hz and A_L = 0.2, for [L]₀ = 0.001, 0.005, 0.018, 0.064, 0.81, and 2.9 mM.

To test this invariance of τ_m more directly, we subjected cells to exponential sinusoid inputs, 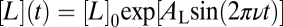, which are perceived as pure sinusoids with amplitude A_L and frequency v under logarithmic input coupling (15, 20). We recorded the phase delay ϕ_D of the response by fitting another sinusoid, 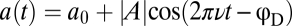, to the FRET response time series. 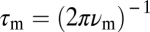At a fixed background concentration, the dependence of ϕ_D on ν was recently shown (20) to follow that expected for a linear filter, , so any dependence of on [L]₀ can be detected as a change in ϕ_D upon stimulation at frequency ν. We measured this dependence at ν = 0.006 Hz (Fig. 5B). The change in ϕ_D, if any, was very small (∼0.02π per decade), corresponding to a <20% increase in τ_m over a >1,000-fold increase in [L]₀. Thus, both the time- and frequency-domain data strongly indicate that the adaptation timescale remains constant over a broad range of background concentrations.

Discussion

We have shown that response rescaling in E. coli follows not only Weber's law at short times after stimulation, but also FCD over the entire response time series, in agreement with a recent theoretical prediction (8). Unexpectedly, we identified two distinct FCD regimes that share a common adaptation timescale, but differ in their response amplitudes. As noted in a previous study of receptor sensitivity (14), a plausible explanation for these changes in the response amplitude for MeAsp is that more than one receptor species is involved in the response to MeAsp. Future experiments using mutant strains with altered receptor complements could shed light on this question.

The manner in which bacteria respond to temporal gradients is captured most succinctly by the system's response to impulsive stimuli (Fig. 4C), whose characteristic biphasic shape demonstrates how inputs from different times in the past are weighed to produce the output at every instant. The particular shape of this time-dependent response function is expected to be under strong selection, as it determines how time derivatives are computed by the bacterium and, as such, encodes the basic chemotactic strategy. The optimal response function for a given environment will depend on the typical distribution of nutrient sources and the shapes of the concentration fields they generate by diffusion. Much theoretical work has been devoted to the effects on chemotaxis of different response functions under a variety of environmental conditions (27–31), based on the impulse response obtained in classic experiments (11, 32) that measured the response of flagellar rotation in cells tethered to a surface through their flagella. However, no systematic comparisons of impulse responses at different background concentrations have been reported to date. Our observation that the adaptation timescale is invariant with respect to the background level of input (Fig. 5) validates the approach of using impulse response functions of the same shape to study gradient responses over the entire range of [L]₀ tested here, provided that the dependence of the amplitude of response on [L]₀ (Fig. 2E) is taken into account.

How might FCD benefit a chemotactic bacterium? Shoval et al. (8) suggested that FCD could be advantageous in searching for nutrient sources. Their argument is based on the observation that typical environmental gradients generated by diffusion or convection from a source can have complex spatial profiles, but their characteristic shapes—when divided by the source strength—are invariant; i.e., the time-dependent spatial profile of the chemoeffector can be decomposed as 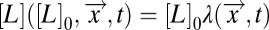, where [L]₀ is the chemoeffector concentration at the source and 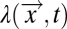is a dimensionless profile that depends on the spatial coordinate, 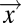, and time, t, but not [L]₀. In this context, FCD enables a bacterium to focus on the shape of the profile as a signal encoding the source location, irrespective of the source strength. Such a strategy could be optimal when “any source is a good source”; that is, the payoff for reaching even a weak nutrient source exceeds that for discriminating between the richness of nutrient sources. The search for nutrient patches by bacteria in the ocean, where microscale sources of dissolved organics are few and far between and highly variable in intensity (33), represents a tangible example of such a scenario. Comparatively little is known about the natural habitats of enteric bacteria such as E. coli, but the fact that this species, noted for its highly optimized physiology, demonstrates FCD invites further investigations about phases in its life cycle and ecology that favor this robust search strategy.

Our results provide a unique experimental demonstration of FCD in biological sensory systems and of the consequences of FCD on organism- and population-level behavior. Given the arsenal of experimental and theoretical tools available for characterizing this minimal sensory network and its behavioral output, bacterial chemotaxis can serve as an ideal model system for further studies of FCD-type response rescaling, from the level of molecular mechanisms to its physiological and ecological implications.

Materials and Methods

In Vivo FRET Measurements and Data Analysis.

FRET microscopy of bacterial populations was performed as described in ref. 17. The FRET donor–acceptor pair (CheZ-CFP and CheY-YFP) was expressed from a plasmid pVS88 (18) in a Δ(cheY-cheZ) derivative of E. coli RP437. Cells, attached to a poly-l-lysine–coated coverslip, were seated at the top face of a bespoke flow cell (34) and subjected to time-varying input modulations, generated by a computer-controlled fluid mixer (SI Text). The change in FRET efficiency upon stimulation, ΔFRET(t), was computed from recordings of the donor and acceptor fluorescence (ref. 17 and SI Text) and normalized to the absolute magnitude of the response to saturating attractant step stimuli |ΔFRET_sat|, to compensate for variations due to different absolute signal levels between experiments.

Microfluidic Experiments.

Microfluidic chemotaxis experiments were performed in a hydrogel-based gradient generator (Fig. 3A) (23), inspired by a design pioneered by Wu and colleagues (22), as described in SI Text. Briefly, a stable linear gradient was generated in a layer of agarose hydrogel, between a source channel and a sink channel, through which constant concentrations of MeAsp were flowed. The MeAsp concentrations in the source and sink channels were varied between 0.005 and 10.3 mM, to generate gradients between 0.003 and 6.9 mM/mm.

Bacteria were observed at test channel middepth, using phase contrast microscopy and a 20× objective. To obtain the spatial distribution of bacteria, a 200-frames sequence was captured at 10 frames/s every 2 min, from 1 to 39 min after injection of bacteria. Image analysis was performed to determine bacterial positions in each frame and yield the cell distribution B(x) along the direction of the gradient (SI Text).