Learning Biomarkers of Pluripotent Stem Cells in Mouse

Abstract

Pluripotent stem cells are able to self-renew, and to differentiate into all adult cell types. Many studies report data describing these cells, and characterize them in molecular terms. Machine learning yields classifiers that can accurately identify pluripotent stem cells, but there is a lack of studies yielding minimal sets of best biomarkers (genes/features). We assembled gene expression data of pluripotent stem cells and non-pluripotent cells from the mouse. After normalization and filtering, we applied machine learning, classifying samples into pluripotent and non-pluripotent with high cross-validated accuracy. Furthermore, to identify minimal sets of best biomarkers, we used three methods: information gain, random forests and a wrapper of genetic algorithm and support vector machine (GA/SVM). We demonstrate that the GA/SVM biomarkers work best in combination with each other; pathway and enrichment analyses show that they cover the widest variety of processes implicated in pluripotency. The GA/SVM wrapper yields best biomarkers, no matter which classification method is used. The consensus best biomarker based on the three methods is Tet1, implicated in pluripotency just recently. The best biomarker based on the GA/SVM wrapper approach alone is Fam134b, possibly a missing link between pluripotency and some standard surface markers of unknown function processed by the Golgi apparatus.

1. Introduction

Classifying high-level phenotypes based on high-throughput gene-level data¹ is a fundamental task in bioinformatics, and analysing corresponding sets of important features improves our understanding of the genotype–phenotype map,² delivering basic insights into the biology underlying a particular phenotype. For the cellular phenotype commonly called ‘pluripotent stem cell’³ and its more heterogeneous counterpart ‘differentiated’ or ‘non-pluripotent stem’ cell, we set out to collect data in the form of gene expression data (microarrays) from the GEO (Gene Expression Omnibus database⁴). Gene expression data are among the most abundant molecular data, and they are still very close to the true genotype of the (static) genome; they may inform us about which genes are responsible for the phenotype we wish to understand. This information comes in several ways. It is of interest:

• (a) Which genes are differentially expressed, i.e. expressed more or less strongly in the pluripotent stem cell state, compared to the differentiated one?

• (b)  Which sets of genes enable the best distinction of the pluripotent stem cell state from the differentiated one, considering their (differential) expression?

• (c)  Which small sets of genes still enable a good distinction of the two states?

A univariate statistical testing approach (often involving normalization/regularization) together with the inspection of ‘fold change’ is a standard approach to answer question a.^5–7 Answers to question b shall yield a comprehensive description of the molecular basis of pluripotency, based on machine learning and feature selection approaches. Answers to question c shall highlight the ‘tips of the iceberg’, and are useful to define small sets of best biomarkers for pluripotency; such ‘minimal-best’ approaches to machine learning have gained popularity in recent years, in particular in search for cancer biomarkers.^8–13

In the past years, the difference between pluripotent stem cells (e.g. embryonic stem/ES cells) and differentiated (e.g. fibroblast) cells has triggered a great deal of interest; it is at the centre of basic research into developmental biology.^3,14 At the same time, there are a multitude of potential applications in regenerative medicine and beyond.¹⁵ Moreover, exciting progress has been made in the in vitro control of basic cellular phenotypes.^16,17 Finally, computational methods such as hierarchical clustering and principal component analysis have been used to investigate pluripotency and differentiation in systematic ways, often based on gene expression data.^18–20 At the end of the Discussion section, further related work will be discussed.

In this paper, we start with a large normalized data set of gene expression experiments obtained from the mouse, using the answer to question a to filter out genes that are not informative. We then tackle question b taking a machine learning approach (including appropriate cross-validation), and we use various machine learning methods resulting in high-accuracy classifiers based on gene expression signatures. Finally, we look into question c by using feature selection methods such as genetic algorithms (GAs)²¹ to obtain classifiers of slightly lower accuracy, working with few features (genes). We evaluate the feature lists obtained to assess their biological plausibility by enrichment analyses. Finally, we discuss the value we may put into the ‘newly discovered’ genes that are supposedly involved in pluripotency.

2. Methods

2.1. Gene expression data

We obtained gene expression data from the GEO database,⁴ taking samples from experiments (data series) related to pluripotency in the mouse, and aiming for a large data set, correctness in class labels and variety in phenotype. As GEO data series usually consist of no more than 5–20 samples, we collected gene expression data from many different GEO series. To ensure straightforward comparability and easy merging of data based on an identical set of probes, we decided to use only data series from the Affymetrix mouse 430.2 oligonucleotide chip (GEO: GPL1261), which is the most popular platform available, containing 45 101 probe sets. To consider a GEO series, it had to contain at least one sample that we could label pluripotent; usually, the GEO series consisted of a mixture of pluripotent and non-pluripotent samples. Based on the sample descriptions, we manually identified samples as pluripotent or non-pluripotent and labelled them as positive (pluripotent) or negative (non-pluripotent). If we were not sure about the label of a sample, we dismissed it rather than risk adding an incorrectly labelled sample. In this paper, pluripotency always refers to stem cells; we do not consider data from cells like zygotes that are pluripotent, but do not have the ability to self-renew. As different microarray platforms have different approaches on how to sample the transcriptome, and about how to represent the concept of ‘genes', the details may differ between different platforms. However, they should converge on the more generic levels of annotation, in particular with respect to most of the UniGene gene symbol annotations of the genes in our analysis; in our analysis, we study mouse genes.

The positively labelled samples are gene expression data of pluripotent stem cells and the inner cell mass (ICM) of the embryo, whereas the negatively labelled samples arise from all sorts of differentiated cells/tissues. We took care to sample a variety of types of pluripotency, including ‘late stages’ up to embryonic day 3.5, pluripotent germline stem cells and induced pluripotent stem (iPS) cells, and of differentiated phenotypes, including ‘early stages’ from embryoid bodies of day 5 onwards, germline stem cells and partially reprogrammed iPS. More specifically, we included samples described as pluripotent from embryonic stem cells (GSE4309, GSE10806, GSE10871 and others), from the ICM up to embryonic day 3.5 (GSE4309), from germline pluripotent stem cells (GSE11274) and from iPS cells (GSE10806, GSE10871 and others). We included samples described as differentiated from embryoid bodies of day 5 (GSE9563) and day 10 (GSE3653), from partially reprogrammed iPS cells (GSE10871), from germline stem cells (GSE10610, GSE11274) and from tissues including testis, ovary and foetus (GSE9954), but also a wide variety of other organs (GSE9954). The final data set contains 286 samples from 25 GEO data series; 146 labelled as pluripotent and 140 labelled as non-pluripotent (Supplementary Table S1).

2.2. Data preprocessing

To summarize the probe sets from the Affymetrix gene expression arrays, we used the robust multi-array average method^22,23 as implemented in the Affymetrix Power Tools.²⁴ First, background adjustment was performed using unmodified perfect match intensities. Then, the intensities were quantile normalized.²⁵ As quantification method we used median polish.^22,23 The resulting expression values are logarithmized on the log2 scale. We then combined all Affymetrix probe set identifiers that correspond to the same gene symbol from the UniGene record²⁶ by calculating the mean value. This way, we obtained the expression values of 20 668 genes. This data set was the starting point for filtering, feature selection and classification, all in the framework of 3-fold cross-validation. Thus, the data set was randomly split into three subsets (folds), to set up a 3-fold cross-validation process. Two-thirds of the data were used to perform filtering, feature selection and finally training of classifiers. The classifiers were then tested on the remaining one-third of the data. This was repeated three times, using different folds for training and testing each time.

As we wanted to identify genes that affect pluripotency, we preferred those having similar expression values within the pluripotent or the non-pluripotent samples and different expression values between these two groups—i.e. differentially expressed genes. Hence, we filtered the genes by applying a two-sample t-test for samples with unequal variances, testing the difference in mean expression of the genes in the respective training set and corrected resulting P-values based on the concept of false discovery rate.²⁷ We dismissed all genes with a q-value (corrected P-value) larger than 0.1. Depending on the training set, we obtained lists of around 16 000 genes. These were sorted by their fold changes determined as log FC_i = |X_i – Y_i|, where X_i is the mean of the gene expression values of gene i for pluripotent samples, and Y_i is the mean of the gene expression values of gene i for non-pluripotent samples, both on the log-scale. The first 5000 and the first 1000 genes of these lists formed our data sets for classification.

As described, filtering, feature selection and training of classifiers were always performed on two-thirds of the data and testing on the remaining third. Only such strict separation of training and test data (which is unfortunately not standard practice, as noted by Rocha et al.²⁸) can ensure that results are not overly optimistic. On each of the three folds, the GA was run 200 times. However, the whole data set was used for calculating feature importance (Fig. 1), for the list of biomarkers we found (Table 2) and for the enrichment analyses (Tables 3 and 4), since these parts of the work did not involve training and testing. In this case, the GA was run 500 times.

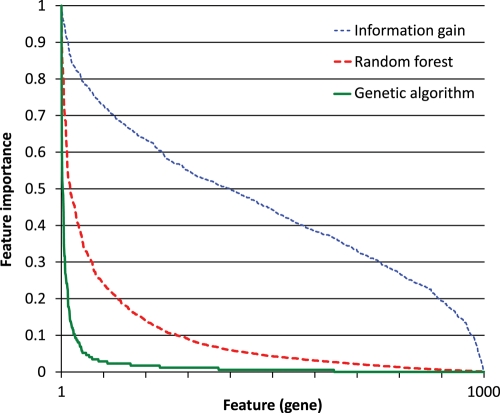
Figure 1.

Feature-importance distribution. Each feature (gene) from the 1000-gene data set was assigned an importance score by each of the three feature selection methods. The scores were scaled to the [0, 1] interval. The features were then sorted by their importance, separately for each method, and their importance was plotted.

Table 2.

Top 20 most important genes

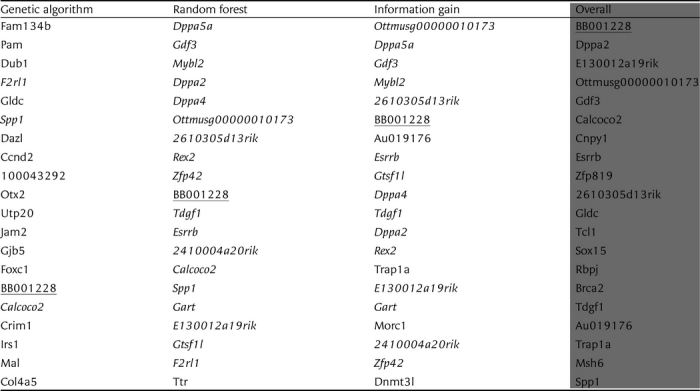The genes that appear in two of the top 20 lists of the individual feature selection methods are shown in italics. The only gene that appears in all three lists (BB001228, also known as Tet1) is underlined. Complete lists are available as Supplementary File S2.

Table 3.

Enrichment of genes in pluripotency networks and embryonic tissue

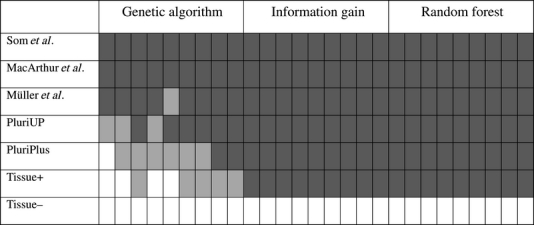Enrichment and its significance of 27 gene sets found by feature selection, using two colours: enrichment in light grey, significant enrichment (P-value ≤ 0.05) in dark grey. See text for abbreviations. Exact counts and p-values can be found in Supplementary File S4.

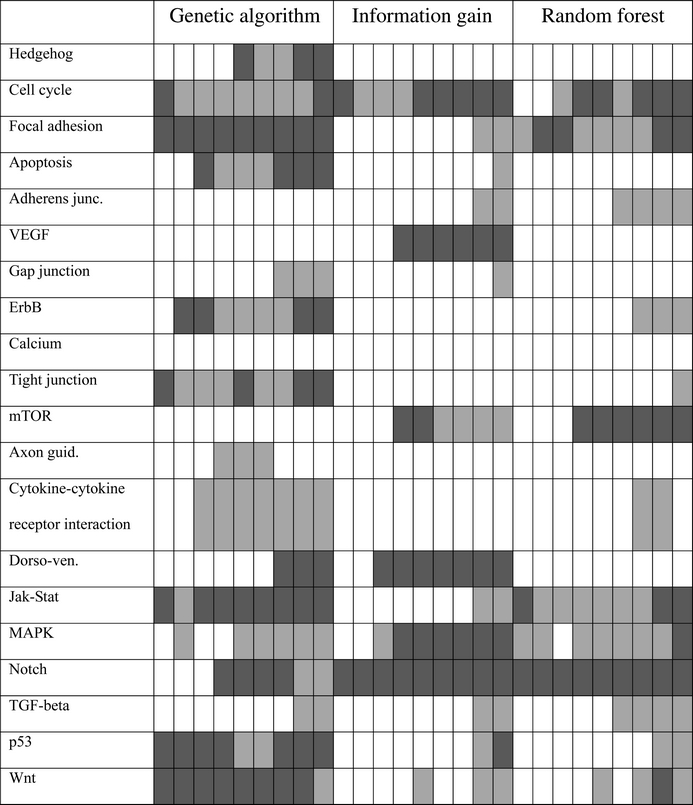
Table 4.

Enrichment of genes in pluripotency pathways (Table 3)

In Supplementary File S2, we provide all lists of input genes we discuss here. Please note that the term ‘gene’ always refers to a gene from the mouse genome (UniGene gene symbol), and its function will be described based on its protein product. Genes are also called ‘features’ in the description of our machine learning methodology. Thus, ‘feature selection’ is synonymous with ‘gene selection’.

2.3. Classification

Classification using both the whole (filtered) data set, and the feature sets selected by the feature selection methods under investigation, was performed with the Weka machine learning suite.²⁹ The following machine learning algorithms were used:

• Naive Bayes³⁰;

• C4.5 decision trees, implemented in Weka as J48³¹;

• Random forest³²;

• Nearest neighbour, implemented in Weka as IBk³³;

• SVM, implemented in Weka as sequential minimal optimization (SMO).³⁴

Concentrating on the discovery of optimal feature sets (biomarkers), we did not tune parameters to maximize classification performance, and all parameters of the machine learning algorithms were kept at Weka's default values. The only exception was the SVM with Gaussian kernel, for which the default LibSVM³⁵ parameter values were used, consistent with the use of LibSVM during feature selection with the GA (see below). We briefly describe two of the machine learning algorithms: the random forest, because of its relevance to feature selection (see below), and the SVM, because it is the algorithm we also used for feature selection with the GA.

The random forest³² is a machine learning approach working with an ensemble of decision trees. Let N be the size of the training set and M the number of features (in our case gene expression values). To grow a tree, N instances from the training set are selected randomly with replacement (which means that some are selected more than once and some never). Then m features (m << M) are selected randomly. Out of these, the one that splits the instances into sets purest with respect to the class is assigned to the root of the tree. This procedure is repeated recursively until the leaves of the tree contain only instances of one class (pluripotent or non-pluripotent in our case). The whole forest consists of a number of such decision trees. To classify an instance, it is classified by all the trees in the forest and the final class is selected by majority voting.

The support vector machine (SVM³⁴) finds a hyperplane across the M-dimensional space occupied by instances that best separates the two classes. In cases where the instances are not linearly separable, their features can be mapped into a higher-dimensional space. Let x_i and x_j be a pair of M-dimensional feature vectors. Let Φ(x_i) and Φ(x_j) be these vectors mapped into a higher-dimensional space. Since computing the hyperplane that separates the instances only involves computing inner products of feature vectors, the mapping can be efficiently accomplished by a kernel function K(x_i, x_j), which returns the inner product of Φ(x_i) and Φ(x_j) without explicitly performing the mapping. The linear kernel function returns the plain dot product: K_lin(x_i, x_j) = x_i · x_j. The Gaussian kernel function is defined as follows: K_Gauss(x_i, x_j) = exp (–γ (x_i − x_j)²). The value of γ controls how much the classifier can adapt to an irregular boundary between classes, and must be selected by the experimenter. As mentioned before, we used the default LibSVM value of γ = 1/number_of_features.

The classification performance was evaluated by 3-fold cross-validation as described in the previous subsection. The performance is presented in terms of the accuracy and the area under the receiver operational characteristics (ROC) curve (AUC). The accuracy is defined as the number of correctly classified instances divided by the total number of instances. It is an appropriate measure when the data set has roughly the same number of instances belonging to each class (as is the case in ours), when misclassifying any class to any other class is equally undesirable and when one is interested in crisp classification. Let one class be considered negative (non-pluripotent in our case) and the other positive (pluripotent) and let the classifier return a continuous value (instead of just one class or the other). The ROC curve is a plot of the true positive rate vs. the false positive rate, obtained by varying the threshold above which the value returned by the classifier is considered to indicate the positive class. The true positive rate is the number of correctly classified positive instances, divided by the number of all positive instances (the probability to recognize pluripotent samples as such). The false positive rate is the number of incorrectly classified negative instances, divided by the number of all negative instances (the probability to mistake a non-pluripotent sample for a pluripotent one). The AUC is an aggregate measure of the performance of the classifier when one considers different thresholds in order to correctly classify more positive instances at the expense of misclassifying negative ones and vice versa. It is appropriate regardless of how many instances belong to each class.

2.4. Feature selection with the information gain

The information gain of a feature F is a measure of how much information one gains about the class C if one knows the value of F. In other words, it is the reduction in uncertainty about C, which is measured by its entropy H(C). The uncertainty about C, if one knows the value of F, is measured by its conditional entropy H(C|F). The information gain is thus defined as

More conveniently, the information gain can be described in terms of joint entropy H(C, F) as follows:

Let f₁,…, f_k be the possible values of the feature F (if the feature is continuous, as in our case, it is discretized first) and c₁,…, c_l the possible values of the class C (only two in our case). The entropies are computed as follows (the computation of H(F) is analogous to the computation of H(C)):

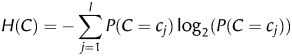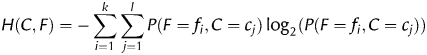Feature selection with the information gain was performed using Weka machine learning suite.²⁹

2.5. Feature selection with the random forest

This subsection describes the procedure to measure feature importance with the random forest³²; an overview of how the random forest works is given in the Classification subsection. To grow a tree in a random forest, N instances from the training set are selected randomly with replacement. N is also the size of the training set, but since the instances are selected with replacement, around one-third of the training instances are left out—these are called the out-of-bag instances. The out-of-bag instances are classified with the tree and the number of correct classifications c_before is counted. For each feature F, its values in the out-of-bag instances are randomly permuted, the out-of-bag instances are classified again and the new number of correct classifications c_after is counted. The difference between c_before and c_after, averaged over all the trees in the forest, is a measure of the importance of F.

Feature selection with the random forest was performed in a custom Weka distribution by Livingston.³⁶ The number of trees in a forest was set to 1000 and the other parameters were kept at default values. A random forest was generated three times and the importance of features was averaged over the three runs.

2.6. Feature selection with the GA

We are looking for small sets of genes that enable us to classify a sample as pluripotent or not, which we call minimal sets of best biomarkers. We search for such sets with the GA²¹ guided by a fitness function. The fitness of a gene set is defined by the classification accuracy of the SVM³⁴ using that set of genes as features, and the size of the set. Thus, the objective of the GA is to find optimal sets of features for classification. Each set of genes/features is binary encoded in a ‘chromosome’. Each bit of the chromosome represents one gene/feature. If a gene belongs to the set of features encoded by the chromosome, the corresponding bit is set to 1, otherwise it is set to 0. (Apart from the binary representation used here, more compact representations may be used, as was done, for example, by Rocha et al.²⁸ A systematic evaluation of such alternative representations is future work.) The initial population of 200 chromosomes is created by setting a random number of bits in each chromosome to 1, and calculating the fitness of the resulting feature set, as follows.

Pseudocode: create initial population

for each chromosome j

for each bit i of j

set i = 0

do with a probability of start_chromosome_size/|set_of_all_genes|

set i = 1

end do

end for

compute fitness of the chromosome

end for

The value |set_of_all_genes| is the number of filtered genes we begin with, in our case 1000. The value start_chromosome_size is the mean number of selected genes for each chromosome of the initial population, which in our case is set to 15. That way each chromosome of the initial population consists of 15 genes on average.

As mentioned before, the fitness of a chromosome is defined by two criteria: the classification accuracy calculated using the SVM, and the number of features/genes. The smaller the number of features and the better the classification accuracy of the feature set, the fitter the chromosome. Following a multiobjective approach, we combine both criteria into one fitness function, f, to be optimized:

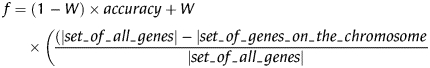The value accuracy is the classification accuracy of the SVM with Gaussian kernel (C = 1, γ = 1/start_chromosome_size), using the LibSVM³⁵ implementation with 6-fold cross-validation. The value |set_of_genes_on_the_chromosome| is the number of selected features. Because the main objective is finding correct biomarkers, accurate classification capability plays a bigger role than the number of selected features. For this reason we choose W = 0.2, as in reference.³⁷

Based on this initial population, we breed a new generation using recombination and mutation. Recombination is implemented as follows.

Pseudocode: recombination

for 1 tosize_of_populationdo

do with a probability of 0.8

select two chromosomes by roulette wheel selection

combine the two chromosomes by uniform cross over

end do

add new chromosome to population

end for

Due to the recombination rate of 0.8, in each generation, about 160 new chromosomes are generated by recombination using uniform crossover.³⁸ Two parent chromosomes are selected using roulette wheel selection, i.e. the probability for a chromosome to be selected is proportional to its fitness. Then, the bits at the same position in both parent chromosomes are compared with each other. If they have the same value, this value is chosen for the child chromosome. If the values are different, the bit in the child chromosome is selected randomly.

Subsequently to the recombination step, all chromosomes are mutated. On average, we flip 1.5 bits on each chromosome, as follows.

Pseudocode: mutation

for each chromosome j of the population

for each bit i of j

do with a probability of 0.1 × start_chomosome_size/|set_of_all_genes|

flip bit i

end do

end for

add new chromosome to population

end for

Finally, following an elitist approach, the resulting chromosomes as well as the chromosomes of the initial population are sorted in descending order of fitness. Then, the first 200 chromosomes are selected to form the new population. This new population serves as the initial population for the next generation. Gene sets with very good cross-validation accuracies were already found after 15 to 20 generations. Thus, the whole process was repeated for 25 generations to obtain the final population.

The best chromosome of the final population contains the potential biomarkers we are looking for. To compare the GA to the other two classification methods, we ran the GA 200 times for each of the three folds. Then, we sorted the genes in decreasing order by frequency of occurrences, generating a ranked list of all genes that is comparable to the lists we obtained with the random forest and the information gain. For those parts of the paper that do not involve training and testing, we ran the GA 500 times, using the whole set of samples.

2.7. Top 20 most important genes

To obtain the list of the top 20 most important genes, an importance score for each gene in the 1000-gene data set was computed by each of the three feature selection methods: the information gain, the random forest and the GA (as described in the previous three subsections). The information gain and the random forest both assign a real-number score to each feature, which we used directly. The GA selects a well-performing set of features that differ from run to run. In our experiments, the size of the set selected by the GA was between 3 and 9 and the features selected varied considerably. Hence we measured the importance of a feature by the number of times it was selected over 500 runs of the GA, using 1000 genes and all the samples in the data set. The genes were ranked by their importance according to each method.

To compute the overall top 20 most important genes, the ranks for each gene were averaged and the overall top 20 genes were chosen by the average rank. We used ranks instead of numeric importance scores because (Fig. 1) the scores assigned by the information gain are on average much larger than those by the random forest and the GA. As a consequence, using the scores instead of ranks would give the information gain much greater weight in the overall ranking.

2.8. Enrichment analysis

To evaluate the biological relevance of our results, we applied gene set enrichment analysis using the hypergeometric distribution.³⁹ We assumed that the genes selected by our feature selection methods are over-represented in gene sets that can be directly associated with the pluripotent status of cells. For this reason, we compared our selected genes with several pluripotency-related networks and pathways^40–46 (http://c-it.mpi-bn.mpg.de/, http://www.genome.jp/kegg/pathway.html). As the reference set, we used the set of all genes in the Affymetrix array. The over-representation analysis (ORA) determines whether a pluripotency-related gene set based on a network or pathway is over- or under-represented in one of the gene sets selected with our feature selection methods, and estimates how likely this is due to our selection method (as opposed to observing the same over- or under-representation by chance).

Let n be the size of an ORA test set (that is, a feature set to be tested for over- or under-representation) and k the number of genes in the set that belong to a pluripotency-related gene set. Furthermore, let m be the number of genes in our reference set and l the number of the genes in the reference set that also belong to the pluripotency-related gene set. The probability for a randomly selected gene from the reference set to belong to the pluripotency-related set is thus l/m, and we expect to find k′ = n l/m genes of the pluripotency-related genes in our test set. If the number of genes actually found (k) is larger than k′, we can say there is an enrichment of pluripotency-related genes, otherwise there is depletion. We then estimate the statistical significance of enrichment by computing the one-tail P-value using the hypergeometric distribution as follows:

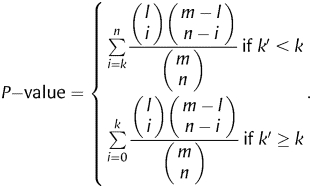3. Results

3.1. Classification without feature selection

Our first objective was to establish how easy it is to classify samples as pluripotent or non-pluripotent with machine learning, and to explore the various machine learning algorithms available for the task. We compared five algorithms chosen to represent different approaches to machine learning: the naive Bayes, the C4.5 decision trees, the random forest (an ensemble of decision trees), the nearest neighbour and the SVM. Two kernels were tried with the SVM: Gaussian and linear. The algorithms were tested on the full set of 20 668 genes as well as on the filtered sets of the 5000 and 1000 most strongly differentially expressed genes. Each sample represented one machine learning instance with gene expression values as features and ‘pluripotent’ or ‘non-pluripotent’ as class labels. The cross-validated classification results are presented in Table 1 in terms of the accuracy and the AUC.

Table 1.

Comparison of machine learning algorithms and data sets

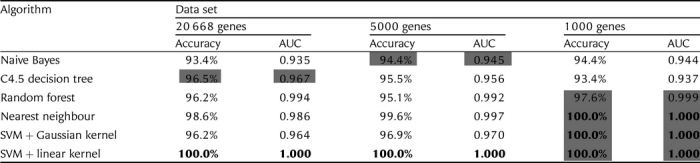The highest cross-validated accuracy and AUC in each column are shown in bold type. The highest accuracy and AUC in each row are shaded in gray.

The first conclusion we can draw from Table 1 is that machine learning classifies very well, in many cases perfectly. Furthermore, the SVM + linear kernel is the algorithm best suited to this task. The reason the SVM + Gaussian kernel performs worse than the SVM + linear kernel on the larger two data sets is probably that we have a lot of features compared to the number of instances, and the Gaussian kernel effectively increases the number of features.^47,48 Using a large number of features is problematic because this approach increases the chance of learning spurious relations (overfitting). Based on these findings, our first choice for testing the classification performance of small feature sets (see the next subsections) was the SVM; both linear and Gaussian kernels were considered because the reduction in the number of features by feature selection may favour the Gaussian kernel.

Table 1 shows that for the three best performing machine learning algorithms (the SVM with both kernels and the nearest neighbour), classification with 5000 genes is better than with all 20 668 genes, and classification with 1000 genes is better than with 5000 genes. Therefore, searching for pluripotency biomarkers in the 1000-gene data set is sufficient and in fact preferable, because many irrelevant genes are already eliminated. Reducing the number of genes further was left to the feature selection methods we investigated (see the next subsection), for which we did not wish to exclude any genes prematurely. Based on Table 1, the list of 1000 genes in Supplementary File S3, sorted by feature importance, may be called the set of genes that enable the best distinction between pluripotent and non-pluripotent, answering question b of the Introduction.

3.2. Feature selection

Feature selection is a technique used in machine learning to reduce the set of features to the most relevant ones, which often improves classification, and, in our case, also identifies biomarkers with potentially important roles in pluripotency. We used three feature selection methods of increasing complexity. The first method is the ranking of features by information gain. The information gain measures how much information about the class one gains by knowing the value of a feature. It considers each feature on its own. The second method is the ranking by feature importance computed by the random forest machine learning algorithm. The importance is obtained by randomly permuting the values of a feature and measuring the resulting decrease in classification accuracy. While this method still evaluates single features, it measures their importance as a part of a classifier that uses other features as well. The third method is feature selection with the GA. Here, the set of features is optimized by the GA guided by the classification accuracy as the main part of the fitness function, computed using the SVM with Gaussian kernel; the size of the feature set also has a minor influence on the fitness function, since we aimed at small sets of best features. This method evaluates whole sets of features.

Figure 1 shows that the three feature selection methods yield considerably different feature-importance distributions. The importance based on the information gain is distributed fairly evenly. The opposite is the case for the importance based on the GA: there are few genes with a high importance and many with a low importance. The random forest is between the two extremes. The most likely explanation for this stems from the well-known redundancy of biomarkers.⁴⁹ Information gain, which considers each gene on its own, finds many of them predictive of pluripotency. The GA selects only the genes most indispensable for classification many times. From the remaining (redundant) genes, different ones are selected in each run due to the random nature of the algorithm, so none ends up with a high importance.

In order to evaluate the performance of the three feature selection methods, we compared cross-validated classification accuracy on the feature sets selected by them. The samples were split in three folds and the first 1000 genes of each fold were selected (see the Methods section), the GA was run 200 times on each of them. For each of the three folds, we sorted the features by their importance (as for Fig. 1) and selected the top 50, 40, 30, 20, 10, 5, 3, 2 and 1 features, and employing these, we computed the classification accuracy using the SVM with the Gaussian and linear kernel, and using the random forest. Then, we calculated the average accuracy over all three folds. The SVM was chosen for its high performance shown in the previous subsection. However, since it was already used as a component of the feature selection with the GA, the feature sets selected by the GA might favour classification with the SVM. We therefore used the random forest for balance. If the features selected by the GA (using the SVM internally) turned out best even for classification with the random forest, we would obtain an unbiased recommendation for using the GA for feature selection. The results are shown in Figs 2–4.

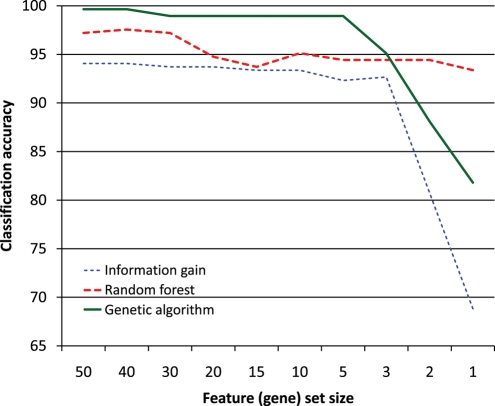
Figure 2.

Classification accuracy measured by the SVM with Gaussian kernel. Feature selection with information gain, random forest and GA was evaluated using incrementally smaller sets of most important features from the 1000-gene data set.

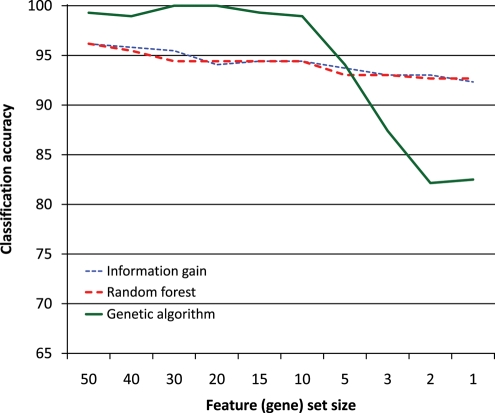
Figure 3.

Classification accuracy measured by the SVM with linear kernel (Fig. 2).

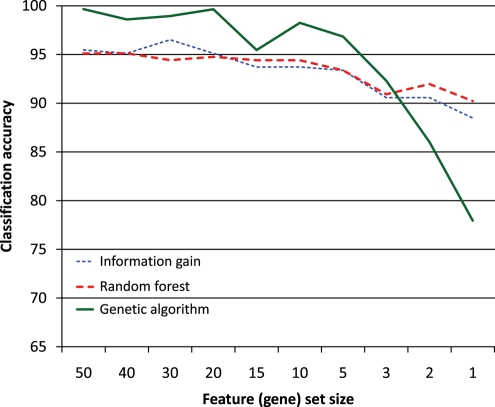
Figure 4.

Classification accuracy measured by the random forest (Fig. 2).

Inspecting Figs 2–4, we can see that classification with SVM does not particularly favour features selected by the GA (using the SVM with Gaussian kernel internally). Likewise, the classification with the random forest does not seem to favour features selected by the random forest. We may thus conclude that the genes selected by these methods are tied to pluripotency in general and not to any particular machine learning algorithm.

Figure 3 shows that the classification accuracy of features selected by information gain and random forest is very similar, starting at around 96% with 50 features and dropping to around 92% with a single feature. The situation is similar in Fig. 4, except that the accuracy is overall slightly lower, because the random forest (Fig. 4) does not classify as well as the SVM (Fig. 3). The difference between feature selection with information gain and random forest in Fig. 2 is larger, which indicates that the random forest may be better at identifying good features than the information gain; however, since this does not occur in Figs 3 and 4, no firm conclusion may be drawn. The behaviour of the features selected by the GA is consistently different from those selected by the other two methods. One feature, two features and in one case three features yield a lower classification accuracy than the same numbers of features selected by the other two methods, but once we have more features, those selected by the GA perform better. This is probably due to the GA selecting sets of features that classify well together but not necessarily individually, whereas the other two methods select features that are good individually.

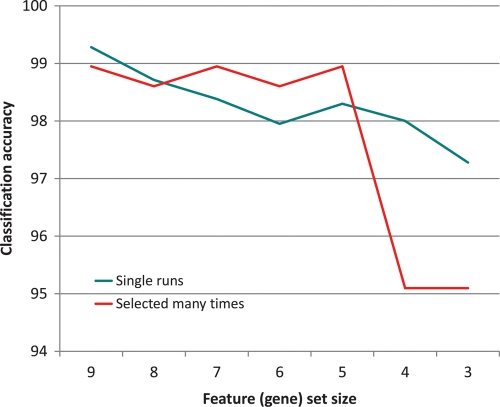
Finally, we compared the classification accuracy of features selected by the GA many times over 200 runs in each fold (shown in Fig. 2, for a large number of feature (gene) set sizes) with the accuracy of features selected in single runs. This comparison enables us to investigate the change of accuracy due to aggregation of output (i.e. merging output lists together). The results are shown in Fig. 5. For feature sets of size 7, 6 and 5, features selected most often over 200 runs performed slightly better. For feature sets of size 9 and 8, features selected in single runs were slightly better, but the difference in accuracy was extremely small. This shows that feature sets consisting of features selected most often by the GA offer reasonable performance, while eliminating the variation in features selected in single runs. Only for feature sets of size 4 and 3 did features selected in single runs perform considerably better. This is because the GA selected so few features only when they achieved sufficient classification accuracy by themselves, in exactly this combination; aggregation of output destroys the exact combinations. The features selected most often came from different sets; one could already observe in Figs 2–4 that such features, if they were too few, performed poorly.

Figure 5.

Classification accuracy measured by the SVM with Gaussian kernel, evaluating features selected many times vs. features selected in single runs by the GA. For feature set size s, the classification accuracy of the features selected by the GA in single runs is averaged over all the final feature sets of size s. The features selected many times are the s features most often selected by the GA (classification accuracy is averaged over the three folds).

Table 2 lists the top 20 most important genes selected from the 1000-gene data set by each of the three feature selection methods. It also lists the overall top 20 genes, which are the ones ranked highest by the three individual methods on average. All the samples in the data set were used and the GA was run 500 times. We can see that the lists by the random forest and the information gain are quite similar, whereas the one by the GA is different. The list of the overall top 20 genes does not contain many of the genes considered important by both the random forest and the information gain, because they were ranked too low by the GA. In the Discussion section, we will describe what is known about the listed genes, with reference to pluripotency.

3.3. Enrichment analysis

The enrichment analysis was done (as described in the Methods section) for the most important genes identified by feature selection with the GA, information gain and random forest. In the absence of a pre-defined number of most important genes to select, we started with the top 40 genes and increased the number in steps of 20 up to 200 genes. This resulted in 27 gene sets, 9 for each of the three feature selection methods.

A significant enrichment (P-value < 0.05) of pluripotency-related genes published by Som et al.,⁴⁰ MacArthur et al.⁴¹ and Muller et al.⁴² can be found for nearly all 27 tested sets, as shown in Table 3. For the sets selected by information gain and random forest, we could also observe a consistent significant enrichment of the genes from two other published pluripotency gene lists (PluriUp and PluriPlus⁴³; for calculating enrichments with respect to human genes, we took their mouse orthologs). The analysis was also done with a set of genes which are enriched or depleted in embryonic tissue (abbreviated ‘Tissue+’ and ‘Tissue–' in the table, obtained from http://c-it.mpi-bn.mpg.de/). For the genes known to be enriched in embryonic tissue, the lists selected by information gain and random forest show a significant enrichment, whereas no significant enrichment can be found in any of the sets chosen by the GA. For the genes which are depleted in embryonic tissues, there is no enrichment in any of the tested sets.

Enrichment could also be observed in different pluripotency-related pathways.^44–46,50 Here, the gene sets selected by the GA show an enrichment in more pluripotency-related pathways than the gene sets selected by the other two methods (Table 4). The larger variety of pathway annotations for the genes selected by the GA reaffirms that this feature selection method selects a broader variety of biomarkers related to different aspects of pluripotency.

4. Discussion

We have shown that on the basis of gene expression data, the distinction between the pluripotent and the differentiated (non-pluripotent stem) cell state can be learned with cross-validated accuracies reaching 100%. We provided evidence that the features (genes) selected by the combination of the GA and the SVM are small sets of features that classify well and that work best in combination (Figs 2–5). We listed these genes as potential biomarkers in Table 2 together with the features (biomarkers) selected by two other methods (information gain and random forest). Analysing each of the top 10 pluripotency biomarkers in the columns of Table 2, we now wish to answer the following questions:

1. What can we find out about the selected genes by literature investigations?

2. Why are the genes generally known to be involved in pluripotency under-represented among the selected genes?

3. How much reliability can be assigned to the selection of genes? What kind of relevance do the selected genes have for pluripotency?

4.1. Literature investigation of the most important pluripotency biomarkers

The sets of pluripotency markers returned by the GA include the Fam134b gene in 35% of the selected gene sets (174 times out of 500), making it the most important feature by a large margin (the Pam gene is the runner-up selected in 21% of the feature sets—106 times out of 500). In human, mutations of FAM134B cause severe neuropathy, leading to a recent effort to characterize the mouse ortholog.⁵¹ Fam134b expression was found predominantly in ganglia. The protein co-localized with the cis-Golgi marker giantin, and (partially) with the trans-Golgi marker TGN38; relocation after brefeldin A treatment followed a pattern typical for Golgi-resident proteins. shRNA knockdown to levels of 19–27% reduced the size of the cis-Golgi compartment and impaired cell proliferation in N2a cells. Interestingly, isoform 2 of Fam134b is found in testis, but not in neural tissue. In the neural context, Golgi-mediated processing and/or transport of neurotrophin precursors and their receptors may be impaired by a lack of Fam134b. In the ES cell context, Golgi-mediated processing and/or transport of two cell surface markers of unknown function in pluripotency, SSEA1 (stage-specific embryonic antigen 1) and AP (alkaline phosphatase) may be impaired; both SSEA1 and AP⁵² are localized in the Golgi, to be transported to the cell surface. The observed role of Fam134b in cell proliferation in the mouse is reflected in human; FAM134b is implicated in oesophageal carcinoma, and it promotes cell proliferation.⁵³ It is also overexpressed in benign tumours (adenomas), but underexpressed in adenocarcinoma.⁵⁴

In 52 cases, the Fam134b gene was selected together with the F2rl1 gene (a.k.a. PAR-2, see below), which is ranked fourth by the GA. By the design of the genetic-algorithm-based feature selection, the most likely ‘connection’ between both genes is that they cover complementary aspects of pluripotency, F2rl1 being concerned with the distinction of pluripotency and multipotency,⁵⁵ acting as a G protein-coupled receptor with a putative role in the mouse blastocyst.⁵⁶

The Pam (peptidylglycine alpha-amidating monooxygenase, a.k.a. Phm) gene is the second-most important feature selected by the GA. The only evidence we could find for its role in pluripotency is provided by Lyczak et al.,⁵⁷ who investigated a putative remote(!) homolog in C. elegans and concluded ‘Our analysis of PAM-1 requirements shows that a puromycin-sensitive aminopeptidase is also required for proteolytic regulation of the oocyte to embryo transition’. Dub1 (deubiquinating enzyme 1) is ranked third; the gene is also a novel candidate involved in pluripotency. (De-)ubiquination of histones has recently been shown to have an important role in repressing developmental control genes in ES cells, however.⁵⁸ As described, the F2rl1 (PAR-2) gene is ranked fourth, and was implicated in the distinction between multipotency and pluripotency.

Positions 5–10 are assigned to genes already implicated in pluripotency. Gldc is discussed by Boue et al.⁵⁹ and Spp1 (a.k.a Osteopontin) is regulated by Pou5f1/Sox2.⁶⁰ Dazl functions in the maintenance of pluripotency of mouse primordial germ cells,⁶¹ and as a translational regulator during ES cell differention.⁶² Ccnd2 is repressed by Tcf3 in embryonic stem cells.⁶³ 100043292 (a.k.a. GM4340) is found only in embryonic tissue in cleavage state (Supplementary File S5) and Otx2 is part of the gene regulatory network in mouse ES cells, working with Oct4 (Pou5f1), possibly to maintain gene expression in early progenitors of ectodermal lineages.⁶⁴ All the named genes just mentioned are listed by Boue et al.⁵⁹ in the human or mouse networks of their Figures 2 and 3; none of them is a well-known pluripotency gene, however.

Genes selected as features by the random forest are more well-known. The top 10 are 3 Dppa (development- and pluripotency-associated) genes, 5 other well-known genes, namely Gdf3,^65,66 Mybl2 (a.k.a. B-Myb),⁶⁷ Rex2,⁵⁵ Zfp42 (a.k.a. Rex1)⁶⁸ and Tet1 (listed by Affymetrix as BB001228, see below) and two unnamed genes (Ottmusg00000010173 and 2610305d13rik).

Information gain highlights the largest set of well-known genes, with Esrrb among the top 10, and 6 of the 10 random forest genes just mentioned. Curiously, however, we find Ottmusg00000010173 (a.k.a. Gm13051) on the top of the list, so we investigated it further. The gene is transcribed predominantly in embryonic tissue in the blastocyst and organogenesis stage (Supplementary File S6). Moreover, NextBio.com lists the study ‘Pluripotent stem cells gene expression at different stages of development in Sox2-deficient embryos’ (GSE15358) as the first study for this gene, reporting its downregulation in epiblast-derived pluripotent stem cells vs. ES cells.

Combining the three lists of features selected by the GA, the random forest and the information gain should highlight those genes which work best as discriminative markers, no matter whether they are used as features in isolation or together with others. The combined list should thus be superior in its general utility and its resistance to outliers, just as combined lists in homology search are.⁶⁹ Three observations are noteworthy. First, the mouse gene BB001228 representing the Tet oncogene 1 (Tet1) according to the Affymetrix array annotation scores best. Tet1 is deemed responsible for the generation of 5-hydroxymethylcytosine (5hmC)⁷⁰ in mouse ES cells under physiological conditions,⁷¹ and during ES cell differentiation, the amount of Tet1 and 5hmC decreases. Also, Tet1 maintains Nanog expression and its knockdown impairs the self-renewal and maintenance of mouse ES cells⁷² by participating in the upregulation of pluripotency factors^73,74 and the downregulation of developmental regulators.⁷³ Secondly, the E130012a19rik gene is ranked third; it was most recently discussed as a Klf5 target with strongest effect (see Figure 2 in Parisi et al.⁷⁵). Finally, Calcoco2 (a.k.a. NDP52l1) and Cnpy1 are now among the top 10; the former has been implicated in pluripotency before,^76–79 and the latter has been reported to be a target of Smad2/3 signalling in mouse ES cells, noting its expression in the embryo (2-cell-stage,⁸⁰ their Table S7), and it is a regulator of FGF signalling in zebrafish, albeit in a neural context.⁸¹

4.2. Underrepresentation of canonical pluripotency genes

We found some generally known genes such as Esrrb, Gdf3, Mybl2, Zfp42, some Dppa (development- and pluripotency-associated) genes and, as the cumulative top scorer, BB001228 (Tet1). This list does not include many generally known genes such as Pou5f1 (a.k.a. Oct4), Sox2, Nanog etc., but not finding these by machine learning is a common phenomenon, as discussed in the subsection on Related Work at the end of the Discussion. The genes Pou5f1, Sox2, Nanog, Lin28 and Klf4 were found at positions 196, 414, 203, 594 and 83 of our list, respectively; the two genes Tcf3 and cMyc are not part of the 1000 gene data set, because the fold changes of these genes are too small.

Our hypothesis is that the latter genes are general indicators of pluripotency (in particular, they are strongly upregulated in pluripotent samples, see Table 5), and with certainty they are involved in its mechanistic basis, but they do not provide crisp classification power because (a) they are involved in other processes such as neural stemness (Sox2⁸²) and germline maintenance (Oct4 (Pou5f1)⁸³) and/or their activity is shut down gradually, and (b) they are redundant in particular in the GA setting: this method may select any one of them for ‘getting the idea’, in combination with more powerful discriminating genes that reflect pluripotency in a complex, context-dependent and non-linear way. With respect to (a), we indeed observed that Sox2 and Oct4 (Pou5f1) are still found in some negative samples, such as GSM272848 or GSM275556. This is not surprising, since, as described, we included pluripotent stages up to embryonal day 3.5 as well as iPS cells as actual positives, and embryonic body stages from day 5 onwards as well as non-pluripotent germline stem cells as actual negatives. With respect to (b), we observe at least one gene of the pluripotency-related network by Som et al.⁴⁰ in 54% of the feature sets selected by the GA. Also, at least one gene of networks published by MacArthur et al. ⁴¹ and Muller et al.⁴² can be found in 33% and 27% of the selected feature sets, respectively. We hypothesize that each feature set includes at least one ‘general indicator’ of pluripotency; some of them are documented in a pluripotency-related network, but some are not known yet.

Table 5.

Gene expression values of pluripotency genes

	Generally known pluripotency genes			First three genes selected by the genetic algorithm
	Pou5f1	Sox2	Nanog	Fam134b	Pam	Dub1
Non-pluripotent	6.02	6.43	4.67	7.38	5.82	4.19
Pluripotent	11.71	11.59	10.91	5.58	4.39	5.69
Fold change	5.69	5.16	6.24	1.79	1.43	1.50

The table shows the mean expression values for the pluripotent samples and the non-pluripotent samples as well as the resulting fold changes for three generally known pluripotency genes. For comparison, the first three genes found by the GA are also listed.

The underrepresentation of canonical pluripotency genes is also reflected by the lower levels of enrichment of relevant genes in the feature sets based on the GA (when compared with information gain and random forest, see Table 3). In turn, the larger variety of relevant pathways enriched in feature sets based on the GA (Table 4) may indicate an overrepresentation of non-canonical pluripotency genes that are (at least peripherically) associated with diverse aspects of pluripotency.

4.3. Reliability and relevance of the most important pluripotency biomarkers found by the GA

The GA is a stochastic search, so we repeated it for a second time with the same data set yielding very similar results, as shown in Table 6, confirming the reliability of our list. The evidence for relevance is given in several ways: (a) the literature investigation at the start of this section revealed that most genes we found are related to pluripotency, even though most of them are not well-known pluripotency genes. (b) Our enrichment analyses show that many genes that are selected as features are implicated in pluripotency, being included in networks describing pluripotency, and being overexpressed in embryonic tissue (Table 3). (c) The enrichment analyses of Table 4, together with the observations of Figs 2–4, imply that the genes selected by the GA cover a wide spectrum of many aspects of pluripotency, and they are most informative about pluripotency in combination.

Table 6.

Similarity of the results of the reference run and the confirmation run of the GA

The table shows the similarity of the top 20 genes from the confirmation (second) run of the GA, compared to the reference (first) run. The colour code for the first, second, third and fourth quartile of the genes of the reference run is carried over to the confirmation run; the two genes coloured white are found up to position 30 in the reference run.

4.4. Related work

Bioinformatics approaches have a long history in pluripotency/stem cell research. The method of ‘Digital differential display’ (http://www.ncbi.nlm.nih.gov/UniGene/help.cgi?item=ddd) may be called a success story, allowing the discovery of the Nanog gene,⁸⁴ which was later recognized to form, together with Oct4 (Pou5f1) and Sox2, the so-called ‘core circuit’ behind pluripotency in both the human and mouse. Basically, Nanog emerged by contrasting transcriptomes from mouse ES cells with those from various other sources, identifying differentially expressed genes and experimentally checking for enhancements in self-renewal triggered by these. Moreover, the discovery of the ‘Yamanaka factors’, transcription factors which can reprogram a fibroblast into an ‘induced pluripotent’ stem cell state (iPS),⁸⁵ was based on testing 24 ES cell marker genes known from several sources, partially discovered by gene expression analyses. There are many approaches^86,87 using gene expression (but also proteomics^88,89) data to derive lists of genes involved in pluripotency. In some publications, the intersection of these lists is studied, and it is long known that such intersections feature only a small number of common genes^90,91; this problem of ‘small overlap’, ‘missing consensus signature' or ‘missing reproducability’ is not confined to investigations into pluripotency, but it is also found in attempts to define cancer biomarkers.^92,93 Moreover, gene lists associated with pluripotency often do not feature the obvious suspects such as the ‘core circuit’ of Oct4 (Pou5f1), Sox2 and Nanog, the other ‘Yamanaka factors’ Klf4 and cMyc,⁸⁵ or other genes commonly associated with pluripotency in the literature,⁴⁰ such as Stat3 or Esrrb; see references^87,94 for examples of gene lists including mostly ‘unexpected markers’. Other analyses based on large data sets feature commonly associated genes, but they also include a large proportion of ‘unexpected markers’.^59,95,96 Literature curation, expression data analysis and machine learning were applied to derive and enhance networks of genes/proteins involved in pluripotency in the mouse⁴¹ and in human,^42,43 yielding even more novel candidates for marker genes.

In contrast to previous work, we investigated and compared two complementary learning approaches: (i) comprehensive learning of pluripotency, employing many features (genes) and striving for maximum accuracy, and (ii) ‘minimal-best’ learning of pluripotency, seeking small sets of best features, akin to ‘biomarker signatures’.^11,86 From a bioinformatics perspective, it is known that small sets of features may even improve classification by reducing noise and overfitting, which is often related to the use of megavariate approaches.⁹⁷ For classification, we used a naive Bayes approach, decision trees, random forest, nearest neighbour and SVM. To select features, we employed information gain, random forest and a wrapper consisting of the GA and the SVM. Wrappers are feature selection methods that search the space of feature subsets and evaluate each subset by testing how well a machine learning algorithm can classify the data using that subset.

Feature selection methods known from machine learning are a standard approach to identifying biomarkers from gene expression data. Wrappers employing the GA to search the space of feature subsets are known to be well suited for biomarker identification, although they were mostly tested on cancer data in the past. Examples include the work of Lin et al.,⁹⁸ Küçükural et al.,⁹⁹ Gan et al.,¹⁰⁰ Zhang et al.¹⁰¹ and Cannas et al.¹⁰² Each group of researchers proposed some enhancement to the basic wrapper approach. Lin et al.⁹⁸ made the final selection of genes based on the number of times they were selected during multiple runs of the GA, which we adopted. Küçükural et al.⁹⁹ ‘restarted’ the GA after every 10 generations to improve the classification accuracy on training data, which was used as a part of the fitness function. We could already achieve perfect classification on training data without such restarts. Gan et al.¹⁰⁰ filtered the initial set of features to make the job of the GA easier. They utilized all their data for filtering instead of using cross-validation. We also filtered our data, but we used an appropriate cross-validation in all steps of our work. Zhang et al.¹⁰¹ used multiple classifiers to evaluate the feature subsets selected by the GA. Cannas et al.¹⁰² also employed filtering and used a combination of classification accuracy and size to evaluate feature subsets; we used feature-subset size in a similar fashion.

5. Conclusions

We demonstrated that the wrapper approach to feature selection using the GA and SVM, which was previously used to identify cancer biomarkers, works well for pluripotency data. It yields high cross-validated classification accuracy even if the accuracy is not measured by the SVM, but by another method such as the random forest. The biomarkers it identifies are enriched in pluripotency-related genes and pathways, and while many of them are ‘unexpected markers’, a literature review can connect most of them to pluripotency. Ultimately, experimental validation of the new markers is required, and we encourage other researchers to scrutinize our approach and, possibly, to investigate the genes we found in an experimental setting.

Authors' contributions

L.S. developed the feature selection based on the GA, performed the enrichment analyses and wrote parts of the manuscript. R.S. carried out classification experiments and feature selection with information gain. M.L. carried out feature selection with the random forest, evaluated feature selection methods and wrote parts of the manuscript. D.R. contributed to the design of the study, regarding cross-validation and gene set enrichment analyses, and improved the manuscript. G.F. coordinated the study and wrote parts of the manuscript, particularly those related to biological relevance. All authors read and approved the final manuscript.

Supplementary data

Supplementary Data are available at www.dnaresearch.oxfordjournals.org.

Funding

Funding by the DFG SPP 1356, Pluripotency and Cellular Reprogramming (FU583/2-1) is gratefully acknowledged.