Reversal in competitive dominance of a toxic versus non-toxic cyanobacterium in response to rising CO₂

Abstract

Climate change scenarios predict a doubling of the atmospheric CO₂ concentration by the end of this century. Yet, how rising CO₂ will affect the species composition of aquatic microbial communities is still largely an open question. In this study, we develop a resource competition model to investigate competition for dissolved inorganic carbon in dense algal blooms. The model predicts how dynamic changes in carbon chemistry, pH and light conditions during bloom development feed back on competing phytoplankton species. We test the model predictions in chemostat experiments with monocultures and mixtures of a toxic and non-toxic strain of the freshwater cyanobacterium Microcystis aeruginosa. The toxic strain was able to reduce dissolved CO₂ to lower concentrations than the non-toxic strain, and became dominant in competition at low CO₂ levels. Conversely, the non-toxic strain could grow at lower light levels, and became dominant in competition at high CO₂ levels but low light availability. The model captured the observed reversal in competitive dominance, and was quantitatively in good agreement with the results of the competition experiments. To assess whether microcystins might have a role in this reversal of competitive dominance, we performed further competition experiments with the wild-type strain M. aeruginosa PCC 7806 and its mcyB mutant impaired in microcystin production. The microcystin-producing wild type had a strong selective advantage at low CO₂ levels but not at high CO₂ levels. Our results thus demonstrate both in theory and experiment that rising CO₂ levels can alter the community composition and toxicity of harmful algal blooms.

Introduction

Climate change scenarios predict that atmospheric CO₂ concentrations will rise to ∼750 p.p.m. by the year 2100 (Solomon et al., 2007). This may have considerable impact on aquatic microbial communities. Cyanobacteria and eukaryotic phytoplankton utilize CO₂ for photosynthesis, and account for almost 50% of the carbon fixation of the world (Field et al., 1998; Behrenfeld et al., 2006). Yet, theory capable of predicting how rising CO₂ will affect the species composition of these communities is still in its infancy.

Resource competition theory aims to predict changes in species composition (Tilman, 1982; Grover, 1997). Mathematical models have been developed that link the population dynamics of competing species with dynamic changes in resource availability. Competition experiments can be run to test the theory, providing a check on the validity of the models or suggesting new directions for research. Competition for nutrients such as nitrogen and phosphorus has been extensively studied in this way (Tilman, 1982; Sommer, 1985; Ducobu et al., 1998; Klausmeier et al., 2004). Competition for light has also been well investigated (Huisman et al., 1999; Litchman and Klausmeier, 2001; Stomp et al., 2004; Passarge et al., 2006). However, with a few exceptions (Williams and Turpin, 1987; Caraco and Miller, 1998), competition for inorganic carbon has not been addressed.

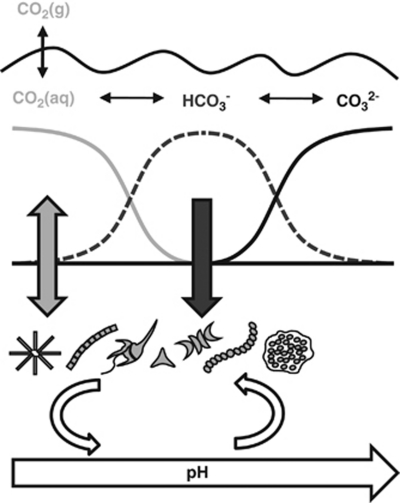
The major challenge here is that competition for inorganic carbon is conceptually and experimentally more complex than competition for other limiting resources (Figure 1). Dissolved CO₂ reacts with water, and subsequently dissociates into bicarbonate and a proton. Hence, rising concentrations of dissolved CO₂ cause a reduction in pH, a phenomenon known as ocean acidification (Orr et al., 2005; Riebesell et al., 2007; Doney et al., 2009). CO₂ uptake for photosynthesis reverses this chemical reaction. High photosynthetic rates can deplete the dissolved CO₂ concentration (Hein, 1997; Ibelings and Maberly, 1998), thereby inducing high pH (Talling, 1976; Maberly, 1996; Hansen, 2002). Changes in pH shift the speciation of dissolved inorganic carbon, from CO₂ at low pH to bicarbonate at intermediate pH and carbonate at high pH (Figure 1). Although phytoplankton species cannot use carbonate as carbon source, many species can take up both CO₂ and bicarbonate (Kaplan and Reinhold, 1999; Martin and Tortell, 2008). However, major species-specific differences exist in relative uptake rates of these two carbon sources (for example, Rost et al., 2003; Price et al., 2008; Maberly et al., 2009), which may affect their competitive interactions (Raven, 1991; Tortell et al., 2002; Rost et al., 2008). Thus, competition for CO₂ involves depletion of the limiting resource (inorganic carbon), a shift in the relative availability of different inorganic carbon sources (CO₂ versus bicarbonate), and a shift in associated environmental conditions (pH).

Figure 1.

Conceptual diagram of the main biological and chemical interactions involved in competition for inorganic carbon.

Competition for inorganic carbon may be particularly relevant in dense algal blooms of eutrophic waters. The high photosynthetic activity of dense algal blooms can strip the surface layer from dissolved inorganic carbon, thereby inducing high pH and carbon-limited growth conditions (Hein, 1997; Ibelings and Maberly, 1998). However, rising atmospheric CO₂ concentrations will enrich surface blooms with inorganic carbon, such that their growth may become limited by other factors. In particular, dense algal blooms also increase the turbidity of the water, thus reducing light availability as a result of self-shading (Huisman et al., 1999, 2004). Hence, competitive interactions within dense blooms might shift from competition for inorganic carbon under low CO₂ conditions to competition for light in a high CO₂ world.

In this paper, we develop a new theory to predict how species compete for inorganic carbon and light. The theory will focus on dynamic changes in carbon chemistry, pH and light conditions during bloom development, and how these environmental changes feed back on the competing species. The theory is tested in chemostat experiments, with full control of CO₂, temperature, light and nutrient conditions. The experiments are carried out with a toxic and non-toxic strain of the freshwater cyanobacterium Microcystis aeruginosa, which is a cosmopolitan species causing harmful algal blooms in many eutrophic waters (Chen et al., 2003; Rinta-Kanto et al., 2005; Verspagen et al., 2006; Paerl and Huisman, 2008).

Theory

We develop a model that considers several phytoplankton species competing for inorganic carbon and light in a dense algal bloom. In this section, we explain the model structure and key assumptions; the full model is presented in the Supplementary Information. The model assumes that all nutrients are in ample supply, such that the specific growth rates of the competing species depend on their intracellular carbon content (Droop, 1973; Grover, 1991a). Let X_i denote the population density of species i, and let Q_i denote its cellular carbon content. The population dynamics of n competing species can then be summarized by two sets of differential equations:

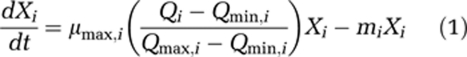i=1,…,n

i=1,…,n

The first set of equations describes the population densities of the competing species, where μ_max,i is the maximum specific growth rate of species i, Q_min,i is its minimum cellular carbon content required for growth, Q_max,i is its maximum cellular carbon content, and m_i is its specific loss rate. The second set of equations describes the cellular carbon contents of the species, which increase through uptake of carbon dioxide ( ) and bicarbonate ( 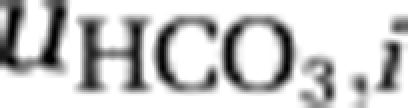), and decrease through respiration (r_i) and through dilution of cellular carbon by growth. We assume that uptake rates of carbon dioxide and bicarbonate are increasing but saturating functions of ambient CO₂ and bicarbonate concentrations, as in Michaelis–Menten kinetics, and are suppressed when cells become satiated with carbon (Morel, 1987; Ducobu et al., 1998). As carbon assimilation requires energy, we further assume that these uptake rates depend on photosynthetic activity and hence on light availability.

Carbon dioxide dissolves in water, and may subsequently dissociate into bicarbonate and a proton. This dissociation depends on pH and is relatively slow (Stumm and Morgan, 1996). Bicarbonate can dissociate further into carbonate and a proton. This is a much faster process, that is essentially in equilibrium with alkalinity and pH (Stumm and Morgan, 1996). Therefore, let [CO₂] denote the total concentration of dissolved carbon dioxide (including carbonic acid), and let [CARB] denote the total concentration of bicarbonate and carbonate. The total dissolved inorganic carbon is DIC=[CO₂]+[CARB]. Changes in dissolved inorganic carbon can then be described by (Johnson, 1982; Stumm and Morgan, 1996):

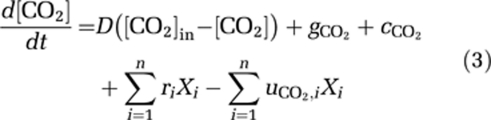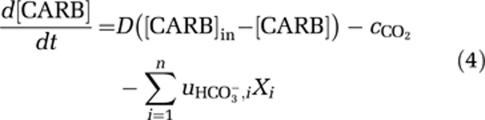The first equation describes changes in the concentration of dissolved carbon dioxide through the influx ([CO₂]_in) and efflux of water containing dissolved CO₂, through gas exchange with atmospheric CO₂ ( 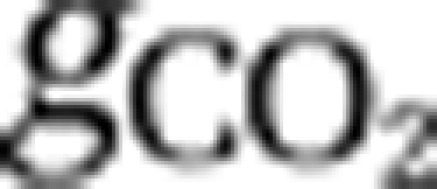), and through the chemical reaction from dissolved CO₂ to bicarbonate and vice versa ( 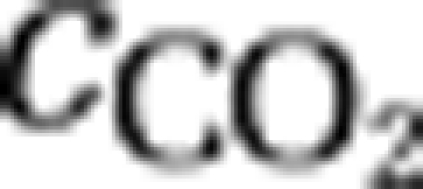). In addition, the concentration of dissolved carbon dioxide increases through respiration (r_i,) and decreases through uptake of CO₂ ( 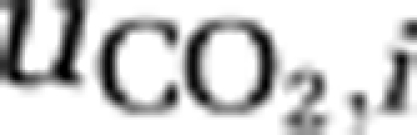) by the species. The second equation describes changes in the summed concentration of bicarbonate and carbonate through in- and efflux of water containing these inorganic carbon species, through the chemical reaction from bicarbonate to dissolved CO₂ and vice versa (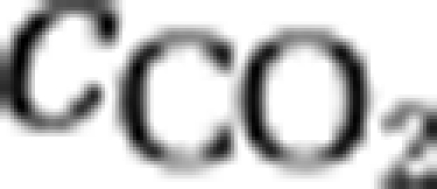), and through uptake of bicarbonate (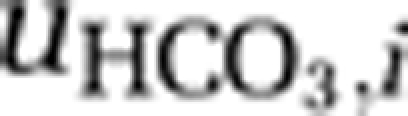) by the species. Concentrations of bicarbonate and carbonate were calculated from [CARB] assuming equilibrium with alkalinity and pH (Stumm and Morgan, 1996; see Supplementary Information for details).

Materials and methods

Species

The model was tested using a toxic and non-toxic strain of the freshwater cyanobacterium M. aeruginosa (Kützing) Kützing. The toxic strain Microcystis CYA140 produces the hepatotoxin microcystin-LR, whereas the non-toxic strain Microcystis CYA43 does not produce microcystins (Van der Grinten et al., 2000). Both strains were obtained from the Norwegian Institute for Water Research, and have been used in many laboratory studies as common representatives of toxic versus non-toxic Microcystis strains. They were grown as single cells and not in colonies. The monoculture experiments were unialgal but not axenic. However, regular microscopic inspection confirmed that abundances of heterotrophic bacteria remained low (that is, <1% of the total biomass) for the entire duration of the experiments.

Chemostat experiments

All experiments were carried out in chemostats specifically designed to study competition among phototrophic microorganisms (Huisman et al., 1999; Stomp et al., 2004; Passarge et al., 2006). Each chemostat consisted of a flat culture vessel illuminated from one side to obtain a unidirectional light gradient. Light was supplied at constant incident irradiance I_in using white fluorescent tubes (Philips PL-L 24W/840/4P, Philips Lighting, Eindhoven, The Netherlands). The chemostats had an optical path length (mixing depth) of z_m=5 cm, and an effective working volume of 1.7 l. The chemostats were run at a dilution rate of D=0.011 h⁻¹, and maintained at a constant temperature of 21.5±1 °C using a metal cooling finger connected to a Colora thermocryostat. The chemostats were supplied with a nutrient-rich mineral medium as described by Van de Waal et al. (2009) to prevent nutrient limitation during the experiments. The mineral medium had a pH of ∼8.2 in the absence of cyanobacteria. The chemostats were aerated with moistened and sterilized (0.2 μm Millex-FG Vent Filter, Millipore, Billerica, MA, USA) N₂ gas enriched with CO₂ to a final gas flow of 25 l h⁻¹ using Brooks Mass Flow Controllers (Brooks Instrument, Hatfield, PA, USA). The gas was moistened with milli-Q water to suppress evaporation of water from the chemostats by the continuous gas flow.

To obtain carbon-limited conditions, we supplied the chemostats with a low partial pressure of pCO₂=200 p.p.m. in the gas flow, a low bicarbonate concentration of 500 μmol l⁻¹ NaHCO₃, and an incident light intensity of I_in=50±1 μmol photons m⁻² s⁻¹. At the onset of the competition experiment, we inoculated the two strains at a 50:50 ratio in terms of cell numbers (corresponding to a 28:72 ratio in terms of the biovolumes of the toxic versus non-toxic strain, as cells of the toxic strain were smaller).

Experimental data under light-limited conditions were obtained from Kardinaal et al. (2007b). They ran monoculture and competition experiments with the same toxic and non-toxic Microcystis strains CYA140 and CYA43 using the same experimental set-up as in our experiments. However, to obtain light-limited conditions, they used a higher partial pressure of pCO₂=1000 to 1250 p.p.m. in the gas flow, a higher bicarbonate concentration of 2000 μmol l⁻¹ NaHCO₃ and a lower incident light intensity of I_in=25±1 μmol photons m⁻² s⁻¹. In their competition experiment, the toxic versus non-toxic strain were inoculated at a 90:10 ratio in terms of biovolume, thus giving the toxic strain an initial advantage. The experimental settings are summarized in Table 1.

Table 1. System parameters used in the chemostat experiments.

Parameter	Description	Carbon-limited chemostats	Light-limited chemostats	Units
D	Dilution rate	0.011	0.011	h−1
Iin	Incident irradiance	50	25	μmol photons m−2 s−1
zm	Mixing depth	0.05	0.05	m
Kbg	Background turbiditya	8 to 12.5	4 to 9	m−1
T	Temperature	21.5	21.5	°C
a	Gas flow rate	25	25	l h−1
γ	Constant of proportionality for gas influxa	1.4 × 10−4 to 2.0 × 10−4	1.4 × 10−4 to 2.0 × 10−4	l−1
pCO2	Partial pressure of CO2 in gas inflow	200	1000 to 1250	p.p.m.
[CO2]in	Concentration of dissolved CO2 at influx	8	29	μmol l−1
[CARB]in	Summed concentration of bicarbonate and carbonate at influx	500	2000	μmol l−1
ALKin	Alkalinity at influx	0.80	2.1	mEq l−1

^aBackground turbidity and the constant of proportionality for gas influx had different values for different chemostat vessels.

Population densities, light, carbon and nutrients

During the experiments, several variables were measured every other day. The incident irradiance (I_in) and the irradiance penetrating through the chemostat vessel (I_out) were measured with a LI-COR LI-250 quantum photometer (LI-COR Biosciences, Lincoln, NE, USA) at 10 randomly chosen positions on the front and back surface of the chemostat vessel, respectively. Cell numbers and biovolumes of Microcystis were determined in triplicate using a Casy 1 TTC cell counter with a 60 μm capillary (Schärfe System GmbH, Reutlingen, Germany). Because the two strains differed in average cell size, and cell size of the non-toxic strain was affected by the experimental treatments, we expressed population densities in terms of biovolume.

DIC concentrations in the chemostats were determined by sampling 15 ml of culture suspension, which was gently filtered over 0.45 μm membrane filters at low pressure (Whatman, Maidstone, UK). DIC was analyzed by a Model 700 TOC Analyzer (OI Corporation, College Station, TX, USA). The concentration of dissolved CO₂ and bicarbonate in the chemostat vessels was calculated from total DIC, pH and temperature (Stumm and Morgan, 1996). The pH was measured with a SCHOTT pH meter (SCHOTT AG, Mainz, Germany). Alkalinity was determined in a 50 ml sample that was titrated in 0.1–1 ml steps with 0.01 mol l⁻¹ HCl to a pH of 3.0. The alkalinity was subsequently calculated using Gran plots according to Stumm and Morgan (1996).

Intracellular carbon, nitrogen, sulfur and phosphorus content were sampled in triplicate. Samples were pressurized at 10 bar to collapse the gas vesicles of Microcystis and subsequently centrifuged for 15 min at 2000 g. After discarding the supernatant, the pellet was resuspended in demineralized water and centrifuged for 5 min at 15 000 g. The supernatant was discarded, pellets were stored at −20 °C and subsequently freeze dried and weighted to determine dry weight. The carbon, nitrogen and sulfur contents of homogenized freeze-dried cell powder were analyzed using a Vario EL Elemental Analyzer (Elementar Analysensysteme GmbH, Hanau, Germany). To determine the phosphorus content, cells were oxidized with potassium persulfate for 1 h at 100 °C (Wetzel and Likens, 2000), and phosphorus concentrations were subsequently analyzed colorimetrically according to Murphy and Riley (1962).

Quantitative PCR

The toxic and non-toxic Microcystis strain looked very similar, and could not be distinguished by means of light microscopy, cell counters or flow cytometry. Therefore, we used quantitative real-time PCR (qPCR) to quantify the population densities of the toxic and non-toxic strain in the competition experiments (Kurmayer and Kutzenberger, 2003; Vaitomaa et al., 2003; Rinta-Kanto et al., 2005). This improves earlier methodology developed by Kardinaal et al. (2007b), who distinguished the same two strains with a less precise semiquantitative method using denaturing gradient gel electrophoresis. We extracted the DNA of all cells and measured the copy numbers of the mcyE region of the microcystin synthetase gene cluster in comparison with the copy numbers of the 16S rDNA gene (16S). The mcyE gene is present only in the toxic strain CYA140, whereas the 16S gene is present in both strains. The mcyE:16S ratios were normalized to the known inoculation ratio of the two strains at the onset of the competition experiment. Thus, the normalized mcyE:16S ratio indicates the relative abundance of the toxic strain in the total Microcystis population, where the total Microcystis population was counted by the Casy 1 TTC cell counter as described earlier.

The mcyE gene was amplified using the Maeru-mcyEF (5′-CCCTAGCATCGGGTTATCAT-3′) and Maeru-mcyER (5′-CGAGTCAATTGATATTCAATTTCTC-3′) primers (modified from Rantala et al., 2004), and the 16S rDNA gene was amplified using the Maeru-16SrDNAF (5′-GCGTGCTACTGGGCTGTA-3′) and Maeru-16SrDNAR (5′-TCGGGTCGATACAAGCC-3′) primers (modified from Doblin et al., 2007).

Aliquots of culture suspension were pressurized at 10 bar to collapse the gas vesicles of Microcystis cells, and subsequently centrifuged for 5 min at 15 000 g. After removal of supernatant, genomic DNA was extracted using a DNeasy Blood & Tissue Kit according to the manufacturer's instruction (Qiagen GmbH, Hilden, Germany). The DNA concentration of the samples was measured using a NanoDrop ND-1000 (Nano-Drop Technologies, Wilmington, DE, USA), and all samples were diluted to an equal density of 10 ng μl⁻¹. The qPCR was performed with a Rotor Gene 6000 thermal cycling system (Corbett Research, Sydney, Australia). Each reaction was performed in triplicate. The reaction mix contained 2 μl of sample DNA in combination with 10 μl ABSolute QPCR SYBR green mix (ABgene, Epsom, UK), 0.3 μl of both the forward and reversed primer of the specific gene tested for, and was filled with 0.1 μm filter sterilized DNase-, RNase- and Protease-free water (Sigma-Aldrich, St Louis, MO, USA) to reach a final reaction volume of 20 μl. The thermal cycle consisted of an initial denaturation at 95 °C for 15 min, followed by 40 cycles of denaturation at 94 °C for 20 s, and annealing for 60 s at 65 °C. Data were acquired at 65 °C, and reaction products were verified by DNA melting curve analysis at a temperature ranging from 60 °C to 95 °C at steps of 0.5 °C. Amplification efficiencies of qPCR reactions were similar in all experiments (data not shown).

Microcystin analysis

According to expectation, the microcystin concentration in the competition experiments should vary with the population density of the toxic strain. The performance of the qPCR analysis could therefore be assessed independently, by comparison of the estimated population densities of the toxic strain against the total microcystin concentration measured in the culture vessel.

Intracellular microcystin content was determined in triplicate by sampling 5–20 ml of culture suspension, which was immediately filtered using Whatman GF/C filters (pore size ∼1.2 μm). Filters were frozen at −20 °C and subsequently freeze dried. Microcystins were extracted in three rounds with 75% MeOH according to Fastner et al. (1998), with an additional step for grinding of the filters using a Mini Beadbeater (BioSpec Products, Bartlesville, OK, USA) with 0.5 mm silica beads (Tonk et al., 2005). Dried extracts were stored at −20 °C and dissolved in 50% MeOH for microcystin analysis using high-performance liquid chromatography with photodiode array detection (Kontron Instruments, Watford, UK). The different microcystin variants were separated using a LiChrospher 100 ODS 5 μm LiChorCART 250-4 cartridge system (Merck, Darmstadt, Germany) and a 30–70% acetonitrile gradient in milli-Q water with 0.05% trifluoroacetic acid at a flow rate of 1 ml min⁻¹. Identification of the different microcystin variants was based on their characteristic ultraviolet spectra (Lawton et al., 1994). This confirmed previous studies that Microcystis CYA140 produces microcystin-LR, whereas Microcystis CYA43 does not produce microcystins (for example, Van der Grinten et al., 2000). Microcystin-LR concentrations were quantified using a gravimetrical standard of microcystin-LR (provided by the University of Dundee).

Extracellular microcystin concentrations were determined in triplicate by filtration of 10 ml culture suspension using Whatman GF/C filters (pore size ∼1.2 μm). Extracellular microcystin concentrations were below the detection limit of the high-performance liquid chromatography (2.5 ng microcystin). Therefore, the filtrate was analyzed using an enzyme-linked immunosorbant assay according to the manufacturer's protocol (EnviroLogix, Portland, ME, USA). This showed that extracellular microcystins comprised <2% of the total microcystin concentrations in all chemostat experiments, which was considered negligible.

Results

Carbon-limited experiments

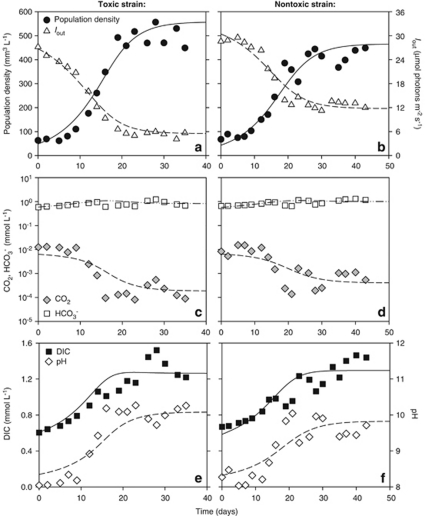
In monoculture experiments under CO₂-limited conditions, population densities gradually increased until a steady state was reached after 20–30 days (Figures 2a and b). Light penetration through the chemostats (I_out) decreased with increasing population density. Steady-state values of I_out ranged from 5 to 12 μmol photons m⁻² s⁻¹, which is well above the I_out values measured under light-limited but CO₂ replete conditions (see below). This indicates that the steady-state chemostats were not light-limited.

Figure 2.

Monoculture experiments in CO₂-limited chemostats. (a, b) Population density (expressed as biovolume) and light intensity penetrating through the chemostat (I_out). (c, d) CO₂ and bicarbonate concentrations. (e, f) Dissolved inorganic carbon (DIC) and pH. Panels a, c and e show data for the toxic strain Microcystis CYA140, whereas b, d and f show data for the non-toxic strain Microcystis CYA43. Symbols represent chemostat data, lines show the model fits. Parameter values are given in Tables 1 and 2.

As a result of increasing population densities, the carbon chemistry and pH in the water changed (Figures 2c–f). Dissolved CO₂ concentrations were rapidly depleted, showing a more than 10-fold drop to steady-state values of ∼0.2 μmol l⁻¹ in the monoculture of the toxic strain (Figure 2c) and ∼0.4 μmol l⁻¹ in the monoculture of the non-toxic strain (Figure 2d). CO₂ depletion was accompanied by an increase of pH to steady-state values of ∼10 for the toxic strain and ∼9.8 for the non-toxic strain (Figures 2e and f). Bicarbonate thus became the predominant carbon species in the water, comprising 65% and 77% of the total DIC in the steady-state monocultures of the toxic and non-toxic strain, respectively. The observation of strong CO₂ depletion and high pH confirms that these monoculture experiments were indeed exposed to CO₂-limited conditions.

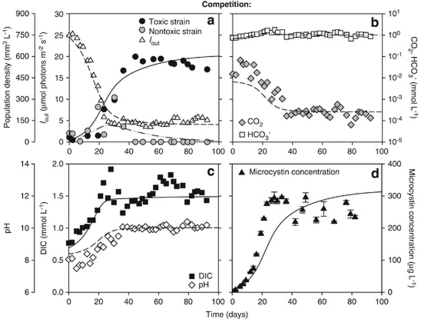
The species parameters were estimated from the monoculture experiments, by fitting the model to the monoculture data (see Supplementary Information for methodology). This showed that the toxic strain has lower half-saturation constants for CO₂ and bicarbonate and a lower minimum carbon content than the non-toxic strain (Table 2). On the basis of these parameter estimates, the model predicts that the toxic strain should be a better competitor for CO₂ and bicarbonate than the non-toxic strain. The model predictions were tested in competition experiments. Under CO₂-limited conditions, both strains initially increased (Figure 3a). After 35 days, dissolved CO₂ was depleted to ∼0.2 μmol l⁻¹ (Figure 3b) and pH had increased to ∼10 (Figure 3c). Hence, the non-toxic strain started to decrease and was gradually displaced by the toxic strain (Figure 3a). After 45 days, the non-toxic strain was completely excluded. The total microcystin concentration increased toward steady-state values, confirming the competitive dominance of the toxic strain (Figure 3d).

Table 2. Parameter values estimated from the monoculture experiments, for the non-toxic strain Microcystis CYA43 and the toxic strain Microcystis CYA140.

Parameter	Description	CYA43	CYA140	Units
μmax	Maximum growth rate	0.80	0.86	Per day
m	Specific loss rate	0.264	0.264	Per day
k	Specific light attenuation coefficient	5.0 × 10−5	6.2 × 10−5	m2 mm−3
HI	Half-saturation constant for light	11	14	μmol photons m−2 s−1
umax,CO2	Maximum uptake rate of CO2	11.2	8.2	μmol mm−3 per day
HCO2	Half-saturation constant for CO2	2.0	0.5	μmol l−1
rmax	Maximum respiration rate	1.0	1.1	μmol mm−3 per day
umax,HCO3	Maximum uptake rate of HCO3−	9.5	7.3	μmol mm−3 per day
HHCO3	Half-saturation constant for HCO3−	200	75	μmol l−1
Qmin	Minimum carbon content	15	9	μmol mm−3
Qmax	Maximum carbon content	17	17	μmol mm−3
yN	Cellular N:C ratio	0.14	0.18	Molar
yP	Cellular P:C ratio	6.0 × 10−3	8.0 × 10−3	Molar
yS	Cellular S:C ratio	5.0 × 10−3	7.6 × 10−3	Molar
V	Cell volume	47–87 × 10−9	35 × 10−9	mm3 per cell
MC	Cellular microcystin content	0	0.52	μg mm−3

Figure 3.

Competition between the toxic and non-toxic strain in a CO₂-limited chemostat. (a) The toxic strain Microcystis CYA140 displaces the non-toxic strain Microcystis CYA43. I_out represents the light intensity penetrating through the chemostat. (b) CO₂ and bicarbonate concentrations. (c) Dissolved inorganic carbon (DIC) and pH. (d) Total microcystin concentration (error bars indicate s.d.). Symbols represent chemostat data, lines show the model predictions. Parameter values are given in Tables 1 and 2.

Light-limited experiments

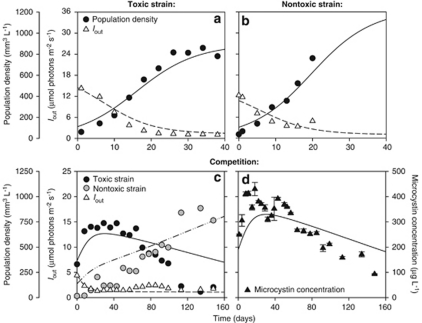
We also tested our model predictions against experiments performed under light-limited but CO₂-replete conditions by Kardinaal et al. (2007b). They measured population densities and light availability, but did not measure alkalinity and inorganic carbon. In their monoculture experiments, population densities increased while light penetration through the chemostats (I_out) was reduced to very low values of ∼1.3 μmol photons m⁻² s⁻¹ (Figures 4a and b). The pH varied between 8.2 and 8.5. This is close to the pH of the mineral medium itself, and far below the pH of 9.8 to 10 measured under carbon-limited conditions (Figures 2e and f). These observations confirm that the experiments were indeed performed under light-limited conditions.

Figure 4.

Monoculture and competition experiments between the toxic and non-toxic strain in a light-limited chemostat. (a, b) Population density (expressed as biovolumes) and light intensity penetrating through the chemostat (I_out) in monoculture experiments of (a) the toxic strain Microcystis CYA140, and (b) the non-toxic strain Microcystis CYA43. (c) In competition, the non-toxic strain Microcystis CYA43 displaces the toxic strain Microcystis CYA140. (d) Total microcystin concentration in the competition experiment (error bars indicate s.d.). Symbols represent chemostat data, lines show the model predictions. Parameter values are given in Tables 1 and 2. The chemostat data in this figure are from Kardinaal et al. (2007b).

According to our parameter estimates, the non-toxic strain has a slightly lower half-saturation constant for light and higher maximum uptake rates for inorganic carbon than the toxic strain (Table 2). Hence, the model predicts that the non-toxic strain should be a slightly better competitor for light. This model prediction is confirmed by the competition experiment. Both strains initially increased while light penetration through the chemostat (I_out) was reduced (Figure 4c). Subsequently, the toxic strain was slowly replaced by the non-toxic strain during a 160-days period. The total microcystin concentration increased during the first 20 days of the competition experiment and subsequently decreased until the end of the experiment, consistent with the gradual replacement of the toxic by the non-toxic strain (Figure 4d).

In total, the competition experiments show that the toxic strain became dominant under CO₂-limited conditions, whereas the non-toxic strain dominated under high CO₂ but light-limited conditions. The model predictions captured this reversal in competitive dominance, and were largely in agreement with the experiments (Figures 3 and 4).

Discussion

Mechanisms of competition

In this study, we have demonstrated that competition for inorganic carbon can be successfully predicted from a relatively simple model that includes the basics of inorganic carbon chemistry and the key physiological traits of the species involved. An important aspect of competition for inorganic carbon is the strong interplay between CO₂, bicarbonate and pH in aquatic ecosystems. More specifically, as observed in our experiments, carbon assimilation leads to CO₂ depletion accompanied by an increase in pH, shifting the carbon chemistry toward a predominance of bicarbonate (Figures 1 and 2). This is consistent with field studies of the inorganic carbon chemistry of eutrophic waters, where dense phytoplankton blooms can deplete the CO₂ concentration, thereby inducing high pH values in both freshwater (Talling, 1976; Maberly, 1996) and marine ecosystems (Hansen, 2002).

Our experiments show that the toxic strain was able to reduce the concentration of dissolved CO₂ to a lower level than the non-toxic strain (Figures 2c and d), and won the competition (Figure 3). That is, the winner of competition had the lowest R^* value for CO₂, as in traditional resource competition models (Tilman, 1982). An alternative explanation for our results is that the pH tolerance differed between the strains. Indeed, in monoculture, the toxic strain enhanced pH to higher values than the non-toxic strain (Figures 2e and f). Hence, the outcome of our experiments might also be explained by differences in pH^* values. However, pH drift experiments (not shown) indicated that both strains could tolerate high pH up to ∼11.2, and that variation in pH had little effect on the specific growth rates of the two strains over the entire pH range covered by our experiments. These findings are consistent with Bañares-España et al. (2006), who showed that the pH tolerance of 19 different Microcystis strains ranged from 10.4 to 11.7, that is, they could all tolerate high pH. Therefore, our model assumed that pH does not have a direct effect on the specific growth rates. Yet, although Microcystis may tolerate high pH, several studies have shown that pH >9 often approaches or even exceeds the pH tolerance of other phytoplankton species (Goldman et al., 1982; Hansen, 2002). Further competition experiments with species of different pH sensitivity are therefore recommended to investigate the impact of changes in pH on phytoplankton community composition.

Given the high bicarbonate concentrations, one may question whether CO₂ depletion by cyanobacteria indeed leads to carbon-limited conditions, as many species can utilize bicarbonate as additional carbon source. CO₂ easily diffuses across cell membranes. In contrast, bicarbonate uptake requires active transport mechanisms to cross the cell membrane or the presence of extracellular carbonic anhydrases converting bicarbonate into CO₂ (Kaplan and Reinhold, 1999; Elzenga et al., 2000; Badger et al., 2006). Hence, phytoplankton species typically have a much lower affinity for bicarbonate than for CO₂ (for example, Rost et al., 2003; Kranz et al., 2009). This is consistent with our study, where we estimated that the half-saturation constant for bicarbonate was more than two orders of magnitude higher than the half-saturation constant for CO₂ (Table 2). This implies that cells strongly rely on CO₂ as their preferred carbon source. For instance, our model estimates that 50–55% of the total carbon uptake during the first days of the competition experiment was attributed to CO₂, even though CO₂ concentrations were much lower than bicarbonate concentrations (Figure 3). When CO₂ was depleted and bicarbonate concentrations increased during the course of the competition experiment, the contribution of CO₂ to the total carbon uptake became lower but still amounted to 29% for the toxic strain and 14% for the non-toxic strain. Similar percentages have been reported for other phytoplankton species (for example, Rost et al., 2003). Thus, the carbon source for phytoplankton growth gradually shifted from combined CO₂ and bicarbonate uptake to predominantly bicarbonate uptake. According to our model simulations, the low uptake rate of bicarbonate was insufficient to sustain high growth rates of the Microcystis strains, such that their growth rates became carbon limited when CO₂ was depleted.

An increase in CO₂ supply and reduction of the incident light intensity shifted our experiments from competition for inorganic carbon to competition for light. This transition caused a reversal in competitive dominance. The strain dominating under carbon-limited conditions lost the competition under light-limited conditions. This finding might be highly relevant. If the reversal in competitive dominance is not restricted to our particular study system but widespread in natural communities, the current rise in atmospheric CO₂ levels may cause major changes in the species composition of algal blooms, from superior carbon competitors to superior light competitors.

The role of microcystins in competition

Harmful cyanobacteria may form dense blooms in eutrophic waters (Reynolds, 1987; Paerl and Huisman, 2008), and can produce a variety of toxins including microcystins that pose a major threat to birds, mammals and human health (Chorus and Bartram, 1999; Carmichael, 2001; Huisman et al., 2005). Interestingly, cyanobacterial blooms often consist of mixtures of toxic and non-toxic strains (Kurmayer and Kutzenberger, 2003; Kardinaal et al., 2007a; Briand et al., 2008; Briand et al., 2009). In our experiments, the toxic strain was the better competitor for inorganic carbon, whereas the non-toxic strain was the better competitor for light. As these results rely on one toxic and one non-toxic strain only, the observed association between toxin production and competitive ability might be mere coincidence.

However, Jähnichen et al. (2001) hypothesized earlier that microcystins might have a possible function in carbon assimilation at low CO₂ availability. Specifically, by drawing an analogy with okadaic acid, they argued that microcystins might suppress carbon losses due to photorespiration by the RuBisCO enzyme. Consistent with this hypothesis, immunogold localization pointed at relatively high densities of microcystin within carboxysomes (Gerbersdorf, 2006), which are intracellular microcompartments containing high RuBisCO concentrations to facilitate the carbon-concentrating mechanism of cyanobacteria (for example, Badger et al., 2006; Price et al., 2008). However, Young et al. (2005, 2008) did not confirm preferential localization of microcystins within carboxysomes, and found instead that microcystins were mainly associated with the thylakoids and polyphosphate bodies. Jähnichen et al. (2007) provided some indirect support for their hypothesis that microcystins are involved in carbon assimilation using a series of ingenious experiments in which they restricted sodium-dependent bicarbonate uptake through replacement of sodium by potassium in the growth medium. Yet, none of these data provide conclusive evidence that microcystin production indeed confers a selective advantage under carbon-limited conditions.

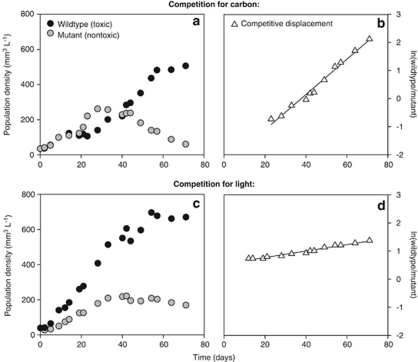
Therefore, we ran additional competition experiments with the microcystin-producing strain M. aeruginosa PCC 7806 and its mcyB mutant. This mutant, which does not produce microcystins, was generated by insertion of a chloramphenicol resistance cassette into the mcyB gene (Dittmann et al., 1997). We quantified population densities of the wild type and mutant during the competition experiments using qPCR targeted at the chloramphenicol resistance cassette of the mutant. For this purpose, we developed two new primers (Maeru-CmF: 5′-TTCGAATTTCTGCCATTCAT-3′ and Maeru-CmR: 5′-ATTATACGCAAGGCGACAAG-3′). The competition experiments were performed using exactly the same conditions as in our other experiments. Under carbon-limited conditions, the wild type displaced the mutant (Figure 5a). Under light-limited conditions, the wild type and mutant coexisted for the entire duration of the experiment, although the wild type was dominant and the mutant slowly declined from day 40 onwards (Figure 5c). To assess the selective advantage of the microcystin-producing wild type, we calculated the rate of competitive displacement (RCD; Grover, 1991b; Passarge et al., 2006). The RCD can be interpreted as the difference in fitness between the wild type and its mutant. Specific growth rates (μ) of the wild type (WT) and mutant (M) are defined as:

Figure 5.

Competition experiments between the wild type strain M. aeruginosa PCC 7806 and its mcyB mutant. (a, b) Competition in a CO₂-limited chemostat. (c, d) Competition in a light-limited chemostat. The rate of competitive displacement (RCD) is estimated from the slope of the linear regression of ln(wild type/mutant) versus time. Comparison of the slopes in (b) and (d) shows that the wild type displaces the mutant at a much faster rate in the CO₂-limited chemostat (RCD=0.063 per day) than in the light-limited chemostat (RCD=0.012 per day). Regression statistics: (b) y=0.063x−2.371 (R²=0.98; P<0.001); (d) y=0.012x+0.518 (R²=0.96; P<0.001).

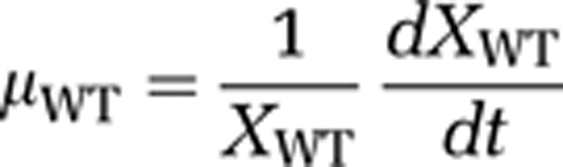and

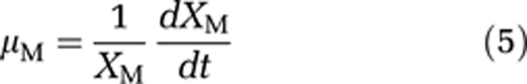As the time derivative of ln(X) equals (1/X)(dX/dt), the RCD is given by:

Hence, the RCD can be estimated as the slope of the linear regression of ln(wild type/mutant) versus time. The RCD estimates confirm that the wild type displaced the mutant at a much faster rate under carbon-limited conditions (Figure 5b; RCD=0.063 per day) than under light-limited conditions (Figure 5d; RCD=0.012 per day). This direct comparison between a microcystin-producing wild type and its mutant demonstrates that microcystin production confers a strong selective advantage under carbon-limited conditions, whereas this selective advantage largely disappears when CO₂ is in ample supply.

Kardinaal et al. (2007b) hypothesized that non-toxic strains are generally better competitors for light, because the energy required for microcystin production is less available under light-limited conditions. However, this hypothesis is not supported by our experiments, as the mutant did not replace the wild type under light-limited conditions (Figures 5c and d). There are several possible explanations for this discrepancy. For instance, energetic costs of microcystin production might be relatively low, as microcystin represents only a minor fraction of the total cellular carbon and nitrogen budgets (Van de Waal et al., 2009). This line of arguments would explain the very slow competitive displacement of toxic strain CYA140 by non-toxic strain CYA43 (Figure 4), and the nearly neutral coexistence of wild type strain PCC 7806 and its mutant under light-limited conditions (Figures 5c and d). Alternatively, it might be that the mutant strain still carries some of the costs associated with microcystin production. Although this mutant cannot produce microcystin because its mcyB gene is disrupted, transcript analyses have shown that transcription of its mcyABC operon remains unaffected (Tillett et al., 2000). Accordingly, even though the hypothesis of Kardinaal et al. (2007b) does not apply to this specific mutant, it might still apply to other non-toxic strains lacking the entire mcy gene cluster. More strains need to be investigated before the hypothesis of Kardinaal et al. (2007b) can be fully evaluated.

In conclusion, our results provide a first step towards a better understanding of competition for inorganic carbon among cyanobacteria. We have shown that microcystin production provides a selective advantage under carbon-limited conditions. In addition, we have demonstrated that rising CO₂ availability can lead to a reversal in the outcome of competition between a toxic and non-toxic strain. However, our work also raises new questions for future research. For instance, what is the role of pH tolerance in competition for inorganic carbon? And what is the underlying molecular mechanism for the observed selective advantage of microcystin production?