Cytoskeletal actin networks in motile cells are critically self-organized systems synchronized by mechanical interactions

Abstract

Growing networks of actin fibers are able to organize into compact, stiff two-dimensional structures inside lamellipodia of crawling cells. We put forward the hypothesis that the growing actin network is a critically self-organized system, in which long-range mechanical stresses arising from the interaction with the plasma membrane provide the selective pressure leading to organization. We show that a simple model based only on this principle reproduces the stochastic nature of lamellipodia protrusion (growth periods alternating with fast retractions) and several of the features observed in experiments: a growth velocity initially insensitive to the external force; the capability of the network to organize its orientation; a load-history-dependent growth velocity. Our model predicts that the spectrum of the time series of the height of a growing lamellipodium decays with the inverse of the frequency. This behavior is a well-known signature of self-organized criticality and is confirmed by unique optical tweezer measurements performed in vivo on neuronal growth cones.

Actin networks are remarkable biological materials essential for the structural stability of eukariotic cells and for many of their vital functions, including motility (1, 2). They are formed by oriented and branched actin fibers (3) and are able to produce compact and relatively stiff two-dimensional structures such as lamellipodia. Within the lamellipodium of a crawling cell, actin networks are capable of organizing over length scales of several micrometers. Moreover, they are able to grow at an approximately constant velocity, independently of the strength of the external force that opposes their growth (4, 5).

The mechanisms underlying this process have been the object of intense theoretical investigation. The reliability of a model is normally judged from its capability of predicting an almost constant force–velocity (Fv) relationship up to a stall force. In autocatalytic nucleation models (6), when the force increases, the actin network—due to the activity of controlling proteins—originates new branches, so that the velocity v remains constant for increasing values of F, while the density increases accordingly. Other models are based on the idea of Brownian ratchets (7–9): thanks to thermal fluctuations of the membrane, actin filament tips in contact with the membrane become accessible to free actin monomers (and hence to growth by polymerization). These models have been used to explain experimental observations on Listeria monocytogenes propulsion (10). The dendritic-nucleation/array-treadmilling model (11) can reproduce the observed geometric structure of actin meshworks near the leading edge of a lamellipodium (12). A symmetric orientation of the actin filaments with respect to the force direction is predicted, provided that branching and capping protection take place only close to the membrane.

The importance of regulatory proteins has been convincingly established in experiments (13–19), and most of the available models focus on biochemical regulation, although mechanical interactions are also known to play an important role (20–30). In refs. 25–28, pulsatile motion of beads propelled by growing actin networks has been observed in models where phases of accumulation of mechanical stresses in the actin filaments alternate with sudden accelerations due to rupture events in the network. These approaches are able to reproduce results from bead and rod motility assays aimed at replicating Listeria motility (24–29). It is suggested in ref. 22 that the mechanical forces arising from actin filament growth against a membrane may provide the basic mechanism for persistent and coordinated cell movement and that, at least in keratocytes, regulatory elements such as signaling molecules may be dispensable or redundant. However, a quantitative assessment of the role of forces in orchestrating organized growth inside protruding lamellipodia is still missing.

Recent advances in experimental techniques have provided detailed information on the dynamics of actin networks (4, 5, 31), both in vivo and in vitro. Very accurate optical tweezer in vivo measurements of the position of a lamellipodium have demonstrated that the leading edge advances with a characteristic “stochastic swing” behavior, in which growth periods alternate with retractions (4). This behavior is observed also when the force exerted by the bead is small, but oscillations increase in size and frequency when the force becomes large. Using the same technique, it was shown that the force necessary to stop completely the growth of the network is of the same order of magnitude of the one exerted by the plasma membrane (4). Thus, also in normal conditions (in the absence of the bead) the propulsive force is almost counterbalanced by the relatively strong tension exerted by the membrane. In this scenario, the retraction periods can be interpreted as due to the pressure exerted by the membrane. Periods of growth alternate with “avalanches” in which the network collapses, at least locally. Why has nature chosen to design the combined system formed by the network and the membrane in this special condition of marginal stability? One may argue that it is not by chance. In fact, the actin network has to produce structures that protrude for several micrometers, and these structures have to be compact and without overhangs in order to be effective for pushing. Avalanches driven by forces arising from the contact with the membrane could be the mechanism that enforces the optimal organization at the micrometer scale.

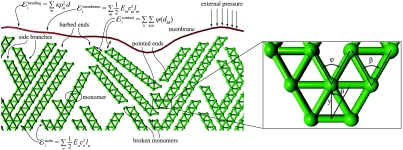
In order to elaborate on this idea on a quantitative basis, we designed a simple model of lamellipodia growth based only on mechanical ingredients. In the model (see Fig. 1 and Methods), the actin network forms by a stochastic process, in which at every “time step” an actin “monomer” is added at the tip (barbed end) of a random filament, forming a time-evolving truss structure. At the beginning of the simulation, “seed” monomers are created at the bottom of the simulation box and kept fixed throughout the computation. Filaments repel each other at a short distance and, with a given probability, branch at a random point. Filaments are allowed to grow and branch if the event does not lead to overlaps with preexisting neighboring filaments or with the membrane (steric hindrance). The network is kept under compressive stress by a flexible membrane, directly interacting with the leading edge of the network. We assume that the polymerization rate is force independent.

Fig. 1.

The model. We consider a two-dimensional network of actin filaments growing against a membrane subject to an external force F directed along the protrusion direction y and opposing the lamellipodium growth. Actin monomers are modeled, as in a truss structure, by two nodes and four connections (edges, the green lines in the figure). Lengths are measured in units of the filament thickness d and forces in units of the filament rupture force F_r. The force F is distributed on a representative cell of width L_cell = 32 d. Periodic boundary conditions are assumed in order to reduce edge effects. At the beginning of the simulation, 12 monomers are created at y ∼ 0 at an angle θ with the y axis. These seeds are kept fixed throughout the simulation. Time is measured in units of growth steps, in each of which a monomer is added at the tip (barbed end) of a randomly chosen filament. One branching event occurs at a random site along the filaments at every growth step with a probability P_b = 0.3. The branching angle φ is fixed at 60° [close to the measured value of 70° (6, 11, 12)]. The contact among different filaments and between filaments and the membrane is modeled by a short-range repulsive potential active for a distance < d. In view of the truss geometry, filaments fail if the absolute value of the force in one of the edges exceeds a critical value f_c = F_r/2, in which case the overcritical monomer is cleaved. Cleaved filaments, which have an exposed pointed end, depolymerize with a speed of 10 monomers per growth step. We assume the filaments to be linearly elastic up to failure, with a persistence length ξ = 1,000 d. This corresponds to approximately 10 μm (35). Reduction to a two-dimensional model is obtained by assuming that a growing planar network deforms a slice of thickness d in the direction orthogonal to the plane of the lamellipodium. The resulting one-dimensional elastic membrane has stretching stiffness of the order of F_r (37) and bending stiffness κ = 0.1F_rd², which results in a persistence length λd with λ ∼ 8 ≪ 10³ (4, 12). The influence of the parameters on the predictions of the model is discussed in detail in SI Text.

The model scale is defined by two independent quantities, the filament diameter d and the filament breaking force F_r. All the other parameters can be expressed in terms of these units as indicated in the caption of Fig. 1. We assumed d = 7 nm (19, 32), whereas the critical force for the filament is assumed in the range F_r = 100–200 pN (33, 34). The persistence length ξ for the filaments is assumed in the range ξ = 1–2 × 10³ d corresponding to about 7–15 μm, which is in agreement with data in refs. 35, 36) (see SI Text for further discussion on the choice of parameters). We further assume that a filament pushing against the membrane deforms a slice of a thickness comparable to the filament diameter d. This assumption allows us to estimate the stiffness parameters for our two-dimensional model from experimental measurements of membrane elastic properties. A stretching stiffness approximately 2F_r used in the model corresponds to an in-plane stretching modulus of the order of 100 pN/nm, in agreement with ref. 37. The bending modulus κ = 0.1F_rd² corresponds to a bending stiffness of approximately 20 K_BT, consistent with refs. 4 and 12.

After each growth event, we compute the local stress on each of the actin monomers by minimizing the total potential energy of the network using a computer program (38). If the stress in a monomer becomes higher than a critical threshold, the monomer breaks and the filament depolymerizes from its pointed end. A similar scheme of filament crushing and disassembly at the trailing edge has been recently proposed in ref. 23 as a key mechanism for shape regulation in fish keratocytes.

We avoided on purpose including in the model the effect of a regulating network based on biochemistry (e.g., we do not model explicitly the selective capping of filaments far from the membrane). This regulating network is present in living cells but, as we will see, its presence is not essential for explaining many key features of the available experimental evidence. For fish keratocytes, this has already been suggested in ref. 22. One may then speculate that biochemical regulation could have appeared later in evolution in order to optimize the performance of the system, building on a simpler prototype based only on mechanical regulation. Also other effects (cross-links between actin fibers, membrane-cytoskeleton adhesion, etc.) are neglected in our model because they are not strictly necessary for stress transmission in the compressive regime arising inside the network when it grows against the membrane, or when the lamellipodium pushes against an obstacle.

Results

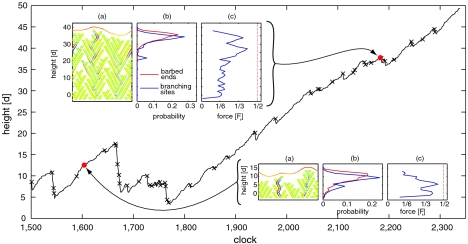
The results reported here refer to the benchmark values of the model parameters reported in Table S1. A typical outcome of our simulations is shown in Fig. 2, where we plot the height of the lamellipodium as a function of time. It is evident that growth proceeds alternating protrusions and fast retractions. Cleavage events are marked by crosses in Fig. 2. This behavior closely resembles the experimental traces at high time resolution (4). The emergence of a strongly organized structure, such as the one depicted in Fig. 2 Inset A, Top Left that leads to a protrusion of almost 50 times the filament thickness d, is obtained after many attempts, in which the system collapses almost completely at much smaller heights (see Movie S1). Less catastrophic retractions are observed also when the system is finally able to grow, after t = 1,800. These retractions are indeed crucial to achieve a sufficient structural stability, as in these events “unfit” filaments are cleaved and eliminated. In other words, if the filaments would not break, the system would not be able to produce a compact and organized structure capable of sustaining a significant external pressure. This scenario, in which mutation is guaranteed by random growth and branching, while selection is achieved through failure of the overstressed filaments, is strongly reminiscent of the evolutionary model in ref. 39. Due to the pressure exerted by the membrane, the actin network organizes itself into a close packed structure, in which each branch is sustained by several other branches (Fig. 2 Inset A, Top Left).

Fig. 2.

Growth, stress diffusion, and localization of the active area near the membrane. Height as function of growth clock for a benchmark simulation of a pushing event against an applied force F of 0.5F_r. Crosses correspond to failure events. Insets A report the network configuration at two different times. Monomers under compressive (respectively, tensile) stress are colored in blue (respectively, red). Insets B show the height distribution of the sites where new monomers can be added (barbed ends) and where new branches can appear (branching sites). Distributions are computed over several independent configurations of height 38 d ∼ 270 nm (Top Left) and 13 d ∼ 90 nm (Bottom Right). Insets C report, for the same configurations as A, the magnitude of the maximum force in the monomers as a function of height.

Just as in autocatalytic (6) and dendritic-nucleation/array-treadmilling models (11), during organized growth all the relevant events (polymerization, branching, and cleavage) happen in a relatively thin layer close to the membrane, while the rest of the network reaches a steady state. This is demonstrated in Fig. 2 Insets B, where we plot the probability of observing a branching and a polymerization event as a function of height (averages are taken over several independent simulations). In contrast with the other models (6, 11), these peaked distributions are not imposed a priori but stem only from the mechanical properties of the system: Monomers buried deeply into the network, and far away from the membrane, are mechanically shielded (low stress levels and no growth or branching because of lateral support and steric hindrance). However, it is obvious that selective localization of suitable proteins and enzymes, which catalyze branching and growth in the proximity of the membrane (6, 11, 40), can greatly enhance the efficiency of the system (e.g., by decreasing the waiting time for the formation of configurations that are fit for pushing).

Another important feature of our model is that during organized growth the stress is uniformly distributed throughout the network. In Fig. 2 Insets A the monomers are colored according to the local stress, with red indicating traction and blue compression. Clearly, the stress is modest and uniformly distributed at all heights. Fig. 2 Insets C show the maximum absolute value of the force as a function of height, highlighting that it is more evenly distributed and lower in average in the case of an organized geometry (Top Left) compared to the cases of a nonorganized one (Bottom Right). Moreover, it is clear how the maximum force near the bottom of the simulation box is high for nonorganized networks, whereas it is close to zero for organized structures. This is an important feature, because ruptures of the network near the bottom cause global, catastrophic avalanches.

Filament Orientation.

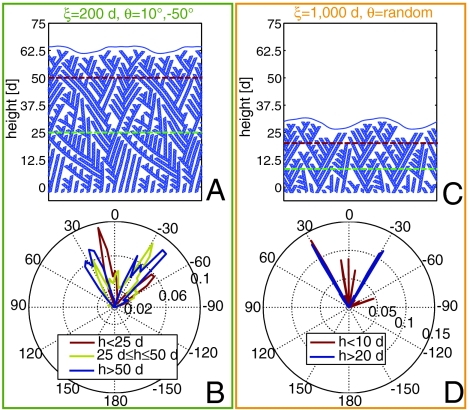
Because of the pressure exerted by the membrane, the network is capable of reaching a global geometric organization by automatically aligning the bisectrix of the branching angle with the external force. In Fig. 3A we show a typical configuration reached starting from an initial state in which the filaments are “misoriented” (i.e., θ = 10°, -50°) but very flexible (ξ = 200 d). Indeed, as shown in Fig. 3B, the orientation of monomers below 25 d is strongly affected by the initial orientation of the seeds that, in the example in Fig. 3B, are generated with a probability strongly peaked around -10° and 50° (red curve). The distribution above 50 d, instead, shows only two significant peaks around ± 30° (blue curve). The symmetric pattern we obtain is in agreement with experiments (39) and reproduces, relying only on mechanics, the results obtained in ref. 11. A similar numerical experiment has been conduced for randomly oriented, regularly stiff filaments (ξ = 1,000 d). The configuration reported in Fig. 3C shows how only the filaments with symmetric orientation with respect to the force direction are selected by the growth-cleavage-depolymerization process. The selection is extraordinarily clear in the sharp orientation distribution reported in Fig. 3D and takes place on a very short length scale (about 20 d). Thus the mechanics of the system suggests two distinct mechanisms to explain the observed symmetry of filaments orientation: rotation due to filament flexibility (over a long range) and selection due to cleavage–depolymerization of misoriented filaments (over a shorter range).

Fig. 3.

Network reorientation. (A) Representative configuration of a simulation of a pushing event against an applied force 1/2F_r with ξ = 200 d and seeds oriented at θ = 10°, -50°. This small persistence length allows an easy angular reorganization of the filaments. (B) Distribution of filament orientation for different height ranges for cases like the one in A. (C) Representative configuration of a simulation of a pushing event against an applied force 1/2F_r with ξ = 1,000 d and random orientation of the initial seeds. (C) Distribution of filament orientation for different height ranges for cases like the one in C.

Velocity.

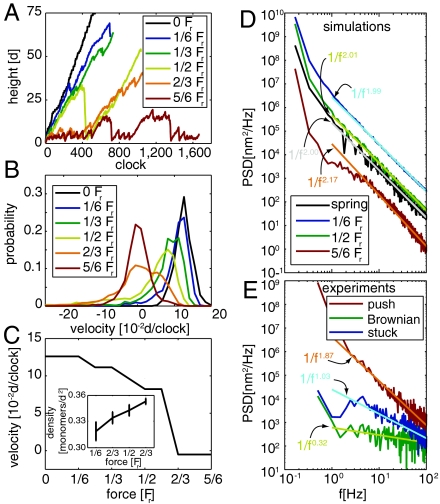
The model also predicts that fit networks grow with an almost constant force–velocity relationship. In Fig. 4A we report the time histories of the network height for different values of the forces. It is evident that, when organized growth takes place, the height traces are roughly parallel to each other independent of the level of the force. However, retraction events are more frequent and severe for higher values of the force. In Fig. 4B we report the distribution of the velocity of the advancing front. Increasing the force broadens the velocity distribution, but affects much less the position of the maximum. At F > 0.6F_r, the center of the distribution collapses to zero, and the observation of positive velocities becomes unlikely. The value of the most likely velocity is plotted against force intensity in Fig. 4C. Such a plot shows a strong nonlinear dependence of the velocity on the force, with an almost flat behavior at low forces and a stalling force of about 0.6F_r. This behavior closely resembles the experimental Fv curves, measured by atomic force microscopy (AFM) (5, 31) and optical tweezers (4). The curve is well fitted by the relation v = v₀(1 - F/F_stall)⁴, where F_stall is the stalling force and v₀ is the velocity under zero force, similar to the one proposed in ref. 22. In our model, the approximately constant Fv behavior is a consequence of the capability of the network of adjusting to variable force levels by reorganizing its geometric structure. At the same time, the network becomes slightly more dense as reported in Fig. 4C, Inset, in agreement with numerical findings in ref. 6.

Fig. 4.

Growth velocities, hysteresis, stochastic swing, and self-organized criticality. (A) Representative traces for simulated pushing experiments at different force levels. (B) Probability distribution of the velocity at different force levels. The velocity is estimated from the slope of the linear regression over a rolling window of 100 growth steps. Histograms are computed taking the average over at least 10 independent simulations like those depicted in A. (C) Most likely velocity as a function of the force. (Inset) Reports the average density of the network as a function of the applied force. Error bars represent the standard deviation of this quantity. (D) PSDs and their best linear fit for simulated traces at different values of force and growth against linear spring. (E) PSDs and their best linear fit for the traces measured in optical tweezer experiments on neuronal growth cones during Brownian oscillation of the bead, for the bead stuck on the coverslip, and pushing action of the lamellipodium. Experimental PSDs are shown up to the cutoff frequency of the trap (100 Hz) as above this frequency the spectrum is strongly modified by the experimental setup (4).

Given the geometry that we consider in this work (see Fig. 1), a stalling force of 0.6F_r corresponds to approximately 0.05F_r acting on each filament in contact with the membrane. With F_r ∼ 100 pN, we find that, according to our model, the growth of a lamellipodium can be stopped by applying an external force of a few piconewtons per filament in contact with the membrane. As already found elsewhere (4), this force is of the order of magnitude of the restraining force exerted by the membrane: For a lamellipodium slice of thickness d and width L_cell = 32 d this force is of the order of 2γL_cell where γ = 0.005 K_BT is the membrane surface tension (4, 12). The resulting estimated force per filament is 0.09F_r corresponding to 9 pN. This estimate is probably an upper bound, as it assumes that most of the surface tension is sustained by a single layer, as it would happen if the front is rounded (12). In order to be more quantitative on this estimate, one should model the system in three dimensions.

In the simulations, branch junctions are usually assumed to have the same resistance as the filaments. To check the effect of possible preferential breaking at branching sites, we performed simulations doubling the filaments resistance without changing the resistance of the branching points. We obtain very similar results in terms of filament orientations and Fv diagrams, with geometries showing shorter side branches (see SI Text). These results suggest that the Fv curve is controlled by the resistance of the weak points in the network.

Hysteresis.

Because the network geometry may evolve, the growth velocity at a given force level depends on the load history, as also observed experimentally (31). Indeed, a network that has survived a high force level is extremely fit and can withstand lower forces more easily. In this network, large avalanches will be more unlikely, and the velocity distribution will be shifted toward larger positive values (see SI Text). We conclude that the multiplicity of velocities under the same applied force, and the resulting hysteretic Fv response are natural consequences of the morphological changes from one stable network structure to another, occurring when a lamellipodium grows against a time-dependent applied force. A similar idea has been put forward in ref. 41, where hysteresis arises from transitions between two fixed metastable geometric configurations. In our approach hysteresis is triggered by the same selection mechanism that leads to organized growth.

Self-Organized Criticality.

The most peculiar feature of our model is that mechanical stress is the key factor that leads to geometric organization. Systems evolving in conditions of spatial or temporal self-organization as a consequence of an external stress or pressure are rather common in nature. A clear signature of this scenario is the onset of a power-law distribution in spatial or time correlations (42). Not surprisingly, our model shows very clearly this signature, as it is basically equivalent to a two-dimensional sand pile, with the membrane tension playing the role of gravity. As shown in Fig 4D, the power spectral density (PSD) of the front height decays as 1/f^α, where f is the frequency, and the exponent α is approximately equal to two regardless of the intensity of the force. The same signature is observed for the simulated growth against a linear spring. One immediately wonders if also experimental traces show these features.

In order to answer this question, we performed accurate measurements of the position of the front of a lamellipodium by an optical tweezer. Neurons from dorsal root ganglia (DRG) of P10-P12 rats were isolated and plated on poly-L-lysine-coated glass coverslips, positioned on the stage of an inverted microscope used for imaging and for force measurements (4). After 1 or 2 d of incubation, lamellipodia emerged and silica beads were trapped with an infrared optical tweezer in front of the lamellipodia. The bead position was measured at 10-kHz temporal resolution with a quadrant position detector using back focal plane interferometry (43). As the lamellipodium grows, the bead is pushed away from the center of the trap. This allows for a simultaneous measurement of the force and of the velocity of the lamellipodium front (4). In a typical experiment the bead remains detached from the lamellipodium, and its position fluctuates significantly due to Brownian motion. In these conditions, the PSD of the position of the front is flat up to the cutoff frequency of the trap (10² Hz in our case). In rare cases, adhesion forces caused the bead to seal onto the lamellipodium. In these conditions, the amplitude of fluctuations of the bead decreases significantly, and it is possible to measure the position of the lamellipodium front with a very good temporal resolution. In Fig. 4E we report the PSD of bead displacements during such an adhesion phase. Remarkably, it decays as 1/f², in a manner that closely resembles the numerical results of Fig. 4D. For comparison, in Fig. 4E we also show the spectrum in a noncontact phase and in a control experiment in which the bead is stuck on the poly-L-lysine-coated coverslip. The different PSD decay in this latter case proves that the signature of the lamellipodium growth is not due to environmental noise.

Discussion

In summary, we have shown that a model based on the mechanical interaction between a growing stiff network of collaborating filaments and a flexible membrane is capable of explaining many seemingly unrelated features of the observed behavior of growing lamellipodia: a growth velocity initially insensitive to the external force up to a stalling value; the capability of the network to organize its orientation with respect to the applied force; a load-history-dependent growth velocity; the concentration of the branching/capping protection zone near the membrane. The model predicts that the range of external forces for which growth can take place is in the 10^-2–10^-1 pN/nm range. In normal conditions, this is exerted by the membrane, which is then responsible for exerting the “selective pressure” on the network. The range of forces predicted by our model is just marginally larger than 2 ∗ 0.02 pN/nm, the restraining force per unit length exerted by surface tension on a growing lamellipodium (12), and of the same order of magnitude of 2 ∗ 0.1 pN/nm, the force exerted by the membrane according to the estimate for a crawling keratocyte (22).

In our model, we assumed for simplicity that the polymerization rate is not explicitly force-dependent. However, the filaments on which a monomer is added are not chosen at random, as growth events that would lead to overlaps with preexisting filaments or with the membrane are not allowed (see Methods). As a consequence, the axial forces on filaments selected for growth are always rather low. In fact, we computed the probability distribution of the axial forces acting on the filaments on which a new monomer is added during 12 statistically independent histories of growth against different external forces (see SI Text). Even when the network grows against the comparatively large external force of 0.5F_r, the axial force on growing filaments is zero in 40% of the cases and is larger than 1/6F_r only in about 1% of the cases. Introducing a genuine force-dependent rate of polymerization would certainly be an interesting theme for further studies. However, modeling exactly this effect may require precise experimental information on the growth dynamics of isolated filaments, extending the results in ref. 44.

Our model provides an explanation for the stochastic nature of the motion of the leading edge observed in experiments, where growth periods alternate with fast retractions. In fact, we claim that these retractions are essential in order to make our growth mechanism robust. This has an important and nontrivial consequence on the statistics of these retractions, whose amplitude and frequency are predicted to obey a power-law distribution, as in critically self-organized systems. This prediction is confirmed by our experiments on neuronal growth cones, showing that the PSD of the time series of the height of a growing lamellipodium decays with the square inverse of the frequency. It is well known that in conditions of self-organized criticality power-law distributions should emerge also in other observables, such as the amplitude of the retractions or the correlation between the height of the front in two different locations. The presence of these power laws is a direct consequence of the model we propose here and offers a direct manner of falsifying or confirming its validity when even more accurate experimental data will become available.

Retraction events may play an important role in all processes where motility rests on the buildup of compressive stresses in actin filaments (structures that, without some form of organization and coordination, would be ill-equipped to sustain compressive and bending stresses). These are ubiquitous in actin cell motility, including systems exhibiting pulsatile motion such as Listeria and motility assays (25–28). In bead motility assays, for example, pauses (during which stresses accumulate in the growing network) alternate with sudden accelerations of the whole bead (due to the breakup of transient attachments and fracture of shells of filaments encapsulating the bead). Although these velocity fluctuations involve macroscopic spatial and temporal scales, the ones occurring in the active layer forming at the leading edge of a protruding lamellipodium, between the plasma membrane and the previously grown, immobilized network, take place at microscopic scales. In our scheme, these fluctuations are the means to achieve network geometries that are effective for pushing the lamellipodium forward and generate sustained motility. Retractions and jerky motion at microscopic scales are compatible with smooth motion without significant oscillations at macroscopic scales. Thus, we believe that our scheme of mechanical self-organization through accumulation of mechanical stresses and avalanches of breaking events may be relevant for other actin-based motile systems, besides the neural growth cones studied in this paper.

Model

In the model developed in this work, the actin network forms by a stochastic process driven by an energy function defining the interaction between the filaments and between the filaments and the membrane. At the ith growth step, the energy of the system 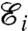is a function of the position of the nodes {u}_i. The equilibrium configuration of the nodes {u^eq}_i is obtained by minimizing 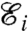numerically, via a conjugate gradient method implemented in the Surface Evolver package (38)

[1]

We assume the actin filaments to be linearly elastic up to failure and the membrane to have a linear elastic in-plane behavior. The filaments are represented by a truss structure, namely, a bead and spring model where the spring constant is the stretching stiffness E_a of the edges. The bending stiffness of the filaments is related to the persistence length ξ by the classical statistical mechanics result κ_a = 2ξK_BT, where κ_a is the equivalent bending stiffness of the truss structure modeling the actin filaments. In turn, from simple geometry and statics, the bending stiffness of the filament κ_a can be related to the stiffness of the trusses, namely κ_a = 2E_a(a tan β/4)², where β = 60° is the characteristic angle of the truss edges (see Fig. 1). Equating the two expressions for κ_a, we obtain

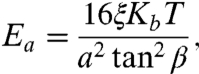[2]

and the elastic energy for the whole actin network is

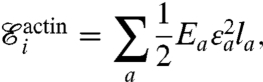[3]

where ϵ_a is the extensional strain of the actin edge a, and l_a is its undeformed length. A similar energy is considered for the membrane

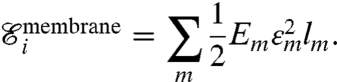[4]

The membrane is assumed to have also a bending stiffness κ that penalizes its curvature ρ. The bending energy of a slice of thickness d is of the form

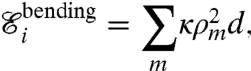[5]

where ρ_m is the curvature computed distributing the angle at the node m of the discretized membrane over a length d (equal to the membrane discretization length). The bending stiffness of the membrane corresponds to a persistence length ξ_m = κ/2 K_BT ∼ 8 d for the parameter values used in the model.

Contact among different filaments is modeled by introducing a short-range repulsion energy ψ between the nodes. Given a pair of nodes h and k, ψ is a function of the distance d_hk between the two nodes, and the contribution to the overall energy of the system is given by

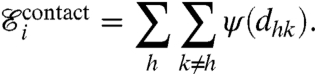[6]

We take for ψ the functional form

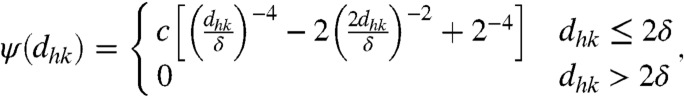[7]

where c is a constant. The contact force goes to infinity for vanishing distance and vanishes smoothly when the distance is larger than the threshold length 2δ. Contact between filaments and membrane is modeled in precisely the same way except that, in this case, the contact length parameter 2δ is used. Besides governing force transmission and mechanical collaboration between filaments, detection of contact also allows us to limit uncontrolled growth of the filaments. Indeed, we discard growth events on a filament that would lead to overlap with neighboring filaments. This makes an explicit modeling of capping unnecessary. This approximation should probably be reconsidered if the model is extended to 3D. The larger contact length parameter for filament–membrane interactions leads to a typical separation between filaments and membrane larger than one monomer and mimics the impact of the high flexibility of the membrane (20, 35, 37) on the dynamics of growth: Adding a monomer against the membrane is allowed because membrane ripples, triggered by thermal fluctuations, allow monomers to reach the barbed ends. Instead, growth against other filaments is less likely, as filaments are more rigid and fluctuations are unlikely to create enough room for an extra monomer. We typically consider constant external forces of intensity F pushing down the membrane nodes: 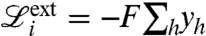. We also seek to model the protrusion of a lamellipodium against an elastic spring. In this case the work of the external forces is given by 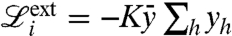, where 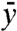is the mean height of the membrane and K is a stiffness constant. Summarizing, the energy of the system is

[8]

Experimental Methods

Neuron preparation.

Rats (P10-P12) were anesthetized with CO₂ and sacrificed by dislocation in accordance with the Italian Animal Welfare Act. DRGs were incubated with trypsin (0.5 mg/mL, Sigma-Aldrich), collagenase (1 mg/mL, Sigma-Aldrich), and DNase (0.1 mg/mL, Sigma-Aldrich) in 5 mL neurobasal medium (Gibco, Invitrogen) in a shaking bath (37 °C, 35–40 min). DRGs were mechanically dissociated, centrifuged at 300 × g, resuspended in culture medium, and plated on poly-L-lysine-coated (0.5 μg/mL, Sigma-Aldrich) coverslips. Cells were incubated for 24 to 48 h followed by the addition of nerve growth factor (50 ng/mL; Alomone) before the measurements.

Optical Tweezer Setup.

The optical tweezers setup was built as previously described (43). The dish containing the differentiating neurons and the beads (PSI-1.0NH2, G.Kisker GbR) was placed on the microscope stage, which could be moved by a three-axis piezoelectric nanocube (17 MAX 301, Melles Griot Inc.). The temperature of the dish was kept at 37 °C by a Peltier device. The bead position was determined in the x, y, and z planes with a lateral and axial accuracy of 2 and 5 nm, respectively, which was obtained from the analysis of the interference between forward scattered light from the bead and unscattered light (43, 45). The back focal plane of the condenser was imaged onto a QPD (C5460SPL 6041, Hamamatsu), and the light was converted to differential outputs digitized at 10 kHz and low pass filtered at 5 kHz. Both the lateral and axial trap stiffness, k_xy = (k_x,k_y) and k_z, respectively, as well as the detector sensitivity were calibrated using the power spectrum method (43) with voltage signals filtered and digitized at 5 kHz. In order to reduce and possibly avoid all mechanical perturbations affecting the measurement of x = (x,y,z), the optical tweezers setup was kept in an isolated and soundproof room, and the scientists performing the experiments controlled all operations remotely from a separate room, in order to reduce perturbations, which could have affected previous investigations.