Abstract
Radial sampling in multidimensional NMR experiments offers greatly decreased acquisition times while also providing an avenue for increased sensitivity. Digital resolution remains concern and depends strongly upon the extent of sampling of individual radial angles. Truncated time domain data leads to spurious peaks (artifacts) upon FT and 2D FT. Linear prediction is commonly employed to improve resolution in Cartesian sampled NMR experiments. Here, we adapt the linear prediction method to radial sampling. Significantly more accurate estimates of linear prediction coefficients are obtained by combining quadrature frequency components from the multiple angle spectra. This approach results in significant improvement in both resolution and removal of spurious peaks as compared to traditional linear prediction methods applied to radial sampled data. The ‘averaging linear prediction’ (ALP) method is demonstrated as a general tool for resolution improvement in multidimensional radial sampled experiments.
Keywords: radial sampling, linear prediction, resolution enhancement
Introduction
Sparse sampling of multidimensional NMR experiments has proven useful for studies of biopolymers in many contexts [1-7]. Radial sampling is particularly appealing because of the predictability of the resulting artifacts, the ability to collect a minimal data set to extract the information of interest without regard to processing artifacts and the statistical nature of the data. This sampling scheme allows for a simultaneous optimization of both acquisition time and resolution, while in principle retaining information equivalent to a traditional Cartesian sampled experiment [8, 9]. Further if the appropriate criteria are met an increase in signal-to-noise of the final spectrum is achievable [9]. The advantages of radial sampling result from the circumvention of the strict orthogonal sampling requirements imposed by traditional Cartesian sampling. In the case of a three-dimensional NMR experiment, radial sampling is achieved by simultaneously evolving the two indirect time domains such that t1 is sampled at τ cos(α) and t2 is sampled at τsin(α), where α is a selected angle between the two orthogonal time domains and τ is a common incremented time [10]. The directly acquired dimension is sampled traditionally resulting in a 2D plane of data points for each angle sampled. An important result of the radial sampling scheme is the fact that the underlying frequency components are underdetermined, which results in artifactual ridges of intensity in the spectrum when processed with either projection reconstruction [10] or the direct multidimensional Fourier transform [11-13].
The details of radial sampling artifacts have been extensively analyzed and a variety of schemes have been developed to remove them [6, 10, 14]. Two commonly preferred methods for generating a final spectrum are the lower value (magnitude) algorithm, which strives to remove the ridges, and the additive back projection algorithm, which attempts to enhance the signal while still retaining the artifacts. Both approaches exploit the fact that the ridge artifacts vary in a known way as a function of the sampling angle. The lower magnitude algorithm compares the individual angle spectra and retains the minimum absolute value at each frequency pair to generate a spectrum free of ridge artifacts. The additive back projection method simply sums equivalent points from the angle spectra which results in a final spectrum containing ridge artifacts at a fraction of the intensity of the authentic peaks.
The success of radial sampling primarily depends upon the set of angles employed. In the case of the lower magnitude algorithm artifacts are only removed if baseline is present at the equivalent chemical shifts of the ridge in at least one angle spectrum. In the case of additive back projection, artifact peaks are reinforced if artifact ridges intersect in multiple sampling angle spectra. Appropriate angle selection minimizes these intersections. We have previously presented a methodology for optimized angle selection and have shown that angle selection can often be dependent upon the effective line width of the peaks in the spectrum [15]. Thus, it is essential to obtain the narrowest possible effective linewidth. As with classic multidimensional NMR spectra, the true linewidth is often never reached in the explicitly sampled time domain. In this context, the forward-backward linear prediction method [16] is routinely used to extend the experimentally sampled time domain data where independent coefficients are determined for forward and backward application of linear prediction and averaged respectively. Here we extend these ideas in an effort to reduce linewidths of radial sampled data. This is accomplished by exploiting the redundancy of radial sampled data to more accurately determine linear prediction coefficients.
Results
Using the averaging concept inherent to forward-backward linear prediction, linear prediction methodology is extended for application to radial sampled NMR data here by exploiting the fact that multiple angle data sets are collected to generate a final spectrum. While conventional linear prediction can be applied to the multiple angle data sets independently, the coefficients obtained from different sampling angles are not directly comparable. Here we develop a means to combine the coefficients of data from multiple sampling angles by estimating and averaging the underlying frequency components. This allows a set of coefficients with improved accuracy to be generated. The approach is outlined in Fig. 1. The mathematical basis of linear prediction is well known [17, 18] and only those details needed for optimizing linear prediction of radial sampled data are recapitulated here.
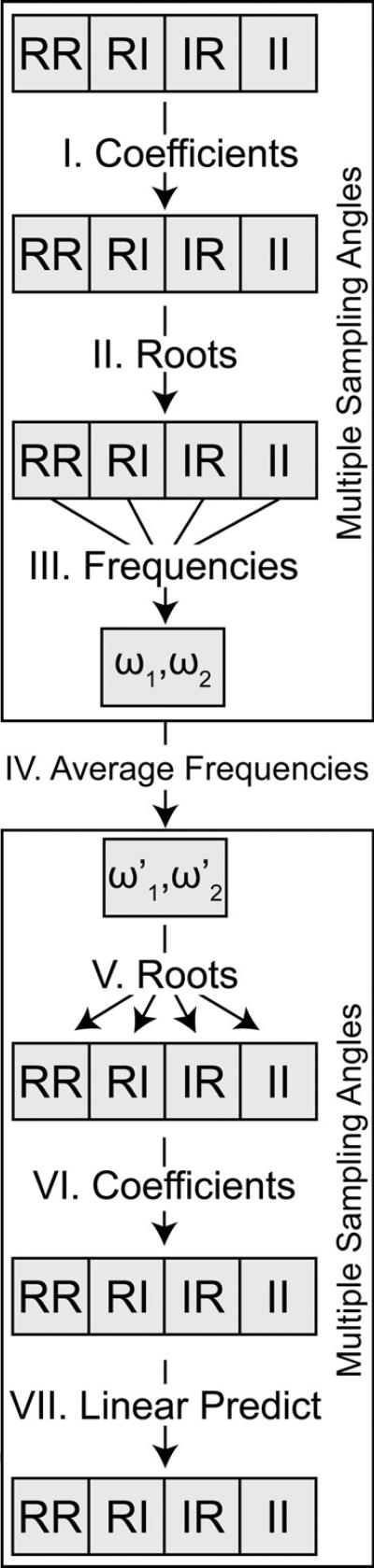
Fig. 1.
A general overview of the average linear prediction algorithm. The algorithm works by calculating a set of linear prediction coefficients in parallel for each radial sampling angle data set quadrature component. The coefficients are then used to solve for the characteristic polynomial roots, which in turn are combined to estimate the underlying amplitude and frequency components. The frequency components are averaged across all angle data sets. Finally, an improved set of coefficients are back-calculated. The improved set of coefficients can be used to predict additional data points with improved accuracy.
In the case of a three-dimensional NMR experiment with radial sampling of the two indirectly sampled time domains, the time series for the co-evolved indirect dimension may be written as:
| (1) |
Where i and j are quaternion numbers, ω1k and ω2k are the frequency components in t1 and t2 indirect time domains, respectively, and M is the total number of frequency components. R12 and R22 are the effective transverse relaxation rates in t1 and t2 indirect time domains, respectively. The acquisition dimension of the experiment is treated traditionally and will be excluded from this analysis.
Consistent with Eq. (1), four quadrature components are collected and stored independently. Previously, the individual quadrature components have been combined according to the quadrature rules of projection reconstruction and linear prediction was used to extend the projection data [10]. Alternatively, linear prediction could be applied to each of the four components separately and then combine the terms subsequently to reconstitute the signal before any final processing. As we will show below, treating the four quadrature components independently is necessary to appropriately model the underlying frequency. Additionally, treating the components independently further exploits the inherent redundancy of radial sampled data. Therefore, the linear prediction coefficients are calculated in parallel for the four quadrature components of each sampling angle using the forward linear prediction approach (step I of Fig. 1). Forward linear prediction is commonly represented as:
| (2) |
where ak are the linear prediction coefficients, xn-k are the existing data points, xn are future data points and M is the number of prediction coefficients. Among the various methods available to solve for the linear prediction coefficients single value decomposition (SVD) is used here to determine the set of coefficients because of its optimal noise handling [19].
Once a set of coefficients are determined for quadrature components of each angle, they are utilized independently to generate a characteristic polynomial describing the time series for each component. The polynomial, described in Eq. (3), is a function of the arbitrary variable z and ak are the coefficients defined in the previous step.
| (3) |
The polynomial is equated to zero and factored to determine the roots of the equation in parallel for each angles quadrature set (step II of Fig. 1). In the present case, we have found that the factoring is efficiently performed by generating a companion matrix and solving for the eigenvalues [20].
From Eq. (1) the roots for each of the quadrature components for each of the M coefficients can be modelled as:
| (4a) |
| (4a) |
| (4c) |
| (4d) |
The roots of each of the four quadrature components of the radial sampled data are modelled as functions of frequencies ω1k, ω2k, sampling angle, α, and amplitudes Ak. It is important to note that Eqs. (4a-d) are models of the roots. The two frequencies used in the model are apparent frequencies defined by the model and not the actual frequency values inherent to the data. The four root components arising from the four quadrature components are designated by whether the time domains are modulated with respect to cosine or sine for either time domain t1 or t2. Unlike forward-backward linear prediction, where the roots are averaged to calculate a new set of coefficients, variation of the sampling angles used in the data sets requires that the model frequency components be determined prior to comparison (step III of Fig. 1). Model frequencies ω1k and ω2k are determined independently by solving the appropriate ratios of the corresponding roots. At this point, the combination of all four quadrature components also provides a means to reduce the noise in the model frequency calculation. The expressions for ω1k and ω2k are written as:
| (5a) |
| (5b) |
Correspondingly, Ak is given by:
| (6) |
Typically the calculation of frequencies using linear prediction is avoided because of the inaccuracy of the determined frequency components. The inaccuracies arise in the first step of linear prediction when the coefficients are determined and are propagated in all subsequent steps. Therefore, the accuracy of the model frequency values determined in Eqs. (5a,b) are directly dependent on both the signal-to-noise of the data and the linewidth variation as a function of the sampling angle[10]. The data noise causes the model frequencies error to vary according to the noise distribution intensity. Accordingly, the errors of the model frequencies increase as the linewidths increase. The linewidths increase as a function of cos(α) and sin(α) for ω1 and ω2 respectively. The same model is used for all angle data sets and therefore the model frequency and amplitude values are directly comparable across the entire data set and are averaged (step IV of Fig. 1). Averaging across multiple angle data sets increases the accuracy of the estimated frequencies, by reducing the noise related error of the frequency according to the variance sum law. The accuracy of the final model frequency components is further increased by accounting for the linewidth related error by weighting the average according to 1/sin(α) and 1/cos(α) for the ω1 and ω2 components respectively. The new roots are calculated for each quadrature component using Eqs. (4a-d) (step V of Fig. 1). Finally, the new improved sets of coefficients for each sampling angle, are calculated from the new roots by using the characteristic polynomial which can be formulated from the new roots (step VI of Fig. 1).
| (7) |
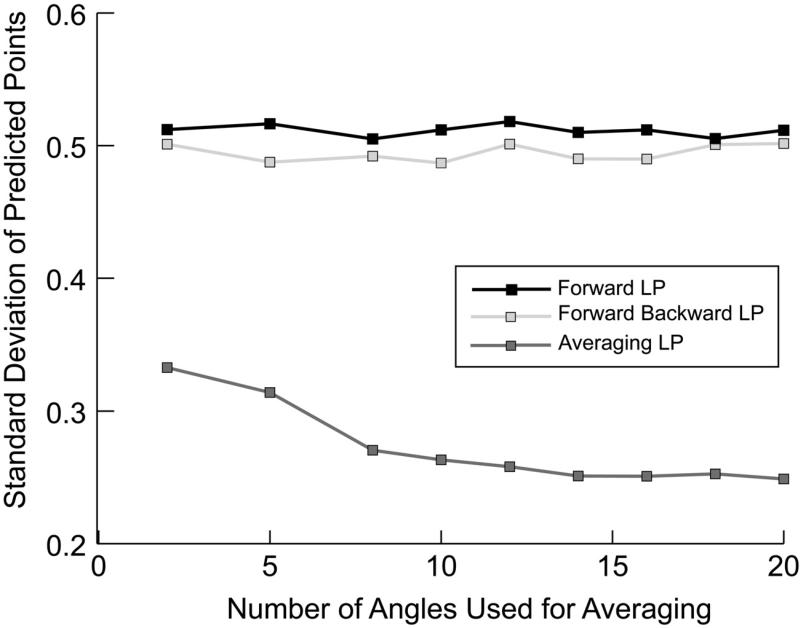
The polynomial utilizes the improved roots, R'k. This method for calculating coefficients from the roots using the characteristic polynomial is opposite of that of calculating roots from coefficients using the polynomial described in Eq. (3). The improved set of coefficients evaluated by expanding Eq. (7) are the coefficients terms of the polynomial zk, where i belongs to [0, M − 1]. The improvement in the accuracy of the linear prediction coefficients versus the number of radial sampling angle data sets is demonstrated for generated data in Fig. 2. This test was performed by generating a noise free radial sampled data set according to Eq. (2) composed of 40 increments. Subsequently, this data set was truncated to 24 increments and random noise was added. Linear prediction coefficients were calculated using forward, forward-backward or the new averaging linear prediction. Using the calculated linear prediction coefficients an additional 16 increments were generated and compared to the corresponding points from the original untruncated data set. This procedure was repeated to determine the standard deviation of the predicted points from the actual values. Inspection of the figure demonstrates that the error in prediction decreases exponentially as the number of angles increases.
Fig. 2.
The improvement in linear prediction coefficient accuracy is assessed through generated data. A radial sampled data set was generated according to Eq. (1). The noise free data contained 10 peaks using 40 quaternion data points. This data set was truncated to 24 quarternion points and random noise was then added. Using 10 coefficients for each of forward, forward-backward or averaging linear prediction with an increasing number of angles, an additional 16 quarternion points were generated. The newly generated 16 points were compared to the noiseless points. The procedure was repeated to generate a standard deviation from the actual values, each time with varying random noise.
The final step of extending the data using linear prediction applies the new improved coefficients to Eq. (2) in step VII of Fig. 1. Ideally, the number of predicted points should be less than or equal to half the number of data points in order to be accurately solved using SVD, provided the number of coefficients used is greater than or equal to the number of frequency components. Here, using averaging linear prediction we stretch this limit by predicting more than half the number of data points used and demonstrate the advantage of this method over both forward and forward-backward LP in the upper limits of the number of points that can be accurately predicted.
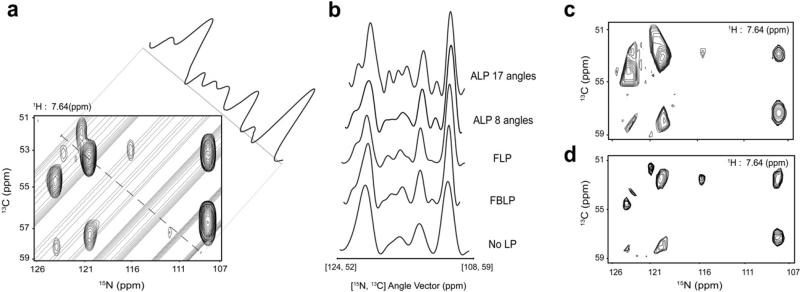
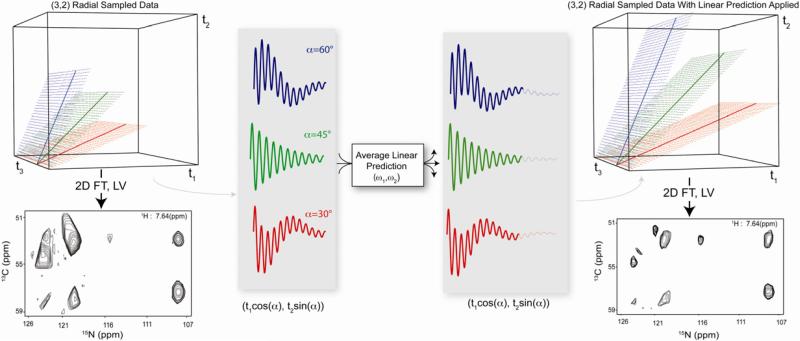
To illustrate the improvement in resolution achieved by averaged linear prediction (ALP), we collected a (3,2) radial sampled HNCA with 24 quaternion data points for each of 17 angles spanning 5° through 85°. A comparison of the various linear prediction methods is shown in Fig. 3 using a perpendicular slice through the radial sampled dimension of the +25° ridge spectrum As evident in the figure, average linear prediction produces superior resolution for equivalent data. The improvement in resolution is a direct result of increased accuracy of the linear prediction coefficients which is clearly indicated by increasing the number of angle data sets averaged from 8 to 17. Further, the figure also demonstrates the increased performance of the lower value algorithm to resolve all of the peaks in a final spectrum when the peaks are appropriately resolved in the component spectra.
Fig. 3.
Demonstration of the advantage of averaged linear prediction in processing radial sampled NMR data. Panel A shows the two-dimensional indirect frequency plane of a linear predicted (ALP) radial sampled HNCA sampled at 25°. The equivalent peaks from the traditionally sampled Cartesian spectrum are overlaid to indicate the authentic intensity. The overlaid dashed line indicates the vector perpendicular to the artifact ridges, the intensity along which is indicated as a projection outside the spectrum. Panel B compares the same spectrum slice from each of the spectra processed with the noted type of linear prediction. It is clear that average linear prediction accurately increases the resolution of all of the peaks in the spectrum resolves all of the peaks in the spectra when 17 sampling angles are used. Panels C and D demonstrate the advantage of applying averaging linear prediction to generate a final spectrum using the lower value comparison. Panel C shows the indirect plane processed without any linear prediction while Panel D shows the equivalent plane processed with average linear prediction. In all cases the data was linear predicted from 24 quaternion data points to 40 quaternion points using 10 linear prediction coefficients.
Discussion and Conclusion
Radial sampling has shown tremendous potential for overcoming the sampling limitations of multidimensional NMR experiments. Efficient application of radial sampling depends on the optimal angle selection and collection of high quality angle plane data in order to generate an accurate final spectrum [15]. We have previously presented means to optimally determine a set of sampling angles. Here, we have presented the means to enhance the quality of the sampling angle data. A novel linear prediction method, averaging-LP, is introduced and its application to radial sampled data has been tested. Averaging-LP exploits the inherent redundancy of radial sampled data sets and results in increased accuracy of linear prediction coefficients which in turn decreases the linewidths and truncation artifacts, which manifest themselves as a ripple pattern in the component angle spectra [8]. The advantages of a decreased linewidth are at least two-fold. First, the decreased linewidth directly affects the efficient generation of a final spectrum when either additive back-projection or lower value methods are used. Second, the decreased linewidth indirectly affects the number of increments necessary to obtain a suitable linewidth which in turn, allows for the collection of more angles per unit time. The availability of additional angles serves to aid in the reduction of reconstruction artifacts. Although tested in the context of the direct two-dimensional Fourier transform and the lower value comparison, averaging-LP is apparently applicable to any method capable of processing radial sampled data. Finally, it is noted that the fundamental limitations of traditional linear prediction also apply to averaging-LP. The presence of a large number of frequency components or poor sensitivity in a particular vector of the indirect dimension constrains the applicability of averaging-LP to radial sampled data.
Methods
Recombinant ubiquitin was prepared as described [21]. NMR data was collected on a 1 mM 13C, 15N uniformly labeled sample of human ubiquitin at 25°C on a Bruker Avance III 500 MHz NMR spectrometer equipped with a 5 mm triple resonance TCI cryogenic probe. The sample was prepared in 50 mM potassium phosphate buffer pH 5.5 with 50 mM NaCl and 0.04% sodium azide in 90% H2O/10% D2O. Data was collected using a standard HNCA [22] or a modified version for radial sampling, such that t1 = t1 cos(α) and t2 = t1 (sw1/sw2)sin(α). The Cartesian experiment was collected using 36 complex points in both of the indirect dimensions for a total of 5184 FIDs. Each FID was the average of 4 transients and contained 512 complex points requiring approximately 6 hours of measurement time. The spectral width was set to 12, 27 and 35 ppm for proton, nitrogen and carbon respectively. The carriers for each dimension were set to 7.73, 117.98 and 54 p.p.m. for proton, nitrogen and carbon respectively. The maximum acquisition times for the nitrogen and carbon dimensions were 0.0264 and 0.0082 seconds, respectively. In the case of radial sampling all experimental parameters, excluding the incremented times, were set to equivalent values as the Cartesian experiment. All of the radial sampled experiments utilized 24 quatrion data points, requiring 4 quadrature components per data point. Each sampling angle plane required 6.5 minutes of measurement time. The angle spectra were processed independently using a direct 2D Fourier transform. Prior to Fourier transforming, the data was linear predicted and apodized with cosine squared function to remove truncation artifacts. Following processing, individual angle spectra were compared using the lower value (magnitude) algorithm to remove the ridge artifacts [10]. The Cartesian sampled data was processed with corresponding apodization and zero filling. The fast Fourier transform was used in place of the direct 2D Fourier transform. All processing was done using an in-house program to be described elsewhere and visualized using Sparky [23].
Radial sampling of multidimensional NMR spectra is often limited by resolution
Standard linear prediction is not directly applicable to radial data
Here we present a linear prediction method specific to radial sampling
Improved accuracy is obtained by combining quadrature components of multiple angles
Acknowledgements
This work was supported by NIH grants GM 085120 and DK 39806 and NSF grants MCB 0842814 and DMR05-200020.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Eghbalnia HR, Bahrami A, Tonelli M, Hallenga K, Markley JL. High-resolution iterative frequency identification for NMR as a general strategy for multidimensional data collection. J. Am. Chem. Soc. 2005;127:12528–12536. doi: 10.1021/ja052120i. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gledhill JM, Walters BT, Wand AJ. AMORE-HX: A multidimensional optimization of radial enhanced NMR-sampled hydrogen exchange. J. Biomol. NMR. 2009;45:233–239. doi: 10.1007/s10858-009-9357-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hiller S, Fiorito F, Wuthrich K, Wider G. Automated projection spectroscopy (APSY) Proc. Natl. Acad. Sci. USA. 2005;102:10876–10881. doi: 10.1073/pnas.0504818102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jiang L, Coggins BE, Zhou P. Rapid assignment of protein side chain resonances using projection-reconstruction of (4,3)D HC(CCO)NH and intra-HC(C)NH experiments. J. Magn. Reson. 2005;175:170–176. doi: 10.1016/j.jmr.2005.03.014. [DOI] [PubMed] [Google Scholar]
- 5.Tugarinov V, Choy WY, Kupce E, Kay LE. Addressing the overlap problem in the quantitative analysis of two dimensional NMR spectra: Application to 15N relaxation measurements. J. Biomol. NMR. 2004;30:347–352. doi: 10.1007/s10858-005-1549-y. [DOI] [PubMed] [Google Scholar]
- 6.Venters RA, Coggins BE, Kojetin D, Cavanagh J, Zhou P. (4,2)D projection-reconstruction experiments for protein backbone assignment: Application to human carbonic anhydrase II and calbindin D-28K. J. Am. Chem. Soc. 2005;127:8785–8795. doi: 10.1021/ja0509580. [DOI] [PubMed] [Google Scholar]
- 7.Kazimierczuk K, Stanek J, Zawadzka-Kazimierczuk A, Kozminski W. Random sampling in multidimensional NMR spectroscopy. Prog. Nucl. Mag. Res. Sp. 2010;57:420–34. doi: 10.1016/j.pnmrs.2010.07.002. [DOI] [PubMed] [Google Scholar]
- 8.Coggins BE, Venters RA, Zhou P. Radial sampling for fast NMR: Concepts and practices over three decades. Prog. Nucl. Mag. Res. Sp. 2010;57:381–419. doi: 10.1016/j.pnmrs.2010.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gledhill JM, Wand AJ. SEnD NMR: Sensitivity enhanced n-dimensional NMR. J. Magn. Reson. 2010;202:250–258. doi: 10.1016/j.jmr.2009.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kupce E, Freeman R. Projection-reconstruction technique for speeding up multidimensional NMR spectroscopy. J. Am. Chem. Soc. 2004;126:6429–6440. doi: 10.1021/ja049432q. [DOI] [PubMed] [Google Scholar]
- 11.Coggins BE, Zhou P. Polar Fourier transforms of radially sampled NMR data. J. Magn. Reson. 2006;182:84–95. doi: 10.1016/j.jmr.2006.06.016. [DOI] [PubMed] [Google Scholar]
- 12.Kazimierczuk K, Kozminski W, Zhukov I. Two-dimensional Fourier transform of arbitrarily sampled NMR data sets. J. Magn. Reson. 2006;179:323–328. doi: 10.1016/j.jmr.2006.02.001. [DOI] [PubMed] [Google Scholar]
- 13.Marion D. Processing of ND NMR spectra sampled in polar coordinates: a simple Fourier transform instead of a reconstruction. J. Biomol. NMR. 2006;36:45–54. doi: 10.1007/s10858-006-9066-1. [DOI] [PubMed] [Google Scholar]
- 14.Yoon JW, Godsill S, Kupce E, Freeman R. Deterministic and statistical methods for reconstructing multidimensional NMR spectra. Magn. Reson. Chem. 2006;44:197–209. doi: 10.1002/mrc.1752. [DOI] [PubMed] [Google Scholar]
- 15.Gledhill JM, Wand AJ. Optimized angle selection for radial sampled NMR experiments. J. Magn. Reson. 2008;195:169–178. doi: 10.1016/j.jmr.2008.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhu G, Bax A. Improved linear prediction of damped NMR signals using modified forward backward linear prediction. J. Magn. Reson. 1992;100:202–207. [Google Scholar]
- 17.Barkhuijsen H, Debeer R, Bovee WMMJ, Creyghton JHN, Vanormondt D. Application of linear prediction and singular value decomposition (LPSVD) to determine NMR frequencies and intensities from the FID. Magn. Reson. Med. 1985;2:86–89. doi: 10.1002/mrm.1910020111. [DOI] [PubMed] [Google Scholar]
- 18.Gesmar H, Led JJ. Spectral estimation of complex time-domain NMR signals by linear prediction. J. Magn. Reson. 1988;76:183–192. [Google Scholar]
- 19.Tufts DW, Kumaresan R. Singular value decomposition and improved frequency estimation using linear prediction. IEEE Trans. ASSP. 1982;30:671–675. [Google Scholar]
- 20.Anton H. Elementary linear algebra. John Wiley; New York: 1994. [Google Scholar]
- 21.Wand AJ, Urbauer JL, McEvoy RP, Bieber RJ. Internal dynamics of human ubiquitin revealed by 13C-relaxation studies of randomly fractionally labeled protein. Biochemistry. 1996;35:6116–6125. doi: 10.1021/bi9530144. [DOI] [PubMed] [Google Scholar]
- 22.Muhandiram DR, Kay LE. Gradient-enhanced triple-resonance 3-dimensional NMR experiments with improved sensitivity. J. Magn. Reson. Ser. B. 1994;103:203–216. [Google Scholar]
- 23.Goddard TD, Kneller DG. SPARKY 3. University of California; San Francisco: [Google Scholar]