Abstract
Transcript elongation by RNA polymerase involves the sequential appearance of several alternative and off-pathway states of the transcript elongation complex (TEC), and this complicates modeling of the kinetics of the transcription elongation process. Based on solutions of the chemical master equation for such transcription systems as a function of time, we here develop a modular scheme for simulating such kinetic transcription data. This scheme deals explicitly with the problem of TEC desynchronization as transcript synthesis proceeds, and develops kinetic modules to permit the various alternative states of the TECs (paused states, backtracked states, arrested states, and terminated states) to be introduced one-by-one as needed. In this way, we can set up a comprehensive kinetic model of appropriate complexity to fit the known transcriptional properties of any given DNA template and set of experimental conditions, including regulatory cofactors. In the companion article, this modular scheme is successfully used to model kinetic transcription elongation data obtained by bulk-gel electrophoresis quenching procedures and real-time surface plasmon resonance methods from a template of known sequence that contains defined pause, stall, and termination sites.
Introduction
Overview of what must be included in a model of transcript elongation
Gene expression begins with initiation of RNA transcription by an RNA polymerase holoenzyme at the promoter of a gene or operon, followed by elongation and eventually termination of the nascent RNA. These events are tightly regulated, because mistakes in gene expression can compromise the survival of single-celled organisms and potentially lead to disease in higher eukaryotes. The transition from the initiation to the elongation phase of transcription is complete once the nascent transcript has grown to ∼11–14 nucleotide residues in length. At this point the specificity subunit (σ-factor) is released, the mature nucleic acid scaffold of the transcription elongation complex (TEC) is fully formed, and the core RNA polymerase (RNAP) binds to it tightly. The nucleic acid framework of the TEC consists of an open transcription bubble that carries within it the RNA-DNA hybrid, comprising the terminal 8–9 RNA nucleotide residues (nts) of the 3′-end of the nascent RNA chain that are paired with the complementary nts of the DNA template strand (see (1,2) and references therein). The transcription bubble and the RNA-DNA hybrid remain approximately constant in length and move along the template DNA with the core RNAP as transcription proceeds.
For survival it is vital that cells regulate the transcript elongation process in response to environmental signals, and also that elongation be tightly coupled to the downstream events of gene expression, such as RNA splicing and translation. This coupling is significantly controlled by pause and termination signals coded in the template DNA, as well in the nascent RNA, and also by regulatory protein (and small RNA) cofactors that bind to the TEC (1–3). Unlike DNA polymerases and other processive enzymes that also extend primed nucleic acid chains by template-directed sequential addition of the next required nucleoside triphosphate (NTP), the RNA polymerases extend the nascent transcript at highly variable and sequence-dependent rates (2,4). This reflects, at least in part, the fact that the TEC has some probability of entering one or more alternative states at any given template position. This probability of entry into alternative states often depends on local template sequence, but may also reflect sequence-independent processes (4).
Pausing of the TEC on the template generally precedes entry into alternative states. These pauses vary in length and type. Ubiquitous pauses are of short duration (usually <4 s) and may be caused by a slight fraying of the 3′-end of the nascent RNA from the template DNA, together with an associated sequence-dependent misalignment of the incoming template NTP in the active site (4,5). Paused states with longer half-lives may be triggered by: 1), backtracking at template positions that contain thermodynamically weak hybrid sequences; 2), hairpins that form in the nascent RNA upstream of the TEC, which may allosterically perturb the conformation of the active site; and 3), roadblocks on the downstream template DNA, including nucleoid proteins in prokaryotes and nucleosomes in higher organisms (4,6).
All of these types of pauses can play important roles in the regulation of RNA transcription, permitting, for example, the triggering of termination by transcription cofactors such as ρ-helicase in bacteria (7). Pauses also participate synergistically in the processes of intrinsic termination and anti-termination (8) (see also Epshtein et al. (9) and Datta and von Hippel (10)).
Finally, termination is often viewed as a kinetic competition or “race” between the processes of elongation and termination (8,11). Terminators at defined sites before the end of a gene are thought to act as “expression switches” that can be tuned by cofactors to alter the balance between these competing pathways. During termination the RNA-DNA hybrid is unwound, the transcription bubble collapses, and the RNAP and the nascent transcript are released from the template DNA (1,9). To fully understand how the balance between pausing and termination regulates RNA transcription, it is necessary to determine the rate constants for these competing processes.
Modeling the transcription process
Given these complexities and the central importance of transcription in controlling the dynamics of cells and entire organisms, the establishment of procedures to model the kinetics of the transcription process has attracted much attention and thought from many investigators. These models range widely in mathematical complexity and in purpose. Some start with the biology, and seek to define the mechanistic elements that must be taken into account in modeling the overall transcription process, and then deal with them at a predetermined level of detail within an appropriate mathematical framework.
These modeling efforts can be further divided into those that are primarily concerned with modeling entire biological regulatory networks, in which transcription is often “lumped” as a single component, effectively “coarse-graining” the entire transcription process by assuming that the rate-limiting step for this process is initiation. Such approaches often boil down to asking—at the biological regulatory level—the “yes or no” question of whether transcription at a particular gene does or does not occur, and then—if it does—treating the remainder of the transcription process (including transcript elongation, termination, editing, etc.) as a lumped nonrate-limiting single step.
Other models of this genre do not make the assumption that initiation is rate-limiting for the whole transcription process, or indeed explicitly proceed on the assumption that it is not. These approaches, focusing instead on the elements of the elongation process, have sometimes proven difficult to use in a predictive or descriptive capacity by experimentalists, both because the mathematics often appears formidable and because many of the needed kinetic and thermodynamic parameters that are central to the model are either unknown or not well defined.
Yet another class of kinetic models is more heavily focused on integrating known kinetic parameters that have been experimentally deduced into an overall predictive model for what can be expected from transcript elongation based on gene sequence and cofactor binding. Such models attempt to recognize specific regulatory sequence elements and then describe and ultimately predict how the kinetic parameters associated with these sequence elements will interact to control the rates of both the local and the integrated elongation process. These approaches have led to a number of predictive models to assist in understanding transcriptional regulation through the effects of pausing and termination (12–20).
However, these models have often relied heavily on relatively few values of kinetic parameters that have been deduced predominantly from time-resolved single-molecule experimental work focused primarily on transcript elongation, the role of the nucleotide addition cycle, and pausing (21–25). In this work, we extend this general approach to take into account additional features not previously considered explicitly, such as the statistical desynchronization of multiple TECs in bulk-solution studies and related complexities. By proceeding in this way, we have sought to develop an intuitive framework of modular models that can be assembled in various combinations to simulate the events of “real” transcription elongation. This approach permits us to describe the effects of pausing, arrest, and termination events on the progression of elongation complexes along any template sequence.
We hope that experimentalists will find this modular modeling approach to be particularly intuitive and easy to use. Our approach is essentially based on initial information from the coding sequence, and thus includes terms that correspond to molecular events other than straightforward elongation (e.g., pausing, stalling termination, back-tracking, etc.) only as required by the template sequence. This makes it easy to simulate the resulting transcription elongation kinetics with “consensus” parameters that can illustrate the effects of each additional modular element on the rate of the overall elongation process. In the companion article (26), as a fully worked-out example of this approach, we apply a comprehensive kinetic scheme developed in this way to a dataset developed by monitoring the kinetics of transcription of the well-known tR2 template of phage λ by two complementary assay procedures: one (bulk-quenched-gel-electrophoresis) that measures the distribution of chain lengths during the transcript elongation from a known stall site as a function of time, and the other (surface plasmon resonance, SPR) that tracks increases and decreases in the effective mass of the TEC as a function of elongation time.
The results include the application of statistical tests to analyze the parameter space and estimate the confidence intervals, and show that this way of modeling and describing the dynamics of transcription elongation is both robust and informative. In addition, we emphasize that the method is general, because it can equally well be used to model any processive (or “n-step”) process of sequential steps (27) that involves template-dependent chain synthesis (for example, DNA replication or protein synthesis), as well as processes that do not produce a molecular product but can be tracked by cyclical NTP hydrolysis events (for example, the movement of molecular motors or helicases along appropriate molecular “tracks”).
Materials and Methods
Simulations
Simulations based on the simple kinetic modular models for different transcription events were programmed into the Berkeley Madonna equation solver (University of California, Berkeley, CA) as described in the Supporting Material. Simulated data from these models were exported as text files and assembled into graphs using SigmaPlot (Systat Software, San Jose, CA).
Results
A simple model for RNA transcription
We begin with the simplest model of RNA transcription that deals with the essential components of the process. Fig. 1 A presents a model of bulk RNA transcription by TECs that assumes: 1), there is only one TEC per DNA template; 2), the concentration of NTPs is not limiting and the concentration of pyrophosphate is negligible; 3), the effect of DNA sequence on the rate constants for elongation and pyrophosphorolysis (the chemical reverse of elongation) are uniform at all template positions; 4), the steps of each single nucleotide addition or pyrophosphorolysis cycle can be described by single forward and reverse rate constants (kF or kR); and 5), there are no off-pathway elongation-incompetent states.
Figure 1.
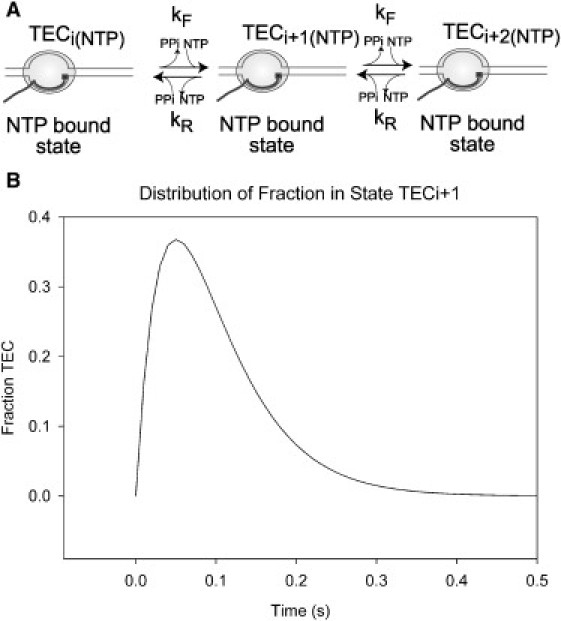
Simple model for transcription. (A) Depiction of a simple model for transcript elongation by a transcription elongation complex (TEC) across three template positions from the NTP-bound state at position (i) to position (i + 2), showing RNA polymerase (pale shaded oval), template DNA (fine lines), nascent RNA (dark line), and bound NTP (solid square). The events that occur during the forward reaction (NTP catalysis, pyrophosphate release, TEC translocation, and binding of the next templated NTP), or the reverse reaction (pyrophosphorolysis), are lumped together within the rate constants for the forward (kF) and reverse (kR) reactions between each position and represented by the reaction arrows. (B) Simulation of movement into, and out of, template position TECi+ 1 during transcription under standard conditions, using forward and reverse rate constants of 20 and 1 × 10−4 nt s−1, respectively. (Solid curve) Fraction of total TECs at position TECi+ 1 as a function of time.
We note that all of these assumptions can be relaxed as further modules are added and “real” complexities are introduced.
A series of coupled differential equations was written to simulate the nucleotide addition or pyrophosphorolysis events that describe the occupancy [TEC(i), TEC(i + 1), and TEC(i + 2)] of template positions (i), (i + 1), and (i + 2) in terms of the rate constants of entry into, and exit from, these positions. For transcription over these three template positions, the change with time in the fraction of TECs at a particular template position is described by the subtraction (from the original fraction of TECs at this position) of all the TECs that are removed by reaction steps that lead away from each of these positions and the addition of all the TECs that are added by steps leading into these positions. This simplest kinetic model is shown schematically in Fig. 1 A.
The rate constants of movement from position (i) to (i + 1) by nucleotide addition, and from position (i+1) to position (i) by pyrophosphorolysis, are described by Eq. 1:
| (1) |
Here kF and kR represent, as a function of time, the forward and reverse rate constants, respectively, and TEC(i) and TEC(i + 1) represent the fractions of the total TEC population that are located at template positions (i) and (i + 1). Similarly, the time dependence of the fractions of TECs located at template positions (i + 1) and (i + 2) is represented by Eqs. 2 and 3:
| (2) |
and
| (3) |
Here TEC(i + 2) is the relative fraction of total TECs at template position (i + 2). Equations 1 and 3 each describe only one possible entry or exit pathway because positions (i) and (i + 2) represent the “ends” of this idealized transcription template, whereas Eq. 2 has two potential entry or exit pathways because position (i + 1) can be accessed from either direction. Because the fraction of total TECs at each template position is dependent on the fractions at the other positions, these equations can be coupled and solved concurrently to determine the fraction of TECs at each elongation position as a function of time.
The average rate constants for nucleotide addition or pyrophosphorolysis during in vitro, single-round RNA transcription reactions for Escherichia coli transcription complexes at 25–30°C under nonlimiting NTP concentrations and at nonpausing positions have been estimated experimentally to be ∼20 and ∼10−4 nt s−1, respectively (25,28–32). Although limiting concentrations of NTPs and high concentrations of pyrophosphate are known to alter these rates, we have here specifically modeled the conditions commonly used for in vitro studies. Parameters determined in this way were used as rate constants to determine the fraction of total TECs at template position (i + 1), assuming that at time zero all TECs were located at template position (i) (Fig. 1 B). Note that movement to or from a particular template position is a stochastic or random process, and that the TEC occupancy profiles for each template position ((i), (i + 1), and (i + 2)) as a function of time can also represent the probability of a single TEC entering or leaving this template position. Hence, for this simple model, the position of the peak representing movement into or out of template position (i + 1) is based on an average dwell-time of ∼50 ms at each template position, and the breadth of the distribution shows that dwell-times for individual TECs may be significantly shorter or longer than this.
Coupled equations for multiple nucleotide addition events covering template positions (i) to (i + n) were generated iteratively (see Fig. S1 in the Supporting Material) and result in the replacement of Eqs. 2 and 3 with Eqs. 4 and 5:
| (4) |
| (5) |
Here j represents each template position from (i + 1) to (i + n − 1). Because n has been set equal to 20 for this simulation, Eq. 4 describes all of the equations representing template positions between (i + 1) and (i + 19) (represented by the dots in Fig. S1). This results in a total of 21 equations, with the final equation (Eq. 5) representing the rate constant for the change of the fraction of TECs at position 20 (TEC(i + 20)). Kinetic fitting programs, such as Berkeley Madonna (used in this work) or other differential equation solvers, can be set up to process these coupled iterative events (see the Supporting Material). More-detailed models can utilize additional mathematical methods to simplify the equations and reduce the computation time required to “solve” the models for such coupled events (13,14,16,33,34). However, the assumptions required to achieve this simplification can introduce other complications and are beyond the “intuitive” aims of this study (33).
The stochastic nature of these events also means that movement out of the first template position, (i), after addition of the next templated NTP, is not completely synchronous, even in this idealized simulation. This is consistent with observations for “bulk” solution transcription reactions described below and elsewhere (24,35,36). The fraction of TECs located at position (i) decays exponentially with time (Fig. 2 A) because the rate of nucleotide addition is significantly faster than that for pyrophosphorolysis and high steady-state concentrations of NTP also favor the forward reaction. The TECs accumulate at the run-off position, represented by TEC(i + 20) in Fig. 2 A, as also seen experimentally at the run-off position in bulk solution transcription reactions (26).
Figure 2.
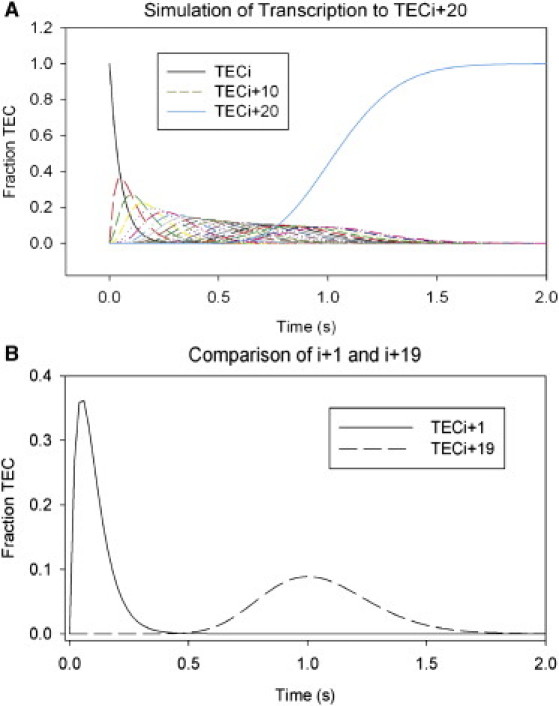
Model for transcription elongation. (A) Simulation of TEC movement during transcription across multiple template positions to position (i + n) (see Fig. S2; n = 20 for this simulation) under standard conditions (described for Fig. 1B above). (Curves) Fraction of total TECs present at each sequential template position as a function of time, beginning with template position (i) (black curve) and ending at position (i + 20) (light-blue curve). (B) Comparison of the fraction of total TECs at template positions (i) (solid curve) and position (i + 19) (dashed curve) over the time-course of the reaction.
The curves representing the fraction of TECs at each successive template position broaden with time, with distribution widths increasing and peak heights decreasing. The progressive decrease in the maximum fraction of TECs at each sequential template position at any one time is a hyperbolic function, in that the rate constant of “spreading” of the TEC population at sequential template positions decreases with time as the template length increases. These differences are most readily apparent when we compare early and late template positions, such as (i + 1) and (i + 19), corresponding to template positions one basepair after the first addition event and one basepair before the end of the (defined and idealized) template (Fig. 2 B). The fraction of total TECs at template position (i + 19) at any given time is significantly reduced relative to the fraction at (i + 1). However, the total time over which one or more TEC(s) is(are) located at position (i + 1), relative to one or more having arrived at position (i + 19), increases from 0.5 s to >1 s.
These simulations can partially explain the variability in apparent forward rate constants observed in single-molecule experiments. For example, if each nucleotide addition event between template positions (i) and (i + 19) occurs within the shortest possible time, the average transcription rate for this TEC would be ∼40 nt s−1, corresponding to the position (at 0.5 s) of the leading edge of the (i + 19) occupancy curve. Conversely, if these events all occurred over relatively long timescales, the average apparent transcription rate for this TEC molecule would appear to be ∼10 nt s−1, as seen for the trailing edge of the (i + 19) curve at 1.5 s (Fig. 2 B). The stochastic effects that create leading and trailing edges of the bulk TEC population have also been observed, particularly for longer templates, in the sensitive real-time SPR data presented elsewhere (8,26).
This difference between the leading and trailing edges of the TEC population at this forward rate constant (which might be incorrectly interpreted as suggesting that the slowest and fastest TECs have different transcription rates) would increase as the number of chain extension events is increased, suggesting that the distribution of TEC velocities sometimes observed in single-molecule experiments may not reflect chemical “microheterogeneity” of the individual TEC complexes (33,35,37), but instead may have been due, at least in part, to the stochastic nature of multiple sequential nucleotide addition events over many template positions. However, as noted elsewhere, this random aspect of nucleotide addition cannot account for the entire range of heterogeneous elongation rates observed (33). In bulk-solution experiments, TECs that lie at the edge of the possible distribution for transcription events do not provide detectable experimental signals, and therefore these events are only “seen” in experiments with high resolution or in simulations such as those presented here.
Adding a “generic” pause to RNA transcription elongation models
One of the basic assumptions made in setting up the simple transcription models described above is that off-pathway alternatives to the elongation-competent state (such as paused states) are specifically excluded. Therefore, such “simple” models cannot be used to describe transcription on a real template, which invariably contain pause signals. We therefore developed a transcription “module” for our overall kinetic scheme that includes such off-pathway states. This permits us to add a paused transcription complex (P) at template position (i + x), where x is less than n, to the basic transcription model described above (see Fig. S2). Although, as discussed elsewhere in this article, three distinct types of long pauses have been described in other studies, this simple model makes no distinction between these pause types. Two new equations were added to the coupled equations above to permit inclusion of such pauses in the model:
| (6) |
| (7) |
Here P denotes the fraction of TECs in the paused state, while kpause and kPE are the rate constants for the movement of the TEC into and out of this alternative state. In Eq. 4, j now represents each template position located upstream (between positions (i + 1) and (i + x − 1)) and downstream (between positions (i + x + 1) and (i + n − 1)) of the pause at template position (i + x). For this simulation the pause was positioned at template site x = 10 (corresponding to TEC(i + 10)), with the rate constants for entry into this position and state (kpause), and exit from this position and state (kPE), taken as 10 and 0.01 s−1, respectively. This corresponds to a relatively weak pause compared to those easily detected in bulk-solution experiments on natural templates. As before, the run-off position was set at n = 20, corresponding to (TECi + 20 in Fig. 2 A), with all TECs initially located at template position (i) and with the corresponding forward and reverse reaction rate constants set at 20 and 0.0001 s−1, as before.
The shapes of the curves describing the arrival of the TECs at run-off template position (i + 20) (Figs. 2 A and 3 A) as a function of time are directly dependent on the rate constants of the transcription events that occur at all of the positions that precede position i + 20 on both the pause- and nonpause-containing templates (Fig. 3 B). Due to the stochastic nature of the movement of the TECs, the arrival of these complexes at the run-off position in the model that includes a pause begins at the same time as in the simple model, because, of course, a fraction of the TECs do not enter the paused state. However, because other TECs do pause, the run-off position is populated at a slower rate, and the final fraction of TECs in this state at the end of the simulation (t = 2–3 s) is smaller than that observed for the run-off band in the simple model. This difference represents the sum of the fractions of the total TEC population that did not pause and those that did pause and then escaped slowly at the rate constant for pause exit (kPE), before completing transcription of the template. As expected, when the simulation was run for 500 s, all the TECs reached the run-off position after escaping from the paused state.
Figure 3.
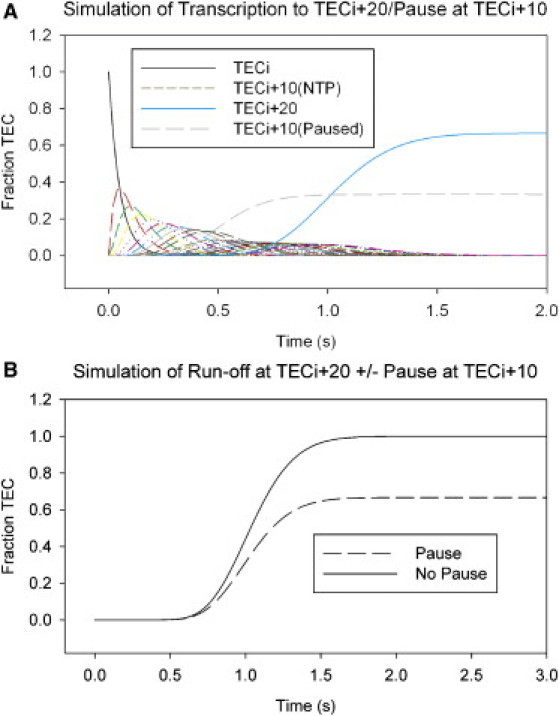
Addition of a paused state to the model for transcription elongation. (A) Simulation of TEC movement from template position (i) to position (i + x), where the TEC may enter a paused state (Fig. S2), to position (i + n) (x = 10 and n = 20 for this simulation), under standard conditions as described for Fig. 1B above, with values for kpausex and kPEx of 10 and 0.1 nt s−1, respectively. (Curves) Fraction of total TECs present at each sequential template position with time, beginning with template position (i) (black curve) and ending at position (i + 20) (light-blue curve), including the fraction of total TECs in the alternative paused state (dashed gray curve). (B) Comparison of TEC entry into template position (i + 19) in simulations with and without a paused alternative state at position (i + x) (dashed and solid curves, respectively), during the time-course of the simulation.
The fraction of TECs that enter the paused state at template position (i + 10) increases rapidly to its peak value and is largely defined by the rate constant kpause that relates to the “efficiency” of the pause (Fig. 3 A) (4,38). In this simulation, the maximum fraction of TECs that are present in the paused state at any one time is 0.35 (Fig. 3 A). The paused TECs then slowly decay (with rate constant kPE) into an elongation-competent state at a rate that is related to the pause half-life by ln(2/kPE) (4), equivalent to ∼5 s in this simulation (Fig. 3 A). Addition of this simple pause also accelerates the previously observed spreading of the curves that represent the entry into, and exit from, successive template positions downstream of this pause site (Fig. 3 A). Although strong pause signals reconcentrate the TECs at the pause position, producing strong bands in bulk-solution gel assays, the above result shows that in addition these signals act to further spread the average population of TECs across the template DNA over time, compared to the spreading on the same template without a pause. This is due to the rate constant of pause escape being significantly slower than the elongation rate constant (Fig. 3 A), consistent with pause escape rates seen in single-molecule and stopped-flow experiments (24,35).
A kinetic model for RNA transcription that includes both elongation and termination
In addition to pausing and related “reversible” events in transcript elongation, termination of RNA elongation represents an important alternative pathway in gene expression and thus an irreversible termination process must also be included in kinetic schemes that seek to describe elongation kinetics in realistic terms. In addition, termination-antitermination systems in bacteria add an effective layer of regulatory response to environmental signals, while termination in all organisms prevents interference with the expression of downstream genes or operons by TECs that would otherwise transcribe-through from upstream promoters. Pausing has previously been found to be an integral event in the transcription termination process, including termination at the intrinsic terminators of prokaryotes (39,40). Hence, the simple kinetic scheme outlined above to describe pausing during transcription can easily be extended to incorporate termination and antitermination processes by defining a “terminated state” (Fig. 4 A). To this end, Eq. 7 was altered to yield Eqs. 8 and 9, which include terminated state T, with krelease designating the rate constant for entry into this state. Because termination is irreversible, there is no rate constant for the reverse reaction:
| (8) |
| (9) |
This total kinetic scheme was used to simulate transcription elongation, pausing, and termination, with the rate constant for termination and release of TECs from the DNA template (krelease) set at 1 s−1, consistent with data from previous work (8,40–44). Under the standard conditions described above for the simple transcription model, the run-off position was set at n = 20, corresponding to TEC(i + 20) in Fig. 4 B, with all TECs assumed to be at template position (i) at time zero, and the forward and reverse reaction rate constants were left unchanged at 20 and 0.0001 s−1, respectively.
Figure 4.
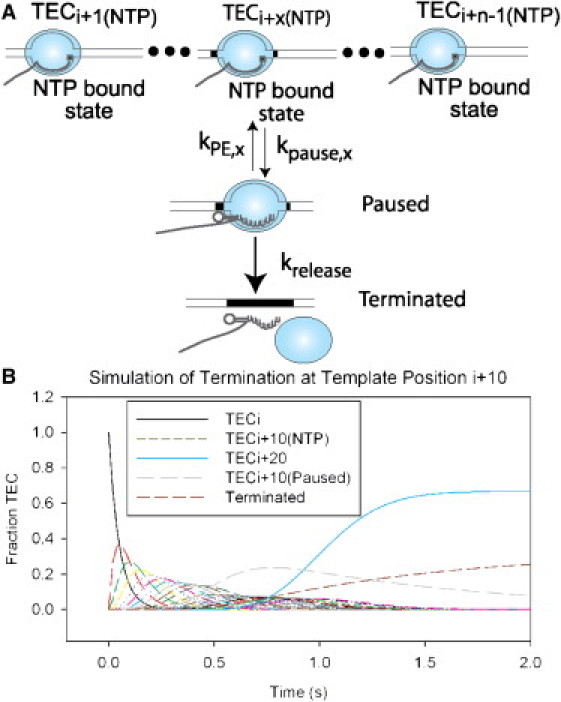
Addition of a terminated alternative state to the model for transcription elongation. (A) Depiction of a model for transcript elongation by a TEC over many template positions (as for Fig. 1A above), excepting RNAP (light-blue oval), with the addition of a potential termination event after the off-pathway paused alternative state. TECs in the paused state at (i + x) may also irreversibly enter a terminated state with rate constant, krelease. An intrinsic terminator, represented by a hairpin in the nascent RNA immediately upstream of a weak RNA/DNA hybrid, is also shown. (B) Simulation of TEC movement across multiple template positions through position (i + x), where the TEC may enter a paused state and potentially undergo termination, to position (i + n) (x = 10 and n = 20 for this simulation) under standard conditions (see Fig. 1B above), with a value for krelease of 1 nt s−1. Sequential curves represent the fraction of total TECs at each template position with time, beginning with template position (i) (black curve) and ending at position (i + 20) (light-blue curve). The fraction of the total TECs present in alternative paused or terminated states is also shown (dashed gray and black curves, respectively).
The termination position was set at x = 10, corresponding to TEC(i + 10), with rate constants of 10 and 0.01 s−1, respectively, for entry into (kpause) and exit from (kPE) the pretermination paused state as described for the transcription model above, which includes a reversible defined pause. This simulation results in a termination efficiency of ∼0.3. This value is largely dependent on the efficiency of pause entry, because the rate constant of release at the terminator is significantly faster than the rate constant of pause escape (Fig. 5). This is supported by simulations in which the rate constant for kpause was varied from 10 to 50 s−1, whereas those for kPE and krelease were held at 0.01 and 1 s−1, respectively, resulting in significant alteration in the fraction of TECs that terminate (Fig. 5 A). Conversely, altering kPE while holding kpause and krelease at constant values of 10 and 1 s−1, respectively, did not greatly affect the terminated fraction (Fig. S3). Increasing the rate constant for release to >1 s−1 also altered the fraction of TECs terminated, particularly for situations where the pause signal was efficient (rate constants of 30 s−1 or greater; see Fig. 5 B). Thus, as expected, a TEC at a termination position will either undergo termination or continue elongation in these simulations, consistent with what is seen in single-molecule experiments (45).
Figure 5.
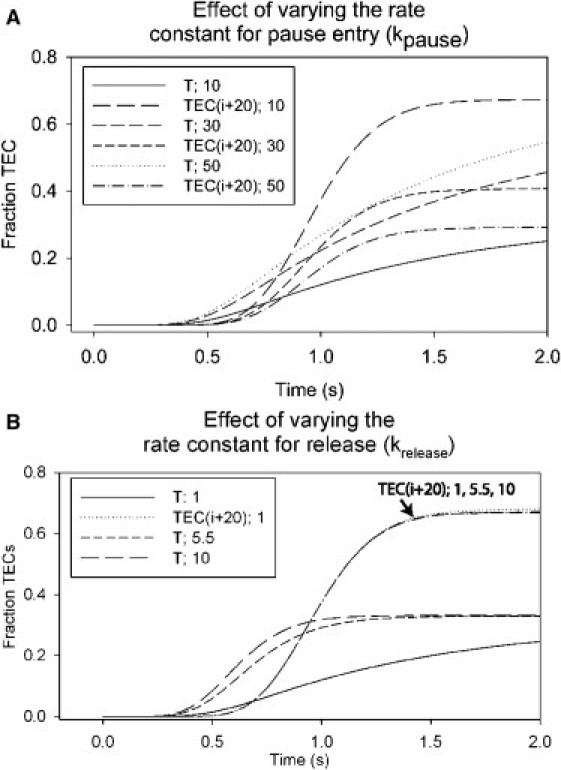
Effect on termination efficiency of kpause and kPE. The fraction of total TECs terminated (T) or run-off (TEC(i + 20)), when the rate constants for pause entry (A; kpause) or release (B; krelease) are varied. Units for the rate constants in the legend are s−1. When not varied kpause was set to 30 s−1 (B), while kPE and krelease were maintained at 0.01 and 1 s−1, respectively.
Adding kinetic terms to describe “stall escape”
Kinetic aspects of transcript elongation are typically studied using TECs that have been initially “stalled” by the absence of the next template-required NTP. Such states are typically created by assembling a nucleic acid scaffold consisting of the transcription bubble and the RNA-DNA hybrid, described above, or by initiation of transcription at the promoter of a particular template and elongation in the presence of three NTPs, until a position is reached where the missing NTP is required. A one-step or multistep nucleotide addition (elongation) reaction is initiated at a defined time by adding a defined concentration of the next required NTP, or by adding all four NTPs together. However, we note that TECs stalled in either of these ways also do not form a uniform synchronized population, because they may enter into paused or arrested alternatives to the elongation-competent state at the NTP-deprived template position ((22,46) and Fig. 6). These include various backtracked positions, which can decay into arrested states, along with the pre- and posttranslocated positions (see the Supporting Material and the companion article (26)).
Figure 6.
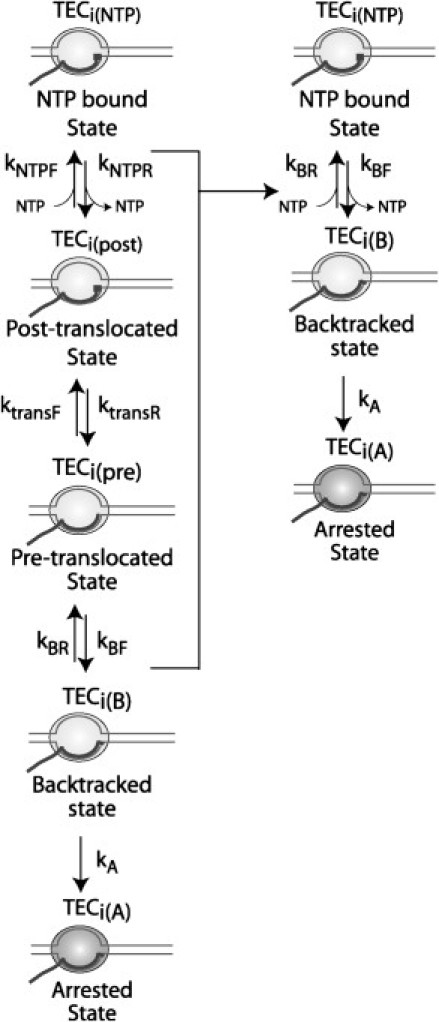
Model describing the alternative states that occur for TECs stalled in the absence of the next templated NTP. Schematic representations are as in Fig. S1, Fig. S2, and Fig. S3, with the addition of an empty NTP binding site in the posttranslocated state (open square). TECs may enter three or more states at stall positions (22,46), including arrested (A; shaded oval); backtracked by one template position (B; extension of solid line); pretranslocated (pre; no square) and posttranslocated (post; open square) states, respectively. Rate constants for movement of TECs into, or out of, these states are denoted with subscripts F and R, respectively. Arrested states cannot undergo nucleotide addition without transcription cofactors and hence only one rate constant (kA) was used to describe movement into this state. Backtracked TECs are considered as paused states with entry and exit rate constants kBF and kBR, respectively. TECs oscillate rapidly between the pre- and posttranslocated states, with rate constants ktrans,F and ktrans,R. Binding of the next templated NTP (solid square) with rate constant kNTP,F traps the TEC in the posttranslocated NTP bound state, which may then undergo nucleotide addition to the next template position. Because the rate-limiting steps here comprise the entry and exit pathways into the backtracked state, the model was simplified by combining the pre- and posttranslocated states with the backtracked state and by lumping the rate constants for these reactions into a single rate constant kBR.
This information was used to design an overall kinetic scheme that can describe the various the events that can occur during elongation (Fig. 6). For simplicity, and consistent with experiments on numerous templates, the model includes only one backtracked state, which can decay into an arrested state with rate constant kA. Because this is an irreversible reaction in the absence of Gre factors, the model does not include the reverse rate constant. Upon NTP addition, this backtracked state returns to the NTP-bound active state via sequential diffusion-driven translocation events through the intervening pre- and posttranslocated states and then NTP binding, with rate constants kBR, ktrans,F, and kNTP,F, respectively (Fig. 6). Escape from the stall position by movement of TECs through these states and into the active NTP-bound state and finally—by nucleotide addition—to the next template position, can be described by the following differential equations:
| (10) |
| (11) |
| (12) |
Here TEC(i)B represents a state that has backtracked by one position and TEC(i)A represents the arrested state at this template position. The rate constants for entry into, and exit from, the backtracked state are denoted kBF and kBR, respectively, whereas kA represents the rate constant for decay into the arrested state.
A kinetic model (or module) of this type can easily be added to the previous models to create a comprehensive (and custom-designed) model that describes all of the events that are known to occur between the resumption of transcription from the stall position to the appearance of the terminated and run-off products. In the accompanying article (26), we use this model to fit “real” data obtained on defined DNA templates by bulk RNA gel electrophoresis and surface plasmon resonance transcription assays.
Discussion
In this study we set out to develop a set of kinetic elements that could be combined to provide molecular models of appropriate complexity to describe (and simulate) the steps of transcription (including alternative pathways) and related repeating cyclic processes involved in gene expression of any given template. Two types of mechanistic models have previously been proposed to describe the central events of transcript elongation. In models of the Brownian ratchet type, the energy provided by thermal fluctuations causes the TECs to oscillate between their pre- and their posttranslocated states (13,33,46,47). The incoming templated NTP then traps these oscillating TECs in the posttranslocated state, leading to nucleotide addition at the 3′ end of the nascent RNA and repetition of the cycle. In contrast, power-stroke models suggest that the net free energy produced by phosphodiester bond transfer during the nucleotide addition cycle drives the TEC forward, inducing one or more conformational changes in the active site of the polymerase and also driving the translocation of the RNAP along the template strand. The kinetic approaches presented here make no distinction between these two types of elongation models, although the observation that TECs can accumulate in the pretranslocated state in the absence of the next templated NTP does provide some support for models of the Brownian ratchet type (13,16,33,34,46,48).
Our kinetic “modules” (essentially introducing additional elements into a purely elongation model to allow for pausing, termination, back-tracking, etc.) are based on the chemical master equation and can be used to fit transcription elongation, pausing, and termination data obtained both from traditional bulk-solution electrophoresis assays and real-time SPR experiments (26). This modular approach can provide a relatively complete mechanistic picture of the steps that are involved in the various processes of transcript elongation.
Finally, our results and analysis can also be used to reveal how these kinetic parameters interact in controlling the overall process, and thus can be used to help define rate-limiting steps and how they shift with changes in reaction conditions and parameters.
Clearly this modular approach can be customized to simulate different events, such as pausing or termination that might occur during transcription elongation. Indeed, in the companion article we have developed such a customized model to fit transcription elongation data from a real template containing the tR2 terminator (26). We note, as in the kinetic modeling performed in our previous study (8), that we have assumed in applying this modular modeling scheme to simulate transcription that the rates of hairpin folding and nucleic scaffold rearrangement during transcript elongation are fast relative to elongation. Although this assumption can easily be relaxed if necessary, making it reduces the termination switch into a “race” between the elongation and the pause entry parameters. We note also that this type of modular kinetic scheme can be expanded to account for the activity of termination factors, such as the ρ-helicase in prokaryotes, by the addition of a separate module describing the binding of these enzymes to, and translocation along, the nascent RNA (1,7).
In summary, in this article we have developed a series of kinetic models of increasing complexity that can be assembled into a custom comprehensive model that can be used to successfully simulate experimental transcription data from specific templates under defined conditions. These models can, in principle, easily be extended to apply to other regulatory events that involve other forms of kinetic competition between alternative reaction pathways. Thus essentially the same master equation framework, but containing different or additional terms, can be used for modeling the template-directed elongation process in DNA replication by including terms for initiation, base misincorporation, and termination; for template-directed DNA repair by including terms for replication restart and error removal; for RNA translation (i.e., template-directed protein synthesis) by including terms dealing with mRNA binding to and translocation on ribosomes and the regulatory effects of translation factors; and for many other “n-step” processes (27).
Acknowledgments
This research was supported in part by National Institutes of Health grant R01-GM-15792 (to P.H.v.H.), by the Marie Curie Incoming International Fellowship (to S.J.G.), and by Biotechnology and Biosciences Research Council (UK) Institute Strategic Program Grants to the John Innes Centre. P.H.v.H. is an American Cancer Society Research Professor of Chemistry.
Footnotes
Sandra J. Greive's present address is Department of Biochemistry, University of Cambridge, Cambridge, UK.
Jim P. Goodarzi's present address is Pulmonary and Critical Care Medicine, Oregon Health and Science University, Portland, OR.
Supporting Material
References
- 1.Greive S.J., von Hippel P.H. Thinking quantitatively about transcriptional regulation. Nat. Rev. Mol. Cell Biol. 2005;6:221–232. doi: 10.1038/nrm1588. [DOI] [PubMed] [Google Scholar]
- 2.Borukhov S., Nudler E. RNA polymerase: the vehicle of transcription. Trends Microbiol. 2008;16:126–134. doi: 10.1016/j.tim.2007.12.006. [DOI] [PubMed] [Google Scholar]
- 3.Proshkin S., Rahmouni A.R., Nudler E. Cooperation between translating ribosomes and RNA polymerase in transcription elongation. Science. 2010;328:504–508. doi: 10.1126/science.1184939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Landick R. The regulatory roles and mechanism of transcriptional pausing. Biochem. Soc. Trans. 2006;34:1062–1066. doi: 10.1042/BST0341062. [DOI] [PubMed] [Google Scholar]
- 5.Sydow J.F., Brueckner F., Cramer P. Structural basis of transcription: mismatch-specific fidelity mechanisms and paused RNA polymerase II with frayed RNA. Mol. Cell. 2009;34:710–721. doi: 10.1016/j.molcel.2009.06.002. [DOI] [PubMed] [Google Scholar]
- 6.Hodges C., Bintu L., Bustamante C. Nucleosomal fluctuations govern the transcription dynamics of RNA polymerase II. Science. 2009;325:626–628. doi: 10.1126/science.1172926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Rosonina E., Kaneko S., Manley J.L. Terminating the transcript: breaking up is hard to do. Genes Dev. 2006;20:1050–1056. doi: 10.1101/gad.1431606. [DOI] [PubMed] [Google Scholar]
- 8.Greive S.J., Weitzel S.E., von Hippel P.H. Monitoring RNA transcription in real time by using surface plasmon resonance. Proc. Natl. Acad. Sci. USA. 2008;105:3315–3320. doi: 10.1073/pnas.0712074105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Epshtein V., Cardinale C.J., Nudler E. An allosteric path to transcription termination. Mol. Cell. 2007;28:991–1001. doi: 10.1016/j.molcel.2007.10.011. [DOI] [PubMed] [Google Scholar]
- 10.Datta K., von Hippel P.H. Direct spectroscopic study of reconstituted transcription complexes reveals that intrinsic termination is driven primarily by thermodynamic destabilization of the nucleic acid framework. J. Biol. Chem. 2008;283:3537–3549. doi: 10.1074/jbc.M707998200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.von Hippel P.H., Rees W.A., Wilson K.S. Specificity mechanisms in the control of transcription. Biophys. Chem. 1996;59:231–246. doi: 10.1016/0301-4622(96)00006-3. [DOI] [PubMed] [Google Scholar]
- 12.Bai L., Shundrovsky A., Wang M.D. Sequence-dependent kinetic model for transcription elongation by RNA polymerase. J. Mol. Biol. 2004;344:335–349. doi: 10.1016/j.jmb.2004.08.107. [DOI] [PubMed] [Google Scholar]
- 13.Tadigotla V.R., O Maoiléidigh D., Ruckenstein A.E. Thermodynamic and kinetic modeling of transcriptional pausing. Proc. Natl. Acad. Sci. USA. 2006;103:4439–4444. doi: 10.1073/pnas.0600508103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Xie P. A dynamic model for transcription elongation and sequence-dependent short pauses by RNA polymerase. Biosystems. 2008;93:199–210. doi: 10.1016/j.biosystems.2008.04.013. [DOI] [PubMed] [Google Scholar]
- 15.Xie P. Dynamics of backtracking long pauses of RNA polymerase. Biochim. Biophys. Acta. 2009;1789:212–219. doi: 10.1016/j.bbagrm.2008.11.005. [DOI] [PubMed] [Google Scholar]
- 16.Woo H.J. Analytical theory of the nonequilibrium spatial distribution of RNA polymerase translocations. Phys. Rev. E. 2006;74:011907. doi: 10.1103/PhysRevE.74.011907. [DOI] [PubMed] [Google Scholar]
- 17.Ribeiro A.S., Smolander O.P., Yli-Harja O. Delayed stochastic model of transcription at the single nucleotide level. J. Comput. Biol. 2009;16:539–553. doi: 10.1089/cmb.2008.0153. [DOI] [PubMed] [Google Scholar]
- 18.Yamada Y.R., Peskin C.S. A look-ahead model for the elongation dynamics of transcription. Biophys. J. 2009;96:3015–3031. doi: 10.1016/j.bpj.2008.12.3955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Voliotis M., Cohen N., Liverpool T.B. Fluctuations, pauses, and backtracking in DNA transcription. Biophys. J. 2008;94:334–348. doi: 10.1529/biophysj.107.105767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Voliotis M., Cohen N., Liverpool T.B. Backtracking and proofreading in DNA transcription. Phys. Rev. Lett. 2009;102:258101. doi: 10.1103/PhysRevLett.102.258101. [DOI] [PubMed] [Google Scholar]
- 21.Holmes S.F., Santangelo T.J., Erie D.A. Kinetic investigation of Escherichia coli RNA polymerase mutants that influence nucleotide discrimination and transcription fidelity. J. Biol. Chem. 2006;281:18677–18683. doi: 10.1074/jbc.M600543200. [DOI] [PubMed] [Google Scholar]
- 22.Toulokhonov I., Zhang J., Landick R. A central role of the RNA polymerase trigger loop in active-site rearrangement during transcriptional pausing. Mol. Cell. 2007;27:406–419. doi: 10.1016/j.molcel.2007.06.008. [DOI] [PubMed] [Google Scholar]
- 23.Toulokhonov I., Landick R. The role of the lid element in transcription by E. coli RNA polymerase. J. Mol. Biol. 2006;361:644–658. doi: 10.1016/j.jmb.2006.06.071. [DOI] [PubMed] [Google Scholar]
- 24.Kireeva M.L., Kashlev M. Mechanism of sequence-specific pausing of bacterial RNA polymerase. Proc. Natl. Acad. Sci. USA. 2009;106:8900–8905. doi: 10.1073/pnas.0900407106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Johnson R.S., Strausbauch M., Register J.K. Rapid kinetic analysis of transcription elongation by Escherichia coli RNA polymerase. J. Mol. Biol. 2008;381:1106–1113. doi: 10.1016/j.jmb.2008.06.089. [DOI] [PubMed] [Google Scholar]
- 26.Greive S.J., Dyer B.A., Hippel P.H.v. Fitting experimental transcription data with a comprehensive template-dependent modular kinetic model. Biophys. J. 2011;101:1166–1174. doi: 10.1016/j.bpj.2011.07.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lucius A.L., Maluf N.K., Lohman T.M. General methods for analysis of sequential “n-step” kinetic mechanisms: application to single turnover kinetics of helicase-catalyzed DNA unwinding. Biophys. J. 2003;85:2224–2239. doi: 10.1016/s0006-3495(03)74648-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Uptain S.M., Kane C.M., Chamberlin M.J. Basic mechanisms of transcript elongation and its regulation. Annu. Rev. Biochem. 1997;66:117–172. doi: 10.1146/annurev.biochem.66.1.117. [DOI] [PubMed] [Google Scholar]
- 29.Rees W.A., Weitzel S.E., von Hippel P.H. Regulation of the elongation-termination decision at intrinsic terminators by antitermination protein N of phage-λ. J. Mol. Biol. 1997;273:797–813. doi: 10.1006/jmbi.1997.1327. [DOI] [PubMed] [Google Scholar]
- 30.Chamberlin M.J., Nierman W.C., Neff N. A quantitative assay for bacterial RNA polymerases. J. Biol. Chem. 1979;254:10061–10069. [PubMed] [Google Scholar]
- 31.Kassavetis G.A., Chamberlin M.J. Pausing and termination of transcription within the early region of bacteriophage T7 DNA in vitro. J. Biol. Chem. 1981;256:2777–2786. [PubMed] [Google Scholar]
- 32.Schafer D.A., Gelles J., Landick R. Transcription by single molecules of RNA polymerase observed by light microscopy. Nature. 1991;352:444–448. doi: 10.1038/352444a0. [DOI] [PubMed] [Google Scholar]
- 33.Roussel M.R., Zhu R. Stochastic kinetics description of a simple transcription model. Bull. Math. Biol. 2006;68:1681–1713. doi: 10.1007/s11538-005-9048-6. [DOI] [PubMed] [Google Scholar]
- 34.Bai L., Fulbright R.M., Wang M.D. Mechanochemical kinetics of transcription elongation. Phys. Rev. Lett. 2007;98:068103. doi: 10.1103/PhysRevLett.98.068103. [DOI] [PubMed] [Google Scholar]
- 35.Herbert K.M., La Porta A., Block S.M. Sequence-resolved detection of pausing by single RNA polymerase molecules. Cell. 2006;125:1083–1094. doi: 10.1016/j.cell.2006.04.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Neuman K.C., Abbondanzieri E.A., Block S.M. Ubiquitous transcriptional pausing is independent of RNA polymerase backtracking. Cell. 2003;115:437–447. doi: 10.1016/s0092-8674(03)00845-6. [DOI] [PubMed] [Google Scholar]
- 37.von Hippel P.H. Transcriptional pausing caught in the act. Cell. 2006;125:1027–1028. doi: 10.1016/j.cell.2006.06.006. [DOI] [PubMed] [Google Scholar]
- 38.Hauser C.A., Sharp J.A., Hatfield G.W. Pausing of RNA polymerase during in vitro transcription through the ilvB and ilvGEDA attenuator regions of Escherichia coli K12. J. Biol. Chem. 1985;260:1765–1770. [PubMed] [Google Scholar]
- 39.Greive S.J., Lins A.F., von Hippel P.H. Assembly of an RNA-protein complex. Binding of NusB and NusE (S10) proteins to boxA RNA nucleates the formation of the antitermination complex involved in controlling rRNA transcription in Escherichia coli. J. Biol. Chem. 2005;280:36397–36408. doi: 10.1074/jbc.M507146200. [DOI] [PubMed] [Google Scholar]
- 40.Gusarov I., Nudler E. The mechanism of intrinsic transcription termination. Mol. Cell. 1999;3:495–504. doi: 10.1016/s1097-2765(00)80477-3. [DOI] [PubMed] [Google Scholar]
- 41.Wilson K.S., von Hippel P.H. Transcription termination at intrinsic terminators: the role of the RNA hairpin. Proc. Natl. Acad. Sci. USA. 1995;92:8793–8797. doi: 10.1073/pnas.92.19.8793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Yin H., Artsimovitch I., Gelles J. Nonequilibrium mechanism of transcription termination from observations of single RNA polymerase molecules. Proc. Natl. Acad. Sci. USA. 1999;96:13124–13129. doi: 10.1073/pnas.96.23.13124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kashlev M., Komissarova N. Transcription termination: primary intermediates and secondary adducts. J. Biol. Chem. 2002;277:14501–14508. doi: 10.1074/jbc.M200215200. [DOI] [PubMed] [Google Scholar]
- 44.Arndt K.M., Chamberlin M.J. Transcription termination in Escherichia coli. Measurement of the rate of enzyme release from ρ-independent terminators. J. Mol. Biol. 1988;202:271–285. doi: 10.1016/0022-2836(88)90457-3. [DOI] [PubMed] [Google Scholar]
- 45.Larson M.H., Greenleaf W.J., Block S.M. Applied force reveals mechanistic and energetic details of transcription termination. Cell. 2008;132:971–982. doi: 10.1016/j.cell.2008.01.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Bar-Nahum G., Nudler E. Isolation and characterization of σ(70)-retaining transcription elongation complexes from Escherichia coli. Cell. 2001;106:443–451. doi: 10.1016/s0092-8674(01)00461-5. [DOI] [PubMed] [Google Scholar]
- 47.Svetlov V., Nudler E. Macromolecular micromovements: how RNA polymerase translocates. Curr. Opin. Struct. Biol. 2009;19:701–707. doi: 10.1016/j.sbi.2009.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Guajardo R., Sousa R. A model for the mechanism of polymerase translocation. J. Mol. Biol. 1997;265:8–19. doi: 10.1006/jmbi.1996.0707. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


