The Binding Process of a Nonspecific Enzyme with DNA

Abstract

Protein-DNA recognition of a nonspecific complex is modeled to understand the nature of the transient encounter states. We consider the structural and energetic features and the role of water in the DNA grooves in the process of protein-DNA recognition. Here we have used the nuclease domain of colicin E7 (N-ColE7) from Escherichia coli in complex with a 12-bp DNA duplex as the model system to consider how a protein approaches, encounters, and associates with DNA. Multiscale simulation studies using Brownian dynamics and molecular-dynamics simulations were performed to provide the binding process on multiple length- and timescales. We define the encounter states and identified the spatial and orientational aspects. For the molecular length-scales, we used molecular-dynamics simulations. Several intermediate binding states were found, which have different positions and orientations of protein around DNA including major and minor groove orientations. The results show that the contact number and the hydrated interfacial area are measures that facilitate better understanding of sequence-independent protein-DNA binding landscapes and pathways.

Introduction

The process of a protein-DNA complex formation comprises at least two major steps. Upon meeting a partner, first an encounter complex is formed, which then either proceeds toward the final complex or dissociates instead. During this formation of the encounter complex, a protein reaches a random nonspecific location on DNA by three-dimensional diffusion, and then uses intramolecular translocation processes involving one-dimensional sliding along the DNA, hopping, and/or intersegmental transfer. This process can be described as a facilitated diffusion mechanism (1–6) and mainly is steered by electrostatic and steric interactions nonspecifically. The formation of the final specific complex is governed by specific hydrogen bonds and van der Waals (vdW) contacts, where water molecules and ions may be released from the interface of the final complex. In many cases, global or local conformational changes of protein and DNA occur concomitantly.

Although information characterizing final specific complexes comes from conventional crystallography and NMR spectroscopy, little is known about the nature of the encounter complexes due to their weaker and less ordered association. There are a few crystal structures of nonspecific proteins in complex with DNA that have been resolved, which include Vvn from Vibrio vulnificus complexed with an 8-bp and a 12-bp DNA (7,8), the nuclease domain of colicin E7 (N-ColE7) from Escherichia coli with 8, 12, and 18 bp of DNA (8–11), and the nuclease domain of colicin E9 (N-ColE9) from E. coli with 8 bp of DNA (12). These structures have provided the structural basis for better understanding of the nonspecific and consequently, specific protein-DNA association.

Recently, a few single-molecule experiments (13–15) have illustrated protein translocation along DNA and estimated one-dimensional diffusion constants for proteins sliding/hopping along double-stranded DNA. In addition, paramagnetic relaxation enhancement NMR (16–18) has detected the transient intermediate states in many macromolecular binding processes. In the case of HoxD9 homeodomain protein binding to DNA, encounter complexes were detected in which the protein is bound to various sites along the DNA. The binding modes observed during the target searching shared similarity to that in the specific complex. Both intramolecular sliding and intermolecular translocation were seen to contribute to the recognition events before specific binding.

Here we take a familiar multiscale simulation approach to these questions (19). Because the process of formation of the encounter complex is diffusion-limited, it can be modeled by Brownian dynamics (BD) simulations. The BD method has been successfully applied to study protein-protein association in a variety of cases (20–24). In most BD simulations, proteins are treated as simple rigid bodies moved by Brownian forces. The long-range electrostatic force and intermediate ranged solvation effects are considered as mean field effects, while short-range interactions such as vdW forces, hydrogen-bonding formation, and salt bridges are only seen at the end when BD is no longer appropriate.

Gabdoulline and Wade (24) previously studied the association rate for six protein-protein pairs with BD. Computed association rates for three of them were in excellent agreement with experimental data, but the other three were overestimated possibly because of the flexibility of the proteins. Camacho et al. (22) utilized the local minimum in the free energy landscape to study the role of shorter-ranged desolvation forces in protein binding kinetics. They found that partial desolvation is not only a major contributor to the free energy but also adds to increases in the diffusion-limited rate for complexes. Spaar and Helms (23) reported a six-dimensional free energy landscape for Barnase-Barstar association on the encounter pathway as well as the association rate. Compared to BD simulations of protein-protein pairs, simulations of protein-nucleic acid association are less well explored (25).

Here we consider the nuclease domain of colicin E7 from E. coli (N-ColE7) in complex with 12 bp of DNA (Fig. 1 A) as a model system to consider how a protein approaches, encounters, and associates with DNA. N-ColE7 is a nonspecific nuclease capable of cleaving phosphodiester bonds at many positions along the DNA (9,10). The active site of N-ColE7 contains an HNH motif which has been identified in hundreds of homing and restriction endonucleases and DNA repair enzymes (26,28). In this motif, the three most conserved histidine and asparagine residues are in the nucleic acid binding and cleavage module. The motif is a ββα-Me finger topology which is composed of two β-strands, one α-helix as well as one metal ion. The structure serves as a scaffold for a catalytic center for hydrolysis. Not only is such a ββα-Me finger found in HNH motif proteins, it is also identified as a common core in the active site of the His-Cys homing endonuclease I-Ppol (27), the endonuclease from bacteria Serratia marcescens (SMNase) (29), the endonuclease Vvn from V. vulnificus (7), phage T4 endonuclease VII (30), and caspase-activated DNase (31). Sharing this similar motif in their active sites is suggestive that those proteins might share the cleaving mechanism and possibly have aspects of the binding mode in common.

Figure 1.

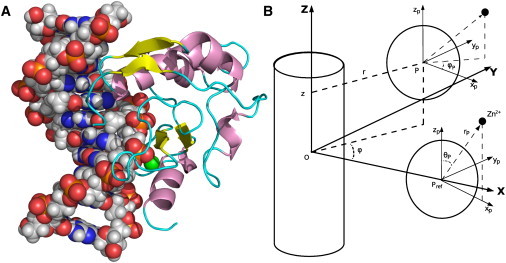
(A) The structure of N-ColE7 in complex with DNA. Zn²⁺ (in green sphere), two β-strands, and one α-helix compose the ββα-Me fold at the active site. (B) Definition of the positional coordinate of the protein (r, z, ϕ) in a cylindrical coordinate system and the orientational coordinate of the protein (r_p, θ_p, ϕ_p) in a spherical coordinate system.

The hydrolysis is metal-ion-dependent. The Mg²⁺ ion is essential to SMNase, I-Ppol, phage T4 endo VII, and Vvn, the transition metal ion Zn²⁺ to N-ColE7 and caspase-activated DNase, and Ni²⁺ or Mg²⁺ to N-ColE9. However, it is still not clear:

• 1.What structural, energetic, and dynamic features guide the enzyme to recognize DNA and
• 2.How the hydration properties of both partners are related to the recognition, association, and function.

In this study, we used a multiscale simulation approach (19) to consider the recognition and complexation of N-ColE7 with a 12-bp DNA. At larger distances, we carried out a swarm of BD simulations to determine the premolecular contact spatial and orientational aspects required for protein association with DNA. This also allowed us to characterize the association pathway based on the free energy landscape. Next, near molecular contact distances we performed a set of molecular dynamics (MD) simulations in explicit water and ions on several model initial condition geometries suggested from the crystallography. The initial model structures for the set of MD trajectories have N-ColE7 and the DNA at some separation with different orientations. The resulting structures and free energies are then analyzed. The use of both BD and MD simulations provides an opportunity for better understanding of sequence-independent protein encountering, searching, and binding with DNA at varying scales of resolution. How DNA is recognized by such proteins may address the mode of DNA interactions for many of the nonspecific nucleases carrying the ββα-Me fold.

Methods

Structures

Both bound and unbound forms of the protein have been structurally studied. The structure of the N-ColE7-DNA complex was taken from the x-ray structure of a mutant N-ColE7-DNA (PDB code: 1ZNS), in which His⁵⁴⁵ in the wide type is mutated to Glu. Crystallographic water molecules were removed before solvation. The residues 443–449, 548–554, and 575–576, not given by the diffraction results, were rebuilt by superimposing the protein partner on the structure of the protein in the absence of substrate (PDB code: 1M08). Similarly, for our study the mutation Glu⁵⁴⁵ was also corrected to the wild-type His⁵⁴⁵. Hydrogen atoms were added, and their positions were optimized by energy minimization with the ESP program (32). Partial atomic charges and atomic radii were assigned from CHARMM27 parameter set (33,34). The protonation states of titratable residues were assigned according to their standard protonation states at pH of 7.0. Histidine was treated as neutral. For H544 and H545, one proton was attached to the ε-nitrogen atom of the imidazole ring, while for H569 and H573, the δ-nitrogen atom was protonated.

Definition of system coordinates

In protein-DNA recognition, mutual translation and rotation occurs. It is necessary to define the system coordinates which take into account the rodlike structure of the DNA and the asymmetric form of the protein. As illustrated in Fig. 1 B, the origin of the coordinates was set at the geometric center of the DNA with the helical axis of the DNA placed along the Z axis. The position of the protein with respect to the DNA was described in a DNA-centric cylindrical coordinate system, in which r is the projection of the center of the protein into the XY-plane. Relative to the crystal structure, z is the displacement of the protein translating along the DNA, and ϕ (in degrees) is the azimuthal angle displacement of the protein. The orientation of the protein was described in a spherical coordinate system, in which r_p is the distance between the center of the protein and the zinc atom at the active site, θ_p is the polar angle, and ϕ_p is the displacement of the azimuthal angle of the orthogonal projection of r_p relative to the crystal reference structure. Such a choice gives the coordinates of the protein with respect to the DNA in the crystal reference structure as (r, z, ϕ, r_p, θ_p, ϕ_p) = (16.7 Å, 0 Å, 0°, 10.6 Å, 152.3°, 0°).

BD simulations

For the BD simulation, we used the software package SDA (35), which was modified to be appropriate for a protein-DNA system and allow a detailed analysis of trajectories. The equation of motion is solved by the Ermak-McCammon algorithm (36).

The intermolecular forces and torques are given by the sum of electrostatic and steric forces. Instead of using the finite difference Poisson-Boltzmann (PB) method (39) to compute the electrostatic potential energy, a set of effective charges for the protein (or DNA) is computed and placed on the electrostatic potential grid of the DNA (protein). The grid is centered on each molecule and has a dimension of 150 × 150 × 150 Å with a spacing size of 1.0 Å. The solvent dielectric constant ε_out is 78.0, and the solute interior dielectric constant ε_in is 4.0. The electrostatic potential grid around protein (DNA) was calculated using the APBS package (40) to solve the full PB equation at the given ionic strength. The effective charges on the protein (DNA) were calculated by the ECM module (58) in the SDA package. A further contribution is computed for the interaction of the effective charges of protein (DNA) with the precomputed desolvation grid (see the Supporting Material) representing the penalty due to the low dielectric of the molecular interior (37).

In the BD simulations, we use mutual translation and rotation diffusion constants (38), so there is no loss of generality by fixing the DNA molecule at the origin. The BD simulations start with the protein randomly placed and oriented at a center-to-center distance of 100 Å. At this distance, the intersolute forces are centrosymmetric. The simulations are terminated when the protein moves outside of a center-to-center distance of 500 Å. The time step is 1.0 ps when r is <50 Å or the absolute value of z is <60 Å, and then increased linearly with a slope of 0.475 ps/Å. This corresponds to an average random displacement of 0.4 Å at small distance and 5.9 Å at long distance (up to 500 Å).

Free energy landscape calculations from the BD trajectory

The free energy landscape calculation is similar to that used by Spaar et al. (23) for protein-protein encounters. The free energy may be approximately computed as

$$\Delta G_{BD}=\Delta G_{ele,BD}-T\Delta S_{BD}=\Delta E_{ele,BD}+\Delta G_{ds,BD}-T\left(\Delta S_{tran,BD}+\Delta S_{rot,BD}\right),$$ (1)

where ΔG_ele,BD is the total effective interaction energy with the electrostatic potential energy component ΔE_ele,BD and the desolvation energy component ΔG_ds,BD. We expect that PV work can be ignored. ΔS_BD is the total configurational entropy loss of protein-DNA encounter, which is the sum of the translational (ΔS_tran,BD) and rotational (ΔS_rot,BD) entropy loss. At each time step of the simulated trajectories, the spatial (r, z, ϕ) and orientational (r_p, θ_p, ϕ_p) coordinates of the protein were obtained. These coordinates were then assigned to a six-dimensional grid, on which minimum total energy, the spatial and orientational occupancy of the protein, and entropy loss were stored. The grid spacing was Δr = 1.0 Å, Δz = 1.0 Å, Δϕ = 2.0°, Δθ_p = 2.0°, and Δϕ_p = 2.0°. The value r_p was fixed because the solutes were considered as rigid bodies for the BD. The entropy loss which depends on the spatial and orientational distributions of the protein can be computed from the distribution by

$$\Delta S=-k_{\text{B}}\sum _{n=1}^N{P}_n\text{ln}{P}_n-k_{\text{B}}\text{ln}N,$$ (2)

where P_n is the probability at bin n, and N is the number of spatial/orientational occupancy bins within the locally accessible volume, V. In the translational entropy calculation, V was defined as a sphere around the spatial occupancy point at (r_i, z_i, ϕ_i) with a radius of 3 Å. The value ΔS_rot,BD was computed with the rotational resolution of θ_p,i ± 3° and ϕ_p,i ± 3°.

MD simulations

To better represent protein-DNA recognition at the shortest distances and timescales, we simulated the association of N-ColE7 with DNA in explicit solvent with molecular dynamics. Six initial condition model structures were considered with the protein at different positions and orientations with respect to the DNA. This ensemble is large enough to give a reasonable picture of the process, but we do not claim that all possibilities are covered. The crystal structure of the protein-DNA complex constitutes our reference structure, and, with the protein moved radially outward from the DNA, was taken as the initial structure of Model I. For the other initial models, the intermolecular zone should contain at least three layers of water. For convenience in the initial model structures, z and θ_p were fixed as in the reference, and ϕ_p was set equal to ϕ. Thus, the active site of the protein started facing the DNA as in the reference structure. In order to choose r and ϕ, we estimated the total electrostatic binding energy in variation of r and ϕ.

The total electrostatic binding energy ΔG_ele,MD was approximated as the sum of the electrostatic potential energy component ΔE_ele,MD and the polar solvation energy component ΔG_p,MD, where the latter was computed by solving the PB equation using the APBS package (40). Fig. S1 in the Supporting Material shows the plot of ΔG_ele,MD dependence with respect to r and ϕ at 0.1 M monovalent salt. For r = 25 Å, two maxima near ϕ = 50° and 180° are identified. The maxima correspond to the configurations, where the negatively charged Asp⁴⁸ from the protein is in close contact with the backbone phosphate atoms of the DNA. In contrast, two energy minima are found at ∼ϕ = 0° and 110°. Three initial models were then constructed with r = 36.5 Å: ϕ = 0° for Model II, ϕ = 50° for Model III, and ϕ = 110° for Model IV, respectively. Model II differs from Model I only in the radial distance r. The values ϕ = 50° and ϕ = 110° are the maximum and minimum observed in the energy, which represent a possible unfavorable and favorable protein approach to DNA. In addition to Models I–IV, two more models were also considered to illustrate the possible influence of orientation of the protein on the binding process. Starting from Model II, Models V and VI have the protein reoriented by ϕ_p = +90° and −90°, respectively. The initial coordinates of the protein with respect to the DNA are listed in Table S1 in the Supporting Material.

Each initial model structure was put into a preequilibrated box of TIP3P water using standard procedures (see Chen et al. (41)). The system contains 9945 water molecules for Model I and ∼20,350 for the other models. A total of 38 Na⁺ and 33 Cl⁻ were added to neutralize the system and set the salt concentration. The simulations were run using the in-house program ESP (32) and the all-atom CHARMM27 parameter set (33,34). Equations of motion were integrated with a 2-fs time step in the microcanonical ensemble (NVE) with periodic boundary conditions. Electrostatic interactions were treated with an Ewald sum using a fast linked-cell algorithm (42). After several steepest-descent energy minimization steps, each system was equilibrated at 300 K for 1.0 ns for all the models. Each trajectory was then continued to 100 ns, and coordinates were saved for analysis at an interval of 0.1 ps.

Binding free energy calculations from MD simulations

An approximate binding free energy was estimated using molecular mechanics/Poisson-Boltzmann surface area methodology (43,44), which has been employed in a variety of applications. The molecular mechanics/Poisson-Boltzmann surface area binding free energy was estimated from the molecular mechanical energy E_MM, the solvation free energy G_sol,MD, and the vibrational, rotational, and translational entropies S_MD, as

$$\Delta G_{tot,MD}=\Delta E_{MM}+\Delta G_{sol,MD}-T\Delta S_{MD}=\Delta E_{\mathrm{int}}+\Delta E_{ele,MD}+\Delta E_{vdw,MD}+\Delta G_{p,MD}+\Delta G_{np,MD}-T\Delta S_{MD},$$ (3)

where ΔE_int is internal binding energy, which is the sum of bond, angle, and dihedral energies. The value ΔE_ele,MD is electrostatic binding energy, and ΔE_vdw,MD is vdW binding energy. The value ΔG_p,MD is the electrostatic solvation binding free energy, computed by solving the full PB equation in the APBS package (40) on the MD structures, and ΔG_np,MD is nonpolar desolvation binding free energy estimated using ΔG_np,MD = gΔSASA + b, where g = 0.23 kJ/Ų, b = 3.85 kJ/mol, and ΔSASA is the buried solvent-accessible surface area. The sum of ΔE_ele,MD and ΔG_p,MD defines the total electrostatic binding energy ΔG_ele,MD. Because ΔE_int will be canceled out in the calculation of the binding energy, the total binding free energy can also be decomposed into

$$\Delta G_{tot,MD}=\Delta G_{ele,MD}+\Delta G_{np,MD}+\Delta E_{vdw,MD}-T\Delta S_{MD}.$$ (4)

The computation of ΔG_ele,MD, ΔE_vdw,MD, and ΔG_p,MD were made at a 100-ps and 50-ps intervals for Model I and Model II, respectively. For the other models, during the first 10-ns trajectory, a 20-ps interval was used; after 10 ns, a 40-ps interval was used due to the nature of the statistical convergence seen. The configurational entropy ΔS_MD is approximated with mass-weighted covariance analysis or quasiharmonic analysis (45,46). The calculation of the entropy is sensitive to the length of the simulation and the position of the sampling window. When a system has a rough energy landscape containing multiple minima, the entropy will change as different regions are explored. So, to reduce convergence problems to some extent, the quasiharmonic calculation was averaged over the intermediate binding states.

Results

BD simulations

We performed BD simulations of N-ColE7-DNA at six different ionic strengths: 0.1, 0.15, 0.2, 0.3, 0.4, and 0.5 M. At each ionic strength a total of 40,000 trajectories were generated and analyzed in order to investigate the nature of the kinetics and the probabilistic paths to the encounter state as a function of salt concentration. The average length of a single trajectory was ∼1.8 μs at 0.1 M ionic strength, although many were far longer.

Fig. 2 displays the free energy landscape with the protein at r = 22.0 Å at 0.1 M salt. Except for the configurations in which vdW overlap occurs (in black), the majority of the configurations are energetically favorable, as expected from the overall charges. Two regions having a local free energy minimum were found near the minor and major grooves.

Figure 2.

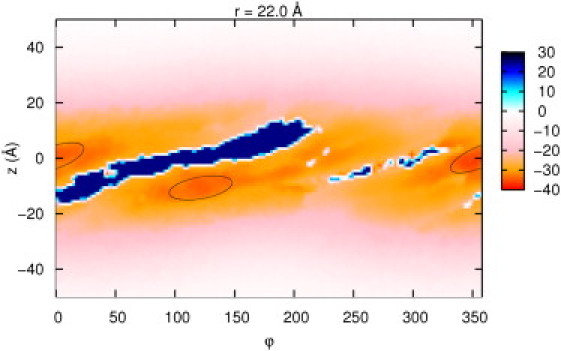
The free energy encounter landscape map generated from the BD simulation at r = 22.0 Å. The energy is in units of kJ/mol. (Circled regions) Energy minima.

Based on the free energy landscape, a reaction path can be obtained defined as the path along the local minimum of the binding free energy. The center-to-center distance d_cc or the minimum contact distance d_min are often used to define the reaction coordinate in the protein-protein or protein-ligand systems. However, as mentioned by Spaar and Helms (23), neither d_cc nor d_min is enough to describe the orientation of the interface of large asymmetric partners. The average distance of all contact pairs d_ave is another choice. Here we identified 50 contact pairs in the crystal structure where the atom-to-atom distance between N-ColE7 and the DNA were within 4.5 Å.

The free energies along reaction paths at different ionic strengths from 0.1 to 0.5 M are shown in Fig. 3. Generally, the variation of the ionic strength has little impact on the overall shape of the free energy curves but quantitative changes are revealed. As expected, the interaction free energy becomes weaker at higher ionic strength. When the distance is ∼80 Å, the interaction free energies are close to 0. As the distance decreases, the interaction free energies become more negative. Along the path or profile, encounter states can be identified which will have a free energy minimum. The first energy minimum is reached near d_ave = 26.0 Å when the protein is around the major groove, denoted as BD_major; we calculate ΔG_BD to be −34.8 ± 0.2 kJ/mol. Desolvation ΔG_ds,BD and −TΔS_BD each make a contribution of 14.9 kJ/mol and 0.8 kJ/mol, respectively, indicating the electrostatic interactions dominate the approach process. The statistical error of the total interaction free energy was estimated by dividing the runs into four different sets.

Figure 3.

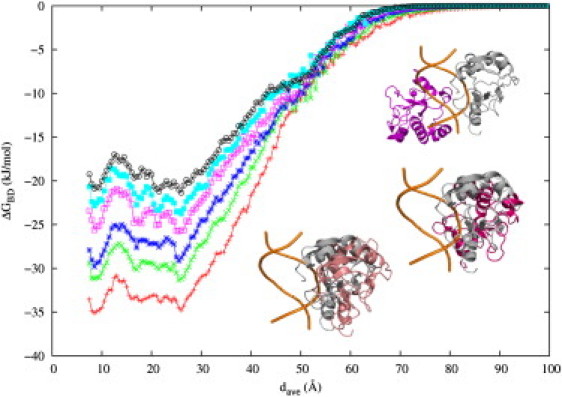
The binding free energy along the reaction path at different ionic strengths: 0.1 M (red), 0.15 M (green), 0.2 M (blue), 0.3 M (magenta), 0.4 M (cyan), and 0.5 M (black). (Inset) Complex configuration at d_ave = 26.0 Å (top), 13.0 Å (middle), and 8.5 Å (bottom). The protein structure in the reference is in gray.

Relative to the reference structure not only may the protein be placed on the opposite side of the DNA and downwards along the helical axis of the DNA by nearly four basepairs, but we also find a large polar angle variation of 130.4°. Nevertheless, the active site of the protein remains facing the DNA, as shown in Fig. 3 (inset). A second free energy minimum was found at d_ave = 8.5 Å, with ΔG_BD = −35.1 kJ/mol, ΔG_ds,BD = 17.9 kJ/mol, and −TΔS_BD = 1.5 kJ/mol. At this state, BD_minor, the position and orientation of the protein with respect to the DNA is similar to the crystallographic reference except that the protein is not as close. In BD_major and BD_minor, the minimum distances between the heavy atoms of the protein and DNA are 4.3 and 3.2 Å, respectively, although the surfaces are atomically rough, do not have perfect steric complementarity, and considerable solvent intervenes. With BD, there is no observation of direct salt bridges, hydrogen bonds, or hydrophobic contacts. The buried solvent-accessible surface area is 169.4 Å² in BD_major and 660.7 Å² in BD_minor. Compared to 2193 Å² in the reference complex, the protein-DNA interfaces of both BD-explored encounter states are nearly fully hydrated.

Between BD_major and BD_minor, an energy barrier of 3.9 ± 0.4 kJ/mol was found at d_ave = 13 Å with ΔG_BD = −31.1 ± 0.4 kJ/mol, ΔG_ds,BD = 13.0 kJ/mol, and −TΔS_BD = 0.5 kJ/mol. The coordinates at the barrier are (24.0 Å, 1.0 Å, 38.0°, 10.6 Å, 155.1°, 11.9°). The electrostatic interactions there are weaker than those in BD_major and BD_minor. Along the reaction coordinate profile within d_ave = 26 Å, several paths along the DNA were observed. The protein translates and orients so that the protein active site remains facing the DNA.

MD simulations

The MD binding free energy for all model systems had stable averages and fluctuations after 25 ns of simulation. Fig. S2 shows that binding free energy without the configurational entropy and Fig. S3, Fig. S4, Fig. S5, Fig. S6, Fig. S7, and Fig. S8 show the time development of the position and orientation of the protein with respect to the DNA. We view the overall binding process as separated into three stages: approach, encounter, and association. During the first stage, it takes N-ColE7 nano- to milliseconds to reach an encounter location from the starting points. At the end of the approach stage, the protein makes molecular-scale encounters with the DNA. This process is dominated by fast fluctuations in structure and reflected in the total electrostatic binding energy ΔG_ele,MD. During the encounter stage, the protein continues to build stronger contacts with the DNA by some sliding movement coupled with rotation around the binding site. The encounter process takes ∼50 ns, in which ΔE_vdw,MD, becomes stronger. The third stage of final association to form the complex is characterized by a relatively stable (but fluctuating) binding free energy and structure. The structure identified at the end of this process may be seen as a Michaelis-like complex, from which the protein might continue to react with the DNA or dissociate.

During the binding process, we analyzed the protein sliding movement along the DNA and whether the protein maintains the active site facing the DNA. Therefore, three components of the protein movement required are sliding along the DNA indicated by change of z, rotation about the DNA monitored by ϕ, and self-rotation on XY-plane indicated by ϕ_P. If the variation of z, Δz, is accompanied by the variation of ϕ, Δϕ, the sliding movement may be helical. If the variation of ϕ and ϕ_P are in phase, the active site can be oriented to face the DNA. For details, see Table S1, which lists the coordinates of the protein at its starting point and end of each binding stage for each MD simulation.

In Model II, the protein starts at (36.5 Å, 0 Å, 0°, 10.6 Å, 152.3°, 0°) with d_min = 13.5 Å. Then it moves to (26.0 Å, −8.7 Å, −18.0°, 11.1 Å, 143.1°, −35.3°) with d_min = 4.4 Å to make the first contacts with the DNA. After experiencing several positional and orientational adjustments, it settles near (20.2 Å, 0.17 Å, −3.7°, 10.9 Å, 125.2°, 1.9°).

In Model III, during the approach process, as the protein slides downward along the DNA by 5.7 Å, it also rotates about the DNA by −38°. This corresponds to a helical slide by ∼1–2 bp. In addition, ϕ_P changes by −42°. Because the decrease of ϕ is accompanied by the decrease of ϕ_P, it indicates that the protein tries to orient the active site to face the DNA during its movement. Similarly, during the encountering process, the protein continues to move downward along the DNA by 8 Å, rotates about the DNA by −55°, and self-rotates by −70°, respectively. The combination of all the movements results in a protein helical slide by ∼3 bp coupled with self-rotation when it approaches and encounters DNA.

In Model IV, as the protein approaches the DNA, it only rotates about the DNA helix by 44°. Then it slides downward by ∼6 Å and reorients by 34.4° to make the encounter with the DNA. So, the protein does not simultaneously undergo slide, rotation, and self-rotation. Similar to Model III, the encounter stage ends up with the protein's active site facing the DNA.

The initial structures of Model V and Model VI differ from that of Model II only in the orientation angle ϕ_P. The protein's orientation is driven by the electrostatic field of the DNA to make the active site face the DNA. From the MD simulation, Δϕ and Δϕ_P from the initial state to the end of the encountering stage are −32° and −54° for Model V and 47° and 51° for Model VI, respectively, indicating that rotation and orientation are coupled, but the active site does not face the DNA. This is because the system is trapped in a local minimum on the landscape.

After the encounter stage, an intermediate binding state is formed. The coordinates of the protein and each component of the binding free energy were averaged over the association stage for all model simulations and listed in Table 1. The contributions from ΔE_ele,MD and ΔG_p,MD are balanced with each other. The differences in the total binding energy can be largely attributed to ΔE_vdw,MD and −TΔS_MD. During the association stage, ΔE_vdw,MD (the drive to make more atomic intermolecular contacts) is the controlling factor in hundreds of kJ/mol.

Table 1.

Binding free energies during the association stage

	Model I	Model II	Model III	Model IV	Model V	Model VI
ΔEele,MD	−5962(170)	−5086(160)	−4897(179)	−5539(160)	−4394(120)	−3825(97)
ΔGp,MD	5942(161)	5064(155)	4894(184)	5528(160)	4377(124)	3840(94)
ΔGnp,MD	−46(2)	−30(3)	−25(4)	−38(4)	−24(3)	−26(2)
ΔEvdw,MD	−341(32)	−220(28)	−216(28)	−284(35)	−193(21)	−249(22)
ΔGele,MD	−20(22)	−23(15)	−4(25)	−12(18)	−17(13)	14(12)
ΔGtot,MD (w/o ΔSMD)	−406(31)	−272(29)	−245(30)	−333(34)	−234(22)	−261(23)
−TΔSMD	166	91	72	109	132	90
ΔGtot,MD (w/ΔSMD)	−240	−182	−172	−224	−102	−171
ΔΔGtot,MD (w/ΔSMD)	0	58	68	16	138	69

All energies have units of kJ/mol with the average followed by standard deviation in parentheses except for the entropy term. ΔΔG_tot,MD is the relative total binding energy compared to Model I.

Generally, the total binding free energies in all models are negative, indicating that all the associations are favorable even though the protein approaches the DNA from different starting points. The trend of the total binding free energy ΔG_tot,MD follows the order I < IV < II < III < VI < V. Among all the models, as expected, Model I that starts from the crystal structure, has the strongest association and possesses the largest buried solvent-accessible interfacial area. As for Model II, it differs from Model I only in the starting distance between the protein and DNA. So the binding in Model II might be expected to be the next most favorable one just after Model I. However, Model II is ranked third although it does have the smallest root mean-square deviation from the crystal structure (heavy atoms) at 5.47 ± 0.45 Å. The Model II binding site is consistent with BD_minor predicted in our BD simulations. The second ranked structure is Model IV, which is only 16 kJ/mol higher than Model I. Compared to Model II, its ΔE_vdw,MD is much stronger. The protein locates consistent with BD_major identified in the BD simulations.

The low binding free energy in Model IV appears to be a combination of a tight association of the protein and DNA with good mutual hydration. Compared to the other models (Fig. 4), it has a total of 29 contacts between the binding partners, just two less than in Model I, and seven more than in Model II. Moreover, the interface is more hydrated with 11 water molecules mediating the hydrogen-bonding interactions, four less than in Model I, one more than in Model II, and approximately four more than in other three models. For each model, we see some fraying of the DNA beyond that expected from pure DNA simulations indicating that protein encounter has affected the DNA structure, possibly coupled to disturbing the ion atmosphere.

Figure 4.

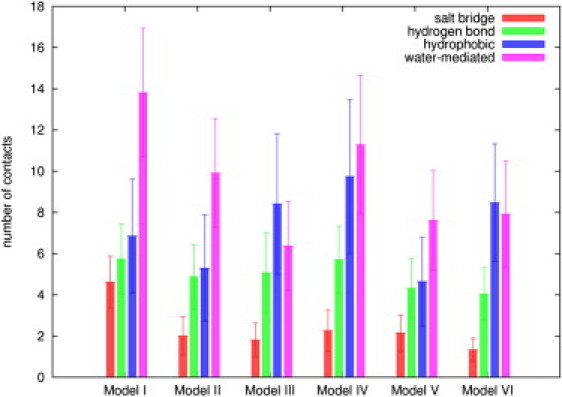
The number of contacts between the protein and DNA for all the models.

Water is an important participant in the protein-DNA recognition, association, and function (47,48) reducing the electrostatic field between the protein and DNA. Here we also see evidence of it acting as a partner in the steric recognition. This is where the merging of the mutual solvation shells, maintaining a layer of water (the solvent-separated configuration), is a structural feature. Water molecules in Models I, II, and IV reduce the repulsion between negatively charged Asp⁴⁸, Asp⁴⁹, and Glu⁹⁷ and the backbone phosphate atoms. Particularly for Asp⁴⁸, the experiment (49) reveals that mutation to Asn or Gln largely improves the binding affinity and cleavage activity, and it also changes the cleavage preference. The finding of a relatively low binding energy, tight contact, and wet interface indicates that in addition to the binding site revealed by the experiment, the major groove site found in Model IV is likely to be a reasonable candidate binding site.

Experiments (50) propose a cleaving mechanism for N-ColE7. In this mechanism, the essential divalent metal ion Zn²⁺ binds directly to the phosphate oxygen of the DNA backbone. His⁵⁴⁵, polarized by a backbone carbonyl group, functions as a general base to activate a water molecule for nucleophilic attack on the scissile phosphate. The phosphoanion transition state is then stabilized by the side chain of Arg⁴⁴⁷. In the simulation of Model I, the water-mediated hydrogen bond contact happens between His⁵⁴⁵ and Ade⁵ with the frequency of 77% and between Arg⁴⁴⁷ and Ade⁵ with 15%. As mentioned above, the active sites of the protein in Models I, II, III, and IV all face the DNA at the end of the simulation. We can speculate about the possibility of the functionality of the intermediate state formed in these models. Unlike the crystal structure, Zn²⁺ binds indirectly to the DNA in Models II–IV via a shared water molecule. In Model II, the zinc binding site is Ade⁵, whereas Arg⁴⁴⁷ mostly interacts with Gua¹³, which is five basepairs away from Ade⁵, so it is improbable that Arg⁴⁴⁷ stabilizes the transition state as proposed based on our calculations. However, we find that Arg⁵³⁸, also in the binding interface, has a strong water-mediated contact with Ade⁵ with the frequency of 85%. Similarly, in Model IV, Arg⁴⁴⁷ is approximately four basepairs away from the zinc binding site Cyt¹⁹. Arg⁵³⁸ interacts with Cyt¹⁹ via water with the frequency of 62%.

In both Models II and IV, no contacts between His⁵⁴⁵ and the DNA were observed—which does not mean no occurrences of His⁵⁴⁵ interacting with the DNA. Previous work on SMNase (51) showed that the catalytic histidine residue interacts with DNA via two more water molecules in the monomer state. It is thus reasonable that a similar mechanism likely obtains in Models II and IV as well. As for Model III, despite the difference of the binding locations, the binding face between the protein and DNA is similar to that in Model I. Analysis of the contacts at the active site suggests that although the protein approaches the DNA from different positions, if the active site keeps facing the DNA, there exists a possibility that the intermediate state formed could be functional. In addition, either Arg⁴⁴⁷ or Arg⁵³⁸ could play a role in the cleavage of DNA by stabilizing the transition state. Two more arginine residues participating in the cleavage of DNA might improve the catalytic activity of N-ColE7 non-sequence-specifically.

Discussion and Conclusions

Two initial encounter states, denoted BD_major and BD_minor, have been identified along the binding pathway based on the free energy landscape map generated from the BD simulations. BD_minor has position and orientation similar to that in the crystal structure, whereas BD_major is located on the side opposite to BD_minor and close to the major groove. Along a pathway from BD_major to BD_minor, the protein maintains close proximity to the DNA. A small 3.9 kJ/mol (∼1.6 k_BT) energy barrier was observed between the two minimum states. Such a small energy barrier is fairly consistent with the results from both a previous theoretical estimate and experimental observation.

In the study of the mechanism of protein-DNA recognition and binding, Slutsky and Mirny (52) concluded that a roughness of the binding energy landscape <2 k_BT is required for a protein's one-dimensional search. Experimental studies (15) on several protein-DNA systems found that when a nonspecifically bound protein diffuses along the DNA helix, an energy barrier of ∼1.1 ± 0.2 k_BT was encountered. If the energy barrier is much larger than 2 k_BT, the diffusion of a protein along the DNA helix will be lowered and the protein cannot find its site in biologically relevant time (52) via their mechanism. We found a relatively small free energy barrier along part of the one-dimensional diffusion search path, which could facilitate a local search for a binding site but this mechanism competes with the faster diffusion in solvent.

The BD estimate of the free energy barrier based on the binding pathway is approximate. Only long-range electrostatic forces and desolvation effects are primarily considered, and short-range repulsive forces are treated by an exclusion. If one configuration has vdW overlap, it was not considered. As a result, such a treatment is too rough to describe short-range interactions. Internal degrees of freedom of the solutes were not sampled in the BD encounters. As a consequence, the possibility of a conformational change during that part of the binding process cannot be determined here. It has been shown that several DNA binding proteins have partially disordered structures in the unbound states, and induced folding happens upon binding to DNA (52–54). Moreover, DNA conformational fluctuation also leads to a larger configurational space, and thus affects the association rate as well. Hydrodynamic interaction (HI) was not incorporated in the BD simulations, which reduces the association rate but has no effect on thermodynamics (55). Because the effects of HI and flexibility on the association are opposite, they could oppose each other to some extent (56). In addition, calculation of the association rate is not the primary aim of this study, so the neglect of HI will not influence the identification of the encounter states.

We performed studies of the final binding process by MD simulations. The binding process was analyzed by stages. The first stage of approach is completely dominated by the total electrostatic interactions which steer and orient the protein to approach the DNA. This effect is clearly salt-concentration-dependent. Then water correlations and vdW interactions build up to hold the protein in proximity to the DNA. The protein undergoes sliding, and self-rotating movement into an intermediate binding state. However, the sliding movement along the DNA is not always within a helical groove. This might be due to the limitations of our sampling of initial conditions. We found that the protein's translation is often accompanied by strongly correlated reorientation, which is common in all the models studied. The coupling helps maintain the active site of the protein to face the DNA, which is in agreement with the experimental study on several protein-DNA binding systems (15). Such coupling is also found in protein-protein systems which have strong electrostatic interactions (22).

One of the results from our study using BD and MD simulations is that in addition to the minor groove binding site found by the x-ray crystallography, a site close to the major groove is likely to be favorable for N-ColE7. Except for Model I, the binding state of Model IV has the lowest binding free energy, the largest contact number, and the largest hydrated interfacial area. In Model IV, the long side chains of Lys⁹² and Arg¹²⁹ insert into the major groove of the DNA and have strong hydrogen-bond contacts with the base atoms. The frequency of such contacts can reach as high as 37%, compared to 50% in Model I and 45% in Model II. In both later models, the side chains of Arg⁹³/Lys⁹² and Arg¹²⁹ contact with the minor groove. Hence, either the minor groove or major groove can accept the insertion of the lysine and/or arginine residues in the recognition of DNA by N-ColE7. In addition, the binding states in Models II and IV could be functional. Zn²⁺ binds the phosphate oxygen via a water molecule, and Arg⁵³⁸ interacts with the zinc binding site to be a candidate in the cleavage of DNA. Note that N-ColE7 hydrolyzes DNA without sequence specificity, so participation of either Arg⁴⁴⁷ or Arg⁵³⁸ in the cleavage of DNA could be a special feature of N-ColE7 to improve its functional activity.

As a case study, we have explored the binding process of N-ColE7 with a DNA fragment. We found encounter states which play an important role in a variety of dynamic processes leading to molecular recognition. Mutually shared waters of hydration play a central role in the recognition complex. Previously, experiments have considered a sequence-specific enzyme in contact with a noncognate sequence (59) which can be contrasted to our study of an enzyme which is inherently non-sequence-specific. The nonspecific binding mechanism found here could be a common prerequisite to specific (59).