Three-Dimensional Electron Microscopy Simulation with the CASINO Monte Carlo Software

Abstract

Monte Carlo softwares are widely used to understand the capabilities of electron microscopes. To study more realistic applications with complex samples, 3D Monte Carlo softwares are needed. In this paper, the development of the 3D version of CASINO is presented. The software feature a graphical user interface, an efficient (in relation to simulation time and memory use) 3D simulation model, accurate physic models for electron microscopy applications, and it is available freely to the scientific community at this website: www.gel.usherbrooke.ca/casino/index.html. It can be used to model backscattered, secondary, and transmitted electron signals as well as absorbed energy. The software features like scan points and shot noise allow the simulation and study of realistic experimental conditions. This software has an improved energy range for scanning electron microscopy and scanning transmission electron microscopy applications.

Introduction

Electron microscopes are useful instruments used to observe and characterize various types of samples: observation of complex integrated circuits, small nanoparticles in biological samples or nano-precipitates, and dislocations by cathodoluminescence just to name a few examples. They can even be used to manufacture integrated circuits by electron beam lithography. To fully understand and extract all the information available from these instruments, the complex electron-matter interactions have to be understood. The Monte Carlo method is useful to help understand these instruments (Joy, 1995b).

Monte Carlo software was used to understand the capabilities of electron microscopes at higher energy (> 10 keV) (Newbury and Yakowitz, 1976) or at lower energy (< 5 keV) (Hovington and others, 1997). For various reasons, but principally because of the long simulation time and large computer memory needed, the previous version of CASINO was limited to simple geometry (Drouin and others, 2007). To apply the Monte Carlo method to more realistic applications with complex sample, three-dimensional (3D) Monte Carlo softwares are needed.

Various softwares and code systems were developed to fill this need of a 3D Monte Carlo software (Babin and others, 2006; Ding and Li, 2005; Gauvin and Michaud, 2009; Gnieser and others, 2008; Johnsen and others, 2010; Kieft and Bosch, 2008; Ritchie, 2005; Salvat and others, 2006; Villarrubia and Ding, 2009; Villarrubia and others, 2007; Yan and others, 1998). However, either because of their limited availability to the scientific community or their restriction to expert users only, we have extended the software CASINO (Drouin and others, 2007) to 3D Monte Carlo simulation. The development of the 3D version of CASINO was guided by these goals: a graphical user interface, an efficient (in relation to simulation time and memory use) 3D simulation model, accurate physic models for electron microscopy applications, and lastly to make it available to the scientific community as done with the previous versions (Drouin and others, 2007; Hovington and others, 1997).

Two main challenges were encountered with the simulation of 3D samples: the creation of the 3D sample by the user and the slowdown inherent to the more complex algorithm needed for a true 3D simulation. This paper presents how we responded to these challenges and goals. We also present the new models and simulation features added to this version of CASINO and examples of their applications.

Features and Structure

The simulation of electron transport in a 3D sample involves two computational aspects. The first one is the geometry computation or ray tracing of the electron trajectory inside the sample. For complex geometry, the geometry computation can involve a large effort (simulation time), so fast and accurate algorithms are needed. The second aspect is the physical interaction with the matter inside the sample. Both are needed to successfully simulate the electron trajectory.

Using the electron transport 3D feature, the beam and scanning parameters allow the simulation of realistic line scans and images. From the simulated trajectories, various distributions useful for analysis of the simulation are calculated. The type of distribution implemented was driven by our research need and various collaborations. Obviously, these distributions will not meet the requirements of all users. To help these users use CASINO for their research, all the information from the saved electron trajectories, such as each scattering event position and energy, can be exported in a text file for manual processing. Because of the large amount of information generated, the software allows the filtering of the exported information to meet the user needs.

3D Sample

The main aim of this work was to simulate more realistic samples. To achieve that goal a 3D sample model was implemented in CASINO. Specifically, the Monte Carlo software should be able to build a 3D sample and track the electron trajectory in a 3D geometry.

Shapes

The 3D sample modeling is done by combining basic 3D shapes and planes. Each shape is defined by a position, dimension and orientation. Except for trivial cases, 3D structures are difficult to build without visualization aids. In CASINO, the creation of the 3D sample is helped by using the OpenGL (http://www.opengl.org) technology to display the sample and the display is also used when the simulation options are chosen. The 3D navigation tool (rotation, translation and zoom of the camera) allows the user to assert the correctness of the sample manually. In particular, the navigation allows the user to see inside the shape to observe imbedded shape.

Seven shapes are available in CASINO and they are separate arbitrary in three categories. The first category has only one shape, a finite plane. The finite plane is useful to define large area of the sample like a homogenous film. However, the user has to be careful that the plane dimension is larger than the electron interaction volume because the plane does not define a closed shape and unrealistic results can happen if the electron travels beyond the lateral dimensions of the plane (see Figure 2E and next section). The second category with two shapes contains 3D shape with only flat surfaces, like a box. The box is often used to define a substrate. Also available in this category is the truncated pyramid shape which is useful to simulate interconnect line pattern. The last category is 3D shape with curved surface and contains 4 shapes. For these 3D shapes the curved surface is approximated by small flat triangle surfaces. The user can specify the number of divisions used to get the required accuracy in the curved surface description for the simulation conditions. This category includes sphere, cylinder, cone, and rounded box shapes.

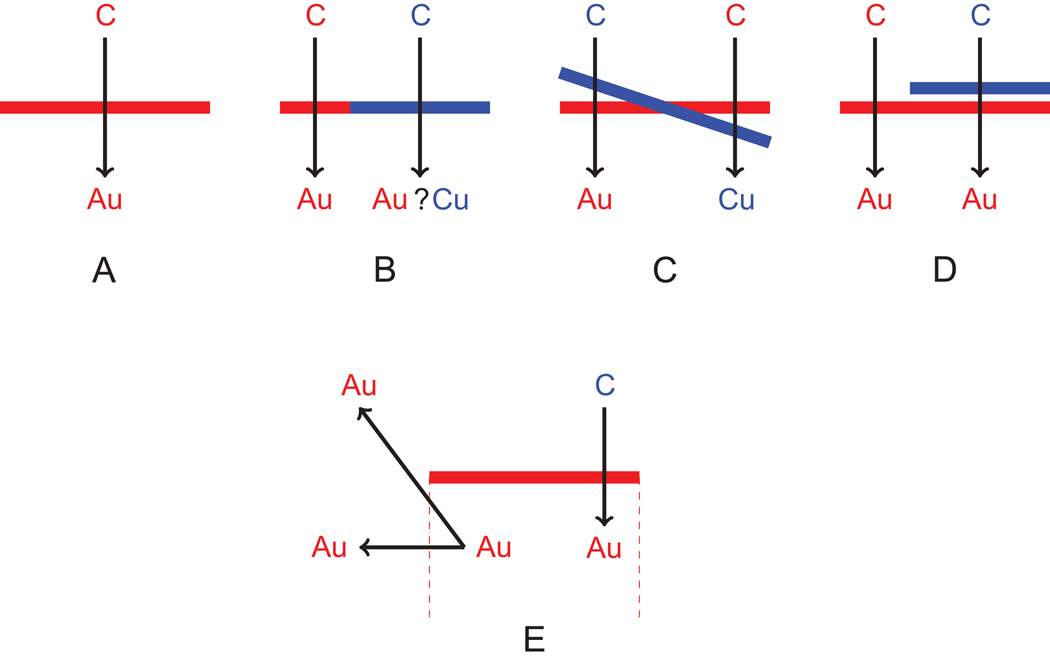
Figure 2.

Schema of the intersection of an electron trajectory and a triangle and the change of region associate with it. A: single triangle where the new region is Au. B: two triangles overlap and ambiguity in the determination of the new region. C: intersection of two triangles with discontinuity in the determination of the new region. D: small gap approach to resolve these two problems. E: another ambiguity in the determination of the new region (the red dash lines define the lateral limit of the Au region of the plane shape).

Complex 3D sample can thus be modeled by using these basic shapes as shown in the examples presented in this paper.

Regions

Each shape is characterized by two sides: outside and inside. A region, which defines the composition of the sample, is associated to each side. The definition of outside and inside is from the point of view of an incident electron from the top (above the shape) toward the bottom (below the shape). The outside is the side where the electron will enter the shape. The inside is the side right after the electron crosses the shape surface for the first time and is inside the shape.

The chemical composition of the sample is set by regions. For each region, the composition can be a single element (C) or multiple elements like a molecule (H₂O) or an alloy (Au_xCu_1-x). For multiple elements, either the atomic fraction or the weight fraction can be used to set the concentration of each element. The mass density of the region can be specified by the user or obtained from a database. For a multiple elements region, the mass density is calculated with this equation

$$\rho =\frac{1}{{\displaystyle \sum _i^n}\frac{c_i}{{\rho }_i}},$$ (1)

where c_i is the mass concentration and ρ_i is the mass density of element i. This equation assumes an ideal solution for a homogeneous phase and gives a weight-averaged density of all elements in the sample. If the true density of the molecule or compound is known, it should be used instead of the value given by this equation. Also the region composition can be added and retrieved from a library of chemical compositions.

For complex samples, a large number of material property regions (two per shape) have to be specified by the user; to accelerate the sample set-up, the software can merge regions with the same chemical composition into a single region.

Triangles and Mesh

The change of region algorithm has been modified to allow the simulation of 3D sample. In the previous version, only horizontal and vertical layers sample were available (Drouin and others, 2007; Hovington and others, 1997). An example of a complex sample, an integrated circuit, is shown in Figure 1A.

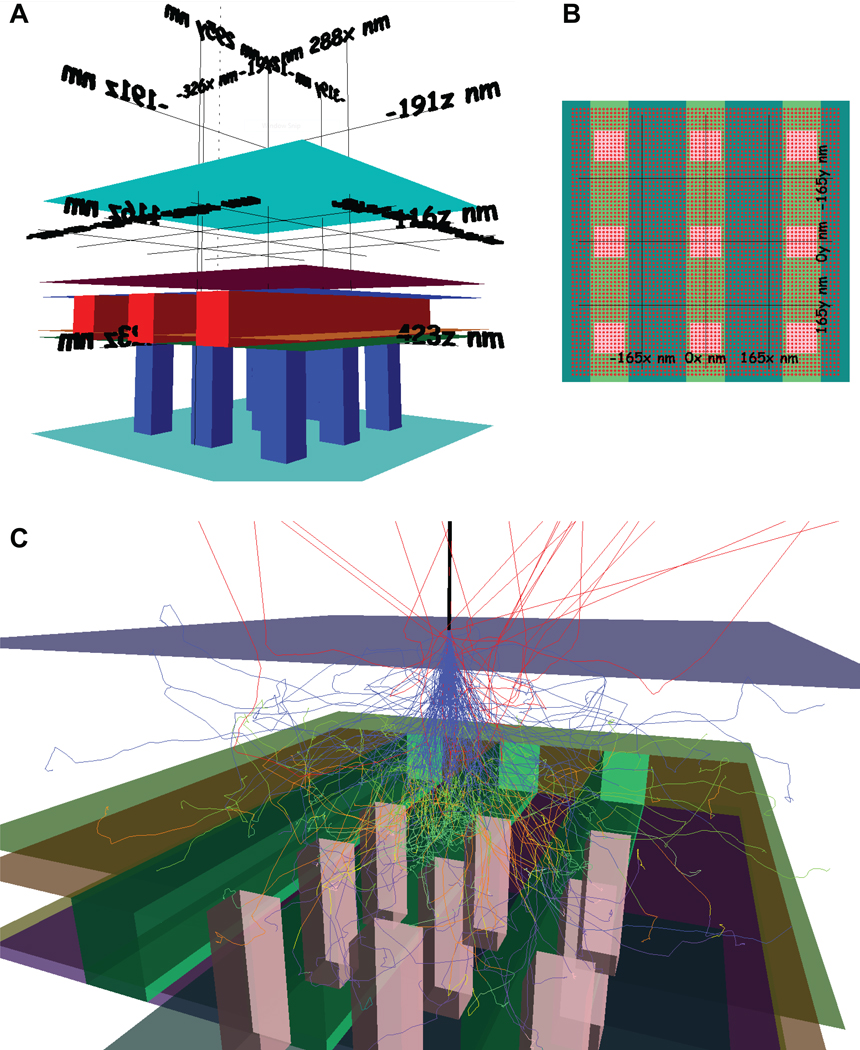
Figure 1.

Screenshots from CASINO software of a 3D sample. A: 3D view of the sample showing the different shapes and regions. B: Top view of the sample with the scan points used to create an image. C: Electron trajectories of one scan point with trajectory segments of different color for each region. The sample used is a typical CMOS stack layer for 32 nm technology node with different dielectric layers, copper interconnects and tungsten via.

The electron trajectory ray tracing algorithm (Akenine-Möller, 1997) does not work with the basic shapes directly, but only with triangles. When the creation of the sample is finished, the software transforms all the shape surfaces into triangles. Each triangle inherits the outside/inside material properties of its parent shape.

During the ray tracing of the electron trajectory, the current region is changed each time the electron intersects a triangle. The new region is the region associated with the triangle side of emerging electron after the intersection. Figure 2A illustrates schematically the electron and triangle interaction and the resulting change of region. For correct simulation results, only one region should be possible after an intersection with a triangle. This condition is not respected if, for example, two triangle surfaces overlap (Figure 2B) or intersect (Figure 2C). In that case, two regions are possible when the electron intersects the triangle and if these two regions are different, incorrect results can occur. The software does not verify that this condition is valid for all triangles when the sample is created. The best approach is to always use a small gap (0.001 nm) between each shape as shown in Figure 2D. No overlapping triangles are possible with the small gap approach and the correct region will always been selected when the electron intersects a triangle. The small gap is a lot smaller than the electron mean free path, i.e., no collision occurs, and the simulation results are not affected by the presence of the gap.

Another type of ambiguity in the determination of the new region is shown in Figure 2E when an electron reaches another region without crossing any triangle boundaries. In CASINO, the change of region only occurs when the electron trajectory cross a triangle boundary. As illustrated in Figure 2E, the region associated with an electron inside the Au region define by the finite plane (the dash lines define the lateral limit) and going out of the dimension define by the plane, either on the side or top, does not change and the electron continue his trajectory as inside a Au region.

A typical 3D sample will generate a large number of triangles, for example 106,082 triangles (6240 triangles per sphere) are required to model accurately the tin balls sample studied in the application section. For each new trajectory segment, the simulation algorithm needs to find if the electron intersects a triangle by individually testing each triangle using a vector product. This process can be very intensive on computing power and thus time. To accelerate this process, the software minimizes the number of triangles to be tested by organizing the triangles in a 3D partition tree, an octree (Mark de Berg, 2008), where each partition a box that contains ten triangles. The search inside the partitions tree is very efficient to find neighbour partitions and their associated triangles. The engine generated a new segment from the new event coordinate, see electron trajectory calculation section. The 10 triangles in the current partition are tested for interception with the new segment. If not, the program found the nearness partition that contains the new segment from the 8 neighbour partitions and created a node intersection event at the boundary between the two partition boxes. From this new coordinate, a new segment is generated from the new event coordinate as described in the electron trajectory calculation section. The octree algorithm allows fast geometry calculation during the simulation by testing only 10 triangles of the total number of triangles in the sample (106,082 triangles for the tin balls sample) and 8 partitions; and generating the minimum of number of new segments.

Electron Trajectory Calculation

The Monte Carlo calculation scheme used in CASINO is based on the previous version of CASINO (v2.42) (Drouin and others, 2007) and reviewed in Joy’s book (Joy, 1995b). The detailed description of the Monte Carlo simulation method used in the software is given in these references. In this section, a brief description of the Monte Carlo method is given and the physical models added or modified to extend the energy range of the software are presented.

The Monte Carlo method uses random numbers and probability distributions, which represent the physical interactions between the electron and the sample, to calculate electron trajectories. An electron trajectory is described by discrete elastic scattering events and the inelastic events are approximated by mean energy loss model between two elastic scattering events (Joy and Luo, 1989). It is also possible to use a hybrid model for the inelastic scattering where plasmon and binary electron-electron scattering events are treated as discrete events, i.e., just like the elastic event, and the rest of inelastic event is calculated with the mean energy loss model (Joy and Luo, 1989; Lowney, 1996). The calculation of each electron trajectory is done as follow. The initial position and energy of the electron are calculated from the user specified electron beam parameters of the electron microscope. Then, from the initial position, the electron will impinge the sample, which is described using a group of triangle surfaces (see previous section). The distance between two successive collisions is obtained from the total elastic cross section and a random number is used to distribute the distance following a probability distribution. The elastic scattering θ angle is determined from another random number and using the differential elastic cross section calculated using analytical models or from tabulated values. When the electron trajectory intercept a triangle, the segment is terminated at the boundary and a new segment is generated randomly from the properties of the new region as described previously. The only difference is that the electron direction does not change at the boundary. This simple method to handle region boundary is based on the assumption that the electron transport is a Markov process (Salvat and others, 2006) and past events does not affect the future events (Ritchie, 2005). These steps are repeated until the electron either leaves the sample or is trapped inside the sample, which happens when the energy of the electron is below a threshold value (50 eV). If the secondary electrons are simulated, the region work function is used as threshold value. Also, CASINO keeps track of the coordinate when a change of region event occurs during the simulation of the electron trajectory.

The tabulated values calculated from the ELSEPA cross section software (Salvat and others, 2005) were added to CASINO. This electron elastic cross section (EECS) model is also used by the Electron Elastic Scattering Cross Section Database (Jablonski and others, 2003) available from NIST (Gaithersburg, MD). This EECS model involves the calculation of the relativistic (Dirac) partial-wave for scattering by a local central interaction potential. The total and differential EECS were pre-calculated using ELSEPA for all chemical elements in the energy range 10 eV to 500 keV. The calculations of the cross sections used the default parameters suggested by the authors of the software ELSEPA (Salvat and others, 2005). These pre-calculated values were then tabulated and included in CASINO to allow accurate simulation of the electron scattering. The energy grid used for each element tabulated data was chosen to give an interpolation error less than one percent when a linear interpolation is used.

A more accurate algorithm, using the rotation matrix, was added for the calculation of the direction cosines. The implementation is based on the MONSEL code (Lowney, 1995; 1996) from NIST.

The generation of secondary electrons was added in CASINO using the hybrid energy loss model mentioned previously. The fast secondary electrons (FSE) are calculated using the Möller equation (Reimer, 1998). The slow secondary electrons (SSE) are generated from the plasmon theory (Kotera and others, 1990). The implementation is based on the MONSEL code (Lowney, 1995; 1996) from NIST. To generate SE in a region, two parameters, the work function and the plasmon energies, are needed. Values for some elements and compounds are included, but the user can add or modify these values. The SSEs are low energy electrons (< 50 eV) and are very sensitive to the electron physical models and SE parameters used. The modified Bethe equation with residual energy constant is used to calculate the energy loss at very low energy (< 50 eV) (Lowney, 1996).

We did not validate the very low energy range (<50 eV) used in CASINO used for the simulation of secondary electrons as the goal was to have a qualitative description of secondary emission. We refer the user to the original article of each model for the validity of the models.

Microscope and Simulation Properties

CASINO allows the user to choose various microscope and simulation properties to best match his experimental conditions. Some properties greatly affect the simulation time or the amount of memory needed. These properties can be deactivated if not required.

The nominal number of simulated electrons is used to represent the electron dose (with beam diameter) or beam current and dwell time. The simulation time is directly proportional to the number of electrons. The shot noise of the electron gun (Reimer, 1998) is included as an optional feature, which results in the variation of the nominal number of electrons N used for each pixel of an image or line scan. The number of electrons for a specific pixel N_i was obtained from a Poisson distribution P_N random number generator with:

$$P_N(N_i)=\frac{N^{N_i}}{N_i!}{e}^{-N}.$$ (2)

Such features allows the user to study the impact of the electron source which can greatly affect the results at low dose (< 1000e−).

The SE feature is very demanding on computing resource. For example, each 20 keV primary incident electron can generate a few thousands of SE electrons.

Three types of scan point distributions can be used in the simulations: a single point, a line scan, and an image. For all types, the positions are specified in 3D and a display is used to set-up and draw the scan points, see Figure 1B, or alternatively they can be imported from a text file.

To manage the memory used in the simulation, the user can choose to keep or not the data (enabled distributions, displayed trajectories) for each simulated scan point. The cost of keeping all the data is the large amount of memory needed during the simulation and the large file size. The main advantage is to have access to all the results for each scan point which allows further post-processing. For example, the energy absorption results presented in Figure 7 needed 4 GB of memory during the simulation.

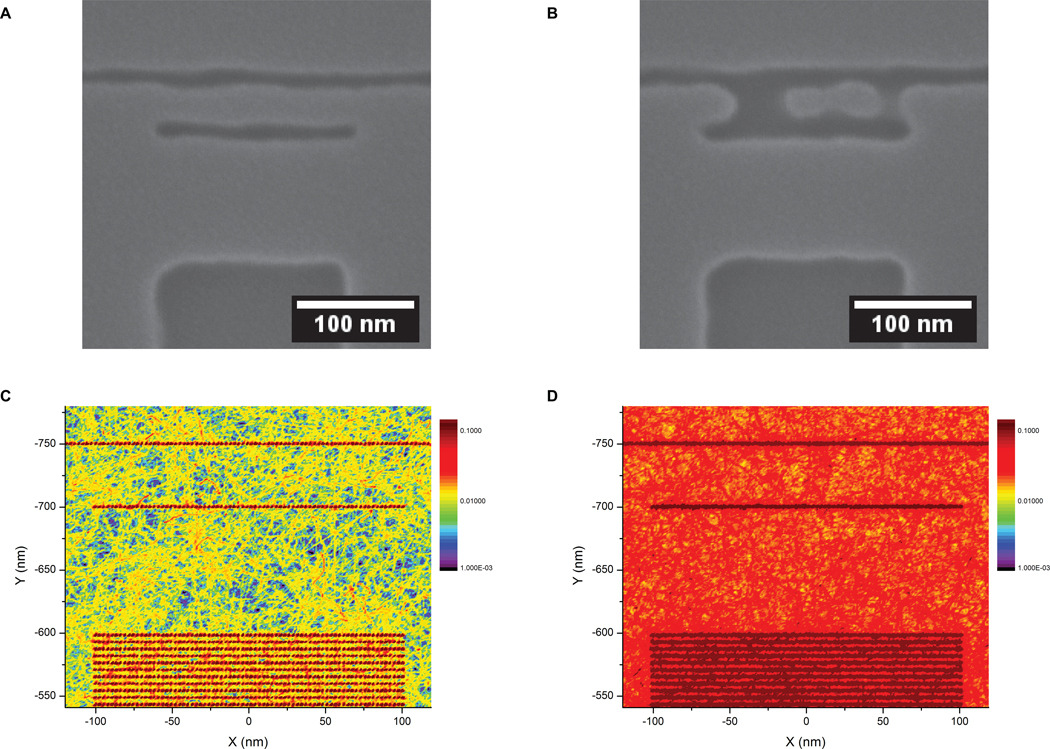
Figure 7.

Simulation of the electron dose effect on electron beam lithography. Two experimental secondary electron images, after electron beam lithography, where the pattern was A: successfully developed and B: incorrectly developed. C: and D: top view of the energy absorbed in the resist from the electron beam pattern simulated with CASINO. The number of electrons per scan point was: C: electron dose of 130 µC/cm² and D: electron dose of 700 µC/cm². The energy absorbed is normalized and displayed on a logarithmic scale.

The simulation of STEM image of amorphous sample is another important feature added to CASINO. The beam parameters now include the semi-angle and focal point, the energy range of the physical models are extended up to 500 keV and the transmitted electrons are detected by an annular dark field detector (ADF). These changes are described in detail elsewhere (Demers and others, 2010).

Finally, the whole sample can be globally rotated in axial (Y) and/or azimuthal (Z) directions. The user should note that the rotation is applied around the Y axis first, when values are given for both directions.

Distributions Calculated by CASINO

Two types of distributions are calculated by CASINO. For the first, distributions are calculated for each scan point independently of the other scan points. For the second type, the distributions are obtained from the contribution of all scan points either as line scan or area scan (image).

Before the description of these distributions, some definitions used by CASINO are needed. The primary electron (PE) which is incident on the sample is either at the end of the trajectory simulation: a backscattered electron (BSE) if the electron exits the sample toward the top direction and with energy greater than 50 eV; an absorbed electron (AE) if the electron is trapped inside the sample when the electron energy reaches below a threshold value (by default 50 eV); a transmitted electron (TE) if the electron exit the sample toward the bottom (same direction than the incident electron). Secondary electron (SE) and PE that exit the sample with energy less than 50 eV are used to calculate the secondary yield. If the energy is greater than 50 eV, they are either a BSE or TE depending of their exit direction.

Distributions for Each Scan Point

The following distributions are used to understand the complex interaction between incident electron and the sample.

The maximum penetration depth in the sample of the primary and backscattered electrons, the energy of BSEs when escaping the surface of the sample, the energy of the transmitted electrons when leaving the bottom of the thin film sample, the radial position of BSEs calculated from the primary beam landing position on the sample, and the energy of BSE escaping area as a function of radial distance from the primary beam landing position are distributions available in CASINO and described in detail elsewhere (Drouin and others, 2007).

A new distribution calculated for each scan point is the energy absorbed in a 3D volume. The volume can be described in Cartesian, cylindrical, or spherical coordinate. The 3D volume options are the position relative to the scan point, the size and number of bins for each axis. To help choosing the 3D volume setting, a display shows the distribution volume position and size relative to the sample. Care must be taken when choosing the number of bins as the memory needed grows quickly. A typical simulation of energy absorbed can use 2 GB of memory for one scan point.

Global Distributions

The following distributions either sum the contribution of all scan points or compare the information obtained from each scan point.

The total absorbed energy distribution is the sum of energy absorbed for all the electron trajectories of all scan points for a preset 3D volume. In this case, the 3D volume position is absolute, i.e., fixed relative to the sample for all scan points.

Intensity distributions related to line scan and image are also calculated. The intensities calculated are the backscattered electrons, secondary electrons, absorbed energy, and transmitted electrons. The absorbed energy intensity is defined by the sum of all energies deposited by the electron trajectories in the selected region for a given scan point. The absorbed energy intensity signal will extend the scan point position and will be limited by the interaction volume. The intensity is either for the total number of electrons simulated or normalized by the number of electrons simulated. The intensity variation between scan points is a combination of the shot noise effect, if selected, and sample interaction.

Representation of Collected Data

For the analysis of the distributions presented previously it is useful to visualize the data directly in a graphic user interface before doing further processing using other software. In this section, the visualization aids available in CASINO are described.

Figure 1A shows the user interface to create and visualize the sample in a 3D display. Figure 1C shows an example of electron trajectories simulated on sample shown in Figure 1A. Through this interface one can visualize the electrons interaction with the sample. The color of the trajectories can be used to represent the type of trajectory: red for a backscattered electron, green for a secondary electron and blue for the other electron (absorbed or transmitted). Another color scheme available allows to follow the regions in which the electron go through, as shown in Figure 1C, by selecting the color of the electron trajectory segment according to the region that contains it. Another option for the visualization of the trajectory is to represent the energy of the electron by different colors. Also the collision (elastic, inelastic and change of region events) that occurs along the trajectory can be displayed with the help of small green sphere at the location of the collision.

The distributions obtained for all scan points are displayed as 2D graphic if the scan points form a straight line. In the case that the scan points form an image, an intensity image is displayed with a color bar mapped to the intensity value. The color scale and minimum and maximum of the scale can be specified by the user.

The signals or results obtained from the electron simulation of all scan points that can be used to form a line scan or an image are: the backscattered electrons (BSE), secondary electrons (SE), transmitted electrons (TE) and the absorbed energy inside the sample. For TE signal, the user can choose to see the effect of the detector on the intensity by using an ADF detector with user specified semi-angles and detector quantum efficiency (DQE).

For most of the displays, the mouse allows to change the zoom, translate, or rotate the information presented. For all displayed graphics, the corresponding data can be exported/copied for further analysis by the user or the graphic itself can be exported/copied. In addition, the intensity image can be saved as a high intensity resolution TIFF image (32-bit float per pixel).

Special Software Features

The simulation of an image needs a large number of scan points. Depending of the results selected, the memory needed by CASINO can be large and exceed the 2 GB limit of a 32-bit Windows system. Naturally the total simulation time increases with the number of scan points. For these reasons, CASINO uses multi-processors/cores and can swap memory of a 32-bit system. On a 64-bit system there is no memory limitation, so the software can use all memory available.

For the more advanced user requiring to investigate the parameterization effect of one or a few simulating parameters a console version of CASINO is available with a basic scripting language. This feature allows the user to avoid to manually create a large numbers of simulation setting using the graphical user interface which can be time consuming when one requires a specific results such as the evolution of the backscattered electron coefficient with the incident energy shown in Figure 3 for example. This feature allows the batch simulation of many simulations and to change one or more parameters for each simulation. Also the console version only uses portable C++ code, so that the software can be available on other operating systems like Linux and Mac OS X.

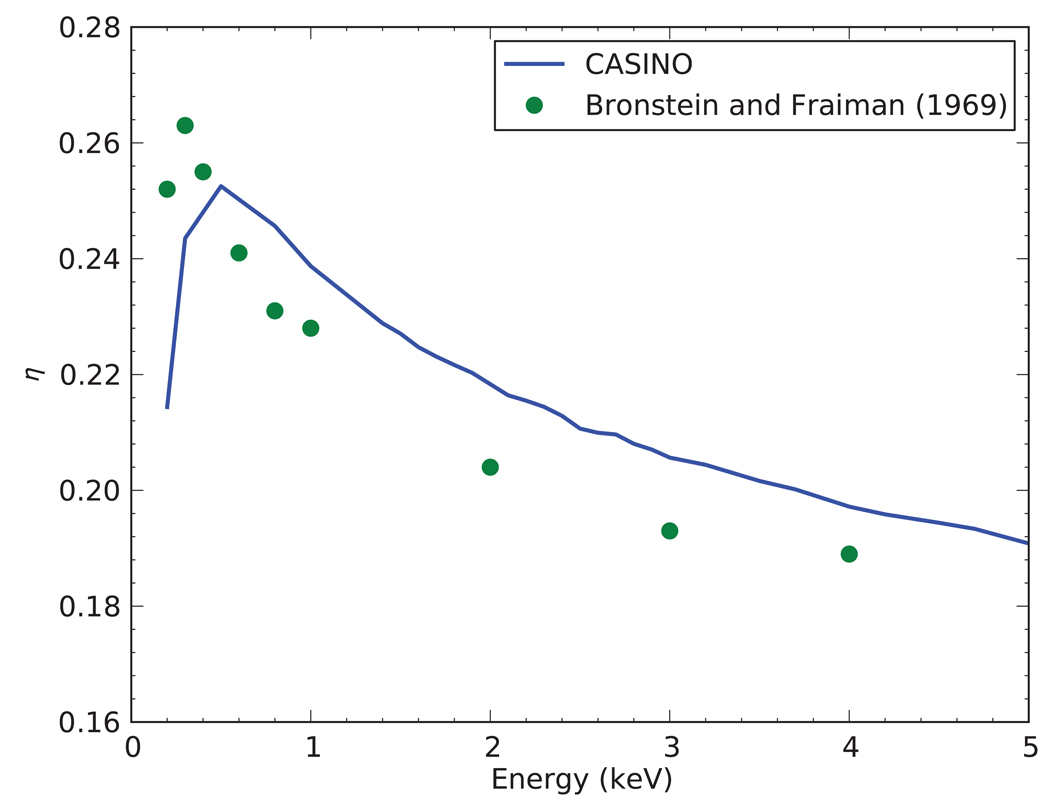
Figure 3.

Simulated backscattered electron coefficients η in silicon at low electron energy compared with experimental data (Bronstein and Fraiman, 1969; Joy, 1995a). 1,000,000 electrons were used in the simulations.

Application Examples

The following examples illustrate the application of the simulation tool in relation to backscattered electron (BSE) and secondary electron (SE) imaging, electron gun shot noise, and electron beam lithography.

Backscattered Electron Coefficient

The backscattered electron coefficient η is useful to validate a Monte Carlo software. The η value is the ratio of the number of trajectories leaving the sample surface over all primary electron trajectories. The accuracy of η depends mainly on the electron elastic cross section, the energy loss models and also the number of primary electron simulated. The smooth variation of η with incident electron energy helps identify problem with the Monte Carlo implementation.

Figure 3 compares the simulation of backscattered electron coefficient for the electron incident energy lower than 5 keV with experimental values (Bronstein and Fraiman, 1969; Joy, 1995a) for a silicon sample. The simulated values are in agreement with the measured values except at very low energy (less than 500 eV) where the simulation and experimental values do not follow the same trend. It is difficult to assert the accuracy at very low energy of the simulation models from this difference. The experimental values at these energies strongly depend on the contamination or oxidation of the sample surface, which results in large variation of the values obtained experimentally (Joy, 1995a).

The linear interpolation problem reported in some Monte Carlo softwares (El Gomati and others, 2008) was not observed in Figure 3. The interpolated energy grid for the elastic electron cross section data was chosen for each element to produce an interpolation error less than one percent when a linear interpolation model is used. This approach is similar to the one used in PENELOPE (Salvat and others, 2006). The power law interpolation model proposed to correct this problem (El Gomati and others, 2008) can increases the simulation time by 20 % versus a linear interpolation model.

Secondary Electron Yield

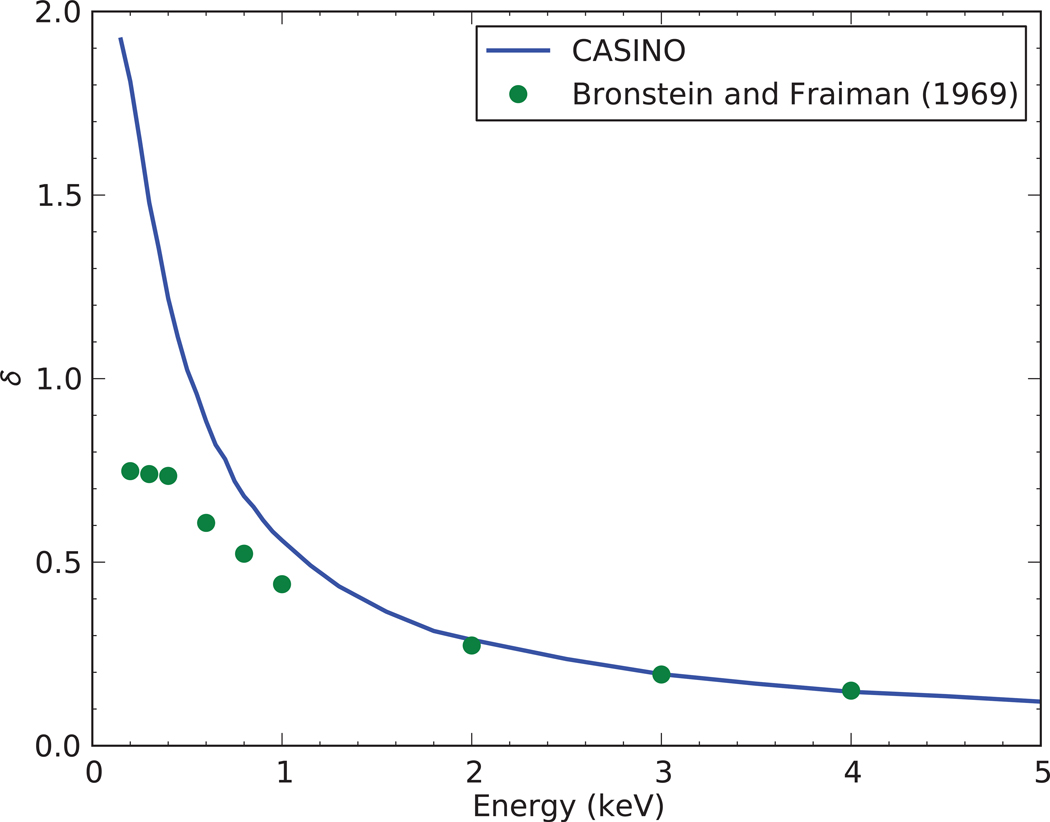
In a similar manner, the evolution of secondary electron yield with the incident electron energy was used to validate the secondary electron generation implementation in CASINO.

Figure 4 compares the simulation of secondary electron yields for the electron incident energy lower than 5 keV with experimental values (Bronstein and Fraiman, 1969; Joy, 1995a) for a silicon sample. The simulated values are in agreement with the measured values except at very low energy (less than 500 eV) where the simulation and experimental values do not follow the same trend.

Figure 4.

Simulated secondary electron yields δ in silicon at low electron energy compared with experimental data (Bronstein and Fraiman, 1969; Joy, 1995a). 100,000 electrons were used in the simulations.

The generation of secondary electrons in the simulation increases the simulation time drastically. For example, in bulk Si sample at 1 keV, the generation of SE increase the simulation time by a factor of 17, and 44 at 5 keV. For each primary electron trajectory, a large amount of secondary electron trajectories are generated and simulated. For example at 1 keV, 100 secondary electron trajectories are generated for each primary electron. The amount of SE trajectories increases with more energetic primary electron, e.g., 1300 SE trajectories for each primary electron at 20 keV. The increase of the simulation time is not directly proportional to the number of SE trajectories, because, most of these new electron trajectories are low energy electron (slow secondary electron) and will have few scattering events, which take less time to simulate than a primary electron.

Tin Balls Imaging

Another useful feature in CASINO is the ability to simulate a set of scan points, e.g., a line scan or an image. Figure 5 shows backscattered electron and secondary electron images simulated with CASINO. The sample consists of Sn balls with different diameters on a carbon substrate. Two different incident electron energies were used 1 keV and 10 keV.

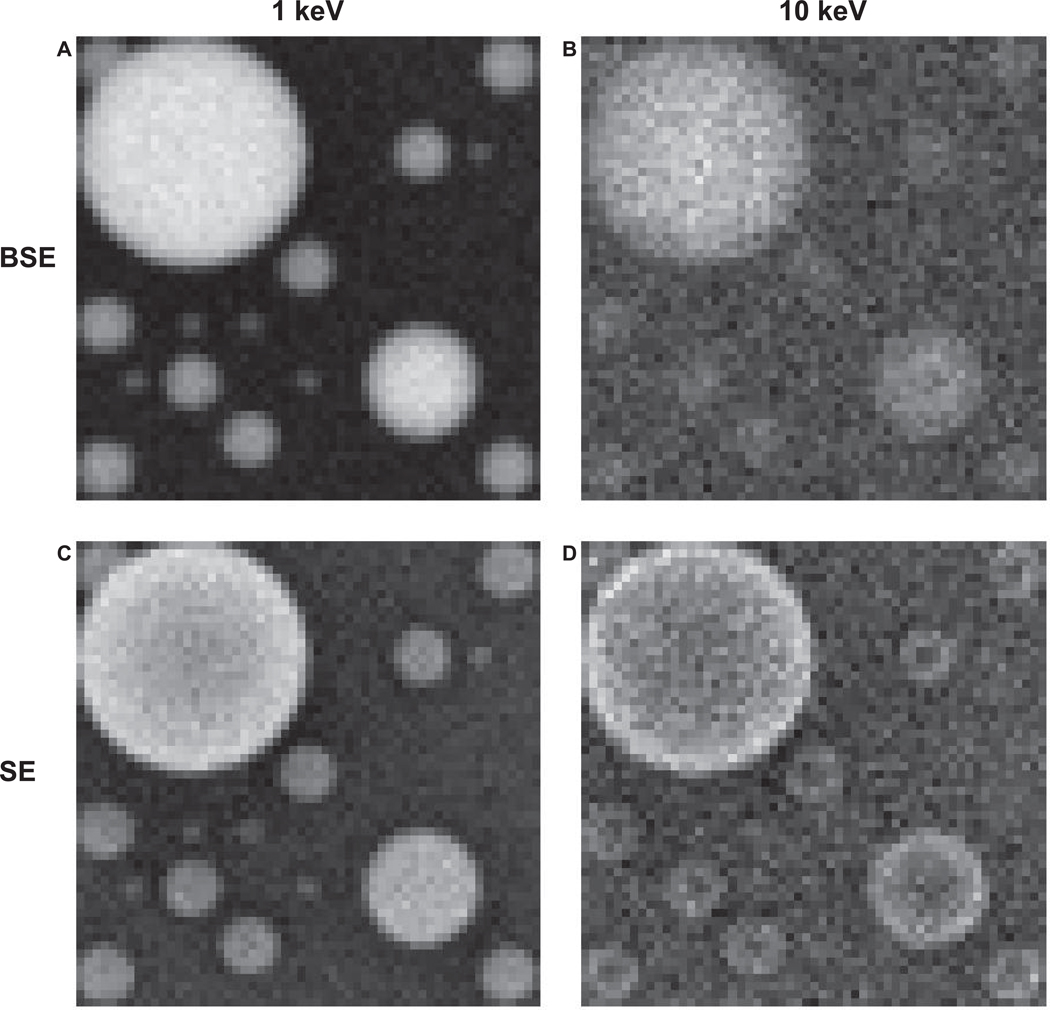
Figure 5.

Simulated images of tin balls on a carbon substrate. A, B: backscattered electron images. C, D: secondary electron images. The incident energy of 1 keV (A, C) and 10 keV (B, D). The tin ball diameters are 20, 10, 5, and 2 nm. The field of view is 40 nm with a pixel size of 0.5 nm. The nominal number of electrons for each scan point was 1,000.

For each image, the contrast range was maximized to the minimum and maximum intensity of the image. The contrast C was calculated to compare the images using the following definition (Goldstein and others, 1992)

$$C=\frac{S_2-S_1}{S_2},$$ (3)

where S₁ and S₂ are the minimum and maximum pixel values in the image, respectively. These three quantities are reported in Table I for each image.

Table I.

Comparison of the contrast values calculated from backscattered electron and secondary electron images shown in Figure 5 for 1 and 10 keV incident electron energies.

Signal	Energy (keV)	Minimum	Maximum	Contrast
BSE	1	0.042	0.61	0.93
	10	0.037	0.16	0.77
SE	1	0.61	2.9	0.79
	10	0.063	0.35	0.82

At 1 keV, the contrast obtained with the BSE signal is better than the SE signal, because the BSE emission has a stronger dependence on the atomic number difference. For both signals, the smaller Sn nanoparticles are visible, because the interaction volume at 1 keV is of the order of few nanometers for both BSE and SE signals. At 10 keV, a similar contrast was obtained for BSE and SE images.

For BSE images, the contrast decreases with the increase of incident energy. The larger interaction volume decreases the signal from Sn nanoparticles as less electron interaction occurs in the particle. The decrease of the contrast at 10 keV increases the importance of the noise on the image resolution. The resolution changes drastically between the two energies. At 10 keV, the smaller tin balls (2 nm diameter) are not visible and the 5 nm diameter balls are barely visible. Similar change in resolution are observed on the SE images for the smaller tin balls (2 nm diameter), but the 5 nm diameter balls are easier to see than on the BSE image. The SE emission decreases by a factor 10 when the incident energy is increase from 1 to 10 keV. The decrease does not change the contrast as both the carbon substrate and Sn nanoparticle are similarly affected. Again the decrease of the signal, increases the effect of the noise on the image resolution.

The topographic information from the SE signal is clearly observed in the large ball where the edges are brighter than the center. The corresponding BSE image in other hand looks flat and doesn’t show topographic information.

These images are used to understand the impact of microscope parameters on image resolution and features visibility.

Shot Noise Effect on Imaging

The number of electrons emitted by the electron gun is not constant, but oscillates around an average value. This is the shot noise from the source and CASINO can include this effect in the simulation of line scan or image.

Figure 6 shows the effect of two different numbers of electrons on the BSE image quality. The sample is a typical microelectronic integrated circuit shown in Figure 1A. At 20 keV, the interaction volume reaches the copper interconnects, which are buried 250 nm depth from the sample surface and increase the BSE emission. The presence of the tungsten via will increase the BSE emission. The increase by the W via was barely observed in Figure 6B with 10,000 electrons, but not visible in Figure 6A with 1,000 electrons. The decrease of the nominal number of electrons from 10,000 to 1,000 illustrates the impact of the electron source noise on image quality. The shot noise feature in CASINO is useful to calculate the visibility of feature of interest with different instrument parameters and feature size. A detailed example of such study with CASINO is given elsewhere (Demers and others, 2010).

Figure 6.

Effect of the shot noise on the backscattered electron images of integrated circuit ST sample. The nominal number of electrons for each scan point was A: 1,000 and B: 10,000. The incident electron energy was 20 keV. The field of view is 700 nm with a pixel size of 10 nm.

Energy Absorption in Electron Beam Lithography

The energy absorption feature of CASINO was used to study a problem encountered with electron beam lithography (EBL) of a pattern shown in Figure 7A and 7B. Under certain conditions, two close line patterns, separated only by 50 nm, are connected after the development of the resist. The sample consists of a 50 nm PMMA film on a 100 nm thick SiO₂ film with a Si substrate and the EBL was done at 20 keV.

Monte Carlo simulations of the sample and pattern were done for two different electron doses (number of electrons): 130 (33) and 700 µC/cm² (175). The total energy absorbed from the pattern was calculated from the 3D matrix obtained with CASINO. Top view of the total energy absorption, normalized and on logarithmic scale, is shown in Figure 7C and 7D for 130 and 700 µC/cm² electrons doses, respectively.

The expected patterns are clearly observed by their dark red color. The absorbed energy in the pattern mainly comes from the incident beam. At 20 keV the electrons pass through the 50 nm resist film and 100 nm dielectric film with little deviation. Most of the elastic collisions occur in the Si substrate. However, the substrate generates backscattered electron that can emerge of the sample as far as 4 µm from the beam impact. With a pattern composed of more than 225,000 scan points, the contribution of the BSE on the absorbed energy cannot be neglected. This is the background energy observed between patterns in Figure 7C and 7D. The long range combined with the random nature of the BSE exit position created a uniform and noisy background signal. The average value of the absorbed energy background is proportional to the electron dose. We suspect that for a specific value of the electron dose, the absorbed energy background reaches the threshold value for the breakdown of the PMMA molecule and development of the resist occurs outside the expected patterns as observed in Figure 7B. However, this is just one possible explanation of the failure. The electron exposure is only the first step of electron beam lithography. The resist development and profile evolution could be the source of the problem as well.

Conclusions

Improved simulation software for modeling signals generation in electron microscope from electron – sample interactions, which include a full 3D sample geometry and efficient 3D simulation model, has been developed. All features are available through a graphical user interface. It can be used for modeling BSE, SE, and TE signals and absorbed energy, which is useful for electron beam lithography. The software features like scan points and shot noise allowing for the simulation and study of realistic experimental conditions. With the improved energy range, this software can be used for SEM and STEM applications, but with the limitation that the sample is considered as amorphous by the models and the simulation scheme used. The software can be downloaded at this website: www.gel.usherbrooke.ca/casino/index.html¹ and used freely. The software is in constant development for our research need and from user comments.