Asymptotic conditional singular value decomposition for high-dimensional genomic data

Summary

High-dimensional data, such as those obtained from a gene expression microarray or second generation sequencing experiment, consist of a large number of dependent features measured on a small number of samples. One of the key problems in genomics is the identification and estimation of factors that associate with many features simultaneously. Identifying the number of factors is also important for unsupervised statistical analyses such as hierarchical clustering. A conditional factor model is the most common model for many types of genomic data, ranging from gene expression, to single nucleotide polymorphisms, to methylation. Here we show that under a conditional factor model for genomic data with a fixed sample size, the right singular vectors are asymptotically consistent for the unobserved latent factors as the number of features diverges. We also propose a consistent estimator of the dimension of the underlying conditional factor model for a finite fixed sample size and an infinite number of features based on a scaled eigen-decomposition. We propose a practical approach for selection of the number of factors in real data sets, and we illustrate the utility of these results for capturing batch and other unmodeled effects in a microarray experiment using the dependence kernel approach of Leek and Storey (2008).

1. Introduction

High-dimensional data are now common across disciplines as diverse as genetics (Carlson et al., 2004; Diabetes Genetics Initiative et al., 2007), marketing (Shaw et al., 2001), chemical screening (Inglese et al., 2006), and brain imaging (Worsley et al., 1996; Geneovese et al., 2002; Schwartzman et al., 2008). In many of these experiments, particularly in the biomedical sciences, the number of features is orders of magnitude greater than the sample size. The data from these experiments consist of a sample of m-dimensional feature vectors x_j, for j = 1, … , n. The data are often either implicitly or explicitly assumed to follow a conditional factor model, where a small set of common factors are associated with the levels of many features simultaneously. For example, this is the usual model for differential expression analysis. The simplest factor model has the form x_j = Γ^mg_j+u_j where Γ^m is an m×r matrix of non-random coefficients with r < n, g_j is a fixed r-vector representing the factor values for sample j, and u_j ~ F^m is a sample from an m-dimensional multivariate distribution. Written in matrix form:

$${\mathit{X}}^m={\Gamma }^m\mathit{G}+{\mathit{U}}^m$$ (1)

Here X^m is an m × n matrix of data, G is an r × n matrix of factors, and U^m is an m × n matrix of mutually independent mean zero random variables, where m is the number of features and n is the number of samples. For this type of data, the singular value decomposition – or principal components analysis – is one approach to estimating common patterns due to unknown factors (Mardia et al., 1979). Under model (1), the right singular vectors of X^m, or equivalently, the eigenvectors of ${\mathit{Z}}^m=\frac{1}{m}{\mathit{X}}^{mT}{\mathit{X}}^m$, can be thought of as estimators of the column-space of the matrix G. So each right singular vector can be thought of as a linear combination of the common factors associated with the data for each feature. Because of this, the singular value decomposition has come to play a central role in the analysis of genome-wide gene expression (Alter et al., 2000) and genetic (Price et al., 2006) data.

There is a well-known duality between the singular value decomposition and principal components analysis (Holmes, 2001; Jolliffe, 2002). The asymptotic properties of both the singular value decomposition and the principal components of large factor models have been studied extensively. Anderson (1963), Anderson and Amemiya (1988) and Connor and Korajczyk (1993) studied the asymptotic properties for a fixed number of features as the sample size goes to infinity. Similarly, Paul and Peng (2009) considered maximum restricted maximum likelihood estimates of principal components under the assumption of Gaussianity. But unlike many traditional experiments, high-dimensional experiments in genomics have a small sample size and a much larger number of measured features (n << m). In this case it is more appropriate to consider asymptotic results for a fixed sample size and an infinite number of features. Asymptotic results for multiple testing follow this approach by considering the behavior of error rate estimates as the number of P-values goes to infinity (Storey, 2002; Storey et al., 2004). More recently, Fan et al. (2008) studied the sampling properties of the covariance matrix under the assumption of fixed sample size, but a large number of features. In this article I show that estimates of G in model (1) based on a scaled eigen-decomposition of Z^m are asymptotically consistent in the number of features for a fixed sample size. I also propose new estimators for the dimension, r, of G and show that they are consistent for the true dimension of G.

One application of these theoretical results is to use singular vectors to address multiple testing dependence. Leek and Storey (2008) recently proposed a general framework for multiple testing dependence based on estimating a dependence kernel for high-dimensional data. The dependence kernel is a low-dimensional set of vectors that quantifies the dependence in high-dimensional data. They suggest estimating the dependence kernel with surrogate variables, a set of low-dimensional vectors estimated from the data that approximate the dependence kernel. We show that when the dependence kernel is orthogonal to the model being tested a scaled eigen-decomposition of the least squares residuals from the high-dimensional data are consistent estimates of the surrogate variables. We demonstrate this approach in both simulated data and in removing batch and lab effects from gene expression data. The usual approach to removing batch effects involves using the date the arrays were processed as a surrogate for batch (Johnson et al., 2007). However, in general this surrogate does not capture all of the dependent variation in gene expression due to technical factors such as PCR, lab personnel, or different reagents. We show that the SVD captures both the effects quantified by the measured batch variable and by other unmeasured sources of bias.

2. Asymptotic Singular Value Decomposition

The SVD has been applied across a variety of disciplines to estimate common factors in high-dimensional data sets. Principal components analysis and factor analysis have been used to estimate eigengenes (Alter et al., 2000), common econometric factors (Connor and Korajczyk, 1993; Bai and Ng, 2002), latent covariates (Price et al., 2006; Leek and Storey, 2007), and for clustering (Yeung and Ruzzo, 2001). Anderson and Amemiya (1988) and Connor and Korajczyk (1993) studied the asymptotic properties of singular vectors and values in the limit of large sample sizes. Cui et al. (2003) consider the asymptotic behavior of a robust dispersion matrix, again for large sample sizes. Bai and Ng (2002) described an approach for consistently estimating the number of factors in the limit as both the number of features and the sample size grew large at defined rates. Solo and Heaton (2003) and Hallin and Liska (2007) also considered the problem of determining the number of factors as both m and n diverge. Neither of these assumptions is practical for a high-dimensional experiment such as a gene expression study, where the number of features is orders of magnitude larger than the number of samples. Here we fix the sample size, and consider the asymptotic properties of the eigenvectors and eigenvalues of a random matrix that consistently estimate the dimension, r, and latent factors, G, in model (1) as the number of features grows large.

2.1 Assumptions

We assume the data from a high-dimensional genomic experiment are distributed according to model (1), where u_j ~ F^m with E(u_j) = 0 and the u_ij mutually independent. We will consider the case where the number of features m is growing and hence the distribution of u_j will depend on m. We also assume the following properties hold.

1. $0<\mathrm{E}\left(u_{ij}^4\right)\le B$ and hence $0<\mathrm{var}\left(u_{ij}\right)={\sigma }_i^2\le B^{\ast }$ by Liapounov’s inequality.

2. $\underset{m\to \infty }{\lim }{\Vert \frac{1}{m}{\mathit{G}}^T{\Gamma }^{mT}{\Gamma }^m\mathit{G}-{\mathit{G}}^T\Delta \mathit{G}\Vert }_F=0$, where Δ is positive definite and ∥.∥_F is the Frobenius norm (Horn and Johnson, 1985).

3. G^TΔG has eigenvalues λ₁, … , λ_n where λ₁ > … > λ_r > λ_r+1 = … = λ_n = 0.

Here G is considered to be a fixed matrix of constants and Γ^m is a matrix of non-random constants that grows with the number of features m. These assumptions define a flexible class of distributions that represent most continuous high-dimensional data, such as gene expression data. The technical and biological constraints on microarray measurements generally imply assumption 1 holds for biological high-throughput data. For example, it is common to assume that log transformed microarray data are normally distributed (Konishi, 2004).

The remaining assumptions relate to the level and structure of influence of the factors in a high-throughput experiment. In high-dimensional data, the assumptions is that G is a fixed matrix and that Γ^m is a matrix of constants which grows with the number of features. For example, this is the usual model when performing a differential expression analysis. Typically, a relatively small subset of influential factors in a high-dimensional experiment will influence the data for many tests. Returning to the example of microarray data, key environmental and genetic factors have been shown to affect the expression for thousands of genes simultaneously (Alter et al., 2000; Price et al., 2006; Leek and Storey, 2007). Technical factors such as batch have also been shown to have a global impact on gene expression (Johnson et al., 2007). It is these common factors that we propose to estimate with the eigen-decomposition of Z^m.

2.2 Asymptotic Consistency of Eigenvalues and Eigenvectors

Given model (1) and assumptions 1-3 we now consider the problem of estimating the common factors G using the eigen-decomposition of Z^m. The eigenvectors of the matrix ${\mathit{Z}}^m=\frac{1}{m}{\mathit{X}}^{mT}{\mathit{X}}^m$ are equal to the right singular vectors of X^m, and the eigenvalues of Z^m are equal to the squared singular values of X^m divided by m. To obtain consistent estimates of the dimension of G, the matrix Z^m must be centered to account for the gene specific background variation. Centering by an estimate of the background variation ensures that the centered eigen-values corresponding to background noise will converge to zero. So instead of the singular value decomposition of X, we consider the eigenvalues, λ₁(W^m), … , λ_n(W^m), and eigenvectors, v₁(W^m), … , v_n(W^m), of the centered random matrix:

$$\begin{array}{cc}\hfill {\mathit{W}}^m=& \frac{1}{m}{\mathit{X}}^{mT}{\mathit{X}}^m-{\widehat{\sigma }}_{\mathit{ave}}^{2}I\hfill \\ \hfill {\widehat{\sigma }}_{\mathit{ave}}^2=& \frac{1}{m(n-\kappa )}{\Vert {\mathit{X}}^m-{\widehat{\Gamma }}_{\kappa }^m{V}_{\kappa }\left({\mathit{Z}}^m\right)\Vert }_F\hfill \\ \hfill =& \frac{1}{m}\sum _{i=1}^m\frac{1}{(n-k)}\sum _{j=1}^m{\left(x_{ij}-\sum _{k=1}^{\kappa }{\widehat{\gamma }}_{ik}^m{v}_{kj}\left(Z^m\right)\right)}^2\hfill \end{array}$$

where I is the n × n identity matrix, V_κ(Z^m) = {v₁(Z^m), … , v_κ(Z^m)} is a matrix of the first κ eigenvectors of Z^m, ${\widehat{\Gamma }}_k^m$ are the least squares estimates from the regression of X^m on V_κ(Z^m), ∥.∥_F is the Frobenius norm, defined as the sum of the squared elements of a matrix (Horn and Johnson, 1985), and κ > r. Under model (1) and assumptions 1-3, the eigenvectors and eigenvalues of this matrix converge almost surely to the true eigenvalues {λ_j(G^TΔG), j = 1, … , n} and eigenvectors {v_j(G^TΔG), j = 1, … , n} of G^TΔG.

Theorem 1

Suppose the data X have a distribution defined by model (1) and subject to assumptions 1-3, then:

$$\begin{array}{cc}\hfill & {\lambda }_j\left({\mathit{W}}^m\right){\to }_{a.s.}{\lambda }_j\left({\mathit{G}}^T\Delta \mathit{G}\right)j=1,\cdots ,n\hfill \\ \hfill & {\mathit{v}}_j\left({\mathit{W}}^m\right){\to }_{a.s.}{\mathit{v}}_j\left({\mathit{G}}^T\Delta \mathit{G}\right)j=1,\cdots ,r\hfill \end{array}$$

The proof of Theorem 1 and other theoretical results appear in supplementary appendix A. Theorem 1 implies that the eigenvectors corresponding to unique eigenvalues in model (1) consistently estimate the eigenvectors of G^TΔG for a fixed sample size, n, and diverging number of features, m. The matrix Z^m is centered by an estimate of the average background variation. Centering is necessary for convergence of the eigenvalues, but not required for almost sure convergence of the eigenvectors of Z^m to the eigenvectors of G^TΔG with unique eigenvalues. A corollary of Theorem 1 is that the first r right singular vectors of X are consistent for the first r eigenvectors of G^TΔG, which in turn span the same column space as G. As we will demonstrate in the next section, centering the matrix is important for identifying m-consistent estimators of the dimension of the column space of G based on the eigenvalues of W^m.

2.3 Consistent Estimation of r

Estimating the dimension, r, of G is a key step in any application of factor analysis to high-dimensional data. There are a large number of methods that have been developed for estimating the dimension of a factor model for data of both standard dimension, and for high-dimensional data. Graphical methods such as scree plots and heuristic cuto s based on the percent of variation explained are popular in a variety of disciplines (Hastie et al., 2001; Jolliffe, 2002). Permutation hypothesis tests based on permuting each row of the data matrix X to break cross-feature structure have also been proposed for estimating the significant singular vectors from a SVD (Buja and Eyuboglu, 1992). Bai and Ng (2002) showed that under the assumptions 1-3 and the following additional assumptions,

5. $\mathrm{E}\left[u_{ij}^8\right]\le B_3$

6. $\underset{n\to \infty }{\lim }\frac{1}{n}{\sum }_{j=1}^n{\mathit{g}}_j^T{\mathit{g}}_j={\Delta }_{\mathit{G}}$ where Δ_G is positive definite.

the number of factors in a principal component analysis can be consistently estimated as the number of features and the number of samples goes to infinity. The Bai and Ng estimate is:

$${\widehat{r}}_{bn}={\mathrm{argmax}}_k\log \left({\Vert {\mathit{X}}^m-{\widehat{\Gamma }}_k^m{\mathit{V}}_k\left({\mathit{Z}}^m\right)\Vert }_F\right)+k\left(\frac{m+n}{mn}\right)\log \left(\frac{mn}{m+n}\right).$$

where V_κ(Z^m) = {v₁(Z^m), … , v_κ(Z^m)} is a matrix of the first κ eigenvectors of Z^m, $b{\widehat{\mathit{Gamma}}}_k^m$ are the least squares estimates from the regression of X on V_κ(Z^m). The Bai and Ng (2002) estimates are useful in econometric data, where both the number of features and the sample size may be assumed to be large. But we will show in simulated examples that the Bai and Ng (2002) estimates may not behave well for data typically encountered in high-dimensional genomics applications where there are a large number of features and a relatively small sample size.

It is possible to consistently estimate the number of factors as only the number of features grows large. The number of non-zero eigenvalues of G^TΔG is equal to the dimension of the column space of the matrix G. Since the eigenvalues of the normalized random matrix, W^m, converge almost surely to the eigenvalues of G^TΔG, one potential estimator for the dimension r is the number of non-zero eigenvalues of W^m. But for any finite sample size, the eigenvalues of W^m will not exactly equal zero. Instead we estimate the dimension of W^m by the number of eigenvalues that are larger than a threshold based on the number of features m.

Lemma 1

Suppose the data follow model (1) and assumptions 1-3 hold where n is fixed. Then 1 {λ_k(W^m) ≥ c_m} →_P 1 for k = 1, … , r and 1 {λ_k(W^m) ≥ c_m} →_P 0 for k = r + 1, … , n provided c_m = O(m^−η), $0<\eta <\frac{1}{2}$.

Lemma 1 illustrates the importance of centering the matrix Z^m by an estimate of the average feature specific variances. Without centering, the eigenvalues of Z^m corresponding to the zero eigenvalues of G^TΔG converge to the unknown average of the feature specific variances. The indicator functions of Lemma 1 would then require an eigenvalue threshold that is dependent on the unknown row-wise variances. Lemma 1 also suggests a simple and asymptotically consistent estimate of r:

$$\widehat{r}=\sum _{k=1}^{n}1\left\{{\lambda }_k\right({\mathit{W}}^m)\ge c_m\}.$$

In the next section we will show this estimate of r may be a practically useful tool for estimating the number of significant factors in high-dimensional data using simulated examples with dimensionality typical of high-throughput experiments in genomics.

3. Simulation Results

In this section we demonstrate both the behavior of the right singular vectors from Theorem 1 and the estimate, $\widehat{r}$, defined in Lemma 1. We also compare the behavior of $\widehat{r}$ to the behavior of the Bai and Ng (2002) estimate, ${\widehat{r}}_{bn}$, and the permutation estimate defined in Buja and Eyuboglu (1992), ${\widehat{r}}_{be}$. Briefly, Buja and Eyuboglu (1992) calculate the singular values of the matrix X, then permute each row of the matrix individually, breaking the structure across rows. For each permutation, they recalculate the singular values of the permuted matrix and compare the ordered observed singular values to the ordered permuted singular values to obtain a P-value for each right singular vector. The estimate, ${\widehat{r}}_{be}$ of the number of factors is the number of P-values less than the Bonferroni corrected 0.05 significance level.

We simulated data varying the dimension of the data, (m, n) and the number of factors in the model, r. In each case, the elements of U were a random sample from the N(0, 1)distribution. We let the dimension m = 1000, 5000, and 10000 and the dimension n = 10, 20, and 100, which are typical values for the number of genes and arrays, respectively, in a microarray experiment. We set r = 3, 5, 10 and 18 and we sampled the elements of G from the Bernoulli(0.5) distribution. We choose the Bernoulli distribution since it is common to think of factors as dichotomous. However, all of the theoretical results presented here are conditional on a fixed value of G as the number of features grows large, which suggests that the distribution of G should not affect the accuracy of the estimates. Indeed, the qualitative behavior of the simulated examples is nearly identical when G is simulated from a normal distribution.

For each combination of parameters we simulated 100 data sets from model (1). We report the mean and standard deviation of the r estimates from Lemma 1 (c_m = nm^−1/3, e.g. $\eta =\frac{1}{3}$ and κ = n), Bai and Ng (2002), and Buja and Eyuboglu (1992). η was chosen near the center of the interval (0, 1/2) to avoid small sample biases. κ was set to be the sample size, since κ must be larger than the column dimension of G to hold and in practice the dimension of G is unknown. We also report the average and standard deviation of the root mean square Frobenius error (RMSFE) for the singular vector estimates. The RMSFE is defined as follows.

$$\mathrm{RMSFE}\{\mathit{G},{\mathit{V}}_{\widehat{r}}({\mathit{W}}^m\left)\right\}=\sqrt{\left\{{\Vert \mathit{G}-\widehat{\mathit{B}}{V}_{\widehat{r}}\left({\mathit{W}}^m\right)\Vert }_F+{\Vert {\mathit{V}}_{\widehat{r}}\left({\mathit{W}}^m\right)-\widehat{\mathit{A}}\mathit{G}\Vert }_F\right\}∕\left(nr\right)}$$

Where $\widehat{r}$ is the estimate of r from Lemma 1, ${\mathit{V}}_{\widehat{r}}\left({\mathit{W}}^m\right)=\left\{{\mathit{v}}_1\right({\mathit{Z}}^m),\dots ,{\mathit{v}}_{\widehat{r}}({\mathit{Z}}^m\left)\right\}$ is a matrix of the first $\widehat{r}$ eigenvectors of W_m, $\widehat{B}$ are the least squares regression estimates from the regression of G on ${\mathit{V}}_{\widehat{r}}\left({\mathit{W}}^m\right)$, $\widehat{A}$ are the least squares regression estimates from the regression of ${\mathit{V}}_{\widehat{r}}\left({\mathit{W}}^m\right)$ on G and ∥.∥_F is the Frobenius norm, defined as the sum of the squared elements of the matrix. If G spans the exact same linear space as ${\mathit{V}}_{\widehat{r}}\left({\mathit{W}}^m\right)$, $\mathit{RMSFE}\{\mathit{G},{\mathit{V}}_{\widehat{r}}({\mathit{W}}^m\left)\right\}=0$. The first component of the RMSFE quantifies how much of the linear space of G is explained by ${\mathit{V}}_{\widehat{r}}\left({\mathit{W}}^m\right)$ and the second quantifies the amount of the linear space of ${\mathit{V}}_{\widehat{r}}\left({\mathit{W}}^m\right)$ spanned by G. Including both terms ensures that the RMSFE will be non-zero whenever $\widehat{r}\ne r$.

The results in Table 1 show that the estimator defined by Lemma 1 performs as well or better than either the asymptotic estimates of Bai and Ng (2002) or the permutation approach of Buja and Eyuboglu (1992). It is not surprising that the Bai and Ng (2002) estimator behaves poorly when the sample size is much smaller than the number of features; the estimate was designed to consistently estimate the number of factors, r, as both (m, n) → ∞. The comparison is therefore meant only to illustrate that estimates focused on the situation where n ≪ m scenario are needed. The Bai and Ng (2002) estimator performs best when n = 100 and for smaller number of factors. The Buja and Eyuboglu (1992) estimator is relatively accurate across the range of dimensions presented here, although it underestimates r compared to the proposed approach.

Table 1.

Results from a simulation experiment. For each combination of m, n and r, 100 independent microarray data sets were simulated according to model (1), the average (s.d.) of the r estimates from Lemma 1, Bai & Ng (2002), and Buja & Eyuboglu (1992) are reported. The average (s.d.) RMSFE, a measure of how well the eigenvectors of W_m span the linear space spanned by G, is also reported.

(m, n)	r	$\widehat{r}$	${\widehat{r}}_{bn}$	${\widehat{r}}_{be}$	$\mathrm{RMSFE}\{\mathit{G},{\mathit{V}}_{\widehat{r}}({\mathit{W}}^m\left)\right\}\times {10}^5$
(1000,10)	3	2.87 (0.34)	2.40 (0.57)	2.74 (0.44)	403.84 (773.88)
(5000,10)	3	2.95 (0.22)	2.21 (0.43)	2.68 (0.47)	78.44 (271.25)
(10000,10)	3	2.94 (0.24)	2.24 (0.51)	2.69 (0.46)	50.18 (215.60)
(1000,20)	3	3.00 (0.00)	2.87 (0.33)	2.99 (0.10)	109.77 (23.18)
(5000,20)	3	3.00 (0.00)	2.90 (0.30)	3.00 (0.00)	22.49 (4.67)
(10000,20)	3	3.00(0.00)	2.96 (0.20)	3.00 (0.00)	10.42 (2.22)
(1000,100)	3	3.00 (0.00)	3.00 (0.00)	3.00 (0.00)	101.24 (7.29)
(5000,100)	3	3.00 (0.00)	3.00 (0.00)	3.00 (0.00)	20.26 (1.57)
(10000,100)	3	3.00(0.00)	3.00 (0.00)	3.00 (0.00)	10.11(0.82)
(1000,10)	5	4.20 (0.56)	3.21(0.57)	3.18 (0.52)	822.46 (624.17)
(5000,10)	5	4.62 (0.49)	3.21 (0.62)	3.25 (0.56)	224.48(309.48)
(10000,10)	5	4.77 (0.42)	3.38 (0.53)	3.37 (0.51)	129.70(245.14)
(1000,20)	5	4.79 (0.41)	4.33 (0.51)	4.75 (0.44)	395.34 (591.32)
(5000,20)	5	4.97 (0.17)	4.36 (0.50)	4.86 (0.35)	46.95 (151.17)
(10000,20)	5	4.99 (0.10)	4.47 (0.50)	4.86 (0.35)	18.00 (78.65)
(1000,100)	5	5.00 (0.00)	5.00 (0.00)	5.00 (0.00)	99.65 (7.22)
(5000,100)	5	5.00 (0.00)	5.00 (0.00)	5.00 (0.00)	20.11(1.31)
(10000,100)	5	5.00 (0.00)	5.00 (0.00)	5.00 (0.00)	10.10 (0.63)
(1000,20)	10	7.97 (0.58))	7.32 (0.65)	6.35 (0.74)	1108.28 (435.75)
(5000,20)	10	9.18 (0.66)	7.38 (0.60)	6.62(0.56)	297.95 (245.09)
(10000,20)	10	9.35 (0.52)	7.41 (0.55)	6.65 (0.58)	198.12 (164.99)
(1000,100)	10	10.00 (0.00)	10.00 (0.00)	10.00 (0.00)	96.40 (5.31)
(5000,100)	10	10.00 (0.00)	10.00 (0.00)	10.00 (0.00)	19.30 (1.06)
(10000,100)	10	10.00 (0.00)	10.00 (0.00)	10.00 (0.00)	9.60 (0.44)
(1000,20)	18	11.71 (0.62))	10.98(0.64)	7.12 (0.71)	1148.48 (273.08)
(5000,20)	18	13.22 (0.60)	11.00 (0.67)	7.39 (0.60)	497.17(144.31)
(10000,20)	18	13.86 (0.62)	11.00 (0.64)	7.46 (0.61)	336.51 (104.66)
(1000,100)	18	17.57 (0.56)	18.00 (0.00)	17.98 (0.14)	314.30 (293.42)
(5000,100)	18	18.00 (0.00)	18.00 (0.00)	18.00 (0.00)	17.88 (0.74)
(10000,100)	18	18.00 (0.00)	18.00 (0.00)	18.00 (0.00)	8.88 (0.34)

The values of r in Table 1 are for the most part much smaller than the sample size n, which is the expectation in practice for most biological experiments. Typically only a small number of technical or biological factors will have a global influence on the measurements for a large number of features. None of the approaches presented here are designed for the case where r > n, since there are only at most n right singular vectors. However the case of r = 18 and n = 20 gives some indication of how the estimates perform when the number of unmodeled factors nearly matches the sample size. In this case, it appears the proposed estimator performs slightly better than either the Buja and Eyuboglu (1992) or Bai and Ng (2002) estimates but all of the approaches consistently underestimate the true number of factors.

The results of Table 1 also indicate that the combination of dimension selection and singular value estimates are accurate even for the smallest number of features (1000), with small values of the RMSFE. The accuracy steadily increases as the number of features grows. In supplementary appendix C, a table of the values of RMFSE are shown for the three estimators. The table shows that accurately estimating r can have a large impact on the RMFSE, hence for small samples the proposed estimator produces much smaller values of RMFSE. Taken together, these results suggest that for the sample sizes and number of features typically encountered in a high-dimensional biology experiment, the right singular vectors are accurate estimates of the space spanned by the true underlying factors particularly when the dimension r is accurately estimated. Correctly estimating the appropriate linear space is important in multiple hypothesis testing, as will be illustrated in Section 5.

4. Practical Estimation of The Number of Factors

The consistency result in Lemma 1 can easily be shown to hold with the threshold c_m replaced with a × c_m where a is any fixed positive constant. In the limit the constant a does not have any effect, but in real examples the choice of a can be critical. Both the results of (Bai and Ng, 2002) and those proposed in this paper suffer from this limitation. A criteria for the practical selection of the number of factors based on consistency results like those proposed here was developed by Hallin and Liska (2007). The idea is to calculate the estimated number of factors using the threshold a × m^−η for a range of values of a and for an increasing set of features S₁ ⊂ S₂ ⊂ S₃, … ⊂ {1, … , m}.

The Hallin and Liska (2007) proceeds by plotting the estimated number of factors for the whole data set across a range of values of a. For each value of a, we also calculate the empirical variance of $\widehat{r}$, ${\widehat{\sigma }}^2\left(a\right)=\frac{1}{\ell }{\sum }_{i=1}^{\ell }{\left(\widehat{r}\right(a,S_i)-\stackrel{‒}{r}(a,\cdot \left)\right)}^2$, where $\widehat{r}(a,S_i)$ is the estimated number of factors at value a, set size S_i, and $\stackrel{‒}{r}(a,\cdot )=\frac{1}{\ell }{\sum }_{i=1}^{\ell }\widehat{r}(a,S_i)$. The estimated number of factors and the empirical variance are both plotted versus the threshold a. Hallin and Liska (2007) suggested that a useful practical criteria is to estimate the number of factors by the value of $\widehat{r}$ at the second “stability interval”, or the second interval where the variance is small.

Figure 1 shows an example of this approach applied to a simulated data set with 1000 genes, 20 arrays, r = 3, and $\eta =\frac{1}{3}$. In general, any value $0<\eta <\frac{1}{2}$ can be used with the Hallin and Liska (2007) estimator, although values near the middle of the range avoid potential biases due to a small number of features. The plot shows the estimated number of factors using the whole data set for a range of values of a (blue) and the variance for each value of a (red). The second stability point (green bracket) is the second place, moving from left to right, where the variance of the estimate reaches a trough. Hallin and Liska (2007) suggest using the estimate corresponding to this second stability point as a practical choice for the number of factors in the factor model. The estimate at the second stability point is $\widehat{r}=3$. In supplementary appendix B, figures 1-8 the Hallin and Liska (2007) approach is applied to eight simulated data sets for varying r. For r = 3, 5, 10 the approach produces a clear and correct estimate of $\widehat{r}$.

Figure 1.

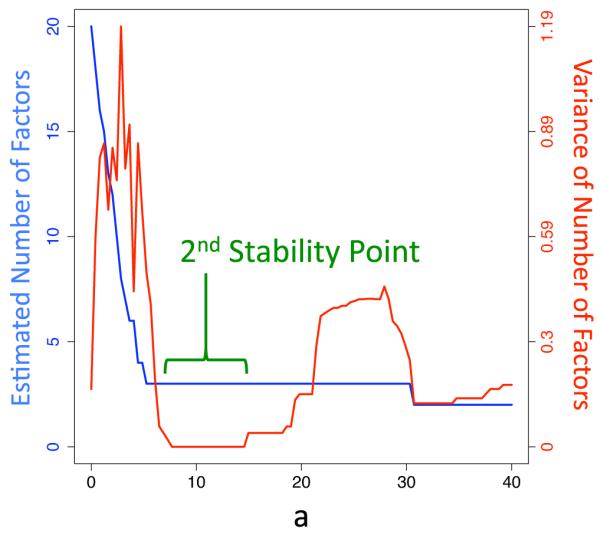
A plot of the estimated number of factors $\widehat{r}$ (blue and left axis) and the empirical variance of the estimate for varying set sizes (red and right axis) across a range of coefficients a. The second stability point (green bracket) is the second point, moving from left to right, where the variance finds a trough. Hallin & Liska (2007) suggest using the estimate corresponding to this second stability point as a practical estimator of the number of factors.

5. Example: Application to Genomics

In high-throughput experiments, the goal typically is to assess the effect of one or more factors on the gene expression levels across a very large set of genes. This process generally involves application of multiple testing procedures. In this type of analysis, it is necessary to account for possible dependence across the genes, which may arises from batch effects or other important biological or technical source of variability. Recently, Leek and Storey (2008) showed that the dependence can be satisfactorily characterized in terms of a “dependence kernel” matrix of low column dimension. The results of Theorem 1 and Lemma 1 in the present paper can be used to estimate this matrix.

We illustrate this process on a data set from Johnson et al. (2007). The goal of this study was to assess the effect of exposure to nitric oxide (NO) on gene expression. The investigators collected NO-exposed and control samples at the time of transcription inhibition and 7.5 hours later. A total of 21,171 genes were assessed. The measurement of gene expression levels was carried out in two batches (Table 1). Batch is a surrogate for a number of unmeasured variables, such as which reagents were used, which people processed the microarrays, and what the lab conditions were when those arrays were processed. All of these variables can lead to dependence across genes, which may bias significance analyses. The usual approach to adjusting these effects is to simply fit a model including the measured batch variable (Johnson et al., 2007). As we will show, this approach may miss important sources of dependence across genes. The surrogate variable approach captures both the variation quantified by the batch variable and additional important sources of dependence across genes.

The approach to the problem, in a general setting, is as follows. Suppose that high-throughput data are distributed according to the model:

$${\mathit{X}}^m={\mathit{B}}^m\mathit{S}+{\mathit{E}}^m$$ (2)

where B^m is an m × d matrix of coefficients, S is a d × n design matrix, and $e_j\sim F_e^m$ where $F_e^m$ is an m-dimensional multivariate distribution allowing for dependence across features. Leek and Storey (2008) showed that there exists a decomposition:

$${\mathit{X}}^m={\mathit{B}}^m\mathit{S}+{\Gamma }^m\mathit{G}+{\mathit{U}}^m$$ (3)

where the elements of $u_j\sim F_u^m$ are independent across rows. They also show that knowing and including the matrix G when fitting model (3) results in independent parameter estimates and inference across features. Leek and Storey (2008) call G a dependence kernel for the data X. When G is orthogonal to S, then a corollary of Theorem 1 gives a consistent estimator of the G matrix.

Corollary 1

Suppose high-throughput data are distributed according to model (3), where Γ, G, and U^m follow assumptions 1-3 and G is orthogonal to S. Let ${\mathit{R}}^m={\mathit{X}}^m-{\widehat{\mathit{B}}}^m\mathit{S}$ be the residuals obtained from the least squares fit using model (2) and let ${\mathit{W}}_{\mathit{R}}^m={\mathit{R}}^{mT}{\mathit{R}}^m-{\widehat{\sigma }}_{\mathit{ave}}^2{P}_{\mathit{S}}$ where P_S = I−S^T (SS^T)⁻¹S, ${\widehat{\sigma }}_{\mathit{ave}}^2=\frac{1}{m(n-\kappa -d)}{\Vert {\mathit{X}}^m-{\widehat{\Gamma }}_{\kappa }^m{\mathit{V}}_{(\kappa +d)}\left({\mathit{Z}}^m\right)\Vert }_F$, and κ > r. Then:

$$\begin{array}{cc}\hfill & {\lambda }_j\left({\mathit{W}}_{\mathit{R}}^m\right){\to }_{a.s.}{\lambda }_j\left({\mathit{G}}^T\Delta \mathit{G}\right)j=1,\cdots ,n\hfill \\ \hfill & {\mathit{V}}_j\left({\mathit{W}}_{\mathit{R}}^m\right){\to }_{a.s.}{\mathit{v}}_j\left({\mathit{G}}^T\Delta \mathit{G}\right)j=1,\cdots ,r\hfill \end{array}$$

In other words, the first r right singular vectors of the residual matrix formed by regressing out the model, S, consistently estimate the dependence kernel, G, as the number of features goes to infinity. The requirement that G and S be orthogonal is strong, however there are a number of special cases where this assumption may hold exactly or approximately. For example, in the current application, the batch and the biological group vectors are balanced and orthogonal. Many high-dimensional biology studies are designed such that technical factors are orthogonal to the group variable. In a randomized study the orthogonality of biological and technical factors with the groups of interest may approximately hold. Similarly, in experiments combining genetic data with gene expression data randomized inheritance of alleles may lead to genetic variation that is approximately orthogonal to population or group differences.

Of course, it is also important to estimate the unknown dimension, r, of the dependence kernel. A corollary of Lemma 1 motivates a consistent estimate of the dimension of the row-space of G.

Corollary 2

Suppose the data follow model (3) and assumptions 1-3 hold where n is fixed. Then $1\left\{{\lambda }_k\right({\mathit{W}}_{\mathit{R}}^m)\ge c_m\}{\to }_{P}1$ for k = 1, … , r and $1\left\{{\lambda }_k\right({\mathit{W}}_{\mathit{R}}^m)\ge c_m\}{\to }_{P}0$ for k = r + 1, …, n provided $c_m=O\left(m_{-\eta }\right),0<\eta <\frac{1}{2}$.

As before, we can use corollary 2 to define a consistent estimate of r as m → ∞:

$$\widehat{r}=\sum _{k=1}^{n}1\left\{{\lambda }_k\right({\mathit{W}}_{\mathit{R}}^m)\ge c_m\}.$$

We now present the application of the foregoing procedure to the Johnson et al. (2007) microarray data set. We first show what happens under a naive analysis where inter-gene dependence is ignored. We fit the simple linear model for the expression, x_ij, of the ith gene on the jth array.

$$\begin{array}{cc}\hfill x_{ij}& =b_{i0}+b_{i1}1({\text{Treat}}_j=\mathit{NO})+b_{i2}1({\text{Time}}_j=7.5)\hfill \\ \hfill & +b_{i3}1({\text{Treat}}_j=\mathit{NO}).1({\text{Time}}_j=7.5)\hfill \end{array}$$ (4)

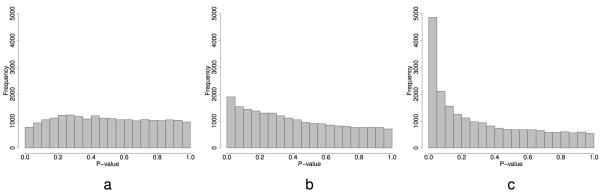
Then we test the null hypothesis that the interaction between treatment and time is zero (b_i3 = 0) for each gene. Performing this analysis for each gene, and calculating a P-value for each gene based on the Wald statistic results in the distribution of P-values in Figure 2a. The P-values have unusual behavior; they are stochastically greater than the uniform. Leek and Storey (2007) demonstrated that this behavior may be due to unmodeled factors influencing the expression of thousands of genes. In this case, equation (4) ignores the effect of batch on gene expression. We can also see this effect in the correlation among genes. For each gene we can calculate the residuals from model 4, then we can look at a randomly sampled set of 1,000 genes from the data set. The distribution of pairwise correlations has mean (s.d.) 0.08 (0.45) which is significantly greater than zero, suggesting there is at least one factor inducing correlation between genes.

Figure 2.

Histograms of the P-values from testing for a time-treatment interaction in the Johnson et al. (2007) data set. a) The P-values from an analysis without adjusting for the batch variable. b) The P-values from an analysis adjusting for a factor model for batch. c) The P-values from an analysis adjusting for the eigenvectors $v_1\left(W_R^m\right)$ and $v_2\left(W_R^m\right)$.

Next, we show what happens when the measured batch variable is entered into the model explicitly. We fit a model including the batch effect,

$$\begin{array}{cc}\hfill x_{ij}& =b_{i0}^{\ast }+b_{i1}^{\ast }1({\text{Treat}}_j=\mathit{NO})+b_{i2}^{\ast }1({\text{Time}}_j=7.5)\hfill \\ \hfill & +b_{i3}^{\ast }1({\text{Batch}}_j=1)+b_{i4}^{\ast }1({\text{Batch}}_j=2)+b_{i5}^{\ast }1({\text{Treat}}_j=\mathit{NO}).1({\text{Time}}_j=7.5)\hfill \end{array}$$ (5)

and test the null hypothesis that the interaction between treatment and time is zero ($b_{i5}^{\ast }=0$) for each gene using the Wald test, we get the distribution of P-values in Figure 2b. The P-values in this case take the familiar form from a multiple testing experiment with a large number of small P-values corresponding to the alternative distribution, mixed with a uniform distribution corresponding to the null. However, if we fit model (5) to each gene and calculate residuals, the distribution of pairwise correlations between genes still has a nonzero mean (s.d.) of 0.08 (0.51), very similar to the correlations when batch is ignored.

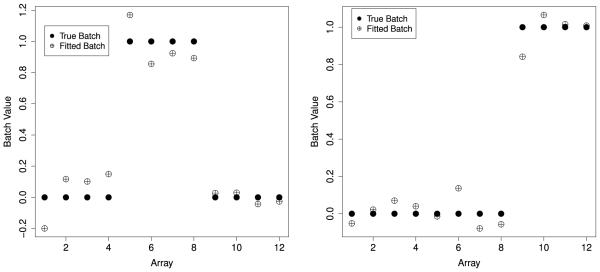
Finally, we show what happens when the methods of this paper are used to parse the inter-gene dependence. The first step is to estimate the dependence kernel matrix, G. We let S be the design matrix from model 4 including the treatement, time, and time-treatment interaction terms. If the dependence kernel, G, only consisted of the design matrix corresponding to a factor model for batch, then G and S would be orthogonal orthogonal (Table 2). Application of Corollary (2) in combination with the Hallin and Liska (2007) approach from Section 4 results in an estimate of $\widehat{r}=3$. Then using the result of Corollary (1) we calculate an estimate of the linear space of G as the first two eigenvectors of ${\mathit{W}}_{\mathit{R}}^m$. Figure 3 shows the two components of the true batch variable, and the fitted values from the regression of the true batch on the eigenvectors of ${\mathit{W}}_{\mathit{R}}^m$. The adjusted multiple R² values for the two components are 0.92 and 0.97, respectively. These results indicate that the singular vectors capture most of the variation due to the measured batch variable.

Table 2.

Sample description for data set 1 from Johnson et al. (2007).

Sample	1	2	3	4	5	6	7	8	9	10	11	12
Treatment (C = Control)	C	C	NO	NO	C	C	NO	NO	C	C	NO	NO
Time (hours)	0	7.5	0	7.5	0	7.5	0	7.5	0	7.5	0	7.5
Batch	1	1	1	1	2	2	2	2	3	3	3	3

Figure 3.

A plot of the true indicators 1(Batch_j = 2) and 1(Batch_j = 3) and the fitted values from the regression of the indicator functions on the estimated eigenvectors ${\mathit{v}}_1\left({\mathit{W}}_{\mathit{R}}^m\right)$ and $v_2\left({\mathit{W}}_{\mathit{R}}^m\right)$, the correlation between the true value and the fitted value is 0.72 for the left panel and 0.79 for the right panel.

We now repeat the analysis of the NO effect with the eigenvectors entered into the model to reduce the dependence due to batch. We performed the significance analysis for the time-treatment interaction using the following model.

$$\begin{array}{cc}\hfill x_{ij}& =b_{i0}^e+b_{i1}^{e}1({\text{Treat}}_j=\mathit{NO})+b_{i2}^{e}1({\text{Time}}_j=7.5)+b_{i3}^e{v}_{1j}\left({\mathit{W}}_{\mathit{R}}^m\right)\hfill \\ \hfill & +b_{i4}^e{v}_{2j}\left({\mathit{W}}_{\mathit{R}}^m\right)+b_{i5}^e{v}_{3j}\left({\mathit{W}}_{\mathit{R}}^m\right)+b_{i6}^{e}1({\text{Treat}}_j=\mathit{NO}).1({\text{Time}}_j=7.5)\hfill \end{array}$$ (6)

Again we tested the null hypothesis that the treatment-time interaction is zero ($b_{i6}^e=0$) using the Wald test. Figure 2c is a histogram of the P-values obtained from model (6). Since the eigenvectors capture most of the variation due to the batch variable, it is expected that the behavior of the P-values from the analysis adjusted for the eigenvectors would show similar characteristics to the analysis adjusted for batch. The eigenvector-adjusted P-values, like the P-values including the true batch adjustment, have the expected form for P-values from a multiple hypothesis testing experiment, with a number of small P-values mixed with a uniform distribution. However, after fitting model (6) and calculating residuals, the mean (s.d.) pairwise correlation among genes 6.24 × 10⁻³(0.46) is much smaller than for either the naive analysis or the analysis including the measured batch variable. This suggests that the SVD better captures the dependence across genes than even the measured batch variable.

Quantitatively, adjustment for the eigenvectors and adjustment for the true batch variable give similar results. The correlation between the P-values adjusted for batch and the P-values adjusted for the eigenvectors is 0.90. Meanwhile, the estimated proportion of true nulls tests is 0.68 for the batch adjusted analysis and 0.52 for the eigenvector analysis, but 0.95 for the unadjusted analysis. Taken together, these results indicate that the eigenvectors account for the dependent variation due to the batch variable, but also other unmodeled sources of dependence that may not be captured by the measured batch variable, which improves significance. This is not surprising, since batch is only a surrogate for the truly important unmeasured confounders in a molecular biology experiment.

6. Discussion

We showed that right singular vectors of a high-dimensional data matrix are asymptotically consistent for latent factors in a factor model for high-dimensional data (1) with a fixed sample size and diverging number of features. These results provide a justification of the singular value decomposition both as a tool for discovering structure in high-dimensional data and as estimates of surrogate variables for multiple testing dependence. we also proposed a new estimator for the number of significant factors in a high-dimensional data set based on the scaled eigenvalues of the high-dimensional data. This new estimator behaves well for the sample sizes and number of features commonly encountered in high-throughput genomic studies. Application of these new estimators resulted in accurate estimates of an unmodeled batch variable, and correction of dependence between genes in a study of the relationship between nitric oxide and gene expression. Using the SVD in place of the measured batch variable is more effective, since batch is usually a surrogate for a large number of unmeasured confounders. The results presented in this paper assume a flexible class of continuous distributions that describe most quantitative high-throughput data. An interesting avenue for future research is to investigate the asymptotic behavior of singular vectors and values for binary data, which are often encountered in high-throughput genetic experiments.