A model of calcium-activation of the cardiac thin filament

Abstract

The cardiac thin filament regulates actomyosin interactions through calcium-dependent alterations in the dynamics of cardiac troponin and tropomyosin. Over the past several decades many details have been discovered regarding the structure and function of the cardiac thin filament and its components. We propose a dynamic, complete model of the thin filament that encompasses known structures of cardiac troponin, tropomyosin and actin and show that it is able to capture key experimental findings. By performing molecular dynamics simulations in two conditions, one with calcium bound and the other without calcium bound to site II of cardiac troponin C (cTnC), we found that subtle changes in structure and protein contacts within cardiac troponin resulted in sweeping changes throughout the complex that alter tropomyosin (Tm) dynamics and cardiac troponin-actin interactions. Significant calcium-dependent changes in dynamics occur throughout the cardiac troponin complex resulting from the combination of: secondary structural changes in the N-lobe of cTnC at and adjacent to sites I and II and the link between them; secondary structural changes of the cardiac troponin I (cTnI) switch peptide, the mobile domain, and in the vicinity of residue 25 of the N-terminus; secondary structural changes in the cardiac troponin T (cTnT) linker and Tm-binding regions; and small changes in cTnC-cTnI and cTnT-Tm contacts. As a result of these changes, we observe large changes in the dynamics of the following regions: the N-lobe of cTnC; the mobile domain of cTnI; the I-T arm; the cTnT linker; and overlapping Tm. Our model demonstrates a comprehensive mechanism for calcium-activation of the cardiac thin filament consistent with previous, independent experimental findings. This model provides a valuable tool for research into the normal physiology of cardiac myofilaments and a template for studying cardiac thin filament mutations that cause human cardiomyopathies.

The Ca²⁺-based control of cardiac muscle function has long been known to reside in the thin filament. A molecular level understanding of this control, both in health and disease, is not fully available. The work reported in this article presents a fully atomistic model of the cardiac troponin (cTn) complex in interaction with tropomyosin (Tm). This model represents the culmination of our efforts(1, 2) to apply molecular dynamics simulations to clarify, on a molecular level, the function of the thin filament. The question we are addressing is: Can a complete, dynamic model of the thin filament be constructed that captures both known structural elements and experimental findings? If so, we believe it will: 1) assist in describing how various, isolated findings can coexist; 2) reveal new details involving thin-filament activation; and 3) provide a useful tool for investigators.

Calcium-activation of the thin filament results from cTn’s allosteric regulation of Tm dynamics on actin.(3, 4) cTn is a complex consisting of three subunits, each of which interacts with the other two. Cardiac troponin C (cTnC) is the site of Ca²⁺-specific binding at site II in the N-lobe of cTnC. Cardiac troponin I (cTnI), the inhibitory subunit, is responsible for inhibition of actomyosin ATPase activity via its interactions with actin(3–5) and forming key inter-subunit interactions, including the formation of a stable coiled coil with cTnT.(6, 7) Cardiac Troponin T (cTnT) is a link between the calcium-binding core region of cTn and Tm. From structural and biochemical evidence, cTnT-Tm interactions are likely a key step of Ca²⁺-signaling propagation between cTn and Tm.(7–9)

The cTn complex can be divided into two regions: a rather stationary globular core domain consisting of portions of cTnC, cTnI, and cTnT;(10) and two highly variable regions consisting of the region of cTnT that interacts with Tm and the mobile domain of cTnI that interacts with actin.(7) The flexibility of various regions throughout cTn appears to be fine-tuned, making them sensitive to mutations.(1, 2) We hypothesize cTn is also finely tuned to propagate changes in dynamics as a result of Ca²⁺-binding.

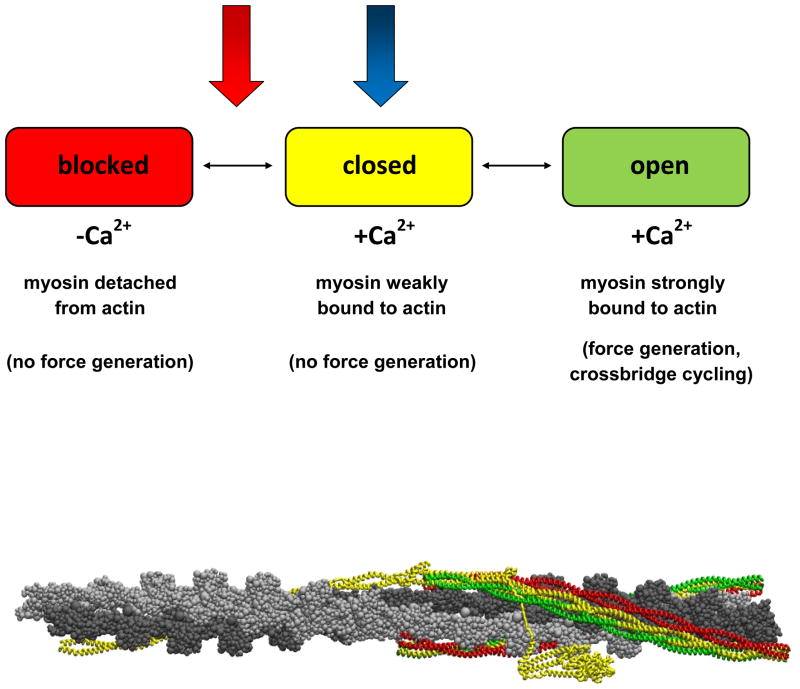
Tm, a long, flexible coiled-coil that bends anisotropically,(11) is in equilibrium between three states of myosin-actin-troponin binding: blocked (Ca²⁺ not bound to troponin C, myosin not bound to actin); closed (Ca²⁺ bound to troponin C, myosin weakly bound to actin); and open (Ca²⁺ bound to troponin C, myosin strongly bound to actin).(12, 13) Only when Tm is in the open state does one observe actomyosin ATPase activity necessary for force generation of the actin-myosin crossbridge.(13, 14) Ca²⁺-binding to cTnC alone is necessary but not fully sufficient to explain Ca²⁺-activation of the thin filament.(15) A Ca²⁺-induced signal must propagate through the cTn complex, beginning with Ca²⁺-binding in cTnC and ending with cTnT’s interactions with Tm, in order for cTn to regulate Ca²⁺-activation of the thin filament. The atomic level mechanism of this propagation remains obscure, and at the present time, is not accessible via experiment alone.

It was the ability to study the subtle structural and dynamic effects of mutation of this system, along with the possibility of obtaining an atomic level understanding of the function of the thin filament, that motivated the work in this article. In order to investigate the Ca²⁺-based regulation of cardiac tissue, a complete model of cTn is necessary. We have constructed a complete, dynamic, atomistic model of cTn in conjunction with overlapping Tm to simulate cTn in two states: Ca²⁺ bound (Ca²⁺-saturated) and Ca²⁺ not bound (Ca²⁺-depleted) to site II of the N-lobe of cTnC. This model, the validation presented herein, and its application to calcium control of the cardiac sarcomere is part of our long term goal of an integrated computational and experimental elucidation of the mechanisms of thin filament regulation and disease causing thin filament mutations in cardiac tissue.

We demonstrate that it is possible to construct a dynamic, atomistic model of the entire cTn complex at all temperatures. With this model we find significant changes in dynamics throughout the cTn subunits as a result of Ca²⁺-binding to site II of cTnC, representing equilibrium states of the closed state and a position between the closed and blocked. We also show that these alterations in cTn dynamics effectively propagate through the cTn complex, resulting in changes to the dynamics of the overlapping region of Tm. Our goal is to make this work accessible to the widest range of biochemists and in particular people beyond the pure simulation community. For this reason, we have elected to put much of the numerical detail in the supporting information.

Methods

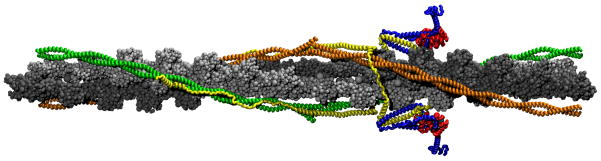
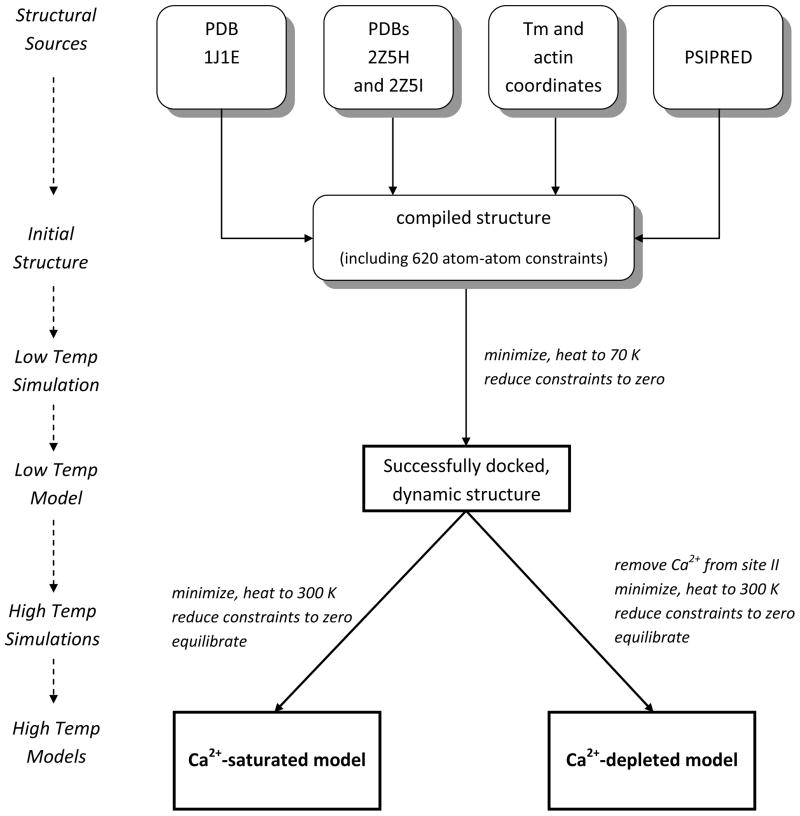
We constructed a thin filament consisting of cTn and overlapping Tm in the closed state oriented to an actin backbone by synthesizing numerous existing atomistic models, including: an atomistic model of the cTn core complex from PDB ID 1J1E,(7) an atomistic model of Tm based on the Lorenz-Holmes model,(16, 17) an overlapping model of Tm based on PDB ID 2Z5I,(9) cTnT-Tm interactions based on PDB ID 2Z5H,(9) and an atomistic model of the thin filament including actin, non-overlapping Tm and the cTn core.(10) Missing regions of cTn were constructed using secondary structure prediction (PSIPRED)(18, 19) and homology with chicken fsTn.(20). The biochemical stoichiometry of the thin filament 7:1:1 (actin:Tm:cTn) may be more accurately described in this case as 14:2:1, where one cTn requires two overlapping Tm to properly bind, thus requiring 14 actin monomers and two Tm per each cTn. Figure 1 shows our model. 14 actin monomers colored in silver are associated with the two green overlapping Tm linked to the top cTn. The second set of 14 actin monomers colored dark gray in Figure 1 are associated with the orange overlapping Tm linked to the bottom cTn. A schematic of the detailed method by which we built our model is diagrammed in Figure 2.

Figure 1.

Representation of the human thin filament containing human cTn, Tm and actin: yellow=cTnT; blue=cTnI; red=cTnC; cyan=calcium ion; green/orange=overlapping Tm; silver/gray=actin filament (The same color scheme is used in the provided movies, except calcium ions in the movie are colored black vice cyan). This figure was obtained by orienting the cTn and Tm to an actin backbone, docking cTnT to overlapping Tm, and performing a 50 ps simulation in equilibrium at 70 K using CHARMM version 33b1(23) of cTn and the overlapping Tm without actin. The resulting cTn-Tm complex is shown here in duplicate with actin added.

Figure 2.

Schematic of the building and simulation processes of our model.

The thin filament was constructed in the closed state by fixing non-overlapping tropomysin in the closed positions on actin while cTn and overlapping tropomyosin were allowed to move freely. Two cTn atoms were held in place with harmonic constraints of 2 kcal/mol/ to anchor cTn over actin (see Supporting Information sections 1–10).

In the construction of our model we used 629 pertinent “known” interactions of cTn, Tm, and cTn-Tm. This includes 620 protein-protein interactions and 9 water bridge interactions based on PDB ID 1J1E, 2Z5H, and 2Z5I.(21) (rf. to Supporting Information, “Protein-protein interactions”) These atom-atom interactions were simulated using NOE constraints in CHARMM version 33b1 but were relaxed to zero as the model stabilized.(22, 23) NOE constraints are designed to introduce a distance restraint between two atoms, using harmonic forces to guide the system toward an optimal equilibrium state. In this case the optimal equilibrium state was expected to satisfy the structural conditions provided by PDB ID 1J1E, 2Z5I and 2Z5H without NOE constraints in place, which was successfully accomplished. The total cTn-Tm-Tm complex consists of 28,847 atoms, including 1,781 residues, four waters, and three calcium ions.

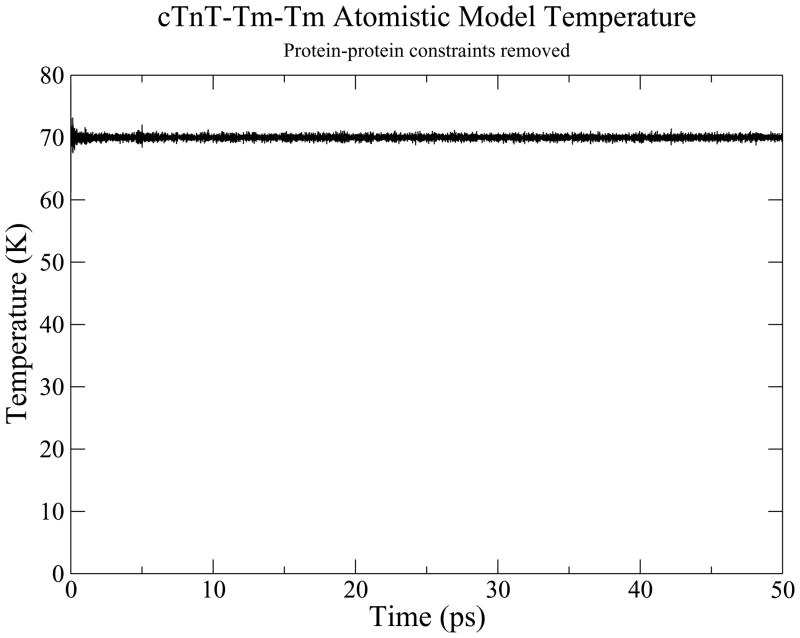
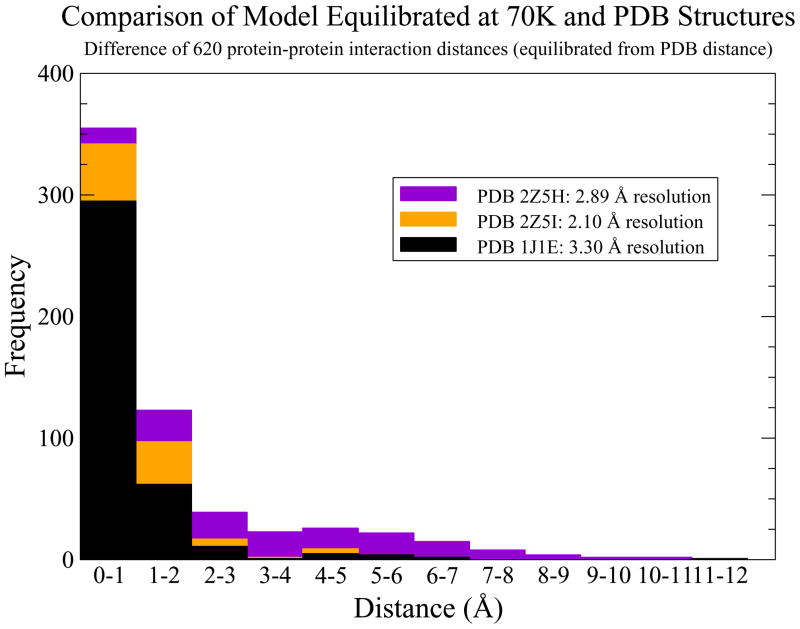
An initial simulation was performed to finalize the building of our model, specifically to dock the N-tail of cTnT to overlapping Tm while orienting the rest of cTn to actin. A 30 ps simulation was performed at cryogenic temperature while the NOE constraints were gradually reduced to zero. The resulting structure successfully reached thermodynamic equilibrium as shown by Figure 3 and was allowed to evolve for 50 ps. We validated this low temperature model by subtracting equilibrium atom-atom distances of our model from atom-atom distances of the structural sources. The results, shown in Figure 4, prove that our low temperature dynamic model is faithful to its separate structural sources. We used this low temperature structure as a common starting structure for simulations at physiologic temperature.

Figure 3.

Temperature monitoring for 50 ps equilibration of docked cTn-Tm complex.

Figure 4.

Histogram of the absolute value of equilibrated atom-atom distances subtracted from PDB atom-atom distances to demonstrate the validity of the model.

We took two thin filament models at low temperature and removed a calcium ion from site II of cTnC from one of them. The two models were then subjected to identical minimization, heating, and equilibration conditions. They were minimized by alternating the SD and ABNR methods until energy optimized (final gradient less than 0.0001 kcal/mol/Å), then the Berendsen thermostat was used to gradually heat the systems from 0K to 300K over 30 ps. Upon reaching 300 K, non-overlapping regions of tropomyosin were constrained in their closed state positions while allowing the overlapping region of Tm to move freely; harmonic force constraints of 2 kcal/mol/Ų were placed on C_α of residues 205 and 277 cTnT while the remainder of cTn was allowed to move freely. The system was again allowed to equilibrate for 30 ps in this free state. The system was now evolved for 1 ns.

We recognize that one ns simulations will seem relatively short to the general population; however, one ns simulations of a system this size are at the limit of current computational possibilities and preclude its explicit solvation. It has been shown that multiple short simulations are more likely indicative of molecular behavior than a single long simulation;(30) therefore, we ran 12 separate simulations with random initial conditions, six with and six without calcium in site II. We show the results of one below, but we report that qualitatively all results are the same for the remaining simulations.

This provided us with equilibrium MD simulations of the entire cTn-overlapping Tm complex virtually free of constraints whose starting structures differed only by a single atom, a Ca²⁺ ion in site II cTnC. These represent our calcium-saturated and calcium-depleted state models at physiologic temperature. Figure 5 identifies where these two models fall within the three-state model. The calcium-saturated model is the thin filament in the closed state; the calcium-depleted model is the thin filament without calcium bound between the closed and blocked state. Our calcium-depleted model is not entirely in the blocked state because the non-overlapping tropomyosin remains fixed in the closed state.

Figure 5.

Tm explores three states of equilibrium (blocked, closed, and open) while the cTn core remains relatively stationary with respect to actin,(10) This system is in constant flux between the three equilibrium positions of Tm, where an entire cardiac contraction cycle involving all three of these states is on the order of 100 ms.(15) We investigate how calcium directly affects the regulatory proteins cTn and Tm by looking at two representative equilibrium states with 1 ns simulations in the closed state and a position between the closed and blocked states and by comparing the changes between them. These two states are represented by the blue and red arrows, representing the Ca²⁺-saturated and Ca²⁺-depleted state, respectively.

The simulations were visualized with VMD(24). Root mean square fluctuation (RMSF), hydrogen bond (cutoff of 2.4 Å), and and root mean square deviation (RMSD) analyses were performed using CHARMM version 33b1.(22, 23) Only the backbone atoms (amine N, C_α, and carboxyl C) were used in calculating RMSF and RMSD. Secondary structure analyses were performed with STRIDE.(25) Contact maps were constructed using SPACE.(26)

Statistical Methods

The nature of proteins and protein dynamics present unique challenges in analysis of their data. The data from these simulations are complex multivariate data clearly correlated by the nature of their peptide bonds as well as their secondary, tertiary, and quaternary structure interactions. Both RMSF and hydrogen bond data appear to follow a gamma distribution pattern. There does not appear to be a standard statistical technique to address the analysis of our data since it is non-linear, highly correlated, and non-Gaussian in nature. Because of this, the method of generalized estimating equations (GEE) appears to be a good choice to compare Ca²⁺-saturated and Ca²⁺-depleted data. GEE is a general method for analyzing longitudinal data that is correlated.(27) A gamma model was fit with an inverse link function using an independent working correlation matrix with the robust sandwich variance estimator.(28, 29) Statistical analyses were conducted with the software package R 2.11.1 for Windows. The test statistic used with GEE in R is the Wald test statistic.(29) p<0.05 is defined as statistically significant.

Results and Discussion

Files containing 3D structural information for the cTn-Tm complex in the Ca²⁺-saturated state at low temperature, Ca²⁺-saturated state at physiologic temperature, and Ca²⁺-depleted state at physiologic temperature are available in PDB format. Movies of the 1 ns simulations at 300 K in the Ca²⁺-saturated and Ca²⁺-depleted states prepared in VMD are available in Moving Picture Expert Group (.mpg) format. Similarly prepared movies of the switch peptide of cTnI interacting with the N-lobe of cTnC in the Ca²⁺-saturated and Ca²⁺-depleted states are also available.

Low Temperature Simulation

The results of our low temperature simulation show that it is possible to create a complete, dynamic model from multiple structural models. The temperature of the system for the 50 ps equilibration phase of the low temperature simulation, shown in Figure 3, demonstrates that the system is in thermodynamic equilibrium. The RMSD over the course of equilibration decreased from 8 Å to about a constant of 1 Å. The cTnT-Tm NOE constraints effectively docked TNT1, an N-terminal domain of cTnT, to the overlapping Tm with close similarity to the distance constraints detailed by PDB ID 2Z5H and 2Z5I, as shown in Figure 4. With all NOE constraints removed, 81% of the 620 dynamic protein-protein interactions differ by less than 4 Å from the static structural solutions. The resolution of the various crystal structures against which these equilibrated, dynamic distances are being compared ranges from 2.10 to 3.30 Å. The majority of differences fall within 0–2 Å, reflecting a high degree of fidelity. The overall structure of our model displays a similar appearance to recent experimental results including the close association of the N-tail of cTnT with Tm.(31)

Physiologic Temperature Simulations

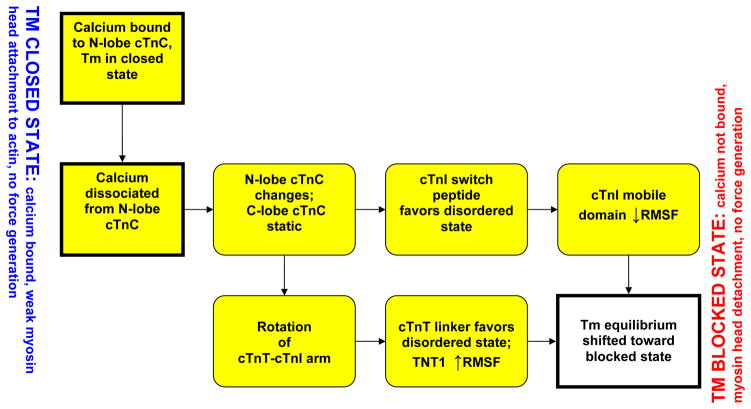
We observe two major routes by which cTn dynamics are able to shift Tm equilibrium toward the closed state as a result of the removal of a calcium ion from site II of cTnC, summarized in Figure 6. First, the known, direct interactions of the N-lobe of cTnC with the switch peptide of cTnI causes fluctuations of the inhibitory and mobile domains of cTnI favoring favor the shift in Tm equilibrium toward the blocked state.(32, 33) Second, the changes in the N-lobe of cTnC alter the apex of the I-T arm while interactions between the static C-lobe of cTnC and cTn-actin stabilize the base of the I-T arm; thus, causing a rotation of the I-T arm. These changes in the I-T arm propagate downstream through the cTnT linker to overlapping Tm via the cTnT-Tm interactions ultimately causing significant changes in overlapping Tm.

Figure 6.

A schematic of the two prong mechanism of Ca²⁺-activation of the thin filament via regulatory proteins. The mechanistic changes captured by our model are highlighted in yellow.

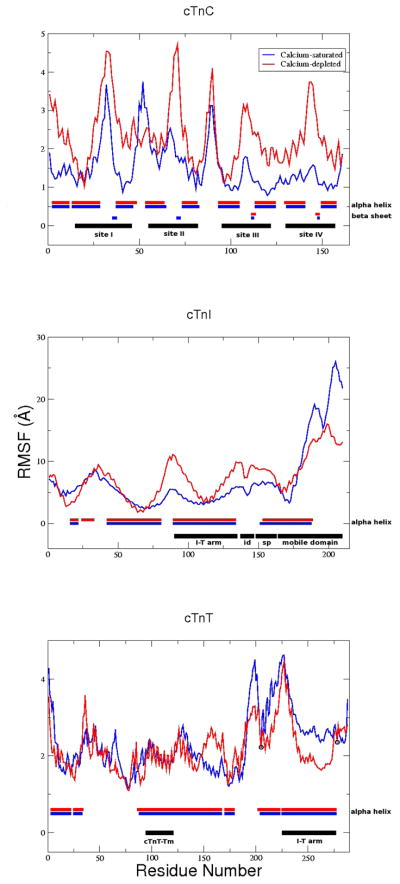
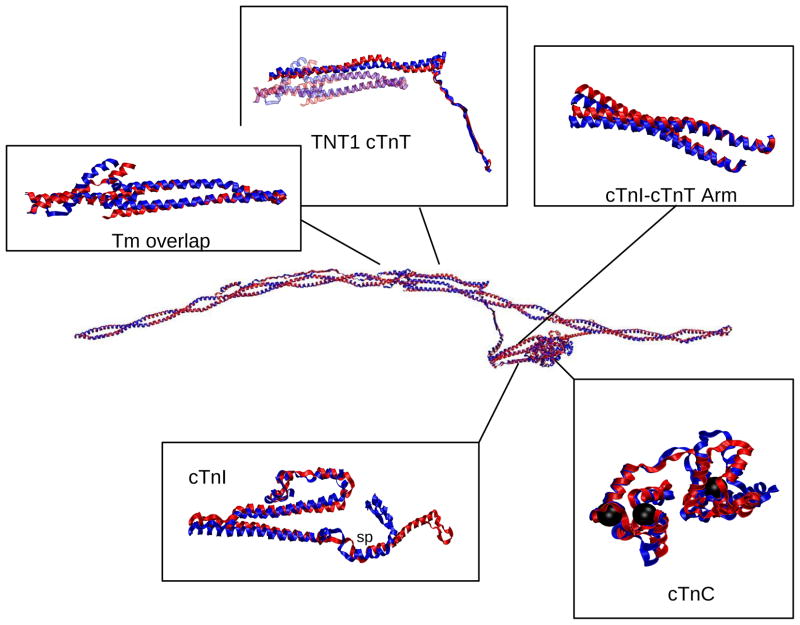
The RMSD over the course of the 1 ns simulations were stable at 5 Å for both Ca²⁺-saturated and Ca²⁺-depleted states. Figure 7 demonstrates areas where subtle change in structure are seen in our model as a function of calcium binding include: the N-lobe of cTnT sites I and II and the linker between them; the switch peptide, the vicinity of residue 25 and the mobile domain of cTnI; and the linker and Tm-bind regions of cTnT (shown in “RMSF analyses for cTn subunits and subsets”, “Secondary structure analysis” and “Contact maps” of Supporting Information). The calcium-dependent changes apparent in Figure 7 are more easily visualized with structural images. Average structures of each model, the calcium-saturated (blue) and calcium-depleted (red), are shown in Figure 8. It identifies key structural regions that are important for the propagation of calcium-signaling through the thin filament: 1) changes in the N-lobe of cTnC directly alter the switch peptide and surrounding domains of cTnI; 2) changes in the N-lobe of cTnC cause a rotation of the I-T arm, which relays the signal downstream through the cTnT linker to overlapping Tm. (Connections between Figure 7 and Figure 8 are shown in “RMSF and structural correspondence” in Supporting Information)

Figure 7.

RMSF analysis for 1 ns simulations. Top: cTnC; Middle: cTnI; Bottom: cTnT. Regions of structural/functional interest are identified in black horizontally along the bottom of each graph. Average secondary structure is identified horizontally along the bottom of each graph where structured residues are blocked, blue for Ca²⁺-saturated and red for Ca²⁺-depleted, and unstructured residues are left blank. cTnI and cTnT secondary structure consists solely of α-helices (blocked) and coils (blank). “id” = inhibitory domain; “sp” = switch peptide; black circles = constraints on C_α 205 and 277 cTnT, all other atoms are allowed to move freely.

Figure 8.

Alignment of Ca²⁺-saturated and Ca²⁺-depleted average structures of the complete cTn complex with overlapping Tm and highlighted regions of interest. The color scheme for this and the other structural images is: Blue=Ca²⁺-saturated; Red=Ca²⁺-depleted. In cTnC, the black spheres are the locations of calcium ions. In cTnI box, “sp” = switch peptide.

cTnC-cTnI interactions are altered as a function of Ca²⁺-binding

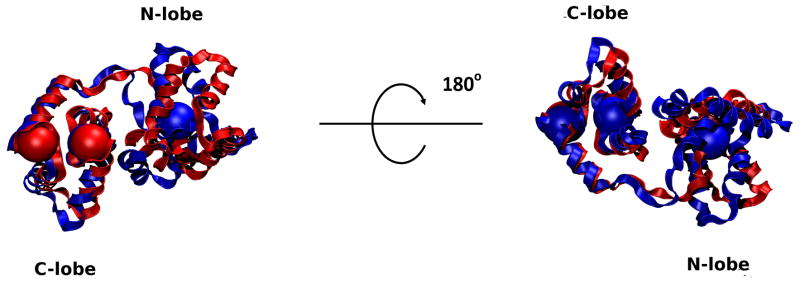
The N-lobe of cTnC undergoes significant change when Ca²⁺ is removed from site II, but the C-lobe does not as shown in Figure 9. Our results match existing solution structures of calcium-depleted and calcium-saturated cTnC, including regions of α-helices, β-sheets, and less well-defined regions which correspond to regions of increased fluctuations in our results (such as the N-and C-terminal residues, sites I [residues 30–34] and II [residues 65–70], the B-C linker [residues 49–53] and the central linker [residues 84–93], as shown in Figure 7).(34, 35) We also observe an increase in fluctuations in sites I and II in the calcium-depleted state which results in them being less well-defined. This is in direct agreeance with NMR observations.(34) These results are reflected in all of our calcium-saturated and depleted simulations.

Figure 9.

Alignment of Ca²⁺-saturated and Ca²⁺-depleted average structures of cTnC. Calcium ion locations are shown as large spheres colored according to their appropriate state. Note the lack of a calcium ion in the N-lobe in the Ca²⁺-depleted state. There is significant change in the conformation of the N-lobe while the C-lobe remains mostly unchanged. The Ca²⁺ ion positions bound to the C-lobe in the two states are virtually superimposed. Binding sites I and II as well as the linker between them are significantly altered as a result of removing Ca²⁺. This corresponds to the changes in RMSF that we see in Figure 7.

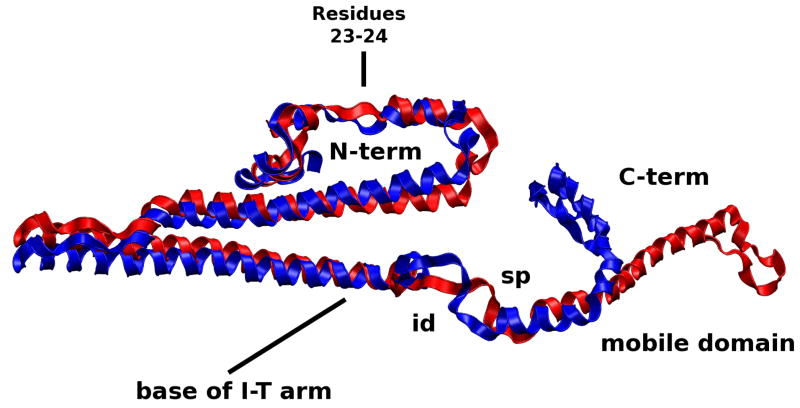
The switch peptide of cTnI and its surrounding regions, the inhibitory and mobile domains, are significantly affected by changes in the N-lobe of cTnC. Our results concur with the “fly-cast” mechanism by which alterations in the switch peptide translate its alternating order-disorder into the altered dynamics of nearby regions.(32, 33, 36) We see greater folding occur in the switch peptide in the Ca²⁺-saturated state allowing this hydrophobic-rich region of cTnI to differentially interact with the N-lobe of cTnC, visually demonstrated in the movies. As a result, the nearby inhibitory and mobile domains are less likely to interact with actin, allowing Tm to more easily shift to the open state.

The Ca²⁺-depleted behavior of the mobile domain of cTnI shown in Figure 10, however, shifts the equilibrium of Tm toward the blocked position. The decreased RMSF of the mobile domain in the Ca²⁺-depleted suggests it is more rigid, a finding that is experimentally confirmed.(33) This is clearly seen in the movies of simulation (see Supplementary Information); it is the single greatest change observed when visually comparing the two simulations. In approximately 500 ps, the mobile domain of cTnI in the Ca²⁺-depleted state “reaches out” toward Tm and binds to it. The rigid nature of the mobile domain of cTnI in the Ca²⁺-depleted state puts it in a more advantageous position to interact with Tm or actin and sterically blocks Tm more toward the states of equilibrium farthest from the cTn core, which as shown in Figure 5 are the closed and blocked states. The mobile domain in the Ca²⁺-saturated state is far more flexible as shown in Figure 7 and the movies, findings which are also experimentally confirmed,(33) which would allow Tm to maximally explore equilibrium states near to and far from the cTn core, i.e., open, closed or blocked states. These results were qualitatively the same for all of our calcium-saturated and depleted simulations. A recent experiment demonstrated findings similar to our simulations, namely that the C-terminal of TnI, residues 157–163, interacted with Tm residue 146 in the absence of Ca²⁺.(37) In our model, cTnI in the vicinity of residues 190–195 is capable of interacting with C-terminal Tm in the vicinity of residue 120 only in the Ca²⁺-depleted state. More recently, it was shown that the last 17 residues of cTnI stabilize Tm in the closed state.(5) Our simulations show the same region of cTnI interacting with Tm in the closed state position.

Figure 10.

Alignment of Ca²⁺-saturated and Ca²⁺-depleted average structures of cTnI. The N-terminus and switch peptide and surrounding regions of the C-terminus interact with the N-lobe of cTnC and are altered as a function of Ca²⁺-binding. As a result, fluctuations in the dynamics of the N-lobe cTnC alter the dynamics of switch peptide of the C-terminus cTnI and the N-terminus of cTnI. id=inhibitory domain; sp=switch peptide.

Ca²⁺-dependent changes in the N-terminus of cTnI

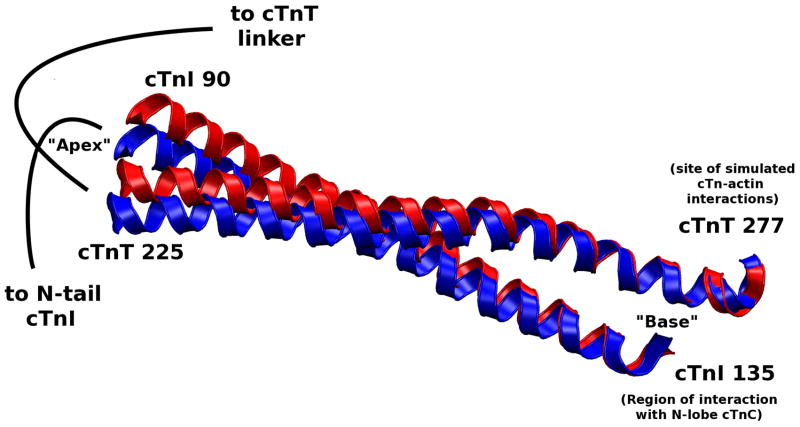
We also see the N-terminus region of cTnI affected by the calcium-dependent change in the N-lobe of cTnC, which results in a rotation of the I-T arm shown in Figure 11. The “apex” of the I-T arm is directly affected by the mobility of the N-terminus of cTnI while the “base” of the I-T arm is stabilized by the C-lobe of cTnC. We found through hydrogen bond analysis that the I-T arm is the most stable region of the complex in terms of subunit-subunit interactions. This concurs with recent experimental findings using hydrogen-deuterium exchange.(6) (see “Hydrogen bond analysis” in Supporting Information) The stable nature of the I-T arm makes it function like a rigid rod capable of moving as a single unit. While the N-terminus of cTnI causes the apex of the I-T to move, the base is relatively fixed due to interactions with the C-lobe of cTnC and cTn-actin interactions. The average position of the I-T arm differs by an RMSD of 1.2 Å and a rotation of 5 degrees between the coiled coils shown in Figure 11. This confirms speculation that a small rotation occurs about a pivot point at the C-terminus of the I-T arm.(7) Due to the I-T arm’s stable base, its helical components appear to rotate about one another at the apex. We also observe significant changes in the position and dynamic behavior of residues 23–24 of cTnI, the cardiac specific phosphorylation sites responsible for the inotropic effects of β-adrenergic agonists,(38, 39) as a function of Ca²⁺ binding. We observe significant change in the mobility of the protein complex at the phosphorylation sites in the calcium saturated and depleted models even though the average secondary structure is not greatly effected by calcium binding. Thus, dynamic properties cannot be inferred from static structures, and are rather dependent on interactions throughout the complex. These results are qualitatively similar for all calcium-saturated and depleted simulations.

Figure 11.

Alignment of Ca²⁺-saturated and Ca²⁺-depleted average structures of the cTnI-cTnT coiled coil (I-T arm). This is the most stable region of the entire complex (in terms of subunit-subunit interactions), allowing the I-T arm to behave as united pair. The stable portion of the arm (in terms of dynamics) is at the “base” of the arm which is where cTnI interacts with the C-lobe of cTnC and where cTnT is simulated to interact with actin. The stable base allows the “apex” of the I-T arm to rotate due to fluctuations in the N-terminus of cTnI. The I-T arm rotation causes fluctuations in the cTnT linker.

This brings to light a plausible mechanism in atomic detail by which the cTnT linker region, residues 170–204 of cTnT, may act to propagate calcium-signaling; it is a dynamic filter fine-tuned to calcium-binding. This means it functionally connects the C-terminus (core) and N-terminus (Tm binding) domains of cTnT.

The dual functionality of cTnT

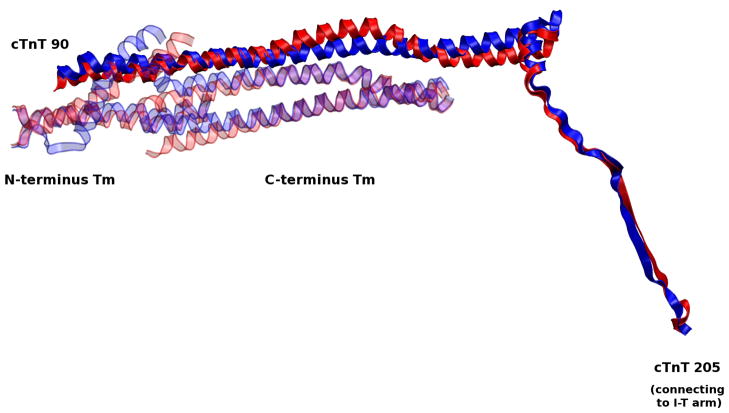
Significant changes in the I-T arm are transduced to Tm via the cTnT linker, which connects the I-T arm to overlapping Tm, shown in Figure 12. This observation helps to explain the underlying reason why early experimental results found that the cTnT C-terminal was necessary for cTnT-cTnI-cTnC Ca²⁺-sensitive interactions(40) while the N-tail of cTnT is required for cooperative activation of the thin filament.(41) The cTnT linker physically and functionally connects the two distinct roles of cTnT’s N- and C-tail domains, as was hypothesized by recent experimental findings.(42) Here we see it demonstrated in a dynamic model with atomic detail. The importance of this region is underscored by the evolutionary conservation of its primary sequence and the lack of disease-causing mutations.(7, 43)

Figure 12.

Alignment of Ca²⁺-saturated and Ca²⁺-depleted average structures of the cTnT linker. Fluctuations from the apex of the I-T arm are passed on through the cTnT linker to overlapping Tm.

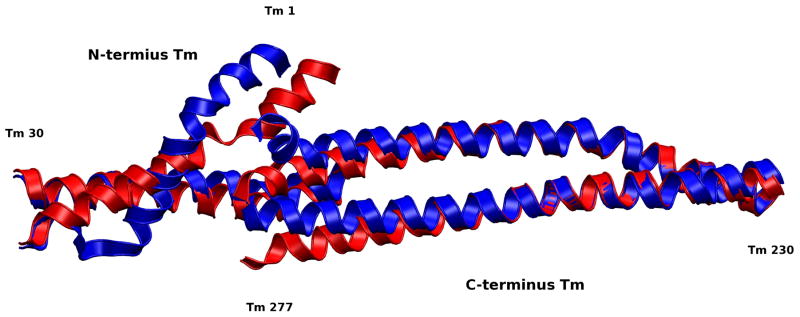
The cTnT linker, in a final step of signal transduction, relays fluctuations to the TNT1 region of cTnT, which is directly bound to overlapping Tm (Figure 12 and Figure 7). Unfolding occurs in the linker region, 170–204, in the Ca²⁺-depleted state. As a result, the region distant from the core, 150–170, swings relatively freely, perturbing Tm equilibrium. The region of cTnT-Tm binding is relatively stable, allowing the cTnT-Tm complex to move as a single unit, reminiscent of the I-T arm. This is confirmed by early experimental studies demonstrating the Ca²⁺-insensitive nature of cTnT-Tm binding in this region;(44) here, we observe it in a complete dynamic model. Gordon notes that in this position, cTnT is “in a position to influence the flexibility of Tm, since the Tm overlap region is responsible for much of the affinity of Tm for actin and Tm shows its greatest flexibility in this region.”(15) Biophysical studies have suggested the importance of stability in this crucial region and the dysfunction caused by mutations here due to alterations in flexibility.(8) Simulations of protein segments in this region by our labs have demonstrated physical mechanisms by which these mutants act, specifically changes in bending forces as a result of hotspot mutations.(1, 2) Despite the relatively small region of freely moving Tm in our model, we notice significant changes in the overlapping Tm. A loss of secondary structure in Tm at the junction between constrained and free Tm are visually observed between the Ca²⁺-saturated and Ca²⁺-depleted states, as seen in Figure 13. This net structural change is a reflection of differential forces transmitted through the cTn complex as a function of Ca²⁺-binding. These significant dynamic changes in overlapping Tm, coupled to the fact that Tm bends anisotropically,(11) support the idea that these small variations in overlapping Tm dynamics induced by cTn may be sufficient to perturb Tm dynamics toward a new equilibrium, favoring either a blocked or open state.(9)

Figure 13.

Alignment of Ca²⁺-saturated and Ca²⁺-depleted average structures of overlapping Tm. The overlapping region of Tm is important for its affinity to actin and flexibility.(15) The significant changes we observe in this region appear despite the fact that both strands of Tm are constrained at each end by the remaining Tm in the closed position. The loss of secondary structure we observe in these average structures is likely the result of resistance to fluctuations by these constraints, an indicator that changes in this region could shift the equilibrium of more than just the overlap region. We expect that the loss of secondary structure would not occur if the remainder of Tm was allowed to move freely and that Tm would shift toward the closed state when our model is in the Ca²⁺-depleted state, and possibly toward the open state when our model is in the Ca²⁺-saturated state which would work in tandem with actomyosin interactions. In our model residues 245–277 of the C-terminus Tm and residues 1–30 of the N-terminus Tm are allowed to move freely, the remaining residues have their alpha carbons fixed in the closed position.

Since our model is only capable of capturing changes in overlapping Tm, we cannot observe the entire shift in equilibrium state of the entire strands. While we can not say definitively that the Tm would shift to the blocked state rather than the open state due to these changes, based on the overwhelming agreement our results with respect to experimental findings, it is relatively safe to assume that the changes we observe in overlapping Tm as a result of the removal of a calcium ion from site II cTnC would assist the shift of the entire strands of Tm toward the blocked state rather than to the open state.

Conclusion

We have presented a dynamic model of the thin filament compiled from existing structures and models of cardiac troponin, tropomyosin and actin that it is capable of replicating key experimental findings with atomic detail. Through molecular dynamics simulations we were able to find that small changes in structure and protein contacts within cardiac troponin result in large changes throughout the complex. These cTn changes affect tropomyosin dynamics and cardiac troponin-actin interactions. The minor changes in structure as a function of calcium binding we saw are: the N-lobe of cTnT sites I and II and the linker between them; the switch peptide, the vicinity of residues 20–25 and the mobile domain of cTnI; and the linker region and N-tail of cTnT. The large changes in the dynamics we saw are: the mobile domain of cTnI; the I-T arm; the cTnT linker; and overlapping Tm. Our model demonstrates a comprehensive mechanism for calcium-activation of the cardiac thin filament validated by experimental findings.

Abbreviations

cTn

cardiac troponin

cTnC

cardiac troponin C

cTnT

cardiac troponin T

cTnI

cardiac troponin I

Tm

tropomyosin