Abstract
In all species studied, afferents from semicircular canals and otolith organs converge on central neurons in the brainstem. However, the spatial and temporal relationships between converging inputs and how these contribute to vestibular behaviors is not well understood. In the current study, we used discrete rotational and translational motion stimuli to characterize canal- and otolith-driven response components of convergent non-eye movement (NEM) neurons in the vestibular nuclear complex of alert pigeons. When compared to afferent responses, convergent canal signals had similar gain and phase ranges but exhibited greater spatial variability in their axes of preferred rotation. Convergent otolith signals also had similar mean gain and phase values to the afferent population but were spatially well-matched with the corresponding canal signals, cell-by-cell. However, neither response component alone nor a simple linear combination of these components was sufficient to predict actual net responses during combined canal-otolith stimulation. We discuss these findings in the context of previous studies of pigeon vestibular behaviors, and we compare our findings to similar studies in other species.
Keywords: vestibular, sensory convergence, brainstem
INTRODUCTION
The vestibular system consists of biological sensors that detect head movements in space. The semicircular canals and otolith organs detect angular and linear head accelerations, respectively. In the brainstem, canal and otolith afferents terminate on neurons in the vestibular nuclear complex (VNC). Neuroanatomical studies in many species have shown overlap between canal and otolith afferent projection regions in the brainstem (Carleton and Carpenter 1984; Dickman and Fang 1996; Kevetter and Perachio 1986; Kuruvilla et al. 1985; Newlands and Perachio 2003; Schwarz and Schwarz 1986). Direct convergence of canal and otolith afferents onto single VNC neurons has also been demonstrated using electrical nerve stimulation (Uchino et al. 2000; Zakir et al. 2000). Further, electrophysiological recordings from VNC neurons using discrete rotational and translational stimuli have characterized the dynamic properties and tuning characteristics of both convergent and non-convergent cells (Dickman and Angelaki 2002; Kasper, Schor and Wilson 1988; Tomlinson, McConville and Na 1996; Yakushin, Raphan and Cohen 2006).
What are the functional implications of canal-otolith convergence in the VNC? One of the primary functions of VNC neurons is to generate compensatory eye, head and limb movements that stabilize gaze and posture during motion. In primates and many other animals, eye-in-head responses (vestibuloocular, VOR) make a significant contribution to gaze stability during passive body rotation (Keshner and Peterson 1995; Meier and Dieringer 1993; Newlands et al. 1999). Eye responses are driven by the activity of distinct categories of eye movement-related (EM) neurons in the VNC (Angelaki, Green and Dickman 2001; Beraneck and Cullen 2007; Brettler and Baker 2001; Cullen, Chen-Huang and McCrea 1993; McConville, Tomlinson and Na 1996; Precht 1979; Roy and Cullen 2002; Scudder and Fuchs 1992). However, head-on-body responses (vestibulocollic, VCR) also contribute to gaze stability (Keshner and Peterson 1995; Peng et al. 1999), driven in part by a heterogeneous population of non-eye movement related (NEM) neurons in the VNC (Gdowski and McCrea 1999; Kasper, Schor and Wilson 1988; McCrea et al. 1999; Roy and Cullen 2004; Wilson and Peterson 1978). In pigeons, the head response provides the primary means for active gaze stabilization, with magnitudes that far exceed that of the eye-in-head response when the head is free to move (Gioanni 1988; Haque and Dickman 2005). In a previous study, we used discrete combinations of canal and otolith stimulation to demonstrate that pigeons integrate these signals when generating eye and head responses to rotation (McArthur and Dickman 2008). Results were consistent with a linear combination of canal- and otolith-generated response components during rotational VOR. However, while canal and otolith components of rotational VCR were spatially aligned, the net head responses to combination stimuli were inconsistent (particularly in phase) with a simple linear combination model. Thus, the convergence of canal- and otolith-related inputs onto the central neurons generating these head responses needs to be characterized, to give some insight into how these signals might be integrated to produce the observed behavior.
In the current study, we used simple motion stimuli to characterize canal-otolith convergence onto single NEM neurons in the VNC. Earth-vertical axis (EVA) rotations were used to characterize neural responses to canal inputs in the absence of dynamic otolith stimulation. Linear translations were used to characterize responses to otolith inputs in the absence of dynamic canal stimulation. Earth-horizontal axis (EHA) rotations dynamically stimulate the canals and otolith organs, since these rotations reorient the head relative to gravity and change the net linear acceleration sensed by the otolith organs. Thus, EHA rotations were used to characterize responses to combined canal and otolith stimulation, to provide a foundation for our understanding of how these signals are neurally integrated.
EXPERIMENTAL PROCEDURES
Twelve adult pigeons (Columba livia, 400–700g, Double T Farm, Glenwood IA) were used in accordance with the guidelines set forth by the National Institutes of Health Guide for the Care and Use of Animals in Research, as well as those approved by the Institutional Animal Studies Committee. The animals were housed and cared for in the Laboratory Animal Facilities under veterinary supervision. The protocol and analyses were adapted from a previous study in primates (Dickman and Angelaki 2002).
Surgical procedures
General anesthesia was achieved using isofluorane gas (3–5% in O2) via endotracheal intubation. Heart rate was monitored, and core temperature (40°C) was maintained with a heating pad. Each bird was surgically implanted with a delrin head stud and a recording electrode guide platform. An incision was made along the skull midline, and the underlying periosteum was removed from the bone. The head was positioned stereotaxically with the beak angled approximately 12° downward, such that upright orientation of the head stud and recording platform corresponded on average to alignment of the horizontal canals with an earth-horizontal plane (Dickman 1996). The head stud (5x5x10mm) was attached to the skull with titanium self-tapping screws and secured with dental acrylic. In addition, a circular delrin recording platform (15mm diameter, 5mm depth) was attached to the skull posterior to the head stud. The platform was pre-drilled with a staggered array of holes (0.8mm apart) that extended from the midline to the area overlying the vestibular nerves (bilaterally). After surgery, butorphanol (10mg/kg) was administered for post-operative pain, and the head wound margin was kept clean with betadine washes and antibiotic ointment.
Following a 5–7 day recovery period, five pigeons underwent an additional surgery to implant a scleral search coil in one eye to monitor eye movements. The coil was constructed of three turns of multi-stranded wire (Teflon-coated, 41-gauge stainless steel, A-M Systems) and coated in a thin layer of Araldite epoxy (Huntsman). Under surgical anesthesia (as described above), a circumferential incision was made in the conjuctiva to allow visualization of the sclera. In pigeons, the sclera is calcified near the cornea, so the coil was attached to the posterior margin of the scleral globe with 8-0 prolene sutures. Coil wire leads were threaded through the bone of the posterior orbit and underneath the skin to exit near the head stud. The conjuctiva was approximated over the coil and closed with 8-0 vicryl sutures. Lead wires were soldered to a nanoconnector (Omnetics) and secured next to the head stud with dental acrylic. After surgery, butorphanol (10mg/kg) was administered for post-operative pain, and ophthalmic antibiotic ointment (bacytracin/neomycin) was applied to the operated eye. Pigeons were allowed to fully recover (7–10 days) before being used in experiments.
Recording procedures
For each experiment, the pigeon was placed in a padded body holder, and the head stud was fixed in an upright position to the body holder. The holder was then secured to a servo-controlled rotator/sled system (Neurokinetics) driven by a PC and programmable interface (CED Model 1401plus, Cambridge Electronic Design). Stimulus control and data acquisition were performed using custom scripts written for the interface environment (Spike2, Cambridge Electronic Design). All stimuli were delivered along axes that passed through the center of the pigeon’s head (i.e. intersection of nasooccipital and interaural axes), and all experiments were performed in total darkness with the pigeon head-fixed. Stimulus delivery was monitored using a rate sensor and 3-axis linear accelerometer mounted near the animal’s head, the outputs of which were low-pass filtered (200Hz, 6-pole Bessel), digitized, and stored for off-line analyses.
A three-field AC magnetic coil system (CNC Engineering) mounted to the motion system was used to monitor eye movements. The coil system provided a 5-in homogeneous magnetic field cube centered about the pigeon’s head. Eye coil signals were also low-pass filtered (200Hz, 6-pole Bessel), digitized, and stored. However, the eye movement signals were primarily used online to categorize cells as eye movement sensitive (EM) or non-eye movement sensitive (NEM) neurons.
Extracellular recordings from single neurons in the vestibular nuclei were obtained using epoxy-coated tungsten microelectrodes (FHC, 10–15MΩ). The electrode was inserted into a 26-gauge stainless steel guide tube, advanced through one of the pre-drilled guide holes in the recording platform, then manipulated in depth with a remote control hydraulic microdrive (FHC). Neural activity was amplified, filtered (300Hz-10kHz), and passed through a dual time-amplitude window discriminator (BAK Instruments). Single-unit spikes triggered acceptance pulses that were stored as events for off-line analyses. The stereotaxic coordinates of the vestibular nuclei have been mapped in pigeons (Dickman and Fang 1996), and we used these coordinates to guide our recording site locations. Reconstruction of electrode tracks indicated that most neurons were recorded from the superior (SVN) or lateral (LVN) vestibular nuclei.
Experimental protocol
During each electrode penetration, we searched for spontaneously active neurons that were sensitive to 0.5Hz sinusoidal rotations and linear translations along any of the three cardinal head axes. We also monitored spontaneous activity in the absence of motion, to determine if each cell was responsive to extra-vestibular cues such as eye movements. For the subset of pigeons implanted with a scleral search coil, voltages corresponding to eye movements were monitored and compared to neural firing in real time. For pigeons without a search coil, large eye movements (gaze shifts) were directly observed by the experimenter in the light. If a neuron’s firing rate correlated with eye movements (i.e. modulation with changes in eye position, burst and/or pause in firing during saccades), that neuron was classified as eye movement-sensitive (EM) and excluded from the current study. Some neurons exhibited firing rate modulations in the absence of motion that were not clearly correlated with eye movements, possibly due to proprioceptive, somatosensory, or motor efferent input. In practice, only those motion-sensitive neurons that did not significantly modulate their firing rates in the absence of motion were classified as non-eye movement (NEM) neurons and studied further.
Once identified, each NEM neuron was tested during sinusoidal rotational and translational stimuli. Stimulus orientations were expressed relative to a head-fixed right-handed coordinate system (see Figure 1). The x-, y- and z-axes corresponded to the pigeon’s nasooccipital, interaural and dorsoventral axes, respectively. Positive rotations were right ear-down, nose-down, and leftward. Positive translations were forward, leftward, and upward. Each neuron was typically tested at a minimum of five different axes of earth-horizontal linear translation (0.5Hz, +0.2g), including fore-aft (x-axis) and lateral (y-axis) motion. Earth-vertical axis (EVA) rotations (0.5Hz, +20o/s) were also delivered, with the pigeon’s head (and body) positioned at a minimum of five static orientations relative to the earth-vertical axis – including upright, 30° nose-up, 30° nose-down, 30° right ear-down, and 30° left ear-down. Finally, a subset of neurons were also tested during earth-horizontal axis (EHA) rotations (0.5Hz, 20°/s), with a minimum of five different axis orientations including roll (x-axis) and pitch (y-axis).
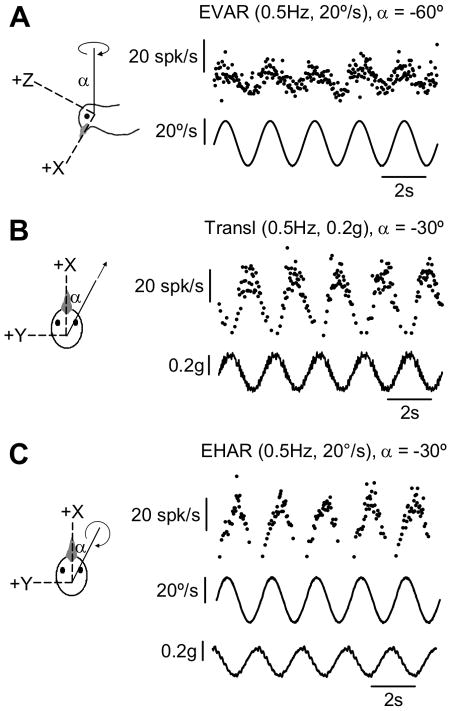
FIGURE 1.
Responses of a single representative convergent neuron to dynamic motion stimulation of semicircular canals only (A: Earth-vertical axis rotation, EVAR), otolith organs only (B: Linear translation), and both canals and otolith organs simultaneously (C: Earth-horizontal axis rotation, EHAR). Single-unit action potentials are plotted as instantaneous firing rates (IFR). Stimulus feedback for each motion trial is also shown (angular velocity, °/s; linear acceleration, g). Axis orientations are expressed relative to the head cardinal axes, using the right-hand rule.
Data analyses
All data analyses were performed off-line using custom scripts in Matlab (Mathworks). For each motion trial, a neuron’s stored spike times (events) were converted to instantaneous firing rates (IFR), computed as the inverse of the interspike intervals and assigned to the end of each interval. Steady-state stimulus feedback and IFR data were fit with sinusoidal functions at the fundamental stimulus frequency using nonlinear least-squares minimization (Levenberg-Marquardt). The relationship between motion stimulus and neural response was evaluated by comparing the parameters of their sinusoidal fits. Neural sensitivity (also referred to as gain) served as a comparison of the amplitude of the neural response (DC-to-peak) to the amplitude of the stimulus. Neural phase indicated the temporal relationship between the peak of the neural response and the peak of the stimulus, expressed as a phase angle (°) within a single representative sinusoidal cycle. For example, if the stimulus frequency was 0.5Hz and the peak of the neural response preceded the peak of the stimulus by 0.5s, the phase of the neural response relative to the stimulus would be computed as +90° (since 0.5s corresponds to one-fourth of a full cycle). For translational stimuli, neural sensitivity was expressed as the amplitude of IFR modulation divided by the amplitude of linear acceleration modulation (spk/s per g), and neural response phase was computed as the phase angle difference (°) between peak IFR and peak head-horizontal linear acceleration. For rotational stimuli, sensitivity was expressed as the amplitude of IFR modulation divided by the amplitude of angular velocity modulation (spk/s per °/s), and phase was computed as the phase angle difference (°) between peak IFR and peak angular velocity.
Based on their sensitivity to rotation and translation, neurons were classified according to their likely vestibular afferent inputs (Angelaki, Bush and Perachio 1993; Dickman and Angelaki 2002; Estes, Blanks and Markham 1975). EVA rotation dynamically stimulates the semicircular canals but not the otolith organs, so neurons that responded to at least one axis of EVA rotation were considered to receive either direct or indirect input from semicircular canal afferents. Similarly, since linear translation dynamically stimulates the otolith organs but not the canals, neurons that responded to at least one axis of linear translation were considered to receive direct or indirect otolith afferent inputs. After examining the distribution of gain values across neurons, we selected a value of 0.1 spk/s per °/s during EVA rotation or 10 spk/s per g during linear translation (for at least one axis of stimulation) as the minimum gain of a neuron identified as receiving canal or otolith input, respectively. Neurons with gains exceeding the criterion value for both EVA rotation and linear translation were classified as canal-otolith convergent neurons, and only these neurons were considered further. This method may have excluded some neurons that in fact received convergent inputs but with lower sensitivities.
For each convergent neuron, we characterized the nature of its canal and otolith inputs by fitting cosine tuning functions to the responses recorded during EVA rotation and linear translation, respectively. Then, we used these tuning functions to determine the orientation of the earth-horizontal axis (EHA) rotation that would evoke maximum modulation of each input (canal- and otolith-related) and the corresponding amplitude and timing of that modulation relative to the EHA rotation stimulus. Finally, for a subset of neurons, we characterized the actual net response to EHA rotation and compared its tuning parameters to those predicted by a simple linear summation of the canal and otolith inputs. For any cosine tuning function, there will be two possible orientations of the maximum sensitivity vector, oriented 180° apart in space with equal gains but opposite phase values. For each cell, we have reported data for the maximum sensitivity vectors corresponding to phase values within the range +90°, unless otherwise noted. Though neurons were recorded bilaterally, maximum sensitivity vector orientations and phase values were reported as though all neurons were recorded from the left hemisphere. For example, a neuron with a maximum sensitivity EVA rotation vector oriented upward preferred ipsilateral (leftward) rotation, according to the right hand rule.
EVA rotation
A three-dimensional cosine tuning function was fit to the sensitivity and phase values obtained from each neuron’s responses during EVA rotations (0.5Hz, 20o/s), yielding a maximum sensitivity vector for the semicircular canal (CANAL) inputs with direction αCANAL, sensitivity SCANAL, and phase θCANAL (Dickman 1996; Dickman and Angelaki 2002).
Linear translation
A two-dimensional cosine tuning function was fit to the sensitivity and phase values obtained from each neuron’s responses during earth-horizontal translations (0.5Hz, 0.2g), yielding a maximum sensitivity vector for otolith organ (OTO) inputs with direction αOTO, sensitivity SOTO, and phase θOTO. A two-dimensional spatiotemporal convergence (STC) tuning function was also fit to the translation response data (Angelaki, Bush and Perachio 1993; Angelaki and Dickman 2000; Bush, Perachio and Angelaki 1993; Dickman and Angelaki 2002) and compared to the cosine tuning function for goodness-of-fit, using the variance accounted for: VAF = 1 − (sum square error of the fit/sum square difference of the data from its mean) (Dickman and Angelaki 2002). For each neuron, we used the translation tuning function with the best fit (i.e. highest VAF) for further analyses. However, since the simple cosine function provided a good description of tuning for most neurons tested, we did not consider STC response behavior further in the current study.
EHA rotation – otolith stimulation
To facilitate an understanding of the analyses used to predict and characterize responses to EHA rotation, we present here a description of the canal and otolith organ components of EHA rotational stimulation experienced by the animal. When the head was positioned upright, the head-vertical axis was considered to be parallel to earth-vertical, and the otolith organs responded to a static linear acceleration due to gravity, represented as a 1g vector directed upward along the head-vertical axis. (Note: This vector is oriented upward because the otolith organs – like all linear accelerometers – signal the vector deviation from freefall, not the vector of force due to gravity.) During sinusoidal EHA rotation, the orientation of the linear acceleration vector swings in the head within the plane of rotation. One can decompose the vector orientation into a head-vertical modulation component and a head-horizontal component, both of which vary as a function of the head’s angular displacement (i.e. orientation relative to gravity). The head-horizontal component of linear acceleration modulates at the same frequency as rotation, with peak amplitude equal to one minus the sine of the peak displacement angle. The head-vertical component of net linear acceleration modulates at the 2nd harmonic of the rotation frequency, with an amplitude equal to one minus the cosine of the peak displacement angle. For example, consider the case of 0.5Hz EHA rotation about the pitch axis with peak velocity of 20°/s. The peak head tilt is ~6.4° ( = peak velocity/2*pi*frequency), and the head rotates between +6.4° (nose-down) and −6.4° (nose-up). The head-horizontal (fore-aft/nasooccipital) linear acceleration modulates around 0g with modulation amplitude of sin(6.4 °); thus, it modulates from −0.1g (nose-down) and +0.1g (nose-up). The head-vertical (up-down/dorsoventral) linear acceleration modulates around +1g with modulation amplitude of cos(6.4°). However, this modulation in head-vertical acceleration modulates at the 2nd harmonic of the rotation frequency, equal to +0.99g at both nose-down and nose-up positions. Note that the modulation in head-vertical linear acceleration (0.01g) is an order of magnitude smaller than the modulation in head-horizontal linear acceleration (0.1g).
EHA rotation – predicted canal and otolith inputs
To predict the canal input response to EHA rotation (0.5Hz, 20°/s), we projected the three-dimensional EVA rotational maximum sensitivity vector (αCANAL) into the head-horizontal plane and expressed its orientation as a polar angle relative to the positive x-axis (canalvec). The corresponding sensitivity (canalS) and phase (canalphase) values were computed from the three-dimensional EVA rotation tuning function. To predict the otolith input response to EHA rotation, we needed to account for the fact that head-horizontal linear acceleration along the neuron’s preferred axis (αOTO) would result from EHA rotation along a perpendicular axis. Thus, there were two axes of maximum otolith sensitivity during EHA rotation, each 90o away from αOTO. For each neuron, we chose the axis orientation (otovec) closest to that cell’s canalvec, also expressed as a polar angle relative to the positive x-axis (though this analysis was repeated in some cases with the otovec chosen to match canal and otolith phase values). The two-dimensional translation tuning function was used to compute the corresponding otolith response sensitivity (otoS) and phase (otophase), which were expressed relative to the apparent EHA angular velocity to facilitate comparison to canalS and canalphase. For EHA rotation, otolith-related sensitivity relative to angular velocity equals the sensitivity relative to linear acceleration times the ratio of peak linear acceleration to peak angular velocity (0.1g/20°/s). Otolith input phase relative to angular velocity equals the phase relative to linear acceleration plus 90° (since linear acceleration leads angular velocity by 90° during EHA rotation; see Figure 1C).
The relationship between predicted canal- and otolith-driven contributions to EHA rotation responses was assessed cell-by-cell, by fitting linear regressions relating canalvec to otovec, canalS to otoS, and canalphase to otophase, using a procedure modified for use with two dependent variables. This procedure minimizes perpendicular errors between actual data points and the estimated linear regression through them, and the corresponding 95% confidence intervals (obtained by bootstrapping) may be asymmetrical. The significance of the regression was assessed by calculating R and p values (alpha = 0.05). If the linear regression provided a significant fit to the data and if the range defined by the confidence intervals on the slope included a value of one, we concluded that the regression slope was not significantly different from unity, indicating a cell-by-cell match between canal and otolith inputs for a given response parameter. If the linear regression did not provide a significant fit to the data, we concluded that canal and otolith input values were not linearly related, and the regression was not plotted in the corresponding figure.
EHA rotation – actual vs. predicted net responses
For the subset of neurons with sufficient data, actual responses to EHA rotation were compared to responses predicted by a linear combination of canal and otolith response components. Actual EHA rotation maximum sensitivity vectors (αEHAR), sensitivity (SEHAR), and phase (θEHAR) values were obtained by fitting a two-dimensional cosine tuning function to the available EHA rotation data. We selected the axis of EHA rotation that yielded the highest predicted sensitivity value and defined the corresponding axis orientation. sensitivity, and phase as the predicted αEHAR, SEHAR, and θEHAR, respectively. To calculate the predicted αEHAR, SEHAR, and θEHAR values, we performed a linear summation (in the complex plane) of the canal and otolith responses to each axis of EHA rotation (sampled every 1°), based on the EVA rotation and linear translation tuning functions, respectively. To assess the relationship between actual and predicted values, we fit a linear regression for two dependent variables (as described above) to the data for αEHAR, SEHAR, and θEHAR. If the linear regression provided a significant fit to the data and if the range defined by the confidence intervals on the slope included a value of one, we concluded that the regression slope was not significantly different from unity, indicating that the linear summation model provided a good estimate of the actual response to EHA rotation. If the linear regression did not provide a significant fit to the data, we concluded that there was not a significant linear relationship between actual and predicted values, and the regression was not plotted in the corresponding figure.
RESULTS
Responses were obtained from 56 convergent neurons in the vestibular nuclear complex (VNC), each of which was sensitive to both rotational and linear translational motion. Responses from a single representative convergent neuron are shown in Figure 1. To characterize the canal and otolith response components separately, we used stimuli that dynamically stimulated only one receptor type at a time: earth-vertical axis (EVA) rotations to stimulate the canals (Figure 1A) and linear translations to stimulate the otolith organs (Figure 1B). Then, we recorded neural responses to earth-horizontal axis (EHA) rotations (Figure 1C), which stimulated both otolith organs and the semicircular canals. We compared the actual neural responses to EHA rotation with the predicted combined response based on a linear combination of canal- and otolith-related responses.
Canal-only responses: earth-vertical axis rotations
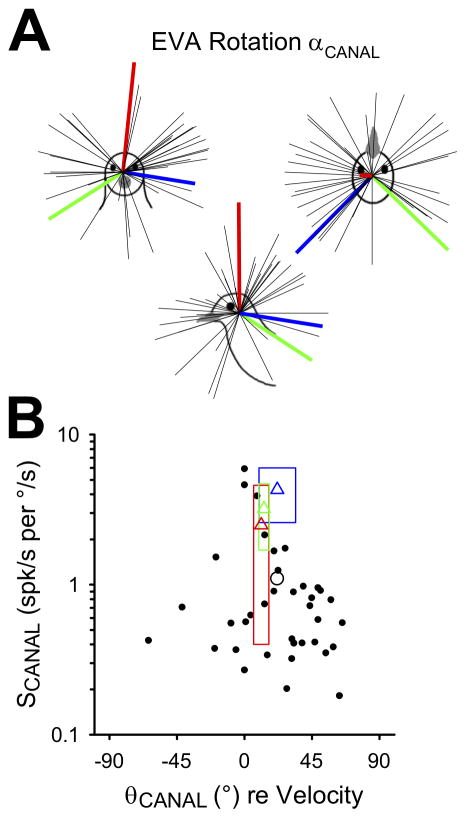
Thirty-seven convergent neurons were characterized during EVA rotations (0.5Hz, 20°/s). The static orientation of the head was varied relative to the earth-vertical axis, and three-dimensional cosine tuning functions were fit to the responses for each neuron. From these tuning functions, we derived each cell’s maximum canal-related sensitivity vector (αCANAL), which corresponded to the axis of EVA rotational motion that would drive the strongest firing rate modulation for that neuron. These unit vectors are plotted in head-referenced space in Figure 2A. For comparison, the mean maximum sensitivity vector orientations for horizontal (red), anterior (blue) and posterior (green) canal afferents in pigeons were also plotted (Dickman 1996). Maximum sensitivity vectors were distributed throughout head-centered space and were not clustered around canal afferent vectors, similar to convergent neurons observed in macaques (Dickman and Angelaki 2002). However, there were relatively few neurons that preferred rotation around the nasooccipital (roll) axis, in contrast to previous studies in both cats (Kasper, Schor and Wilson 1988; Perlmutter et al., 1999; Wilson et al., 1992) and primates (Dickman and Angelaki 2002). Next, maximum neural sensitivities (SCANAL) and phase values (θCANAL) were plotted for each neuron (Figure 2B). Semicircular canal afferent response means (triangles; ± standard deviations indicated by rectangles) were plotted for comparison (Dickman 1996). Convergent neuron sensitivity values varied between 0.2 and 5.9 spk/s per °/s, with a mean value of 1.1 spk/s per °/s (SD = 1.2 °), lower than the typical sensitivity values for canal afferents. Phase values varied widely, from −64.1° to 65.2°, but generally led head velocity by 10–30° (mean = 21.7°, SD = 29.5°), similar to the typical phase behavior of canal afferents. There was no apparent systematic relationship between sensitivity and phase for the neurons sampled.
FIGURE 2.
Responses of convergent neurons (n=37) to earth-vertical axis (EVA) rotation (0.5Hz, 20°/s). A: Axes of maximum sensitivity (αCANAL) are plotted as unit vectors in three-dimensional head space. Mean maximum sensitivity vectors for pigeon horizontal (red), anterior (blue), and posterior (green) canal afferents are also shown (thick lines; Dickman 1996). B: Maximum sensitivity (SCANAL) and phase (θCANAL) values are expressed relative to angular velocity, with the population mean indicated by the open circle. Mean sensitivity and phase values (open triangles) are also shown for pigeon horizontal (red), anterior (blue), and posterior (green) canal afferents (Dickman 1996). Boxes indicate afferent means ± standard deviation.
Otolith-only responses: linear translations
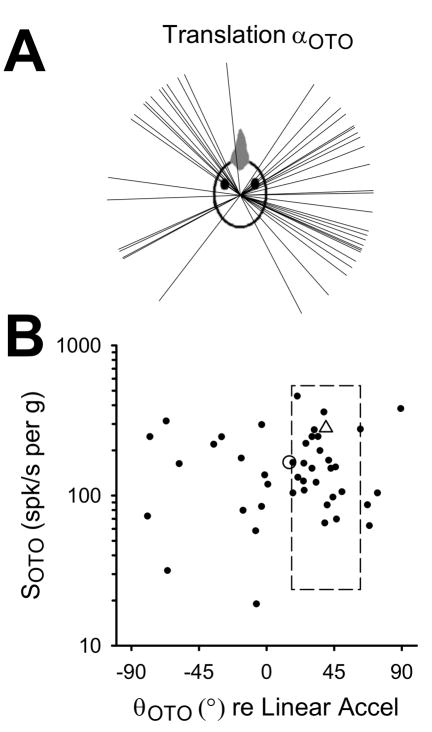
Forty-three convergent neurons were characterized during earth-horizontal axis linear translations (0.5Hz, 0.2g), and two-dimensional cosine tuning functions were fit to each cell’s responses. The response for each cell was represented by the maximum otolith-related sensitivity vector (αOTO) and plotted in head-referenced space (Figure 3A). Pigeon otolith afferents innervating the utricle (i.e. those oriented to respond maximally to head-horizontal linear accelerations) had maximum sensitivity vectors that clustered near the interaural axis (68% fell within +30° of the interaural axis; Si, Angelaki and Dickman 1997). In contrast, central convergent neurons preferred a wider range of horizontal translation directions, with some tendency to cluster near canal planes (Figure 3A). The scarcity of neurons with maximal responses to nasooccipital translation agrees with previous findings in rodents (Angelaki, Bush and Perachio 1993), cats (Kasper, Schor and Wilson 1988; Perlmutter et al. 1999; Wilson et al. 1992), and primates (Dickman and Angelaki 2002). Maximum sensitivity values (SOTO) and the associated response phases (θOTO) were plotted in Figure 3B, and mean pigeon otolith afferent data were plotted for comparison (Si, Angelaki and Dickman 1997). Convergent neuron sensitivity values ranged between 19.0 and 460.2 spk/s per g, with a mean value of 166.7 spk/s per g (SD = 98.9). Thus, the distribution of sensitivity values for convergent neurons was lower than but overlapping with the distribution for otolith afferents (Si, Angelaki and Dickman 1997). Phase values also varied widely and included both phase lags and phase leads (between −79.4° and 89.2°), with a mean value of 15.1° (SD = 41.1) – in contrast to the otolith afferents, which primarily led head acceleration by 10° to 45°. As with semicircular canal inputs, there was no apparent systematic relationship between sensitivity and phase in this sample of convergent central neurons.
FIGURE 3.
Responses of convergent neurons (n=43) to earth-horizontal linear translation (0.5Hz, 0.2g). A: Axes of maximum sensitivity (αOTO) are plotted as unit vectors in two-dimensional head space. B: Maximum sensitivity (SOTO) and phase (θOTO) values are expressed relative to linear acceleration, with the population mean indicated by the open circle. The mean pigeon otolith afferent sensitivity and phase is indicated by the open triangle, and the box indicates the corresponding standard deviation (Si, Angelaki and Dickman 1997).
Relationship between canal and otolith inputs
Next, we examined the relationship between canal- and otolith-related responses for 25 convergent VNC neurons. In a previous study, we demonstrated that pigeons integrate canal and otolith signals to generate compensatory responses to EHA rotation (McArthur and Dickman 2008). Thus, we transformed the maximum sensitivity vectors for canal (αCANAL) and otolith (αOTO) response components, to predict each component’s maximum sensitivity vector for EHA rotation (see Methods for details). Each vector was expressed as its orientation relative to the forward nasooccipital axis (canalvec for canal input, otovec for otolith input; Figure 4A). For most neurons, their convergent canal and otolith inputs were spatially aligned, such that both response components would be maximally stimulated by EHA rotation around the same axis. Thus, the linear regression relating canalvec and otovec values had a slope that was not significantly different from unity (slope = 1.2, 95% CI = [0.9, 1.4], R = 0.92, p < 0.001). A similar spatial alignment between convergent inputs was observed in rats (Angelaki, Bush and Perachio 1993) and cats (Perlmutter et al. 1999) but not monkeys (Dickman and Angelaki 2002; Yakushin, Raphan and Cohen 2006).
FIGURE 4.

Predicted responses of canal and otolith inputs to convergent neurons (n=25) during earth-horizontal axis (EHA) rotation (0.5Hz, 20°/s). Significant linear regressions (solid) are plotted through the available data, and the unity slope line (dotted) is plotted for comparison. A: Axes of maximum sensitivity for canal (canalvec) and otolith (otovec) inputs to each neuron, expressed as polar angle orientations relative to the positive x-axis. Regression slope = 1.2 (95% CI = [0.9, 1.4], R = 0.92, p < 0.001. Unity slope line +30° (shaded) is plotted for comparison. B: Response sensitivity values of canal (canalS) and otolith (otoS) inputs to each neuron, expressed relative to angular velocity. Open symbols indicate those neurons with very low (<0.1) predicted canal sensitivity to EHA rotation. C: Response phases of canal (canalphase) and otolith (otophase) inputs to each neuron, expressed relative to angular velocity.
The corresponding sensitivity and phase values for each response component (both expressed relative to EHA rotation velocity), however, did not match. As shown in Figure 4B, canal (canalS) and otolith (otoS) response components were predicted to have sensitivity values that could vary significantly from one another for a single convergent neuron, with the canal sensitivity sometimes higher and sometimes lower than the otolith sensitivity. There was not a consistent linear relationship between these values, even when those neurons with very small predicted canal sensitivity to EHA rotation were excluded from the data (linear regression: R = 0.13, p = 0.55; excluded neurons indicated by open symbols in Figure 4B). There also was not a significant linear relationship between canalphase and otophase (linear regression: R = 0.18, p = 0.39; Figure 4C). During EHA rotation around the maximum sensitivity axis, the canal-driven response modulated approximately in-phase with or slightly leading angular velocity, while the otolith-driven response tended to respond in-phase with angular position or acceleration (i.e. lag or lead angular velocity by 90°). It was possible that this temporal mismatch was a result of how we selected the orientation of the otovec. Due to the nature of a cosine tuning function, there are two maximum sensitivity vectors in a given plane, with equal sensitivity values but opposite orientations and phase values. For each neuron, we originally selected the otovec orientation that aligned it more closely with the corresponding canalvec. However, when we selected the otovec to maximize temporal alignment between canal and otolith phase values instead, these values (canalphase and otophase) were still mismatched (data not shown). Thus, convergent canal and otolith inputs onto single central vestibular neurons were spatially matched for synergistic modulation during EHA rotation, but convergent inputs had different gains and phases relative to the rotational stimulus.
Combined canal and otolith stimulation: responses to EHA rotation
For eleven neurons with sufficient data, we fit two-dimensional tuning functions to observed EHA rotation responses (0.5Hz, 20°/s), yielding the orientation of each cell’s actual maximum sensitivity vector (αEHAR) and the corresponding response sensitivity (SEHAR) and phase (θEHAR). These values were compared to those predicted by a simple linear summation of canal- and otolith-driven responses (Figure 5), derived from EVA rotation and linear translation responses, respectively. Actual and predicted maximum sensitivity vectors were well-aligned spatially across neurons, as indicated by the fact that the actual and predicted αEHAR values were linearly related with a slope that was not significantly different from unity (slope = 0.99, 95% CI = [0.7, 1.4], R = 0.9, p < 0.001; Figure 5A). However, actual and predicted sensitivity and phase values were not so well-matched. The linear combination model underestimated the maximum sensitivity value (SEHAR) of some neurons and overestimated it for others (Figure 5B), though the linear regression through the data might have reached significance with the addition of more neurons with similar properties (slope = 0.7, 95% CI = [0.1, 2.1], R = 0.6, p = 0.06). Further, the model yielded phase values that were further out of phase with angular velocity than the actual EHA responses, which were clustered around 0° (Figure 5C), and there was no significant linear relationship between actual and predicted phase values (linear regression: R = 0.4, p = 0.3). Thus, convergent neurons kept their responses approximately in-phase with angular velocity during EHA rotation (similar to the canal-driven input alone), despite the phase offset that would have been introduced by the otolith response if canal and otolith components were simply summed.
FIGURE 5.
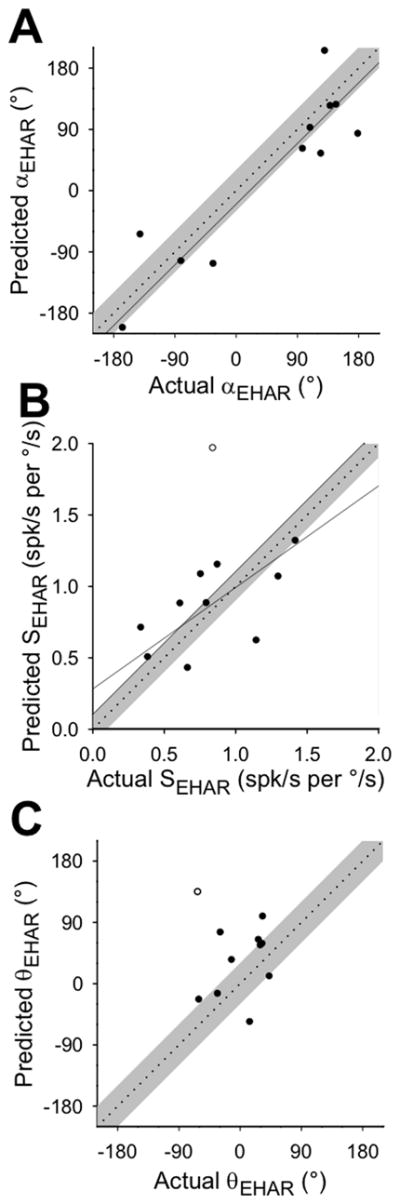
Actual responses to earth-horizontal axis (EHA) rotation (0.5Hz, 20°/s) were compared to predicted responses based on a linear summation of canal- and otolith-related responses. Significant linear regressions (solid) are plotted through the available data, and the unity slope line (dotted) ± 0.1 or 30° (shaded) is plotted for comparison. A: Axes of maximum sensitivity to EHA rotation (αEHAR), expressed as polar angle orientations relative to the positive x-axis. Regression slope = 0.99 (95% CI = [0.7, 1.4], R = 0.90, p < 0.001. B: Response sensitivity (SEHAR) values for EHA rotation around the maximum sensitivity axis, expressed relative to angular velocity. Regression slope = 0.7 (95% CI = [0.1, 2.1]), R = 0.6, p = 0.06 (outlier plotted with an open symbol). C: Response phase (θMAX) values for EHA rotation around the maximum sensitivity axis, expressed relative to angular velocity (outlier plotted with an open symbol).
DISCUSSION
We characterized the canal- and otolith-related contributions to convergent NEM neuron responses using motion that dynamically stimulated one set of receptor inputs at a time. Earth-vertical axis (EVA) rotations stimulated the semicircular canals but not the otolith organs, and earth-horizontal linear translations stimulated the otolith organs but not the canals. Central neuron responses to EVA rotation resembled canal afferent responses in that they were approximately in-phase with rotational velocity or led it by <90° (Dickman 1996). Also, convergent neuron responses led translational linear acceleration by <45°, on average, similar to otolith afferents (Si, Angelaki and Dickman 1997). However, spatial preferences differed significantly between central convergent neurons and vestibular afferents. While canal afferents prefer rotation in canal planes, convergent VNC cells preferred axes of rotation that varied widely in space. Further, otolith-driven responses in the VNC were spatially matched to canal-driven responses, such that the same axis of earth-horizontal axis (EHA) rotation dynamically modulated both components. However, during EHA rotation about this preferred axis, canal and otolith inputs were typically 90° out of phase with one another and had different sensitivities.
Canal-related spatial preferences are more closely related to behavior than to canal afferents
The canal component responses modulated approximately in-phase with angular velocity but had preferred axes of EVA rotation that were widely distributed in the head, in contrast to the restricted spatial preferences of the canal afferents (Dickman 1996). In other species, central convergence of multiple afferents innervating non-coplanar canals has been suggested as a mechanism for producing this spatial diversity in central neurons (Angelaki, Bush and Perachio 1993; Dickman and Angelaki 2002; Eron et al. 2008; Kasper, Schor and Wilson 1988; Perlmutter et al. 1999; Wilson et al. 1992; Yakushin, Raphan and Cohen 2006). The need to have central NEM neurons with preferred axes of rotation that differ from canal planes is likely tied to the demands of vestibulospinal reflexes. Muscles receiving vestibulospinal inputs are often maximally activated by rotation about the nasooccipital or roll axes (Baker, Goldberg and Peterson 1985; Wilson et al. 1986). In fact, although central neurons’ response vectors are not restricted to canal planes, their distribution in head-referenced space is not homogeneous and appears to be related to species-specific behaviors. For example, in cats, vestibular limb responses are stronger during roll rotation than during pitch rotation (Wilson et al. 1986), and the majority of central neurons indeed prefer roll or near-roll rotation (Kasper, Schor and Wilson 1988; Perlmutter et al. 1999; Wilson et al. 1992). In pigeons, we found that most central convergent neurons preferred pitch or near-pitch rotations. While the pigeon head response is larger overall for yaw rotation than for either pitch or roll (Gioanni 1988; Dickman, Beyer and Hess 2000; Haque and Dickman 2005), the vestibular tail response during flight is most prominent for pitch rotations (McArthur and Dickman 2011). Thus, the distribution of canal-related maximum sensitivity vectors is likely biased to accommodate the behavioral needs of each animal according to the specific instabilities encountered under natural conditions.
Convergent canal- and otolith-related responses are spatially aligned
Convergent VNC neurons showed a stronger preference for linear translation within canal planes than did the otolith afferents, which loosely tend to prefer interaural translation (Si, Angelaki and Dickman 1997). There was also a paucity of convergent VNC cells with maximum sensitivity vectors near the nasooccipital axis, similar to central convergent neuron populations recorded in rats (Angelaki, Bush and Perachio 1993) and monkeys (Dickman and Angelaki 2002; Zhou et al. 2006). Further, VNC convergent neurons exhibited a striking spatial alignment between canal- and otolith-driven responses, consistent with maximal activation of both canal and otolith inputs during EHA rotation around the same axis. Similar spatial alignment has been observed in rats (Angelaki, Bush and Perachio 1993) and cats (Perlmutter et al. 1999), while the majority of convergent neurons in monkeys did not exhibit this spatial input alignment (Dickman and Angelaki 2002).
What is the functional significance of the spatial alignment of convergent inputs in NEM neurons in the vestibular brainstem? For pigeons and other lateral-eyed animals, both canal and otolith stimulation contribute to compensatory eye and head responses that stabilize gaze during rotation relative to gravity (i.e. EHA rotation; pigeon: Dickman and Angelaki 1999; Dickman, Beyer and Hess 2000; McArthur and Dickman 2008; mouse: Harrod and Baker 2003; rat: Brettler et al. 2000; rabbit: Barmack 1981). Specifically in pigeons, we have demonstrated that a dynamic net head-horizontal linear acceleration signal improves the phase of both eye and head responses to EHA tilt (McArthur and Dickman 2008). Indeed, the canal- and otolith-driven components of these responses are spatially aligned with one another when examined separately (Dickman and Angelaki 1999; McArthur and Dickman 2008). Thus, the fact that otolith inputs were spatially aligned with canal inputs for central neurons supports the idea that the functional role of otolith signals in pigeons is to cooperate with primarily canal-driven reflexes, rather than generating other, primarily otolith-driven reflexes with different spatial demands (e.g. translational VOR in primates).
Sensitivity and phase for convergent canal- and otolith-related inputs are mismatched
While the spatial preferences of convergent canal and otolith inputs to VNC neurons were coincident, the sensitivity and phase values predicted for these inputs during EHA rotation were not. In fact, though canal and otolith EHA rotational sensitivities were distributed across a similar range, the values for any given neuron could be quite different in that either input could be much higher than the other. Moreover, both canal and otolith inputs seemed to retain the phase characteristics of their afferent populations on average, with canal inputs responding in-phase with angular velocity (Dickman and Correia 1989) and otolith inputs in-phase with linear acceleration (Si, Angelaki, and Dickman 1999). Thus, there was little overlap in the phase distribution for canal and otolith input phases, and these values were mismatched for individual neurons. In a previous study, we demonstrated that the canal and otolith components of the rotational VCR in pigeons also had mismatched gain and phase values (McArthur and Dickman 2008). The otolith component was nearly in-phase with angular velocity (phase ~ 0°), while the canal component had a nearly compensatory phase for angular velocity (phase ~ −180°). Further, the gain of the canal-driven VCR was an order of magnitude larger than the gain of the otolith-driven component. Thus, both behavioral and neural responses were consistent with mismatched sensitivity and phase values for canal- and otolith-associated components in the reflex circuitry of the vestibular nuclei.
Convergent inputs do not sum linearly during EHA rotation
EHA rotation dynamically modulates both canal and otolith inputs to convergent neurons. How do neurons integrate these two types of inputs when both are dynamically stimulated? One possibility was that convergent neurons simply computed a linear sum of canal and otolith inputs during EHA rotation. In a previous study (McArthur and Dickman 2008), we demonstrated that linear summation of canal- and otolith-driven response components provided a good characterization of compensatory eye (VOR) but not head (VCR) response gain and phase during EHA rotation. In the current study, linear summation failed to provide a good fit to the available gain and phase data for convergent neurons, consistent with nonlinear integration of canal and otolith inputs.
Two aspects of the stimulus protocol might introduce error into our characterization of the otolith input and might, therefore, account for some of the observed mismatches between actual and predicted gain and phase values during EHA rotation. First, we characterized the otolith input based on neural responses to horizontal linear acceleration only. Though EHA rotations primarily modulate the head-horizontal component of linear acceleration, there is an additional modulation in head-vertical linear acceleration (see Methods for details). However, since the head-vertical modulation was much smaller in amplitude and occurred at twice the frequency of the head-horizontal modulation, the response to the head-horizontal modulation was likely to dominate the otolith-driven response. Second, the translations used to characterize the otolith input generated a larger modulation of head-horizontal linear acceleration than the EHA rotations used to test the linear summation model (0.2g versus 0.1g, respectively). Though a subset of central vestibular neurons in monkeys vary their gain as a function of linear acceleration amplitude (Marlinski and McCrea 2009), there is no evidence that NEM neurons in pigeons display similar tendencies. Thus, despite these possible sources of error in our characterization of the otolith-driven input, we believe that the failure of the linear summation model to predict EHA response sensitivity and phase indicates that convergent neurons are carrying out real nonlinear integration of canal and otolith inputs.
Spatiotemporal matching: different species, different stages?
What kind of nonlinear processing might be carried out by convergent VNC neurons, and what purpose might this serve for the animal? We can only speculate regarding this issue, as there was insufficient data in the current study to rigorously fit alternative models of canal-otolith integration. However, others have provided insight from studies in non-human primates, where canal and otolith signals are combined to construct central representations of the animal’s movements in space. Canal afferents alone cannot reference the animal’s rotations to a space-fixed reference frame, since the semicircular canals are fixed in the head. Otolith afferents alone cannot disambiguate gravitational and translational linear accelerations, as the otolith organs detect net gravito-inertial linear acceleration. Populations of central neurons can perform these computations via nonlinear integration of canal and otolith afferent signals, whereby rotational signals are decomposed into EHA and EVA components and linear acceleration signals are decomposed into gravitational and translational components (Angelaki et al., 2004; Yakusheva et al., 2010). Modeling studies, grounded in behavioral and electrophysiological data, suggest that these computations require intermediate populations of convergent neurons, whose canal and otolith inputs are spatiotemporally matched (Green and Angelaki, 2004; 2007).
This matching need not occur at the level of an individual neuron, however, as long as the distributions of spatial preference, sensitivity, and phase match on average (Green and Angelaki, 2004; 2007). Further, each type of matching need not occur at the same level, i.e. the same anatomical location in the brain. In primates, distinct populations of neurons in the brainstem, cerebellar cortex, and deep cerebellar nuclei exhibit different degrees of input matching and nonlinear processing. Convergent neurons in the primate VNC not only exhibit a wide distribution of gain and phase values, but also lack the degree of input spatial matching that we saw in the pigeon (Dickman and Angelaki 2002). While there was a trend across the primate population for convergent canal and otolith inputs to prefer the same axis of EHA rotation, this was not generally observed for individual cells. In the cerebellar cortex, however, convergent canal- and otolith-driven inputs were tightly matched for both sensitivity and phase (Angelaki et al. 2010).
Perhaps the convergent neurons of both primates and pigeons perform similar functions, constructing meaningful representations from ambiguous afferent inputs. However, each species may display different levels of single-cell matching and may perform each type of matching at different places in the central vestibular system. In primates, convergent inputs to VNC neurons are not tightly matched for spatial preference, sensitivity, or phase, leaving this function for populations in the cerebellum to perform. In pigeons, convergent VNC neurons have relatively well-matched input spatial preferences, though the sensitivity and phase values are still mismatched. It may be necessary for pigeons to spatially match canal and otolith inputs in the brainstem in order to use the otolith-driven net linear acceleration signal to enhance the performance of the VOR and VCR along short-latency reflex pathways (McArthur and Dickman 2008). Future studies should characterize how the pattern of convergence in avian cerebellum compares to primates.
HIGHLIGHTS.
We characterize brainstem neurons receiving convergent canal and otolith input.
Convergent inputs were spatially aligned when co-stimulated during tilt.
Convergent inputs were temporally out of phase during tilt co-stimulation.
Net responses to tilt were not predicted by a linear combination of convergent inputs.
Acknowledgments
The authors thank Dr. Dora E. Angelaki for insight and suggestions regarding data analysis and presentation and for review of the manuscript. The authors also thank David Huss and Isabel Acevedo for expert assistance and support. Finally, the authors thank Dr. Jacob Nadler and Dr. Sally McIver, who recorded some of the data presented herein. This work was supported in part by funding from NIDCD Grants DC003286 and DC007618, NIH Training Grant T32-GM008151, and NASA Grant NNA-04CC52G.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Angelaki DE, Bush GA, Perachio AA. Two-dimensional spatiotemporal coding of linear acceleration in vestibular nuclei neurons. J Neurosci. 1993;13:1403–1417. doi: 10.1523/JNEUROSCI.13-04-01403.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Angelaki DE, Dickman JD. Spatiotemporal processing of linear acceleration: primary afferent and central vestibular neuron responses. J Neurophysiol. 2000;84:2113–2132. doi: 10.1152/jn.2000.84.4.2113. [DOI] [PubMed] [Google Scholar]
- Angelaki DE, Green AM, Dickman JD. Differential sensorimotor processing of vestibulo-ocular signals during rotation and translation. J Neurosci. 2001;21:3968–3985. doi: 10.1523/JNEUROSCI.21-11-03968.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Angelaki DE, Yakusheva TA, Green AM, Dickman JD, Blazquez PM. Computation of egomotion in the macaque cerebellar vermis. Cerebellum. 2010;9:174–182. doi: 10.1007/s12311-009-0147-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker J, Goldberg J, Peterson B. Spatial and temporal response properties of the vestibulocollic reflex in decerebrate cats. J Neurophysiol. 1985;54:735–756. doi: 10.1152/jn.1985.54.3.735. [DOI] [PubMed] [Google Scholar]
- Barmack NH. A comparison of the horizontal and vertical vestibulo-ocular reflexes of the rabbit. J Physiol. 1981;314:547–564. doi: 10.1113/jphysiol.1981.sp013724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beraneck M, Cullen KE. Activity of vestibular nuclei neurons during vestibular and optokinetic stimulation in the alert mouse. J Neurophysiol. 2007;98:1549–1565. doi: 10.1152/jn.00590.2007. [DOI] [PubMed] [Google Scholar]
- Brettler SC, Baker JF. Directional sensitivity of anterior, posterior, and horizontal canal vestibulo-ocular neurons in the cat. Exp Brain Res. 2001;140:432–442. doi: 10.1007/s002210100836. [DOI] [PubMed] [Google Scholar]
- Brettler SC, Rude SA, Quinn KJ, Killian JE, Schweitzer EC, Baker JF. The effect of gravity on the horizontal and vertical vestibulo-ocular reflex in the rat. Exp Brain Res. 2000;132:434–444. doi: 10.1007/s002210000357. [DOI] [PubMed] [Google Scholar]
- Bush GA, Perachio AA, Angelaki DE. Encoding of head acceleration in vestibular neurons. I. Spatiotemporal response properties to linear acceleration. J Neurophysiol. 1993;69:2039–2055. doi: 10.1152/jn.1993.69.6.2039. [DOI] [PubMed] [Google Scholar]
- Carleton SC, Carpenter MB. Distribution of primary vestibular fibers in the brainstem and cerebellum of the monkey. Brain Res. 1984;294:281–298. doi: 10.1016/0006-8993(84)91040-0. [DOI] [PubMed] [Google Scholar]
- Cullen KE, Chen-Huang C, McCrea RA. Firing behavior of brain stem neurons during voluntary cancellation of the horizontal vestibuloocular reflex. II. Eye movement related neurons. J Neurophysiol. 1993;70:844–856. doi: 10.1152/jn.1993.70.2.844. [DOI] [PubMed] [Google Scholar]
- Dickman JD. Spatial orientation of semicircular canals and afferent sensitivity vectors in pigeons. Exp Brain Res. 1996;111:8–20. doi: 10.1007/BF00229550. [DOI] [PubMed] [Google Scholar]
- Dickman JD, Angelaki DE. Three-dimensional organization of vestibular-related eye movements to off-vertical axis rotation and linear translation in pigeons. Exp Brain Res. 1999;129:391–400. doi: 10.1007/s002210050907. [DOI] [PubMed] [Google Scholar]
- Dickman JD, Angelaki DE. Vestibular convergence patterns in vestibular nuclei neurons of alert primates. J Neurophysiol. 2002;88:3518–3533. doi: 10.1152/jn.00518.2002. [DOI] [PubMed] [Google Scholar]
- Dickman JD, Beyer M, Hess BJ. Three-dimensional organization of vestibular related eye movements to rotational motion in pigeons. Vision Res. 2000;40:2831–2844. doi: 10.1016/s0042-6989(00)00128-0. [DOI] [PubMed] [Google Scholar]
- Dickman JD, Fang Q. Differential central projections of vestibular afferents in pigeons. J Comp Neurol. 1996;367:110–131. doi: 10.1002/(SICI)1096-9861(19960325)367:1<110::AID-CNE8>3.0.CO;2-6. [DOI] [PubMed] [Google Scholar]
- Dickman JD, Correia MJ. Responses of pigeon horizontal semicircular canal afferent fibers. I. Step, trapezoid, and low-frequency sinusoid mechanical and rotational stimulation. J Neurophysiol. 1989;62:1090–1101. doi: 10.1152/jn.1989.62.5.1090. [DOI] [PubMed] [Google Scholar]
- Eron JN, Cohen B, Raphan T, Yakushin SB. Differential coding of head rotation by lateral-vertical canal convergent central vestibular neurons. Prog Brain Res. 2008;171:313–318. doi: 10.1016/S0079-6123(08)00645-6. [DOI] [PubMed] [Google Scholar]
- Estes MS, Blanks RHI, Markham CH. Physiologic characteristics of vestibular first-order canal neurons in the cat. I. Response plane determination and resting discharge characteristics. J Neurophysiol. 1975;38:1232–1249. doi: 10.1152/jn.1975.38.5.1232. [DOI] [PubMed] [Google Scholar]
- Gdowski GT, McCrea RA. Integration of vestibular and head movement signals in the vestibular nuclei during whole-body rotation. J Neurophysiol. 1999;81:436–449. doi: 10.1152/jn.1999.82.1.436. [DOI] [PubMed] [Google Scholar]
- Gioanni H. Stabilizing gaze reflexes in the pigeon (Columba livia). II. Vestibulo-ocular (VOR) and vestibulo-collic (closed-loop VCR) reflexes. Exp Brain Res. 1988;69:583–593. doi: 10.1007/BF00247311. [DOI] [PubMed] [Google Scholar]
- Green AM, Angelaki DE. An integrative neural network for detecting inertial motion and head orientation. J Neurophysiol. 2004;92:905–925. doi: 10.1152/jn.01234.2003. [DOI] [PubMed] [Google Scholar]
- Green AM, Angelaki DE. Coordinate transformations and sensory integration in the detection of spatial orientation and self-motion: from models to experiments. Prog Brain Res. 2007;165:155–180. doi: 10.1016/S0079-6123(06)65010-3. [DOI] [PubMed] [Google Scholar]
- Harrod CG, Baker JF. The vestibuloocular reflex (VOR) in otoconia deficient head tilt (het) mutant mice versus wild type C57BL/6 mice. Brain Res. 2003;972:75–83. doi: 10.1016/s0006-8993(03)02505-8. [DOI] [PubMed] [Google Scholar]
- Haque A, Dickman JD. Vestibular gaze stabilization: different behavioral strategies for arboreal and terrestrial avians. J Neurophysiol. 2005;93:1165–1173. doi: 10.1152/jn.00966.2004. [DOI] [PubMed] [Google Scholar]
- Kasper J, Schor RH, Wilson VJ. Response of vestibular neurons to head rotations in vertical planes. I. Response to vestibular stimulation. J Neurophysiol. 1988;60:1753–1764. doi: 10.1152/jn.1988.60.5.1753. [DOI] [PubMed] [Google Scholar]
- Keshner FA, Peterson BW. Mechanisms controlling human head stabilization. I. Head-neck dynamics during random rotations in the horizontal plane. J Neurophysiol. 1995;73:2293–2301. doi: 10.1152/jn.1995.73.6.2293. [DOI] [PubMed] [Google Scholar]
- Kevetter GA, Perachio AA. Distribution of vestibular afferents that innervate the sacculus and posterior canal in the gerbil. J Comp Neurol. 1986;254:410–424. doi: 10.1002/cne.902540312. [DOI] [PubMed] [Google Scholar]
- Kuruvilla A, Sitko S, Schwartz IR, Honrubia V. Central projections of primary vestibular fibers in the bullfrog: I. The vestibular nuclei. Laryngoscope. 1985;95:692–707. doi: 10.1288/00005537-198506000-00012. [DOI] [PubMed] [Google Scholar]
- Marlinski V, McCrea RA. Self-motion signals in vestibular nuclei neurons projecting to the thalamus in the alert squirrel monkey. J Neurophysiol. 2009;101:1730–1741. doi: 10.1152/jn.90904.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McArthur KL, Dickman JD. Canal and otolith contributions to compensatory tilt responses in pigeons. J Neurophysiol. 2008;100:1488–1497. doi: 10.1152/jn.90257.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McArthur KL, Dickman JD. State-dependent sensorimotor processing: gaze and posture stability during simulated flight in birds. J Neurophysiol. 2011;105:1689–1700. doi: 10.1152/jn.00981.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McConville KMV, Tomlinson RD, Na E-Q. Behavior of eye-movement-related cells in the vestibular nuclei during combined rotational and translational stimuli. J Neurophysiol. 1996;76:3136–3148. doi: 10.1152/jn.1996.76.5.3136. [DOI] [PubMed] [Google Scholar]
- McCrea RA, Gdowski GT, Boyle R, Belton T. Firing behavior of vestibular neurons during active and passive head movements: vestibulo-spinal and other non-eye-movement related neurons. J Neurophysiol. 1999;82:416–428. doi: 10.1152/jn.1999.82.1.416. [DOI] [PubMed] [Google Scholar]
- Meier RK, Dieringer N. The role of compensatory eye and head movements in the rat for image stabilization and gaze orientation. Exp Brain Res. 1993;96:54–64. doi: 10.1007/BF00230438. [DOI] [PubMed] [Google Scholar]
- Newlands SD, Ling L, Phillips JO, Siebold C, Duckert L, Fuchs AF. Short- and long-term consequences of canal plugging on gaze shifts in the rhesus monkey. I. Effects on gaze stabilization. J Neurophysiol. 1999;81:2119–2130. doi: 10.1152/jn.1999.81.5.2119. [DOI] [PubMed] [Google Scholar]
- Newlands SD, Perachio AA. Central projections of the vestibular nerve: a review and single fiber study in the Mongolian gerbil. Brain Res Bull. 2003;60:475–495. doi: 10.1016/s0361-9230(03)00051-0. [DOI] [PubMed] [Google Scholar]
- Peng GC, hain TC, Peterson BW. Predicting vestibular, proprioceptive, and biomechanical control strategies in normal and pathological head movements. IEEE Trans Biomed Eng. 1999;46:1269–1280. doi: 10.1109/10.797986. [DOI] [PubMed] [Google Scholar]
- Perlmutter SI, Iwamoto Y, Baker JF, Peterson BW. Spatial alignment of rotational and static tilt responses of vestibulospinal neurons in the cat. J Neurophysiol. 1999;82:855–862. doi: 10.1152/jn.1999.82.2.855. [DOI] [PubMed] [Google Scholar]
- Precht W. Vestibular mechanisms. Ann Rev Neurosci. 1979;2:265–289. doi: 10.1146/annurev.ne.02.030179.001405. [DOI] [PubMed] [Google Scholar]
- Roy JE, Cullen KE. Vestibuloocular reflex signal modulation during voluntary and passive head movements. J Neurophysiol. 2002;87:2337–2357. doi: 10.1152/jn.2002.87.5.2337. [DOI] [PubMed] [Google Scholar]
- Roy JE, Cullen KE. Dissociating self-generated from passively applied head motion: neural mechanisms in the vestibular nuclei. J Neurosci. 2004;24:2102–2111. doi: 10.1523/JNEUROSCI.3988-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarz DW, Schwarz IE. Projection of afferents from individual vestibular sense organs to the vestibular nuclei in the pigeon. Acta Otolaryngol. 1986;102:463–473. doi: 10.3109/00016488609119432. [DOI] [PubMed] [Google Scholar]
- Scudder CA, Fuchs AF. Physiological and behavioral identification of vestibular nucleus neurons mediating the horizontal vestibuloocular reflex in trained rhesus monkeys. J Neurophysiol. 1992;68:244–264. doi: 10.1152/jn.1992.68.1.244. [DOI] [PubMed] [Google Scholar]
- Si X, Angelaki DE, Dickman JD. Response properties of pigeon otolith afferents to linear acceleration. Exp Brain Res. 1997;117:242–250. doi: 10.1007/s002210050219. [DOI] [PubMed] [Google Scholar]
- Tomlinson RD, McConville KM, Na EQ. Behavior of cells without eye movement sensitivity in the vestibular nuclei during combined rotational and translational stimuli. J Vestib Res. 1996;6:145–158. [PubMed] [Google Scholar]
- Uchino Y, Sato H, Kushiro K, Zakir MM, Isu N. Canal and otolith inputs to single vestibular neurons in cats. Arch Ital Biol. 2000;138:3–13. [PubMed] [Google Scholar]
- Wilson VJ, Bolton PS, Goto T, Schor RH, Yamagata Y, Yates BJ. Spatial transformation in the vertical vestibulocollic reflex. Ann N Y Acad Sci. 1992;656:500–506. doi: 10.1111/j.1749-6632.1992.tb25231.x. [DOI] [PubMed] [Google Scholar]
- Wilson VJ, Peterson BW. Peripheral and central substrates of vestibulospinal reflexes. Physiol Rev. 1978;58:80–105. doi: 10.1152/physrev.1978.58.1.80. [DOI] [PubMed] [Google Scholar]
- Wilson VJ, Schor RH, Suzuki I, Park BR. Spatial organization of neck and vestibular reflexes acting on the forelimbs of the decerebrate cat. J Neurophysiol. 1986;55:514–526. doi: 10.1152/jn.1986.55.3.514. [DOI] [PubMed] [Google Scholar]
- Yakushin SB, Raphan T, Cohen B. Spatial properties of central vestibular neurons. J Neurophysiol. 2006;95:464–478. doi: 10.1152/jn.00459.2005. [DOI] [PubMed] [Google Scholar]
- Zakir M, Kushiro K, Ogawa Y, Sato H, Uchino Y. Convergence patterns of the posterior semicircular canal and utricular inputs in single vestibular neurons in cats. Exp Brain Res. 2000;132:139–148. doi: 10.1007/s002210000336. [DOI] [PubMed] [Google Scholar]
- Zhou W, Tang BF, Newlands SD, King WM. Responses of monkey vestibular-only neurons to translation and angular rotation. J Neurophysiol. 2006;96:2915–2930. doi: 10.1152/jn.00013.2006. [DOI] [PubMed] [Google Scholar]