Skip to main content
PMC home page
Bioinformatics logoLink to Bioinformatics
. 2011 Jul 22;27(18):2610–2611. doi: 10.1093/bioinformatics/btr431

GenSSI: a software toolbox for structural identifiability analysis of biological models

Oana Chiş 1, Julio R Banga 1, Eva Balsa-Canto 1,*
PMCID: PMC3167050  PMID: 21784792

Abstract

Summary: Mathematical modeling has a key role in systems biology. Model building is often regarded as an iterative loop involving several tasks, among which the estimation of unknown parameters of the model from a certain set of experimental data is of central importance. This problem of parameter estimation has many possible pitfalls, and modelers should be very careful to avoid them. Many of such difficulties arise from a fundamental (yet often overlooked) property: the so-called structural (or a priori) identifiability, which considers the uniqueness of the estimated parameters. Obviously, the structural identifiability of any tentative model should be checked at the beginning of the model building loop. However, checking this property for arbitrary non-linear dynamic models is not an easy task. Here we present a software toolbox, GenSSI (Generating Series for testing Structural Identifiability), which enables non-expert users to carry out such analysis. The toolbox runs under the popular MATLAB environment and is accompanied by detailed documentation and relevant examples.

Availability: The GenSSI toolbox and the related documentation are available at http://www.iim.csic.es/%7Egenssi.

Contact: ebalsa@iim.csic.es

1 INTRODUCTION

Mathematical modeling can be regarded as the central element in computational systems biology. The process of developing a model involves several tasks, among which the estimation of unknown parameters of the model from a certain set of experimental data is of key importance (Ashyraliyev et al., 2009; Banga and Balsa-Canto, 2008; Jaqaman and Danuser, 2006). This problem of parameter estimation, also known as the inverse problem, has many possible pitfalls, and modelers should be very careful to avoid them. Many of such pitfalls arise from a fundamental (yet often overlooked) property of this inverse problem: the so-called structural (or a priori) identifiability (Jaqaman and Danuser, 2006; Srinath and Gunawan, 2010; Walter and Pronzato, 1997).

Global identifiability considers the issue of uniquely estimating all the free parameters of a model from data (Ljung and Glad, 1994). If a model is non-identifiable, then the estimated parameters will lead, irrespective of the applied method, to artifacts in the model calibration and errors in subsequent model predictions. Thus, there is a fundamental need of reliable methods and tools to detect non-identifiability as soon as a new model is proposed. Structural (a priori) non-identifiability is usually caused by over-parameterization of the model (including its observation function), while practical (a posteriori) non-identifiability is generally due to lack of information in the available data. Here, we will focus in a priori global identifiability, which is a structural property of the model, and must be considered a prerequisite for reliable parameter estimation. It should be noted that structural identifiability assumes an ideal context of error-free model structure and noise-free measurements.

The vast majority of models in current systems biology are non-linear and dynamic. Testing the identifiability of this class of models (typically composed of sets of non-linear ordinary differential equations) is an extremely challenging mathematical problem. Currently, most of the software tools allow for practical identifiability analysis (see, for example, the Profile Likelihood Approach, PLE(Raue et al., 2009) or AMIGO (Balsa-Canto and Banga, 2011). The analysis is performed for a given dataset and parameter values. DAISY (Differential Algebra for Identifiability of SYstems) (Bellu et al., 2007) allows for the structural identifiability analysis; however, it is limited in the size and the functional form of the non-linearities that can be handled (only polynomial or rational).

Here we present a new software, GenSSI (Generating Series approach for testing Structural Identifiability), implemented as a free toolbox for the MATLAB computing language. GenSSI can handle any linear or non-linear dynamic model described by arbitrary analytic functions. GenSSI is easy to use and does not require user knowledge of higher mathematics, a programming language or computer algebra system (other than basic familiarity with MATLAB). The user only needs to specify the model equations, input variables (controls), output variables (observables), initial conditions and relevant parameters for model calibration. After a series of automatic symbolic computations (see methods below), the toolbox produces rich text and graphical output describing the identifiability of such model. The toolbox is accompanied by a users guide with several examples and detailed documentation describing the methods and their implementation.

2 METHODS AND IMPLEMENTATION

GenSSI can handle systems represented by a set of linear/non-linear differential equations of the form given below:

graphic file with name btr431m1.jpg (1)

where x∈Rn is the n-dimensional state variable, u∈Rm a m-dimensional control, y∈Rr is the r-dimensional output which may be in principle any function of the state variables and x0(p) are the initial conditions that may depend on the parameters. The model response will depend on a number of unknown parameters, denoted by p∈P (P⊆Rq).

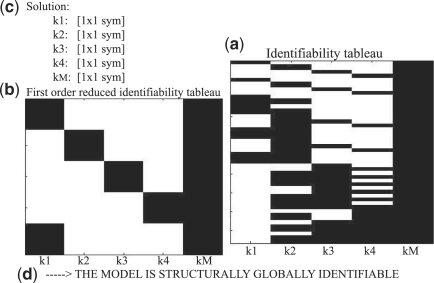
GenSSI is based on the generating series approach coupled with the use of identifiability tableaus (Balsa-Canto et al., 2010). The underlying idea is to generate a non-linear system of equations on the parameters from the computation of the successive Lie derivatives of f and g. If the solution of the system of equations is unique then the parameters are globally identifiable. Note that at least a number of r(1+m)NrDerivatives should be computed. But it is possible that extra derivatives are needed if the kernel (initial conditions) is not informative, thus zero or dependent Lie derivatives are generated. Once the Lie derivatives are computed, the identifiability tableaus (see Fig. 1 for an illustrative example) help not only to devise global identifiable parameters, but also to decide on the appropriate way to handle the non-linear system of equations on the remaining parameters.

Fig. 1.

Fig. 1.

Open in a new tab

Example of output from GenSSI: (a) Identifiability tableau of rank equal to the number of parameters (5); (b) reduced identifiability tableau—the first five linear independent rows (associated to the corresponding Lie derivatives components); (c) symbolic solution of the parameters (in this case unique).

GenSSI will automatically perform all symbolic computations and will finally present, after reasonable computation times, text and figures describing the structural identifiability of the set of parameters. GenSSI will produce one of the following diagnosis: structurally globally identifiable (SGI), structurally locally identifiable (SLI) and structurally non-identifiable (SNI) up to the current derivative. SGI is guaranteed if a unique solution of the parameters p can be obtained from the set of algebraic equations generated using input–output data. If SGI cannot be proved, GenSSI will try to establish if there is a finite number of indistinguishable parameter values, in which case the model will be SLI. Otherwise the model will be SNI. The model Σ(p) will be SNI if at least one of its parameters is SNI.

3 EXAMPLES

In order to illustrate the use and capabilities of GenSSI, the software distribution includes a detailed users guide and several relevant examples:

  • the Goodwin oscillator: a model of oscillatory behavior in enzymatic control, with three dynamic state variables, six parameters and three observables.

  • (an Arabidopsis thaliana circadian network model), with seven dynamic state variables, 27 parameters, one control variable and two observables.

  • a glycolysis-inspired metabolic pathway, with five dynamic state variables, five parameters, four controls and five observables.

In the toolbox documentation, we discuss in detail the results of GenSSI for these examples, which are obtained with a very reasonable computational effort. Further, we also illustrate how, in cases of structural non-identifiability, subsets of parameters can be chosen in order to make the system identifiable.

4 CONCLUSION

Here we present a software toolbox, GenSSI, which can be used to test the structural identifiability of arbitrary non-linear dynamical models of biological systems (i.e. described by sets of non-linear ordinary differential equations). In case of detection of non-identifiability for a given model, this toolbox can also be used to determine which subsets parameters can be identified (or at least locally identified), therefore guiding in the reformulation of the model when needed. GenSSI is cross-platform (using the MATLAB computing environment, available in most operating systems) and is easy to use, not requiring high-level programming or advanced mathematical skills from users.

Funding: Spanish MICINN project ‘MultiSysBio’ (ref. DPI2008-06880-C03-02); CSIC intramural project ‘BioREDES’ (ref. PIE-201170E018).

Conflict of Interest: none declared.

REFERENCES

  1. Ashyraliyev M., et al. Systems biology: parameter estimation for biochemical models. FEBS J. 2009;276:886–902. doi: 10.1111/j.1742-4658.2008.06844.x. [DOI] [PubMed] [Google Scholar]
  2. Balsa-Canto E., Banga J.R. AMIGO, a toolbox for advanced model identification in systems biology using global optimization. Bioinformatics. 2011 doi: 10.1093/bioinformatics/btr370. [Epub ahead of print; doi:10.1093/bioinformatics/btr370] [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Balsa-Canto E., et al. An iterative identification procedure for dynamic modeling of biochemical networks. BMC Syst. Biol. 2010;4:11. doi: 10.1186/1752-0509-4-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Banga J., Balsa-Canto E. Parameter estimation and optimal experimental design. Essays Biochem. 2008;45:195. doi: 10.1042/BSE0450195. [DOI] [PubMed] [Google Scholar]
  5. Bellu G., et al. DAISY: a new software tool to test global identifiability of biological and physiological systems. Comp. Meth. Prog. Biomed. 2007;88:52–61. doi: 10.1016/j.cmpb.2007.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Jaqaman K., Danuser G. Linking data to models: data regression. Nat. Rev. Mol. Cell Biol. 2006;7:813–819. doi: 10.1038/nrm2030. [DOI] [PubMed] [Google Scholar]
  7. Ljung L., Glad T. On global identifiability for arbitrary model parametrizations. Automatica. 1994;30:265–276. [Google Scholar]
  8. Raue A., et al. Structural and practical identifiability analysis of partially observed dynamical models by exploiting the profile likelihood. Bioinformatics. 2009;25:1923. doi: 10.1093/bioinformatics/btp358. [DOI] [PubMed] [Google Scholar]
  9. Srinath S., Gunawan R. Parameter identifiability of power-law biochemical system models. J. Biotech. 2010;149:132–140. doi: 10.1016/j.jbiotec.2010.02.019. [DOI] [PubMed] [Google Scholar]
  10. Walter E., Pronzato L. Commun. Control Eng. ed. London: Springer; 1997. Identification of parametric models from experimental data. [Google Scholar]

Articles from Bioinformatics are provided here courtesy of Oxford University Press

RESOURCES