Neutral Evolution of Robustness in Drosophila microRNA Precursors

Abstract

Mutational robustness describes the extent to which a phenotype remains unchanged in the face of mutations. Theory predicts that the strength of direct selection for mutational robustness is at most the magnitude of the rate of deleterious mutation. As far as nucleic acid sequences are concerned, only long sequences in organisms with high deleterious mutation rates and large population sizes are expected to evolve mutational robustness. Surprisingly, recent studies have concluded that molecules that meet none of these conditions—the microRNA precursors (pre-miRNAs) of multicellular eukaryotes—show signs of selection for mutational and/or environmental robustness. To resolve the apparent disagreement between theory and these studies, we have reconstructed the evolutionary history of Drosophila pre-miRNAs and compared the robustness of each sequence to that of its reconstructed ancestor. In addition, we “replayed the tape” of pre-miRNA evolution via simulation under different evolutionary assumptions and compared these alternative histories with the actual one. We found that Drosophila pre-miRNAs have evolved under strong purifying selection against changes in secondary structure. Contrary to earlier claims, there is no evidence that these RNAs have been shaped by either direct or congruent selection for any kind of robustness. Instead, the high robustness of Drosophila pre-miRNAs appears to be mostly intrinsic and likely a consequence of selection for functional structures.

Introduction

Robustness or canalization is the extent to which a genotype can produce the same phenotype in the face of perturbations (Gibson and Wagner 2000; Meiklejohn and Hartl 2002; de Visser et al. 2003; Flatt 2005; Wagner 2005). These perturbations can be genetic, such as mutation, recombination, and horizontal gene transfer, or environmental, such as fluctuations in temperature, food availability, or salinity. Mutational robustness is thought to be a fundamental property of biological systems, from individual molecules to gene regulatory networks (de Visser et al. 2003; Kitano 2004a, 2004b; Stelling et al. 2004; Wagner 2005). For example, Guo et al. (2004) found that 74% of nucleotide substitutions preserved at least some of the function of human enzyme 3-methyladenine DNA glycosylase (3MDG). High tolerance against mutations has been observed in many other proteins (Miller 1979; Reddy et al. 1998; Bloom et al. 2005; Lind et al. 2010). In addition, conserved elements of secondary structure from the genomes of RNA viruses were found to be significantly more resistant to mutations than nonconserved elements (Wagner and Stadler 1999).

How did this high mutational robustness evolve? One possibility is that it resulted from direct selection for high mutational robustness (de Visser et al. 2003). The strength of selection for mutational robustness is at most the magnitude of the deleterious mutation rate, U_del (Kimura 1967; Proulx and Phillips 2005). For a single RNA or protein molecule, the deleterious mutation rate is given by $U_{\text{del}}=\mu L{P}_{\text{del}}$, where μ is the mutation rate per site, per generation, L is the length of the sequence, and P_del is the probability that a mutation is deleterious. (Note that 1–P_del is a measure of neutrality or mutational robustness.) For example, the human enzyme 3MDG has L = 894 nucleotides [nt] and P_del = 26% (Guo et al. 2004). Assuming that μ = 2.5×10⁻⁸ per base pair per generation (Nachman and Crowell 2000), we estimate that U_del ≈ 5.8 × 10⁻⁶. Thus, selection for mutational robustness is expected to be weak in human 3MDG, as well as in the vast majority of individual gene products.

The main factor determining the extent to which mutational robustness will respond to direct selection is the effective population size, N_e (Kimura 1968a; Wagner et al. 1997; van Nimwegen et al. 1999; Wilke et al. 2001; Azevedo et al. 2006; Forster et al. 2006). For example, a diploid population is expected to respond provided that it obeys the condition $2N_{\text{e}}{U}_{\text{del}}>>1$ (Wright 1931; Kimura 1968b; Li 1978). Therefore, according to theory, mutational robustness should only evolve under direct selection in taxa with high N_eU_del, such as certain RNA viruses, prokaryotes, and unicellular eukaryotes (Drake et al. 1998; Lynch and Conery 2003). In agreement with this prediction, experimental evidence for evolution of mutational robustness under direct selection has only been observed in an RNA virus (Sanjuán et al. 2007). In contrast, the mutational robustness of individual protein or RNA molecules is expected to be effectively neutral in most multicellular eukaryotes (Lynch and Conery 2003), suggesting that direct selection is an unlikely explanation for the findings of high mutational robustness.

An alternative explanation, known as congruence, is that mutational robustness evolved as a by-product of selection for another form of robustness (Ancel and Fontana 2000; Gibson and Wagner 2000; Meiklejohn and Hartl 2002; de Visser et al. 2003; Wagner 2005; Masel and Siegal 2009), such as thermodynamic stability (Ancel and Fontana 2000), robustness to recombination (Azevedo et al. 2006; Gardner and Kalinka 2006; Misevic et al. 2006; Szöllósi and Derényi 2008), or robustness to transcriptional or translational errors (Ninio 1991; Wilke and Drummond 2006). For example, RNA molecules alternate rapidly among several different low-energy secondary structures. Some molecules are more thermodynamically stable than others at a constant temperature. Using computer simulations, Ancel and Fontana (2000) showed that the thermodynamic stability of an RNA molecule is positively correlated with its robustness to mutation, such that selection for the ability to produce a given structure at constant temperature caused both thermodynamic stability and mutational robustness to increase. Recently, Montville et al. (2005) demonstrated that mutational robustness evolved congruently in strains of an RNA virus selected for high and low levels of coinfection.

A third hypothesis is that mutational robustness is intrinsic (Gibson and Wagner 2000; de Visser et al. 2003; Wagner 2005; Masel and Siegal 2009), that is, it evolved as a by-product of selection for a gene's function. For example, the binding affinity of an enzyme for its ligand might be genetically correlated to the robustness of the enzyme, such that selection on the enzyme activity would drive the evolution of robustness.

In the last decade, RNA molecules such as microRNA precursors (pre-miRNAs) have emerged as a model system for the study of the evolution of robustness (Wagner and Stadler 1999; Bonnet et al. 2004; Borenstein and Ruppin 2006; Sanjuán et al. 2006; Shu et al. 2007, 2008; Szöllósi and Derényi 2009; Churkin et al. 2010). Mature microRNAs (miRNAs) are short sequences ∼21–23 nt in length that regulate gene expression in eukaryotes (Bartel 2004). Mature miRNAs originate from longer primary miRNA transcripts. In animals, miRNA maturation includes four steps (Bartel 2004): (i) a ∼60- to 70-nt pre-miRNA is cleaved in the nucleus by the RNase III endonuclease Drosha and then (ii) exported to the cytoplasm by the RanGTP-dependent double-stranded RNA-binding protein Exportin 5, where (iii) another RNase III endonuclease, Dicer, cuts it into a 21- to 23-nt RNA duplex; (iv) one strand of the RNA duplex—the mature miRNA—gets incorporated preferentially into a protein complex that inhibits target gene expression. Pre-miRNA molecules fold into a stem–loop hairpin structure (Bartel 2004) (fig. 1A). The pre-miRNAs of multicellular eukaryotes are not expected to respond to direct selection for mutational robustness because they are small molecules in organisms with small populations: if we assume L = 100 and P_del = 100% (the maximum possible value), we expect that 2N_eU_del ≈ 2N_eμ to range from 0.054 to 0.74 for the pre-miRNAs of human, mouse, Drosophila melanogaster, and Caenorhabditis elegans (Lynch and Conery 2003).

FIG. 1.

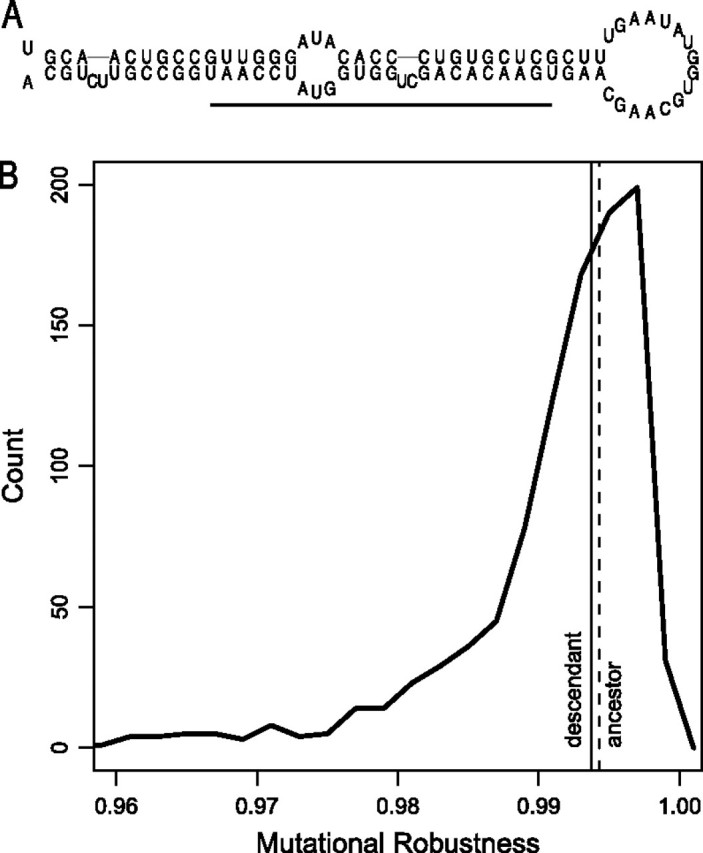
No evidence of evolution of mutational robustness in Drosophila pseudoobscura mir-317. (A) Secondary structure of dps-mir-317. The pre-miRNA folds into a stem–loop hairpin structure. The horizontal line marks the location of the mature miRNA. (B) Density plot of the structure-constrained null distribution of mutational robustness for dps-mir-317. The null distribution consists of 1000 sequences differing from the predicted ancestor in any k = 5 nucleotide positions but with exactly the same length (L = 90 nt) and structure as dps-mir-317. See supplementary figure S1 (Supplementary Material online) for additional null distributions.

Surprisingly, Borenstein and Ruppin (2006) reported evidence for direct selection for mutational robustness in pre-miRNAs from, among others, the above-listed species. They found that these RNAs have a higher mutational robustness than random sequences with the same secondary structure, even after controlling for the robustness arising from the pre-miRNA hairpin structure (fig. 1 and supplementary fig. S1, Supplementary Material online) and correcting for nucleotide composition bias. Furthermore, real and random pre-miRNAs did not differ significantly in their thermodynamic stability, which led them to conclude that the high mutational robustness was caused by direct, rather than congruent, selection (Borenstein and Ruppin 2006). If correct, these results would imply that, either current population genetics theory is wrong or that we have grossly underestimated the effective population sizes and/or the deleterious mutation rates in multicellular eukaryotes, including humans.

Subsequent studies (Shu et al. 2007; Szöllósi and Derényi 2009) have challenged some of Borenstein and Ruppin's results, although they have confirmed the finding that the mutational robustness of natural pre-miRNAs is higher than that of random sequences with the same structure. However, previous studies on the evolution of pre-miRNA robustness have two important limitations (Bonnet et al. 2004; Borenstein and Ruppin 2006; Shu et al. 2007, 2008; Szöllósi and Derényi 2009). First, they assume that random or shuffled sequences provide adequate null models for the evolution of pre-miRNAs, whereas natural sequences tend to evolve over much shorter sequence distances (Ehrenreich and Purugganan 2008; Liang and Li 2009; Nozawaet al. 2010). Second, the pre-miRNAs considered are not phylogenetically independent (Felsenstein 1985). Here we use a rigorous phylogenetic framework (fig. 2) to test whether or not the mutational and environmental robusteness of Drosophila pre-miRNAs have been subject to selection during ∼60 My of evolution.

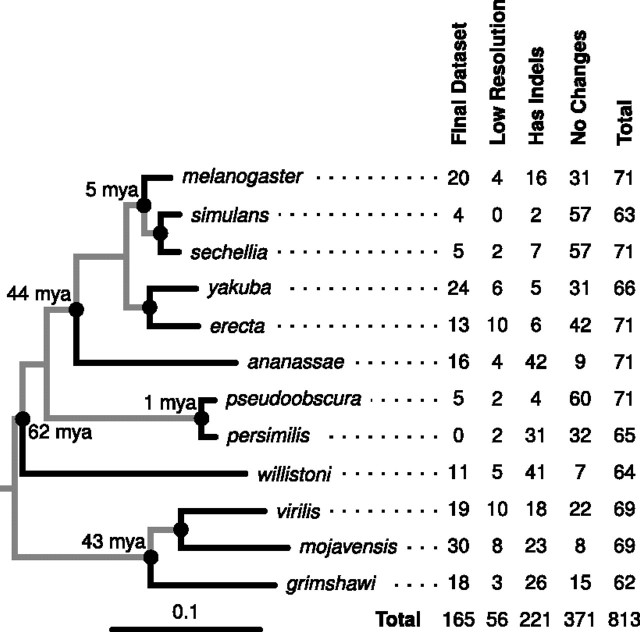
FIG. 2.

Summary of the pre-miRNA data set. Seventy-one sets of orthologous pre-miRNA genes from Drosophila were analyzed using the above phylogenetic tree (Siepel et al. 2005; Rosenbloom et al. 2010). (See http://tinyurl.com/drostree for original.) Divergence dates were taken from (Tamura et al. 2004). Only evolutionary events that occurred on the terminal branches (black lines) were counted. For genes found in all 12 species, inferred ancestors were used at the nodes with black circles. The table summarizes the number of branches/sequences for each species that were filtered for (1) showing no evolution, (2) containing indels, or (3) having null distributions with low resolution, that is, fewer than 20 unique values for mutational robustness. The remaining branches were part of the final data set. See Materials and Methods for more details.

Materials and Methods

Pre-miRNA Genes and Ancestral Sequence Reconstruction

We constructed a data set of pre-miRNAs by downloading Drosophila sequences from miRBase version 14 (Sept. 2009) (Griffiths-Jones et al. 2008). If a pre-miRNA gene had orthologs in at least 8 of the 12 Drosophila species found in miRBase (see list in fig. 2), we included it for ancestral sequence reconstruction. If a species had multiple copies of a gene, we excluded all copies in that species. The pre-miRNA sequences in miRBase include the product of Drosha cleavage and a small amount of flanking sequence (Griffiths-Jones et al. 2008).

We gathered a total of 71 pre-miRNA orthologous gene sets (supplementary table S1, Supplementary Material online) and aligned the sequences for each gene using MAFFT v6.717b (global pair/G-INS-i alignment algorithm with default parameters and maximum iterations at 1000) (Katoh and Toh 2008). The guide tree used for the alignments was the phylogenetic tree in figure 2 (Siepel et al. 2005; Rosenbloom et al. 2010). When a gene had orthologs in fewer than 12 species, the tree was pruned to remove the missing species. To reconstruct ancestral sequence states, we used the web server ANCESTORS v1.0 (http://ancestors.bioinfo.uqam.ca/ancestorWeb/), which implements a maximum likelihood method (Blanchette et al. 2008; Diallo et al. 2010). Ancestry was inferred from our alignments and guide trees using the “best exact scenario” option and default parameters. Ancestral state reconstruction did not take into account the secondary structures of the sequences involved. We restricted our analyses to the terminal branches in the ancestral reconstruction that included at least one substitution and no insertions or deletions (indels), resulting in 221 usable branches (fig. 2).

Secondary Structure Prediction and Simulation of Alternative Descendants

For each of the 221 terminal branches included in our analysis, we predicted the minimum free energy (MFE) structure of the ancestor and descendant using the folding algorithm developed by Zuker and Stiegler (1981) and implemented in the RNAfold program of the Vienna RNA package version 1.8.4 (Hofacker et al. 1994). We then simulated alternative descendants for each branch by randomly mutating the ancestral sequence based on the number of substitutions in the natural descendant and keeping sequences that had the same structure as our descendant sequence (Zuker and Stiegler 1981). The number of possible descendants that are k substitutions away from an ancestor of sequence length L is $\left(\begin{array}{c}L\\ k\end{array}\right)3^k$ (assuming no back mutations). Because this number quickly becomes very large, we exhaustively searched all possible descendants for branches that contained k = 1 or 2 substitutions. For branches that contained k ≥ 3 substitutions, we uniformly generated random descendants with replacement. For these searches, the sampling algorithm stopped when either it found 1,000 descendants with the same MFE structure (a success) or the probability of finding a descendant with the same MFE structure was less than ${10}^{-6}$. To estimate this probability, we used pseudocounts:

where S is the number of successes and N is the total number of sequences tried.

In addition to simulating possible descendants with the same MFE structure, we also simulated possible descendants without constraining on structure. As before, we uniformly generated random descendants of the ancestors of each sequence in our 221-branch data set. However, we simply kept the first 1,000 simulated descendants for any value of k. Because structure was not constrained, these sets contained some sequences with the same MFE structure as the natural descendant and some with a different structure. We refer to the two sets of simulations as structure constrained and structure unconstrained, respectively.

Measuring Robustness

Robustness is best measured as a variance (Wagner et al. 1997; Rice 1998; Gibson and Wagner 2000), but the robustness metrics used in previous studies of pre-miRNAs (Borenstein and Ruppin 2006; Shu et al. 2007; Szöllósi and Derényi 2009) do not capture this principle. (Note, however, that employing the metrics defined in those studies does not change our results qualitatively.) Here we introduce variance measures of robustness based on the base-pair distance (d) between two structures calculated using the bp_distance algorithm in the Vienna RNA package (Hofacker et al. 1994) (the number of base pairs present in one structure, but not the other).

We define the mutational “fragility” of a sequence of length L as

where d_i is the MFE structural distance between the sequence and its mutant neighbor i. This statistic is inversely related to robustness ($f_m=0$ for a maximally robust sequence). We measure mutational robustness as $r_m=1-f_m$.

We define the environmental fragility of a sequence of length L as the variance of its structural ensemble:

where d_j is the distance between a sampled pair of structures from the ensemble, and N is the number of sampled pairs. As before, environmental robustness (or thermodynamic stability) is calculated as $r_e=1-f_e$. We generated ensembles via Vienna RNA's partition function folding algorithm (pf_fold) using the default temperature of 310 K and calculated f_e from N = 10⁶ sampled pairs.

The distributions of r_m and r_e for the 165 Drosophila pre-miRNAs were similar and skewed towards the maximum of 1, indicating that these natural sequences are highly robust (supplementary fig. S4A, Supplementary Material online). Furthermore, the two types of robustness were strongly correlated (Spearman's rank correlation: $\rho =0.703$; fig. S4B, Supplementary Material online).

Drosophila pre-miRNA Trees

Reconstruction of the 71 pre-miRNA genes produced a total of 813 terminal branches, approximately half had no changes, a quarter had indels, and a quarter had only substitutions. Figure 2 shows the phylogeny of the Drosophila species used in this study and the number of branches that were in the final data set or excluded for one of three reasons. As expected, the branches where species had recently diverged such as D. simulans, D. sechellia, D. pseudoobscura, and D. persimilis were most likely to have branches with no changes.

The number of terminal branches with only substitutions was 221. About half of these branches contained a single substitution, but 18% had 4 or more substitutions allowing us to explore a broad range of evolutionary divergences (table 1). Eighty branches had at least 100 samples, and 86 had between 20 and 99 samples. Notably, six branches produced no samples with the same structure.

Table 1.

Number of Substitutions and Size of Structure-Constrained Null Distributions Per Branch

		Number of Substitutionsa
		1	2	3	4	5	6+	Total
Size of null distribution	0–19	36	13	0	1	1	4	55
	20–99	75	11	0	0	0	0	86
	100–999	1	12	1	0	4	5	23
	1000+	0	11	21	12	8	5	57
	Total	112	47	22	13	13	14	221

^aBranches with indels or no substitutions are excluded.

We further pruned these 221 branches by estimating the mutational and environmental robustness values of each of the samples in their null distributions and excluding branches that had less than 20 unique mutational robustness values. This produced a final data set that contained 165 branches (fig. 2). The 165 branches came from 62 orthologous genes; nine orthologous genes—miR-1, miR-124, miR-125, miR-283, miR-289, miR-2a-2, miR-2c, miR-307, and miR-iab-4—produced no branches that made the final data set. For each Drosophila species, except D. persimilis, we were able to retain at least four terminal branches with only substitutions and a sufficient number of unique robustness values of simulated sequences (supplementary table S1, Supplementary Material online). Including lower-resolution branches or excluding branches with a single substitution did not affect our conclusions.

Test of Selection

To determine whether pre-miRNA sequences have been selected for increased robustness, we compared the robustness of the natural sequences to null distributions produced in our simulations. On some branches, the descendant structure was so unusual that we did not have enough robustness values to make a meaningful comparison (table 1). Out of the 221 branches, we excluded ones for which the simulations produced less than 20 unique values for r_m. This gave us 165 branches to test whether there had been selection for increased robustness (fig. 2). (Note that one branch from rows 2–4 of table 1 is excluded due to the uniqueness criteria, resulting in 165 not 166 branches in this data set.) Significance was assessed by first calculating the quantile q of each natural descendant's r value in the null distribution provided by the set of simulated descendants selected to have the same MFE structure. Because ties between r values were possible, we calculated q as the mid-point of any r values in the null-distribution that were the same as the descendants:

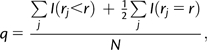where r is the robustness value (mutational or environmental) for the natural descendant, r_j is the value for the j-th element of the null sample, N is the number of values in the null sample for that branch, and I is an indicator function. If the natural descendants were not systematically selected for robustness, then we would expect them to follow their associated null distributions, so that the values of q should be uniformly distributed.

To evaluate the uniformity of the distribution of q, we used the Anderson–Darling goodness-of-fit test (Anderson and Darling 1952; Marsaglia and Marsaglia 2004). The Anderson–Darling test statistic, A, is based on the area between a sample cumulative distribution function (CDF) and the diagonal (the uniform CDF):

where $x_1<x_2<\dots <x_n$ is an ordered set of samples (Marsaglia and Marsaglia 2004). If this statistic is greater than expected, then the sample is considered to deviate significantly from uniformity. The significance of A was measured with the statistical software R (R Development Core Team 2009), using the method of Marsaglia and Marsaglia (2004) implemented in the ADGofTest package. Because our data set contained uneven sample sizes and ties, we confirmed the significance levels via simulation. We constructed 1000 simulated data sets by randomly sampling robustness values from the null distribution of each of our branches and calculating the A statistic for each data set.

Under the null hypothesis, the CDF consists of uniform order statistics, which follow a beta(k, n–k+1) distribution, where k is the rank of a point and n is the sample size. From the null distribution, we determined the 95% concentration band for the simultaneous and equal-tail test of points in the CDF. We found that a pointwise concentration band with α = 0.000925 rejected only 5% of uniform Monte Carlo simulations with 165 points.

Results

Mutational and Environmental Robustness Have Not Increased

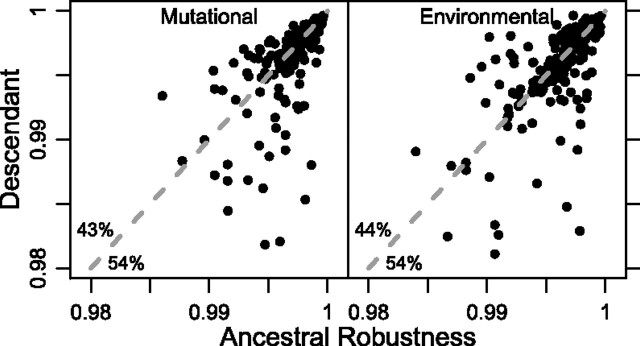
If a substantial fraction of Drosophila pre-miRNAs has experienced a recent history of selection (direct or indirect) for increased robustness, then we might expect descendant (extant) pre-miRNAs to be more robust than their ancestors. When we compare the 221 descendants and their predicted ancestors, we find that both mutational robustness (r_m) and environmental robustness (r_e) have decreased slightly (median Δr_m = –0.0015% and Δr_e = –0.0031%; fig. 3 and supplementary fig. S2, Supplementary Material online) and that the change is marginally statistically significant (paired Wilcoxon test: p_m ≈ p_e ≈ 0.05). These results suggest that Drosophila pre-miRNAs have not evolved increased levels of either kind of robustness.

FIG. 3.

Mutational and environmental robustness have not increased from ancestor to descendant. Comparisons of mutational and environmental robustness in the 221 natural pre-miRNAs used in this study with estimated values in corresponding ancestors. Numbers in the bottom left of panels indicate the percentage of points in either half of the panel, defined by the y = x diagonal. Some outlying points (<10) are not plotted (see supplementary fig. S2, Supplementary Material online).

Neutral Evolution of Both Mutational and Environmental Robustness

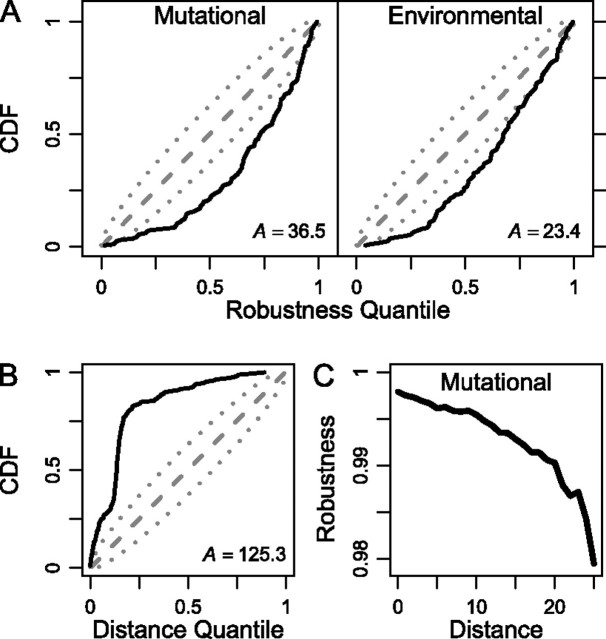
The previous test assumed that neutral evolution of robustness would cause robustness not to change (on average) between ancestor and descendant. However, this assumption would not be met if, for example, most mutations caused a reduction in pre-miRNA robustness. To take such a possibility into account, we replayed the tape of evolution (Gould 1989); we generated a null distribution of descendant pre-miRNA sequences at the same sequence distance (k) from the ancestor and with the same secondary structure as the real descendant (i.e., with base pair distance, d = 0). Figure 1B shows the resulting null distribution for mutational robustness for a representative sequence, the D. pseudoobscura mir-317. The null distribution allows us to measure the extent to which a real descendant pre-miRNA is more or less robust than expected under neutral evolution, when structure is the only constraint. For example, dps-mir-317 corresponds to the q = 54.7% quantile of the null distribution, implying that it is slightly more robust than expected, despite being slightly less robust than its ancestor (fig. 1B). If the robustness of Drosophila pre-miRNAs has been evolving neutrally, then we expect that values of q over the entire data set should be uniformly distributed. The CDFs of q for mutational and environmental robustness are plotted in figure 4A and do not differ significantly from a uniform distribution (Anderson–Darling test: $p_m=0.469$ and $p_e=0.480$, N = 165). The insignificance of thesegoodness-of-fit tests was confirmed by simulation ($p_m=0.463$and $p_e=0.481$; fig. 4B). These results suggest that the robustness of Drosophila pre-miRNAs has evolved neutrally.

FIG. 4.

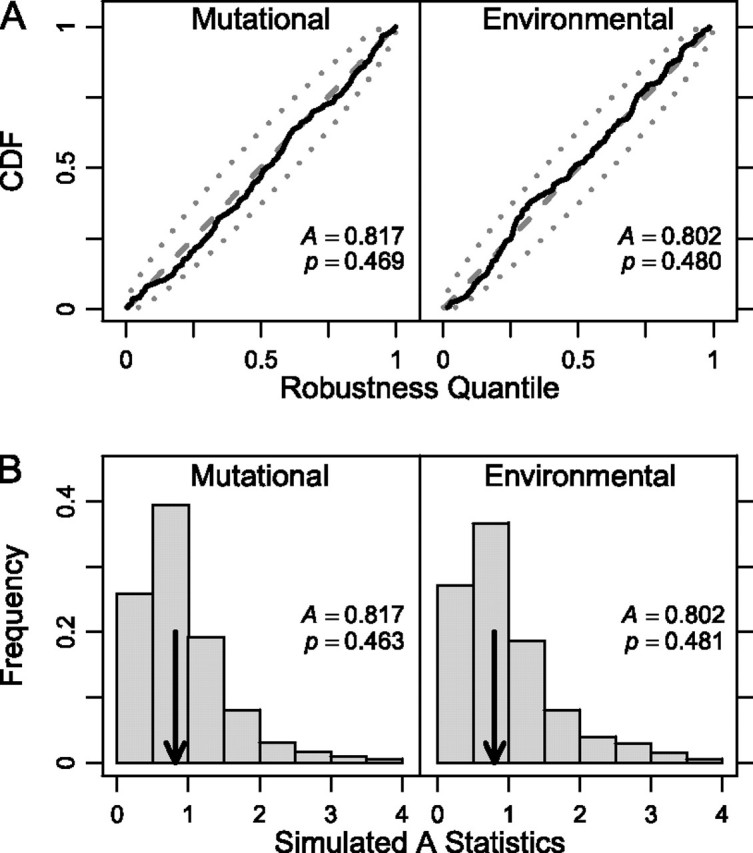
Neutral evolution of robustness. (A) The CDF of q values (black lines) of the robustness of pre-miRNAs compared with their corresponding structure-constrained null distributions. Anderson-Darling test statistics (A) and their associated P values are also shown. The dashed lines represent the expected values of points in a CDF for a uniform distribution, and dotted lines mark 95% concentration bands (only 5% of uniform CDFs of this size are expected to have at least one point outside this region). (B) Histograms of the simulated distributions for each A statistic; P values do not change noticeably.

Strong Purifying Selection Against Changes in Secondary Structure

So far, we have imposed an absolute constraint on the structure of the natural pre-miRNAs, as did earlier studies (Borenstein and Ruppin 2006; Shu et al. 2007; Szöllósi and Derényi 2009). Does this assumption make a difference for the outcome of our analysis? To test this assumption, we generated a new null distribution of descendant pre-miRNA sequences. These were at the same sequence distance (k) from the ancestor as the real descendant, but their structure was not constrained in any way (i.e., we allowed any value of d between real and simulated descendant). We then repeated the analysis described in the previous section. The CDFs of q are plotted in figure 5A and show a highly statistically significant deviation from a uniform distribution (Anderson–Darling test: $p<4\times {10}^{-6}$ for both r_m and r_e): ∼75% of descendants are more robust than expected (q > 0.5). These results are caused by variation in structure; that is, both mutational and environmental robustness tend to decrease as the structures of simulated sequences deviate more from the structure of the corresponding (natural) descendant pre-miRNA (fig. 5C). This result indicates that the constraint on structure is a crucial assumption in these analyses. What might cause such a constraint? One possibility is that there is strong purifying selection against all mutations altering the pre-miRNA structure. If so, then the structures of descendants should be closer to those of their ancestors than expected by chance. To test this prediction, we used the structure-unconstrained null distribution of descendant pre-miRNA sequences and employed the same approach we used for robustness in the previous section. Over 90% of descendants were, indeed, structurally closer to their ancestors than expected under neutral evolution (q > 0.5; Anderson–Darling test: $p<4\times {10}^{-6}$; fig. 5B). Therefore, the evolution of Drosophila pre-miRNAs is consistent with the operation of strong purifying selection in which the functional constraint is the secondary structure.

FIG. 5.

Strong purifying selection against changes in secondary structure. (A) CDF of q values of the robustness of pre-miRNAs compared with their corresponding structure-unconstrained null distributions. (B) CDF of q values of the structural distance between ancestor and descendant pre-miRNAs compared with their corresponding structure-unconstrained null distributions. (C) Median mutational robustness of the sequences from the structure-unconstrained null distributions binned according to their structural distance from the natural descendant pre-miRNA. Robustness decreases as the distance to natural structures increases.

The results so far could be explained by an alternative scenario, in which robustness is under strong directional selection, whereas the secondary-structure constraint is a by-product of this selection. This hypothesis may also account for the observation that the structure of pre-miRNAs is robust (de Visser et al. 2003), when compared with the structures of random or shuffled sequences of the same length (Bonnet et al. 2004; Borenstein and Ruppin 2006; Shu et al. 2007). This is illustrated in supplementary figure S1 (Supplementary Material online) for the structure of dps-mir-317; random sequences with the same structure as the natural pre-miRNA are, on average, more robust than random sequences unconstrained for structure. We tested this “inverted” selection hypothesis and found that our data does not support it (supplementary fig. S3, Supplementary Material online). Another argument against this scenario is that selection should act more strongly on the “mean” structure expressed by individual organisms than on the “variance” in structure, either within those organisms (environmental robustness) or among their offspring (mutational robustness). Indeed, it would be difficult to imagine how selection for robustness in structure could take place in the absence of some form of purifying selection on structure.

In conclusion, our data are best explained by an evolutionary scenario of neutral evolution of robustness acting in combination with strong selection against changes in pre-miRNA structure.

Discussion

Theoretically, the strength of direct selection for mutational robustness is at most the magnitude of the deleterious mutation rate (Kimura 1967; Proulx and Phillips 2005); thus, direct selection for mutational robustness should not operate on the pre-miRNAs of multicellular eukaryotes. Against this expectation, Borenstein and Ruppin (2006) concluded that eukaryotic pre-miRNAs are under direct selection for mutational robustness. We investigated the ∼60-My evolutionary history (Tamura et al. 2004) of mutational and environmental robustness of Drosophila pre-miRNAs. We replayed the tape of pre-miRNA evolution based on several explicit evolutionary models. Our analyses provided no evidence that either kind of robustness evolved under any form of direct selection.

Our conclusion, like those from earlier studies (Borenstein and Ruppin 2006; Shu et al. 2007; Szöllósi and Derényi 2009), postulates the existence of a strong constraint on pre-miRNA structure. We have shown that one plausible mechanism for this constraint—strong purifying selection—can explain the observed pattern of evolution in secondary structure (fig. 5B). Strong purifying selection can also account for the observation that Drosophila pre-miRNAs evolve ∼30% slower than nonsynonymous sites of protein-coding genes (Nozawa et al. 2010). Indeed, there is strong evidence that pre-miRNAs are subject to stringent structural constraint: the precise structure of a pre-miRNA influences several aspects of its maturation including recognition and cleavage by Drosha and nuclear export by Exportin 5 (Zeng and Cullen 2003, 2004, 2005; Zeng et al. 2005; Han et al. 2006).

Selection against changes in pre-miRNA structure may indirectly result in mutational and environmental robustness. Borenstein and Ruppin (2006) claimed that the pre-miRNAs of multicellular eukaryotes show signs of direct selection for mutational robustness. Our results refute this claim, providing no evidence that Drosophila pre-miRNAs have experienced direct selection for mutational robustness in the last ∼ 60 My. This is in agreement with theoretical expectations. If we assume L = 95 and P_del = 85% (Nozawa et al. 2010), then we predict that 2N_eU_del ≈ 0.60 < 1 in D. melanogaster (Lynch and Conery 2003). Under these conditions, direct selection for mutational robustness would be ineffectual. We also find that inverse folding produces invalid null distributions. For example, for mir-317-dps, inverse folding of random sequences (Borenstein and Ruppin 2006; Szöllósi and Derényi 2009) is nearly equivalent to simulating alternative descendants without constraining for structure (supplementary fig. S1 Supplementary Material online).

Our results also contradict the results of other studies that concluded that pre-miRNAs have experienced direct selection for environmental robustness (e.g., thermal stability) (Shu et al. 2007; Szöllósi and Derényi 2009). Simultaneous selection for robustness to recombination, robustness to transcriptional errors, robustness to thermodynamic fluctuations, and robustness to all other perturbations failed to cause congruent evolutionary increase in either mutational robustness or thermal stability. This is surprising because (1) multiple buffering mechanisms are expected to act congruently on robustness, and (2) congruent selection is predicted to be much stronger than direct selection for mutational robustness (Gibson and Wagner 2000; Meiklejohn and Hartl 2002; de Visser et al. 2003; Wagner 2005; Masel and Siegal 2009). The mutational robustness and thermal stability of extant Drosophila pre-miRNAs are strongly and positively correlated (supplementary fig. S4B Supplementary Material online), and changes between ancestral and descendant sequences caused highly correlated changes in both kinds of robustness (ρ = 0.644, data not shown). However, there might be trade-offs with other types of robustness. For example, Cooper et al. (2006) found a tradeoff between robustness to mutational and environmental perturbations in Escherichia coli growth rate. Alternatively, congruent selection on these different types of robustness may not be as strong or consistent as previously thought.

Despite the clear advantages of our approach over those employed in earlier studies, it does have four limitations. First, we only consider a single high likelihood reconstruction of the evolutionary history of each orthologous gene. The uncertainty involved in ancestral state reconstruction could be incorporated into these analyses through Bayesian phylogenetic methods (Robinson et al. 2003). Second, we allowed nucleotide substitutions to occur anywhere in a sequence, when it is clear that different regions of Drosophila pre-miRNA sequences evolve at different rates (Nozawa et al. 2010). Third, we did not consider indels, when they have obviously played an important role in pre-miRNA evolution. However, there is no reason to assume that these limitations have biased our analyses.

A final potential limitation of our study, as well as of previous work on pre-miRNA (e.g., Borenstein and Ruppin 2006; Shu et al. 2007; Szöllósi and Derényi 2009), may be that the MFE predictions of the secondary structures of pre-miRNAs have not been experimentally validated. We note, however, that in a recent, detailed study of the structures of 10 human pre-miRNAs (Krol et al. 2004), structure prediction correctly inferred close to 90% of base pairs. One way to improve our methods is to extend our measures to consider the ensemble of alternative equilibrium structures with a free energy within some threshold of the MFE structure (McCaskill 1990; Ancel and Fontana 2000; Mathews 2006).

In conclusion, contrary to earlier claims, there is no evidence that pre-miRNAs have been shaped by either direct or congruent selection for any kind of robustness. Instead, the high robustness of Drosophila pre-miRNAs appears to be mostly intrinsic, and likely a consequence of selection for functional structures. Our study should serve as a cautionary tale for claims on the adaptive value of robustness (e.g., von Dassow et al. 2000; Meir et al. 2002; Eldar et al. 2003).

Supplementary Material

Supplementary figures S1–S4 and table S1 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).