Modeling Transport Through Synthetic Nanopores

Abstract

Nanopores in thin synthetic membranes have emerged as convenient tools for high-throughput single-molecule manipulation and analysis. Because of their small sizes and their ability to selectively transport solutes through otherwise impermeable membranes, nanopores have numerous potential applications in nanobiotechnology. For most applications, properties of the nanopore systems have to be characterize at the atomic level, which is currently beyond the limit of experimental methods. Molecular dynamics (MD) simulations can provide the desired information, however several technical challenges have to be met before this method can be applied to synthetic nanopore systems. Here, we highlight our recent work on modeling synthetic nanopores of the most common types. First, we describe a novel graphical tool for setting up all-atom systems incorporating inorganic materials and biomolecules. Next, we illustrate the application of the MD method for silica, silicon nitride, and polyethylene terephthalate nanopores. Following that, we describe a method for modeling synthetic surfaces using a bias potential. Future directions for tool development and nanopore modeling are briefly discussed at the end of this article.

I. Introduction

Synthetic nanopores have arisen as a convenient means of characterizing single molecules, with DNA being one of the most popular subjects. By applying an electric field, ions and charged biomolecules like DNA can be compelled to interact with or translocate through nanopores in thin membranes. The use of the nanopore method for characterizing nucleic acids gained initial momentum in 1996 with a landmark paper by Kasianowicz et al. [1]. The researchers observed step-like reductions of ionic current through a pore furnished by the protein α-hemolysin, apparently associated with the passage of single nucleic acid molecules. The duration of the reductions was found to be proportional to the length of the molecules. Subsequent research showed that different DNA homopolymers and block copolymers [2] and, later, molecules differing by a single nucleotide [3] could be discriminated by the values of the ionic current. It was also possible to determine the orientation of the DNA (led by the 5′- or 3′-end) [4] in this way.

Rather than using proteinaceous nanopores to probe the properties of single molecules, many researchers turned to synthetic nanopores [5], [6], [7], [8], [9], [10], [11], [12] which can operate under less restrictive ranges of temperature, pH, electrolyte concentration, and external bias. Furthermore, one can fabricate nanopores of almost any desired size; thus, the pore geometry can be optimized for the application at hand. Synthetic membranes made from semiconductors, such as silicon, also permit electronic devices to be integrated with the pores [9]. Synthetic nanopores have been fabricated from hard ceramic materials, such as silicon nitride [5], [7], [9], [11] and silicon oxide [6], [8], [10], multilayer silicon [13], [14], and polymer films, such as polyethylene terephthalate (PET) [15], [16]. Among potential applications of synthetic nanopores are low-cost and high-throughput technology for sequencing DNA [17], [18], [14], genotyping [19], protein detection [20], [21] and separation [22], stochastic sensing [23], [24], single molecule manipulation [25], [26], [27], [28], and nanofluidic electronics [29], [30], [31].

Due to the nanoscale confinement and the high surface-to-volume ratio, nanopores can produce unexpected phenomena not observed at the macroscale. Currently, no experimental technique has enough resolution to visualize the atomic level dynamics in such systems. Computer simulations can provide information that is needed to implement successful design strategies. Indeed, different computational approaches, such as all-atom molecular dynamics (MD) [32], coarse grained MD [33] and lattice Boltzmann models [34], have already been used to study nanochannels. In particular, molecular dynamics (MD) simulations do provide an atomistic description of systems with lengths up to hundreds of nanometers, becoming valuable tools for interpreting experimental results.

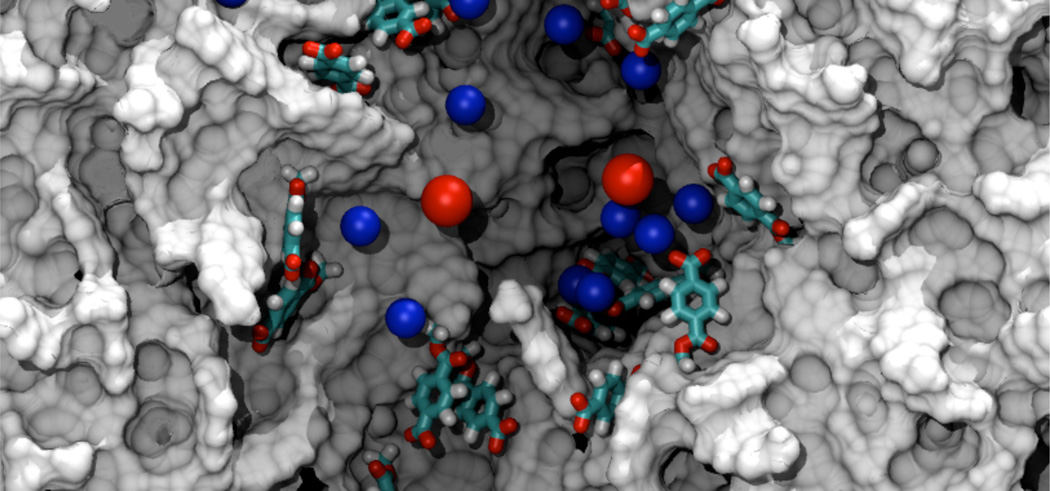
Simulating biomolecules such as DNA and proteins in synthetic nanopores, e.g., the system shown in Figure 1, presents a number of challenges. First, MD simulations require force fields from which the interaction between atoms of the simulated systems can be calculated. Conventional force fields for simulating biomolecular systems usually do not include synthetic materials such as silicon-based membranes. Second, the composition and structure of the surfaces of nanopores are not fully known and often depend on fabrication techniques, making it difficult to develop protocols for creating realistic models of pore surfaces. Below we describe our efforts to meet these challenges, for which we have created general tools for modeling synthetic nanopores as well as developed simulation protocols specific to several materials.

Fig. 1.

Molecular dynamics study of a biomolecule-nanopore system. The figure shows an atomic-scale model of a nanopore (gray surface), DNA (green and purple strands), protein (light blue and orange surfaces) and Cl⁻ and K⁺ ions (red and blue spheres). Water molecules are not shown. Through MD simulations the atomic-level dynamics inside the nanopore can be elucidated.

II. Setting up nanopore models

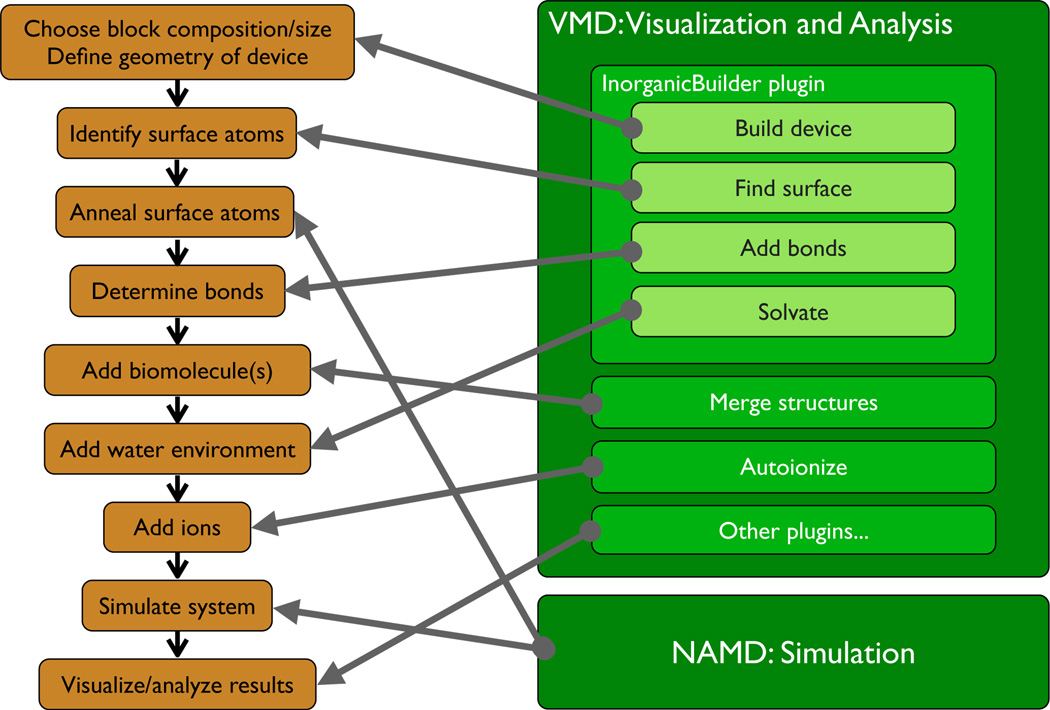
Creating an all-atom model of a synthetic nanopore or of any other nanodevice begins with a set of tasks to define the basic geometry of the device. These tasks include creating a block of the bulk material the device in made of and sculpturing in that block the nanodevice according to the specified geometry. In addition, some modeling techniques require bond connectivity to be computed, and, in some cases, it is desirable to identify surface atoms for special treatment. Furthermore, in biological simulations, one or more biomolecules are arranged in the vicinity of the device, and the device is submerged in an environment resembling a physiological solution (water and dissociated salt). The sequence of activities required to perform a typical simulations of interactions of biomolecules with a prototype nanodevice model is shown in Figure 2. Setting up such a simulation typically requires coordinating the actions of a number of tools for performing these tasks, and the creation of specialized scripts that connect the tools together to produce the input files for simulation of a particular nanopore configuration, a skill that is tedious, demanding significant initial training. Then, to study another nanopore configuration, the script must be manually reworked for the new model parameters.

Fig. 2.

Steps associated with a typical nanodevice/biomolecular simulation (left), and software components developed to perform these tasks efficiently (right).

The Inorganic Builder is a tool developed by the authors that simplifies many tasks associated with setting up device simulations. It is implemented as a plugin module to the molecular visualization program, VMD [35]. VMD provides a framework for visualizing molecular structures, and a versatile atom selection language that allows plugins to access and manipulate atom information efficiently. Through VMD’s embedded Tcl/Tk-based scripting language, a plugin such as the Inorganic Builder can include an easy-to-use graphical interface that is integrated into the main VMD interface, and can take advantage of VMD’s high-performance visualization interface to display a 3-D interactive model of the device as it is built.

A fundamental step in setting up a device simulation is defining the geometry of the device model. To build the model using the Inorganic Builder, the user first selects a material for the device. The Inorganic Builder includes a library of several common materials, (e.g. crystalline SiO₂ and Si₃N₄, amorphous SiO₂, PET), but also allows the user to add new materials by supplying files specifying atom types, coordinates for a small basic block of the material, and parameters describing the geometry of the basic block. After selecting a material, the size of the block in which the device will be embedded is described by specifying how many copies of the basic block are needed in each dimension. Although it is possible to create blocks of arbitrary size, often it is desirable to have the size of the final block an integer multiple of the size of the basic block. Such a choice preserves correct spacing between atoms when simulations are performed under periodic boundary conditions. By requiring an integer number of basic blocks, this condition is enforced in the Inorganic Builder. Next, the geometry of the device is described by specifying a set of exclusions, which are regions of various shapes (cylinders, cones, spheres, etc.) that will be removed from the material block. As each exclusion is added, an updated diagram of the structure is displayed by VMD. After defining the structure of the device, the Inorganic Builder produces the all-atom model by populating the geometrical structure with atoms.

Typically a model produced using the device building capability of the Inorganic Builder requires additional processing to better reproduce the characteristics of the physical device. Often the desired model has a crystalline interior embedded inside an amorphous surface layer. Such a model may be produced for SiO₂ using the Inorganic Builder in conjunction with a development version of the molecular dynamics simulation program, NAMD [36], which implements the BKS force field [37] for melting silica materials. The Inorganic Builder has a tool for identifying surface atoms of a structure, defined by their proximity to empty space, which can extract a surface layer of a desired thickness. An amorphous surface is created by fixing the positions of the interior atoms in the NAMD simulation, and allowing the surface atoms to melt and resolidify. Changes to the geometry of the pore during melting may be prevented using the grid-steered MD (G-SMD) feature of NAMD [38]. In the G-SMD method, the motion of atoms can be controlled by applying external potentials defined on regular grids. By applying a grid potential designed according to the shape of the pore, the shape of the latter can be enforced even when the pore surface is in a liquid state.

Unlike the BKS potential, force fields compatible with biological molecules generally include terms for both bonded and non-bonded interactions. Accordingly, the Inorganic Builder includes a tool for determining bonds. For biomolecules and crystalline solids, bond information may be determined by the topology of the structure, but for many amorphous materials, bond information needs to be determined by locating all pairs of atoms separated by less than some bond cutoff length. The bond search also takes into account atom types, so that, for example, in a SiO₂ model, bonds are only defined between a silicon and an oxygen atom, never between two silicons, or two oxygens. As most simulations are performed using periodic boundary conditions, the bond search can also find bonds that wrap around the boundaries of the periodic cell.

Like most biomolecular simulations, nanopore simulations usually require a physiologically-realistic environment of water and ions. Such an environment is generated using a combination of Inorganic Builder with other tools in VMD. VMD includes a Solvate tool that adds a box of water molecules around some molecular structure, but is only capable of producing orthorhombic boxes. Since the periodicity of device simulations is often based on the non-orthorhombic symmetry of the underlying crystal structure of the material, the Inorganic Builder provides a tool that uses Solvate to create a water box, but then post-processes the results to create the desired shape for the water box. Finally, VMD includes an Autoionize tool, that takes the model, including device, biomolecule, and water molecules, and adds a specified concentration of ions.

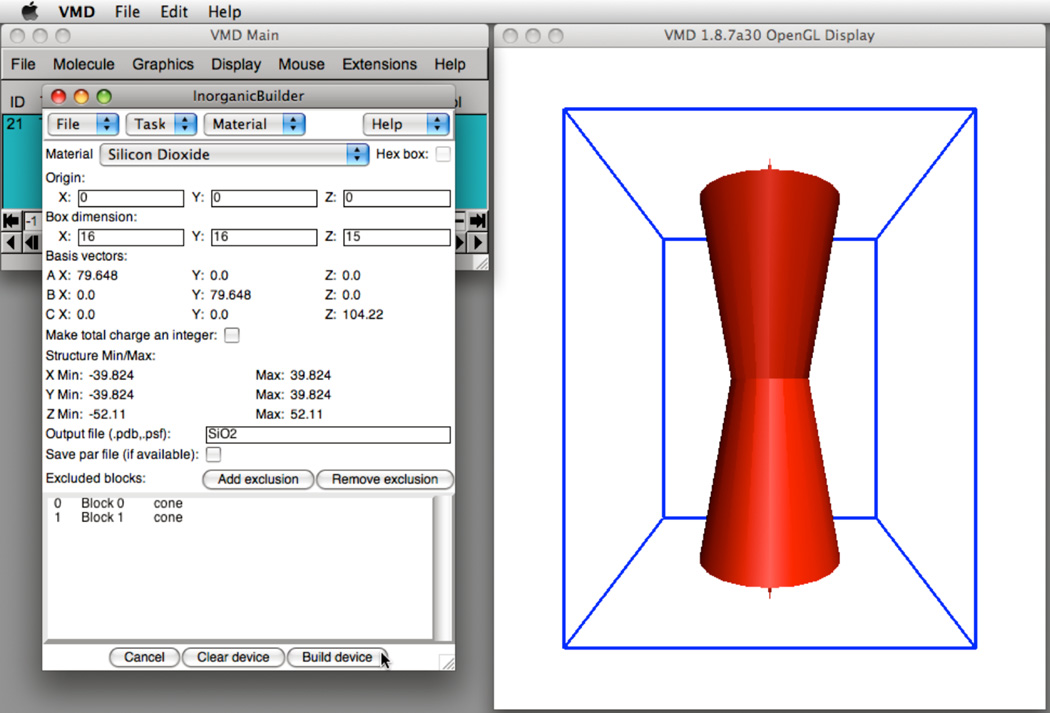
Several of the steps for creating a model of a nanopore in a crystalline silicon dioxide membrane are illustrated in Figure 3. The desired model is to be built from a block of the material 80 Å ×80 Å on side and approximately 100 Å thick. The nanopore is formed by removing cones of atoms from the top and bottom of the block, such that the surface of the nanopore forms an angle of 10° with the vertical axis, and the center of the nanopore narrows to a diameter of 22Å. To produce a block of material that can accommodate the device, the unit cell of the silicon dioxide crystal is replicated 16 × 16 × 15 times such that the final dimensions of the block are 79.6 Å ×79.6 Å ×104.2Å. Producing the pore in the specific geometry requires two cones of a 40.4 Å diameter and a 104.2 Å height. Next, the user specifies the pore by excluding material from the block. The two cone exclusions are added by specifying the center and radius of the base and the coordinates of the apex of each cone. As each exclusion is added to the device, the schematic view of the device is updated in the VMD window. Once satisfied with the geometry of the device, the user selects Build Device to populate the model with atoms; the resulting atomic structure is stored.

Fig. 3.

(Left) The Inorganic Builder user interface. (Right) Construction of a nanopore formed by two cones in a block of silicon dioxide.

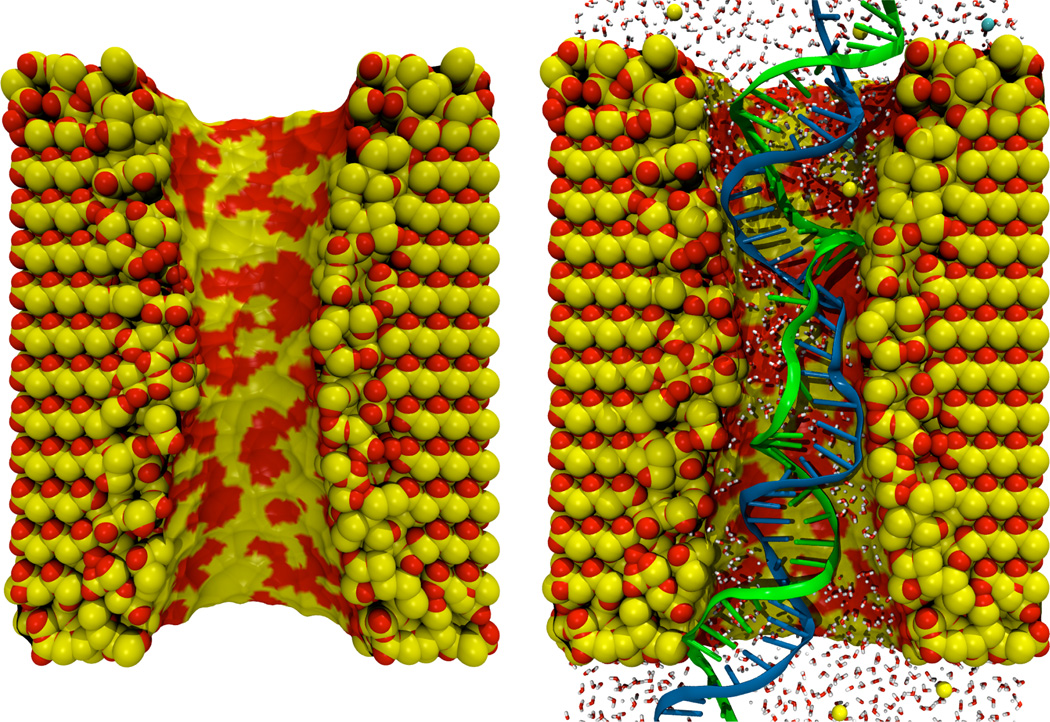
Figure 4 shows a model of a nanopore-DNA system created using the Inorganic Builder, The Inorganic Builder Find Surface tool was used to identify a 10 Å thick surface layer which was melted to produce amorphous SiO₂. Then, a strand of DNA was placed inside the pore, a water box was generated around the combined structure, and ions were added to produce an electrically neutral system.

Fig. 4.

A silicon dioxide pore (left) created using the Inorganic Builder, and the same pore after including a fragment of DNA and an environment of water and ions (right).

Although the details of the subsequent simulations depend on the system and process being studied, several common steps are involved. Common force fields for biomolecular systems (e.g. AMBER [39], CHARMM [40], [41]) do not include parameters for inorganic material such as silicon-based membranes. Force field parameterization for three popular inorganic materials is described below. After the force field parameters have been determined, the system is minimized and equilibrated for a period of time using standard MD protocols [36]. To induce permeation of ions and biomolecules through the nanopores, an external electric field directed normal to the membrane is imposed. As the simulation proceeds, atom coordinates are saved in a trajectory file for subsequent analysis. Finally, analysis of the trajectory is performed using analysis tools included with VMD, (e.g. electrostatic potential map calculation, RMSD analysis) as well as custom data-analysis calculations implemented using VMD’s Tcl scripting interface.

III. Silica nanopores

When immersed in an aqueous solution, silicon-based devices develop a coating layer of amorphous silica (a-SiO₂). Thus, an accurate MD model of a-SiO₂ is relevant to simulation of any pores build on silicon-based membranes, such as Si₃N₄, crystalline SiO₂, and crystalline Si. In this section, we present molecular dynamics (MD) studies of a-SiO₂ nanopores. First, we describe the parameterization of silica-water interactions based on the hydrophobicity of the silica surface. This parameterization strategy differs from conventional ab-initio parameterization schemes. Second, with our custom silica-water force field, we present a study of ionic current rectification.

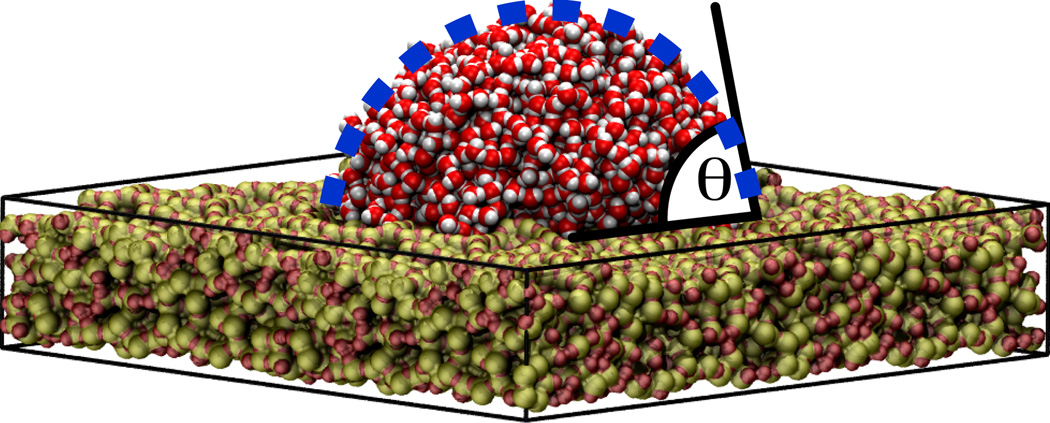
In all present nanopore applications, the interactions between biomolecules and silica occurs in an aqueous environment. Therefore, a first step is to develop an empirical force field for a-SiO₂ that is able to reproduce the intermolecular silica-water interactions. We parametrized the silica surface using the experimentally known wettability of this surface. The contact angle (θ) of a water droplet on a silica surface was used as a quantitative observable to tune the intermolecular interactions, as illustrated in Figure 5. The mathematical form of the force field was chosen compatible with the CHARMM potential, composed of a Lennard-Jones potential plus an electrostatic term. For parameterization, a water droplet was placed on top of each surface and then equilibrated for 2 ns. By testing more than 30 different parameter combinations, we were able to determine a set of parameters that reproduced the experimental water contact angle [42].

Fig. 5.

Contact angle of a water droplet (θ) on a silica surface. The picture shows a water droplet composed of 2000 water molecules on top of a rectangular silica slab of 11.4 nm length and 2 nm thick. The system was equilibrated for 2 ns in a molecular dynamics simulation. The water contact angle (θ) is the angle between the tangent of the drop surface and the silica slab.

Most nanopore experiments are based on ionic current measurements; however, a detailed understanding the ion dynamics is still needed. For instance, at opposite voltage polarities, nanopores can produce remarkably different ionic currents, generating I–V curves that deviates from the expected linear ohmic response. This non-linear response is known as ionic current rectification. We performed a systematic MD study of the conductance of a KCl electrolyte through silica nanopores having different arrangement of their surface atoms. It was found that ion-binding spots on the surface, such as dangling atoms, affect the ionic concentration and electrostatic potential inside the pore, producing current rectification [43]. The simulations revealed, for the first time, that the presence of ion-binding spots at the nanopore surface can play a major role in ionic conduction.

IV. PET nanopores

Polyethylene terephthalate (PET) is a carbon-based linear polymer widely used in synthetic fibers, beverage bottles, and other plastic containers. Due to its unique properties, such as high melting point, high mechanical strength and non-reactivity to many chemicals [44], PET is an excellent material also for nanotechnology applications. In particular, PET membranes have been used for building nanopores. For this purpose, a thin PET foil of 12 µm is penetrated by a single heavy ion (e.g. Au, Xe), followed by chemical etching of the ion’s track [45]. The size and shape of these pores are tailored by controlling temperature and duration of etching, producing pores with radii as small as 1 nm. Such nanopores have been proposed as a nanofluidic diode for nanofluidic electronic devices [30]. Furthermore, PET nanopores are being used to test ion channel theories [46].

Several fascinating results have been observed in PET nanopores, such as ion selectivity [47], oscillation in current due to small addition of Ca⁺² [48], reverse rectification due to Ca⁺² [49] and nanoprecipitation [50]. However, the physical basis behind these phenomena is not fully understood. It has been proposed that the stated effects are due to a combination of nano-scale confinement and high surface charge. After the chemical etching, the PET surface is covered with benzoic groups, shown in Figure 6, that produce a negative surface charge of 1 e nm⁻². As in the case of silica nanopores, MD simulations can shed light onto the atomic scale dynamics inside PET nanopores.

Fig. 6.

Molecular dynamics simulation of PET nanopores. The figure shows a PET nanopore of a 1.5 nm radius. The nanopore is cut in the middle to reveal the interior of the pore. The gray surface shows the carbon-based structure of the nanopore. Deprotonated benzoic groups at the surface of the nanopore are shown in licorice representation. Blue and red spheres represent K⁺ and Cl⁻ ions, respectively. Water molecules are not shown.

Atomistic simulations of PET have reached a level where they are now useful in gaining insights into the molecular origins of the behavior of bulk material [51], [52], [53]. Nevertheless, most of the work has been focused on studying the mechanical bulk properties and there is still relatively little known about the properties of the PET surface and how the surface affects the transport through PET nanopores. Until now, an accurate description of the polymer surface at the atomic level was not available.

We have developed the needed protocol to build PET bulk structures and PET surfaces. First, we constructed a computational a model for a 9-mer PET polymer based on available biomolecular force fields [40], [54]. Second, we arranged 245 PET polymers into a matrix of 7×7×5. The separation distance in the matrix was enough to avoid any contact among the polymers. By using the capabilities of NAMD to apply custom potentials, the matrix was collapsed and annealed into a periodic cube that reproduced the bulk properties of PET. Third, we created a conical pore by removing atoms and patching the exposed ends with benzoic groups. The concentration and protonation state of benzoic groups can be controlled in our protocol, allowing us to match the experimental surface charge concentration and mimic different pH conditions.

With this model, we are presently studying the ionic transport properties through PET nanopores: the KCl conduction using different pH conditions and also the effect of divalent ions on the ionic conduction. Preliminary results are not only showing good agreement with experiments, but also providing the molecular details of the ionic conduction mechanism in PET nanopores.

V. Silicon nitride nanopores

Silicon nitride is an extremely hard ceramic material from which membranes housing nanopores can be constructed. To model silicon nitride pores, a block of the material can be produced by replicating the β-Si₃N₄ cell with Inorganic Builder. By adjusting the forces that hold the atoms of the material in the solid crystal structure, one can calibrate the dielectric constant [11] so that the electric field within the pore in simulations is realistic.

To form the pore, geometrical constraints are used to remove atoms. However, the removal process does not result in a realistic relaxed surface, but one with many dangling atoms and cavities. The structure of the real surfaces of such pores is not known and, depending on the details of fabrication, different quantities of oxygen are attached chemically to the surface [55]. In earlier simulations of Si₃N₄ nanopores, single-stranded DNA were found to interacted strongly with the surface of crystalline Si₃N₄, preventing the observation of DNA transport on the timescale accessible to MD [56]. It was found that the nucleobases of DNA adhere to the Si₃N₄ surface via hydrophobic attraction, while the charged phosphate groups interacted strongly with cavities and dangling atoms. This behavior appeared unrealistic. To improve the model of the pore surface, an approach involving calibration of the wettability, like that performed for SiO₂ [42], was a possible choice. However, we chose instead to leave the structure of the Si₃N₄ surface like that of the crystal and apply an external force to the DNA to control the DNA–nanopore interaction.

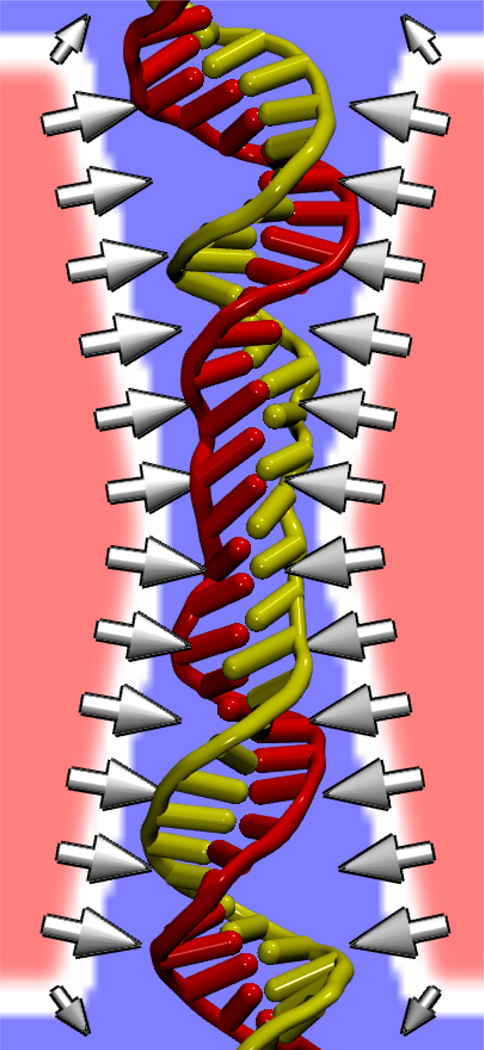
The external force was applied to DNA atoms by interpolation from a three-dimensional grid using the G-SMD method [38]. The force was adjusted to prevent close contact between DNA and the pore surface. Figure 7 shows a potential map used to modify the interaction between DNA and Si₃N₄. Applying this DNA-specific surface force, we could simulate transport through nanopores of hairpin DNA, which consists of a portion with the properties of single-stranded DNA and a double-helical portion with the secondary structure of double-stranded DNA [57]. The simulations revealed that hairpin DNA can translocate nanopores having minimum diameters from 1.3 to 2.2 nm by three modes: unzipping of the double helix and—in two distinct orientations—stretching/distortion of the double helix. Furthermore, each of these modes can be selected by an appropriate choice of the pore size and voltage applied transverse to the membrane [57].

Fig. 7.

DNA-specific surface force imposed via a potential defined on a grid. An image of the DNA is overlaid on a cross section of the potential energy grid. Regions of low potential energy are shown in blue, while regions of high potential energy are shown in red. Arrows show the resulting force at the pore surface that repels the DNA. Water and ions are not shown.

VI. Phantom nanopores

Taking the idea of applying an external force to model the pore surface a step farther, it is possible to dispense with the pore atoms altogether and model an idealized pore using only surface forces from a grid. Such a pore is smooth and can be used to study DNA behavior in the absence of the effects of friction and surface roughness.

Translocation of single-stranded DNA through very small pores (1.0 nm in diameter) is dramatically slower than that through slightly larger pores. Using phantom pores, the origin of the change in speed could be elucidated. The translocation speed in simulations where both the DNA and electrolyte were confined by a phantom pore was an order of magnitude smaller than that in simulations where only the DNA was confined by the phantom pore [11]. Thus, it was shown that, in the absence of the surface friction forces, the DNA translocation velocity is determined mainly by the condensation of counterions on the DNA backbone rather than by the steric restraints imposed by the pore surface on the DNA conformation.

VII. Outlook

Several new capabilities are planned for the Inorganic Builder plugin described above. Surface-refinement techniques will produce even more accurate models of realizable device surfaces by repairing the surface anomalies that result from geometrically “cutting” a block of material. Closer integration with simulation tools will simplify generation of amorphous regions within crystalline material. Furthermore, although force field parameter generation has been shown to be a challenging task, it is also the task most necessary for modeling. One solution being considered is to provide parameters using values determined by the Universal Force Field (UFF) [58], with the caveat that the force field has not been tested in biomolecular simulations, and must be evaluated first to determine its usefulness in such simulations. Determining and evaluating parameters for silica and silicon nitride nanopores has set the stage for further studies of DNA interaction with those materials. The force fields for these nanopores could be further refined by calibrating their interaction with biomolecules with experimentally measurable quantities. Examining ionic current in PET pores also points to further use of MD simulation for understanding PET-biomolecule interaction. Finally, the phantom pore method is a computationally efficient method for studying biomolecule–nanopore systems, especially for situations where the properties of the particular material may not matter.

The computational methods presented above are expected to greatly aid development of the bionanotechnological applications of inorganic nanopores such as high-throughput DNA sequencing and genotyping. The methods will also find application in simulations of various lab-on-chip processes including transport of biomolecules through nanofluidic systems, self-assembly of nanoparticles or nanoparticle-biomolecular conjugates into inorganic nanostructures, protein and DNA microarray technologies, and field-effect biosensors such as immunosensors and silicon nanowires.

Biographies

Aleksei Aksimentiev (aksiment@uiuc.edu) is an assistant professor in the Department of Physics at the University of Illinois.

Robert K. Brunner (M’92) (rbrunner@illinois.edu) is a senior research programmer with the Theoretical and Computational Biophysics Group at the Beckman Institute at the University of Illinois.

Eduardo Cruz-Chú (chucruz@ks.uiuc.edu) is a Ph.D. candidate with the Center for Biophysics and Computational Biology at the University of Illinois.

Jeffrey Comer (jcomer@ks.uiuc.edu) is a Ph.D. candidate with the Department of Physics at the University of Illinois.

Klaus Schulten (kschulte@ks.uiuc.edu) is the director of the Theoretical and Computational Biophysics Group at the Beckman Institute and is Swanlund Professor of Physics at the University of Illinois.