Abstract
Ratios of effective populations size, Ne, to census population size, N, are used as a measure of genetic drift in populations. Several life-history parameters have been shown to affect these ratios, including mating system and age at sexual maturation. Using a stochastic matrix model, we examine how different levels of persistent individual differences in mating success among males may affect Ne/N, and how this relates to generation time. Individual differences of this type are shown to cause a lower Ne/N ratio than would be expected when mating is independent among seasons. Examining the way in which age at maturity affects Ne/N, we find that both the direction and magnitude of the effect depends on the survival rate of juveniles in the population. In particular, when maturation is delayed, lowered juvenile survival causes higher levels of genetic drift. In addition, predicted shifts in Ne/N with changing age at maturity are shown to be dependent on which of the commonly used definitions of census population size, N, is employed. Our results demonstrate that patterns of mating success, as well as juvenile survival probabilities, have substantial effects on rates of genetic drift.
Keywords: effective population size, reproductive success, individual quality, age at maturity
1. Introduction
Genetic diversity is of central importance in evolutionary biology and conservation. Random genetic drift is a major cause of loss of this diversity, and a lot of studies have focused on the rates at which this loss can be expected to occur in natural populations (reviewed in [1]). Wright [2] introduced the concept of effective population size, Ne, defined as the size of an ideal population that would experience the same amount of genetic drift as the population in question. An ideal population refers to a population of constant size with discrete, non-overlapping generations and reproduction by random sampling of gametes. In a diploid population, the expected rate of allele frequency change owing to drift, and the loss of (selectively neutral) heterozygosity, is proportional to 1/(2Ne) per generation.
Most real populations have an effective population size which is lower than their census size (N), and thus experience higher levels of genetic drift [3–6]. It has proven difficult to find any general relationship between the effective population size and the actual size of populations [4], but a number of factors that influence the effective population size have been identified. Some of the most important of these are fluctuations in population size [2,4], variation in reproductive success [7,8] and unequal sex ratios [2,9]. Different mating systems give rise to different patterns of male mating success. When the distribution of mating success is skewed, like in harem polygyny, the effective population size is lower. This has been demonstrated both theoretically [7–12] and experimentally [13]. Other factors that affect the variance in reproductive success, and thus Ne, are multiple paternity within broods [14], population subdivision [15] and variance in female fecundity [16–18]. Nunney [16] examined different types of variation in female fecundity and found that consistent individual effects decreased the effective population size more than random effects or age-related effects. The effects of mating system on Ne can be influenced by other factors [19–22], and may often be overwhelmed by stronger effects, such as fluctuating population size [23]. However, many species have life-history characteristics that allow Ne to be substantially affected by mating system [5,23–25].
Values of Ne/N have been reported for a number of populations of different species (e.g. [3,4,6]). The range of values reported is extensive (studies reviewed by [4] include values of Ne/N from 10−6 to 1.07), and techniques for obtaining these estimates vary [3,4,26]. One problem with these numbers is that several different definitions of N are used [3]. Sometimes N is reported as the census size of the entire population, sometimes it refers to the adult population only and sometimes only breeding individuals are counted. Nunney & Elam [3] discussed this issue, and concluded with a recommendation that N be counted as the number of adults in the population.
There are two main types of effective population size. Inbreeding effective size focuses on the rate of increase of identity by descent, whereas the variance effective size is concerned with the sampling variance in allele frequency from one generation to the next [27,28]. These two types of effective population size can differ substantially in populations of increasing or decreasing size [8,29], but are identical when populations are of constant size with stable stage distributions, as is the case in this paper [30].
The study of effective population size is often complicated by the presence of overlapping generations [1,31]. Several authors have addressed this point, and presented formulas for calculating the effective population size in populations in which generations overlap ([10,11,31–36], among others). As shown by Hill [32], it is the variance in lifetime reproductive success that matters when determining effective size in such populations. Fluctuations in age structure make the problem even more complex. Engen et al. [37] showed how diffusion theory and matrix models can be used to derive the effective population size in populations subject to fluctuations in age structure. Studying a subpopulation of individuals carrying a selectively neutral allele allows calculation of the sampling variance in the frequency of this allele per time step [37]. Thus, this method can be used to study genetic drift per time step, and when it is combined with the generation time, it gives Ne/N per generation.
Generation time has been shown to influence the effects of other factors on the effective population size. For example, a skewed sex ratio tends to cause Ne/N to decrease more when the generation time is short than when it is long [10,38]. Also, Nunney [10,11] found that although some mating systems have the potential to lower Ne/N significantly, this effect all but disappeared as the generation time in their model was lengthened, and Ne approached N/2 regardless of mating system. This was explained by a decrease in the variance in male mating success as the generation time increased. When each male participated in several mating seasons they had more chances to be successful, and reproductive success could even out among them. This assumes that male mating success is independent each season, which is not necessarily the case. Several recent studies have highlighted the importance of recognizing that populations consist of individuals with different vital parameters, and that the individual differences may be persistent over time [39–47]. Mating success is one area in which persistent individual differences may exist in some species (e.g. [44,48–50]), thus potentially causing correlations in individual success from year to year.
Delayed maturity has been shown to increase the effective population size [11,51–53]. In fact, Waite & Parker [51] found that the convergence of Ne/N to 0.5 at long generation times reported by Nunney [11] was dependent on a low ratio of age at maturity to adult lifespan. When the age at maturity was increased in relation to the adult lifespan, Ne/N was found to increase linearly. Both age at maturity, adult lifespan and the relationships between the two vary among species and taxonomic groups, making this particularly relevant [51].
In this paper, we use a stochastic matrix model to investigate how the effective population size is influenced by the presence of persistent individual differences in mating success among males, and how this may depend on generation time. We also examine how juvenile survival rates influence the effects of delayed maturity. In addition, we demonstrate that the definition of N used to calculate Ne/N when studying age at maturity has the potential to influence the results in ways not previously considered.
2. The model
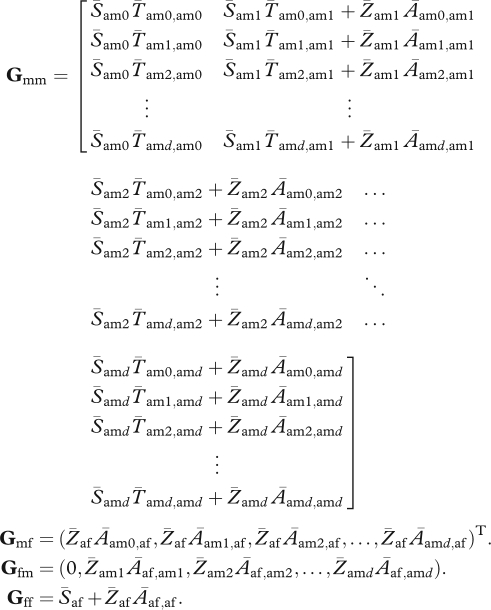
Consider a diploid population with two sexes. Based on well-known theory, we use a matrix model to study a subpopulation of heterozygote individuals carrying a certain rare allele (e.g. [8,37,54,55]). The number of individuals in this subpopulation will be called X. Pre-reproductive individuals are divided into classes according to age and sex. Adult males are classed according to mating success (number of mates, from 0 to d), and adult females are all assumed to have the same individual parameters (survival probability and expected number of offspring) and are therefore collected in a single group. This means that there are a total of (rm + d + rf) classes in the model, where rm is the age at sexual maturity of males, d is the maximum number of mates a single male can obtain and rf is the female age at maturity. The population vector can then be written as X = (Xym1, … , Xym(rm −1), Xam0, … , Xamd, Xyf1, … , Xyf(rf −1), Xaf)T where the superscript T indicates matrix transposition. Subscripts denote young (pre-reproductive) males of age 1 to rm − 1 (ym1, … , ym(rm − 1)), adult males who obtain 0 to d mates (am0, … , amd), young females of age 1 to rf − 1 (yf1, …, yf(rf − 1)), and adult females (af). Note that offspring are not included in the model until they reach 1 year of age (any individuals that die before that age are ignored). The population vector for the next time step is obtained from the current population vector by matrix multiplication with the stochastic projection matrix, G. Thus, Xt+1 = GXt. The stochastic projection matrix can be partitioned into four parts,
where Gmm is the contribution from the male part of the population to next time step's males, Gmf is the contribution from females to males, Gfm from males to females and Gff is the contribution from females to next time step's females.
If all individuals become sexually mature at age 1 (rm = rf = 1), the stochastic projection matrix can be written as a composite of the following submatrices:
 |
In these matrices
 |
where Si,k is an indicator variable for survival of individual k in group i,
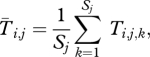 |
where Ti,k is an indicator variable indicating which of the Sj survivors from group j move to group i,
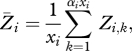 |
where Zi,k is the number of offspring produced by individual k in group i,
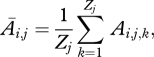 |
where Ai,j,k is an indicator variable indicating which of th Zj offspring from group j move to group i (based on presence of the rare allele, sex and mating probability).
We assume a constant environment, so the stochastic projection matrix G includes demographic stochasticity but not environmental stochasticity. Adult males are assumed to have a survival probability sm (sf for females). The probability of a male obtaining ν mates, and thus being in class amν is called tν. Since the variance effective population size is defined by the variance in allele frequency, the actual distribution of females among males does not need to be known. It is the variance in reproductive success among males (or females) that matters. In order to find t-values that give a particular variance in male mating success, we have used the model from Lee et al. [56]. The t-values represent the probability of a new male in the population ending up in a certain class (and mating a certain number of times) in his first season. If there are no permanent individual differences among males, these are also the probabilities of surviving males moving to each class in later seasons. However, the mating probability of a male in a given season is not necessarily independent from his mating success in previous seasons. This is incorporated by introducing a parameter c. This parameter can increase the probability of obtaining the same number, one more or one less mate than the previous season. At the limits, if c = 0, mating is independent among seasons. If c = 1, a surviving male is guaranteed to end up in the same class, or one of the neighbouring classes (one more or one less mate) the next season. The adjusted probabilities of these three classes are 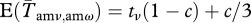 (for ν = ω − 1, ω, ω + 1). The only exception is the group of unmated males, where we assume that c affects only the probability of staying unmated the next season (without increasing the probability of obtaining a single mate). Thus,
(for ν = ω − 1, ω, ω + 1). The only exception is the group of unmated males, where we assume that c affects only the probability of staying unmated the next season (without increasing the probability of obtaining a single mate). Thus, 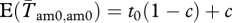 . All other classes have an adjusted probability of
. All other classes have an adjusted probability of 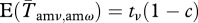 . In this way, the ratio between the other classes is not altered. It would also be possible for c to be negative, but we have not considered that here.
. In this way, the ratio between the other classes is not altered. It would also be possible for c to be negative, but we have not considered that here.
We assume that survival and reproduction are independent within years, and can therefore treat the survival and reproduction terms separately. We also assume independence among columns as we are studying a small group of individuals found in a much larger population. Within columns, however, there must be some covariance. To see this, consider the surviving males from adult class one at a given time step. At the next time step, each of these survivors will be in one and only one of the d classes of adult males. A single individual cannot move to more than one class. Thus, survival terms in Gmm have a multinomial distribution in which the Samω survivors from group j = amω have probabilities  of ending up in each of the d + 1 classes of adult males. Equivalently, the reproduction terms also have a multinomial distribution in which the Zj offspring from class j have a probability
of ending up in each of the d + 1 classes of adult males. Equivalently, the reproduction terms also have a multinomial distribution in which the Zj offspring from class j have a probability 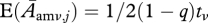 of ending up in class i = amν (this is the probability of an offspring having the rare allele, being male and ending up in quality group amν), as well as a probability
of ending up in class i = amν (this is the probability of an offspring having the rare allele, being male and ending up in quality group amν), as well as a probability 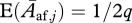 of being female. Assuming that females produce a mean of μz offspring each, the number of offspring produced in group j can be written as:
of being female. Assuming that females produce a mean of μz offspring each, the number of offspring produced in group j can be written as: 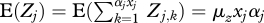 , where αj is equal to ν for amν, ν=0, …, d and equal to 1 for adult females. For simplicity, we assume that the number of offspring produced per female per time step has a Poisson distribution. The total number of offspring produced in the population at a given time step, and the total number of offspring produced by a single female over her entire lifetime, are then also Poisson-distributed.
, where αj is equal to ν for amν, ν=0, …, d and equal to 1 for adult females. For simplicity, we assume that the number of offspring produced per female per time step has a Poisson distribution. The total number of offspring produced in the population at a given time step, and the total number of offspring produced by a single female over her entire lifetime, are then also Poisson-distributed.
When rm and/or rf are greater than 1, offspring of each sex are born into a single class. Male offspring pass through rm − 1 pre-reproductive classes (and females pass through rf − 1 pre-reproductive classes) before entering an adult class. Survival probability in these pre-reproductive classes is called sym for males and syf for females. The projection matrix G for this case is presented in appendix A.
Ignoring environmental stochasticity, the demographic variance of the subpopulation of heterozygotes with the rare allele can be written as [37]:
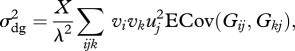 |
1.1 |
where λ is the growth rate of the subpopulation, found as the dominant eigenvalue of the expected projection matrix, vi is the reproductive value of class i (found from the left eigenvector), uj is the proportion of individuals found in class j once a stable stage distribution has been reached (found from the right eigenvector), and Gij is the entry in the ith row and jth column of G. The stable stage distribution is scaled such that ∑uj = 1, and the reproductive values are scaled to get ∑uj vj = 1. We use uad to denote the proportion of a population that is found in adult classes (as opposed to pre-reproductive classes).
Assuming xj = Xuj, equation (1.1) becomes
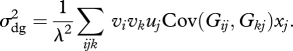 |
1.2 |
Expressions for Cov(Gij, Gkj) in the different cases described above can be found in appendix B. These covariances are all proportional to 1/xj, causing the xj's in equation (1.2) to cancel out. Thus, σd,g2 is independent of the size of the subpopulation, X.
As shown by Engen et al. [37], the ratio of effective population size to census population size can be calculated as:
| 1.3 |
where T is the generation time (defined as the average age of parents of newborn offspring), and N is the total population size. Given age-independent survival and reproduction in adults, the average generation time, T, can be written as T = (Tm + Tf)/2, where Tm = rm + sm /(λ − sm) and Tf = rf + sf/(λ − sf) [38,57].
In equation (1.3), N is the total number of individuals in the population. In order to find Ne/N for an alternate definition of N (e.g. only adults or only mated individuals), one can simply multiply equation (1.3) by N/Nalt. This ratio can be found from the relevant values of uj (the stable stage distribution).
This model is used here to study genetic drift by looking at the sampling variance in allele frequency per time step, and the effective population size (per generation). The growth rate of the subpopulation X is held constant at λ = 1 at all times. The effect of persistent differences in mating probability among individual males is examined by adjusting the parameter c while holding all other parameters constant. We look at three specific cases, with c = 0, 0.5 and 1, which span the gradient from completely independent mating success among seasons (c = 0) to permanent individual differences (c = 1). We also look at four different levels of variance in male mating success (1, 2, 5 and 10). By increasing survival probabilities, we also investigate the effect of generation time on these populations. As survival is increased, female fecundity is decreased such that the growth rate stays constant at 1.
We look at how age at maturity affects σd,g2 and Ne/N, and how this effect may vary depending on the survival probability of pre-reproductive individuals. We assume that males and females mature at the same age (rm = rf), and adjust female fecundity in such a way that a stable population size is maintained. Finally, we examine whether the outcome of these analyses is dependent on the definition of N used when calculating the ratio Ne/N.
3. Results
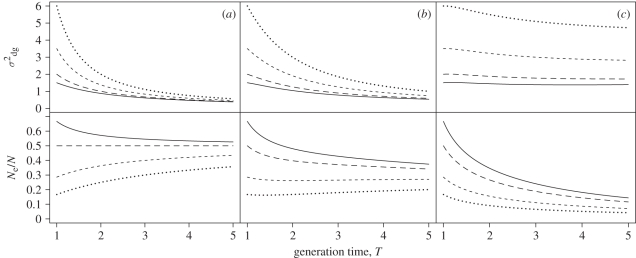
In the absence of persistent individual differences among males, the mating success of each individual male is independent among years. In this situation, the ratio of effective population size to adult or census population size becomes less affected by differences in mating system as the generation time increases (figure 1a). Differences in mating system are here defined by differences in the variance in male mating success. Mean male mating success is constant at 1 (the sex ratio is even and all females mate), and age at maturity is set to 1, so all individuals in the population are assumed to be adults. Nunney [11] has previously shown that the ratio of effective population size to adult population size converges towards 0.5 as the generation time increases. This result was confirmed by Waite & Parker [51] and is supported by our figure 1. In fact, the graph shown in figure 1a can be exactly reproduced by inserting our parameters into the equations of Nunney [10]. However, if there are persistent individual differences among males, Ne/N approaches a lower value than 0.5 (figure 1b,c). Effects of mating system differences on Ne/N still decrease with increasing generation time, and the speed with which this happens does not seem to differ much from the case with no persistent individual differences. The demographic variance, on the other hand changes much more slowly as individual differences become more persistent (top panel in figure 1). Thus, the fact that differences in mating system become less important as the generation time increases does not seem to be caused by a reduction in the variance in male reproductive success (as suggested by Nunney [11]). Such a reduction in the variance is expected when the mating success of males is independent from year to year, allowing different males to be successful at different times, thereby reducing the variance in lifetime reproductive success when compared with the variance in reproductive success in a single season. However, even when the probability of the same males being successful year after year is very high, causing the demographic variance to stay high as the generation time is increased, Ne/N still seems to converge (figure 1c). This suggests that the convergence is a result of the way the effective population size is defined. This can be seen from equation (1.3). As T becomes large, changes in σdg2 become less influential. Analogously, when σdg2 is large, changes in T have less effect on Ne/N.
Figure 1.
Effects of generation time, T, on the genetic drift per time step, σdg2, and the ratio of effective population size to census (total) population size, Ne/N, in populations with different mating systems and different levels of persistent individual differences in mating success among males; (a) c = 0 (no persistent differences), (b) c = 0.5 and (c) c = 1. See §2 for a more detailed description of the parameter c. Different mating systems are represented by the variance in annual male mating success, which is equal to 1 (solid lines), 2 (long dash), 5 (short dash) and 10 (dotted). Generation time is increased by increasing the annual survival probability, s from 0 (T = 1) to 0.8 (T = 5), simultaneously decreasing the expected number of offspring per female from 2 to 0.4. Other parameters are sex ratio at birth, q = 0.5, and age at maturity, r = 1.
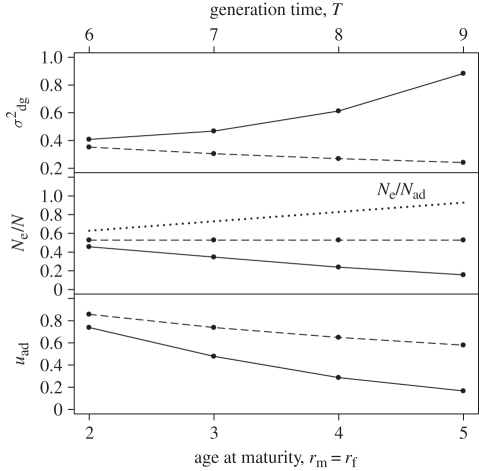
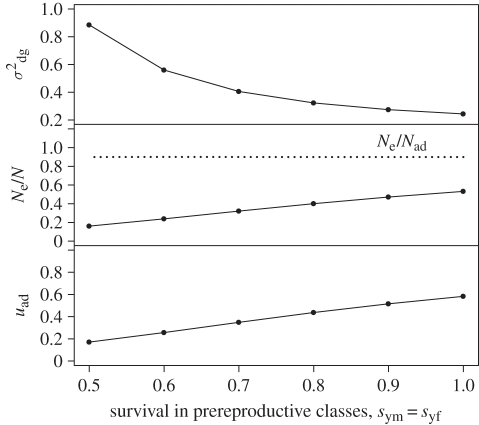
Increasing the age at maturity also affects Ne/N (figure 2). The direction and magnitude of this effect depends on the survival probability of pre-reproductive individuals, sym, as well as the definition of N used in the calculation of Ne/N. When the annual survival probability of juveniles is close to 1, an increase in the age at maturity causes σdg2 to decrease (figure 2). At lower juvenile survival probabilities, on the other hand, σdg2 increases as the age at maturity increases (figure 2). This increase becomes greater as the survival probability decreases (figure 3). Changes in the age at maturity are also reflected in the average generation time, T. When N is defined as the (total) census population size, changes in σdg2 and T described above cause Ne/N to decrease as the age at maturity increases (figure 2). When sym is close to 1, the observed decrease in Ne/N is very slight. On the other hand, if Nad denotes the size of the adult population only, Ne/Nad increases linearly with age at maturity. With this definition of population size, the ratio Ne/Nad is also not affected by changes in juvenile survival rate (figure 3). The substantial difference between the behaviour of the two ratios Ne/N and Ne/Nad can be explained by the changes in stage structure that accompany changes in the age at maturity and/or juvenile survival rate. Since the denominator of Ne/Nad includes only adult individuals, changing the proportion of the population that is in the adult state (uad) will alter this ratio. Thus, a decrease in uad causes Ne/Nad to increase with age at maturity, even when both σdg2 and T increase (figure 2). When juvenile survival is altered, the resulting change in σdg2 is cancelled out by the change in uad, leaving Ne/Nad unchanged, while Ne/N is shifted.
Figure 2.
Effects of age at maturity, r, on the genetic drift per time step, σdg2, the ratio of effective population size to census (total) population size, Ne/N, and the proportion of adults at stable stage structure, uad, in populations with different levels of juvenile survival. Annual survival probability of prereproductive individuals, sym = syf, is equal to 0.5 (solid lines) and 1 (dashed lines). In the middle panel, the dotted line shows the ratio Ne/Nad, where Nad is the adult population size (as opposed to the total population size used in the ratio Ne/N represented by the solid and dashed lines). Variance in annual male mating success is equal to 2, the sex ratio, q, is equal to 0.5, and the expected number of offspring is adjusted to maintain a growth rate, λ, of 1.
Figure 3.
Effects of annual juvenile survival probability on the genetic drift per time step, σdg2, the ratio of effective population size to census (total) population size, Ne/N, and the proportion of adults at stable stage structure, uad. Parameters are age at maturity, r = 5, generation time, T = 9 and sex ratio, q = 0.5. Variance in annual male mating success is equal to 2. The expected number of offspring is adjusted to maintain a growth rate, λ, of 1. The dotted line in the middle panel shows the ratio Ne/Nad, where Nad is the adult population size, whereas the solid line shows Ne/N, where N is the total population size.
4. Discussion
Effective population size, Ne, is influenced by a number of different factors, including mating system and generation time. In a study on the influence of mating systems on Ne, Nunney [11] found that the effective population size should approach half the size of the adult population, Nad/2, as generation time becomes large. Later, Waite & Parker [51] showed that the result of Nunney only held when the age at maturity was low when compared with the adult lifespan. Using a matrix model, we have re-examined these ideas, taking persistent individual differences and juvenile survival probabilities into account.
Persistent individual differences in mating success among males cause Ne/N to converge to a value lower than 0.5 as the generation time increases (figure 1). There is evidence to support the existence of such persistent individual differences in natural populations (e.g. [43,44,48–50,58,59]). Basically, when male mating success is dependent on certain male traits and the expression of these traits is not independent among breeding seasons, mating success will not be independent among seasons either. Some physical attributes that may affect mating success are permanent, like colour morph [58,60–62], while the expression of other traits may vary from season to season but still be correlated. One such trait is male body weight. In species where males engage in physical combat over females or territories, body weight may be important in determining reproductive success. Accordingly, body weight (at birth or capture) is positively correlated with lifetime reproductive success of males in some studied populations [49,63–68]. If there is strong site fidelity in a population, the distribution of territories may cause correlations in reproductive success among years, even without persistent differences in fighting ability [48,69–71].
A common pattern, especially in birds, is that lifespan is the main predictor of lifetime reproductive success [72,73]. However, even in long-lived seabirds, a considerable part of the variation in lifetime reproductive success can be traced back to factors other than lifespan, and reproductive parameters are often found to be consistent between years [43]. Sometimes traits that increase annual reproductive success also promote longevity, intensifying the effect [44,48,50,59,74,75]. In other cases reproduction is costly. This can cause negative correlation in reproductive success among years [76], or negative effects of reproduction on survival [77–80]. The model presented in this paper can easily be extended to include both of these cases.
It has previously been demonstrated that increasing the age at maturity in relation to the adult lifespan causes an increase in Ne/N [51]. We have shown that this result is very dependent on the definition of N used. Waite & Parker [51] used the number of adults, Nad, as their measure of population size, following recommendations from Nunney & Elam [3]. When the pre-reproductive part of the life cycle is lengthened when compared with the adult part, the proportion of individuals found in the pre-reproductive state also increases. Thus, Nad then represents a smaller proportion of the population, and Ne/Nad increases. This does not necessarily mean, however, that the amount of genetic drift decreases. In fact, depending on the survival probability of juveniles, the genetic drift per time step (measured by σdg2) may increase substantially (figure 2). This is reflected in Ne/N if N is counted as the total population size (both adults and juveniles).
The use of different definitions of N when reporting values of Ne/N has previously been discussed by Nunney & Elam [3]. They called attention to the fact that estimates of Ne/N become impossible to compare when different definitions of N are used. The total census number was deemed an impractical measure of population size because it is often difficult to obtain and is also prone to fluctuations (juvenile numbers are more likely to vary with seasonal conditions). Thus, practical considerations make the number of adults a better choice [3]. This is not a problem as long as the consequences of this choice are kept in mind. As we have shown, the definition of N used is not only an issue when comparing ratios of Ne/N from different studies. Results from theoretical analyses must also be interpreted in light of the definition used.
Waite & Parker [51] mention that having delayed maturity could restrict the genetic effects of a catastrophic (short-term) loss of adults. Any possible advantage of having a large proportion of the population in a juvenile state during catastrophic events is obviously dependent on the relative vulnerability of juveniles and adults to such events. In figure 3, we have shown that σdg2 increases as the survival probability of juveniles decreases. Koons et al. [81] demonstrated that environmental uncertainty can drive the evolution of delayed maturity in iteroparous populations if juveniles have a higher survival probability than adults. However, environmental uncertainty did not have the same effect in the more common case of juvenile survival being lower than that of adults.
In general, low juvenile survival would be expected to oppose the evolution of delayed maturation [82]. What would be considered ‘low’ in this context is however dependent on the benefits that delayed maturation confer. In a study using data from 109 populations of snakes, lizards and turtles, Pike et al. [83] found that juvenile survival in these species did not differ substantially from adult survival. These are taxa in which the age at maturity is often quite high in relation to their lifespan [51]. Survival probabilities shown in figure 3 are within the range presented by Pike et al. [83]. Thus, these combinations of age at maturity and juvenile survival rate seem to be realistic.
In figures 1–3 mating systems are represented by their variance in male mating success (with mean mating success constant at 1). This is in accordance with previous studies [10,11,51] and accommodates comparison with other results. It is worth noting, however, that the mean number of recruits per season is changed as the generation time is altered (in order to maintain a stable population size), so the variance in reproductive success does not necessarily stay constant even if the mating system (mating success) does.
The model presented here assumes that survival rate and fecundity are independent of age once adulthood is reached. However, it is not uncommon for these parameters to be age-specific (e.g. [72]), and there is a possibility that this may affect patterns of genetic drift. Although we have chosen not to include adult age classes as an additional complicating factor in this study, the model can easily be expanded to accommodate this.
As shown by Hill [32], it is the variance in lifetime reproductive success that is important when estimating the effective size of populations with overlapping generations, and most formulas for Ne contain this parameter (e.g. [1,11,32,84]). However, estimates are often available for reproductive success in single seasons only [11]. Using seasonal measures for estimating Ne could be a problem if fecundity varies with age, but Nunney [11] and Nunney & Elam [3] demonstrated that corrections can be made to minimize this problem. Our results highlight another potential problem using seasonal estimates. We have shown that persistent individual differences in mating success over time can have a strong influence on genetic drift. Establishing the presence or absence of such differences will therefore be an important step in the venture to quantify genetic drift in natural populations.
Acknowledgements
We thank D. Koons and R. Waples for helpful comments that improved this paper. The work was financed by the Research Council of Norway (project STORFORSK).
Appendix A. Projection matrix for the case of delayed maturation
If one or both sexes have delayed maturation (i.e. rf or rm, or both, are greater than 1), the projection matrix G consists of the following submatrices:
 |
 |
Expected values of the entries in these submatrices are basically the same as in the case with rm = rf = 1, except that the survival and reproduction terms are separate. A few things that must be noted are that pre-reproductive survival may differ from adult survival and that the mating success of male offspring does not come into play until they enter the adult population at age rm. Thus, 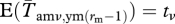 . It would also be possible to let mating probabilities be lower for these first-year males.
. It would also be possible to let mating probabilities be lower for these first-year males.
Appendix B. Variances and covariances of G
Survival and reproduction are assumed to be independent within years. We can therefore treat survival and reproduction terms separately.
Var(Gi,j,survival×xj) is simply the variance in a multinomial distribution in which the xj individuals from class j have probabilities 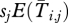 of surviving and moving to class i. Here, sj is either sm (for males) or sf (for females). Thus,
of surviving and moving to class i. Here, sj is either sm (for males) or sf (for females). Thus,
In order to calculate Var(Gi,j,reproduction×xj), we first find the conditional variance given Zj (the number of offspring produced in class j), and then use the law of total variance to obtain
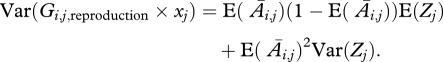 |
The expressions for sj, E(Zj), Var(Zj), 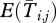 and
and  for different values of i and j are all presented in the main text. Note that
for different values of i and j are all presented in the main text. Note that 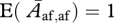 .
.
Since the xj values are known, we have
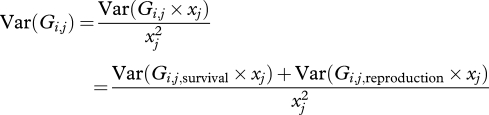 |
As explained in the main text, there are no covariances between columns. Within columns we have
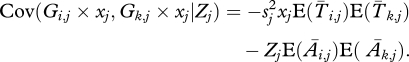 |
This means that
 |
and
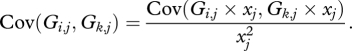 |
References
- 1.Caballero A. 1994. Developments in the prediction of effective population-size. Heredity 73, 657–679 10.1038/hdy.1994.174 (doi:10.1038/hdy.1994.174) [DOI] [PubMed] [Google Scholar]
- 2.Wright S. 1931. Evolution in mendelian populations. Genetics 16, 97–159 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Nunney L., Elam D. R. 1994. Estimating the effective population size of conserved populations. Cons. Biol. 8, 175–184 10.1046/j.1523-1739.1994.08010175.x (doi:10.1046/j.1523-1739.1994.08010175.x) [DOI] [Google Scholar]
- 4.Frankham R. 1995. Effective population size/adult population size ratios in wildlife: a review. Genet. Res. 66, 95–107 10.1017/S0016672300034455 (doi:10.1017/S0016672300034455) [DOI] [PubMed] [Google Scholar]
- 5.Creel S. 1998. Social organization and effective population size in carnivores. In Behavioral ecology and conservation biology (ed. Caro T.), pp. 246–265 Oxford, UK: Oxford University Press [Google Scholar]
- 6.Palstra F. P., Ruzzante D. E. 2008. Genetic estimates of contemporary effective population size: what can they tell us about the importance of genetic stochasticity for wild population persistence? Mol. Ecol. 17, 3428–3447 10.1111/j.1365-294X.2008.03842.x (doi:10.1111/j.1365-294X.2008.03842.x) [DOI] [PubMed] [Google Scholar]
- 7.Wright S. 1938. Size of population and breeding structure in relation to evolution. Science 87, 430–431 [Google Scholar]
- 8.Crow J. F., Kimura M. 1970. An introduction to population genetics theory. New York, NY: Harper & Row [Google Scholar]
- 9.Nomura T. 2002. Effective size of populations with unequal sex ratio and variation in mating success. J. Anim. Breed. Genet. 119, 297–310 10.1046/j.1439-0388.2002.00347.x (doi:10.1046/j.1439-0388.2002.00347.x) [DOI] [Google Scholar]
- 10.Nunney L. 1991. The influence of age structure and fecundity on effective population-size. Proc. R. Soc. Lond. B 246, 71–76 10.1098/rspb.1991.0126 (doi:10.1098/rspb.1991.0126) [DOI] [PubMed] [Google Scholar]
- 11.Nunney L. 1993. The influence of mating system and overlapping generations on effective population size. Evolution 47, 1329–1341 10.2307/2410151 (doi:10.2307/2410151) [DOI] [PubMed] [Google Scholar]
- 12.Balloux F., Lehmann L. 2003. Random mating with a finite number of matings. Genetics 165, 2313–2315 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Briton J., Nurthen R. K., Briscoe D. A., Frankham R. 1994. Modelling problems in conservation genetics using Drosophila: consequences of harems. Biol. Cons. 69, 267–275 10.1016/0006-3207(94)90426-X (doi:10.1016/0006-3207(94)90426-X) [DOI] [PubMed] [Google Scholar]
- 14.Pearse D. E., Anderson E. C. 2009. Multiple paternity increases effective population size. Mol. Ecol. 18, 3124–3127 10.1111/j.1365-294X.2009.04268.x (doi:10.1111/j.1365-294X.2009.04268.x) [DOI] [PubMed] [Google Scholar]
- 15.Basset P., Balloux F., Perrin N. 2001. Testing demographic models of effective population size. Proc. R. Soc. Lond. B 268, 311–317 10.1098/rspb.2000.1359 (doi:10.1098/rspb.2000.1359) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Nunney L. 1996. The influence of variation in female fecundity on effective population size. Biol. J. Linn. Soc. 59, 411–425 10.1111/j.1095-8312.1996.tb01474.x (doi:10.1111/j.1095-8312.1996.tb01474.x) [DOI] [Google Scholar]
- 17.Bouteiller C., Perrin N. 2000. Individual reproductive success and effective population size in the greater white-toothed shrew Crocidura russula. Proc. R. Soc. Lond. B 267, 701–705 10.1098/rspb.2000.1059 (doi:10.1098/rspb.2000.1059) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Stiver J. R., Apa A. D., Remington T. E., Gibson R. M. 2008. Polygyny and female breeding failure reduce effective population size in the lekking Gunnison sage-grouse. Biol. Cons. 141, 472–481 10.1016/j.biocon.2007.10.018 (doi:10.1016/j.biocon.2007.10.018) [DOI] [Google Scholar]
- 19.Anthony L. L., Blumstein D. T. 2000. Integrating behaviour into wildlife conservation: the multiple ways that behaviour can reduce Ne. Biol. Cons. 95, 303–315 10.1016/S0006-3207(00)00037-9 (doi:10.1016/S0006-3207(00)00037-9) [DOI] [Google Scholar]
- 20.Dobson F. S., Smith A. T., Gao W. X. 2000. The mating system and gene dynamics of plateau pikas. Behav. Processes 51, 101–110 10.1016/S0376-6357(00)00122-4 (doi:10.1016/S0376-6357(00)00122-4) [DOI] [PubMed] [Google Scholar]
- 21.Twiss S. D., Thomas C., Poland V., Graves J. A., Pomeroy P. 2007. The impact of climatic variation on the opportunity for sexual selection. Biol. Lett. 3, 12–15 10.1098/rsbl.2006.0559 (doi:10.1098/rsbl.2006.0559) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sæther B.-E., Engen S., Solberg E. J. 2009. Effective size of harvested ungulate populations. Anim. Cons. 12, 488–495 10.1111/j.1469-1795.2009.00278.x (doi:10.1111/j.1469-1795.2009.00278.x) [DOI] [Google Scholar]
- 23.Parker P. G., Waite T. A. 1997. Mating systems, effective population size, and conservation of natural populations. In Behavioral approaches to conservation in the wild (eds. Clemmons J. R., Buchholtz R.), pp. 243–261 Cambridge, UK: Cambridge University Press [Google Scholar]
- 24.Kelly M. J. 2001. Lineage loss in Serengeti cheetahs: consequences of high reproductive variance and heritability of fitness on effective population size. Cons. Biol. 15, 137–147 [Google Scholar]
- 25.Waples R. S. 2006. Seed banks, salmon, and sleeping genes: effective population size in semelparous, age-structured species with fluctuating abundance. Am. Nat. 167, 118–135 10.1086/498584 (doi:10.1086/498584) [DOI] [PubMed] [Google Scholar]
- 26.Blackwell B. F., Doerr P. D., Reed J. M., Walters J. R. 1995. Inbreeding rate and effective population-size: a comparison of estimates from pedigree analysis and a demographic-model. Biol. Cons. 71, 299–304 10.1016/0006-3207(94)00050-Z (doi:10.1016/0006-3207(94)00050-Z) [DOI] [Google Scholar]
- 27.Crow J. F. 1954. Breeding structure of populations. II. Effective population number. In Statistics and mathematics in biology (eds Kempthorne O., Bancroft T. A., Gowbk J. W., Lush J. L.), ch. 43, pp. 543–556 Ames, IA: Iowa State College Press [Google Scholar]
- 28.Kimura M., Crow J. F. 1963. Measurement of effective population number. Evolution 17, 279–288 10.2307/2406157 (doi:10.2307/2406157) [DOI] [Google Scholar]
- 29.Waples R. S. 2002. Definition and estimation of effective population size in the conservation of endangered species. In Population viability analysis (eds. Beissinger S., McCullough D.), ch. 8, pp. 147–168 Chicago, IL: The University of Chicago Press [Google Scholar]
- 30.Allendorf F. W., Luikart G. 2007. Conservation and the genetics of populations. Malden, MA: Blackwell Publishing [Google Scholar]
- 31.Felsenstein J. 1971. Inbreeding and variance effective numbers in populations with overlapping generations. Genetics 68, 581–597 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hill W. G. 1972. Effective size of populations with overlapping generations. Theor. Popul. Biol. 3, 278–289 10.1016/0040-5809(72)90004-4 (doi:10.1016/0040-5809(72)90004-4) [DOI] [PubMed] [Google Scholar]
- 33.Emigh T. H., Pollak E. 1979. Fixation probabilities and effective population numbers in diploid populations with overlapping generations. Theor. Popul. Biol. 15, 86–107 10.1016/0040-5809(79)90028-5 (doi:10.1016/0040-5809(79)90028-5) [DOI] [Google Scholar]
- 34.Pollak E. 2000. The effective population size of some age-structured populations. Math. Biosci. 168, 39–56 10.1016/S0025-5564(00)00041-9 (doi:10.1016/S0025-5564(00)00041-9) [DOI] [PubMed] [Google Scholar]
- 35.Orive M. E. 1993. Effective population-size in organisms with complex life-histories. Theor. Popul. Biol. 44, 316–340 10.1006/tpbi.1993.1031 (doi:10.1006/tpbi.1993.1031) [DOI] [PubMed] [Google Scholar]
- 36.Waples R. S. 2010. Spatial-temporal stratifications in natural populations and how they affect understanding and estimation of effective population size. Mol Ecol Res 10, 785–796 10.1111/j.1755-0998.2010.02876.x (doi:10.1111/j.1755-0998.2010.02876.x) [DOI] [PubMed] [Google Scholar]
- 37.Engen S., Lande R., Sæther B.-E. 2005. Effective size of a fluctuating age-structured population. Genetics 170, 941–954 10.1534/genetics.104.028233 (doi:10.1534/genetics.104.028233) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Engen S., Ringsby T. H., Sæther B.-E., Lande R., Jensen H., Lillegard M., Ellegren H. 2007. Effective size of fluctuating populations with two sexes and overlapping generations. Evolution 61, 1873–1885 10.1111/j.1558-5646.2007.00155.x (doi:10.1111/j.1558-5646.2007.00155.x) [DOI] [PubMed] [Google Scholar]
- 39.McGraw J. B., Caswell H. 1996. Estimation of individual fitness from life-history data. Am. Nat. 147, 47–64 10.1086/285839 (doi:10.1086/285839) [DOI] [Google Scholar]
- 40.Cam E., Link W. A., Cooch E. G., Monnat J. Y., Danchin E. 2002. Individual covariation in life-history traits: seeing the trees despite the forest. Am. Nat. 159, 96–105 10.1086/324126 (doi:10.1086/324126) [DOI] [PubMed] [Google Scholar]
- 41.Link W. A., Cooch E. G., Cam E. 2002. Model-based estimation of individual fitness. J. Appl. Stat. 29, 207–224 10.1080/02664760120108700a (doi:10.1080/02664760120108700a) [DOI] [Google Scholar]
- 42.Pfister C. A., Stevens F. R. 2002. The genesis of size variability in plants and animals. Ecology 83, 59–72 10.1890/0012-9658(2002)083[0059:TGOSVI]2.0.CO;2 (doi:10.1890/0012-9658(2002)083[0059:TGOSVI]2.0.CO;2) [DOI] [Google Scholar]
- 43.Moreno J. 2003. Lifetime reproductive success in seabirds: interindividual differences and implications for conservation. Scientia Marina 67, 7–12 [Google Scholar]
- 44.Pelletier F., Hogg J. T., Festa-Bianchet M. 2006. Male mating effort in a polygynous ungulate. Behav. Ecol. Sociobiol. 60, 645–654 10.1007/s00265-006-0208-y (doi:10.1007/s00265-006-0208-y) [DOI] [Google Scholar]
- 45.Ezard T. H. G., Becker P. H., Coulson T. 2007. Correlations between age, phenotype, and individual contribution to population growth in common terns. Ecology 88, 2496–2504 10.1890/06-2020.1 (doi:10.1890/06-2020.1) [DOI] [PubMed] [Google Scholar]
- 46.Pelletier F., Clutton-Brock T., Pemberton J., Tuljapurkar S., Coulson T. 2007. The evolutionary demography of ecological change: linking trait variation and population growth. Science 315, 1571–1574 10.1126/science.1139024 (doi:10.1126/science.1139024) [DOI] [PubMed] [Google Scholar]
- 47.Vindenes Y., Engen S., Sæther B.-E. 2008. Individual heterogeneity in vital parameters and demographic stochasticity. Am. Nat. 171, 455–467 10.1086/528965 (doi:10.1086/528965) [DOI] [PubMed] [Google Scholar]
- 48.McVey M. E. 1988. The opportunity for sexual selection in a territorial dragonfly, Erythmis simplicicollis. In Reproductive success: studies of individual variation in contrasting breeding systems (ed. Clutton-Brock T. H.), ch. 4, pp. 44–58 Chicago, IL: University of Chicago Press [Google Scholar]
- 49.Höglund J., Alatalo R. V. 1995. Leks. Princeton, NJ: Princeton University Press [Google Scholar]
- 50.McElligott A. G., Hayden T. J. 2000. Lifetime mating success, sexual selection and life history of fallow bucks (Dama dama). Behav. Ecol. Sociobiol. 48, 203–210 10.1007/s002650000234 (doi:10.1007/s002650000234) [DOI] [Google Scholar]
- 51.Waite T. A., Parker P. G. 1996. Dimensionless life histories and effective population size. Cons. Biol. 10, 1456–1462 10.1046/j.1523-1739.1996.10051456.x (doi:10.1046/j.1523-1739.1996.10051456.x) [DOI] [Google Scholar]
- 52.Storz J. F., Bhat H. R., Kunz T. H. 2001. Genetic consequences of polygyny and social structure in an Indian fruit bat, Cynopterus sphinx. II. Variance in male mating success and effective population size. Evolution 55, 1224–1232 [DOI] [PubMed] [Google Scholar]
- 53.Broquet T., Jaquiery J., Perrin N. 2009. Opportunity for sexual selection and effective population size in the lek-breeding European treefrog (Hyla arborea). Evolution 63, 674–683 10.1111/j.1558-5646.2008.00586.x (doi:10.1111/j.1558-5646.2008.00586.x) [DOI] [PubMed] [Google Scholar]
- 54.Caswell H. 2001. Matrix population models: construction, analysis, and interpretation, vol. 2 Sunderland, MA: Sinauer Associates [Google Scholar]
- 55.Engen S., Lande R., Sæther B.-E., Gienapp P. 2010. Estimating the ratio of effective to actual size of an age-structured population from individual demographic data. J. Evol. Biol. 23, 1148–1158 10.1111/j.1420-9101.2010.01979.x (doi:10.1111/j.1420-9101.2010.01979.x) [DOI] [PubMed] [Google Scholar]
- 56.Lee A. M., Engen S., Sæther B.-E. 2008. Understanding mating systems: a mathematical model of the pair formation process. Theor. Popul. Biol. 73, 112–124 10.1016/j.tpb.2007.09.003 (doi:10.1016/j.tpb.2007.09.003) [DOI] [PubMed] [Google Scholar]
- 57.Lande R. 1988. Demographic models of the northern spotted owl (Strix occidentalis caurina). Oecologia 75, 601–607 10.1007/BF00776426 (doi:10.1007/BF00776426) [DOI] [PubMed] [Google Scholar]
- 58.Goldsmith S. K., Alcock J. 1993. The mating chances of small males of the cerambycid beetle Trachyderes mandibularis differ in different environments (coleoptera, cerambycidae). J. Insect Behav. 6, 351–360 10.1007/BF01048116 (doi:10.1007/BF01048116) [DOI] [Google Scholar]
- 59.Lescroel A., Dugger K. M., Ballard G., Ainley D. G. 2009. Effects of individual quality, reproductive success and environmental variability on survival of a long-lived seabird. J. Anim. Ecol. 78, 798–806 10.1111/j.1365-2656.2009.01542.x (doi:10.1111/j.1365-2656.2009.01542.x) [DOI] [PubMed] [Google Scholar]
- 60.Madsen T., Shine R. 1992. A rapid, sexually selected shift in mean body size in a population of snakes. Evolution 46, 1220–1224 10.2307/2409767 (doi:10.2307/2409767) [DOI] [PubMed] [Google Scholar]
- 61.Krüger O., Lindström J. 2001. Lifetime reproductive success in common buzzard, Buteo buteo: from individual variation to population demography. Oikos 93, 260–273 10.1034/j.1600-0706.2001.930209.x (doi:10.1034/j.1600-0706.2001.930209.x) [DOI] [Google Scholar]
- 62.Wang Q. 2002. Sexual selection of Zorion guttigerum westwood (Coleoptera: Cerambycidae: Cerambycinae) in relation to body size and color. J. Insect Behav. 15, 675–687 10.1023/A:1020747907490 (doi:10.1023/A:1020747907490) [DOI] [Google Scholar]
- 63.Clutton-Brock T. H., Albon S. D., Guinness F. E. 1988. Reproductive success in male and female red deer. In Reproductive success: studies of individual variation in contrasting breeding systems (ed. Clutton-Brock T.), ch. 21, pp. 325–343 Chicago, IL: University of Chicago Press [Google Scholar]
- 64.Le Boeuf B. J., Reiter J. 1988. Lifetime reproductive success in northern elephant seals. In Reproductive success: studies of individual variation in contrasting breeding systems (ed. Clutton-Brock T.), ch. 22, pp. 344–362 Chicago, IL: University of Chicago Press [Google Scholar]
- 65.Hanks L. M., Millar J. G., Paine T. D. 1996. Body size influences mating success of the eucalyptus longhorned borer (Coleoptera: Cerambycidae). J. Insect Behav. 9, 369–382 10.1007/BF02214016 (doi:10.1007/BF02214016) [DOI] [Google Scholar]
- 66.Kruuk L. E. B., Clutton-Brock T. H., Rose K. E., Guinness F. E. 1999. Early determinants of lifetime reproductive success differ between the sexes in red deer. Proc. R. Soc. Lond. B 266, 1655–1661 10.1098/rspb.1999.0828 (doi:10.1098/rspb.1999.0828) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.McElligott A. G., Gammell M. P., Harty H. C., Paini D. R., Murphy D. T., Walsh J. T., Hayden T. J. 2001. Sexual size dimorphism in fallow deer (Dama dama): do larger, heavier males gain greater mating success? Behav. Ecol. Sociobiol. 49, 266–272 10.1007/s002650000293 (doi:10.1007/s002650000293) [DOI] [Google Scholar]
- 68.Jenkins J. M., Jackman R. E. 2006. Lifetime reproductive success of bald eagles in northern California. Condor 108, 730–735 10.1650/0010-5422(2006)108[730:LRSOBE]2.0.CO;2 (doi:10.1650/0010-5422(2006)108[730:LRSOBE]2.0.CO;2) [DOI] [Google Scholar]
- 69.Orians G. H., Beletsky L. D. 1989. Red-winged blackbird. In Lifetime reproduction in birds (ed. Newton I.), ch. 12, pp. 183–197 London, UK: Academic Press [Google Scholar]
- 70.Currie D., Thompson D. B. A., Burke T. 2000. Patterns of territory settlement and consequences for breeding success in the northern wheatear Oenanthe oenanthe. Ibis 142, 389–398 10.1111/j.1474-919X.2000.tb04435.x (doi:10.1111/j.1474-919X.2000.tb04435.x) [DOI] [Google Scholar]
- 71.Arlt D., Part T. 2007. Nonideal breeding habitat selection: a mismatch between preference and fitness. Ecology 88, 792–801 10.1890/06-0574 (doi:10.1890/06-0574) [DOI] [PubMed] [Google Scholar]
- 72.Clutton-Brock T. H. E. 1988. Reproductive success: studies of individual variation in contrasting breeding systems. Chicago, IL: The University of Chicago Press [Google Scholar]
- 73.Newton I. 1989. Lifetime reproduction in birds. London, UK: Academic Press [Google Scholar]
- 74.Partridge L. 1988. Lifetime reproductive success in Drosophila. In Reproductive success: studies of individual variation in contrasting breeding systems (ed. Clutton-Brock T.), ch. 2, pp. 11–23 Chicago, IL: University of Chicago Press [Google Scholar]
- 75.Clinton W. L., Leboeuf B. J. 1993. Sexual selections effects on male life-history and the pattern of male mortality. Ecology 74, 1884–1892 10.2307/1939945 (doi:10.2307/1939945) [DOI] [Google Scholar]
- 76.Wolff J. O. 1998. Breeding strategies, mate choice, and reproductive success in American bison. Oikos 83, 529–544 10.2307/3546680 (doi:10.2307/3546680) [DOI] [Google Scholar]
- 77.Geist V. 1971. Mountain sheep: a study in behavior and evolution. Chicago, IL: University of Chicago Press [Google Scholar]
- 78.Madsen T., Shine R. 1994. Components of lifetime reproductive success in adders, Vipera berus. J. Anim. Ecol. 63, 561–568 10.2307/5222 (doi:10.2307/5222) [DOI] [Google Scholar]
- 79.Alcock J. 1996. Male size and survival: the effects of male combat and bird predation in Dawson's burrowing bees, Amegilla dawsoni. Ecol. Ent. 21, 309–316 10.1046/j.1365-2311.1996.00007.x (doi:10.1046/j.1365-2311.1996.00007.x) [DOI] [Google Scholar]
- 80.Mills S. C., Grapputo A., Jokinen I., Koskela E., Mappes T., Poikonen T. 2010. Fitness trade-offs mediated by immunosuppression costs in a small mammal. Evolution 64, 166–179 10.1111/j.1558-5646.2009.00820.x (doi:10.1111/j.1558-5646.2009.00820.x) [DOI] [PubMed] [Google Scholar]
- 81.Koons D. N., Metcalf C. J. E., Tuljapurkar S. 2008. Evolution of delayed reproduction in uncertain environments: a life-history perspective. Am. Nat. 172, 797–805 10.1086/592867 (doi:10.1086/592867) [DOI] [PubMed] [Google Scholar]
- 82.Charlesworth B. 1994. Evolution in age-structured populations. Cambridge, UK: Cambridge University Press; 10.1017/CBO9780511525711 (doi:10.1017/CBO9780511525711) [DOI] [Google Scholar]
- 83.Pike D. A., Pizzatto L., Pike B. A., Shine R. 2008. Estimating survival rates of uncatchable animals: the myth of high juvenile mortality in reptiles. Ecology 89, 607–611 10.1890/06-2162.1 (doi:10.1890/06-2162.1) [DOI] [PubMed] [Google Scholar]
- 84.Hill W. G. 1979. Note on effective population-size with overlapping generations. Genetics 92, 317–322 [DOI] [PMC free article] [PubMed] [Google Scholar]