Percentile-based Empirical Distribution Function Estimates for Performance Evaluation of Healthcare Providers

Summary

Hierarchical models are widely-used to characterize the performance of individual healthcare providers. However, little attention has been devoted to system-wide performance evaluations, the goals of which include identifying extreme (e.g., top 10%) provider performance and developing statistical benchmarks to define high-quality care. Obtaining optimal estimates of these quantities requires estimating the empirical distribution function (EDF) of provider-specific parameters that generate the dataset under consideration. However, the difficulty of obtaining uncertainty bounds for a square-error loss minimizing EDF estimate has hindered its use in system-wide performance evaluations. We therefore develop and study a percentile-based EDF estimate for univariate provider-specific parameters. We compute order statistics of samples drawn from the posterior distribution of provider-specific parameters to obtain relevant uncertainty assessments of an EDF estimate and its features, such as thresholds and percentiles. We apply our method to data from the Medicare End Stage Renal Disease (ESRD) Program, a health insurance program for people with irreversible kidney failure. We highlight the risk of misclassifying providers as exceptionally good or poor performers when uncertainty in statistical benchmark estimates is ignored. Given the high stakes of performance evaluations, statistical benchmarks should be accompanied by precision estimates.

1. Introduction

Performance evaluation is an important activity in health policy research. Policy motivations for these evaluations include improving patient outcomes, increasing accountability among providers of services, and enhancing quality of health care. Much attention has been given to the development of analytic methods to estimate provider-level performance (Christiansen and Morris, 1997; Normand et al., 1997; Landrum et al., 2003; Liu et al., 2004; Normand and Shahian, 2007) and to rank providers (Goldstein and Spiegelhalter, 1996). A common characteristic of such evaluations is that provider-level performance is measured using patient-level outcomes. Hierarchical Bayesian modeling is well-suited to such evaluations given the data structure, with the first stage of the model representing the sampling distribution of the outcome measured on patients, the second stage the sampling distribution from which provider-specific parameters are drawn, and the third stage a hyper-prior distribution. This model is readily extendible for larger numbers of stages (Lindley and Smith, 1972).

Far less attention has been devoted to developing statistical methods to evaluate the performance of a system (or population) of K providers. Examples of such system-wide performance evaluation goals include identifying hotspots (Wright et al., 2003) or estimating threshold exceedances (Conlon and Louis, 1999) in environmental risk assessment; implementing pay-for-performance programs like those considered by the Centers for Medicare and Medicaid Services in the United States that identify performance of the top 20% of hospitals with respect to performance on quality of care measures (Centers for Medicare and Medicaid Services, 2005); and establishing a performance monitoring system within the Veterans Health Administration in the U.S. to improve vaccination rates (Jha et al., 2007).

A related goal to system-wide performance monitoring is the ongoing development of statistical benchmarks to define high-quality care. The demand for data-driven performance benchmarks has been informed in part by the desire to effectively motivate health care providers to improve their performance. For example, the Achievable Benchmarks of Care (Kiefe et al., 2001) is a statistical benchmarking approach that defines a ‘realistic standard of excellence’ as the performance attained by the top (e.g., 90^th percentile) of health care providers. Kiefe et al. (2001) found that providers who received feedback about how their performance compared to that of their strongest peers provided higher quality care than those who did not receive such feedback. One of the most well-known collections of statistical benchmarks is provided by the Healthcare Effectiveness Data and Information Set (HEDIS). Further emphasizing the widespread use of statistical benchmarks is the fact that over 90% of health plans in the U.S. use HEDIS to measure their performance (National Committee on Quality Assurance, 2009). HEDIS summarizes 71 performance measures collected across eight domains of care in terms of a national performance benchmark (e.g., the 90^th percentile of overall performance) as well as other percentile thresholds.

An open issue is that these statistical benchmark estimates are not reported with accompanying uncertainty statements. This is in contrast to other related inferential targets, such as provider-specific posterior means and ranks, for which the importance of reporting uncertainty is well-established (Goldstein and Spiegelhalter, 1996). The statistical benchmark could be estimated under a Bayesian hierarchical modeling framework from the conditional expected empirical distribution function (EDF) of the provider-specific parameters, but statistical methods are lacking for obtaining its uncertainty bounds. Though one could construct approximate uncertainty bounds using its posterior mean and variance (Shen and Louis, 1998), a more principled approach that avoids relying on the central limit theorem would be desirable.

In this paper, we develop and study alternative EDF estimates for univariate provider-specific parameters that are based on computing order statistics of Markov Chain Monte Carlo (MCMC) samples drawn from the posterior distribution of the provider-specific parameters under a hierarchical Bayesian model. Our method could be used to obtain uncertainty bounds on the EDF estimate and features of it, such as thresholds and percentiles. We apply our method to data from the Medicare End Stage Renal Disease (ESRD) Program, a national health insurance program in the U.S. for people with irreversible kidney failure. Congress established a network to support the U.S. government in monitoring the quality of the care ESRD patients receive throughout the entire system of Medicare-certified dialysis facilities and kidney transplant centers (Crow, 2005). We illustrate how to characterize acterize provider performance with respect to provider-level risk-adjusted mortality. Our work also has broader relevance whenever the analytic objective is to produce an ensemble of parameter estimates to describe the distribution of cluster-specific parameters or to identify clusters that fall above or below a pre-specified threshold, such as for small area estimation (Rao, 2003, Section 9.6; Louis and DerSimonian, 1986) and subgroup analysis (Tukey, 1974; Louis, 1984).

We proceed as follows. Our three-stage hierarchical modeling framework is presented in Section 2. Estimation of the EDF and our order statistics-based approach for estimating its uncertainty is presented in Section 3. We study the properties of our method by simulation in Section 4. We illustrate our approach in Section 5 using data from our motivating ESRD application. We use this motivating application to illustrate the importance of incorporating uncertainty about the EDF estimate into inferences about the distribution of provider-level mortality rates as well as its effect on statistical benchmarks. We conclude with discussion of our results and implications for performance evaluation in Section 6.

2. Hierarchical Model

We consider a three-stage, compound sampling model

$$\begin{array}{ccc}\hfill \mathit{\eta }& \hfill \sim \hfill & H\hfill \\ \hfill {\theta }_k\mid G& \hfill \stackrel{\mathit{\text{iid}}}{\sim }\hfill & G(\cdot \mid \mathit{\eta }),k=1,\dots ,K\hfill \\ \hfill Y_k\mid {\theta }_k& \hfill \stackrel{\mathit{\text{indep}}}{\sim }\hfill & f_k(Y_k\mid {\theta }_k)\hfill \end{array}$$ (1)

We assume that the θ_k's and η are continuous and that Y = (Y₁, …, Y_k) (k = 1, …, K). The provider-specific observations, Y_k, come from a sampling distribution f_k that depends on θ_k. The provider-specific parameter, θ_k, comes from a population distribution, G, that depends on hyperparameters, η, and η is assumed to have a hyperprior distribution, H. In the ESRD context, patient outcomes for the k^th provider are represented by Y_k and are nested within dialysis provider having target parameter θ_k. Two instances of this model will be explored in Section 4. Let g and h be the density functions of G and H, respectively; then, the posterior distribution of θ_k is,

$$g({\theta }_k\mid \mathbf{\text{Y}})=\int g({\theta }_k\mid {\mathbf{\text{Y}}}_k,\mathit{\eta })h(\mathit{\eta }\mid Y)d\mathit{\eta }$$ (2)

where

$$\begin{array}{c}g({\theta }_k\mid Y_k,\mathit{\eta })=\frac{f_k(Y_k\mid {\theta }_k)g({\theta }_k\mid \mathit{\eta })}{\int f_k(Y_k\mid s)g(s\mid \mathit{\eta })\mathit{\text{ds}}}=\frac{f_k(Y_k\mid {\theta }_k)g({\theta }_k\mid \mathit{\eta })}{f_{\mathit{\eta }}(Y_k)}\hfill \\ h(\mathit{\eta }\mid Y)=\frac{f_{\mathit{\eta }}(Y_k)h(\mathit{\eta })}{\int f_{\text{u}}(Y_k)h(\mathbf{\text{u}})d\mathbf{\text{u}}}\hfill \end{array}$$

3. Estimating the EDF

Our target of interest is the empirical distribution function (EDF) of θ = (θ₁, …, θ_K):

$$G_K(t\mid \mathit{\theta })=K^{-1}\sum I_{\{{\theta }_k\le t\}},$$ (3)

and let q_K(p) be the p^th quantile of G_K(t ∣ θ). Though G_K is consistent for G (Shen and Louis, 1998), note that G_K is preferred to the superpopulation distribution, G, as an inferential target for system-wide performance evaluation and for developing statistical benchmarks. Statistical benchmarks are performance standards developed from existing data on a population of K providers that are used for setting performance targets by, for example, identifying the 90^th percentile of provider performance. G_K summarizes the distribution of the K providers who are actually in the system, rather than generalizing to a hypothetical population of all such providers represented by G. To further emphasize this point, in our motivating application, K is the total number of providers in the system. It is this set of providers that is the focus to decision-makers and policy-makers using this information.

3.1. Posterior Mean Estimate

Let A(t) be a candidate estimate of G_K(t ∣ θ). Under integrated squared error loss (ISEL),

$$\text{ISEL}(A,G_K)=\int {\{A(t)-G_K(t)\}}^2\mathit{\text{dt}},$$ (4)

Shen and Louis (1998) show that the optimal estimate is

$${\overline{G}}_K(t\mid \mathbf{\text{Y}})=E[G_K(t\mid \mathit{\theta })\mid \mathbf{\text{Y}}]=K^{-1}\sum \mathit{\text{Pr}}({\theta }_k\le t\mid \mathbf{\text{Y}})$$ (5)

The optimal discrete distribution estimate with at most K mass points is Ĝ_K, with mass K⁻¹ at

$${\widehat{U}}_j={\overline{G}}_K^{-1}\left(\frac{2j-1}{2K}\mid \mathbf{\text{Y}}\right),j=1,\dots ,K$$ (6)

To compute Ĝ_K from MCMC draws, after burn-in pool all θs and order them. The Û_j are the (2j − 1)/(2K)^th order statistics.

3.2. Percentile-based Estimates

We present two percentile-based EDF estimates that can be derived using MCMC output that summarizes the marginal posterior distributions of model parameters θ. These approaches allow one to estimate uncertainty bounds without relying on the central limit theorem to construct approximate uncertainty intervals using the estimated mean and variance of the estimate of (3). Denote the number of MCMC draws (after burn-in) by n.

3.2.1. Posterior percentiles of G_K(t ∣ θ) for a fixed t

Let A(t) be a candidate estimate of G_K(t ∣ θ). Under integrated absolute error loss (IAEL),

$$\text{IAEL}(A,G_K)=\int \mid A(t)-G_K(t)\mid \mathit{\text{dt}}.$$ (7)

Let $G_K^{(0.5)}(t\mid \mathbf{\text{Y}})$ be the 50^th posterior percentile, which is the optimal estimate of G_K(t ∣ θ) under IAEL. More generally, for 0 < α < 1, $G_K^{(\alpha )}(t\mid \mathbf{\text{Y}})$ is the α^th posterior percentile of G_K(t ∣ θ). For all α, $G_K^{(\alpha )}(t\mid \mathbf{\text{Y}})$ is non-decreasing in both α and t. By definition, for a fixed α it is discrete with a maximum of K mass points. Using a standard argument, for each t, $G_K^{(\alpha )}(t\mid \mathbf{\text{Y}})$ minimizes (α, 1 − α)-weighted absolute value loss for estimating G_K(t ∣ θ). That is, $G_K^{(\alpha )}(t\mid \mathbf{\text{Y}})$ minimizes the posterior risk induced by the loss function:

α· |Ĝ_K(t) − G_K(t ∣ θ)| I_{{ĜK(t)≤GK(t∣θ)}} + (1 − α)· |Ĝ_K(t) − G_K(t ∣ θ)| I_{{ĜK(t)>GK(t∣θ)}}

Also, it minimizes (α, 1 − α)-weighted IAEL. For 0 < α < 0.5 use $\left(G_K^{(\alpha )}(t\mid \mathbf{\text{Y}}),G_K^{(1-\alpha )}(t\mid \mathbf{\text{Y}})\right)$ for a (1 − 2α) credible interval. To estimate G_K(t ∣ θ), replace Ḡ_K(t ¯ Y) by $G_K^{(0.5)}(t\mid \mathbf{\text{Y}})$. To compute $G_K^{(\alpha )}(t\mid \mathbf{\text{Y}})$, order the draws of θ from the MCMC sampler at iteration m, θ^(m), and place them in row m of a matrix of MCMC samples of θ, so that ${\theta }_j^{(m)}$ is the j^th largest value in θ. Then, column j of this matrix of MCMC samples summarizes the posterior distribution of the j^th order statistic. Obtain the desired α^th percentiles from each column. Then, set $G_K^{(\alpha )}(t\mid \mathbf{\text{Y}})=(2j-1)/2K$ for t equal to the α^th percentile of column j.

3.2.2. Posterior percentiles of q_K (p)

Define $q_K^{(\alpha )}(p)$ to be the α^th posterior percentile of the p^th quantile of G_K(t). The q_K(p) can be obtained using order statistics, represented approximately as $G_K^{-1}(p\mid \mathit{\theta })$ and exactly as θ_([pK]+1), 0 < p < 1, where θ_(k) is the k^th order statistic and […] is the greatest integer function. To compute $q_K^{(\alpha )}(p)$, at each MCMC iteration order the draws θ so that column j is the j^th order statistic. Then, for each column (order statistic), compute the desired α^th percentile. Use $q_K^{(0.5)}(p)$ for the estimated p^th quantile and $\left(q_K^{(\alpha )}(p),q_K^{(1-\alpha )}(p)\right)$ for the (1 − 2α) credible interval.

3.3. Compatibility of $G_K^{(\alpha )}(t\mid \mathbf{\text{Y}})$ and $q_K^{(\alpha )}(p)$

Due to the discrete distributions involved, $G_K^{(\alpha )}(t\mid \mathbf{\text{Y}})$ and $q_K^{(\alpha )}(p)$ are not necessarily compatible but are so asymptotically (in K). See the Appendix for the proofs showing that:

$$\left|G_K^{(\alpha )}\left(q_K^{(\alpha )}(p)\mid \mathbf{\text{Y}}\right)-p\right|\to 0\text{and}\left|q_K^{(\alpha )}\left(G_K^{(\alpha )}(t\mid \mathbf{\text{Y}})\right)-t\right|\to 0.$$ (8)

4. Simulation Study

We evaluate $G_K^{(0.5)}(t)$ and Ĝ_K(t) as point estimates of G_K(t) with respect to both ISEL (for which Ĝ_K is optimal) and IAEL (for which $G_K^{(0.5)}(t)$ is optimal), examining scenarios of K = 20, 60, and 100, to cover a range of relatively small to moderate-sized providers. Furthermore, we evaluate coverage (Rubin, 1984) of the (1 − 2α) tolerance intervals for G_K, for α = 0.005, 0.025, 0.05, 0.125 on a grid of t-values along the support of G, represented by T*:

$$\frac{1}{C}\sum _{j=1}^C\left\{\frac{1}{T}\sum _{t\in T\ast }I\left[G_K\in \left(G_K^{(\alpha )}{(t\mid \mathbf{\text{Y}})}^{(j)},G_K^{(1-\alpha )}{(t\mid \mathbf{\text{Y}})}^{(j)}\right)\right]\right\},$$ (9)

where I(·) is the indicator function, C is the number of Monte Carlo cycles and T is the cardinality of T*. Similarly, we evaluate coverage probabilities for quantiles, q_K(p), for α = (0.005, 0.025, 0.05, 0.125) and p = (0.01, 0.05, 0.1, 0.25, 0.5).

4.1. The Gaussian model

The data-generating Gaussian-Gaussian model for the simulation study is,

$$\begin{array}{l}[{\theta }_k\mid \mu ,{\tau }^2]\sim N(\mu ,{\tau }^2)k=1,\dots ,K\\ [Y_k\mid {\theta }_k]\sim N({\theta }_k,{\sigma }_k^2),\end{array}$$ (10)

with μ = 0 and τ² = 1. To evaluate via simulation how performance depends on the size of the sampling variance relative to the prior variance and on the variation in the ${\sigma }_k^2$, we fix the ${\sigma }_k^2$ as follows:

$${\sigma }_k^2=(\mathit{\text{gm}})\times {(\mathit{\text{rls}})}^{-0.5}\times {(\mathit{\text{rls}})}^{\frac{k-1}{K-1}}$$

where,

$$\begin{array}{l}\mathit{\text{rls}}={\sigma }_k^2/{\sigma }_1^2(\text{the ratio of the largest to the smallest variance})\\ \mathit{\text{gm}}={\left(\prod _{k=1}^K{\sigma }_k^2\right)}^{1/K}(\text{the geometric mean})\end{array}$$

and study gm = (0.1, 1.0) and rls = (1.0, 100).

Model (10) is the analysis model for data sets generated for the simulation study, along with the additional specification of hyper-prior:

$$[\mu ,{\tau }^2]\mathrm{ind}\mu \sim N(m_0,M_0);{\tau }^{-2}\sim \text{Gamma}(d_0,d_1),$$ (11)

such that E(τ⁻²) = d₀/d₁, m₀ = 0, M₀ = 100, d₀ = 1, and d₁ = 1. The joint posterior distribution of (θ₁, …, θ_K, μ, τ⁻²) is,

$$P({\theta }_1,\dots ,{\theta }_K,\mu ,{\tau }^{-2}\mid Y)\propto \left\{\sum _{k=1}^K{\sigma }_k^{-1}\mathit{\text{exp}}\{-{(y_k-{\theta }_K)}^2/2{\sigma }_k^2\}\times \mathit{\text{exp}}\{-{({\theta }_k-\mu )}^2/2{\tau }^2\}\right\}\times \mathit{\text{exp}}\{-{(\mu -m_0)}^2/2M_0)\mathit{\text{exp}}(-d_1/{\tau }^2)/{\tau }^{2(d_0-1)}$$

4.2. The Poisson-Gamma Model

The data-generating Poisson model for the simulation study is,

$$\begin{array}{l}[{\theta }_k\mid \alpha ,\beta ]\sim \text{Gamma}(\alpha ,\beta )k=1,\dots ,K\\ [Y_k\mid {\theta }_k]\sim \text{Poisson}(m_k{\theta }_k)\end{array}$$ (12)

Here, E(Y_k ∣ m_k, θ_k) = V(Y_k ∣ m_k, θ_k) = m_kθ_k. We generate data using fixed (α, β) = (20, 0.02), so E(θ_k ∣ α, β) = 0.4, V(θ_k ∣ α, β) = 0.008 and to induce a range of conditional variances, we set m_k = 5 + 2(k − 1), analogous to rls > 1 in the Gaussian model.

For the analysis model, we specify hyperpriors for α and β, which result in a Poisson-Gamma model that allows for the possibility of over-dispersion relative to a Poisson model (George et al., 1993):

$$[\alpha ,\beta ]\mathit{\text{ind}}\alpha \sim \text{Gamma}(a_0,a_1);\beta \sim \text{Gamma}(b_0,b_1),$$ (13)

where a₀ = a₁ = b₀ = b₁ = 0.001, and the resulting joint posterior distribution is:

$$P({\theta }_1,\dots ,{\theta }_K,\alpha ,\beta \mid Y)\propto \left\{\prod _{k=1}^K\mathit{\text{exp}}(-m_k{\theta }_k){(m_k{\theta }_k)}^{yk}\times ({\beta }^{\alpha }/\Gamma (\alpha )){\theta }_k^{\alpha -1}\mathit{\text{exp}}(\beta {\theta }_k)\right\}\times {\alpha }^{a_0-1}\mathit{\text{exp}}(a_1\alpha )\times {\beta }^{b_0-1}\mathit{\text{exp}}(b_1\beta )$$

We ran each simulation for 10, 000 Monte Carlo cycles. For each cycle, MCMC implemented by the BRugs package in R (Thomas, 2006) was used to sample model parameters from their joint posterior distribution. For the compound Gaussian model (10-11), 1000 parameter draws were saved after a 1000 burn-in; for the Poisson-Gamma model (12-13), every fifth draw of the 5000 following a burn-in of 5000 were saved, with the thinning done to speed up the Monte Carlo simulation since the sorting required at each cycle for computing order statistics was relatively computationally expensive. We examined the efficiency of $G_K^{(0.5)}(t)$ relative to Ĝ_K(t) using the ratios,

$$\begin{array}{c}\text{ISEL}.\text{R}=\frac{\text{ISEL}\{G_K^{(.5)}(t)\}}{\text{ISEL}\{{\widehat{G}}_K(t)\}}\\ \text{IAEL}.\text{R}=\frac{\text{IAEL}\{G_K^{(.5)}(t)\}}{\text{IAEL}\{{\widehat{G}}_K(t)\}},\end{array}$$ (14)

along with their Monte Carlo standard errors (MCSEs) for the Gaussian-Gaussian and the Poisson-Gamma models, respectively.

4.3. Simulation Study Results

Tables 1-4 display results. ISEL.R and IAEL.R are near 1, ranging from 0.99-1.02 for all scenarios examined for selected values of {K, gm, rls} under the Gaussian-Gaussian model. The associated MCSEs are very small, ranging from 0.0001 – 0.0010. Results for the Poisson-Gamma model (Table 1) are similar, except ISEL.R is largest for K = 20, with IAEL.R closer to 1.

Table 1.

Poisson-Gamma model: Ratios of integrated squared error loss (ISEL.R) and ratios of integrated absolute error loss (IAEL.R) of $G_K^{(0.5)}(t)$ versus ${\widehat{G}}_K(t)$. Mean values are subscripted by their MCSEs.

K	ISEL.R(MCSE)	IAEL.R(MCSE)
20	1.14(0.0028)	1.04(0.0019)
60	1.02(0.0006)	1.01(0.0005)
100	1.01(0.0003)	1.00(0.0003)

Table 4.

Poisson-Gamma model: Coverage of the 100(1 − α/2)% credible intervals for selected quantiles, q_K (p), p = 0.05, 0.10, 0.25, 0.50.

K	Nominal Coverage				K	Nominal Coverage
	75%	90%	95%	99%		75%	90%	95%	99%
	qK (0.05):					qK (0.10):
20	77	92	96	99	20	77	92	96	99
60	74	89	94	99	60	73	89	94	99
100	75	90	95	99	100	74	89	95	99
	qK (0.25):						qK (0.50):
20	77	91	96	99	20	75	90	95	99
60	74	89	95	99	60	75	90	95	99
100	75	90	95	99	100	74	89	95	99

The percentile-based tolerance intervals perform well over all models and scenarios considered. Table 2 shows that the average (with respect to t) coverage probabilities of intervals for G_K(t) (Equation 9) is at the expected nominal level for both models across all choices of simulation parameters. Tables 3 and 4 display coverage probabilities of tolerance intervals for quantiles, q_K(p), for P = 0.05, 0.10, 0.25, 0.50, under the Gaussian-Gaussian and Poisson-Gamma models, respectively, with all intervals at or near the nominal levels. Since MCSEs are very small and equal across simulations (MCSEs for {75%, 90%, 95%, 99%} = {0.44, 0.31, 0.23, 0.11}), they are omitted from Tables 2-4.

Table 2. Coverage probabilities averaged over t of 100(1 − α/2)% credible intervals ( $(G_K^{(\alpha )}(t),G_K^{(1-\alpha )}(t))$) for Gaussian-Gaussian and Poisson-Gamma models.

K	gm	rls	Nominal Coverage
			75%	90%	95%	99%
Gaussian-Gaussian model:
100	1	100	74	90	95	99
100	1	1	74	89	95	99
100	0.1	100	75	90	95	99
100	0.1	1	75	90	95	99
60	1	100	75	90	95	99
60	1	1	75	90	95	99
60	0.1	100	75	90	95	99
60	0.1	1	75	90	95	99
20	1	100	75	90	95	99
20	1	1	75	90	95	99
20	0.1	100	74	89	94	99
20	0.1	1	75	90	95	99
Poisson-Gamma model:
20			76	91	96	99
60			74	89	94	99
100			75	90	95	99

Table 3.

Gaussian-Gaussian model: Coverage of the 100(1 − α/2)% credible intervals for selected quantiles, q_K (p), p = 0.05, 0.10, 0.25, 0.50.

K	gm	rls	Nominal Coverage				Nominal Coverage
			75%	90%	95%	99%	75%	90%	95%	99%
			qK (0.05):				qK (0.10):
100	1	100	74	89	95	99	74	90	95	99
100	1	1	73	89	94	99	74	89	94	99
100	0.1	100	75	90	95	99	75	89	94	99
100	0.1	1	74	90	95	99	74	90	95	99
60	1	100	74	90	95	99	74	90	95	99
60	1	1	75	90	95	99	75	90	95	99
60	0.1	100	75	90	95	99	74	89	94	99
60	0.1	1	75	89	95	99	74	90	95	99
20	1	100	76	91	96	99	77	91	96	99
20	1	1	78	92	96	99	78	92	96	99
20	0.1	100	75	90	95	99	74	90	95	99
20	0.1	1	76	90	95	99	75	90	95	99
			qK (0.25):				qK (0.50):
100	1	100	75	90	95	99	74	90	95	99
100	1	1	74	90	94	99	74	89	94	99
100	0.1	100	75	90	95	99	75	89	94	99
100	0.1	1	75	90	95	99	74	90	95	99
60	1	100	76	90	95	99	74	90	95	99
60	1	1	76	90	95	99	75	90	95	99
60	0.1	100	74	89	94	98	74	89	94	99
60	0.1	1	74	89	94	99	74	90	95	99
20	1	100	75	90	95	99	77	91	96	99
20	1	1	77	91	95	99	78	92	96	99
20	0.1	100	74	89	94	99	74	90	95	99
20	0.1	1	76	90	95	99	75	90	95	99

5. Performance Evaluation of Dialysis Providers

The providers in this analysis include Medicare-certified dialysis facilities and kidney transplant centers. The data consist of ESRD provider-specific profiles constructed by the United States Renal Dialysis System (USRDS) from the ESRD Facility Survey data, patient-level data, and ESRD Medicare claims for 1998 (K = 3, 428 providers) and 2001 (K = 4, 007 providers). The USRDS provided to us the number of provider-specific observed (Y_k) and expected (m_k) deaths, which are treated as known. Expected deaths are produced by a case mix adjustment with respect to age, race, gender, ESRD primary diagnosis, number of years with ESRD (“vintage”), year, and all two-way interactions among age, race, gender, and ESRD primary diagnosis. To stabilize the estimates USRDS provided to us, three years of data (1996, 1997, and 1998) were used with weights 1/3, 1/2, and 1, respectively, to derive estimates for 1998 (Liu et al., 2004), and a similar weighting scheme was used to derive provider-specific estimates for 2001. To provide a sense of the potential variability in provider mortality, the number of patients per provider in the 1998 data ranges from 1 to 697, with the median equal to 66 (10^th percentile= 13; 25^th percentile= 33; 75^th percentile=111; 90^th percentile= 163). The distribution of patients per provider in the 2001 data is very similar.

We fit the model presented in Equations (12-13) to data from each year (1998 and 2001) to estimate the standardized mortality ratio (SMR) for provider k, θ_k, and their distribution for the given year. We favored this approach over conducting a longitudinal analysis because our substantive questions pertain to characterizing system-wide performance in a given year as opposed to facility-level performance. Further emphasizing this fact is that the set of facilities in the ESRD network change from year to year: 248 facilities dropped out of the universe between 1998 and 2001 while 827 entered the universe by 2001. Focusing only on the 3, 180 of the 4, 255 facilities that remained in both years would provide an incomplete picture of performance in each of these years. Additionally, this approach also serves the dual purpose of examining the development of statistical benchmarks using data such as the USRDS data set, since the typical statistical benchmarking approach is to use one data set to derive the statistical benchmark estimate while using a second data set to obtain provider-specific performance estimates and compare them to an externally-derived benchmark.

For the analysis, hyperparameters were set to a₀ = a₁ = b₀ = b₁ = 0.0001; the results obtained were insensitive to this prior parameterization relative to other priors we examined, including a₀ = a₁ = b₀ = b₁ = 1 as well as specifying independent U(0, 1000) priors for α and β (Gelman, 2006). We confirmed the appropriateness of allowing for extra-Poisson variation by using the Poisson-Gamma model by comparing posterior mean deviances of the Poisson-Gamma versus Poisson models and examining posterior predictive distributions for Y_k's versus observed y_k's (Gelman et al., 2003).

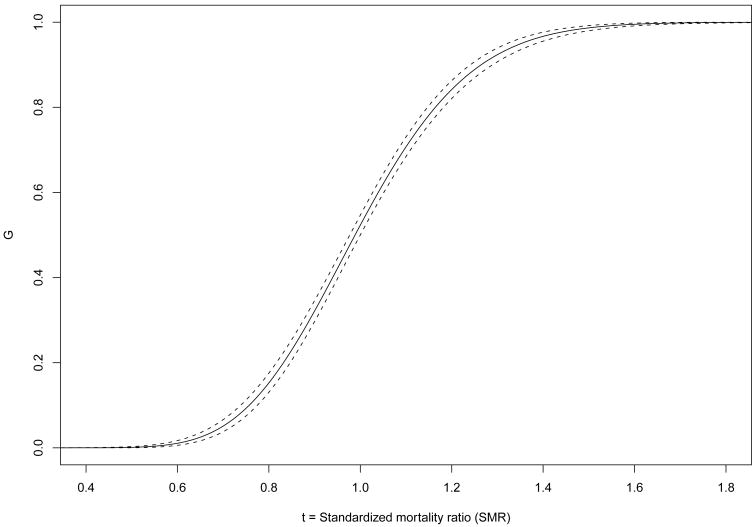
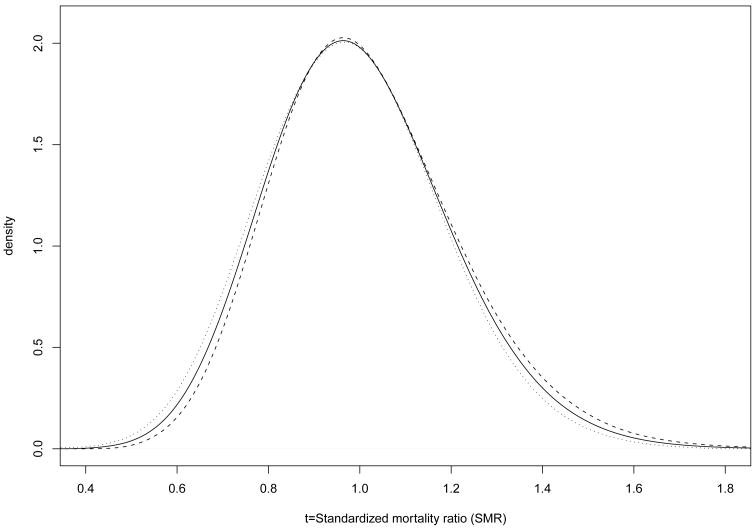
Figure 1 displays as a solid line the percentile-based, estimated EDF, $G_K^{(0.5)}(t)$ based on the 1998 data (the estimate Ĝ_K(t) is virtually identical and is omitted), with the upper and lower 95% bounds displayed as dashed lines. The distance between bounds is wider for higher SMR estimates and narrower for SMR estimates near 1.0. Figure 2 shows $g_K^{(0.5)}(t)$, the probability density function associated with $G_K^{(0.5)}(t)$, as a solid line along with the corresponding 95% credible interval (CI) in dashed lines.

Fig. 1.

$G_K^{(0.5)}(t)$ versus t, the standardized mortality ratio (SMR), and 95% credible interval (dashed lines) for the K = 3428 facilities in the 1998 USRDS data.

Fig. 2.

Left: $g_K^{(.5)}(t)$ (solid line) and 95% credible interval, with the lower bound given by the dashed line and the upper bound by the dotted line for the K = 3428 facilities in the 1998 USRDS data.

We now turn to developing statistical benchmarks for characterizing system-wide performance with respect to mortality. We use the USRDS 1998 data to estimate several candidate statistical benchmark values for SMR performance based on various quantiles of the distribution of θ_k's using $q_K^{(\alpha )}$. Results for each of these benchmarks are provided in Table 5(i), with the posterior mean estimates of the statistical benchmarks (SBs) and their 95% CIs.

Table 5.

Statistical benchmark (SB) estimates and corresponding 95% credible intervals (CIs). (a): Number of facilities in 2001 (N) classified as falling below the SB estimate. (b): N classified as falling below the SB CI. (c): Difference between (b) and (a). (d): N classified as falling above the SB estimate. (e): N classified as falling above the SB CI. (f): Difference between (d) and (e).

pth quantile	SB (CI), 1998	(a)	(b)	(c)	(d)	(e)	(f)
(i) Using $q_K^{(\alpha )}(p)$ to define statistical benchmark
5th	0.697 (0.676, 0.720)	0	0	0	2379	1899	480
10th	0.756 (0.738, 0.775)	0	0	0	1268	1006	262
25th	0.861 (0.847, 0.875)	0	0	0	251	196	55
75th	1.128 (1.112, 1.143)	184	144	40	2	2	0
90th	1.265 (1.240, 1.289)	1134	870	264	0	0	0
95th	1.353 (1.320, 1.384)	2301	1844	457	0	0	0
(ii) Using q(p) to define statistical benchmark
5th	0.697 (0.675, 0.718)	0	0	0	2373	1927	446
10th	0.756 (0.736, 0.774)	0	0	0	1271	1014	257
25th	0.861 (0.846, 0.875)	0	0	0	251	194	57
75th	1.129 (1.112, 1.146)	191	144	47	2	2	0
90th	1.265 (1.241, 1.291)	1141	876	265	0	0	0
95th	1.352 (1.321, 1.385)	2301	1877	424	0	0	0

We then analyzed 2001 USRDS data to determine whether each provider k was significantly higher or lower than the 1998-based statistical benchmark estimate, as determined by the benchmark estimate, $q_K^{(0.5)}(p)$, for p = 0.05, 0.10, 0.25, 0.75, and 0.90 falling outside of the 95% credible interval for θ_k obtained from the 2001 USRDS data analysis. We examined the effect of uncertainty in the statistical benchmark estimate on this assessment by conservatively classifying a facility as being different from the statistical benchmark if it fell entirely above or below the 95% credible interval for the statistical benchmark.

Table 5(i) shows a discrepancy in the numbers of facilities classified as falling below the statistical benchmark for each candidate statistical benchmarking threshold, depending on whether the classification is based on the SB or the CI that reflects the uncertainty in the SB. For example, the statistical benchmark using the 1998 data for the 5^th quantile of SMR is 0.697, with a 95% CI of (0.676, 0.720). Zero facilities in 2001 had 95% CIs that fell completely below the benchmark corresponding to $q_K^{(0.5)}(0.05)$, SMR = 0.697 (column a), nor did any facilities have CIs that fell entirely below the lower bound of the benchmark SMR CI (column b). In contrast, 2379 facilities had significantly higher SMRs than the mean 5^th quantile benchmark (column d), suggesting suboptimal performance with respect to mortality given this performance benchmark. However, the number of facilities with 95% CIs falling above the 5^th quantile statistical benchmark was 1899 (column e), for a decrease of 480 (20%) in the number of facilities deemed to be significantly different from the benchmark. More generally, the misclassification rate across each performance indicator shown in Table 5(i) for which at least some facilities meet the benchmark is about 20%. Practically speaking, these 480 facilities (column f) are misclassified as having substantially higher SMRs than the 5^th quantile statistical benchmark when uncertainty in the benchmark is ignored. This has implications for the use of statistical benchmarks for quality improvement – in this case, resources that could be devoted to implementing and monitoring improvements for the 1899 truly underperforming facilities would instead be partially diverted to 480 facilities that are not actually meaningfully different than the benchmark.

Table 5(ii) shows the same analysis, only this time using quantiles, q(p), from the simulated posterior distribution of G, in order to understand how sensitive inferences are to the choice of estimating G versus G_K given the relatively large number of providers in the data set. Despite the near-equality of these statistical benchmark estimates and 95% CIs to those in Table 5(i), important practical differences arise, particularly for the most extreme (e.g., 5^th and 95^th) quantiles: 33 more facilities were classified as falling below the statistical benchmark CI for the 95^th quantile in Table 5(ii) than for Table 5(i), whereas 28 more facilities were classified as falling above the statistical benchmark CI when using q rather than $q_K^{(\alpha )}$.

6. Discussion

We introduce an effective inferential target for estimating the EDF of K provider-specific parameters for which estimating its posterior uncertainty can be readily obtained from posterior simulations of provider-specific parameters using MCMC. Our method relies on computing order statistics for provider-specific parameters that are derived from MCMC output streams. The ease of implementation is a strength of our approach, which should facilitate greater use of percentile-based EDF estimates and reporting of uncertainties associated with estimates derived from it. This is especially important considering our approach produces the optimal estimate, $G_K^{(0.5)}$, under ASEL and thus should be favored over other non-optimal methods currently in practice for characterizing system-wide performance or developing statistical benchmarks.

Though variation in estimates derived using some commonly-used statistical benchmarking methods has been noted (O'Brien et al., 2008), we are unaware of any previous effort to measure the uncertainty of a given statistical benchmark estimate itself. Our study therefore contributes to the field not only by providing a method to estimate the uncertainty in percentiles derived using EDFs but also by demonstrating the implications of such uncertainty with respect to monitoring providers and improving health care quality and outcomes. Our analysis of the USRDS data highlights the increased risk of misclassifying providers as being exceptionally good or poor performers when uncertainty in the statistical benchmark estimate is ignored. High stakes are involved in performance evaluations, which often include direct financial incentives and penalties (Rosenthal et al., 2006) as well as less direct ones, such as increased or decreased patient referrals (Werner and Asch, 2005). Therefore, a benchmark estimate should always be reported along with an uncertainty statement about its precision.

Future work includes extending our investigation to examine the variation in candidate statistical benchmarking approaches as well as the uncertainties in their estimates. An open question is how do widely-used approaches perform relative to using percentiles derived from G_K. Of particular interest are the Achievable Benchmarks of Care approach (Kiefe et al., 2001) – which involves estimating provider-level performance using a non-hierarchical modeling framework – and selection of top providers using posterior means (O'Brien et al., 2008) – which is limited by the underdispersion of posterior means relative to the EDF estimate. Our approach could also be extended to performance evaluations that focus on multiple levels of interest, such as examining performance simultaneously at the physician, facility, and geographic and/or network levels. Our work has implications for the simultaneously addressing multiple inferential goals using the triple-goal estimation framework of Shen and Louis (1998, 2000), since it relies centrally on estimating the EDF of provider-specific parameters as described in this paper. We did not evaluate the performance of percentile-based EDF estimates when the data-generating and data analysis models differed. Practitioners concerned about model misspecification could modify our analytic approach by modeling the superpopulation distribution, G, nonparametrically (Paddock et al., 2006; Ohlssen et al., 2007), for example, and still be able to obtain percentile-based EDF estimates. Finally, estimating statistical benchmarks using G versus G_K might be reasonable for K very large under a correctly specified analytic model. Bayesian quantile regression may be a competitor in such cases. Bayesian quantile regression for hierarchical data is only now being developed (e.g., Reich et al., 2010) and its performance for estimating parameters such as θ_k's has yet to be examined. Thus, future work includes examining its statistical performance and suitability to large-K statistical benchmarking applications.

Appendix: Compatibility of $G_K^{(\alpha )}(t\mid \mathbf{\text{Y}})$ and $q_K^{(\alpha )}(p)$

To see that ${lim}_{K\to \infty }\left|G_K^{(\alpha )}(q_K^{(\alpha )}(p)\mid \mathbf{\text{Y}})-p\right|=0$, first order each vector obtained from MCMC, $({\theta }_1^{(m)},\dots ,{\theta }_K^{(m)})$, where m indexes the MCMC draws. After sorting the MCMC sampled vectors, each column (order statistic) represents the p = k/(K + 1)^th quantile of G (k = 1, …, K). Then, select the α^th percentile from the column (order statistic) to get $q_K^{(\alpha )}(p)$. Because of discreteness of $G_K^{(\alpha )}$, there are only K unique values of $q_K^{(\alpha )}(p)$ for all p ∈ (0, 1). Thus, if p is not in P = {1/(K + 1), …, K/(K + 1)}, select p₁ closest to p such that p₁ ∈ P. Define $t_1=q_K^{(\alpha )}(p_1)$. By construction, $G_K^{(\alpha )}(t_1)=p_1$ because p₁ ∈ P. Then, ${lim}_{K\to \infty }\left|G_K^{(\alpha )}(t_1)-p\right|={lim}_{K\to \infty }\left|p_1-p\right|$. However, p₁ will be arbitrarily close to p if K is selected to be very large at the outset, so this limit goes to 0 as K → ∞.

To see that ${lim}_{K\to \infty }\left|q_K^{(\alpha )}(G_K^{(\alpha )}(t|\mathbf{\text{Y}}))-t\right|=0$, first select $G_K^{(\alpha )}(t)$ by ordering each vector obtained from MCMC, $({\theta }_1^{(m)},\dots ,{\theta }_K^{(m)})$. Then, select the α^th percentile from each column. The grid, T, is determined in this way, with t ∈ T, where $G_K^{(\alpha )}(t)=p$, with p ∈ {1/(K + 1), …, K/(K + 1)}. Since the grid, T, is determined by the values of $G_K^{(\alpha )}$, the particular t of interest may not be on that grid. Select the closest grid point to t, and call it t₁. $G_K^{(\alpha )}$ is non-decreasing in α and t, so t₁, will be arbitrarily close to t if K → ∞, as the grid becomes finer. By construction, $t_1=q_K^{(\alpha )}(G_K^{(\alpha )}(t_1))$, as t₁ is on the grid T, so the above becomes lim_{K → ∞} |t₁ − t|. Given the choice of t₁ arbitrarily close to t at the outset as K → ∞, |t₁ − t| → 0.