Abstract
Though genome-wide association studies (GWAS) have identified numerous susceptibility loci for common diseases, their use is limited due to the expense of genotyping large cohorts of individuals. One potential solution is to use ‘additional controls’, or genotype data from control individuals deposited in public repositories. While this approach has been used by several groups, the genetically heterogeneous nature of the population of the United States makes this approach potentially problematic. We empirically investigated the utility of this approach in a US-based GWAS. In a small GWAS of pancreatic cancer in New York, we observed clear population structure differences relative to controls from the database of Genotypes and Phenotypes (dbGaP). When we conduct the GWAS using these additional controls, we find large inflation of the test statistic that is properly corrected by using eigenvectors from principal components analysis as covariates. To deal with errors introduced due to different sources, we propose simultaneously genotyping a small number of controls along with cases and then comparing this group to the additional controls. We show that removing SNPs that show differences between these control groups reduces false-positive findings. Thus, through an empirical approach, this report provides practical guidance for using additional controls from publicly available datasets.
Key Words: Genome-wide association studies, Additional controls, dbGaP, Population stratification, Pancreatic cancer
Introduction
In recent years, genome-wide association studies (GWAS) have been used to identify numerous replicable susceptibility loci for many complex diseases. A typical GWAS involves a case-control design in which the investigator analyzes DNA samples from both affected case individuals and matched, healthy control individuals. One hurdle in conducting such studies, in which hundreds of thousands of SNPs are independently tested for association with disease, is the large sample size required to obtain adequate power to detect a modest effect after correcting for multiple testing. To address this problem, many groups have joined efforts to create large consortia with DNA samples from thousands or tens of thousands of individuals to conduct studies that are well powered to detect even a modest genetic effect. Even with large consortia, however, the cost of genotyping such a large number of samples can be prohibitive.
One potential solution to the sample size requirement of GWAS that has been proposed is the use of a common set of control individuals in numerous studies. In 2007, the Welcome Trust Case Control Consortium (WTCCC) used this ‘shared controls’ approach to study seven common diseases [1]. Rather than using controls individually matched to the cases for each disease, the WTCCC genotyped a common set of controls representative of the self-identified white European population of Great Britain and compared allele frequencies from this group with each set of case individuals. This approach has been used by others with case individuals who come from both the UK and elsewhere, including the United States [1,2,3,4,5]. Recently, Zhuang et al. [6] published a simulation study in which they showed the theoretical potential for expanding the control group with publicly available disease samples or reference samples to increase the power of GWAS; we refer to the use of such controls from the database as ‘additional controls’.
Despite the apparent practical success of this approach and simulation studies suggesting its effectiveness, both the power and pitfalls of using additional controls from databases in the genetically heterogeneous population of the United States remain unclear. Genome-wide genotype information, along with limited phenotypic data, is available for numerous healthy individuals from the United States in the database of Genotypes and Phenotypes (dbGaP) at NIH. Therefore, in theory it should be possible to combine these data with genome-wide SNP profiles from a smaller number of cases that an individual investigator is studying to identify disease susceptibility loci. However, population stratification due to differences in genetic ancestry between people in such case and control groups and differential genotyping error from different sources could hinder an effective use of this approach. It is known that even if a study is restricted to self-identified ‘white’ individuals in the United States, genotype frequency at many loci can vary based on from where in Europe the ancestors came [7,8]. While a variety of statistical methods have been developed to identify and correct for such stratification [9,10], how such correction will influence the power and type I error rate of using common controls in US-based studies remains to be seen.
In this paper, we evaluate the use of additional controls from publicly available sources in a US-based GWAS. To do so, we utilize a small pancreatic cancer dataset for which we have genome-wide genotype data on 263 cases and 202 controls. We chose this dataset in part because four recently reported pancreatic cancer-associated SNPs could be used as true positives to estimate the power of this additional controls approach in a real setting [11,12]. We found that the rank and p value of these true disease SNPs improved significantly in our dataset with additional controls, with the added benefit of more controls reaching a plateau after a control:case ratio of 10:1 is obtained. Despite a large amount of population stratification in this joint dataset, the impact of this stratification was effectively captured and corrected by principal component analysis (PCA). We demonstrate the utility of genotyping some controls at the same time as cases for comparison with the additional controls to remove SNPs that show differential allele frequencies due to disparity in data processing and technical artifacts. We thus show systematically for the first time the practical issues that concern the use of controls from different sources. This report can serve as useful guidance when using additional controls from publicly available datasets in future studies.
Subjects and Methods
Ethics Statement
The study was approved by the Memorial Sloan-Kettering Cancer Center's (MSKCC) Institutional Review Board and all participants signed informed consent.
Analytical Power Calculation
We determined the analytical power of GWAS assuming a simple test of allelic association. We computed the power using a non-central χ2 distribution with non-centrality parameter λ [13]. The power was computed under an additive model with the significance threshold α = 1 × 10−7. The genotype relative risk (GRR) was varied from 1.0–3.0 with increments of 0.1, and the disease allele frequency (DAF) was varied from 0.05 to 0.50. The number of cases used ranged from 100 to 3,000, and the control:case ratio ranged from 1:1 to 50:1.
Pancreatic Cancer Study Samples and Genotyping
The pancreatic cancer study dataset was obtained from an ongoing hospital-based case-control study conducted in conjunction with the Familial Pancreatic Tumor Registry (FPTR) at MSKCC. The samples were obtained by the MSKCC FPTR research study assistant. Patients were eligible if they were aged 21 or over, spoke English, and had pathologically or cytologically confirmed adenocarcinoma of the pancreas. Patients were recruited from the Surgical and Medical Oncology Clinics at MSKCC when seen for initial diagnosis or follow-up. Controls were visitors accompanying patients with other diseases to MSKCC or spouses of patients. They had the same age and language eligibility requirements as the cases and were not eligible if they had a personal history of cancer (except for non-melanoma skin cancer). The 263 cases and 202 controls in this analysis were recruited between June 2003 and July 2009. The participation rate among approached and eligible individuals was 76% among cases and 56% among controls. Participants provided a blood or buccal (mouthwash or saliva) sample for DNA and completed risk factor and family history questionnaires administered by the research study assistant by telephone or in person.
Genomic DNA was isolated from buccal cells using the Puregene DNA purification kit (Qiagen, Inc., Valencia, Calif., USA). DNA was also isolated from saliva samples with the Oragene saliva kits (DNA Genotek, Kanata, Ont., Canada) or from blood using the Gentra Puregene blood kit (Qiagen, Inc.). DNA samples were hydrated in 1x TE buffer. Genomic DNA was genotyped on the Illumina 370K SNP chip (either the Illumina CNV370-Duo or Illumina CNV370-Quad) at the Genomics Core Laboratory of MSKCC according to the manufacturer's protocol.
Additional Controls from dbGaP
Genotypes from additional controls were obtained from the NIH's dbGaP. All individuals used are controls in the underlying study and are of European ancestry. Specifically, data from 6 studies in dbGaP genotyped using Illumina chips were used (table 1). These datasets provide 5,485 additional controls in total. Using a common set of markers present in all the datasets, we combined our MSKCC cases and controls with some or all of the additional controls to yield control:case ratios of 5:1, 10:1 or 20:1.
Table 1.
Controls from dbGaP used in the present study
| Abbreviation | Study | Controls, n | dbGaP accession No. | Ref. |
|---|---|---|---|---|
| SAGE | Study of addiction: genetics and environment | 1,285 | phs000092v1 | |
| CGEMS breast cancer | CGEMS breast cancer GWAS – stage 1 – NHS | 1,142 | phs000147v1 | [28] |
| CGEMS prostate cancer | CGEMS prostate cancer GWAS – stage 1 – PLCO | 1,148 | phs000207v1 | [29] |
| CIDR PD | CIDR: genome-wide association study in familial Parkinson disease | 863 | phs000126v1 | |
| SIALS | Study of Irish amyotrophic lateral sclerosis | 211 | phs000127v1 | [26] |
| A genome-wide scan of lung cancer and smoking | A genome-wide scan of lung cancer and smoking | 844 | phs000093v2 | [30] |
Data Processing and Quality Control
All genotype data was processed using PLINK [14]. We performed several steps of quality control (QC). First, we processed the MSKCC samples alone, without additional controls. As we could not be certain of the DNA strand the genotype calls from each study are in reference to, we removed all A/T and C/G SNPs, as strand could be confused for these allele pairs. We removed individuals for whom less than 90% of genotypes were called and SNPs for which less than 10% of genotypes were called. We also removed SNPs with a minor allele frequency of <5%, or SNPs that were out of Hardy-Weinberg equilibrium in controls (p < 1 × 10−7). A total of 314,664 markers passed the QC in the MSKCC data and were used for combining data from various sources. Similar QC steps with the same parameters were performed on each of the additional controls datasets independently. The datasets were then merged using PLINK, restricting analysis to a set of SNPs common to all datasets. We calculated genome-wide identity by descent (IBD) using PLINK (– genome) and 70 individuals with excessive IBD (π^ > 0.4) were removed from our analysis. After these steps, we applied the same thresholds for missing data, minor allele frequency, and Hardy-Weinberg equilibrium as before. We also removed 529 SNPs that showed a significant difference in rates of missing genotype calls between cases and controls (p < 1 × 10−7) and a further 723 markers that show differential missingness (p < 1 × 10−7) between males and females. A test for differences in missingness based on local haplotype also did not reveal any SNPs with strong evidence for differential missingness based on inferred genotype at the SNP (– test-mishap in PLINK; p < 1 × 10−7). We compared allele frequencies and call rates between MSKCC study samples obtained from different DNA sources (buccal, saliva, or blood) and did not find any markers showing different missingness rates or genotype frequencies due to difference in DNA source (p < 1 × 10−7).
Principal Components Analysis
To perform principal components analysis to adjust for population substructure, we used the EIGENSTRAT software from the EIGENSOFT 2.0 package [9]. We first filtered the data by removing markers in high linkage disequilibrium (LD). This gave us a set of 32,619 SNPs for which pairwise r2 values within a window of 50 SNPs are all less than a specified threshold (usually 0.1; – indep-pairwise 50 5 0.1 command in PLINK). This set of markers was then used as input for EIGENSTRAT. Principal components were computed and outliers removed using default parameters. Significant principal components were determined using the Tracy-Widom statistic (p < 0.05).
Additional QC by Control Group Comparisons
To perform additional QC to reduce false-positive findings, we tested for genotype frequency differences between each control group versus the rest of the controls. For each control group, we adjusted for the top 11 principal components and used logistic regression to test for differences in genotype frequency versus the other control groups. For the MSKCC controls, we identified 2,702 SNPs that show a significant difference in genotype frequencies (p < 0.01; online suppl. fig. 1; for all online suppl. material, see www.karger.com/doi/10.1159/000330149); these SNPs were removed from further analysis. For the other control groups, we identified an additional 15 SNPs that showed significant deviation in genotype frequency in at least one control group (p < 1 × 10−7; online suppl. fig. 1). Notably, we found that the 211 controls from the Study of Irish Amyotrophic Lateral Sclerosis (SIALS; phs000127v1) show a strong deviation from the null hypothesis on a quantile-quantile plot (online suppl. fig. 1). Therefore, we chose to remove these 211 controls from the final analysis. This resulted in a final dataset of 263 cases and 5,416 total controls at 267,109 markers.
Association Analysis and Estimation of λ
To test for association between disease phenotype and SNPs, we used logistic regression as implemented in PLINK. When we do not consider population substructure, logistic regression is used without covariate adjustment; otherwise, significant principal components were used as covariates to adjust for population substructure.
We used PLINK's estimate for the genomic control parameter λ, which is a measure of test statistic inflation due to effects such as population stratification. PLINK reports λ (based on median χ2) in the .log file. To test control:case ratios of 1:1, 5:1, 10:1, and 20:1, we selected appropriate subsets of the additional controls to add to the MSKCC case-control dataset.
TaqMan Genotyping Assay
All MSKCC DNA samples were first amplified using the Illustra GenomiPhi v2 DNA amplification kit (GE Healthcare), following the manufacturer's recommendations. The reaction was then diluted by adding 120 μl reduced TE buffer. Prior to use in genotyping, we performed an additional 2-fold dilution to improve assay performance. One SNP, rs2236479, was genotyped using the TaqMan allelic discrimination genotyping assay (Applied Biosystems). Genotyping was conducted according to the manufacturer's instructions as follows: a master mix consisting of 1.375 μl water, 2.5 μl 2× TaqMan master mix, and 0.125 μl SNP assay (probe + primers) for each individual was prepared. Four microliters were aliquoted into each well of a 384 well plate, and 1 μl of amplified and diluted DNA was added. PCR was performed in an ABI Gene Amp 9700 machine under the following conditions: 95°C for 10 min followed by 48 cycles of 92°C for 15 s and 60°C for 1 min. Plates were read on an ABI Prism 7900HT fast real-time PCR system, and genotype calling was performed using the ABI Sequence Detection System software version 2.3. The genotype concordance rate was computed using 346 individuals who were genotyped both with TaqMan and on the Illumina arrays.
Results
Analytical Power
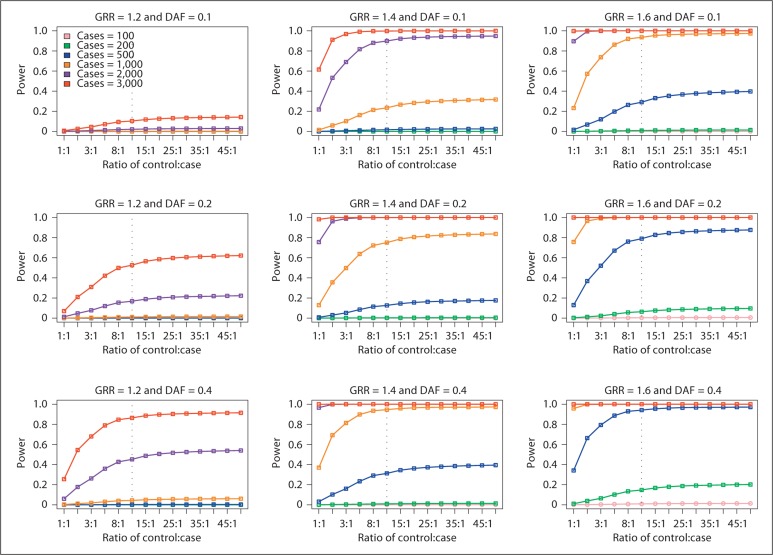
The large number of control individuals currently available in dbGaP and other databases raises the question of limiting returns. In other words, at what point is the improved power obtained through additional controls small enough that it is no longer worth adding controls? We therefore investigated the shape of the curve of power as a function of control:case ratio with a constant number of cases. As expected, the power increases with increasing number of cases, GRR and DAF. The maximum power is achieved when the control:case ratio increases to 10:1; beyond that, the power plateaus (fig. 1). For example, at a GRR of 1.6, a DAF of 20%, and a significance level of 10−7, little increase in power is observed after a control:case ratio of 10:1. Therefore, we consider a 10:1 control:case ratio ideal for using additional controls in a GWAS.
Fig. 1.
Analytical power of GWAS with additional controls. All power calculations assume an additive model and significance level of α = 1 × 10-7. The power computed using GRR of 1.2, 1.4, and 1.6 and DAF of 0.1, 0.2, and 0.4 is plotted.
Population Stratification in New York-Based Data
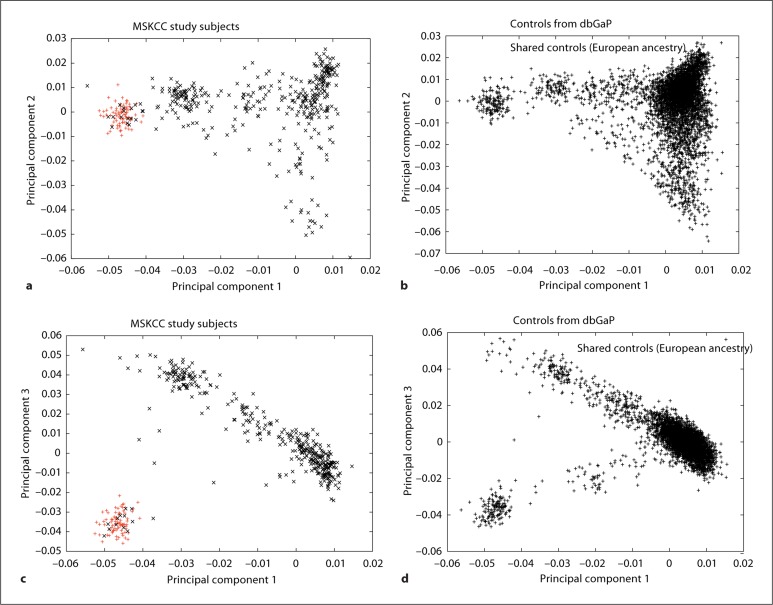
The present study was motivated by our desire to combine data from common controls with data from case individuals ascertained at MSKCC in New York. We were concerned that population stratification could become a significant problem in such a study, even if we restrict our analysis to self-identified ‘white’ individuals, because of subtle genetic differences among different European populations [8,15,16]. The history of immigration to the United States suggests that a larger proportion of white Americans of Ashkenazi Jewish or southern European (e.g. Italian) ancestry would be found in the New York metropolitan area compared to the country as a whole. If this were the case, combining additional controls with our New York-based population would result in the detection of alleles that mark geographic ancestry within Europe rather than disease risk. To investigate whether this concern was well-founded, we performed PCA on 263 cases and 202 controls from the MSKCC pancreatic cancer study combined with 5,416 individuals selected as additional controls from 6 different studies available in dbGaP (table 1). When we examine the first and third principal components in our samples from New York, we observe many individuals along a single gradient which has been previously suggested to represent a cline extending from northwest to southeast Europe [17] (fig. 2). The separate cluster of individuals has been previously suggested to be individuals of Ashkenazi Jewish ancestry; all participants in our study who self-identified as Ashkenazi Jewish cluster in this group, supporting the contention that this cluster represents the Ashkenazi Jewish population (fig. 2). When we compared this PCA plot with one for the controls from dbGaP, we observe marked differences in the distribution of individuals on the plot, suggesting a different distribution of geographic ancestry within Europe. Notably, 18% of the individuals in our study cluster in the ‘Ashkenazi Jewish’ group, compared with 1.7% in the dbGaP control group. These differences could potentially lead to high test statistic inflation when cases and additional controls are analyzed together. Therefore, we conclude that population stratification may be a serious issue when using additional controls with a New York-based case dataset and must be addressed.
Fig. 2.
Population substructure of the MSKCC pancreatic cancer study and additional controls. Principal components were computed for the MSKCC and additional controls samples combined, and plotted separately. a, c Principal components of the 263 cases and 202 controls from the MSKCC (New York) pancreatic cancer study. The first principal component is plotted against the second (a) or third (c). Individuals in red self-identified as Ashkenazi Jewish in the study questionnaire. b, d Principal components of the additional controls from dbGaP. The first principal component is plotted against the second (b) and third (d) principal components.
PCA-Based Correction Method Using Additional Controls
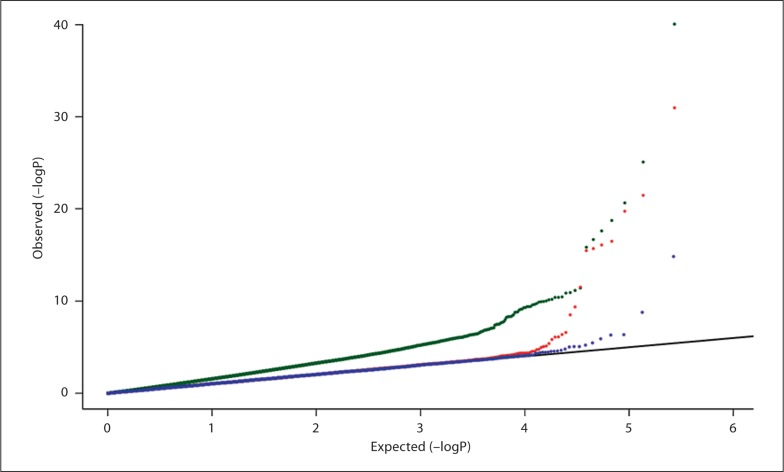
We next asked if stratification between our New York-based case dataset and controls from dbGaP results in false positives and if PCA can properly correct for it. We limited the data to those SNPs that were in common among all studies. As all studies were conducted using the Illumina platform, there were 272,796 overlapping SNPs. The full dataset results in a control:case ratio of 20:1, twice as much as we would recommend based on the analytical power calculations. Using an independent set of markers (all pair-wise LD r2 < 0.1), we determined the significant principal components using EIGENSTRAT [9]. The top principal components were used as covariates in a logistic regression model. As can be seen on the quantile-quantile plot, there is an immense inflation of the test statistic when we do not correct for population structure; we interpret this to be due to stratification rather than any true positive finding (fig. 3). When we correct for population structure by adjusting for the top 21 eigenvectors, the quantile-quantile plot follows the distribution expected for the null hypothesis much more closely (fig. 3), even though there is a little inflation near the tail. Therefore simple adjustment for principal components can largely correct for population stratification introduced when using additional controls.
Fig. 3.
Quantile-quantile plot of GWAS of pancreatic cancer cases with additional controls. At a 20: 1 control:case ratio, this plot compares the association statistics without any population stratification correction (green), after correction with principal components analysis (red), or with both PCA and removal of SNPs that show differences between the MSKCC controls and additional controls (blue). The black line shows the expected result under the null hypothesis of no association.
Additional QC through Comparison of Control Groups
The presence of 6 SNPs at the genome-wide significance threshold of 10−7 concerned us as such highly significant associations should have been found in the previously reported pancreatic cancer GWAS [11,12]. When we examined the previously reported GWAS of pancreatic cancer in dbGaP [11], none of these 6 SNPs was significant (all p > 0.05) (table 2). This failure to replicate raises the possibility that the significant results in our study may represent false positives even after following QC steps used in regular case-control GWAS. We next asked if SNPs that lead to false positives could be detected by comparing the MSKCC controls with the additional controls from dbGaP using logistic regression. The quantile-quantile plot of this comparison shows no inflation of test statistics when correcting for 11 principal components (genomic inflation factor λ = 1.01). Five out of six potential false-positive SNPs showed a nominally significant difference (p < 0.01) in allele frequency between control groups (table 2). We then examined the normalized intensity plots for the sixth SNP, rs1975920, in the data we generated (online suppl. fig. 3). While the plot shows distinct clusters, we noticed that this SNP was monomorphic in the samples we genotyped on the Illumina CNV370-Quad array, while it was polymorphic in the larger number of samples genotyped using the Illumina CNV370-Duo array. As only 20 controls were genotyped using the Illumina CNV370-Quad array, we were not able to detect this artifact through the control group comparison. However, 84 out of 263 cases were genotyped on the CNV370-Quad, presumably driving the signal seen in the case-control analysis. Thus, we introduce an additional QC step by removing 2,863 SNPs that show significant difference (p < 0.01) in allele frequencies between the MSKCC control group and additional controls. We extended this analysis to the other control groups, comparing each group with all other control groups. We excluded 15 markers with significant differences in genotype frequency (p < 1 × 10−7). We also visually inspected the quantile-quantile plot of each test for excess test statistic inflation (online suppl. fig. 1). Notably, we found that the 211 controls from the SIALS (phs000127v1) show deviation from the null hypothesis in the quantile-quantile plot. Thus, we removed these 211 controls from the final analysis. We reanalyzed 263 pancreatic cancer cases with 5,416 additional controls after performing this additional QC step and found that most of the SNPs with an extremely low p value were removed except one (rs2236479). We genotyped rs2236479 in our cohort using a different technology (TaqMan). The concordance rate between the two technologies (TaqMan and Illumina) for rs2236479 was 85%, suggesting that false positives may still be present due to genotyping error. Therefore, we conclude that careful QC using a small control group genotyped simultaneously with cases can effectively reduce false-positive findings when using additional controls by identifying SNPs that show different genotype frequencies between control groups.
Table 2.
SNPs associated with pancreatic cancer at genome-wide significance (p < 1 × 10 7) before additional QC
| SNP | Chr. | Analysis using additional controls (p) | Differential missingness (p) | PanScan analysis (p) | Additional controls vs. MSKCC controls (p) |
|---|---|---|---|---|---|
| rs7503953 | 17 | 2.7 × 10−12 | 7.8 × 10−5 | 0.5273 | 8.2 × 10−5 |
| rs2236479 | 21 | 8.9 × 10−23 | 0.08729 | 0.7827 | 0.003 |
| rs1975920 | 12 | 1 × 10−10 | 0.448 | 0.5081 | 0.55 |
| rs1455311 | 4 | 1.3 × 10−32 | 1 | 0.2184 | 3.5 × 10−15 |
| rs1810636 | 20 | 3.4 × 10−17 | 1 | 0.4524 | 1.5 × 10−5 |
| rs1447826 | 3 | 1.1 × 10−16 | 1 | 0.2049 | 0.0014 |
In the third column, all additional controls (control:case ratio = 20:1) were used. Differential missingness was measured by a test for differences in the missing data frequency between the two groups (p value). The p value for the PanScan analysis is obtained from published data [11, 12]. The last column compared MSKCC controls with additional controls, correcting for population structure. Chr. = Chromosome.
Effect of Data Source on Inflation Factor
We next analyzed how test statistic inflation is influenced by the number and choice of sets of additional controls. We used the genomic control parameter λ as an estimate of the test statistic inflation [18]. We measured λ in both the original case-control dataset (no additional controls) and with the addition of various additional controls from dbGaP. We observe that λ is near 1 when no additional controls are used (table 3), indicative of no test statistic inflation. As the control:case ratio is increased by adding data from different sources, λ increases, suggesting the existence of population stratification and/or other technical artifacts. In this analysis, λ is maximal at 1.81 when data from all 6 different studies are added for a control:case ratio of 20:1 (table 3). When all significant principal components from PCA were used to correct for population stratification, λ reduces to nearly 1 (range 1.01–1.03; table 3). Thus, as expected from our quantile-quantile plot analysis, PCA-based correction can properly account for the population stratification that results when using additional controls.
Table 3.
Genomic inflation factor λ for analyses with various control datasets
| Control:case ratio | Controls used | Controls n | Significant principal components | λ | |
|---|---|---|---|---|---|
| without PCA correction | with PCA correction | ||||
| 1:1 | MSKCC pancreatic cancer study controls | 202 | 3 | 1.009 | 1.005 |
| 5:1 | SAGE | 1,488 | 5 | 1.50 | 1.014 |
| MSKCC pancreatic cancer study controls | |||||
| 5:1 | CGEMS breast cancer | 1,344 | 6 | 1.52 | 1.018 |
| MSKCC pancreatic cancer study controls | |||||
| 5:1 | CGEMS prostate cancer | 1,350 | 5 | 1.64 | 1.019 |
| MSKCC pancreatic cancer study controls | |||||
| 5:1 | CIDR PD | 1,276 | 5 | 1.53 | 1.008 |
| MSKCC pancreatic cancer study controls | |||||
| 10:1 | SAGE | 2,522 | 7 | 1.71 | 1.015 |
| A genome-wide scan of lung cancer and smoking | |||||
| SIALS | |||||
| MSKCC pancreatic cancer study controls | |||||
| 20:1 | SAGE | 5,628 | 20 | 1.81 | 1.03 |
| A genome-wide scan of lung cancer and smoking | |||||
| CIDR PD | |||||
| SIALS | |||||
| CGEMS breast cancer | |||||
| CGEMS prostate cancer | |||||
| MSKCC pancreatic cancer study controls | |||||
Performance of Known Pancreatic Cancer-Associated SNPs
We next turned to the question of whether the use of additional controls in GWAS will enable new discoveries. To investigate this question, we asked whether we would have been able to discover the 4 recently reported pancreatic cancer susceptibility SNPs [11,12] in our data combined with additional controls. We asked what rank and p value are observed for each of these 4 SNPs both in our original cohort and as we add more additional controls. Theoretically, the power to detect each of these SNPs doubles as the control:case ratio increases from 1:1 to 20:1 (table 4). We found that rank and p value of the 4 pancreatic cancer-associated SNPs improved after adding additional controls in a manner that appears to correlate with the computed power. There is a two-fold increase in power for each of the 4 SNPs when the control:case ratio is increased from 1:1 to 20:1. SNP rs9543325 has the highest increase in power and largest improvement in rank and p value. There is some fluctuation in rank and p value for all 4 SNPs when we compare control:case ratios of 10:1 and 20:1. We assume this is due to sampling variability rather than a difference in power as power plateaus out beyond a 10:1 control:case ratio. These results demonstrate that using additional controls in GWAS can help bring true positive hits towards the top of the list, though in this case none of the true positives reached genome-wide significance. These powers should be compared to the power of the original PanScan study, which had 99% power to detect these 4 SNPs at α = 0.05, and reasonable power at α = 10−7, suggesting that our inability to find these true positives at genome-wide significance was to be expected.
Table 4.
Rank and p value of the 4 pancreatic cancer-associated SNPs from analyses with varying numbers of additional controls
| SNP/odds ratio/minor allele frequency | Control:case ratio |
||||
|---|---|---|---|---|---|
| 1:1 | 5:1 | 10:1 | 20:1 | ||
| rs505922/ | rank | 105,668 | 6,769 | 5,302 | 216 |
| 1.2/ | p value | 0.393 | 0.02 | 0.01 | 0.0007 |
| 0.358 | power | 0.20 | 0.33 | 0.349 | 0.364 |
| rs9543325/ | rank | 477 | 21 | 72 | 52 |
| 1.26/ | p value | 0.0019 | 8.2 × 10−5 | 2.5 × 10−4 | 1.6 × 10−4 |
| 0.317 | power | 0.29 | 0.48 | 0.50 | 0.53 |
| rs3790844/ | rank | 102,024 | 7,645 | 1,977 | 1,357 |
| 0.77/ | p value | 0.38 | 0.02 | 0.007 | 0.004 |
| 0.21 | power | 0.265 | 0.49 | 0.51 | 0.53 |
| rs401681/ | rank | 265,649 | 239,819 | 152,561 | 157,875 |
| 1.19/ | p value | 0.99 | 0.91 | 0.57 | 0.58 |
| 0.434 | power | 0.198 | 0.313 | 0.32 | 0.347 |
Correction for population stratification is performed in all analyses. Analytical power is computed assuming an additive model with α = 0.05.
We also asked if, for a given number of additional controls, the choice of dataset(s) from which the additional controls are taken influences our ability to detect association with these 4 SNPs. Using additional controls from 4 different studies of approximately equal size, we asked what rank and p value are observed for each of the 4 known pancreatic cancer risk SNPs. We observed variability in both the rank and p value for each of these 4 SNPs depending on the choice of control samples. As no control group is consistently the best for all 4 SNPs, we attribute this variability to sampling variation rather than intrinsic factors in any of the control groups (table 5).
Table 5.
Effect of choice of control group on association statistics for 4 known pancreatic cancer risk SNPs
| SNP/odds ratio/minor allele frequency | Control datasets |
||||
|---|---|---|---|---|---|
| SAGE | CGEMS prostate cancer | CGEMS breast cancer | CIDR PD and SIALS | ||
| Controls, n: | 1,487 | 1,350 | 1,344 | 1,065 | |
| rs505922/ | rank | 6,769 | 2,866 | 1,131 | 481 |
| 1.2/ | p value | 0.02 | 0.01 | 0.004 | 0.0018 |
| 0.358 | power | 0.333 | 0.328 | 0.32 | 0.315 |
| rs9543325/ | rank | 21 | 101 | 133 | 445 |
| 1.26/ | p value | 8.2 × 10−5 | 0.0004 | 0.0004 | 0.001 |
| 0.317 | power | 0.483 | 0.477 | 0.476 | 0.459 |
| rs3790844/ | rank | 7,645 | 84,087 | 20,488 | 92,396 |
| 0.77/ | p value | 0.02 | 0.31 | 0.075 | 0.34 |
| 0.21 | power | 0.49 | 0.491 | 0.491 | 0.476 |
| rs401681/ | rank | 239,819 | 244,531 | 77,059 | 173,589 |
| 1.19/ | p value | 0.91 | 0.94 | 0.28 | 0.64 |
| 0.434 | power | 0.313 | 0.308 | 0.308 | 0.297 |
Analytical power is computed assuming an additive model with α = 0.05.
Number of Significant Principal Components
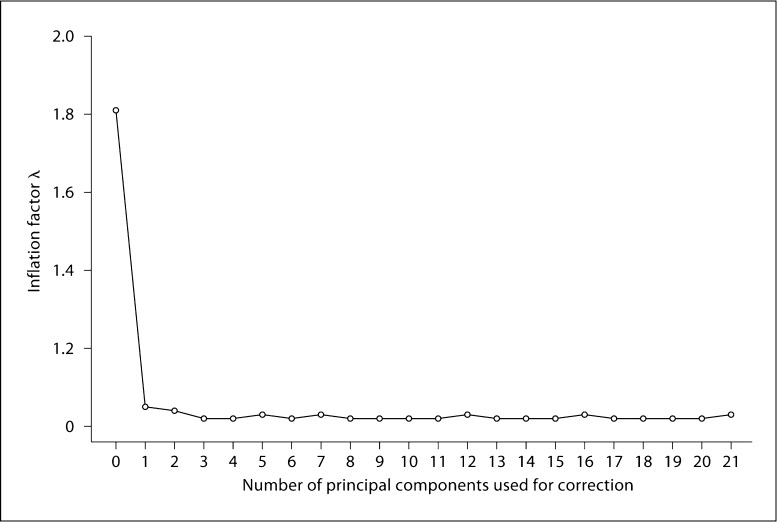
One choice that must be made is how many principal components are included as covariates in the model. If one simply asks which principal components are significant using Tracy-Widom statistics [9], the number of covariates to use increases as additional sources of control individuals are added (table 3). For instance, in our example with a 20:1 control:case ratio there are 21 significant principal components to include. To ask whether these many covariates are necessary, we varied the number of top principal components used as covariates and measured test statistic inflation using the genomic control parameter λ (fig. 4). We find that λ decreases drastically with the first principal component and decreases somewhat more as the next 3 are added (fig. 4). While this suggests that all 21 principal components are not needed as covariates, it does not tell us whether including extra principal components as covariates decreases the power of the test. When we examine the 4 known pancreatic risk SNPs, we find that the ranks of the 4 SNPs do not change dramatically as more principal components are added after the first few (table 6). This suggests that while only 4 principal components may be needed in this situation to correct for population stratification, the risk of decreased power through adding additional principal component covariates is minimal. To address the question of what these 21 significant principal components may represent, we first asked if any of the principal components appear to associate with membership in specific studies. Visual inspection of plots of 2 principal components at a time, with studies color-coded, does not reveal any striking correlation between principal components and study membership. Regression analysis revealed that only the top 4 principal components, for which we recommend adjusting in the GWAS, are associated with study membership (data not shown). We next repeated the PCA with a more stringent r2 threshold for LD-based SNP pruning. When the r2 threshold for pruning is lowered from 0.1 to 0.05, the number of significant eigenvectors (Tracy-Widom p < 0.05) drops from 21 to 11.
Fig. 4.
Genomic inflation factor λ versus number of principal components used for correction. There are 21 principal components that are significant using Tracy-Widom test statistics when the control:case ratio is 20: 1.
Table 6.
Rank of the known pancreatic cancer-associated SNPs after correcting for the specified number of principal components (PC)
| Number of PCs for correction | rs9543325 | rs505922 | rs3790844 | rs401681 |
|---|---|---|---|---|
| 0 | 585 | 103,084 | 103,905 | 264,098 |
| 1 | 197 | 1,795 | 2,692 | 133,722 |
| 2 | 162 | 821 | 2,859 | 140,725 |
| 4 | 76 | 302 | 1,382 | 162,016 |
| 6 | 77 | 294 | 1,382 | 161,914 |
| 10 | 65 | 290 | 1,676 | 156,465 |
| 16 | 56 | 220 | 1,651 | 153,981 |
| 21 | 52 | 216 | 1,357 | 157,875 |
In total, 267,785 markers were analyzed.
Therefore, we conclude that using additional controls can increase the power of relatively small GWAS after strict QC steps and properly correcting population stratification.
Discussion
In this article, we have performed a practical evaluation of using additional controls from publicly available databases to conduct GWAS. This approach can result in improved power by increasing the number of controls without any extra cost of genotyping. By using data from our small pancreatic cancer GWAS, we evaluated this approach through comparison with results from the recently published PanScan GWAS [11,12]. When we analyzed our pancreatic cancer data with additional controls and properly accounted for population stratification, we found improvement in the rank and p value for all 4 known pancreatic cancer SNPs relative to an analysis of our case-control dataset alone. However, while 3 of the 4 SNPs were significantly associated with pancreatic cancer in our analysis with p < 0.05, these results cannot be considered an independent replication of the PanScan results, as a large subset of our cases and controls were included in PanScan.
While statistical theory argues that the power of a GWAS increases as the control:case ratio increases for a fixed number of cases, no clear guidelines exist to determine the maximum number of added controls after which there is little or no added benefit. Using analytical power calculations, we show that power increases rapidly as the control:case ratio moves from 1:1 to 10:1 and then plateaus out. Through our analysis of the pancreatic cancer data, we see improved power with a 20:1 control:case ratio relative to a 10:1 ratio. Based on these data, it appears that when designing a GWAS using additional controls, obtaining at least 10 controls for every case is extremely important, though additional benefit could be had by obtaining up to 20 controls for every case.
It is apparent that the QC steps of GWAS in the context of additional controls obtained from public data sources are different from those of typical case-control GWAS. Recently, Pluzhnikov et al. [19] reported a method to estimate genotyping errors from raw signal intensity data when using GWAS control samples from existing public databases. This method can only be used when the raw signal intensity data is available, which is not always the case. As an alternative approach to deal with errors introduced from genotype data with different origins, we propose including some controls to be genotyped along with the cases. By removing SNPs that show different frequencies between our controls and the additional controls, we effectively reduced the false-positive findings. We consider this step crucial in controlling false positives, especially when raw intensity data is not available.
Beside genotyping errors caused due to different data sources, our results illustrate that population stratification is also a potential problem with additional controls. If there is different underlying genetic ancestry in the populations from which cases and controls are taken, an inflated type I error will result. This is clearly observed in our example, where disproportionately more self-reported white cases from the New York metropolitan area are of southern European or Ashkenazi Jewish ancestry than self-reported white controls from other parts of the United States. This stratification results in artificially high test statistics if we combine data without correcting for population structure. Using simulation studies, it has been demonstrated that correction for population stratification can be achieved successfully by using various methods like multidimensional scaling or PCA [9,10,20,21,22]. We used the popular PCA software EIGENSTRAT to identify principal components in our data and then corrected for these components in logistic regression. Adjusting for the significant principal components substantially reduces the genomic inflation factor in every additional controls dataset we tested.
The proper number of principal components to consider in correcting for population substructure remains unclear. Notably, the number of significant principal components computed using the Tracy-Widom test statistic [9] increased when we increased the control:case ratio by adding data from different sources. With a control:case ratio of 20:1, 21 significant principal components were identified. We explored the effect of including different numbers of principal components in our analysis and found that after 4 principal components are included, no additional benefit is gained by including more principal components. Intriguingly, in a GWAS of Alzheimer's disease, Harold et al. [23] similarly found no additional improvement in λ after accounting for 4 principal components. As we found a reduced number of significant principal components upon lowering the r2 threshold to obtain independent markers for the PCA calculation, we hypothesize that many of the 21 principal components may be picking up local LD patterns in the data rather than population substructure. Therefore, including these additional principal components is not necessary for the analysis.
We acknowledge that the additional controls approach is limited by choice of genotyping platform, as it requires the same SNP to be genotyped in all samples. To maximize overlap between SNPs, we restricted our analysis to projects that used Illumina chips for genotyping and further restricted analysis to only SNPs in common among all studies. Alternatively, imputation techniques have been used to integrate genotype data from different platforms, though how such an approach will perform when different platforms are used to genotype the cases and controls remains unclear.
Besides these technical issues, there are conceptual limitations to this approach. Using additional controls works best in consideration of genetic effects alone. While in theory gene-environment interaction can be considered if appropriate environmental data is present in dbGaP, in practice this information is often found in only some datasets and details of the collection of this data likely vary between studies.
Based on these results, it appears that using this approach with only several hundred cases to study a disease typical of the common diseases studied with GWAS will result in the true disease loci rising to the top of the list of SNPs but not reaching genome-wide significance. Therefore, we propose that the use of additional controls will work best in the context of a large case-control study. In this context, a subset of cases and controls would be selected for genome-wide genotyping. These data would be combined with additional controls. The top 103−104 SNPs from this analysis would then be genotyped in the full case-control study both to increase power and remove false positives. In other words, additional controls may work best when included in stage 1 of a two-stage GWAS design [24,25,26,27]. Standard downstream analyses including independent replication and fine mapping would then be conducted on SNPs that pass the second stage. Thus, the use of additional controls is a promising method to increase sample sizes and thus the power of the study without additional cost.
Supplementary Material
Quantile-quantile (Q-Q) plot for each control group versus all of the other control groups combined. Base 10 logarithms are used on each axis. The figures extend over 4 pages.
Principal component analysis plot comparing pairs of eigenvectors for the top 20 principal components. Each individual is color-coded by sample source, as indicated in the Figures. All figures use the same coding.
Allele intensity scatter plot for rs1975920. Normalized probe intensity, as rederived from the log R ratio and B allele frequency, are shown for cases and controls genotyped using the Illumina CNV370-Duo and Illumina CNV370-Quad arrays.
Supplementary Acknowledgements
Acknowledgements
We are grateful to Heriberto Moran for technical assistance, Jason Willis for extracting the allele intensity data, and Jason Willis and Xing Xu for helpful comments on the manuscript. This work was supported by the Geoffrey Beene Cancer Research Center at MSKCC; the Emerald Foundation, and NIH R03 CA141524 (to R.J.K.). We are extremely grateful to all of the investigators and funding agencies responsible for the data deposited in dbGaP that were used in the study; detailed acknowledgements can be found in the online supplementary Acknowledgements.
References
- 1.WTCCC Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature. 2007;447:661–678. doi: 10.1038/nature05911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Crowther-Swanepoel D, Qureshi M, Dyer MJ, Matutes E, Dearden C, Catovsky D, Houlston RS. Genetic variation in cxcr4 and risk of chronic lymphocytic leukemia. Blood. 2009;114:4843–4846. doi: 10.1182/blood-2009-07-235184. [DOI] [PubMed] [Google Scholar]
- 3.Shete S, Hosking FJ, Robertson LB, Dobbins SE, Sanson M, Malmer B, Simon M, Marie Y, Boisselier B, Delattre JY, Hoang-Xuan K, El Hallani S, Idbaih A, Zelenika D, Andersson U, Henriksson R, Bergenheim AT, Feychting M, Lonn S, Ahlbom A, Schramm J, Linnebank M, Hemminki K, Kumar R, Hepworth SJ, Price A, Armstrong G, Liu Y, Gu X, Yu R, Lau C, Schoemaker M, Muir K, Swerdlow A, Lathrop M, Bondy M, Houlston RS. Genome-wide association study identifies five susceptibility loci for glioma. Nat Genet. 2009;41:899–904. doi: 10.1038/ng.407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Di Bernardo MC, Crowther-Swanepoel D, Broderick P, Webb E, Sellick G, Wild R, Sullivan K, Vijayakrishnan J, Wang Y, Pittman AM, Sunter NJ, Hall AG, Dyer MJ, Matutes E, Dearden C, Mainou-Fowler T, Jackson GH, Summerfield G, Harris RJ, Pettitt AR, Hillmen P, Allsup DJ, Bailey JR, Pratt G, Pepper C, Fegan C, Allan JM, Catovsky D, Houlston RS. A genome-wide association study identifies six susceptibility loci for chronic lymphocytic leukemia. Nat Genet. 2008;40:1204–1210. doi: 10.1038/ng.219. [DOI] [PubMed] [Google Scholar]
- 5.Kilpivaara O, Mukherjee S, Schram AM, Wadleigh M, Mullally A, Ebert BL, Bass A, Marubayashi S, Heguy A, Garcia-Manero G, Kantarjian H, Offit K, Stone RM, Gilliland DG, Klein RJ, Levine RL. A germline jak2 snp is associated with predisposition to the development of jak2(v617f)-positive myeloproliferative neoplasms. Nat Genet. 2009;41:455–459. doi: 10.1038/ng.342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zhuang JJ, Zondervan K, Nyberg F, Harbron C, Jawaid A, Cardon LR, Barratt BJ, Morris AP. Optimizing the power of genome-wide association studies by using publicly available reference samples to expand the control group. Genet Epidemiol. 2010;34:319–326. doi: 10.1002/gepi.20482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Price AL, Butler J, Patterson N, Capelli C, Pascali VL, Scarnicci F, Ruiz-Linares A, Groop L, Saetta AA, Korkolopoulou P, Seligsohn U, Waliszewska A, Schirmer C, Ardlie K, Ramos A, Nemesh J, Arbeitman L, Goldstein DB, Reich D, Hirschhorn JN. Discerning the ancestry of European Americans in genetic association studies. PLoS Genet. 2008;4:e236. doi: 10.1371/journal.pgen.0030236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tian C, Kosoy R, Nassir R, Lee A, Villoslada P, Klareskog L, Hammarström L, Garchon HJ, Pulver AE, Ransom M, Gregersen PK, Seldin MF. European population genetic substructure: further definition of ancestry informative markers for distinguishing among diverse European ethnic groups. Mol Med. 2009;15:371–383. doi: 10.2119/molmed.2009.00094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- 10.Li Q, Yu K. Improved correction for population stratification in genome-wide association studies by identifying hidden population structures. Genet Epidemiol. 2008;32:215–226. doi: 10.1002/gepi.20296. [DOI] [PubMed] [Google Scholar]
- 11.Amundadottir L, Kraft P, Stolzenberg-Solomon RZ, Fuchs CS, Petersen GM, Arslan AA, Bueno-de-Mesquita HB, Gross M, Helzlsouer K, Jacobs EJ, LaCroix A, Zheng W, Albanes D, Bamlet W, Berg CD, Berrino F, Bingham S, Buring JE, Bracci PM, Canzian F, Clavel-Chapelon F, Clipp S, Cotterchio M, de Andrade M, Duell EJ, Fox JW, Jr, Gallinger S, Gaziano JM, Giovannucci EL, Goggins M, Gonzalez CA, Hallmans G, Hankinson SE, Hassan M, Holly EA, Hunter DJ, Hutchinson A, Jackson R, Jacobs KB, Jenab M, Kaaks R, Klein AP, Kooperberg C, Kurtz RC, Li D, Lynch SM, Mandelson M, McWilliams RR, Mendelsohn JB, Michaud DS, Olson SH, Overvad K, Patel AV, Peeters PH, Rajkovic A, Riboli E, Risch HA, Shu XO, Thomas G, Tobias GS, Trichopoulos D, Van Den Eeden SK, Virtamo J, Wactawski-Wende J, Wolpin BM, Yu H, Yu K, Zeleniuch-Jacquotte A, Chanock SJ, Hartge P, Hoover RN. Genome-wide association study identifies variants in the ABO locus associated with susceptibility to pancreatic cancer. Nat Genet. 2009;41:986–990. doi: 10.1038/ng.429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Petersen GM, Amundadottir L, Fuchs CS, Kraft P, Stolzenberg-Solomon RZ, Jacobs KB, Arslan AA, Bueno-de-Mesquita HB, Gallinger S, Gross M, Helzlsouer K, Holly EA, Jacobs EJ, Klein AP, LaCroix A, Li D, Mandelson MT, Olson SH, Risch HA, Zheng W, Albanes D, Bamlet WR, Berg CD, Boutron-Ruault MC, Buring JE, Bracci PM, Canzian F, Clipp S, Cotterchio M, de Andrade M, Duell EJ, Gaziano JM, Giovannucci EL, Goggins M, Hallmans G, Hankinson SE, Hassan M, Howard B, Hunter DJ, Hutchinson A, Jenab M, Kaaks R, Kooperberg C, Krogh V, Kurtz RC, Lynch SM, McWilliams RR, Mendelsohn JB, Michaud DS, Parikh H, Patel AV, Peeters PH, Rajkovic A, Riboli E, Rodriguez L, Seminara D, Shu XO, Thomas G, Tjonneland A, Tobias GS, Trichopoulos D, Van Den Eeden SK, Virtamo J, Wactawski-Wende J, Wang Z, Wolpin BM, Yu H, Yu K, Zeleniuch-Jacquotte A, Fraumeni JF, Jr, Hoover RN, Hartge P, Chanock SJ. A genome-wide association study identifies pancreatic cancer susceptibility loci on chromosomes 13q22.1, 1q32.1 and 5p15.33. Nat Genet. 2010;42:224–228. doi: 10.1038/ng.522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Klein RJ. Power analysis for genome-wide association studies. BMC Genet. 2007;8:58. doi: 10.1186/1471-2156-8-58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MA, Bender D, Maller J, Sklar P, de Bakker PI, Daly MJ, Sham PC. Plink: A tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007;81:559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tian C, Plenge RM, Ransom M, Lee A, Villoslada P, Selmi C, Klareskog L, Pulver AE, Qi L, Gregersen PK, Seldin MF. Analysis and application of European genetic substructure using 300 K SNP information. PLoS Genet. 2008;4:e4. doi: 10.1371/journal.pgen.0040004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Novembre J, Johnson T, Bryc K, Kutalik Z, Boyko AR, Auton A, Indap A, King KS, Bergmann S, Nelson MR, Stephens M, Bustamante CD. Genes mirror geography within Europe. Nature. 2008;456:98–101. doi: 10.1038/nature07331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Paschou P, Drineas P, Lewis J, Nievergelt CM, Nickerson DA, Smith JD, Ridker PM, Chasman DI, Krauss RM, Ziv E. Tracing sub-structure in the European American population with PCA-informative markers. PLoS Genet. 2008;4:e1000114. doi: 10.1371/journal.pgen.1000114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Devlin B, Roeder K. Genomic control for association studies. Biometrics. 1999;55:997–1004. doi: 10.1111/j.0006-341x.1999.00997.x. [DOI] [PubMed] [Google Scholar]
- 19.Pluzhnikov A, Below JE, Konkashbaev A, Tikhomirov A, Kistner-Griffin E, Roe CA, Nicolae DL, Cox NJ. Spoiling the whole bunch: quality control aimed at preserving the integrity of high-throughput genotyping. Am J Hum Genet. 2010;87:123–128. doi: 10.1016/j.ajhg.2010.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kimmel G, Jordan MI, Halperin E, Shamir R, Karp RM. A randomization test for controlling population stratification in whole-genome association studies. Am J Hum Genet. 2007;81:895–905. doi: 10.1086/521372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Epstein MP, Allen AS, Satten GA. A simple and improved correction for population stratification in case-control studies. Am J Hum Genet. 2007;80:921–930. doi: 10.1086/516842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lee S, Sullivan PF, Zou F, Wright FA. Comment on a simple and improved correction for population stratification. Am J Hum Genet. 2008;82:524–526. doi: 10.1016/j.ajhg.2007.10.014. author reply 526–528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Harold D, Abraham R, Hollingworth P, Sims R, Gerrish A, Hamshere ML, Pahwa JS, Moskvina V, Dowzell K, Williams A, Jones N, Thomas C, Stretton A, Morgan AR, Lovestone S, Powell J, Proitsi P, Lupton MK, Brayne C, Rubinsztein DC, Gill M, Lawlor B, Lynch A, Morgan K, Brown KS, Passmore PA, Craig D, McGuinness B, Todd S, Holmes C, Mann D, Smith AD, Love S, Kehoe PG, Hardy J, Mead S, Fox N, Rossor M, Collinge J, Maier W, Jessen F, Schurmann B, van den Bussche H, Heuser I, Kornhuber J, Wiltfang J, Dichgans M, Frolich L, Hampel H, Hull M, Rujescu D, Goate AM, Kauwe JS, Cruchaga C, Nowotny P, Morris JC, Mayo K, Sleegers K, Bettens K, Engelborghs S, De Deyn PP, Van Broeckhoven C, Livingston G, Bass NJ, Gurling H, McQuillin A, Gwilliam R, Deloukas P, Al-Chalabi A, Shaw CE, Tsolaki M, Singleton AB, Guerreiro R, Muhleisen TW, Nothen MM, Moebus S, Jockel KH, Klopp N, Wichmann HE, Carrasquillo MM, Pankratz VS, Younkin SG, Holmans PA, O'Donovan M, Owen MJ, Williams J. Genome-wide association study identifies variants at CLU and PICALM associated with Alzheimer's disease. Nat Genet. 2009;41:1088–1093. doi: 10.1038/ng.440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wang H, Thomas DC, Pe'er I, Stram DO. Optimal two-stage genotyping designs for genome-wide association scans. Genet Epidemiol. 2006;30:356–368. doi: 10.1002/gepi.20150. [DOI] [PubMed] [Google Scholar]
- 25.Ohashi J, Clark AG. Application of the stepwise focusing method to optimize the cost-effectiveness of genome-wide association studies with limited research budgets for genotyping and phenotyping. Ann Hum Genet. 2005;69:323–328. doi: 10.1046/j.1529-8817.2005.00157.x. [DOI] [PubMed] [Google Scholar]
- 26.Skol AD, Scott LJ, Abecasis GR, Boehnke M. Optimal designs for two-stage genome-wide association studies. Genet Epidemiol. 2007;31:776–788. doi: 10.1002/gepi.20240. [DOI] [PubMed] [Google Scholar]
- 27.Satagopan JM, Elston RC. Optimal two-stage genotyping in population-based association studies. Genet Epidemiol. 2003;25:149–157. doi: 10.1002/gepi.10260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hunter DJ, Kraft P, Jacobs KB, Cox DG, Yeager M, Hankinson SE, Wacholder S, Wang Z, Welch R, Hutchinson A, Wang J, Yu K, Chatterjee N, Orr N, Willett WC, Colditz GA, Ziegler RG, Berg CD, Buys SS, McCarty CA, Feigelson HS, Calle EE, Thun MJ, Hayes RB, Tucker M, Gerhard DS, Fraumeni JF, Jr, Hoover RN, Thomas G, Chanock SJ. A genome-wide association study identifies alleles in FGFR2 associated with risk of sporadic postmenopausal breast cancer. Nat Genet. 2007;39:870–874. doi: 10.1038/ng2075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Yeager M, Orr N, Hayes RB, Jacobs KB, Kraft P, Wacholder S, Minichiello MJ, Fearnhead P, Yu K, Chatterjee N, Wang Z, Welch R, Staats BJ, Calle EE, Feigelson HS, Thun MJ, Rodriguez C, Albanes D, Virtamo J, Weinstein S, Schumacher FR, Giovannucci E, Willett WC, Cancel-Tassin G, Cussenot O, Valeri A, Andriole GL, Gelmann EP, Tucker M, Gerhard DS, Fraumeni JF, Jr, Hoover R, Hunter DJ, Chanock SJ, Thomas G. Genome-wide association study of prostate cancer identifies a second risk locus at 8q24. Nat Genet. 2007;39:645–649. doi: 10.1038/ng2022. [DOI] [PubMed] [Google Scholar]
- 30.Landi MT, Chatterjee N, Yu K, Goldin LR, Goldstein AM, Rotunno M, Mirabello L, Jacobs K, Wheeler W, Yeager M, Bergen AW, Li Q, Consonni D, Pesatori AC, Wacholder S, Thun M, Diver R, Oken M, Virtamo J, Albanes D, Wang Z, Burdette L, Doheny KF, Pugh EW, Laurie C, Brennan P, Hung R, Gaborieau V, McKay JD, Lathrop M, McLaughlin J, Wang Y, Tsao MS, Spitz MR, Wang Y, Krokan H, Vatten L, Skorpen F, Arnesen E, Benhamou S, Bouchard C, Metsapalu A, Vooder T, Nelis M, Valk K, Field JK, Chen C, Goodman G, Sulem P, Thorleifsson G, Rafnar T, Eisen T, Sauter W, Rosenberger A, Bickeboller H, Risch A, Chang-Claude J, Wichmann HE, Stefansson K, Houlston R, Amos CI, Fraumeni JF, Jr, Savage SA, Bertazzi PA, Tucker MA, Chanock S, Caporaso NE. A genome-wide association study of lung cancer identifies a region of chromosome 5p15 associated with risk for adenocarcinoma. Am J Hum Genet. 2009;85:679–691. doi: 10.1016/j.ajhg.2009.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Quantile-quantile (Q-Q) plot for each control group versus all of the other control groups combined. Base 10 logarithms are used on each axis. The figures extend over 4 pages.
Principal component analysis plot comparing pairs of eigenvectors for the top 20 principal components. Each individual is color-coded by sample source, as indicated in the Figures. All figures use the same coding.
Allele intensity scatter plot for rs1975920. Normalized probe intensity, as rederived from the log R ratio and B allele frequency, are shown for cases and controls genotyped using the Illumina CNV370-Duo and Illumina CNV370-Quad arrays.
Supplementary Acknowledgements