Summary
HIV dynamics studies, based on differential equations, have significantly improved the knowledge on HIV infection. While first studies used simplified short-term dynamic models, recent works considered more complex long-term models combined with a global analysis of whole patients data based on nonlinear mixed models, increasing the accuracy of the HIV dynamic analysis. However statistical issues remain, given the complexity of the problem. We proposed to use the SAEM (Stochastic Approximation EM) algorithm, a powerful maximum likelihood estimation algorithm, to analyze simultaneously the HIV viral load decrease and the CD4 increase in patients using a long-term HIV dynamic system. We applied the proposed methodology to the prospective COPHAR2-ANRS 111 trial. Very satisfactory results were obtained with a model with latent CD4 cells defined with five differential equations. One parameter was fixed, the ten remaining parameters (eight with between patient variability) of this model were well estimated. We showed that the efficacy of nelfinavir was reduced compared to indinavir and lopinavir.
Keywords: HIV dynamics, Non linear mixed effects models, SAEM algorithm, Model selection
Keywords: Algorithms; Anti-HIV Agents; therapeutic use; Computer Simulation; HIV Infections; drug therapy; epidemiology; Humans; Likelihood Functions; Models, Biological; Models, Statistical; Prevalence; Treatment Outcome
1. Introduction
Understanding variability in response to antiretroviral treatment in HIV patients is an important challenge. HIV dynamic models describe the viral load decrease and the CD4 cells increase under treatment by modeling the interaction between several types of CD4 cells and virions (Perelson et al., 1996; Perelson and Nelson, 1997; Wu and Ding, 1999; Nowak and May, 2000; Rong and Perelson, 2009). They are defined as nonlinear differential systems and have generally no closed-form solutions. As available data are measurements of total number of the CD4 and the total number of virions, these differential systems are partially observed, complicating the parameter estimation. Nonlinear mixed effect models (NLMEMs) are appropriate to estimate model parameters and their inter-patient variability. The first modeling of viral load dynamic, using standard nonlinear regression or mixed models, considered a short time period and assumed non-infected CD4 cells to be constant (Perelson et al., 1996; Wu et al., 1998; Ding and Wu, 2001). Another simplified approach assumed inhibition of any new infection by initiated therapy. Under that unrealistic assumption, the system can be solved explicitly (Wu et al., 1998; Putter et al., 2002). Putter et al. (2002) proposed the first simultaneous estimation of the viral load and CD4 dynamics based on a differential system under this assumption, but had to focus only on the first two weeks of the dynamic after initiation of an anti-retroviral treatment. These two assumptions are unsatisfactory when studying long-term response to anti-retroviral treatment for which the use of complete models expressed as ordinary differential equations (ODEs) is mandatory.
Estimation of NLMEMs is complex because the likelihood has no closed form, even for simple models. Bayesian estimation methods based on Markov Chain Monte Carlo (MCMC) algorithms and informative priors have first been proposed for complex ODE HIV models and NLMEMs (Putter et al., 2002; Wu et al., 2005; Huang et al., 2006). The choice of informative prior distributions can be and issue. Furthermore, Bayesian algorithms can be very slow to converge, especially in this complex context. Wu et al. (2005) adjusted only viral load with a dynamic system describing the long-term HIV dynamics and considering drug potency, drug exposure/adherence and drug resistance during chronic treatment. However, the authors used a simplified model which does not consider separately the compartments of HIV-producing infected cells and the latent cells and does not decompose the virus compartment into infectious and non-infectious virions.
For maximum likelihood estimation in NLMEMs, likelihood approximations such as linearization (Pinheiro and Bates, 1995) or Laplace approximation (Wolfinger, 1993) have been proposed, leading to inconsistent estimates (Ding and Wu, 2001). Guedj et al. (2007a) proposed algorithms based on Gaussian quadrature but these algorithms are cumbersome and were not applied to problems with more than three random effects. Wu and Zhang (2002) proposed a semi-parametric approach. Other new algorithms are stochastic EM algorithms as Monte Carlo EM (Wu, 2004). Among them, the Stochastic Approximation EM algorithm (SAEM) has convergence results (Delyon et al., 1999; Kuhn and Lavielle, 2005), even for ODE models (Donnet and Samson, 2007). It is implemented in the MONOLIX software and has been mainly applied for the analysis of pharmacokinetics models (Lavielle and Mentré, 2007). Another complexity of viral load analysis is left censoring which occurs when viral load are below a limit of quantification (LOQ). The proportion of subjects with viral load below LOQ has increased with the development of highly active anti-retroviral treatment. Although it is known that when ignored, this censoring may induce biased parameter estimates (Samson et al., 2006; Thiébaut et al., 2006), several authors did not take into account this problem (Ding and Wu, 2001; Wu et al., 2005). Conversely, Hughes (1999); Fitzgerald et al. (2002); Thiebaut et al. (2005); Guedj et al. (2007a) proposed different approaches to handle accurately the censored viral load data. Samson et al. (2006) extended the SAEM algorithm to perform maximum likelihood estimation for left-censored data.
The first objective of this work was to estimate parameter of HIV dynamic models with the convergent SAEM algorithm. A second objective was to propose and apply statistical approaches for studying model selection in this context. We applied this approach to data obtained in patients of the clinical trial COPHAR2 - ANRS 111 (Duval et al., 2009) initiating an antiviral therapy with two nucleoside analogs (RTI) and one protease inhibitor (PI). We analyzed simultaneously the HIV viral load decrease and the CD4 increase based on a long-term HIV dynamic system. We considered three dynamic models and compare them with respect to their ability to represent HIV-infected patients after initiation of reverse transcriptase inverse (RTI) and protease inhibitor (PI) drugs therapy.
This article is organized as follows. Section 2 presents three mathematical models for long-term HIV dynamics. In Section 3, we discuss nonlinear mixed effects models and estimation with the SAEM algorithm, model selection, model identifiability and covariate testing. We, then, provide the results obtained in the COPHAR II-ANRS 134 clinical trial using MONOLIX in Section 4. Section 5 concludes this article with some discussion.
2. Mathematical models for HIV dynamics after treatment initiation
Three nonlinear ordinary differential systems modeling the interaction of HIV virus with the immune system after initiation of antiviral treatment containing reverse transcriptase inhibitor (RTI) and protease inhibitor (PI) are presented.
2.1. The basic dynamic model
Let TNI, TI and VI denote the concentration of target noninfected CD4 cells, productively infected CD4 cells and infectious viruses, respectively. Following Perelson and Nelson (1997); Perelson (2002), it is assumed that CD4 cells are generated through the hematopoietic differentiation process at a constant rate λ. The target cells are infected by the virus at a rate γ per susceptible cell and virion. Noninfected CD4 cells die at a rate μNI whereas infected ones at a rate μI. Infected CD4 cells produce virus at a rate p per infected cell. The virus are cleared at a rate μV. Two additional parameters ηRTI and ηPI are introduced to model the effect of antiviral therapy containing RTI and PI. RTI prevents susceptible cells from becoming infected through inhibition of the transcription of the viral RNA into double-stranded DNA. ηRTI denotes the proportion of susceptible cells prevented to be infected and is valued between 0 and 1. A value of ηRTI = 1 corresponds to a completely effective drug. PI leads to the production of noninfectious viruses VNI which is modeled trough an additional equation. VNI are produced at a rate ηPIp where ηPI is a proportion between 0 and 1 and where ηPI = 1 corresponds to a completely effective drug. It is assumed that infectious and non infectious viruses die at the same rate μV. Under combined PI and RTI action, the system is written:
| (1) |
It is assumed that before the treatment initiation, the system has reached an equilibrium state (the steady state values are given in the Web Appendix A). The measured viral load is the total viral load V = VI +VNI and the measured CD4 cell count is the total T = TNI +TI. This basic model is called
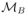 . Its parameters and their definitions are summarized in Table 1.
. Its parameters and their definitions are summarized in Table 1.
Table 1.
Parameters of each HIV dynamic model (
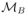 : basic model,
: basic model,
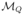 : quiescent model,
: quiescent model,
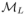 : latent model
: latent model
| Parameter | unit | description | |||
|---|---|---|---|---|---|
| λ | cells/mm3/day | Rate of production of infected CD4 cells | ★ | ★ | ★ |
| γ | Infection rate of CD4 cell per virion | ★ | ★ | ★ | |
| μNI | day−1 | Death rate of uninfected CD4 cells | ★ | ★ | ★ |
| μI | day−1 | Death rate of infected CD4 cells | ★ | ★ | |
| μQ | day−1 | Death rate of quiescent CD4 cells | ★ | ||
| μL | day−1 | Death rate for latently infected CD4 cells | ★ | ||
| μA | day−1 | Death rate for actively infected CD4 cells | ★ | ||
| μV | day−1 | Death rate of virions | ★ | ★ | ★ |
| p | Number of virions production by CD4 cell | ★ | ★ | ★ | |
| ρ | day−1 | Rate of reversion to the quiescent state | ★ | ||
| αQ | Activation rate of quiescent CDA cells | ★ | |||
| αL | Activation rate of latently infected CD4 cells | ★ | |||
| π | Proportion of infected CD4 cells that become activated | ★ | |||
| ηRTI | Efficacy of NRTI | ★ | ★ | ★ | |
| ηPI | Efficacy of PI | ★ | ★ | ★ | |
| Number of parameters | 8 | 11 | 11 | ||
2.2. The quiescent dynamic model
De Boer and Perelson (1998); Guedj et al. (2007a) proposed a more elaborated model which distinguishes quiescent CD4 cells, TQ, target (activated) noninfected cells, TNI, and infected T cells, TI. Only activated CD4 cells become infected with HIV, and quiescent cells are assumed to be resistant to infection. Quiescent CD4 cells TQ are generated through the hematopoietic differentiation process at a constant rate λ. As the CD4 cell compartment is largely maintained by self-renewal, the dynamic model allows the quiescent CD4 cells to become activated at a low constant rate αQ. Quiescent CD4 cells are assumed to die at a rate μQ, and to appear by the deactivation of activated noninfected CD4 cells at a rate ρ. The system of differential equations describing this model after treatment initiation is written as:
| (2) |
As proposed by Perelson et al. (1996), it is assumed that newly produced viruses are fully infectious before the introduction of a PI treatment and that before the treatment initiation, the system has reached an equilibrium state (see the Web Appendix A). The measured viral load is the total viral load V = VI + VNI and the measured CD4 cell count is the total T = TQ +TNI +TI. This quiescent model is called
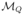 . Its parameters and their definitions are summarized in Table 1.
. Its parameters and their definitions are summarized in Table 1.
2.3. The latent dynamic model
Funk et al. 2001 considered that not all CD4 cells actively produce virus upon successful infection. Infected cell pool is split into actively and latently infected cells. Uninfected CD4 cells are infected by the virus, as previously, at a rate (1 − ηRTI)γVI. But only a proportion π of this infected cells are activated CD4 cells, TA, and a proportion (1 − π) are latently infected CD4 cells, TL. Latently infected CD4 cells die at a rate μL and become activated at a rate αL. Actively infected cells TA die at a rate μA and only these cells produce virus particles. The differential system describing this model after treatment initiation is written:
| (3) |
| (4) |
As previously, it is assumed that before treatment initiation, the system has reached an equilibrium state (see the Web Appendix A). The measured viral load is the total viral load V = VI + VNI and the measured CD4 cell count is the total T = TNI + TL + TA. This latent model is called
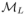 . Its parameters and their definitions are summarized in Table 1.
. Its parameters and their definitions are summarized in Table 1.
3. Statistical Methods
3.1. The nonlinear mixed effects model
Let N be the number of patients. For patient i, we measure ni viral loads at times (tij), j = 1, …, ni and mi CD4 cells at times (τij), j = 1, …, mi. Let us define vi = (vi1, …, vini) where vij is the observed log10 HIV viral load (cp/mL) for individual i at time tij, i = 1, …, N, j = 1, …, ni, and zi = (zi1, …, zimi) where zij is the the CD4 cell count (cells/mm3) for individual i at time τij, i = 1, …, N, j = 1, …, mi. The observed log10 viral load and the CD4 cell count of all patients are analyzed simultaneously using a nonlinear mixed effects model, where V and T are the total number of virus (cp/mm3) and CD4 cells (cells/mm3):
| (5) |
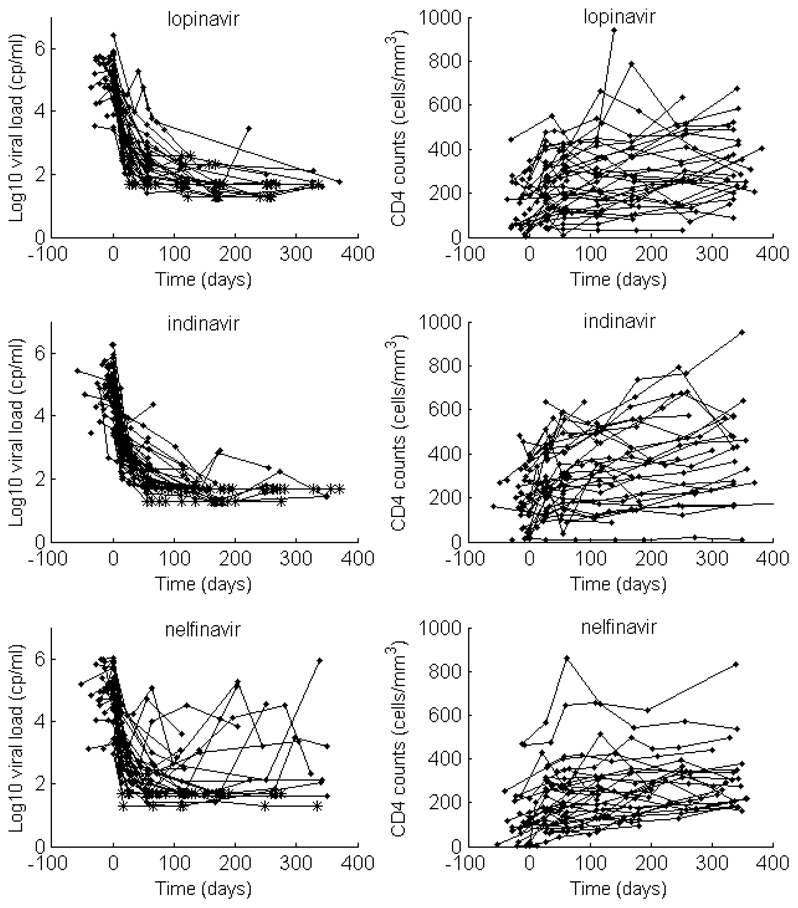
Note that V is expressed in cp/mm3 and the observed v in log10-cp/mL, hence the 1000 in equation (5). Here (eV,ij) and (eT,ij) represent the residual errors. We assume a constant error model for the log viral load and a proportional error model for the CD4 concentration. Several error models will be tested for the CD4 count. Different parametric models for V and T were previously proposed. These models are functions of individual parameters ψi, which are assumed to be independent of the residual errors (eV,i, eT,i). The parameters ψi are assumed to be some transformation h(φi) of a Gaussian random vector φi with mean μ (the vector of fixed effects) and variance-covariance Ω (the covariance matrix of the random effects). As inhibition parameters ηRTI and ηPI take their values in [0, 1], they are defined as the logistic transformation of a Gaussian random variable. For model
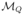 , π is defined as the logistic transformation of a Gaussian random variable. Others parameters are non-negative parameters and defined as the exponential transformation of Gaussian random variables.
, π is defined as the logistic transformation of a Gaussian random variable. Others parameters are non-negative parameters and defined as the exponential transformation of Gaussian random variables.
The observation model is complicated by the detection limit of assays. When viral load data vij is below the limit of quantification LOQ, the exact value vij is unknown and the only available information is vij ≤ LOQ. These data are classically named left-censored data. Let denote Iobs = {(i, j)|vij ≥ LOQ} and Icens = {(i, j)|vij ≤ LOQ} the index sets of respectively the uncensored and censored observations. Finally, we observe
3.2. Parameters estimation
Let be the set of unknown population parameters. Maximum likelihood estimation of θ is based on the likelihood function of the observations (vobs, z):
| (6) |
where is the likelihood of the complete data ( , zi, φi) of the i-th subject. As the random effects φi and the censored observations are unobservable and as the regression functions are nonlinear, the foregoing integral has no closed form. Therefore the maximum likelihood estimate is not available in a closed form.
We propose to use the Stochastic Approximation Estimation Maximisation (SAEM) algorithm, a stochastic version developed by Delyon et al. (1999) of the Expectation-Maximization algorithm introduced by Dempster et al. (1977). This algorithm computes the E-step of the EM algorithm through a stochastic approximation scheme. It requires a simulation of one realization of the non observed data in the posterior distribution at each iteration, avoiding the computational difficulty of independent samples simulation of the Monte-Carlo EM and shortening the time consumption. SAEM algorithm is a stochastic algorithm, for which almost-sure convergence toward the maximum likelihood estimation is ensured under general conditions (Delyon et al., 1999). As the simulation of the non observed data in the posterior distribution is not direct for NLMEMs, Kuhn and Lavielle (2005) proposed to combine the SAEM algorithm with a MCMC method to realize this simulation step. Donnet and Samson (2007) proposed a version of the SAEM algorithm adapted to mixed models defined by differential equations. The SAEM algorithm also enables to take into account the left-censored viral load data accurately with convergent estimator (Samson et al., 2006). The combination of the two extensions of SAEM for differential equations and for left-censored data handling is used in the following analyzes.
3.3. Model selection
Model selection aims at identifying a model that best fits the available data with the smallest possible dimension. The two most popular model selection criteria are the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC). Following the simulation results of Bertrand et al. (2008), the best model is defined here as the model with the lowest BIC. Let
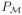 be the number of parameters in the model
be the number of parameters in the model
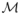 ,
,
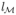 the likelihood function of the observations (vobs, z) and
the likelihood function of the observations (vobs, z) and
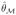 the maximum likelihood estimate of θ in model
the maximum likelihood estimate of θ in model
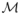 . The BIC penalizes the minimized deviance by log(N) times the number of free parameters.
. The BIC penalizes the minimized deviance by log(N) times the number of free parameters.
Using BIC requires to compute the log-likelihood of model
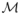 . Following (5), for any model
. Following (5), for any model
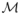 , the likelihood l of the observations (vobs, z) can be decomposed as follows (we omit the subscript
, the likelihood l of the observations (vobs, z) can be decomposed as follows (we omit the subscript
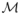 to simplify the notation):
to simplify the notation):
| (7) |
where π is the probability distribution density of φ and π̃ any absolutely continuous distribution with respect to π. Then, l(vobs, z; θ) can be approximated via an Importance Sampling integration method:
draw φ (1), φ (2), …, φ(K) with the distribution π̃ (·; θ),
let
l̂K(vobs, z; θ) is a consistant estimator of the observed likelihood:
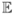 (l̂K(vobs, z; θ)) = l(vobs, z; θ) and Var(l̂K(vobs, z; θ)) =
(l̂K(vobs, z; θ)) = l(vobs, z; θ) and Var(l̂K(vobs, z; θ)) =
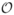 (K−1). Furthermore, if π̃ is the conditional distribution p(φ|vobs, z; θ), the variance of the estimator is null and l̂K(vobs, z; θ) = l(vobs, z; θ) for any value of K. That means that an accurate estimation of l(vobs, z; θ) can be obtained with a small value of K if the sampling distribution is close to the conditional distribution p(φ|vobs, z; θ).
(K−1). Furthermore, if π̃ is the conditional distribution p(φ|vobs, z; θ), the variance of the estimator is null and l̂K(vobs, z; θ) = l(vobs, z; θ) for any value of K. That means that an accurate estimation of l(vobs, z; θ) can be obtained with a small value of K if the sampling distribution is close to the conditional distribution p(φ|vobs, z; θ).
We recommend the following procedure: for i = 1, 2, …, N, one estimates empirically the conditional mean and the conditional variance-covariance matrix of φi as described above. Then, the are drawn with the sampling distribution π̃ as follows:
where ( ) is a sequence of i.i.d. random vectors and where the components of are independent variables distributed with a t–distribution with ν degrees of freedom. The numerical results presented here were obtained with ν = 5 d.f.
Note that recently, several authors proposed conditional Information Criteria for linear mixed models, see Liang et al. (2008) for example. The use of such criteria seems promising but extension to non linear mixed model is not straightforward.
3.4. Model identifiability
If the ODE model is not identifiable, any estimation method may produce unreliable and misleading results. Then, identifiability of the model parameters has to be checked before applying the HIV dynamic model to the data. Usually, many of the model components may not be measurable and several parameters may not be identifiable. We need a trade-off between model complexity and parameter identifiability based on clinical data. If a model has too many components, it may be difficult to analyze. If a model is too simple, some important clinical factors cannot be incorporated, although the viral dynamic parameter can be identified and estimated. Various works on system identification of nonlinear HIV models can be found for example in Perelson and Nelson (1997); Xia and Moog (2003); Jeffrey and Xia (2005); Guedj et al. (2007b); Wu et al. (2008). Xia and Moog (2003) proposed a HIV dynamic model defined with a system of 4 ODEs and checked the algebraical identifiability. Assuming that the non infected cells are observed, their system allows to derive some sufficient conditions which ensure the algebraic identifiability of the model. Unfortunately, the different models that we consider do not allow to separate the problem into two independent problems as proposed by Xia and Moog (2003) or by Wu et al. (2008) and the identifiability of the complete set of the parameters must be discussed on the whole. This problem has no closed form algebraic conditions. As an alternative, we propose to examine the algebraic identifiability problem by performing some sensitivity analysis.
Nevertheless, even if algebraic identifiability is useful, it is not completely appropriate for a population approach where the distribution of the individual parameters is also part of the (statistical) model. In other word, if a parameter is not algebraically identifiable, it can be statistically identifiable (an example is given in the Web Appendix A) and the reverse is also true: some parameters can be difficult to estimate with a very poor design, even if the model is algebraically identifiable. Then, practical identifiability should also be considered (see Guedj et al. (2007b) for example). As a practical diagnostic tool, we propose to use the Fisher Information Matrix for detecting some over-parametrization in the model. From our experience, very large standard errors (or NaN) indicate some issues in the parametrization, but the reverse is not necessarily true … We recommend to perform several runs with slightly different initial guesses. Then, convergence to different solutions can indicate a lack of identifiability, rather than the presence of several isolated local maxima of the likelihood.
3.5. Covariate testing
Another statistical issue in NLMEMs is the utilization of covariates to explain part of inter-individual parameter variability. Comparing models with and without covariates can be performed through model selection with the BIC criterion. For nested models, the likelihood ratio test can be applied by computing the log-likelihoods of the nested models. The Wald test can be used based on the covariates estimated effects and their standard errors.
3.6. The MONOLIX software
Monolix is a free software (http://software.monolix.org), which implements a wide variety of stochastic algorithms such as SAEM, Importance Sampling, MCMC, and Simulated Annealing, all dedicated to the analysis of NLMEMs. The objectives are: a) parameter estimation by computing the maximum likelihood estimator of the parameters without any approximation of the model and standard error for the maximum likelihood estimator; b) model selection by comparing several models using some information criteria (AIC, BIC), testing hypotheses using the Likelihood Ratio Test, testing parameters using the Wald Test and c) Goodness of fit. Monolix version 2.4 was used in this work. We used the code BiM (release 2.0, April 2005) which implements a variable stepsize method for stiff initial value problems for ODEs.
4. Application to the COPHAR II - ANRS 134 trial
4.1. Material and Methods
In the COPHAR II- ANRS 134 trial, an open prospective non-randomized interventional study, 115 HIV-infected patients adults started an antiviral therapy with at least 2 RTIs and one of three different PIs. 48 patients were treated with indinavir (and ritonavir as a booster)(I), 38 with lopinavir (and ritonavir as a booster) (L) and 35 with nelfinavir (N). Patients were followed one year after treatment initiation. Viral load and CD4 cell count were measured at screening, at inclusion and at weeks 2(or 4), 8, 16, 24, 36 and 48. Plasma HIV-1-RNA were measured by Roche monitored with a limit of quantification of 50 copies/ml. The results of this trial are reported in Duval et al. (2009). The proportion of virological failure was higher in the nelfinavir group and similar for indinavir and lopinavir, although lopinavir is supposed to be a more potent PI now widely used. Observed viral load and CD4 cell count are displayed in Figure 1 which clearly shows a large inter-subject variability.
Figure 1.
Observed viral load decrease (left) and CD4 increase (right) after treatment initiation in the three PI groups: lopinavir (top), indinavir (middle) and nelfinavir (bottom)
The models
 ,
,
 and
and
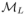 were compared using the BIC criterion. The identifiability of the selected model was studied, the effect of the PI group is tested by adding a covariate on ηPI:
were compared using the BIC criterion. The identifiability of the selected model was studied, the effect of the PI group is tested by adding a covariate on ηPI:
| (8) |
where TRTi is the PI administrated to patient i (L, I or N). The reference group is the lopinavir group (βL = 0). BIC and Wald test were used to study the differences in the 3 PI groups: no PI effect (LIN), only two groups: L vs. IN (L-IN) or LI vs N (LI-N), three groups L-I-N.
4.2. Results
We compared the three dynamic models. For each model, the complete set of fixed effects (Table 1) were estimated. Furthermore, variability on all the parameters was assumed without any correlation between the random effects. The population parameters were estimated with the SAEM algorithm and the log-likelihoods were estimated by Monte Carlo Importance Sampling. The BIC computed for the three models. The latent model
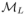 was selected as the best model among the three candidate models: BIC(
was selected as the best model among the three candidate models: BIC(
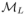 )=8758, BIC(
)=8758, BIC(
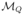 )=9077, BIC(
)=9077, BIC(
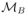 )=9134. Furthermore, the fits for both the viral load and the CD4 counts were better with model
)=9134. Furthermore, the fits for both the viral load and the CD4 counts were better with model
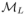 (σV = 0.46 and σT = 0.25) than with model
(σV = 0.46 and σT = 0.25) than with model
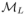 (σV = 0.62 and σT = 0.27) or model
(σV = 0.62 and σT = 0.27) or model
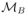 (σV = 0.67 and σT = 0.27).
(σV = 0.67 and σT = 0.27).
We then studied the identifiability of
 . First we studied the mathematical identifiability by performing a sensitivity analysis on a single simulated individual that showed that individual fitting does not allow to estimate simultaneously three sets of parameters: (p, μV), (γ, π, p, μA) and (ηPI, ηRTI) (see Web Appendix B for more details).
. First we studied the mathematical identifiability by performing a sensitivity analysis on a single simulated individual that showed that individual fitting does not allow to estimate simultaneously three sets of parameters: (p, μV), (γ, π, p, μA) and (ηPI, ηRTI) (see Web Appendix B for more details).
The sensitivity analysis showed that only the ratio p/μV can be estimated. The problem of estimating both p and μV was also found in the Fisher Information Matrix obtained after running the SAEM algorithm with very high estimated standard errors (236% and 240% respectively). Therefore, we assumed that μV did not vary and was fixed to the value 30/day (Ramratnam et al., 1999; Guedj et al., 2007a). Fixing μV to any other value around 30/day didn’t change the estimation of the other parameters, except p. We also found that both γ and μL could be correctly estimated (their s.e. were estimated to 43% and 11%) but not their inter-patient variability. We therefore decided to estimate these two parameters, but considering that they do not vary in the population. For the third set, the sensitivity analysis clearly showed that, using the data from only one patient, only the product (1 − ηPI)(1 − ηRTI) can be estimated. Then, we tried to fix ηPI or ηRTI but the results were clearly deteriorated. That means that the probability distribution of (1 − ηPI)(1 − ηRTI) cannot be described assuming that only one of these two parameters is a random variable. Thus, we assumed that both ηPI and ηRTI vary in the population because both are statistically identifiable (see discussion on that in Web supplement).
Table 3 reports BIC and estimated β’s for the different merging of the PI group (BIC and LL are different from Table 2 because parameter μV was fixed in Table 3). Adding a covariate treatment to explain the variability of ηPI did not modify the identifiability of the model. Different starting values always gave similar results for the β’s. The smallest BIC was for LI-N implying a different effect of nelfinavir versus lopinavir and indinavir that were grouped. The estimated parameters of that model are reported in Table 4. The efficacy of PI ηPI was 0.99 for lopinavir-indinavir and 0.75 for nelfinavir, i.e. nelfinavir efficacy for blocking infectious viruses was 25% less important than for lopinavir and indinavir, which are boosted PI. The LRT for the nelfinavir effect was very significant (p = 10−12 for comparison of models LIN and LI-N), no significant improvement was found when separating L and I (comparison of models LI-N vs L-I-N: p = 0.32 ). The Wald tests also agreed that only βN was significatively different from zero.
Table 3.
Estimated fixed effects and standard deviations of the random effects for the latent model
 . The estimated standard errors are in parenthesis. See eq. (5) for the definition of the fixed and random effects.
. The estimated standard errors are in parenthesis. See eq. (5) for the definition of the fixed and random effects.
| Parameter (S.E.); | Inter-patient variability (S.E.) | |
|---|---|---|
| λ (cells/mm3/day) | 2.61 (0.25) | 0.55 (0.044) |
| γ | 0.0021 (0.0009) | 0 (fixed) |
| μNI(day−1) | 0.0085 (0.0010) | 0.44 (0.073) |
| μL(day−1) | 0.0092 (0.0009) | 0 (fixed) |
| μA(day−1) | 0.289 (0.016) | 0.399 (0.047) |
| μV(day−1) | 30 (fixed) | 0 (fixed) |
| p | 641 (110) | 0.9 (0.13) |
| αL | 1.6e-5 (1.7e-6) | 0.678 (0.33) |
| π | 0.443 (0.038) | 0.45 (0.047) |
| ηRTI | 0.90 (0.17) | 2.93 (1.8) |
| ηPI | 0.99 (0.003) | 3.19 (2) |
| βN | −5.6 (2.6) | |
| σV | 0.464 (0.024) | |
| σT | 0.254 (0.009) |
Table 2.
Comparison of different covariate models for PI group. The estimated standard errors are in parenthesis. Here, pβN (resp. pβ I) is the p-value of the Wald test used for testing βN = 0 (resp. βI = 0).
| Model | −2 × log-likelihood | BIC | βN | pβN | βI | pβI |
|---|---|---|---|---|---|---|
| LIN | 8646 (6) | 8741 (6) | ||||
| LI-N | 8635 (6) | 8734 (6) | −5.6 (2.6) | 0.045 | ||
| L-I-N | 8631 (6) | 8735 (6) | −4.9 (2.3) | 0.036 | −1.1 (4.0) | 0.790 |
This model provided good fits of both viral load and CD4 cells as can be seen on the visual predictive check (Figure 2) and on some individual fits for patients in each treatment group (Figure 3).
Figure 2.
Visual predictive checks for the latent model
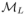 . The observed viral loads and CD4 counts are displayed with dots, the predicted median with a solid line and a 90% prediction interval with dotted lines.
. The observed viral loads and CD4 counts are displayed with dots, the predicted median with a solid line and a 90% prediction interval with dotted lines.
Figure 3.
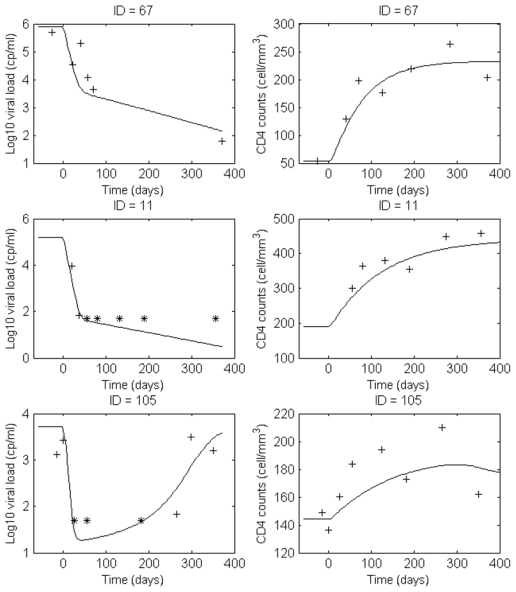
Examples of individual fits obtained with the latent model
 : ID=67 (lopinavir), ID=11 (indinavir) and ID=105 (nelfinavir). The + represent the non censored observations and the * the limit of quantification.
: ID=67 (lopinavir), ID=11 (indinavir) and ID=105 (nelfinavir). The + represent the non censored observations and the * the limit of quantification.
We also tested several error models for the CD4 count. Thiebaut et al. (2005) assumed a constant error model for the CD4 count at the power 0.25 (z1/4 = T1/4 + ε). For this error model as well as for the constant error model, the log-likelihood was lower (−2 × LL = 8680) and the proportional error model was preferred (−2 × LL = 8635) for the final model.
Convergence of SAEM takes about 20mn on a Dual Core laptop. The total time for estimating the population parameters with SAEM, the Fisher Information Matrix, the individual parameters and the log-likelihood is about 1 hour.
5. Discussion
This article proposed the SAEM algorithm to estimate parameters of nonlinear mixed model based on partially observed complex HIV differential systems. The estimation of the parameters of such a mixed model is a dificult statistical and computational challenge. The HIV differential systems defining these mixed models are non linear, consequently without any analytical solution. Furthermore, the ODE system is generally stiff, the classic ODE solver such as Runge-Kutta not being adapted to solve numerically the system. We used the code BiM (release 2.0, April 2005) which implements a variable order-variable stepsize method for (stiff) initial value problems for ODEs. The analysis of such data is also complicated by the left-censoring of the viral load data due to the lower limit of experimental devices detection, and it is well known that omitting to correctly handle this censored data provides biased estimates of dynamic parameters. The SAEM algorithm has theoretical convergence properties and is computationally efficient on these dynamic models.
In this article, we applied it to a clinical trial in HIV infection, using all the data (both viral load and CD4 measurements) obtained during 48 weeks of follow-up in naive patients starting a treatment while most studies of HIV dynamics model studied only viral load data during a shorter period (2–6 weeks) after the initiation of anti-retroviral treatment.
We compared several HIV dynamic models and showed that the latent model was the best one using the BIC criterion. We also studied the practical identifiability of this model. Using likelihood ratio test to compare the efficacy of the three studied PI, we found a significant difference in the efficacy of nelfinavir compared to lopinavir or indinavir. This is in agreement with the results of the trial (Duval et al; 2009) in which virological failure was found in 33% of patients treated with nelfinavir and only in 5% of patients treated by indinavir or lopinavir.
The HIV dynamic model used in this study has some limitations. First, it does not take into account the fact that HIV undergoes rapid mutation in the presence of anti-retroviral therapy. Of course, considering such phenomenon in the model may introduce many more parameters. We attempted to keep the model itself as simple as possible and the goodness of fit were satisfactory. Second, we considered a constant treatment effect, however, the effect of antiviral treatment may change over time, due to pharmacokinetics intra-patient variability, fluctuating patient adherence, emergence of drug resistance mutations and/or other factors. Huang et al. (2006) proposed viral dynamic models to evaluate antiviral response as a function of time-varying concentrations of drug in plasma. A more elaborate model would thus promisingly include this additional extension. Nevertheless, these limitations did not offset the major findings from our modeling approach, although further improvement may be brought. In conclusion, the SAEM algorithm is an useful tool for model development and parameter estimation in this context of HIV dynamics.
Supplementary Material
Acknowledgments
The authors would like to thank the scientific committee of COPHAR II-ANRS111 trial for giving us access to the data, especially the principal investigators Pr Dominique Salmon-Céron from Infectious Diseases Unit at Cochin Hospital, Paris and Dr Xavier Duval from Center for Clinical Investigation, Bichat Hospital, Paris, France. We thank Xavière Panhard (INSERM UMR738) for her help in managing the data of the trial and discussion on the choice of models.
This work was supported by the French ANR (Agence Nationale de la Recherche).
Footnotes
Supplementary Materials
Web Appendices referenced in Section 2 and Section 4 are available under the Paper Information link at the Biometrics website http://www.biometrics.tibs.org.
References
- Bertrand J, Comets E, Mentré F. Comparison of model-based tests and selection strategies to detect genetic polymorphisms influencing pharmacokinetic parameters. Journal of Biopharmaceutical Statistics. 2008;18:1084–1102. doi: 10.1080/10543400802369012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Boer R, Perelson A. Target cell limited and immune control models of HIV infection: a comparison. Journal of Theoretical Biology. 1998;190:201–214. doi: 10.1006/jtbi.1997.0548. [DOI] [PubMed] [Google Scholar]
- Delyon B, Lavielle M, Moulines E. Convergence of a stochastic approximation version of the EM algorithm. Annals of Statistics. 1999;27:94–128. [Google Scholar]
- Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society: Series B. 1977;39:1–38. [Google Scholar]
- Ding A, Wu H. Assessing antiviral potency of anti-HIV therapies in vivo by comparing viral decay rates in viral dynamic models. Biostatistics. 2001;2:13–29. doi: 10.1093/biostatistics/2.1.13. [DOI] [PubMed] [Google Scholar]
- Donnet S, Samson A. Estimation of parameters in incomplete data models defined by dynamical systems. Journal of Statistical Planning and Inference. 2007;137:2815–31. [Google Scholar]
- Duval X, Mentré F, Rey E, Auleley S, Peytavin G, Biour M, Métro A, Goujard C, Taburet A, Lascoux C, Panhard X, Tréluyer J, Salmon-Céron D. Benefit of therapeutic drug monitoring of protease inhibitors in HIV-infected patients depends on PI used in HAART regimen - ANRS 111 trial. Fundamental and Clinical Pharmacology. 2009;23:491–500. doi: 10.1111/j.1472-8206.2009.00693.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitzgerald A, DeGruttola V, Vaida F. Modelling HIV viral rebound using non-linear mixed effects models. Statistics in Medicine. 2002;21:2093–2108. doi: 10.1002/sim.1155. [DOI] [PubMed] [Google Scholar]
- Funk G, Fischer M, Joos B, Opravil M, Günthard H, Ledergerber B, Bonhoeffer S. Quantification of in vivo replicative capacity of HIV-1 in different compartments of infected cells. Journal of Acquired Immune Deficiency Syndromes. 2001;26:397–404. doi: 10.1097/00126334-200104150-00001. [DOI] [PubMed] [Google Scholar]
- Guedj J, Thiébaut R, Commenges D. Maximum likelihood estimation in dynamical models of HIV. Biometrics. 2007a;63:1198–2006. doi: 10.1111/j.1541-0420.2007.00812.x. [DOI] [PubMed] [Google Scholar]
- Guedj J, Thiébaut R, Commenges D. Practical identifiability of HIV dynamics models. Bulletin of Mathematical Biology. 2007b;69:2493–2513. doi: 10.1007/s11538-007-9228-7. [DOI] [PubMed] [Google Scholar]
- Huang Y, Liu D, Wu H. Hierarchical Bayesian methods for estimation of parameters in a longitudinal HIV dynamic system. Biometrics. 2006;62:413–423. doi: 10.1111/j.1541-0420.2005.00447.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughes J. Mixed effects models with censored data with applications to HIV RNA levels. Biometrics. 1999;55:625–629. doi: 10.1111/j.0006-341x.1999.00625.x. [DOI] [PubMed] [Google Scholar]
- Jeffrey A, Xia X. Identifiability of HIV/AIDS models. World Scientific Publications; Singapore: 2005. [Google Scholar]
- Kuhn E, Lavielle M. Maximum likelihood estimation in nonlinear mixed effects models. Computational Statististics and Data Analysis. 2005;49:1020–1038. [Google Scholar]
- Lavielle M, Mentré F. Estimation of population pharmacokinetic parameters of saquinavir in HIV patients and covariate analysis with with the SAEM algorithm implemented in MONOLIX. Journal of Pharmacokinetics and Pharmacodynamics. 2007;34:229–249. doi: 10.1007/s10928-006-9043-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang H, Wu H, Zou G. A note on conditional AIC for linear mixed-effects models. Biometrika. 2008;95:773–778. doi: 10.1093/biomet/asn023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowak M, May R. Virus dynamics: mathematical principles of immunology and virology. Oxford University Press; 2000. [Google Scholar]
- Perelson A. Modelling viral and immune system dynamics. Nature Reviews Immunology. 2002;2:28–36. doi: 10.1038/nri700. [DOI] [PubMed] [Google Scholar]
- Perelson A, Nelson P. Mathematical analysis of HIV-1 dynamics in vivo. SIAM Review. 1997;41:3–44. [Google Scholar]
- Perelson A, Neumann A, Markowitz M, Leonard J, Ho D. HIV-1 dynamics in vivo: virion clearance rate, infected cell life-span, and viral generation time. Science. 1996;271:1582–1586. doi: 10.1126/science.271.5255.1582. [DOI] [PubMed] [Google Scholar]
- Pinheiro J, Bates D. Approximations to the log-likelihood function in the non-linear mixed-effect models. Journal of Computational and Graphical Statistics. 1995;4:12–35. [Google Scholar]
- Putter H, Heisterkamp S, Lange J, de Wolf F. A Bayesian approach to parameter estimation in HIV dynamical models. Statistics in Medicine. 2002;21:2199–214. doi: 10.1002/sim.1211. [DOI] [PubMed] [Google Scholar]
- Ramratnam B, Bonhoeffer S, Binley J, Hurley A, Zhang L, Mittler JE, Markowitz M, Moore JP, Perelson AS, Ho D. Rapid production and clearance of HIV-1 and hepatitis C virus assessed by large volume plasma apheresis. The Lancet. 1999;354:1782–1786. doi: 10.1016/S0140-6736(99)02035-8. [DOI] [PubMed] [Google Scholar]
- Rong L, Perelson A. Modeling HIV persistence, the latent reservoir, and viral blips. Journal of Theor Biol. 2009;260:308–331. doi: 10.1016/j.jtbi.2009.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samson A, Lavielle M, Mentré F. Extension of the SAEM algorithm to left-censored data in non-linear mixed-effects model: application to HIV dynamics model. Compututational Statististics and Data Analysis. 2006;51:1562–74. [Google Scholar]
- Thiébaut R, Guedj J, Jacqmin-Gadda H, Chêne G, Trimoulet P, Neau D, Commenges D. Estimation of dynamical model parameters taking into account undetectable marker values. BMC Medical Research Methodology. 2006;6:38. doi: 10.1186/1471-2288-6-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thiebaut R, Jacqmin-Gadda H, Babiker A, Commenges D Collaboration C. Joint modelling of bivariate longitudinal data with informative dropout and left-censoring, with application to the evolution of CD4+ cell count and HIV RNA viral load in response to treatment of HIV infection. Stat Med. 2005;24:65–82. doi: 10.1002/sim.1923. [DOI] [PubMed] [Google Scholar]
- Wolfinger R. Laplace’s approximations for non-linear mixed-effect models. Biometrika. 1993;80:791–795. [Google Scholar]
- Wu H, Ding A. Population HIV-1 dynamics in vivo: applicable models and inferential tools for virological data from AIDS clinical trials. Biometrics. 1999;55:410–418. doi: 10.1111/j.0006-341x.1999.00410.x. [DOI] [PubMed] [Google Scholar]
- Wu H, Ding A, De Gruttola V. Estimation of HIV dynamic parameters. Statistics in Medicine. 1998;17:2463–85. doi: 10.1002/(sici)1097-0258(19981115)17:21<2463::aid-sim939>3.0.co;2-a. [DOI] [PubMed] [Google Scholar]
- Wu H, Huang Y, Acosta E, Rosenkranz S, Kuritzkes D, Eron J, Perelson A, Gerber J. Modeling long-term HIV dynamics and antiretroviral response: effects of drug potency, pharmacokinetics, adherence, and drug resistance. Journal of Acquired Immune Deficiency Syndromes. 2005;39:272–283. doi: 10.1097/01.qai.0000165907.04710.da. [DOI] [PubMed] [Google Scholar]
- Wu H, Zhang JT. The study of long-term HIV dynamics using semi-parametric non-linear mixed-effects models. Statistics in Medicine. 2002;21:3655–3675. doi: 10.1002/sim.1317. [DOI] [PubMed] [Google Scholar]
- Wu H, Zhu H, Miao H, Perelson AS. Parameter identifiability and estimation of HIV/AIDS dynamic models. Bulletin of Mathematical Biology. 2008;70:785–799. doi: 10.1007/s11538-007-9279-9. [DOI] [PubMed] [Google Scholar]
- Wu L. Exact and approximate inferences for nonlinear mixed-effects models with missing covariates. Journal of the American Statistical Association. 2004;99:700–709. [Google Scholar]
- Xia X, Moog C. Identifiability of nonlinear systems with application to HIV/AIDS models. IEEE Transactions on Automatic Control. 2003;48:330–336. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


