The accuracy of human population maps for public health application

Summary

OBJECTIVES

Human population totals are used for generating burden of disease estimates at global, continental and national scales to help guide priority setting in international health financing. These exercises should be aware of the accuracy of the demographic information used.

METHODS

The analysis presented in this paper tests the accuracy of five large-area, public-domain human population distribution data maps against high spatial resolution population census data enumerated in Kenya in 1999. We illustrate the epidemiological significance, by assessing the impact of using these different human population surfaces in determining populations at risk of various levels of climate suitability for malaria transmission. We also describe how areal weighting, pycnophylactic interpolation and accessibility potential interpolation techniques can be used to generate novel human population distribution surfaces from local census information and evaluate to what accuracy this can be achieved.

RESULTS

We demonstrate which human population distribution surface performed best and which population interpolation techniques generated the most accurate bespoke distributions. Despite various levels of modelling complexity, the accuracy achieved by the different surfaces was primarily determined by the spatial resolution of the input population data. The simplest technique of areal weighting performed best.

CONCLUSIONS

Differences in estimates of populations at risk of malaria in Kenya of over 1 million persons can be generated by the choice of surface, highlighting the importance of these considerations in deriving per capita health metrics in public health. Despite focussing on Kenya the results of these analyses have general application and are discussed in this wider context.

Introduction

Accurate census enumeration combined with information on the spatial distribution of administrative areas is a prerequisite for efficient governance in all nation states (UN 2001). This information, transformed into human population distribution maps, forms an essential population denominator required for many epidemiological studies and for rational public health planning and healthcare provision. Accurate knowledge of human population distribution is needed to define populations at risk of disease for example, to enable exploration of the association of this risk with the environment, poverty and other diseases. It is further necessary to investigate the effectiveness, efficiency and equity of the healthcare system and thus to optimally target and cost interventions through the formal sector (Noor et al. 2003, 2004).

The massive increase in the availability of rasterized (or gridded) imagery of Earth surface conditions, derived primarily from remote sensing, has facilitated a renaissance in the mapping of a range of vector-borne diseases at continental and global scales (Hay 2000; Hay et al. 2000; Randolph 2000; Rogers 2000; Rogers & Randolph 2000; Rogers et al. 2002) and a concomitant improvement in the spatial resolution at which disease risk can be determined. Combinations of these vector-borne disease and demographic data, with assumptions about attributable risk, can be used to generate burden of disease estimates where primary health information system data are wanting (Snow et al. 1998, 1999, 2003, 2005; WHO/UNICEF 2003; Hay et al. 2004, 2005; WHO 2005). The error associated with the population denominator in these calculations is usually ignored.

Similarly, international efforts to quantify the global burdens of a wider range of infectious diseases (Murray & Lopez 1996, 1997; Walker et al. 2002; Williams et al. 2002; Black et al. 2003; Kosek et al. 2003; Morris et al. 2003; de Silva et al. 2003; Zaidi et al. 2004) have traditionally relied on attribution of detailed local information to population data aggregated over large areas; often the national level (Mathers et al. 2003; Murray et al. 2003). Risk is assumed to be equally spatially partitioned among homogenously distributed human populations. It is unlikely that this assumption will be valid for the leading causes of under-five mortality globally; including diarrhoea, pneumonia, malaria (Craig et al. 1999; Hay et al. 2004) and HIV/AIDS (Black et al. 2003; Morris et al. 2003). It is further unlikely that geographical homogeneity is to be found in all of the major underlying risk factors for these causes (Ezzati et al. 2002, 2004), which at the very least will show large urban-rural mortality differentials (Hinrichsen et al. 2002; Dyson 2003; Tatem & Hay 2004; Hay et al. 2005). As techniques for defining disease burdens are moved to sub-national scales to support strategic assessments of progress towards international health and development targets (UNDP 2003), evaluating the fidelity of the associated human population distribution data used will become increasingly important.

Population data is primarily gathered through national census enumeration within country specific administrative boundaries. Methods used to interpolate census polygon data into continuous surfaces are varied and briefly outlined. They include areal weighting, pycnophylactic (mass-preserving) interpolation, dasymetric mapping (density measuring) and various forms of ‘smart’ interpolation (Deichmann 1996; Deichmann et al. 2001) and their use in several public-domain large-area human population distribution maps is also summarized (Table 1, Figure 1).

Table 1.

Characteristics of large-area public-domain raster population data sources: UNEP (URL: http://grid2.cr.usgs.gov/datasets/datalist-php3) (Deichmann 1996), GPW2.0 (URL: http://sedac.ciesin.columbia.edu/plue/gpw/) (Deichmann et al. 2001), GPW3.0 (Balk & Yetman 2004), GPW3.0UR (Balk & Yetman 2004) and LandScan (URL: http://www.ornl.gov/sci/gist/landscan/) (Dobson et al. 2000, 2003)

Dataset	Coverage	Spatial res. km (deg.)	Population Type	Interpolation method	Admin. units Global/Africa/Kenya	Date
UNEP	Africa	5 (2.5′)	Residential	Smart In.	NA/4715/258	1990
GPW2.0	Global	5 (2.5′)	Residential	Areal W.	127083/5939/258	1995
GPW3.0	Global	5 (2.5′)	Residential	Areal W.	364111/105989/6624	2000
GPW3.0UR	Global	1 (0.5′)	Residential	Dasy. M.	364111/105989/6624	2000
LandScan	Global	1 (0.5′)	Ambient	Smart In.	69350/5025/258	2002

Areal W., areal weighting; Dasy. M., dasymetric mapping; Smart In., smart interpolation.

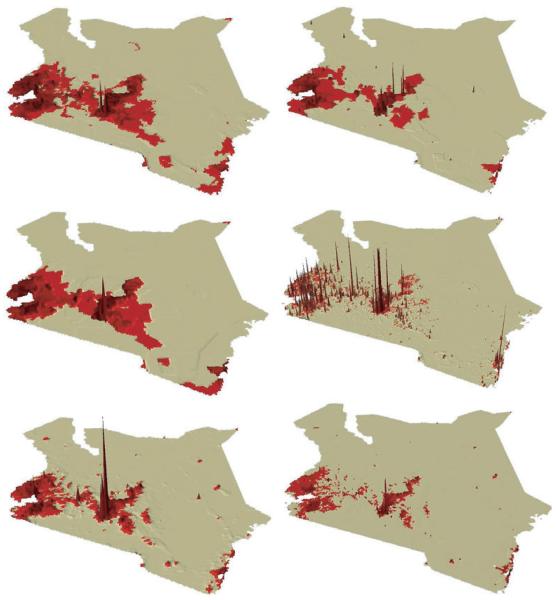
Figure 1.

Raster population maps for Kenya. From top left to bottom right: UNEP99, GPW299, GPW399, GPW3UR99, LS99 and AW99 (areal weighted 1999). To compare population data which is highly skewed (Table 4) it is convenient to express values as standard deviations from the mean value for the entire image. The highest values in each image are 3 standard deviations from the mean allowing inter-comparison. Colours and shading are added to accentuate these differences.

Areal weighting simply overlays a regular grid (raster surface) on administrative unit (polygon) data and assigns population according to the proportion of the polygon area in the raster grid cell (Mennis 2003). For example, imagine an administrative unit x is a perfect square of 3 × 3 km. To turn this into a gridded population map at 1 × 1 km spatial resolution, the population of x/9 would be assigned to each square in the raster grid. Areal weighting was used to generate the Gridded Population of the World version 2.0 (GPW2.0) (Deichmann et al. 2001) and GPW3.0 (CIESIN/CIAT 2004) and while it has the advantage of simplicity it is confounded by the assumption that human populations distribute themselves uniformly in space.

Pycnophylactic interpolation starts identically to areal weighting and then smoothes these raster values iteratively with the weighted average of nearest neighbours; at each iteration the total is adjusted to maintain the population count of the original polygon hence ‘mass-preserving’ (Tobler 1979). The number of nearest neighbours used and iterations applied is subjective and determines the overall level of smoothing required in the output raster surface. Pycnophylactic interpolation is an elegant solution to the problem of generating a continuous surface from discontinuous data and was used to generate GPW 1.0 as part of the Global Demography Project (Tobler et al. 1995, 1997). It unrealistically assumes, however, that no sharp boundaries exist in the distribution of human population (Tobler 1979).

Dasymetric mapping uses ancillary information (often land-use derived from satellite imagery) at higher spatial resolution than the population polygon data to help allocate population (i.e. from forested to urban) who are assumed to differentially inhabit land-use types (Wright 1936; Langford & Unwin 1994; Mennis 2003). Dasymetric mapping again has the merit of relative simplicity and requires little extra data but can be difficult to implement because of the problems of defining the relative weights of the land-use classes. The GPW3.0 with urban-rural reallocation (GPW3.0UR) is an example of dasymetric mapping. GPW3.0UR uses the same global input census data as GPW3.0 but also uses remote sensing [night-time lights (Sutton et al. 2001) and Landsat (Mika 1997)] and other geographic data [Digital Chart of the World (DCW) populated places (Danko 1992)] to define urban extents. Weights are then applied to reallocate urban and rural populations to 1 × 1 km grids, based on the census data and published city population data (Balk & Yetman 2004; CIESIN/IPFRI/CIAT 2004).

Smart interpolation is technically more sophisticated than dasymetric mapping and uses a wide variety of ancillary data to help disaggregate population polygons as humans are known to distribute themselves non-randomly in the environment (Stewart & Warntz 1958; Langford & Unwin 1994; Cohen & Small 1998). For example, people are more likely to be living near roads and navigable rivers than in lakes or at the top of mountains (Tatem & Hay 2004). Weights can therefore be derived from ancillary data to inform the interpolation process to a raster grid. Smart interpolation tries to incorporate geography explicitly into the population distribution process and can vary in complexity from techniques informed predominantly by transport networks and settlement size, such as the accessibility potential interpolation used in UNEP (Deichmann 1996), to those that use a plethora of ancillary data to define occupation probabilities for all pixels in a raster grid, for example the smart interpolation used in Landscan (Dobson et al. 2000, 2003; Openshaw & Turner 2001). Uncertainty regarding the derivation of such weights and their geographical homogeneity are the primary complications for the implementation of smart interpolation (Openshaw & Turner 2001).

The analyses presented here investigate the accuracy of five public-domain, large-area population surfaces with reference to the 1999 Kenya population and housing census. The performance of areal weighting, pycnophylactic interpolation and accessibility potential interpolation techniques at generating new raster population surfaces for Kenya from the 1999 census data are also investigated, as relevant national agencies and affiliated researchers may have access to higher spatial resolution census data than those used in deriving global raster population surfaces. The resolution of the input census polygon data used in creating large area raster representations of human population distribution is also tested as the spatial resolution of available data is highly variable between countries and has rarely been evaluated outside of high-income nations (Fisher & Langford 1995; Martin 1996; Martin et al. 2000). From the outset we have the reservation that the raster population datasets used were often designed and implemented at global and continental scales and were not necessarily conceived for the applications for which they were tested. This paper is not positioned to favour any implementation or technique but to help evaluate the merits and demerits of these sources of human population distribution data used in epidemiology and public health and thereby help identify priority areas for their refinement. The importance of these considerations in epidemiology is highlighted by quantifying the differences in population at different levels of climate suitability for malaria risk obtained when extracting from the different human population distribution maps available for Kenya.

Materials and methods

The Kenyan Government’s Central Bureau of Statistics implemented a complete population and housing census in 1999 (CBS 2001). It was of the de facto type, so that all persons were enumerated where encountered at the time of census in their homes. Kenya’s administrative unit hierarchy (Figure 2) and population data are available in public-domain to the fifth administrative unit or sub-location (CBS 2001). The number, area (mean, minimum and maximum) and average spatial resolution (ASR; the square root of country area/number of admin units) (Deichmann 1996), of each administrative level are detailed (Table 2).

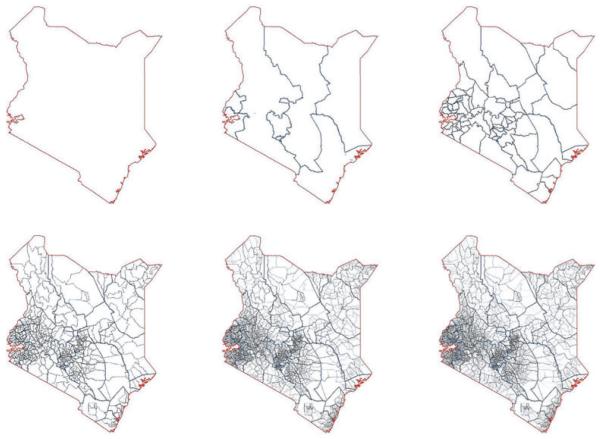
Figure 2.

Administrative boundaries for Kenya 1999. From top left to bottom right: country (administrative level 0); province (administrative level 1); district (administrative level 2); division (administrative level 3); location (administrative level 4); sub location (administrative level 5). A further finer level of stratification, ‘enumeration area’ is used for census counting and is not shown. North is to the top of the page and Kenya is 1126 km from its most northerly to southerly extent.

Table 2.

Spatial characteristics of Kenyan administrative hierarchy divisions

Admin.	n	Mean area	Minimum area	Maximum area	ASR
Country	1	585 055.8	585 055.8	585 055.8	764.9
Province	8	73 132.0	700.3	182 930.7	270.4
District	69	8479.1	231.8	68 229.1	91.8
Division	505	1158.5	10.8	20 783.4	34.0
Location	2436	240.2	0.4	10 755.0	15.5
Sub-location	6624	88.3	0.02	10 755.0	9.4

ASR, $\text{average}\text{spatial}\text{resolution}=\sqrt{\text{country}\_\text{area}∕\text{number}\_\text{of}\_\text{units}}$. (Deichmann 1996).

All units km² save ASR in km.

Public-domain population surfaces

Five public-domain raster datasets of human population distribution for which complete coverages of Kenya could be derived were obtained: UNEP (Deichmann 1996), GPW2.0 (Deichmann et al. 2001), GPW3.0 (Balk & Yetman 2004), GPW3.0UR (Balk & Yetman 2004; CIESIN/IPFRI/CIAT 2004) and LandScan (Dobson et al. 2000, 2003). Hereafter the five human population distribution surfaces are referred to as UNEP99, GPW299, GPW399, GPW3UR99 and LS99. The main characteristics of each of these population surfaces are detailed (Table 1) and the surfaces extracted and displayed for Kenya (Figure 1).

The date for which the human population distribution surfaces were generated and their spatial resolution varied so that two further modifications were required to enable inter-comparison. The first was a correction for enumeration year. An estimate of population in 1999 was produced for each raster population distribution using the following equation; P₁₉₉₉ = P_xe^rt where P₁₉₉₉ is the required 1999 population within a pixel, P_x is the population within the same pixel at year x, t is the number of years between year x and 1999, and r is the average growth rate (Deichmann 1996). Annual growth rates were determined from provincial intercensal population growth rates (Nairobi 4.8%, Central 1.8%, Coast 3.1%, Eastern 2.1%, North Eastern 9.5%, Nyanza 2.3%, Rift Valley 3.5% and Western 2.5%) (CBS 2001) and applied at the district level to generate population distribution maps for 1999. These changes were implemented with Idrisi Kilimanjaro (Clark Labs, Clark University, Worcester, MA, USA). The spatial resolution of the administrative boundaries and hence census information was often significantly finer than the spatial resolution of the raster data (Figure 1, Table 2). A second modification was therefore required to increase the spatial resolution of the raster surfaces to 100 × 100 m using areal weighting to allow reliable population extractions at the highest order administrative levels. This was particularly important in the urban areas of highest population density. These population surfaces were generated and subsequent extractions performed with ArcView 3.2 (Environmental Systems Research Institute Inc., Redlands, CA, USA).

The co-registration of the raster population and census data was checked by shifting each raster image by one 100 × 100 m picture element (pixel) in all orientations (N, W, S, E). In each case the correlation between the human population distribution maps and the census data decreased, showing they were optimally co-registered (aligned); results not shown. The error attributed to using a non-equal-area latitude and longitude reference system for Kenya is minimal as the country straddles the equator and is less than that would be generated by re-sampling the population surfaces to an alternative projection (Bugayevskiy & Snyder 1995). All the population surfaces were therefore analysed in the projection in which they were supplied.

Population interpolation approaches

Human population distribution surfaces at 100 × 100 m were also independently generated from these census data for Kenya using areal weighting, pycnophylactic interpolation and accessibility potential interpolation approaches. Each rubric was performed using census data at the national through to sub-location administrative level. Areal weighting was implemented with the zonal attributes extension of ArcView 3.2 (Environmental Systems Research Institute Inc.). Pycnophylactic interpolation was implemented with C code supplied by Uwe Deichmann and a smoothing factor iterated for 100 times or until no further changes in the cell adjustments were observed (Tobler 1979; Tobler et al. 1995). The accessibility potential interpolation technique was also implemented with C code written by and a methodology devised by Uwe Deichmann and Tom Cova (Deichmann 1998). The ancillary data required for accessibility potential interpolation, the human settlement database, river, road, railway networks and gazetted areas and water-bodies were assembled as follows.

Africover data at full spatial resolution (1:100 000) were requested and downloaded (URL: http://www.africover.org). The Africover roads and rivers themes were produced from visual interpretation of digitally enhanced Landsat Thematic Mapper images (bands 4, 3, 2) acquired mainly in 1995. The land-cover classes using the FAO/UNEP international standard land cover classification system (Di Gregorio & Jansen 1998), were similarly derived from visual interpretation of Landsat Thematic Mapper images but using scenes acquired more recently in 1999, the same year as the Kenya national census (CBS 2001). All landcover polygons classified as an urban area, rural settlement and refugee camp were compared with the sub-location data and aggregated to make them coherent administrative groupings (244 from 327 polygons). For example, the cluster of 12 polygons of urban areas in and around Mombasa were aggregated to one. The centroids of these aggregated polygons were assigned names and population counts using the database of municipalities, town councils and other urban centres from the 1999 population and housing census (CBS 2001) (133 of 244 polygons). Localities that were in the census list but not represented by Africover polygons (n = 144) were added as points using geo-referencing information obtained from Microsoft Encarta 2003 (Microsoft Corporation, Seattle, WA, USA). We were able to locate all of Kenya’s 9 996 991 urban classified population (CBS 2001) in this manner. Finally, we took the population and name of the parent sub-location for all remaining Africover polygons (n = 111) resulting in a total urban associated population of 10 766 874 in 388 localities. The river network was used as supplied by Africover. The newer Africover road network (0.040 km/km² road density for Kenya) was supplemented with the higher density road network supplied with the DCW (Danko 1992) (0.094 km/km² road density for Kenya). A buffer of 600 m around the Africover roads was used to erase duplicate roads in the DCW network and the resulting coverages merged in ArcGIS 8.3 (Environmental Systems Research Institute Inc.) and manually checked and corrected. This resulted in a hybrid road network (0.074 km/km² road density for Kenya) optimizing the more contemporary Africover and more comprehensive DCW. Railway data was used as supplied by DCW as this has not changed since digitization (Danko 1992). Finally, many irregularities were found in the gazetted area polygons for Kenya and their provenance could not be reliably determined. The polygons over land (n = 45) were checked against all ancillary data and manually corrected if their boundaries did not reconcile (i.e. if a gazetted area boundary followed an administrative border, road or river boundary inaccurately it was corrected). These polygons were augmented (n = 21) with all sub-locations that contained National Park, National Reserve or Forest in any of the administrative hierarchy names and had a population density <20 people/km². They were all then classified as gazetted parks (n = 46) or gazetted forests (n = 20).

The road, river and rail layers were merged to create a single transportation network and each component assigned travel speeds as outlined in previous work (Deichmann 1998). The data on settlement size and location were then linked to the transport network by assigning each settlement to the nearest network node. This information was used by the accessibility potential interpolation model to compute a simple accessibility measure for each node in the transport network. This measure is the sum of the population of settlements in the vicinity of each node weighted by a function of network distance. The computed accessibility estimates were then interpolated to a 100 m spatial resolution surface. The water body, gazetted forest and gazetted park polygons were, in turn, used to adjust the accessibility surface to 0%, 50% and 20% of their original value (Deichmann 1998). Finally, the sub-location population totals were distributed in proportion to the accessibility index measured for each pixel.

Accuracy assessment and malaria burden implications

Descriptive statistics (Sokal & Rohlf 1997b) for each administrative level were computed from administrative zone totals and accuracy comparisons between census and human population distribution data determined using the population adjusted coefficient of determination (adjusted r²) (Sokal & Rohlf 1997a) and root mean square error (RMSE) (ASPRS 1989). The RMSE is the square root of the mean of the sum of the squares of the error residuals;

$$\text{RMSE}=\sqrt{\frac{1}{n-1}(d_1^2+d_2^2\dots d_n^2)}$$

where n is the number of observations and d₁ to d_n the residual values and is essentially a normalized confidence interval on the predicted values. In addition, we derived estimates of the kurtosis and skewness of the census and transformed human population distribution for the areal weighting, pycnophylactic interpolation and accessibility potential interpolation data extractions at each administrative level (Sokal & Rohlf 1997c) to show the influence of the processing on the distribution of the human population distribution data. Kurtosis characterizes the relative ‘peakedness’ or ‘flatness’ of a distribution compared with the normal distribution. ‘Skewness’ is the degree of asymmetry of a distribution around its mean (Sokal & Rohlf 1997c).

The map of climate suitability for malaria transmission (Craig et al. 1999) was partitioned into established classes of malaria risk (Snow et al. 2003) (Figure 3). Populations exposed to different levels of risk were calculated by overlaying the five human population distribution surfaces on a Kenya subset of a map (Figure 3). Populations at risk were also determined directly from the census data by assigning population in direct proportion to the area of each sub-location occupied by a transmission intensity class (i.e. equivalent to areal weighting at sub-location). The results are summarized for the national level (Table 5).

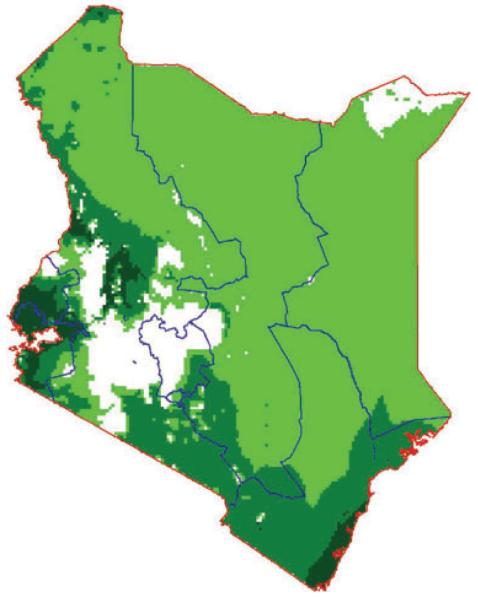
Figure 3.

Model of endemic malaria distribution (Craig et al. 1999) showing fuzzy climate suitability (FCS) for P. falciparum malaria transmission. FCS values vary between zero (totally unsuitable) and 1 (totally suitable) in an average year. The data are grouped (Snow et al. 2003) into class 1 zero risk □ (FCS = 0), class 2 marginal risk (FCS >0–<0.25), class 3 acute seasonal transmission (FCS >0.25 to <0.75) and class 4 stable endemic transmission (FCS > 0.75). The red boundary is national and the blue provincial (see Figure 2).

Table 5.

Population at risk of malaria

	Malaria climate suitability class
Source	1	2	3	4	Total
UNEP99	6 731 815	9 390 026	7 712 139	4 337 786	28 171 766
GPW299	7 087 332	10 014 129	7 967 788	4 587 939	29 657 189
GPW399	7 000 512	10 261 922	7 275 299	5 704 444	30 242 177
GPW3UR99	7 215 219	10 429 831	7 113 859	5 823 280	30 582 189
LS_99	7 033 693	10 423 229	8 855 830	4 791 363	31 104 115
Kpop99	6 526 062	9 684 076	6 709 852	5 766 616	28 686 607
Average	6 932 439	10 033 869	7 605 795	5 168 571

Class 1 zero risk (Fuzzy climate suitability (FCS = 0), class 2 marginal risk (FCS >0 to <0.25), class 3 acute seasonal transmission (FCS >0.25 to <0.75) and class 4 stable endemic transmission (FCS >0.75). See Figure 3. Source, population data source; UNEP99, United Nations Environment Programme in 1999; GPW299, Gridded Population of the World version 2 in 1999; GPW399, GPWv3.0 in 1999; GPW3UR99, GPWv3.0-UR in 1999; LS99, LandScan in 1999; KPOP99, Kenya census enumeration 1999.

Results

Public-domain population surfaces

The five public-domain raster human population distribution surfaces predicted accurately populations at the provincial (mean adjusted r² = 0.988, range 0.961–0.999), district (mean adjusted r² = 0.923, range 0.808–0.998) and divisional levels (mean adjusted r² = 0.803, range 0.665–0.992) (Table 3, Figure 4). The mean RMSEs, when expressed as a percentage of the mean population size of the administrative level (RMSE%), were correspondingly small at 9.8 (range 7.2–12.6) 19.1 (range 8.9–32.7) and 37.9 (range 11.2–54.7) for province, district and division respectively (Table 3, Figure 4). Moving down the administrative hierarchy, predictive skill decreased; at the location (mean adjusted r² = 0.498, range 0.212–0.948) and sub-location (mean adjusted r² = 0.397, range 0.090–0.904) level (Table 3, Figure 4). The mean RMSE%s were higher at 81.3 (range 23.4–111.4) and 107.5 (range 35.6–150.2) for location and sub-location respectively (Table 3, Figure 4).

Table 3.

Population retrievals and correlation structure between publicly-available population products and administrative levels

Admin.	Source	Total	Mean	Min.	Max.	SE	Ad. r2	n	RMSE	RMSE%
Country	KPOP99	28 686 607
Province	UNEP99	28 171 766	3 521 471	520 094	6 972 174	753 273	0.961	8	442 102	12.6
	GPW299	29 657 189	3 707 149	448 080	7 619 123	801 808	0.987	8	467 278	12.6
	GPW399	30 242 177	3 780 272	1 044 904	7 572 937	706 212	0.996	8	270 575	7.2
	GPW3UR99	30 582 189	3 822 774	1 060 776	7 538 830	697 106	0.999	8	275 210	7.2
	LS99	31 104 115	3 888 014	1 020 707	7 776 844	729 965	0.998	8	377 192	9.7
District	UNEP99	28 171 766	408 286	26 382	1 297 872	30 651	0.808	69	133 334	32.7
	GPW299	29 657 189	429 814	26 629	1 658 102	34 252	0.866	69	110 720	25.8
	GPW399	30 242 177	438 292	48 727	2 319 504	39 463	0.993	69	41 516	9.5
	GPW3UR99	30 582 189	443 220	48 359	2 345 870	39 751	0.998	69	39 326	8.9
	LS99	31 104 115	450 784	65 436	2 347 364	39 580	0.947	69	83 633	18.6
Division	UNEP99	28 171 766	55 786	0	352 354	2 209	0.665	505	30 528	54.7
	GPW299	29 657 189	58 727	163	381 012	2 289	0.710	505	28 751	49.0
	GPW399	30 242 177	59 885	23	465 206	2 388	0.949	505	12 519	20.9
	GPW3UR99	30 582 189	60 559	3	468 323	2 414	0.992	505	6 805	11.2
	LS99	31 104 115	61 592	105	440 513	2 664	0.701	505	33 041	53.6
Location	UNEP99	28 171 766	11 565	0	182 679	268	0.248	2 436	12 685	109.7
	GPW299	29 657 189	12 175	0	192 544	282	0.212	2 436	13 562	111.4
	GPW399	30 242 177	12 415	23	129 770	249	0.698	2 436	6 995	56.3
	GPW3UR99	30 582 189	12 554	3	121 153	252	0.948	2 436	2 936	23.4
	LS99	31 104 115	12 769	3	232 858	345	0.381	2 436	13 507	105.8
Sub-loc.	UNEP99	28 171 766	4 253	0	171 907	68	0.115	6 624	6 104	143.5
	GPW299	29 657 189	4 477	0	155 898	76	0.090	6 624	6 725	150.2
	GPW399	30 242 177	4 566	13	107 408	64	0.539	6 624	3 768	82.5
	GPW3UR99	30 582 189	4 617	0	102 842	64	0.904	6 624	1 644	35.6
	LS99	31 104 115	4 696	0	142 766	95	0.237	6 624	6 916	147.3

Admin., administrative level; Source, population data source; Total, total population; KPOP99, Kenya census enumeration 1999; UNEP99, United Nations Environment Programme in 1999; GPW299, Gridded Population of the World version 2 in 1999; GPW399, GPWv3.0 in 1999; GPW3UR99, GPWv3.0-UR in 1999; LS99, LandScan in 1999; Min., minimum; Max., maximum; SE, standard error; Ad. r², adjusted r squared (all correlations highly significant P >> 0.0001); n, number of observations; RMSE, root mean square error. RMSE %, (RMSE/Mean) × 100.

Figure 4.

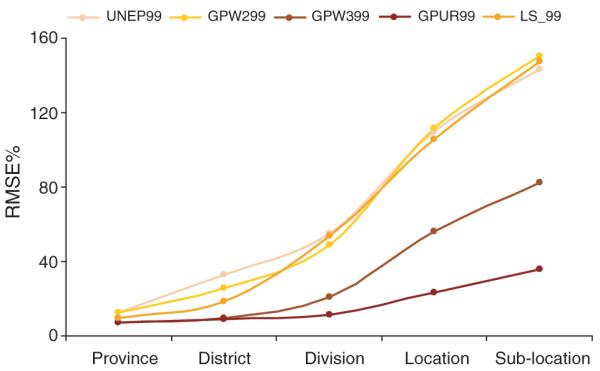
Graph of error structure by administrative level for the five large area public-domain human population distribution surfaces. RMSE% = the root mean square error (see Methods) expressed as a percentage of the mean population size of the administrative level.

GPW3UR maintained the lowest RMSE% (35.6) and highest correlation (r² = 0.904) to the census data at the sub-location level followed by GPW399 (82.5, r² = 0.539). There was little difference between the poorer performing surfaces, all showing RMSEs larger than the average population size of a sub-location (Table 3, Figure 4). All human population distribution surfaces showed an increase in RMSE with population size of the sub-location and performed badly in sub-locations of very low population (Figure 5).

Figure 5.

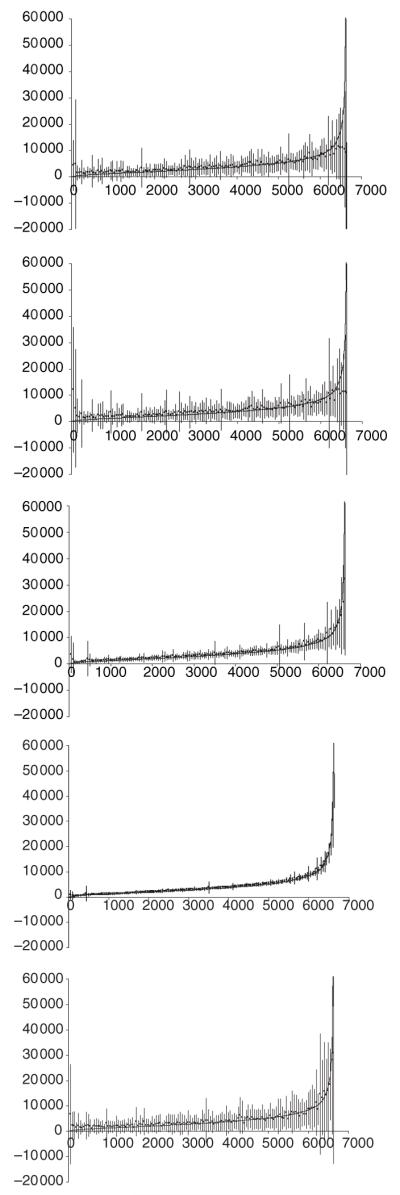
Accuracy of raster population maps for Kenya by sub-location. From top left to bottom right: UNEP99, GPW299, GPW399, GPW3UR99 and LS99. The graphs show population number (y-axis) by sub-location ordered from lowest to highest population (x-axis). The thick black line are the census counts (CBS 2001). The dots and error bars are the mean and root mean square error, respectively, averaged for sequential blocks of 50 sub-locations for clarity.

Population interpolation approaches

The accessibility potential interpolation technique showed more skill at predicting human population distribution at provincial and district admin levels but performed worse than areal weighting or pycnophylactic interpolation at division, location and sub-location levels (Table 4, Figure 6), although these differences are small, and at sub-location level due principally to the rasterization process. The areal weighting technique was most accurate at the admin 3 level and above. Pycnophylactic interpolation had only cosmetic effects on the human population distribution maps and always decreased accuracy over areal weighting. The population data were highly skewed (Table 4, as people tend to aggregate spatially) but implementing areal weighting, pycnophylactic interpolation and accessibility potential interpolation increased skewness; this effect was most apparent at the divisional level.

Table 4.

Population retrievals and correlation structure between interpolated population sources and administrative level 5 population (n = 6624 in all comparisons)

Inter.	Admin.	Total	Mean	Min.	Max.	Kurt.	Skew.	SE	Ad. r2	RMSE	RMSE%
AW	Kpop99	28 686 607	4 331	0	108 234	62	67	6
	Country	28 731 142	4 337	2	527 497	185	304	13	0.004	16 233	375
	Province	28 794 337	4 347	8	378 253	142	333	15	0.002	12 405	286
	District	28 829 542	4 352	1	378 263	112	508	17	0.035	9 572	221
	Division	28 830 286	4 352	0	158 316	76	154	9	0.148	6 301	145
	Location	28 765 445	4 343	0	108 024	63	56	6	0.738	2 698	62
	Sub-loc.	28 864 478	4 358	0	108 260	63	66	6	1.000	116	3
PI	Country	28 731 142	4 337	2	527 497	185	304	13	0.004	16 233	375
	Province	28 794 037	4 347	4	376 291	144	341	15	0.002	12 543	290
	District	28 827 976	4 352	1	376 560	112	507	17	0.037	9 516	220
	Division	28 847 329	4 355	0	150 804	75	145	9	0.156	6 220	144
	Location	28 859 276	4 357	0	108 318	63	57	6	0.750	2 635	61
	Sub-loc.	28 870 545	4 358	0	108 318	63	66	6	0.999	151	3
API	Country	27 577 041	4 163	0	174 879	100	63	6	0.013	9 074	210
	Province	27 640 763	4 173	0	249 225	111	171	10	0.035	9 508	220
	District	27 892 903	4 211	0	249 225	112	170	10	0.088	8 994	208
	Division	28 436 608	4 293	0	130 757	86	71	6	0.177	6 701	155
	Location	28 515 116	4 305	0	108 063	67	51	5	0.671	3 189	74
	Sub-loc.	28 446 519	4 294	0	107 977	62	66	6	0.995	378	9

Inter., interpolation method; Admin., administrative level; AW, areal weighting; PI, pycnophylactic interpolation; API, accessibility potential interpolation; Total, total population; Min., minimum; Max., maximum; Kurt., kurtosis; Skew., skewness; SE, standard error; Ad. r², adjusted r squared (note all correlations highly significant P ⪢ 0.0001); RMSE, root mean square error. RMSE %, (RMSE/Mean) × 100.

Figure 6.

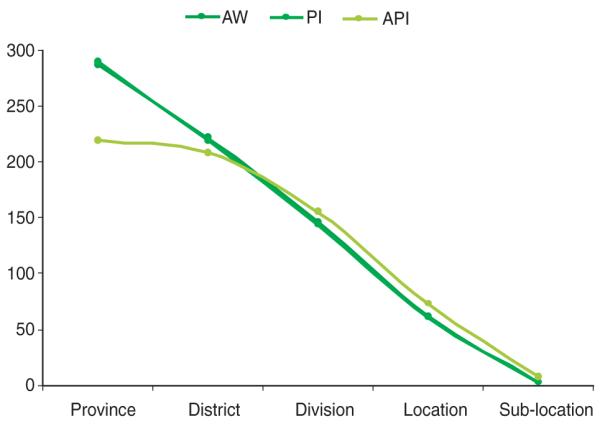
Graph of error structure by administrative level for the three modelled human population distribution surfaces. RMSE% = the root mean square error (see Methods) expressed as a percentage of the mean population size of the administrative level.

The average number of people at risk of malaria in Kenya was 22 808 235 (range 21 439 951–24 070 422) (Table 5). Large discrepancies were also found in each of the classes of categorical risk: the class 2 marginal risk average was 10 033 869 (range 9 390 026–10 429 831), the class 3 acute seasonal transmission risk average was 7 605 795 (range 6 709 852–8 855 830) and the class 4 stable endemic transmission risk average was 5 168 571 (range 4 337 786–5 823 280) (Table 5).

Discussion

It should be pointed out that while Kenya has a large diversity in human population distribution from the intensively urban centres of Nairobi and Mombasa to the rural coastal, lakeside and pastoralist communities, the analyses discussed here arise from one country. While illustrative, it is clear that further evaluation of these human population distribution surfaces in countries of different size and experiencing different levels of urbanization and population aggregation are desirable. Nevertheless, as a result of these simple comparisons, certain characteristics that are helpful for evaluating population surfaces for use in epidemiological and public health applications are apparent. All the human population distribution surfaces tested showed a sharp transition in predictive accuracy when evaluated below the level of the input census data regardless of the interpolation method used. This can be seen by examining the number of admin units available for interpolation (Table 1) and the point at which accuracy metrics rapidly decrease (Table 3). UNEP99, GPW299 and LS99 use 258 units which correspond to division level data (admin3) from the 1989 Kenya census. GPW3UR and GPW399 are the exceptions that prove the rule, as they have no precipitous decline in accuracy at the divisional level and input data at the sub-location level. The fact that all RMSEs exceeded the size of the average population of administrative unit at any spatial resolution division finer than the input census data underscores the importance of investigating the local ASR metric (Table 2) no matter how beguiling the spatial resolution of the gridded surface appears (Figure 1) or the sophistication of the modelling used.

It is important to emphasize therefore that knowledge of local resolution of input polygon data is essential when using population surfaces especially when conducting studies at regional, continental and global scales. For example GPW399 has 25 times more population administrative units for Kenya than any of the other surfaces and more administrative units for Africa than LS99 uses for the entire world (Table 1). In addition, all population surfaces will have some countries and regions that will have input data no better than a national average (admin0) and that they may rely on very old census information (URL: http://www.census.gov). The ability to determine the spatial and temporal fidelity of products is therefore highly desirable and the metadata that are distributed with UNEP99 (Deichmann 1996), GPW299 (Deichmann et al. 2001), GPW399 (Balk & Yetman 2004) and GPW3UR99 (Balk et al. 2004; CIESIN/IPFRI/CIAT 2004) may be extremely useful in this regard. Dissemination of such metadata, as well as information including the details of ancillary data used and weights applied in modelling are also prerequisites for interpreting human population distribution surfaces. The information distributed with Landscan, for example, remains limited in this respect. The provision of details of ancillary data used in such smart interpolation procedures is of importance in avoiding the introduction of bias when these population layers are compared with other information sources based on the same data. Such additional knowledge has never been utilized when deriving burden of disease estimates and part of our future work is directed at using these surfaces to define spatial variation in the confidence of population-based health metrics derived across countries, regions and the globe.

It is clear that the current accuracy of GPW3UR and GPW399 for Kenya is largely due to access to admin5 data. It is also surprising, that despite the difference in complexity between the methods used, and types and ages of data available to generate UNEP99, GPW299 and LS99, the RMSE differences between them are relatively small (Table 3, Figures 4 and 5). Moreover, these differences relate more to how accurately the various maps had defined the national park and forest areas of Kenya in their interpolation processes, than to the techniques used (Figure 5). It is evident therefore that these human population distribution surfaces could be improved simply by using more accurate and contemporary vector files of gazetted locations, although the gains in accuracy due to better ancillary data are insignificant when compared with gains in accuracy due to higher resolution input population data. To a lesser extent the same arguments can be applied to the resolution of the national boundary and coastlines used.

The comparison of simple interpolation techniques through the administrative hierarchy was also illuminating. The accessibility potential interpolation method offered some increased skill at the provincial level but failed to exceed the precision achieved by areal weighting or pycnophylactic interpolation at the lower administrative levels. Pycnophylactic interpolation always decreased accuracy over areal weighting and can thus only be justified on aesthetic grounds. Given the ease of implementation of areal weighting it remains the default technique where the ASR of the population data exceeds that of the ancillary GIS data. The results do point to a role for smart interpolation techniques but that these are going to be strongly influenced by the spatial resolution of the ancillary GIS data used. Smart interpolation procedures are based currently on heuristic rules relating population distribution to socioeconomic factors, without a solid evidence-base for such rules. Finding the balance between the accuracy gained for the increased complexity of smart interpolation, based on reality using high spatial resolution remotely sensed data is the subject of on-going work (Tatem & Hay 2004; Tatem et al. 2004).

The influence of these respective human population surfaces was illustrated dramatically by showing the difference in population at malaria risk for a nation such as Kenya that can be generated simply by the choice of population surface. Differences between the extreme extractions, expressed as a percentage of the average extracted for total population at risk was 10% but reached 28% in the highest endemicity class. Such margins would have very dramatic effects on any disease burden and commodity needs estimation that might use these numbers. It is clear that the assumption of a uniformly distributed human population would generate wildly inaccurate numbers.

We have tested the precision of existing continuous human population distribution surfaces for Kenya and demonstrated the accuracy with which novel human population distribution maps can be generated using a range of available and simple interpolation techniques. The paramount importance of the ASR of the input census data has been highlighted and its consideration when utilizing such data emphasized. Obviously, these results argue primarily for the free distribution of high ASR census data globally but in the real world this will not always be possible. We have therefore further highlighted the issues involved and accuracy that can be obtained using simple interpolation techniques at different administrative levels where these might be locally available. However, a corollary to these findings is that as the ASR of input data for human population distribution surfaces increases with periodic updates, the rationale for modelling human population distribution will decrease. The critical importance of metadata and background information that describes the methodology and data sources used in the construction of the human population distribution, that help the user evaluate the local fidelity of the data, was also laboured. Finally, this is illustrated with the range of population at malaria risk estimates that can be derived from using these various public domain human population distribution maps. The suite of epidemiological application and public health interventions that use human population distribution maps should therefore start to be aware of some the limitations and opportunities we have documented.