Herd behavior in a complex adaptive system

Abstract

In order to survive, self-serving agents in various kinds of complex adaptive systems (CASs) must compete against others for sharing limited resources with biased or unbiased distribution by conducting strategic behaviors. This competition can globally result in the balance of resource allocation. As a result, most of the agents and species can survive well. However, it is a common belief that the formation of a herd in a CAS will cause excess volatility, which can ruin the balance of resource allocation in the CAS. Here this belief is challenged with the results obtained from a modeled resource-allocation system. Based on this system, we designed and conducted a series of computer-aided human experiments including herd behavior. We also performed agent-based simulations and theoretical analyses, in order to confirm the experimental observations and reveal the underlying mechanism. We report that, as long as the ratio of the two resources for allocation is biased enough, the formation of a typically sized herd can help the system to reach the balanced state. This resource ratio also serves as the critical point for a class of phase transition identified herein, which can be used to discover the role change of herd behavior, from a ruinous one to a helpful one. This work is also of value to some fields, ranging from management and social science, to ecology and evolution, and to physics.

Most of the social, ecological, and biological systems that involve a large number of interacting agents can be seen as complex adaptive systems (CASs), because they are characterized by a high degree of adaptive capacities to the changing environment. CAS dynamics and collective behaviors have attracted much attention among physical scientists (1–3). In order to survive, self-serving agents in these CASs must compete against others for limited resources with biased or unbiased distribution by conducting strategic behaviors. This competition can globally result in balanced or unbalanced resource allocation. Examples of such phenomena involve many species like human beings. For instance, drivers select different traffic routes, people bet on horse racing with odds, and so on. In general, the allocation of the resources in a CAS could reach a balanced state due to the preferences and decision making ability of agents, as revealed by investigating a resource-allocation problem (4). In practice, however, it will sometimes fail to reach the balanced state. For this, one important reason is due to the formation of a herd. In fact, herding extensively exists in collective behaviors of many species in CASs, including human beings. Though human decisions are basically made according to individual thinking, people tend to pay heed to what others are doing, emulate successful persons, or those of higher status, and thus follow the current trend. For example, young girls often copy the clothing style of some famous stars named as trendsetters in the fashion world. Similarly, researchers would rather choose to work on a topic that is currently hot in the scientific society. As a result, large numbers of people may act in concert, and this unplanned formation of crowds is called herd behavior (5). Locally speaking, either the irrationality (6, 7) or rationality (8–10), of an individual agent can be the cause of herd behavior. The global view of herding often implies the ruin of balance by causing excessive volatility in the resource allocation system. Accordingly, herd behavior is commonly seen as a tailor-made cause for explaining bubbles and crashes in a CAS with the existence of extremely high volatility. But is this “common sense” always right? Based on results of this study, we argue that herd behavior should not be labeled like the killer of balance and stability all the time. Here we focus on the effect of herding on the whole CAS for resource allocation, because it is most important for as many agents (involving human beings) as possible to survive in various kinds of CASs like social, ecological or biological systems. Therefore, we shall not study or consider the details on how to reach a herd through contagion and/or imitating. In fact, our results are not dependent on the process of herding formation.

Experiment

We design and conduct a series of computer-aided human experiments, on the basis of the resource-allocation system (4, 11–13), in order to study the necessary conditions for a CAS to reach the ideal balanced state. Using this kind of experimental settings will allow us to investigate the herd behavior in a well regulated abstract system for resource allocation, which reflects the fundamental characteristics of many CASs (14–17). Human participants of the resource-allocation experiment are students recruited from several departments of Fudan University. Before the start of experiments, a leaflet (as shown in SI Text: Part I) was provided which explains configurations of the experiment and actions of the participants. There are two rooms (Room 1 and Room 2) and the amounts of resource in these two rooms are M₁ and M₂ (≤ M₁), respectively. As the experiment evolves, M₁ and M₂ are kept fixed and unknown to all the participants. For each experiment round, each participant has to choose one of the two rooms to enter. Those who go into the same room should share alike the virtual resource (M₁ or M₂) in it. Apart from human participants, there are also imitating agents joining the experiment. All the imitating agents are generated by a computer program, because their decisions are simply made by mimicking human participants’ behaviors. In particular, each imitating agent will randomly select a group (of size five) of human participants at every experiment round, and then follow the choice of the best participant (who has the highest score) in the group for the next round. In each round of the experiment, the number of human participants and imitating agents in Room 1 is denoted as N₁ and the number in Room 2 as N₂. Therefore the total number of human participants and imitating agents can be counted as N = N₁ + N₂. The human participants or imitating agents who earned more than the global average (M₁ + M₂)/N are regarded as winners of the round, and the room which the winners had entered as the winning room. The total number of human participants or imitating agents can also be expressed as N = N_n + N_m. Here N_n is the total number of human participants who make decisions by their own, and N_m is the total number of imitating agents who do not have their own ideas. The ratio between imitating agents and human participants is defined as β = N_m/N_n. More details about the experiment can be found at the end of the main text.

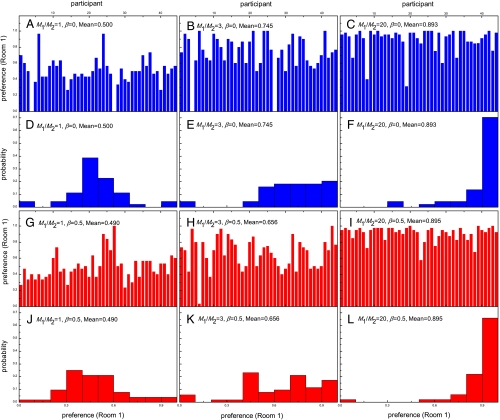
The resource-allocation experiments are conducted repeatedly with different values of M₁/M₂ and β. The modeled system is designed as an open system in which the number of human participants N_n is fixed while the number of imitating agents N_m is increased in an implicit manner. As shown in the previous study (4), the heterogeneity of preferences is an indispensable factor for the whole system to reach the balanced state. Hence the preferences of human participants need to be checked under the influence of imitating agents. For a human participant in the experiment, his/her preference is evaluated as the average rate that he/she chooses to enter Room 1. Preferences of the 44 participants are plotted in Fig. 1 with different M₁/M₂’s and/or β’s. Fig. 1A shows the preferences of human participants when M₁/M₂ = 1 and the imitating agents are absent. Distinctions among the preferences of human participants can be easily identified. For example, the fourth participant is strongly partial to entering Room 2 while the sixth participant prefers Room 1 much more. It can be found in Fig. 1 B and C, that the human participants still have diverse preferences even when M₁ becomes much larger than M₂. In addition, the heterogeneity of preferences remains even for the cases in which N_m = N_n/2 imitating agents are involved; see Fig. 1 G–I. Despite of this heterogeneity, the average of participants’ preferences changes along with M₁/M₂. In other words, human participants have the ability to adapt themselves to fit the environment.

Fig. 1.

Data obtained from the human experiment. (A–C,G–I) Preferences of the 44 participants in sequence to Room 1 for the cases (A–C) without and (G–I) with imitating agents, β = (A-C) 0 and (G–I) 0.5, for the resource distributions M₁/M₂ = (A,G) 1, (B,H) 3, and (C,I) 20. Here, “Mean” denotes the average value of the preferences of the 44 participants. (D–F,J–L) Distribution of the 44 participants’ preferences.

Comparisons of the distributions of human participants’ preferences, as the resource distribution M₁/M₂ is varied and/or the imitating agents are involved, are shown in Fig. 1 D–F, J–L. From Fig. 1 D and E, one can find that when M₁/M₂ is not so biased, human participants alone can do the analysis of the system so well that they can make the whole system reach the balanced state. Note that the preference distribution has a peak at 0.5 in Fig. 1D and the participants’ preferences are mainly distributed around 0.75 in Fig. 1E. Both of the two observations can be deduced from the resource distribution, M₁/M₂ = 1 and M₁/M₂ = 3. When the imitating agents are involved, however, the two preference distributions have some changes in Fig. 1 J and K. In particular, the peak almost disappears in Fig. 1J and the mean value of participants’ preference deviates from the resource distribution bias in Fig. 1K. A possible reason for these changes can be inferred as that human participants may get confused by the behavior of imitating agents. Hence in this case the herd (which is formed by imitating agents) indeed disturbs the system and weakens the analyzing ability of human participants. Things are different if M₁/M₂ gets even larger, as shown in Fig. 1 F and L. Here the involvement of imitating agents does not bring much change to the preference distribution of human participants. One may say that, in this case, herd behavior has no harmful effect on the analyzing ability of the human participants. Finally, it is interesting to note from the same figure, that a minority of human participants with preference to Room 2 can stay alive even in a highly biased system (M₁/M₂≫1) when the imitating agents exist.

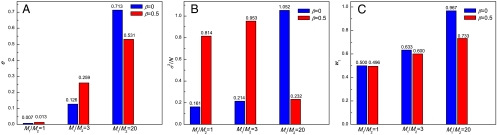
To evaluate the performance of the whole system, we have calculated efficiency (which, herein, only describes the degree of balance of resource allocation), stability, and predictability of the resource-allocation system. The efficiency of the whole system can be defined as 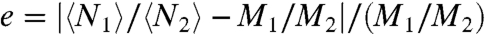. A smaller e means a higher efficiency in the allocation of resources. The stability of the resource-allocation system can be described as 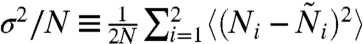, where 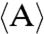denotes the average of time series A. This definition describes the fluctuation (volatility) in the room population away from the balanced state, where the optimal room populations 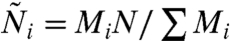can be realized. The predictability of the system is measured by the “uniformity” of the winning rates in different rooms. The winning rate in Room 1 is denoted as w₁. It is obvious that if w₁ is close to 0.5, choices of the two rooms are symmetrical and the system is unpredictable. If the winning rates were too biased, smart participants should be able to predict the next winning room in the experiment. As shown in Fig. 2, when M₁/M₂ is small (M₁/M₂ = 1 or 3), adding some imitating agents will lower the efficiency and cause large fluctuations. On the other hand, when M₁/M₂ get even larger (M₁/M₂ = 20), the formation of herd can improve the efficiency, the stability, and the unpredictability of the resource-allocation system.

Fig. 2.

Experimental results for (A) efficiency e, (B) stability σ²/N, and (C) predictability w₁ of the modeled resource-allocation system, with human participants N_n = 50. β = 0 and 0.5 correspond to imitating agents N_m =0 and 25, respectively. Each experiment lasts for 30 rounds.

Agent-Based Modeling

An agent-based model is developed in order to fully understand the preceding experimental results. Consider a situation where N agents repeatedly join a resource-allocation system. Among these agents, there are N_n normal agents (which correspond to human participants in the preceding experiments) and N_m imitating agents, so that the total number of agents can be calculated as N = N_n + N_m. To play in the resource-allocation system, each normal agent will take S strategies from the full strategy space and compose a strategy book. A strategy for the resource-allocation experiment is typically a choice table which consists of two columns. The left column is for the P possible situations, and the right column is filled with bits of 0 or 1. Bit 1 is linked to the choice for the entrance of Room 1, while bit 0 to that of Room 2. In the strategy book of a normal agent, strategies differ from each other in the preference, which is defined as an integer L (0 ≤ L ≤ P). To model the heterogeneity of preference, let the normal agent pick up a preference number L first. Then each element of the strategy’s right column is filled in by 1 with the probability L/P, and by 0 with the probability (P - L)/P (more detailed explanations can be found in SI Text: Part II). The process will be repeated S times, each time with a randomly chosen L for each normal agent to complete the construction of its strategy book. From the start of the resource-allocation experiment, each normal agent will score all the strategies in its strategy book so as to evaluate how successful they are to predict the winning room. Following the hitherto best performing strategy in their strategy books, normal agents are enabled to make decisions to enter one of the two rooms, once the current situation is randomly given*. Imitating agents in the model behave in a different way during the process of decision making. Before each round of the play starts, each imitating agent will randomly select a group of k (1 ≤ k ≤ N_n) normal agents ^†. Within this group, the imitating agent will find the normal agent who has the best performance so far and imitate its behavior in the following experiment round. It is assumed that the imitating agents know neither the historical record of the winning room nor the details of strategy books of other group members. The only information for them to access is the performance of the normal agents, that is, the virtual money that these normal agents have earned from the beginning of the experiment. If the number of imitating agents N_m kept increasing, there would be more and more positive correlations among agents’ decisions, which would trigger the formation of a herd in the system.

Simulation Results of the Agent-Based Modeling

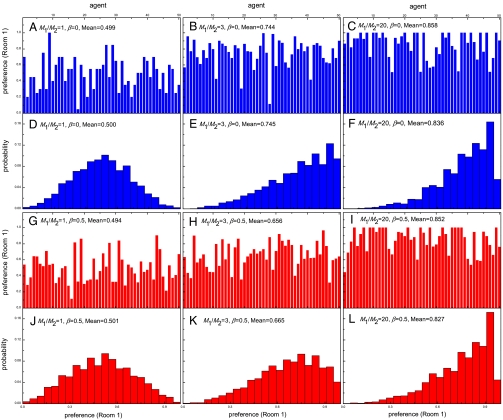
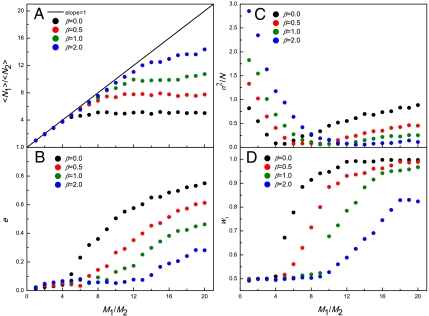
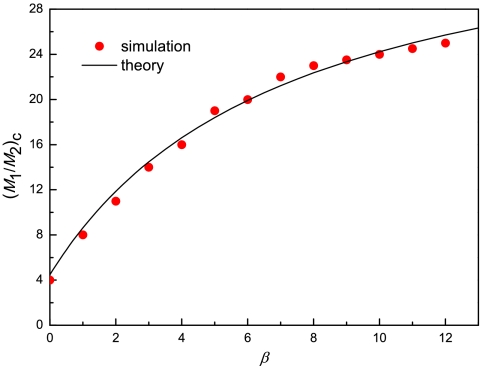
Agent -based simulations are carried out in an open system condition, in reference to the experiments. (Please refer to SI Text: Part III to see the results for a closed system.) Following the analysis of experimental results, we first investigate the simulation results for the preferences of normal agents. Clearly, Fig. 3 shows distributions of the preferences similar to those shown in Fig. 1. The qualitative agreement indicates that our agent-based modeling has taken into account the heterogeneity of preferences with a reasonable modeling of the decision making process for the human participants. (We had also investigated the preferences of normal agents in an alternative way by analyzing the Shannon information entropy; see SI Text: Part IV) Next, efficiency, stability, and predictability of the whole modeled system are calculated according to the definitions made in the experimental study. The change of system behavior along with the variation of the resource ratio M₁/M₂ is shown in Fig. 4. Differently colored symbols in the figure represent results obtained under different values of β. As shown in Fig. 4A, when the resource distribution is comparable (M₁/M₂ ≈ 1), the averaged population ratio 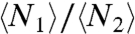can always be in concert with M₁/M₂ no matter imitating agents are involved or not. On the other hand, as the resource distribution gets more and more biased (M₁/M₂ increases), surprisingly the whole system tends to reach the balanced state only if more imitating agents (larger β) join the system. Fig. 4B shows the change of efficiency of the resource-allocation system. The tendency is that when the resource ratio gets more biased, a larger size of herd is needed to realize a higher efficiency of the resource distribution. From both the subfigures, the so-called “M₁/M₂ phase transition” (4), where M₁/M₂ plays the role of control parameter, can also be identified. As shown in Fig. 4C, the increase of the number of imitating agents will cause larger fluctuations in the low M₁/M₂ region. However, as M₁/M₂ increases, more imitating agents can yield higher stability of the resource-allocation systems. Comparing system behaviors for the cases of β = 0 and β ≠ 0, the M₁/M₂ phase transition also indicates the change of role for the herd behavior, namely, from a ruinous herd into a helpful herd. It is clear that the critical point of the M₁/M₂ phase transitions get larger when the number of imitating agents increases. Denoted as (M₁/M₂)_c hereafter, the critical point refers to the M₁/M₂ value where the minimum of σ²/N is achieved. This definition together with the mechanism for the increase of (M₁/M₂)_c will be further discussed in the theoretical analysis of the model. Finally, the effect of herd behavior on the predictability of the resource-allocation system is shown in Fig. 4D. When more imitating agents are introduced to the system for large M₁/M₂, the prediction of the next winning room becomes more difficult as winning rates for the two rooms are more symmetric. Notice that the system behavior under various conditions found herein by the agent-based simulations echoes with the observations in the experiment.

Fig. 3.

Simulation results obtained from the agent-based simulations. (A–C,G–I) Preferences of the 50 normal agents to Room 1 for the cases (A–C) without (β = 0) and (G–I) with (β = 0.5) imitating agents, and for the resource distributions M₁/M₂ = (A,G) 1, (B,H) 3, and (C,I) 20. We have run the simulations for 200 times, each over 400 time steps (first half for equilibration, the remaining half for statistics). (A–C,G–I) are typical results of one of the 200 runs. In (A–C,G–I), “Mean” denotes the mean value of the preferences of the 50 normal agents. (D–F,J–L) Distribution of the 50 normal agents’ preferences. Note that (D–F,J–L) are obtained from the average over the 200 runs, and also the “Mean” in (D–F,J–L) denotes this average. Simulation parameters: S = 4, P = 16, and N_n = 50.

Fig. 4.

(A) 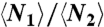, (B) e, (C) σ²/N, and (D) w₁ as a function of M₁/M₂, for an open system in the agent-based simulations. Parameters: N_n = 50, S = 4, P = 16, k = 5, and β = 0, 0.5, 1.0, and 2.0. For each parameter set, simulations are run for 200 times, each over 400 time steps (first half for equilibration, the remaining half for statistics). In (A), “slope = 1” denotes the straight line with slope being 1.

We summarize the simulation results here and make some more comments to emphasize the significance of findings in our study. The performance of the resource-allocation system consisting of normal agents or human participants with the full decision making ability is, in some cases, inferior to those including imitating agents (who form the herd). This argument might seem questionable at first sight. In particular, it may be argued that the failure to reach the balanced resource allocation for large M₁/M₂ when β = 0 is only due to the relatively small population of the normal agents. However, it has been proved in the theoretical analysis [see the equation for the population in the next section or Eq. S6 in SI Text: Part II] and the agent-based simulation of resource-allocation systems (4) that the total number of agents is indeed not a key factor. When the resource distribution is not biased so much, the normal agents can play pretty well so that the resource-allocation system behaves in a healthy manner (efficient or balanced, stable and unpredictable). In such kind of situations, adding imitating agents will only bring about a “crowded system” in which larger fluctuations (volatility) turn up. In this respect, our study shares some common features with the Binary-Agent-Resource model (18, 19). In particular, the “crowd effect” has been observed in these models and the inclusion of imitating agents in our model can be explained as a special kind of networking effects. Only if the resource distribution becomes so biased that most of the normal agents cannot completely solve the decision making problem by referencing their strategy books, adding the imitating agents could become a helpful factor in consuming the remained arbitrage opportunities in the system. The discussion above explains the reason why the herd behavior in the resource-allocation system can effectively help the system to realize the balanced state and reduce instability and predictability in the mean time.

Theoretical Analysis of the Agent-Based Modeling

To further understand the underlying mechanism for these phenomena, we also conduct a theoretical analysis by deriving the critical points (M₁/M₂)_c for the M₁/M₂ phase transition identified in the agent-based simulations. (For the details of derivation, please refer to SI Text: Part II.) As a result of the theoretical analysis, the maximum of population ratio in Room 1 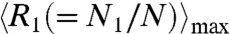can be obtained under the condition M₁≥M₂. Its formula reads as the following (the meaning of the symbols can also be found in SI Text: Part II),

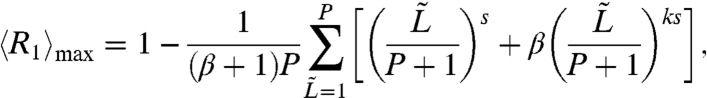where 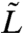stands for the preference of a normal agent’s strategy. If 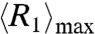is not less than M₁/(M₁ + M₂), the system can fluctuate around the balanced state. Otherwise, the system can never reach the balanced state. Then some insightful comments can be added:

• The state of the resource-allocation system depends only on M₁/M₂, β, k, P, and S. This state has no concern with N_n or N_m.

• An optimized value of β may be calculated by setting 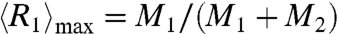, which could make the system most stable. After substituting this expression into the equation for 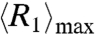, we can obtain numerical solutions for the critical points (M₁/M₂)_c of the phase transitions. Fig. 5 shows a good agreement between the simulation results and those of theoretical derivation for the critical points.

• It is easy to prove that 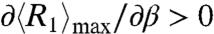, which means that β and 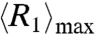are positively related. When β → ∞, the population ratio will converge to 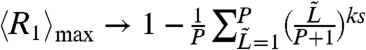. At this limit, the model suggested here will be equivalent to the original resource-allocation model without the imitating agents (4), except that in this case, each agent would occupy kS (instead of S) strategies.

Fig. 5.

Critical points of the M₁/M₂ phase transition, (M₁/M₂)_c, varying with different population ratios β: simulation results (symbols) vs. theoretical results (line). The simulation results are obtained from the data in Fig. 4 A and C.

Discussion and Conclusions

We have revealed that, if the bias between the two resources M₁/M₂ were large and unknown to the participants, a herd of a typical size could help the overall system to reach the optimal state, namely, the state with a minimal fluctuation, a high efficiency, and a relatively low predictability. The corresponding ratio between the two resources also works as the critical point of a class of M₁/M₂ phase transition. The phase transition can be used to discover the role change of herd behavior, namely from a ruinous herd to a helpful herd as the resources distribution gets more and more biased. The main reason for this generalization could be understood as follows. When a large bias exists in the distribution of resource, the richer room will offer more arbitrage opportunities so that it deserves to be chosen without too much deliberation. Because imitating agents learn from the local best human participant or normal agent, the herd formed by these agents will certainly be more oriented to the richer room. To balance a highly biased resource distribution, in fact, it correspondingly needs a suitable number of participants who have a highly biased orientation in their choices. But every coin has two sides. Normal agents will be confused if too many imitating agents are involved. Because in that case, normal agents have to estimate not only the unknown system but also the behavior of the herd. The effect of herd behavior would become negative again under these situations. We emphasize that these arguments are quite general. In particular such arguments are independent of the process of herding. In SI Text: Part V, results of a different agent-based model, in which imitating agents follow the majority of the linked group, rather than the best normal agent, are shown. Similar results are achieved indeed.

This work is also expected to be important to some fields, ranging from management and social science, to ecology and evolution, and to physics. In management and social science, administrators should not only conduct risk management after the formation of herd, but also need to consider system environment and timing to see whether the herd is globally helpful or not. In ecology and evolution, it is not only necessary to study the mechanism of herd formation as usual, but also to pay more attention to the effect of herding on the whole ecological system and/or evolution groups. For physics, this work not only presents the existence of phase transition in such a complex adaptive system, but also proposes a new equilibrium theory. Namely, in the presence of symmetry breaking, a complex adaptive system is likely to reach the equilibrium state only through the performance of typically sized clusters.

About the Computer-Aided Human Experiment

All the experiments are carried out in an online manner. Human participants can get the necessary information only from their computer terminals. The desktop designs of the experiment-control computer program are shown in Fig. S1. The control panel for the experiment coordinator is configurated as panel (A), and that for human participants as panel (B). At the beginning of the experiment, the coordinator input the value of M₁/M₂ and β, and set the time length (60 s) for the human participants to make their decisions. When all the human participants have logged in, the coordinator can click the “start” button to start the experiment. After all the participants have made their choices, the coordinator clicks the “reset” button to end the current round and set anew. On panel (B), buttons with numbers of 1 and 2 are used to choose Room 1 and Room 2. The left of the panel displays the current score (a) of the participant and the current experiment round (t). To keep every participant conducting the experiment independently, procedures and rules of the experiment are designed carefully so that possible direct or indirect communications can be shut off. For example, participants can only make their own choices by clicking the button instead of raising their hands. This limitation could make sure that participants cannot get information from sounds, expressions, or gestures of the others. There is also no need for the experiment coordinator to announce the result of winning room. Participants can only deduce the winning room from the change of their scores on the desktop panels. In addition, no human participants had been kicked off (please refer to SI Text: Part I) during the experiments. For all the experiments with M₁/M₂ = 1, 3, and 20, the total number of human participants was kept to be 50. Among those, 44 human participants played through all the three experiment sessions. On the other hand, we had member-changes for the remained six participants.