Pattern of trauma determines the threshold for epileptic activity in a model of cortical deafferentation

Abstract

Epileptic activity often occurs in the cortex after a latent period after head trauma; this delay has been attributed to the destabilizing influence of homeostatic synaptic scaling and changes in intrinsic properties. However, the impact of the spatial organization of cortical trauma on epileptogenesis is poorly understood. We addressed this question by analyzing the dynamics of a large-scale biophysically realistic cortical network model subjected to different patterns of trauma. Our results suggest that the spatial pattern of trauma can greatly affect the propensity for developing posttraumatic epileptic activity. For the same fraction of lesioned neurons, spatially compact trauma resulted in stronger posttraumatic elevation of paroxysmal activity than spatially diffuse trauma. In the case of very severe trauma, diffuse distribution of a small number of surviving intact neurons alleviated posttraumatic epileptogenesis. We suggest that clinical evaluation of the severity of brain trauma should take into account the spatial pattern of the injured cortex.

Epileptic activity in the brain emerges on several organizational levels from hyperexcitable dynamics of single neurons that result from genetic predisposition (1) or pathological alterations in extracellular ionic concentrations (2–9) to aberrations in network structure that give rise to hypersynchronization of neuronal ensembles and subsequent onset of seizures (10). Such changes in network connectivity and structure may occur after severe brain trauma, which commonly leads to epileptogenesis (11). Trauma-related epileptic activity often occurs after a latent period that offers a potential therapeutic window to reduce the likelihood of later seizure onset. Given this latency, it is imperative to understand how different spatial patterns of trauma affect the propensity of a network (composed of both healthy and traumatized cells) to develop posttraumatic epileptic activity.

A likely effect of brain trauma may include damage to synaptic connectivity between neurons. Such damage would lead to reduction of the long-range excitatory inputs to affected areas, therefore creating islands of partially isolated cortical tissue with strongly reduced neuronal activity. Evidence from in vitro studies suggests that chronic blockade of activity may modify synaptic strengths and intrinsic neuronal excitability. After a few days of pharmacological blockade of activity in cortical cell cultures, the amplitudes of excitatory postsynaptic currents (EPSCs) and miniature EPSCs (mEPSCs) in pyramidal cells increase (12, 13), and quantal release probabilities increase as well (14). Conversely, prolonged enhanced activity levels induced by blockade of synaptic inhibition or elevated extracellular potassium ([K⁺]_o) reduce the size of mEPSCs (12, 15, 16). Similar activity-dependent changes in mEPSC size have been observed in spinal cell cultures (17). There is a similar regulation of NMDA receptor-mediated currents by activity (13, 15). Interestingly, miniature inhibitory postsynaptic currents are scaled down with activity blockade in the opposite direction to excitatory currents. This effect is reversible (18) and accompanied by a reduction in the number of open GABA_A channels and GABA_A receptors clustered at synaptic sites (19). These observations suggest the existence of a fundamental mechanism, termed homeostatic plasticity (20), that controls the levels of neuronal activity, such as the firing rates (12, 14). Similar homeostatic processes were also reported in vivo (21, 22).

We previously showed (23, 24) that homeostatic plasticity, which normally maintains a moderate level of activity in the cortex, may fail to control normal excitability in heterogeneous networks, where there are subpopulations of neurons with different levels of activity—conditions found in the traumatized cortex (25). This unstable balance of excitation and inhibition leads to paroxysmal seizures. However, the role of trauma geometry and size in epileptogenesis remains unknown. In this study, we aimed to understand the combined effects of trauma geometry and homeostatic regulation of synaptic conductances. We constructed a large-scale realistic computational model of cortical network and studied its dynamics in response to different spatial patterns of deafferentation. We specifically focused on cortical undercut experiments. Results of the present study support earlier theories regarding the potential pathological role of excessive homeostatic regulation in posttraumatic epileptogenesis. Furthermore, it predicts that the propensity of homeostatic synaptic plasticity (HSP) to evoke seizure-like dynamics is critically dependent on the spatial profile of cortical trauma.

Results

Characteristics of Collective Burst Discharges in Randomly Deafferented Model Networks Depend on Intrinsic Excitability and Synaptic Plasticity.

We first investigated the response of a network (SI Materials and Methods) to a fixed amount of HSP imposed immediately after trauma. In control conditions, each neuron in the model network received uncorrelated Poisson distributed spike train delivered through AMPA-type receptors; this input simulated spontaneous activity of the rest of the cortical population not included in the biophysical network model. This activity led to asynchronous activity in populations of model pyramidal (PY) cells and interneurons (INs), with PY cells firing at ∼5 Hz. The effect of trauma was simulated by reducing the external input to different degrees (afferent stimulation rate was multiplied by the rate drop factor r_D < 1) to randomly selected fractions of excitatory and inhibitory neurons (controlled by the parameter f_D < 1). These two parameters (f_D and r_D) defined the severity of deafferentation (e.g., f_D = 0.9 and r_D = 0.1), which means that 90% of neurons received only 10% of the original input rate after deafferentation. Immediately after random deafferentation, the strength of PY to PY and IN to PY synapses was changed to model homeostatic synaptic plasticity. Dynamics of the model were then monitored for fixed amounts of HSP (e.g., 100% HSP corresponded to an increase by 100% of PY–PY coupling strength and a decrease by 50% in the strength of IN–PY coupling).

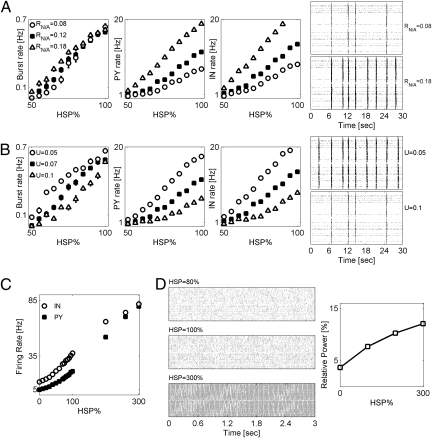
Reduction of afferent input led to the decrease of the averaged firing rate, which was then partially or fully recovered by posttraumatic HSP. Depending on the degree of deafferentation and the strength of imposed HSP, the resulting network's activity could remain asynchronous or could display bursting dynamics. The last was quantified by calculating the burst rate for a given degree of deafferentation and different levels of HSP. An increase of HSP scaling generally led to an increase of bursting rate (Fig. 1). Consistent with the predictions of previous conductance-based models of traumatized cortical networks, the rate of bursts showed very weak dependence on NMDA to AMPA conductance ratio for high levels of HSP (>70%), although somewhat stronger dependence was seen for lower levels of HSP (23) (Fig. 1A). The firing rate of both PY and IN neurons was strongly dependent on the NMDA to AMPA conductance ratio (Fig. 1A). Raster plots of network activity (Fig. 1A) confirm that modulation of NMDA synaptic content mostly affects the intraburst firing rate of model neurons.

Fig. 1.

 Patterns of networks’ activity in 2D deafferented networks depend on synaptic plasticity and neuronal excitability. (A, plot 1) Burst rate vs. HSP for different NMDA–AMPA conductance ratios: R_NIA = 0.08 (circles), R_NIA = 0.12 (squares, baseline model), and R_NIA = 0.18 (triangles). (A, plots 2 and 3) Averaged rates of PY and IN neurons firing vs. HSP for the different scenarios shown in plot 1. (A, plot 4) Raster plots for a fixed level of HSP (60%) and different NMDA–AMPA conductance ratios: R_NIA = 0.08 (top raster) and R_NIA = 0.18 (bottom raster). Neurons (both PY and IN) were randomly sampled from the central block of 20 × 20 neurons. Deafferentation was f_D = 0.9 and r_D = 0.1, and it was spatially random. Data points are mean ± SEM (n = 5). (B, plot 1) Burst rate vs. HSP for different parameters of synaptic depression: U = 0.05 (circles), U = 0.07 (squares, baseline model), and U = 0.1 (triangles). (A, plots 2 and 3) Averaged rates of PY and IN neurons firing vs. HSP for different scenarios shown in plot 1. (A, plot 4) Raster plots for a fixed level of HSP (60%) and different values of U: U = 0.05 (top raster) and U = 0.1 (bottom raster). Neuronal sampling and deafferentation were as shown in A. Data points are mean ± SEM (n = 5). (C) Firing rate of PY (closed squares) and IN (open circles) neurons vs. HSP in an intact model network. (D Left) Raster plots of intact network activity vs. HSP. (D Right) Relative power of collective activity in the γ-band (40–90 Hz) vs. HSP.

The response of a network after deafferentation and HSP also depended on the parameters of synaptic transmission, such as the extent of synaptic depression at model excitatory AMPA and NMDA synapses (captured by the value of U; e.g., U = 0.1 means that 10% of synaptic resources are used by a single synaptic event). Weaker synaptic depression led to an increase in the rate of network burst generation (Fig. 1B), which was accompanied by increases in the firing rate of both PY and IN model neurons (Fig. 1B).

The emergence of network bursting events could simply be a consequence of synaptic scaling. Alternatively, it could represent the nontrivial effect of posttraumatic network reorganization that includes both synaptic scaling and changes in network's excitability (brought about by neuronal deafferentation). To test this issue, we monitored the dynamics of a model intact (without deafferentation) network for different fixed amounts of HSP at model synapses. Both PY and IN neurons had their firing rates increased for higher amounts of HSP (Fig. 1C). For physiologically relevant levels of synaptic scaling (maximal up-regulation of 100%) (12), the collective activity remained asynchronous, and no bursting was observed (Fig. 1D Top Left and Middle Left). Stronger scaling led to the appearance of high-frequency collective oscillations (Fig. 1D Left Bottom), which were characterized by an increase in the relative power in the γ-band (40–90 Hz) (Fig. 1D Right). However, these oscillations were only supported by unrealistically high firing rates of model PY and IN neurons (Fig. 1C) and differed from the interictal-like bursts that had temporal widths of ∼200 ms. Thus, within the physiologically relevant limits, bursting dynamics in our model network reflect the combined effect of neuronal deafferentation and homeostatic synaptic plasticity.

Severity of Spatially Random Deafferentation Determines the Reorganization of Network Activity by Homeostatic Plasticity.

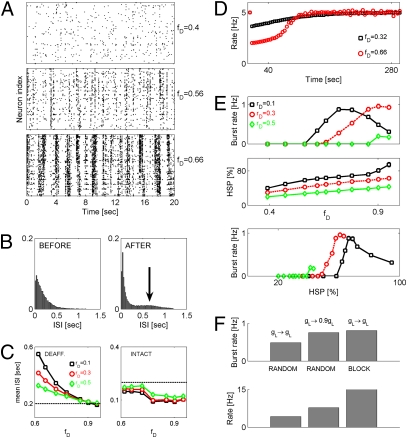
To study the homeostatic response of our model network to the spatially random pattern of neuronal deafferentation, we reduced the rate of afferent synaptic excitation (as captured by the parameter r_D) to a set of randomly selected neurons N_deaff (such that N_deaff = ⌊f_DN⌋, where N = entire network size). After the process of deafferentation, activity of the network was monitored for a long time (more than 300 s of biological time). During that time, the strength of collateral synaptic connections was gradually adjusted according to Eqs. S16 and S17 (SI Materials and Methods) to model HSP until the network reached a new steady state. In this new posttraumatic steady state, the network-averaged firing rate of pyramidal neurons (both deafferented and intact) was equal to the rate before deafferentation (5 Hz) (Fig. 2D). Severe network deafferentation led to the emergence of global, network-wide bursting events, each lasting for ∼200 ms (Fig. 2A shows sample raster plots). After deafferentation and subsequent reorganization of activity by HSP, the distribution of interspike intervals (ISIs) became more concentrated, with a stronger peak at short ISIs (reflecting ISIs within a burst) and a second peak reflecting interburst ISIs (Fig. 2B). The firing rate of deafferented neurons in the steady state was higher (smaller ISI) for smaller decreases in the rate of afferent excitation (captured by r_D; larger values of r_D correspond to a smaller decrease of the afferent stimulation rate) (Fig. 2C). The steady state firing rate of nondeafferented neurons (preserving their external input) was higher than the target rate of 5 Hz but otherwise, showed no consistent dependence on deafferentation parameters. The network-averaged rate of pyramidal neurons firing converged to the target level of 5 Hz (Fig. 2D).

Fig. 2.

Posttraumatic reorganization of activity. (A) Raster plots (in posttraumatic steady state) exemplifying reorganization of activity by HSP: r_D = 0.1 and f_D = 0.4 (Top), r_D = 0.1 and f_D = 0.56 (Middle), and r_D = 0.1 and f_D = 0.66 (Bottom). Neurons were randomly sampled from the central block of 20 × 20 neurons. (B) Distributions of ISIs before (Left) and after (Right) spatially random deafferentation. Location of the second smaller peak in the ISI distribution of posttraumatic network is indicated by an arrow. (C) Mean ISIs (in steady state) of deafferented (Left) and intact (Right) neurons vs. f_D: r_D = 0.1 (squares), r_D = 0.3 (circles), and r_D = 0.5 (diamonds). (D) Dynamics of PY firing rates. Squares: f_D = 0.32 and r_D = 0.1. Circles: f_D = 0.66 and r_D = 0.1. (E Top) Rate of network bursts vs. f_D. Squares: r_D = 0.1. Circles and dashed line: r_D = 0.3. Diamonds: r_D = 0.5. (E Middle) HSP (PY–PY synaptic scaling factor) in steady state vs. f_D. (E Bottom) Burst rate vs. HSP. Data points are mean ± SEM (n = 5). (F Upper) Burst rate in severely deafferented network (r_D = 0.1 and f_D = 0.9) is modulated by 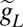(center bar) or the spatial organization of intact neurons (right bar). (F Lower) Firing rates of intact PY neurons for cases shown in F Upper.

The rate of network bursts depended on the extent of deafferentation (captured by the fraction of cells deafferented, f_D), with more severe deafferentation generally resulting in a higher rate of bursting events (Fig. 2E Top). The rate of bursting also depended on the drop in the rate of afferent excitation to deafferented neurons characterized by r_D. Stronger rate drop (smaller r_D) shifted the threshold for burst initiation to smaller values of f_D (Fig. 2E). Interestingly, in the case of a strong afferent rate decrease (r_D), the rate of burst generation first increased with increasing deafferentation levels, but it attained significantly lower values for still higher levels of deafferentation (Fig. 2E) (f_D = 0.6 vs. f_D = 0.9 for r_D = 0.1).

The reduction in burst initiation threshold for smaller values of r_D could simply reflect the fact that burst rate depends on the level of HSP at model synapses, with smaller r_D leading to stronger synaptic scaling and a subsequently higher rate of network bursts generation. To test whether this theory is the case, we plotted, for each deafferentation scenario, the rate of network bursts vs. the amount of HSP at model PY–PY synapses (Fig. 2E Bottom). This plot shows that HSP alone cannot account for the observed change in burst rate—if this case were true, the same levels of HSP (same abscissa points) would have yielded the same burst rates, contrary to what is shown in Fig. 2E Bottom. An alternative explanation is that, in addition to the homeostatic regulation of synaptic conductances, a change in r_D would also affect the nucleation and propagation of bursts through the network. In this view, for relatively mild deafferentation (high r_D and/or low f_D), bursts can be nucleated locally, but their propagation is hampered by the asynchronous activity of sufficiently abundant intact neurons. Therefore, in the network with lesser degree of afferent input deafferentation, a larger fraction of neurons should be deafferented to observe bursting after HSP scaling. A follow up of this latter explanation is that, for spatially random deafferentation, the rate of network bursts should decrease with the increasing size of the region (square block) from which the neuronal activities are sampled, a trend that is observed in our model (SI Materials and Methods). Thus, in the scenario of mild to severe spatially random trauma, the threshold for the appearance of seizure-like activity is modulated by the drop in the rate of afferent excitation, r_D, through modulation of burst propagation through the network.

The explanation provided above accounts for the effects of mild to severe deafferentation on the emergence of epileptic-like activity—more severe deafferentation leads to higher rates of network burst generation (24). A naïve extension of this reasoning would assume that this deafferentation burst rate relation holds for all values of r_D, f_D. However, as shown in Fig. 2E, above the critical level of f_D, a consistent drop in burst rate is observed. The reduction of burst rate was stronger for lower values of r_D (stronger drop in the rate of afferent excitation). Because severely deafferented neurons in our model were not likely to trigger network bursts, we hypothesized that the drop in burst rate was a consequence of the reduced propensity of the intact population to generate bursting events. This failure to nucleate global network bursts could arise because of the insufficient recurrent excitation and could, for example, be alleviated by decreasing the leak conductance of model neurons. Consistent with this last hypothesis, a 10% reduction of leak conductance, g_L, conferred higher excitability on the model neurons, which resulted in higher rates of network bursts even for nearly complete deafferentation (Fig. 2F Upper).

Another way to enhance the nucleation of network bursts by the severely traumatized network is by increasing the recurrent excitation of its remaining intact circuits. As shown in Fig. 2F Upper, when intact neurons were clustered in space (block configuration) to increase the chances of forming a recurrent circuit, network bursts were generated at a much higher rate than for the random deafferentation of comparable severity. The increased rate of burst generation correlated with the increased rate of intact pyramidal neuron firing (Fig. 2F Lower).

Spatial Pattern of Deafferentation Affects the Threshold for Network Burst Emergence.

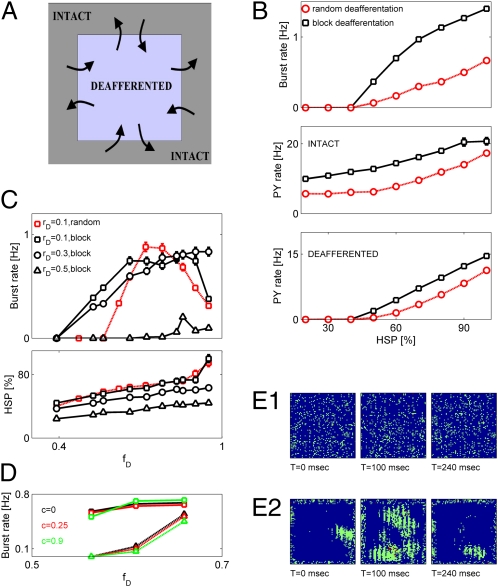
We analyzed the patterns of activity generated by a severely deafferented cortical network under fixed amounts of HSP imposed on the synaptic conductances (Fig. 3 A and B). For the case of spatially structured deafferentation, we focused here on a simple scenario that we term block deafferentation, in which a block of neurons is deafferented by the same r_D. As before, the size of this block was defined by parameter f_D. All boundaries of the deafferented block were connected to the intact part of the network, allowing for symmetric exchange of information between the lesioned and healthy tissue (Fig. 3A). This spatially structured deafferentation was characterized by higher rates of network bursts, higher averaged rate of intact PY neurons firing, and higher averaged rate of deafferented PY neurons firing compared with the scenarios of random deafferentation that targeted the same number of model neurons (Fig. 3B). Hence, the spatial pattern of network lesions might affect the threshold for the emergence of epileptic-like collective burst discharges. This finding suggests that, for mild deafferentation (relatively small f_D), synchronous network bursts are less likely to emerge in the randomly deafferented network, because deafferented neurons are sufficiently diluted in the asynchronous activity of intact population (SI Materials and Methods).

Fig. 3.

Spatially structured cortical deafferentation changes the threshold for network burst emergence. (A) Schematic presentation of the deafferentation setup. (B) Quantification of networks’ activity under the fixed amount of HSP (synaptic conductance scaling) that immediately followed deafferentation. (B Top) Burst rate vs. HSP. Squares, block (structured) deafferentation; circles, spatially random deafferentation. In both cases, r_D = 0.1 and f_D = 0.9. (B Middle) Firing rate of intact PY neurons vs. HSP. Keys are as in B Top. (B Bottom) Firing rate of deafferented PY neurons vs. HSP. Keys are as in B Top. (C Upper) Burst rate vs. f_D. Open red squares, random deafferentation with r_D = 0.1; open black squares, block deafferentation with r_D = 0.1; open black circles, block deafferentation with r_D = 0.3; open black triangles, block deafferentation with r_D = 0.5. (C Lower) HSP (PY–PY synaptic scaling factor) in steady state vs. f_D. Keys are as in C Upper. (D) Effect of correlated afferent inputs. Black, c = 0; red, c = 0.25; green, c = 0.9; solid lines and circles, block deafferentation; dashed lines and triangles, random deafferentation. (E) Collective activity in traumatized network. (E, 1) Snapshots of activity (each dot is model neuronal firing rate in the time bin of 20 ms) in an intact network (before deafferentation). (E, 2) Snapshots of activity in the posttraumatic steady state. Deafferentation parameters are r_D = 0.1 and f_D = 0.75. Color scale is from blue (low firing rates) to red (high firing rates).

Results reported in Fig. 3B suggest that the pattern of spatially structured deafferentation might also affect the threshold (defined in terms of minimal f_D required to observe bursting for a given level of r_D) for pathological network burst generation associated with posttraumatic epilepsy. To address this issue, we analyzed the characteristics of network's activity using different patterns of spatially structured deafferentation (spatially structured deafferentation here is defined as blocks of different dimensions). Fig. 3C Upper shows that the threshold for burst initiation was lower for block deafferentation vs. random deafferentation. Furthermore, for the case of very severely deafferented network (large f_D), block deafferentation led to a higher rate of bursting compared with the case of random trauma; in the last case, the rate of bursting was reduced because of the insufficient excitation of remaining intact neurons. The higher rate of bursting achieved by the network after the spatially structured deafferentation required smaller amounts of HSP at model synapses (Fig. 3C Lower). Collective bursting activity in this scenario of spatially structured trauma nucleated at the boundary separating intact and traumatized regions and engaged many of the deafferented neurons in intense firing before fading away (Fig. 3E, 2). Interestingly, however, introduction of correlation between afferent inputs (SI Materials and Methods) slightly reduced the burst rate around the threshold for spatially random trauma, but it had a minimal effect on the reorganization of network activity after spatially structured trauma (Fig. 3D), thus suggesting that our observations might be robust with respect to different cortical rhythms. Thus, the spatial pattern of cortical trauma can affect the propensity of a network to exhibit seizure-like dynamics.

Spatial Characteristics of Burst Propagation.

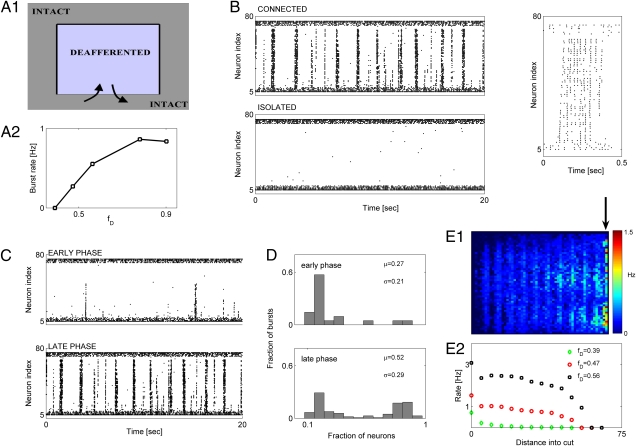
Evidence from cortical undercut experiments (25, 26) suggests that seizure-like discharges originate at the border between relatively intact and deafferented regions, and they propagate into the latter. We set out to determine the spatial characteristics of burst propagation in our model network subject to spatially structured deafferentation. For the sake of clarity in presentation and analysis, we consider, in this section, the case of block-deafferented cortical network in which the synaptic connectivity between the deafferented block region and the intact part is destroyed on three sides of the block; thus, the deafferented and intact networks can communicate only through one side of the block (Fig. 4A). Such model setup was inspired by cortical undercut experiments (25, 26).

Fig. 4.

Characteristics of burst propagation in structurally deafferented model cortical networks. (A, 1) Schematic of deafferentation scenario. (A, 2) Burst rate vs. f_D. For all cases, r_D = 0.1. (B Upper Left) Activity in network for which deafferented region is connected to the intact network (same as in A). (B Lower Left) Activity in network for which deafferented region was completely isolated from the intact network. (B Right) Raster plot showing fine spatiotemporal structure of a sample burst. In all panels, activity of a single column (1D cross-section; 80 neurons), oriented perpendicular to the connecting interface, is shown. Deafferentation parameters are r_D = 0.1 and f_D = 0.56. (C Upper) Partially propagating bursts in the window of 80–100 s after deafferentation. (C Lower) Fully propagating bursts in the window of 280–300 s after deafferentation. Deafferentation parameters are r_D = 0.1 and f_D = 0.56. (D) Distribution of burst intensity during early (D Upper) and late (D Lower) phases of HSP for windows as in C. (E, 1) Spatial map of mean firing rate in posttraumatic steady state. Cool and warm colors are for lower and higher rates of firing, respectively. Contact between the deafferented and intact region is collinear with the arrow. (E, 2) Averaged firing rates of deafferented neurons vs. the distance from the line of contact: f_D = 0.39 and r_D = 0.1 (green diamonds); f_D = 0.47 and r_D = 0.1 (red circles); f_D = 0.56 and r_D = 0.1 (black squares). In E, 1 and 2, the firing rate was computed over a time window of 40 s.

As for the case of deafferented network with fully functional synaptic connections between the deafferented and intact parts (Fig. 3A), homeostatic plasticity of synaptic conductances led to the reorganization of electrical activity. After the trauma and action of HSP, the activity took the form of bursting events (Fig. 4B), with the averaged firing rate of pyramidal neurons settling at the target level of 5 Hz. The rate with which network bursting events were generated in the steady state (after the model pyramidal neurons recovered their averaged firing rate of 5 Hz) depended on the extent of network deafferentation (Fig. 4A, 2). Bursting events were initiated at the border between intact and deafferented areas and propagated inside the deafferented area (Fig. 4B, 1). Furthermore, a complete destruction of synaptic connectivity between the deafferented and intact regions eliminated bursting events altogether, regardless of the degree of HSP (Fig. 4B), suggesting that this mode of collective activity is indeed generated at the border between intact and deafferented regions, which is consistent with experimental observations (25, 26). The speed of burst propagation into the deafferented region was V_burst ∼ 22 footprints/s. Considering that, in real cortical networks, synaptic footprint spans ∼1 mm, the speed of burst propagation in our model networks would translate to ∼2.2 cm/s, an estimate consistent with experimental estimations (27, 28) and results obtained with previous, more detailed models (23).

The constraints on synaptic connectivity imposed by the undercut geometry also allowed us to clearly discriminate between two types of events: (i) full network-wide bursts during which the majority of model neurons fired action potentials (Fig. 4C Lower) and (ii) partial bursts that recruited a fraction of neurons and propagated to a limited distance into the deafferented region (Fig. 4C Upper). Notably, the presence of partial bursts depended on the amount of HSP at model synapses, with the model network generating more partial bursts during the early phase of HSP action. We quantified the relative abundance of partial bursts by building the distributions of burst intensity, which we operationally defined as a fraction of model neurons that was active (firing at least one spike) during the given burst. Both the mean (μ) (Fig. 4D) and SD (σ) (Fig. 4D) of the distribution increased as a function of time elapsed since deafferentation (Fig. 4D). Consistent with this trend, partial bursting events were also observed during the late stage of posttraumatic activity reorganization (after the network had reached the steady state with model pyramidal neurons firing at ∼5 Hz), indicating that this failure of burst propagation depends on the dynamic state of cortical network.

To study the possible effects that lesion size might have on the propagation of bursting events, we computed the mean firing rate of model PY neurons vs. their distance from the interface connecting the intact and deafferented regions for a variety of cut sizes. More severe deafferentation induced stronger HSP and led to a more reliable propagation of bursting events into the deafferented region (Fig. 4E). Thus, network bursts in our model of cortical undercut experiment originated at the interface between the intact and deafferented regions, which is in accordance with observations from cortical undercut experiments (25). The propagation of bursts into the deafferented region (extent of global seizure-like dynamics) depended on the severity of trauma.

Discussion

Epilepsy is a network disease involving interactions between many neurons, with pathological alterations in neuronal intrinsic excitability leading to epileptogenesis (2, 6). Thus, it is important to understand how the network's structure can affect the chances to observe epileptic-like activity (10, 29). Here, we investigated network mechanisms that give rise to posttraumatic epilepsy (PTE) in the setting of traumatic brain injury, when the structure of cortical network is distorted as a result of trauma-induced deafferentation. Our results suggest that spatial pattern of brain trauma can critically affect the threshold for PTE induction. We propose that clinical methods aiming to measure the severity of trauma (in conjunction to PTE emergence) should incorporate pattern-related aspects.

Traumatic brain injury can take different forms (for example, focal contusion, traumatic hemorrhage, and diffuse axonal injury) (30) that may lead to posttraumatic epileptogenesis through different mechanisms. However, the biomarkers and other criteria needed to quantify the different traumatic brain injury subtypes and their role in epileptogenesis are still elusive. From the clinical perspective, the different scenarios of cortical trauma that we studied here might correspond to the focal contusion (block deafferentation) and diffuse axonal injury (random deafferentation). With this correspondence, our model predicts that diffuse head injury should be less prone to develop PTE than the focal brain trauma. Interestingly, the risk of PTE associated with focal contusion is estimated to be approximately three times higher than the risk of diffuse head injury (30). The prediction of the model that diffuse axonal injury is less prone to develop epilepsy than focal contusion is, thus, consistent with these clinical reports.

Our study suggests that the network, which is prone to paroxysmal bursting, should include a population of cells with relatively high density of intact neurons (this population serves as an igniter for epileptic activity) and a population of cells with high levels of deafferentation and therefore, low spontaneous activity (because it is mostly suitable for propagation of bursting events). This suggestion predicts that, in the heterogeneous networks, epileptic activity should arise near the boundary of intact and deafferented areas and propagate to the deafferented population. This finding indeed was observed in vivo in experiments with cortical undercut (25), and it is also captured by our model network (Fig. 4).

Earlier work (23, 24) as well as the present study suggest that interictal-like dynamics, often observed in the posttraumatic cortex, could be caused by the action of homeostatic synaptic plasticity, which tends to compensate for the loss of excitability incurred by trauma. However, synaptic scaling applied within physiologically plausible limits (maximal up-regulation of 100%) (12) failed to induce pathological dynamics in the intact network model. This finding suggests that HSP might be an essential but not sufficient condition to transform the asynchronous activity to bursting dynamics. Indeed, an asynchronous state is maintained when recurrent synaptic conductance is weaker than the conductance associated with afferent excitation (i.e., when G_{PY ← PY} < G_{PY ← EX} and G_{IN ← PY} < G_{IN ← EX}). With the choice of parameters as in SI Materials and Methods, this constraint on synaptic conductance is still satisfied after synaptic scaling is applied to the recurrent synapses. The asynchronous state then can only be breached by reducing the effective afferent conductance or alternatively, by reducing the rate of afferent excitation (and thus, making the impact of random afferent excitation much weaker). Furthermore, such violation of asynchronous condition can occur locally.

These findings highlight the importance of trauma pattern in the nucleation of network bursts—as more regions that violate the asynchronous condition are created closer to each other, burst generation becomes easier. More detailed studies will determine the exact contribution of spatial correlation in trauma pattern to the local breaching of asynchronous network state and its development into population bursting.

Materials and Methods

The model network consisted of 6,400 neurons, 5,120 (80%) of which were excitatory PYs; the remaining 1,280 (20%) were inhibitory INs. Neurons were modeled with Hodgkin–Huxley-like equations. The detailed model of synaptic and neuronal dynamics is provided in SI Materials and Methods.