Automated Real-Space Refinement of Protein Structures Using a Realistic Backbone Move Set

Abstract

Crystals of many important biological macromolecules diffract to limited resolution, rendering accurate model building and refinement difficult and time-consuming. We present a torsional optimization protocol that is applicable to many such situations and combines Protein Data Bank-based torsional optimization with real-space refinement against the electron density derived from crystallography or cryo-electron microscopy. Our method converts moderate- to low-resolution structures at initial (e.g., backbone trace only) or late stages of refinement to structures with increased numbers of hydrogen bonds, improved crystallographic R-factors, and superior backbone geometry. This automated method is applicable to DNA-binding and membrane proteins of any size and will aid studies of structural biology by improving model quality and saving considerable effort. The method can be extended to improve NMR and other structures. Our backbone score and its sequence profile provide an additional standard tool for evaluating structural quality.

Introduction

Protein structure is an indispensable guide to understanding the function of a protein. The Protein Data Bank contains >70,000 protein structures determined by x-ray crystallography, NMR spectroscopy, and cryo-electron microscopy. X-ray crystallography is the main method used to solve these structures; however, crystals of large proteins, complexes, and membrane proteins often diffract to limited resolution as compared with soluble, single-domain proteins.

Computational techniques are essential for structural refinement (1–6). Many algorithms proceed by global minimization of the total energy in schemes that combine prior knowledge of stereochemistry in real space and, for x-ray crystallography, an optimized fitting of the observed structure factor amplitudes in reciprocal space (5,6). The widely used CNS program suite (4) uses a simulated annealing approach to optimize protein structures using either electron densities from x-ray diffraction or distance constraints from NMR measurements. However, simulated annealing methods are unable to surmount high barriers between conformations, which severely restricts their search capabilities. Other schemes, such as RAPPER (2), use distance constraints to provide a wide range of initial conformations that are then inserted into CNS for further optimization. The combined RAPPER/CNS system enables a more extensive conformational search than would be possible with CNS alone.

An obvious approach to structure refinement is the application of all-atom molecular-mechanics simulations. Although such simulations are extremely powerful, they often fail to accurately reproduce backbone geometries and have shown limited success in improving the accuracy of near-native structures, such as low-resolution crystal structures or predicted structures (7–9). Knowledge-based potentials are more successful in this regard (10,11). Many successful approaches alternatively rely on inserting known chain fragments from the Protein Data Bank (PDB) (12). However, fragment insertion methods often encounter problems after the initial model is generated, because the final models typically have higher energies than the native structures. Although the energy functions can correctly identify the native structure, limited sampling of local backbone conformations and side-chain packing arrangements in the condensed state often preclude extensive refinement with these methods.

It is computationally difficult to introduce the requisite Å-level backbone moves without disrupting the structure. For example, a ϕ,ψ pivot move that alters the backbone dihedral angles of a single residue will also translate a large portion of the protein through space. This large displacement generally produces disastrous steric overlaps and destroys the fold. Although it is not fatal for a folding algorithm that starts from an unfolded chain, this move is unsuitable for protein dynamics or refinement of a protein structure, because both of these tasks require fine-scale, Å-level motions to sample nearby conformations. In summary, methods that use real protein motions (e.g., molecular dynamics) fail to surmount large barriers, and those that use artificial moves severely distort the compact protein structure.

Here we present an automated method to identify unfavorable backbone (ϕ,ψ) dihedral angles in structures and transfer them into preferred regions of a Ramachandran map (RamaMap) that is specific to each amino acid (aa) type. The choice of angles accounts for the considerable but often overlooked dependence of the individual preferences on the neighboring residues' chemical identity and conformation. After the backbone geometries are improved, the side chains are reinserted and the entire protein is energy-minimized to fit the real-space electron density. The resulting structures have increased numbers of hydrogen (H)-bonds and similar or better crystallographic R-factors. These two independent metrics support the validity of our rebuilding algorithm. The new angles are closer on average to those observed in a higher-resolution structure than the starting angles. We discuss concerns relating to Rfree and real-space refinement, the use of RamaMaps as part of the target function rather than just as a validation tool, the applicability of our method to membrane proteins, and comparisons with existing methods.

Results

RamaMaps and statistical potentials

Our method requires the unique preferences of three dihedral angles, ϕ, ψ, and ω, to be identified for each residue. Typically, ω lies within ∼5° of either 0° (cis) or 180° (trans), whereas ϕ and ψ are more broadly distributed, as observed in RamaMaps (Fig. 1 a) (13). The ϕ,ψ angle pairs populate four regions: the extended β-basin, the α_R- and α_L-helical basins, and the polyproline II basin (PPII) (14). The distinct separation between the extended and PPII basins is clearly evident in RamaMaps for high-resolution structures (Fig. 1 a) but often is lost in lower-quality structures.

Figure 1.

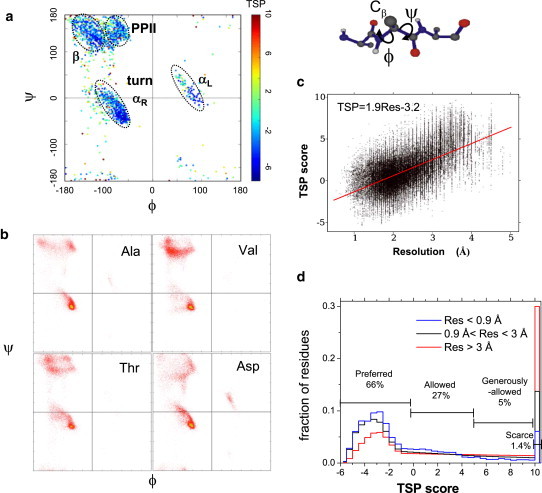
RamaMaps and TSP scores. (a) Protein ϕ,ψ dihedral angles and their distribution (RamaMap) for high-resolution structures (<0.9 Å). (b) RamaMaps for four representative residues. The Ala distribution in the extended region (upper left quadrant) exhibits distinct β and PPII basins, whereas Val, Thr, and Asp display their own individual preferences. (c) <TSP>_residue versus resolution for 140,000 chains in the PDB. (d) Histogram of TSP scores for high-, medium-, and low-resolution structures (percentages are based on data for resolution < 0. 9 Å). The distribution of TSP scores falls into four categories: Preferred ([−6,0), 66%), Allowed ([0,5), 27%), Generously allowed ([5,10), 5%), and Scarce (≥10, 1.4%).

The RamaMaps differ for each amino acid due to interactions between the backbone and side chains. Proline, pre-proline, and glycine RamaMaps are the most distinct, and the 18 other amino acids exhibit smaller but significant variations (Fig. 1 b). However, many crystallographic refinement and evaluation programs ignore the variations among the alanine-like amino acids as well as the distinction between the extended and PPII basins. Another largely disregarded factor is the significant influence of the chemical identity of the neighboring residues on the RamaMaps (15–20).

We use a torsional statistical potential (TSP) that is sensitive to the identities of the amino acid and the adjacent residues (21,22), and demonstrate that the TSP score provides a new, to our knowledge, and extremely valuable tool for structure refinement. We formulate the TSP using moderate- to high-resolution (<2.2 Å), nonredundant (homology < 30%) crystal structures (Rfree ≤ 0.3) (23). The TSP score is proportional to log [observed frequency] and ranges from −6 to +10. This scoring function strongly correlates with the resolution of the structure (Fig. 1, c and d) (20,24–26). A linear fit yields TSP score = 1.9(Resolution) + 1.6.

The validity and sensitivity of our TSP scoring function is established in two ways. First, nearly all residues in 12 high-resolution structures (<0.9 Å) have extremely good TSP scores (Fig. 1, a and d). Thus, the distribution of the well-determined dihedral angles of these high-resolution structures is sharply peaked at the maxima of the individual neighbor-dependent distributions observed in the moderate- to high-resolution structures for each aa type (the angles in the high-resolution structures account for only ∼0.2% of the total used to create the TSP).

Second, the increased sensitivity of our TSP scoring function relative to typical neighbor-independent scoring functions is demonstrated with a 2.6 Å structure of a protein-lipid complex at a late stage of refinement (deposited as 3OV6). Nearly all of its residues fall into the preferred region of the RamaMap (Fig. 2 a) and have excellent backbone scores when we use a standard scoring criterion that treats all alanine-like residues identically, or even one that distinguishes between each type of amino acid (Fig. 2 b). Scoring with our TSP, however, indicates that a majority of the residues actually are in the unfavorable regions once the neighbor dependence is included.

Figure 2.

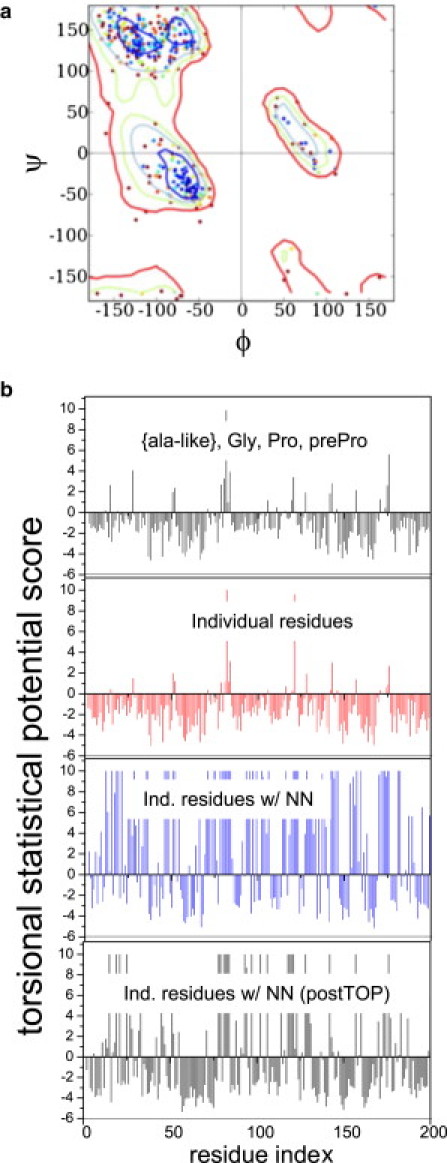
Sensitivity of the TSP to aa type and neighbors. (a) RamaMap for a lipid-binding protein, and (b) the associated backbone Ramachandran scores for the first 200 residues of the input structure using potentials that either group all alanine-like residues together (black) or distinguish individual residue types (red), as compared with our nearest-neighbor (NN)-dependent TSP (blue). Also shown is the neighbor-dependent TSP score after application of TOP (gray).

These two tests instill confidence that the TSP score is capable of recognizing high-quality backbone geometries and thus properly extracts the effects of the neighboring residues. Therefore, our scoring function provides a highly sensitive metric that can be used to identify deficiencies in a backbone model and (if those deficiencies are correctable) that guide the production of a superior-quality structure.

Double-crank move set

It is challenging to correct poor angles across an entire protein during structural refinement, especially for structures that diffract to limited resolution. The most common practice involves a tedious manual process of transferring the ϕ and ψ angles of each outlier into favorable regions of the RamaMap, or, during automated refinement, either restraining the angles to remain near their initial values or discarding disallowed angles using simple criteria (6). However, the adjustment of even a single pair of angles generally degrades the structure by producing unrealistic bond lengths and angles or by introducing large displacements in the main-chain coordinates that produce significant deviations from the electron density and that are often difficult to rectify by refinement protocols in reciprocal space.

Here we present a two-stage torsion optimization procedure (TOP). In the first stage, the quality of the backbone, as defined by our high-fidelity TSP scoring function, is improved and the number of backbone H-bonds is increased. The second stage is an all-atom, real-space refinement step in which the experimental electron density is used to improve the fit of the side chains into the density and obtain even better H-bonding.

Backbone quality is improved in the first stage via a Monte Carlo simulated annealing (MCSA) algorithm that uses our TSP scoring function and a new torsion angle move set that permits one residue to execute motions with arbitrarily large changes in ϕ, ψ while flanking regions remain largely unchanged in Cartesian space. This move set involves a crankshaft rocking of a peptide group in which the ψ angle of the preceding residue is counter-rotated with respect to ϕ for the residue of interest: (ψ_i−1,ϕ_i) → (ψ_i−1 + δ, ϕ_i − δ), mimicking the dominant motion of real protein backbones (27) (Fig. 3 a). Changes in both (ψ, ϕ) of a residue are enabled by two simultaneous crankshaft moves involving three residues and four consecutive angles: (ψ_i−1,ϕ_i,ψ_i,ϕ_i+1) → (ψ_i−1 + δ, ϕ_i − δ,ψ_i − Δ,ϕ_i+1 + Δ). An example of different move sets and the resulting effects on the overall fold of ubiquitin (Ub) are shown in Table S1.

Figure 3.

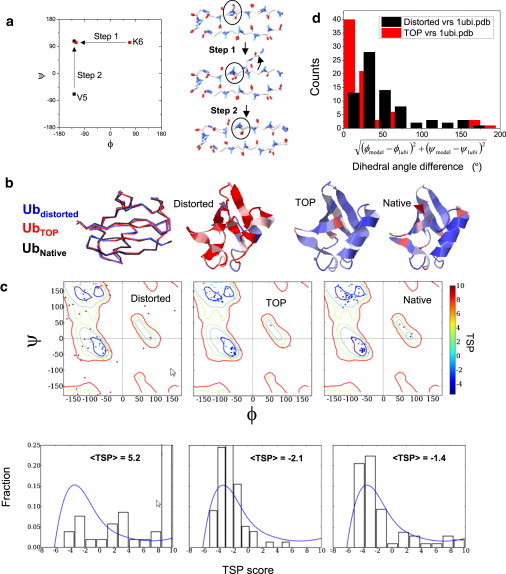
TOP applied to a deliberately highly distorted version of Ub. (a) Single-crank move with overlay of the distorted and native structures for the amino terminal hairpin (upper). The incorrectly positioned carbonyl oxygen of V5 is circled. To correctly reposition this oxygen, ϕ_K6 is changed (step 1), followed by a counter-rotation of ψ_V5 (step 2). This and similar moves lead to the final refined structure. (b) Wire-frame overlay of distorted, backbone-improved, and native structures (1UBI, residues 1–73), with ribbon models colored by TSP score. (c) Corresponding RamaMaps and histograms of TSP scores. The blue line represents values for the high-resolution structures (<0.9 Å). (d) Comparison of angular deviations in the RamaMap of the distorted and refined models with respect to the crystal structure, as illustrated with a histogram.

New angles for the center residue are sampled from a PDB-based library that is conditional on both the chemical identity of the three residues (i.e., triplet) and their secondary structure, as identified using the Dictionary of Protein Secondary Structure (28). The triplets are extracted from the same set of PDB structures used to obtain the TSP. Because of the dependence on the secondary structure of each aa in the triplet, this sampling procedure incorporates additional information that is absent from our TSP, which only accounts for the chemical identity of the three residues. Because it gives investigators the ability to sample the favored regions in torsional angle space without disrupting the overall protein conformation, this double-crank move is ideal for improving backbone torsion angles and optimizing H-bonding during structure refinement.

TOP algorithm

The TOP algorithm integrates the double-crank move with the TSP scoring function to generate protein models with significantly improved H-bonding and backbone torsion angles while maintaining the backbone close to the input models (e.g., C_α root mean-square deviation (RMSD) ≤ 0.9 Å). In the first stage, all side-chain atoms beyond the β carbons are removed during torsional optimization to enhance computational speed and generate a smoother energy landscape. Three substages (substages I, II, and III) are run as independent MCSA simulations using the simulated annealing protocol described by Colubri et al. (29). The lowest-energy conformation from the prior substage is taken as the initial conformation for the next stage. The input reference structure is retained across all stages.

We use a linear combination of five energy functions: 1), our neighbor-dependent TSP; 2), a metric for the similarity to the input reference structure; 3), an H-bond potential; 4), the repulsive portion of the C_β-level statistical potential (22) that is designed to prevent steric clashes; and 5), a neighbor-independent TSP. Each substage uses a slightly different combination of these five energy functions (see Supporting Material). Substage I is designed to optimize the dihedral angles, although the resulting structures tend to drift away from the initial model by up to ∼2 Å C_α-RMSD. In substage II, the errant chain is guided back toward the initial model while the number and quality of the H-bonds are increased. Substage III involves local optimization of both the torsional angles and backbone H-bonds. Each substage contains 10–20 independent MCSA rounds.

The sampling of backbone torsion angles for the central residue (ϕ_i and ψ_i) proceeds with different protocols in the three substages. The ϕ_i and ψ_i angles in stage I are drawn from the center residue of trimers with 3° added Gaussian noise. The possible dihedral angle pairs are extracted from the nonredundant PDB structures used to create the TSP3 score, and are contingent on the primary sequence and secondary structure of the triplet. Substages II and III, however, only permit the ϕ_i and ψ_i angles to vary locally from their current values by an amount determined randomly from a uniform distribution between 0 and 5° (stage II) or 3° (stage III), respectively. In all substages, compensatory adjustments are applied to the torsion angles of the adjacent residues (i − 1, i +1) according to the double-crank move set by Δψ_i−1 = −Δϕ_i and Δψ_i = −Δϕ_i+1. The accompanying ω angle is varied by 1° only in substage I.

Application to a highly distorted protein

We first demonstrate that the double-crank move can aggressively improve the dihedral angle distribution of a distorted Ub (1UBI, resolution = 1.8 Å; Fig. 3 b) while largely maintaining the overall backbone fold. We created a purposely severely distorted model from the crystal structure by heating the structure to 8000 K and then slowly cooling it, using the experimental diffraction data truncated to 3.3 Å (4). The distorted structure contains many unfavorable dihedral angles (Fig. 3, b and c), a greatly inferior R-free parameter compared with the crystal structure (0.17 → 0.49), and a C_α-RMSD of 0.7 Å from the original model. Nevertheless, our TOP protocol, using the double-crank move set, recovers a near-native dihedral distribution, favorable TSP energies, and a C_α-RMSD of 1.1 Å from the input model (and 0.9 Å from the original 1UBI structure). The average TSP score decreases from 5.2 to −2.1, even surpassing the native score of −1.4. Also, the number of the backbone H-bonds increases from 14 to 27 (the native number of 37 is found after our real-space optimization).

More than a dozen angles change by 50–100° and many end within 40° of the native values (Fig. 3 d). Of particular note is the nearly complete rotation of the peptide plane between residues V5 and K6 (Fig. 3 a). This rotation largely reflects a single crank shaft move with Δψ_V5 ∼ −Δϕ_K6 ∼170°. The algorithm recovers the amino-terminal hairpin's native H-bonding pattern wherein successive carbonyl groups point in opposite directions. This example demonstrates that double-crank moves with appropriate dihedral angle sampling are capable of recovering near-native sets of dihedral angles with favorable TSP scores and a near-native complement of H-bonds, even when starting from an extremely poor initial distribution.

TOP recovers angles found in a high-resolution structure

The next test demonstrates that the new angles selected by TOP for a medium-resolution structure are improved to more resemble those found in a higher-resolution structure. This test is applied to the original structure (3HVT, 2.9 Å) and a more recent, high-resolution structure (3DLK, 1.85 Å) of an α/β protein, HIV reverse transcriptase (chain A only, 546 aa). On average, TOP selects angles that are closer to those in the high-resolution structure than those in the initial lower-resolution structure (Fig. 4 and Fig. S1). In the medium-resolution structure, 53% of the ϕ,ψ pairs are within 40° of the corresponding pairs in the high-resolution structure, $\sqrt{{\left(\varphi -{\varphi }_{Hi\mathrm{Re}s}\right)}^2+{\left(\varphi -{\varphi }_{Hi\mathrm{Re}s}\right)}^2}$ < 40°, whereas in the TOP-improved model, 69% of pairs satisfy this criterion. Hence, TOP's backbone refinement protocol selects angles closer to the high-resolution data while improving the average TSP score (<TSP> = 5.7 → −0.1) and increasing the number of backbone H-bonds (102 → 125).

Figure 4.

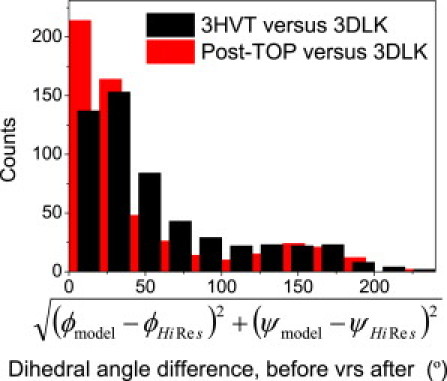
TOP selects native-like angles. Starting from a low-resolution crystal structure of HIV reverse transcriptase (3HVT), the first, backbone-only refinement stage of TOP selects angles that on average are closer to those observed in a medium-resolution crystal structure, as illustrated with a histogram of the dihedral angle differences. The corresponding RamaMaps are shown in Fig. S1.

A repeat of this test on an NMR structure of barnase (2KF3), a 110 aa α/β protein, shows that TOP again produces angles that on average are more similar to those of the 2.05 Å crystal structure (1BNI), and at the same time produces a superior TSP score and an increased number of H-bonds (Fig. S2).

Structure refinement against the electron density

After backbone refinement is completed, the side chains are restored using their original χ rotamer angles. Restored angles generally produce better final structures than angles obtained from a PDB-based, backbone-dependent rotamer library. Presumably, this difference arises because the rotamers in the original model represent a better fit to the electron density. However, the user can insert any desired set of rotamer angles before conducting the real-space refinement procedure and then compare the outcomes.

Portions of the protein, particularly side chains, become displaced from the electron density during the initial stage of TOP, elevating the crystallographic R-values. Hence, the complete TOP procedure includes a second stage in which the backbone-optimized structure is refined in real space against the electron density in the asymmetric unit (Supporting Material). This step mainly improves the fit of the side chains into the electron density and proceeds using a modified version of Trabuco and co-workers' (30) molecular modeling flexible fitting (MDFF) module of the program NAMD 2.7b2, which has been applied to cryo-electron microscopy (cryoEM) structures. Because the models obtained from the double-crank procedure already reside within the electron density (e.g., the C_α-RMSD is <1 Å from the starting structures), there is no need to perform molecular-dynamics simulations; only conjugate gradient energy minimization is utilized.

R-free and real-space refinement

The validity of standard R-free calculations is a potential concern with regard to real-space refinement involving fitting models to electron density maps calculated from the diffraction data. In the R-free calculation, a subset of the diffraction data is set aside and the subset is then compared with the predicted reciprocal space intensities calculated from the final model. To retain the full statistical validity of R-free, the electron density used in the real-space refinement should not use the set-aside diffraction data from the outset. Nevertheless, crystallographers typically retain all reflections, including the free set, in generating the electron density maps, or calculate weights for the 2mFo-Fc map based on reflections in the free set (31). These maps are used in real-space manual rebuilding because the more-stringent maps obtained without the free-set reflections are subject to potential errors due to early truncation of Fourier transforms between reciprocal and real spaces. Because the real-space refinement used by TOP mimics the standard practice of manual real-space refinement, the performance of TOP should be judged in the same manner, i.e., using the maps computed from the full electron density. Regardless, we report in the tables both the conventional R-free and the more stringent R-free where the free set reflections are excluded in the evaluation of the real-space map. Calculations performed with this more stringent procedure produce only small changes in R-free.

Examples

We applied the TOP procedure to a diverse test set of crystal and cryoEM structures that include extremely large membrane and DNA-binding proteins, and arise at different stages of the refinement process with varying resolution (2.1–4.6 Å). (See Tables 1 and 2, Table S2 and Table S3, which show additional analyses, including detailed RamaMap statistics based on TSP and MolProbity.)

Table 1.

TOP structure refinement

Protein		APC22750
		Initial	TOP∗		Initial	TOP∗
			Stage 1	Stage 2		Stage 1	Stage 2
Resolution		2.09–25.0 Å			2.09–25.0 Å
Number of residues		465			480
Starting model		During refinement			Deposited (1VR4)
Cα-RMSD (Å)		N/A	0.71	0.42	N/A	0.46	0.14
<TSP>		3.31	−0.4	0.08	0.45	−1.2	−0.9
No. of H-bonds†		162	190	214	239	249	263
R-work		0.3091	0.3880	0.2979 (0.2983)‡	0.2061	0.3150	0.2087 (0.2074)‡
R-free		0.3537	0.4233	0.3163 (0.3403)	0.2647	0.3507	0.2372 (0.2589)
Map correlation		0.76	0.66	0.77	0.85	0.76	0.85
RMSD from ideal	Bond length (Å)	0.045	0.047	0.040	0.014	0.017	0.016
	Angle (°)	2.567	2.904	3.130	1.692	1.935	1.810
RamaMap statistics (%)
Preferred§		79	88	88	92	92	93
Allowed		6	3	4	5	5	4
Outliers		15	9	8	3	3	3

Protein		Cytochrome b6f complex			A-Cobratoxin-ACHBP complex
		Initial	TOP∗		Initial	TOP∗
			Stage 1	Stage 2		Stage 1	Stage 2
Resolution		3.00–39.30 Å			4.20–25.0 Å
No. of residues		959			1356
Starting model		Deposited (2E74)			Deposited (1YI5)
Cα-RMSD (Å)		N/A	0.78	0.40	N/A	0.8	0.62
<TSP>		2.92	−0.9	−0.7	4.35	0.09	0.68
No. of H-bonds†		410	445	468	332	481	513
R-work		0.2248	0.3515	0.2423 (0.2395)‡	0.2529	0.3404	0.2531 (0.2506)‡
R-free		0.2704	0.3760	0.2726 (0.2802)‡	0.3128	0.3863	0.2857 (0.3107)‡
Map correlation		0.8	0.7	0.75	0.68	0.59	0.68
RMSD from ideal	Bond length (Å)	0.029	0.039	0.035	0.012	0.036	0.026
	Angle (°)	2.659	3.162	2.831	1.579	2.125	2.093
RamaMap statistics (%)
Preferred§		83	91	91	85	91	91
Allowed		11	5	6	10	6	6
Outliers		6	4	4	5	2	3

Protein		A-DNA-binding protein			A-Protein-lipid complex
		Initial	TOP∗		Initial	TOP∗
			Stage 1	Stage 2		Stage 1	Stage 2
Resolution		3.35–20.0			2.60–43.5 Å
No. of residues		364			376
Starting model		Early stage			Final stage (3OV6)
Cα-RMSD (Å)		N/A	0.85	0.97	N/A	0.74	0.32
<TSP>		3.33	−2.0	−1.5	2.92	−0.1	0.13
No. of H-bonds†		147	187	192	168	181	193
R-work		0.2890	0.3874	0.3136 (0.3079)‡	0.2285	0.3611	0.2323 (0.2341) ‡
R-free		0.3722	0.4418	0.3562 (0.3830)	0.2851	0.4076	0.2551 (0.2760)
Map correlation		0.75	0.68	0.74	0.88	0.78	0.86
RMSD from ideal	Bond length (Å)	0.007	0.014	0.016	0.009	0.026	0.017
	Angle (°)‡	1.218	1.689	1.837	1.401	2.147	1.944
RamaMap statistics (%)
Preferred§		81	94	94	93	94	95
Allowed		11	3	3	5	4	3
Outliers		8	3	3	1	2	2

^∗Stage 1 and Stage 2 refer to backbone refinement using the MCSA/double-crank algorithm and all-atom energy minimization using the electron density, respectively.

^†Backbone H-bonds are defined when the amide nitrogen and carbonyl oxygen are within 3.5 Å and the angle between the N-H and O=C bond vectors exceeds 145°.

^‡The values in parentheses are the R and R-free values calculated where the more stringent maps generated after excluding the free reflections are used in the real-space refinement stage of TOP.

^§As defined by the program COOT (36).

Table 2.

TOP structure refinement

Protein		PaBphP-PCD
Resolution No. of residues Starting model		2.60–49.0 Å 3827 Final stage
		Initial	TOP∗		Manual Refinement After Top
			Stage 1	Stage 2
Cα-RMSD (Å)		N/A	0.73	0.33	0.3
<TSP>		2.91	−0.6	−0.2	1.28
No. of H-bonds†		1352	1814	1909	1754
R-work		0.2244	0.3551	0.2338 (0.2375)‡	0.2198
R-free		0.2820	0.3854	0.2567 (0.2803)‡	0.2613
Map correlation		0.80	0.69	0.80	0.82
RMSD from ideal	Bond length (Å)	0.004	0.017	0.016	0.005
	Angle (°)	0.946	1.894	1.893	0.973
RamaMap statistics (%)
Preferred§		90	94	94	95
Allowed		8	4	4	5
Outliers		2	2	2	0.3

Legend is the same as for Table 1.

To test TOP's versatility, we apply it to a structural genomics target, APC22750 (R = 2.1 Å, 480 aa), at two different stages of refinement. The starting model from an early stage of refinement lacks some poorly resolved chain segments and bound water molecules, and the other target is the final deposited structure (1VR4) of this protein of unknown function. The first, backbone optimization stage of TOP retains the model typically within 1 Å C_α-RMSD of the input structure. Real-space refinement reduces the C_α-RMSD. Fig. S3 provides a detail analysis of the backbone movements for this protein.

The RamaMap distribution for the early model significantly improves after the backbone refinement stage, with both tighter clustering in the α helical region and distinct β and PPII clusters—features that are otherwise only observed in high-resolution crystal structures. Between this stage and the final energy-minimization stage, the average TSP score improves from 3.3 → 0.1 and 0.5 → −0.9 when starting from the early and deposited structures, respectively (Table 1). Because the TSP is part of the target function, improvements in TSP are to be expected.

Encouragingly, two independent metrics also support the validity of our procedure. The number of backbone H-bonds is significantly increased for the early-stage model (162 → 214), and R-free also improves (0.36 → 0.32). Similar results are also observed for the deposited model (Table 1). Again, TOP produces angles for the early-stage structure that are more similar to those in the deposited structure (e.g., 71% and 73% of angles in the early-stage and post-TOP models have $\sqrt{{\left(\varphi -{\varphi }_{1VR4}\right)}^2+{\left(\varphi -{\varphi }_{1VR4}\right)}^2}$ < 40°, respectively).

Results for the five other targets are comparable (Fig. 5). These targets include PaBphP-PCD, a crystal structure with eight monomers in the asymmetric unit (3827 aa total, near-final stage refinement model, 2.6 Å resolution), the cytochrome b₆f membrane complex (2E74, 959 aa, 3.0 Å), a cobra toxin acetylcholine-binding complex (1YI5, 1356 aa, 4.2 Å), a DNA-binding protein (early stage, 364 aa, 3.4 Å), and a late-stage lipid-binding protein (3OV6, 376 aa, 2.6 Å). The starting models for 2E74 and 1YI5 are taken directly from the PDB. All TSP scores are improved by 3–5 units, equivalent to a 2–3 Å increase in effective resolution for the backbone quality as estimated from the correlation shown in Fig. 1 b. The number of backbone H-bonds increases by ∼50% for three of the structures, and the R-free improvements range from 0.01 to 0.03 for four targets.

Figure 5.

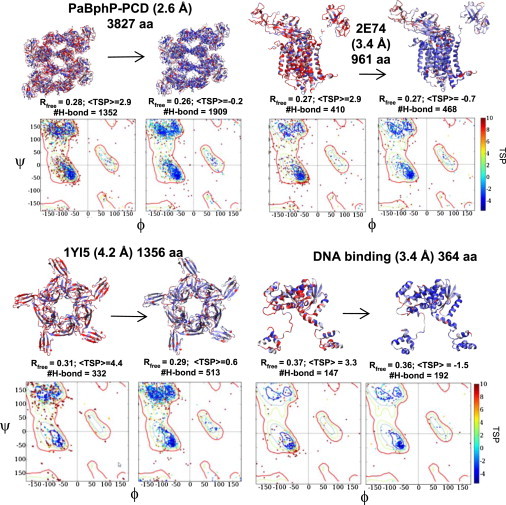
Application of TOP to different protein structures. For PaBphP-PCD, the RamaMap for four of the eight chains is shown. For the DNA-binding protein and cytochrome b₆f membrane complex (2E74) structures, the DNA and a few cofactors are part of the crystal structure but are not displayed.

We have not encountered a situation in which our method fails to converge, except in regions where the electron density is so poor that a realistic backbone could not be built to begin with. Undoubtedly, when the initial model strays outside the electron density, the MDFF algorithm's long-range electrostatic potential will be of considerable benefit (30). This algorithm has produced large domain motions (>10 Å) for cryoEM models.

Subsequent manual rebuilding and insertion of high-occupancy water molecules (either manual or automated) could further improve the structure and R-factors. However, we did not perform these steps here because our focus was on introducing our automated procedure, and manual rebuilding is very dependent on the individual. Nevertheless, we note that three of these targets (PaBphP-PCD, the DNA-binding protein, and 3OV6) have been refined with the use of Phenix (and presumably subsequent manual refinement) within the last year, and hence they serve to illustrate TOP's capabilities relative to modern refinement methods of improving backbone quality, H-bond formation, and R-free.

In addition, we provide an illustration of how the TOP procedure facilitates further manual rebuilding. We manually refined the 3827 aa PaBphP-PCD post-TOP structure to place all but one residue into the preferred or allowed region of the RamaMap with minimal effort (Table 2 and Table S3). The improvement arises in part because TOP fixes regions that were poorly represented in the original model. Other (minor) improvements to TOP's model (e.g., bond lengths and angles of side chains) can be achieved with the use of other programs, such as Phenix. However, we suggest that the backbone be kept fixed; otherwise, TOP's dihedral angle improvements will revert toward the original angles.

Membrane proteins

Our tools, which use Ramachandran statistics for soluble proteins, may appear to be inappropriate for membrane proteins. For example, the noticeable kinks in transmembrane helices might be removed by TOP because it tends to idealize ϕ,ψ angles. However, the applicability of TOP to membrane proteins is supported by the following observations:

First, kinked helices can be found in soluble proteins (e.g., hemoglobin and 1GZX) and the interior of membrane proteins (e.g., 2E76 and 3ABW). Second, there is little reason to believe that the presence of phospholipids exerts a significant influence on the Ramachandran distributions, and even then, any such effects probably should be limited to residues in direct contact with the membrane. High-resolution membrane proteins (e.g., 3ABW and 1.9 Å) have excellent TSP scores, indicating that any existing difference is subtle. Third, if environmental effects are significant, Ramachandran distributions would be expected to depend on burial in soluble proteins. However, in our previous studies of soluble proteins (18), we did not detect observable differences in the RamaMaps as a function of burial, except for some residues at the outermost surface of the protein, an effect that is attributable to the chains turning back around toward the body of the protein and to the increased population of turns. On the basis of these observations, as well as physiochemical principles, we believe that RamaMaps are largely determined by sterics, H-bonding, and other electrostatic interactions, and should be similar for soluble and membrane proteins.

Irrespective of these arguments, we compare the kinked helices in the cytochrome b₆f membrane complex (2E74) with those in the model produced by our TOP procedure. The starting structure has five long transmembrane helices with distinct kinks or curvature (Fig. S4). These helices retain their shapes in our refined model and are superimposable, with only a net C_α-RMSD of 0.43 Å across all of the associated 130 residues. Furthermore, the number of H-bonds for these helices increases from 62 to 84 while the <TSP> is dramatically improved from 4.5 to −2.1. We note that this structure has a relatively low resolution (3.0 Å), which gives our algorithm some leeway in the fitting of the electron density, and would permit straightening of the helices if they were heavily biased in this direction. Nevertheless, our procedure accurately reproduces the irregular secondary structures while enhancing the H-bonding network and backbone geometry. This result, along with the similarity of TSP scores between soluble and membrane proteins and the presence of kinked helices in both classes of proteins, allows us to conclude that the TOP algorithm is also appropriate for membrane proteins.

Application to cryoEM structures

Structures determined by cryoEM can be refined with the same procedures used for the crystallographic structures. We extracted the electron density for a monomer from the 4.6 Å resolution cryoEM structure (2XEA) of the tobacco mosaic virus (TMV). Retaining the electron density within 4 Å of the monomer, we generated a structure with an increased number of backbone H-bonds (22 → 50), better torsional angles (<TSP> = 1.1 → −0.5), and an improved cross-correlation coefficient between our new model and the density map (0.68 → 0.71, calculated using program VMD (32)). The cross-correlation coefficient provides a performance metric to validate our improvements, just as R-free does in our crystallographic studies. Even more impressive improvements are obtained for the 4.0 Å resolution cryoEM structure of a membrane-bound acetylcholine receptor pore (1OED): H-bonds, 241 → 387, <TSP> = 0.9 → −2.3, and cross-correlation coefficient = 0.67 → 0.87 (Fig. S5).

Comparison with other methods

Conceptually and fundamentally, our global refinement procedure of scoring and selecting new angles using a Ramachandran distribution that accounts for neighboring residues has not been successfully incorporated in any commonly used software package that we are aware of. Unlike RAPPER (2), Arp/Warp (33), and Phenix.autobuild (6), TOP does not focus on initial model building. Rather, TOP improves the entire backbone of an existing protein model with no input beyond an initial model and, if real-space refinement is desired, the electron density. Nevertheless, we have compared TOP in detail with some other refinement packages that may appear to have similar features (see Supporting Material).

Discussion

Our real-space refinement algorithm converts protein models at early or advanced stages of refinement to ones with superior H-bonding and similar or better R-factors, as well as improved backbone geometries. Our strategy incorporates knowledge of residue-specific RamaMaps and their significant dependence on the neighboring residues' chemical identity and geometry. This extra prior information is incorporated through our TSP scoring function and our PDB-based sampling protocol. The TOP procedure already was used to refine an anthrax protective antigen octamer (3KWV, >1000 aa, 3.1 Å (34)) and a CD1c/lipid complex (3OV6, 376 aa, 2.5 Å (35)).

The current use of RamaMaps in the refinement process is contrary to the longstanding belief that Ramachandran plots are too valuable a validation tool to be used as part of a target function. This work clearly demonstrates that the final refinement can be improved by the application of this extra knowledge, just as nearly all model building uses the known bond lengths and angles of the backbone and side chains. We stress that our structures have an increased number of H-bonds and similar or improved crystallographic R-free parameters. The improvement of these two independent and powerful metrics of structural quality, combined with our finding that the TOP procedure recovers the dihedral angles found in high-resolution structures when starting from a lower-resolution model, amply justifies the use of RamaMaps in the refinement process.

TOP generally produces models with superior R-free values for input structures that have not undergone extensive manual rebuilding and structure refinement, with smaller improvements for input structures with significant, tedious manual refinement. As illustrated here, further manual improvement of TOP-generated structures can produce even better structures. Iterative recalculation of the electron density map, interspersed with reciprocal space refinement, could potentially improve performance for cases with poor initial maps.

The improvements in backbone geometry are obtained by using a computational scheme that omits the side-chain atoms beyond the C_β carbon, and the omitted atoms are restored only in the final energy-minimization step. Nevertheless, our sampling protocol and scoring functions largely recapture the lost information because backbone dihedral angles strongly correlate with the side-chain rotamer angles, the neighboring residues' identities, and the side-chain conformations. The C_β-level model also permits aggressive backbone moves that are essential to produce better structures. This ability to find new local minima can account for some of the improvement. Potentially, the new minimum could be found manually by the expert crystallographer. In other cases, the improvements are subtler and require knowledge contained in our aa and neighbor-dependent torsional potential and our sampling routine.

After the initial model is created, most other refinement protocols improve the structure by extensively adjusting the side-chain rotamers rather than the backbone dihedral angles, because changes in the backbone either disrupt the structure or distort the bond lengths and angles. Consequently, it becomes difficult to obtain further improvements in backbone. In contrast, the lack of explicit side chains in our first stage and the mimicking of how real proteins move enable us to optimize the backbone geometry and H-bonding throughout the protein before reinserting and optimizing the side chains. This hierarchal protocol follows the protein's intrinsic structural hierarchy and generates superior structures.

TOP works more effectively after major errors in the backbone traces are removed by initial cycles of conventional structure refinement and perhaps manual rebuilding. TOP also can improve individual regions during the chain-building process. In fact, mistraced regions and artificially inserted loops are readily detected by the failure of TOP to produce a favorable TSP score. For example, the membrane protein (2E74) has one region (C170–C238) that lacks noticeable improvements in the TSP score using TOP. Further inspection reveals that the electron density in this region has a less well defined density than most of the protein, and the starting structure has a poor backbone trace in this area. Consequently, we suggest that the TSP score and its sequence profile be included as an additional tool to evaluate structural quality.

Conclusion

Our automated TOP algorithm identifies and improves the backbone torsional angles of a protein structure, increases the number of H-bonds, and generally improves crystallographic R-factors. We have demonstrated the algorithm's effectiveness for nontrivial crystal and cryoEM structures that diffracted to low to moderate resolution. The algorithm requires only an initial backbone trace and may be applied to particularly challenging regions that are recalcitrant to manual intervention. In addition, our move set and sampling procedure can be extended to refine NMR structures and computational models.

Submissions to our refinement and evaluation servers can be made at http://godzilla.uchicago.edu/pages/projects.html.