Abstract
Homologous pairing and braiding (supercoiling) have crucial effects on genome organization, maintenance, and evolution. Generally, the pairing and braiding processes are discussed in different contexts, independently of each other. However, analysis of electrostatic interactions between DNA double helices suggests that in some situations these processes may be related. Here we present a theory of DNA braiding that accounts for the elastic energy of DNA double helices as well as for the chiral nature of the discrete helical patterns of DNA charges. This theory shows that DNA braiding may be affected, stabilized, or even driven by chiral electrostatic interactions. For example, electrostatically driven braiding may explain the surprising recent observation of stable pairing of homologous double-stranded DNA in solutions containing only monovalent salt. Electrostatic stabilization of left-handed braids may stand behind the chiral selectivity of type II topoisomerases and positive plasmid supercoiling in hyperthermophilic bacteria and archea.
Introduction
An ability of homologous DNA molecules to pair without breaking or unwinding the double helix may have profound implications for genome organization, maintenance, and evolution (1,2). Studies in yeast suggest that such pairing may be an essential step in homologous recombination and double-strand break repair of DNA, preceding the formation of protein-covered single strands and subsequent exchange of fragments (recombination) between homologous sequences (1–4). Homologous pairing of intact double-helical DNA fragments was predicted (5) and observed (6,7) in mixtures of DNA and salt. However, existing theories (8,9) could not explain stable pairing of homologous molecules at low DNA concentration in monovalent salt solutions (7).
Braiding is another crucial property of genomic DNA that is incompletely understood, although significant progress has been made in characterizing the enzymes that control it in vivo (10). (We speak of braiding in reference to any winding of two DNA molecules around each other and reserve the term “supercoiling” for braiding in closed DNA loops.) Braiding accompanies DNA replication and has to be relieved by topoisomerases, to prevent polymerase stalling (11). In plasmid DNA, braiding (plectonemic supercoiling) is introduced by gyrases, suggesting that it has some important function (11,12); but it is not entirely clear why negative supercoiling is essential for mesophilic and positive supercoiling for hyperthermophilic bacteria and archea (13). The idea that negative and positive supercoiling have different effects on the double-helix stability is not supported by experiments (14). Positive supercoiling might lead to more tightly wound braids and negative supercoiling to less tightly wound braids; however, studies of the underlying chiral interactions are just beginning (13).
Here we demonstrate that homologous pairing and braiding of DNA double helices may be intricately related, at least in vitro. These two processes are affected by the same DNA-DNA interactions, and so may be synergistic; this is why we discuss them together. Indeed, interactions between highly-charged DNA molecules are predominantly electrostatic, yet DNA is not just a charged rod. DNA-DNA interactions depend both on charge density and the double-helix structure (9). A zipper-like alignment of negatively charged phosphate strands with grooves on the opposing molecule reduces the repulsion between phosphates and favors pairing of homologous double helices (see Fig. 1). Because of sequence-related variations in the helical pitch of DNA, similar pairing of nonhomologous double helices requires costly elastic deformation (5,8). Left-handed wrapping of the double helices around each other enhances, while right-handed wrapping suppresses, the energetically favorable strand-groove alignment. Hence, braiding may significantly affect DNA-DNA interactions and vice versa.
Figure 1.
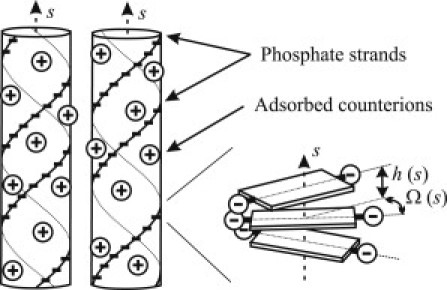
Electrostatic sequence homology recognition and pairing of parallel DNA double helices. Alignment of negatively charged phosphate strands opposite to positively charged counterions in the grooves of the apposing molecule reduces the electrostatic energy. This may lead to intermolecular attraction and pairing, provided that a sufficient fraction of phosphate charges is compensated by bound counterions. Sequence-related variations in the twist Ω(s) and axial rise h(s) per basepair (depicted on the right) lead to variations in the helical pitch. These disrupt the energetically favorable alignment of two apposing molecules with nonhomologous sequences.
A theory of electrostatic interactions between straight, parallel molecules with double-helical patterns of discrete surface charges explained a number of observed features of DNA-DNA interactions (9), including the segregation of homologs in dense, multimolecular aggregates (5,6,8). It predicts that spontaneous association of the homologs into stable pairs might be induced by cations capable of neutralizing >80–90% of the net DNA charge upon binding in DNA grooves (15). Binding of these cations leads to a favorable apposition of negatively charged phosphate strands and positively charged grooves (see Fig. 1), resulting in net attraction, DNA pairing, or formation of multimolecular aggregates (8,9,15). Such strong cation binding is unlikely in monovalent salt solutions (16). Thus, the stable homolog pairing observed by Danilowicz et al. (7) seemed to be inconsistent with this theory. However, these homolog pairs could be braided rather than parallel, in which case the theoretical prediction could be different.
Verifying whether a braided geometry could explain the observed homologous pairing of DNA in monovalent salt solutions was one motivation behind this study. The other was to generate a better general understanding, as well as a systematic theoretical analysis, of the role of electrostatic interactions in braided DNA pairs, e.g., as a first step toward studying these effects in supercoiled plasmids. Most previous studies of DNA braiding and supercoiling focused on the topology and mechanics of the double helices (17–20), although some have included electrostatics (21–23) by treating DNA as a uniformly charged rod. Recent studies suggest that chiral DNA-DNA interactions may actually play a very important role in DNA braiding and plasmid supercoiling (13,24). Yet, to the best of our knowledge, theoretical analysis of chiral electrostatic interactions between DNA double helices has so far been limited to simplified models (9,25) and simulations of crossovers between short oligonucleotides (26).
Here, we develop a theory that implements and extends the idea for calculating the energy of chiral electrostatic interactions between braided helices sketched out in our recent review (9). We show that the association of homologous double helices into stable braids may be favorable in monovalent salt solutions, discuss how electrostatic braiding may rationalize the chiral preference of type II topoisomerases, and speculate on the role of such braiding in positive plasmid supercoiling within hyperthermophilic bacteria and archea.
Using simple geometrical arguments we could predict the handedness of the braid (see Fig. 2). However, rigorous mathematical analysis is needed to derive a reliable estimate of the value of the tilt angle, to evaluate the extent of reduction in the energy of the braid relative to a nonbraided configuration, to determine the critical threshold of charge compensation above which the DNA-DNA attraction takes place, etc. Because of the curved geometry of DNA molecules in the braid and their helical charge distribution, the mathematics of the problem is quite involved. Surprisingly, this analysis leads to simple, although nontrivial, results.
Figure 2.
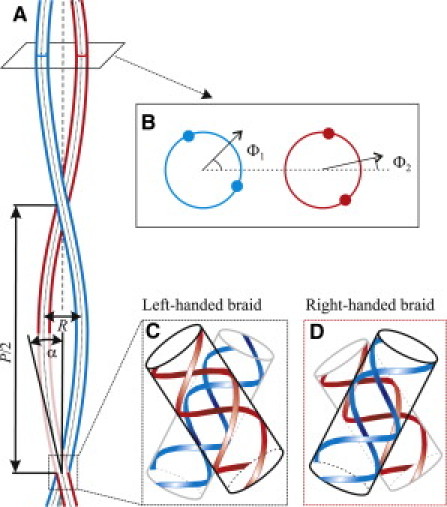
Geometry of a DNA braid. (A) Straight, left-handed braid formed by two DNA molecules (blue and red); P is the braid pitch; R is the braid diameter (distance between the centerlines of the molecules); and α is the tilt angle of the molecules. (B) Lateral cross-section of the braid, after tilting the molecular axes parallel to the braid centerline. Solid circles depict phosphate strands; the angles Φ1 and Φ2 represent azimuthal orientation of the center of the minor groove of each molecule with respect to the line connecting the two centerlines (see the Supporting Material). (C) Crossover geometry in a left-handed braid. Phosphate strands on the back side of the red molecule are aligned parallel to the strands and grooves on the front side of the blue molecule, making this crossover more energetically favorable than parallel alignment (compare to Fig. 1). (D) Crossover geometry in a right-handed braid. Phosphate strands on the back side of the blue molecule are aligned perpendicular to the opposing strands and grooves on the front side of the red molecule, making this crossover less favorable than parallel alignment.
To make the article accessible to a wide audience, we have structured it as follows. In the next section, we describe the basic features of the model and how the calculation was performed, presenting analytical formulas derived for the free energy of the braid and the braid pitch, and discuss advantages and limitations of the model. Derivations and important auxiliary details are provided in the Supporting Material. In Results, we describe predictions of the theory, focusing on qualitative ideas that may be tested experimentally. In Discussion, we interpret the existing data, present ideas for testing these interpretations, and speculate on biological implications of our results.
Model and Methods
Except for the more complex supercoil geometry, we followed the approach to calculating the free energy reviewed in Kornyshev et al. (9) and extended in Lee et al. (15). We accounted for sequence-related and thermal twisting and stretching deformations of the double helices. To calculate the free energy, we optimized the balance between electrostatic interactions and the elastic free energy of the braid. Here we state the basic assumptions of our model and outline the main steps of the calculation for the braid free energy, providing expressions used to generate our results.
Braid geometry
We considered topologically unconstrained braids formed by two infinitely long double helices. We assumed that:
-
1.
The braid is axially symmetric.
-
2.
The centerline of each molecule is an ideal helical line precessing around the braid axis with the constant, small tilt angle α (see Fig. 2).
-
3.
The distance R between the centerlines (braid diameter) remains constant along the braid.
-
4.
The molecules may slide along each other as well as stretch and twist about their centerlines.
Elastic energy
We utilized an elastic rod model (27) to describe both the elastic cost of DNA centerline bending, and the torsional and stretching deformations with respect to the centerline. Specifically, we described the elastic energy by Lee et al. (15),
| (1) |
Here μ labels the two molecules, s is the curvilinear coordinate along the centerline of each molecule, and rμ(s) defines the centerline in Cartesian coordinates. The geometric parameters Ωμ(s) and hμ(s) are the twist and rise per basepair along the centerline (see Fig. 1); is the average rise per basepair; and Ω0μ(s) and h0μ(s) are the intrinsic twist and rise per basepair in unstressed DNA. These are determined by the basepair sequence (9,28). The quantities B, Cs, and Ct are the elastic moduli of bending, stretching, and twisting, which we assume to be independent of s.
Electrostatic energy
We followed the model discussed in Kornyshev et al. (9), in which each DNA is represented by a flexible dielectric cylinder with discrete surface charges forming a double-helical pattern (Fig. 1). These curved cylinders follow the centerlines of the molecules forming the braid. The dielectric constant within them is taken to be much smaller than the bulk water value, used for the surrounding solvent. The radius of these cylinders is an effective parameter of the electrostatic theory rather than a hard-core radius of the molecule.
It is important to note that this approximation captures the most important effects of complex surface charge patterns on DNA electrostatics and is in good agreement with measured DNA-DNA interactions (9,15). Two braided dielectric cylinders model an effective dielectric response of DNA cores and tightly bound water molecules rather than hard-core interactions between the molecules. The corresponding dielectric constant is much lower than in bulk water, but this dielectric boundary is neither sharp nor well characterized. Hence we treat the radius a of the effective dielectric cylinder as a parameter of the theory and find its value a ≈ 11.2 Å by fitting the forces measured between parallel DNA molecules in aggregates (15). This model does not prohibit interpenetration of the dielectric cylinders, but the corresponding expression for the electrostatic energy might be inaccurate at interaxial distances R < 2a ≈ 22.4 Å (15). Hence, this model should not be applied to tightly supercoiled DNA minicircles, in which R might be as small as 19.5 Å (29). However, it is justified for less tightly wound braids considered in this study, in which one might expect R closer to 27–31 Å observed in counterion-condensed aggregates of parallel DNA molecules (30–33).
We described electrolyte ions within a Debye-Bjerrum-like approximation (9), distinguishing bound (condensed) counterions from other electrolyte ions. The former were treated as fixed charges on the cylinder surface that compensate a fraction θ of the DNA charge. The latter were treated within the Debye-Hückel approximation. We assumed that fraction f1 of bound counterions was located in the middle of the minor groove, fraction f2 was in the middle of the major groove, and the remaining fraction 1-f1-f2 was distributed randomly on the cylinder surface (see Fig. 1). The values of f1, f2, and θ were treated as phenomenological parameters and were not self-consistently calculated.
To calculate the electrostatic energy of a DNA braid, we utilized a small tilt angle (α) expansion. The details of this calculation and underlying approximations are discussed in Section SII of the Supporting Material. Briefly, we calculated the potential of a point charge on the dielectric boundary formed by two braided dielectric cores of DNA immersed in electrolyte solution, following the approach described earlier for straight, parallel molecules (34). We summed the contributions from all charges on each molecule (including fixed charges and condensed counterions), and calculated the electrostatic energy of these charges in the net potential. We accounted for the discrete nature and helical organization of the charges (see Fig. 1), but neglected the contributions of the harmonics of the surface charge density related to regular spacing between the charges along the helical strands (expected to be small based on earlier studies of interactions between straight molecules (9)).
The resulting electrostatic energy at small α (α ≈ sinα) is derived in Section SII of the Supporting Material,
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
Here, kB is the Boltzmann constant; T is the absolute temperature; lB is the Bjerrum length (≈ 7 Å at 25°C); is the number of charged phosphate groups per unit length of DNA (lc ≈ 1.7 Å); a is the effective radius of the dielectric cylinder (a ≈ 11.2 Å provides the best fit for forces measured in columnar DNA assemblies (15)); ≈ 2π /34 Å−1 is the mean reciprocal helical pitch of DNA; ≈ 0.4π is the azimuthal half-width of the minor groove; ΔΦ(s) ≈ Φ1-Φ2 (see Fig. 2) is the relative azimuthal alignment of the molecules; κD−1 is the Debye screening length in the electrolyte solution; and In(x), Kn(x), I′n(x), and K′n(x) are the modified Bessel functions and their derivatives, respectively.
The first term in Eq. 2 is the electrostatic interaction energy for parallel, straight molecules (α = 0) at interaxial spacing R (9). The second term is the next order in the expansion of the electrostatic energy at small α, where we have neglected a small repulsive term due to induced charges on the dielectric core (see Section SII in the Supporting Material). In addition, we neglected all higher order terms in the expansion in α.
Helix nonideality
In an unconstrained braid, in which the molecules can slide and rotate along each other, ideal double helices will establish an energetically optimal alignment with the optimal value of ΔΦ that does not depend on s. However, sequence-related variations and thermal fluctuations in the twist Ωμ(s) and rise hμ(s) per basepair disrupt this alignment, resulting in ΔΦ that depends on s. When two molecules are homologous (have the same basepair texts), ΔΦ is affected only by thermal fluctuations in Ωμ(s) and hμ(s). In nonhomologous pairs, uncorrelated sequence-related variations in Ωμ(s) and hμ(s) affect ΔΦ as well.
To describe these effects of nonideal helical structure on DNA braiding, in Section SIIB of the Supporting Material, we construct a partition function that accounts for all possible realizations of ΔΦ(s), due to sequence-related variations and thermal fluctuations in Ωμ(s) and hμ(s). We then calculate the free energy within a variational approximation proposed in Lee et al. (15).
Free energy
The resulting free energy per unit length of the braid at small α (α ≈ sinα) is given by Eqs. S64–S69 in the Supporting Material, which we rewrite as
| (8) |
| (9) |
and
| (10) |
Here and are the average alignment and structural adaptation length of DNA, which are determined by minimization of FDNA; ≈ 500 Å is the bending persistence length of DNA (35); ≈ 350 Å is the helical persistence length of DNA, which characterizes thermal fluctuations in the twist and rise per basepair (9,15); and λc(0) ≈ 150 Å is the intrinsic helical coherence length of DNA, which characterizes sequence-related variations in the twist and rise per basepair (36). The first two terms in Eq. 8 represent the contribution of electrostatic interactions, the third term is associated with the elastic energy and entropy of fluctuations in the twist and rise, and the last term is the bending energy.
The most energetically favorable tilt angle α may be obtained by minimization of Eq. 8, which yields
| (11) |
This is one of the key results of the article, as it relates the tilt angle to the chiral torque F1, caused by helix-specific electrostatic interactions; interaxial distance in the braid, R, which is to be self-consistently calculated (F1 is also R-dependent); and bending elastic modulus . Note that, given a phenomenological chiral torque F1, the forms of Eqs. 8 and 11 could have been deduced from the expected linear dependence of the chiral electrostatic interaction on α at small α (9,37), and the competing bending energy. However, without a full calculation, it would not be possible to say anything about the values of F1 and R, and thereby to evaluate αmin. Most importantly, the effects of sequence-related and thermal distortions in DNA structure as well as the contribution of image-charge interactions into F1 are not intuitive and could not be predicted a priori.
Model limitations
-
1.
The assumption of axially symmetric geometry with constant R and α constrains possible conformations of the braid. This model cannot be applied to supercoiled DNA minicircles, in which topological constraints, distortions of the double-helix structure, and the presence of hairpin loops at the two ends will affect the geometry of the central braid. However, our estimates suggest that it is a reasonable first approximation for long free braids with small tilt angles, in which the geometry is determined primarily by DNA-DNA interactions (provided that the molecules do not have significant intrinsic curvature associated, e.g., with multiple A-tracts). A more general theory, allowing for variable R and α, and possible braid asymmetry, will be developed in future work.
-
2.
The assumption of macroscopic dielectric response of water may not be accurate within 1–2 layers of water molecules separating the two double helices in a braid.
-
3.
Ion size and correlations may also become important at these close interaxial separations, particularly for multivalent counterions (for a discussion on ion correlations, see references (9,38,39)).
-
4.
The distribution of condensed ions (θ, f1, and f2) may depend on α, R, and κD. A self-consistent calculation of these parameters might be based on the ideas proposed in Netz and Orland (40), but it would require poorly characterized local binding potentials in the grooves to describe counterion chemisorption.
-
5.
Equation 8 is valid only at sufficiently large , when the second and higher order terms in the small α expansion are negligible compared to the bending energy at α = αmin, but we do not know whether this is the case for DNA. Nevertheless, we think that our theory captures the main aspects of the physics of DNA braiding and is adequate for an initial analysis and estimates.
Results
Free energy landscapes
Fig. 3 A illustrates the dependence of the free energy on the tilt angle and diameter of the braid for DNA molecules with uncorrelated sequences, θ = 0.7, f1 = 0.4, and f2 = 0.6. At this distribution of bound counterions, pairing of straight molecules (α = 0) is energetically unfavorable. However, topologically unconstrained molecules, which are allowed to bend, will spontaneously form a left-handed braid with R ≈ 24 Å and α ≈ 0.4 rad. (The tilt angle is positive in left-handed and negative in right-handed braids in accordance with the definition of the supercoiling sign in closed DNA loops). Importantly, the small α value obtained here is consistent with the assumptions of the theory. (Note that our theory is limited to braids with relatively small α, because it accounts only for the first term in the electrostatic energy expansion with respect to α—see Eq. 2. Thus, the free energy landscape shown in Fig. 3 A should not be extrapolated to tightly wound braids in which α might become close to 1 rad.)
Figure 3.
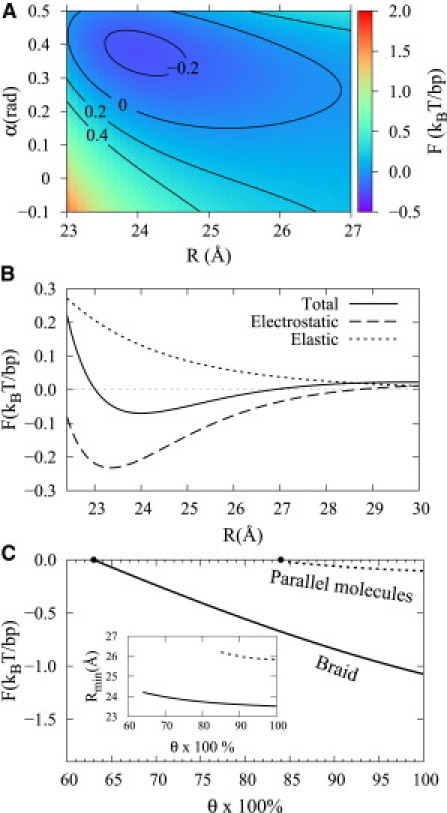
Free energy landscape for a braid formed by two DNA double helices with random, uncorrelated sequences. (A) Dependence of the free energy on the tilt angle α and braid diameter R at 70% compensation of phosphate charges by bound counterions. (B) Optimum energy at a fixed value of R, decomposed into the electrostatic (dashed) and elastic (dotted) components. (C) Dependence of the braid free energy at equilibrium (most favorable) R and α on the charge neutralization fraction θ. (Inset) Dependence of the equilibrium R on θ. The free energy was calculated from Eqs. 3–10 at a = 11.2 Å (15), λD = 7 Å (which corresponds to the physiological ionic strength), f1 = 0.4, and f2 = 0.6. F = FDNA at optimal .
Fig. 3 A shows that left-handed braiding makes DNA-DNA interactions more favorable as a result of better alignment of negatively charged phosphate strands with apposing positively charged grooves (see Fig. 2). The electrostatic benefit exceeds the bending energy cost associated with the braiding (Fig. 3 B). The net energy benefit of the left-handed braiding is further illustrated by Fig. 3 C that compares pairing free energies for an unconstrained braid (optimal α and R) and parallel, straight molecules (α = 0, optimal R). Pairing into a braid becomes favorable at smaller θ and the energetic benefit of the left-handed braiding may be as high as ∼1 kBT per basepair. Braiding also leads to closer spacing between the double helices in the pair (see Fig. 3 C, inset). Strictly speaking, this spacing may be too close to warrant the use of macroscopic electrostatics (R ∼ 24 Å corresponds to 1–2 layers of water molecules between DNA surfaces). Nevertheless, we expect that the qualitative predictions of this study will not be affected. Indeed, the dependence of the free energy on R (Fig. 3 A) suggests that even at larger interaxial separations there will still be a strong impetus for braiding.
Homologous pairing
The energetically favorable alignment of the strands and grooves on apposing DNA surfaces in the braid requires torsional and stretching deformations of the double helices with uncorrelated sequences. Otherwise, uncorrelated sequence-related variations in the helical pitches of the two molecules would disrupt the alignment. The elastic energy cost of the deformations that synchronize the helical pitches reduces the energetic benefit of the pairing (8,15).
In contrast, pairing of homologous double helices with similar sequences facing each other does not require such torsional and stretching deformations. Sequence-related variations in the helical pitches of homologous DNA molecules are the same, enabling the favorable alignment along the entire length of the braid without the additional elastic energy cost. As a result, pairing of homologous double helices is more favorable than pairing of nonhomologous ones by ∼0.3–0.4 kBT per basepair (Fig. 4 A, and see Fig. S1 in the Supporting Material). That difference per basepair translates into ∼50 kBT per bending persistence length of DNA, sufficient to compete with thermal motions (∼1 kBT per persistence length). Sufficiently long homologous DNA molecules may thus spontaneously associate into stable left-handed braids even at θ below 0.6 (e.g., the expected association energy for 200 bp molecules at θ = 0.6 exceeds 10 kcal/mol).
Figure 4.
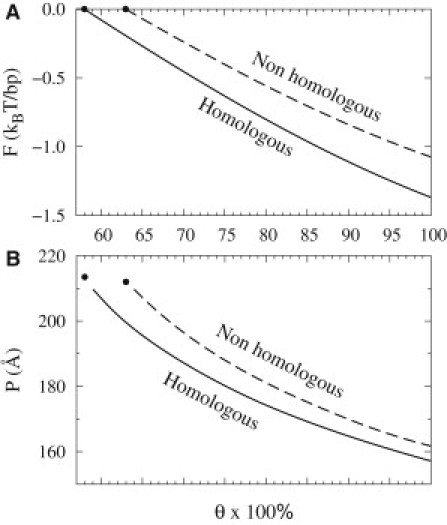
Braid pairing free energy (A) and pitch (B) for homologous and nonhomologous pairs as a function of charge compensation parameter θ. Endpoints denote the thresholds for pair stability. The parameters used to calculate the free energy were as in Fig. 3.
Pitch and handedness of DNA braids
In topologically unconstrained braids (e.g., formed by linear DNAs with free ends), the optimal tilt angle α is determined by the balance of chiral electrostatic interactions and DNA bending. Electrostatic interactions favor left-handed braiding, which enhances the favorable apposition of the negatively charged phosphate strands and positively charged grooves. The energetic cost of DNA bending associated with the braiding restrains the increase in α. At small α, the optimal tilt angle and the corresponding pitch P of the braid (P = 2R/tanα) may be described by Eq. 11 (and see Model and Methods). The pitch decreases with strengthening of the electrostatic interactions at larger θ (see Fig. 4 B). The predicted pitch of the braid is smaller than half of the bending persistence length, which indicates that chiral electrostatic interactions can induce significant bending of the molecules. The value of the pitch depends on the electrolyte composition, yet our model predicts left-handed chirality under all conditions.
Electrolyte effects on the pairing energy
Electrolyte composition affects the energy of DNA braids because different counterions have different preferences for binding the minor and major grooves of DNA (41). Stronger counterion localization in the grooves reduces the average distance between the apposing negative and positive charges (Figs. 1 and 2), thereby enhancing the attraction and pairing of the molecules (see Fig. S2). Interestingly, preferential counterion binding in the minor groove favors DNA association into braided pairs (Fig. S2), yet it suppresses the association of straight DNA molecules into parallel pairs (42).
Changing salt concentration, while keeping θ constant, has two competing effects. On one hand, higher ionic strength favors DNA pairing by diminishing the repulsion associated with the net charge of the molecules. On the other hand, it inhibits the pairing by diminishing the attraction between aligned negatively charged phosphate strands and positively charged grooves. The net-charge repulsion is screened by salt more effectively (see Model and Methods). As a result, increasing salt concentration strengthens the pairing at lower θ (see Fig. 5, curves with θ = 0.6, 0.7), when the net-charge repulsion is significant. Salt may weaken the pairing at larger θ (see Fig. 5, θ = 0.8), when the net interaction is dominated by the strand-groove attraction.
Figure 5.
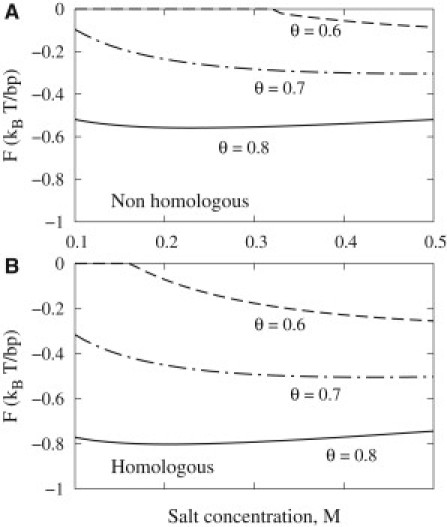
Salt concentration effects on DNA pairing energy of nonhomologous (A) and homologous (B) DNA molecules in 1:1 electrolyte solutions with different ionic strengths. All other parameters were the same as in Fig. 3.
Discussion
This work builds on several previous ideas for the potential role of chiral electrostatic interactions in DNA braids. In particular, the analytical theory of interactions between long, straight molecules (37) and analysis of crystal structures of short oligonucleotides (13) suggested that chiral electrostatic interactions favor right-handed DNA crossovers. Hence, these interactions may indeed stabilize left-handed DNA braids (9,26), in which the crossovers are right-handed (Fig. 2). Recently, Timsit and Várnai (13) proposed that: 1), divalent cations might induce left-handed DNA braiding via stable chiral crossovers; 2), hyperthermophilic bacteria and archaea might exploit chiral DNA-DNA interactions for genome stabilization; and 3), crossovers favored by chiral DNA-DNA interactions might contribute to the chiral selectivity of type II topoisomerases.
However, all these ideas were based on studies of individual crossovers between straight or nearly straight double helices. To the best of our knowledge, no theory or simulations of chiral electrostatic interactions in long DNA braids, in which the molecules are bent and wrapped around each other multiple times, has ever been reported before.
Our theory addresses this issue. It supports and corroborates the ideas discussed in the literature (9,13,26,37). It further develops and extends these ideas as well, by explicitly incorporating DNA bending and demonstrating how competition between the bending and chiral electrostatic interactions might affect the crossover angle and overall braid geometry.
More importantly, this theory predicts significant and nonintuitive effects of sequence homology and electrolyte composition on chiral electrostatic interactions in long DNA braids: 1), pairing of DNA molecules into braids is energetically favorable in a wider range of conditions than DNA condensation; 2), juxtaposition of homologous sequences in a braid is significantly more favorable than juxtaposition of nonhomologous sequences; and 3), spontaneous association of long homologous DNA molecules into stable pairs in monovalent salt solutions reported in Danilowicz et al. (7) might be explained by braiding. These predictions are the focus of our discussion below, although we also revisit and extend some of the older ideas.
Before we proceed, however, we should note that the quantitative accuracy of our theory is limited by the model assumptions (see Model Limitations). Hence, our interpretations of observed phenomena and their biological implications require further experimental testing.
Pairing into braids might be induced by counterions that do not cause DNA condensation
A larger variety of counterions might cause pairing of nonhomologous DNAs into braids than aggregation of DNA into assemblies. In the absence of osmotic stress, DNA self-assembly into columnar aggregates requires counterions (e.g., spermine4+, spermidine3+, and cobalt-hexamine3+) that bind preferentially in the major groove of DNA and compensate for ≥∼90% fraction of the total phosphate charge (43–45). Binding of these counterions induces a zipper-like juxtaposition of negatively charged phosphate strands and positively charged grooves. We argued that columnar aggregates form when the resulting zipper-type attraction between sufficiently long parallel molecules exceeds the repulsion associated with the net charge of DNA (5,9,15). Note, however, that the maximum net attraction energy between parallel molecules is only ∼0.2 kBT per basepair and that this energy is sensitive to the composition of the electrolyte solution and other experimental conditions (31–33). For instance, the attraction between short (<100 bp) DNA fragments induced by the same counterions was observed at some (46) but not other (47) experimental conditions.
This study suggests that pairing of long DNA molecules into braids becomes energetically favorable in a wider range of conditions, e.g., already at ∼70% or even lower compensation of the phosphate charge by counterions bound in either groove. Left-handed braiding leads to a more favorable juxtaposition of the negatively charged strands and positively charged grooves compared to parallel straight molecules (see Fig. 2), significantly enhancing the zipper attraction (see Figs. 3 C and 4 A). As a result, braided pairs might become energetically favorable already in Ca2+ and Mg2+ solutions, in which aggregation of DNA into columnar assemblies is unfavorable. A closely related stabilization of right-handed crossovers between DNA double helices was observed within oligonucleotide crystals (48) and interpreted as salt bridges between phosphates on one oligonucleotide and divalent ions bound to cytosine on the other (26). Note that further assembly of braided pairs into higher-order structures is likely to be unfavorable, e.g., columnar aggregation of the braids would involve unfavorable left-handed DNA crossovers.
At first sight, the prediction of energetically favorable braiding appears to be at odds with the lack of evidence for stable dimers in commonly used solutions of linear DNA, which often contain divalent ions and have been extensively studied in the early years of DNA research. However, spontaneous braid formation might not always occur or be readily apparent when the resulting braid is energetically favorable. For instance, Fig. 3 B predicts attractive interactions at <10 Å and repulsive interactions at larger surface-to-surface separations between braided double helices. The repulsion contributes to an energy barrier, which might prevent noticeable spontaneous pairing of DNA under common experimental conditions (e.g., at physiological or lower ionic strength). Entanglements and the need for large-scale winding of the molecules around each other are likely to further inhibit spontaneous braiding. Testing the possibility of spontaneous pairing of DNA molecules into stable braids might thus require dedicated studies, such as those recently reported by Danilowicz et al. (7). In the latter experiments, efficient DNA pairing was observed for homologous sequences of intermediate length (103−5 104 basepairs) at high ionic strength and elevated temperature.
Chiral electrostatic interactions may affect DNA supercoiling in closed loops
Electrostatic braiding in the presence of divalent ions might be responsible, e.g., for the observed supercoiling of plasmids relaxed with topoisomerase I. Equilibration of circular DNA with topoisomerase I and divalent counterions was found to produce positive (left-handed) supercoiling, after the ions and topoisomerase were removed (49). This observation was explained by assuming that bound divalent ions overwind the double helix and that relaxation of this overwinding after removal of the topoisomerase and ions causes the supercoiling. However, divalent cation binding might cause double-helix unwinding rather than overwinding. Indeed divalent ion binding reduces the electrostatic force that stretches DNA. Recent observations suggest that reduced stretching might cause double-helix unwinding rather than overwinding (50). As follows from our results, as well as simulations of Várnai and Timsit (26), divalent cation binding may cause positive supercoiling via chiral interactions that favor left-handed braiding in topoisomerase-relaxed DNA. This supercoiling is then topologically fixed upon the topoisomerase removal.
Hyperthermophiles may exploit chiral electrostatic interactions for genome stabilization
In vivo, supercoiling of plasmid DNA is controlled by gyrases (51), yet chiral interactions between DNA segments within braided regions of supercoiled plasmids may still be important. For instance, these interactions may affect the accessibility of the plasmid genome by controlling the tightness of the braid (13). Our theory supports this idea. Indeed, left-handed braiding in positively supercoiled plasmids makes the net electrostatic interaction less repulsive or even attractive, leading to more tightly wound braids and reduced genome accessibility (see Fig. 3 A). Mesophilic bacteria and archaea may need gyrases to produce energetically unfavorable right-handed braiding, increasing repulsion, leading to less tightly wound braids and so improving genome accessibility.
In contrast, hyperthermophilic bacteria and archaea may exploit attractive chiral electrostatic interactions in left-handed braids for survival at 80–110°C temperatures, at which these organisms thrive. The only proteins expressed exclusively in hyperthermophiles are reverse gyrases, which induce positive plasmid supercoiling. The need for the positive supercoiling cannot be explained by the double-helix stability or its resistance to thermal degradation, which are similar in negatively and positively supercoiled plasmids (14). It can be explained, however, by assuming that attractive chiral electrostatic interactions prevent excessive thermal loosening of left-handed DNA braids.
Electrostatically favored DNA crossovers might contribute to the chiral selectivity of type II topoisomerases
Speculating even further, stabilization of left-handed DNA braids by chiral electrostatic interactions might also rationalize the observed (52) chiral selectivity of some type II topoisomerases. Indeed, stable braids may not unwind when ATP-independent type I topoisomerases cut one DNA strand and relax topological constraints. For such braids, the cell may require ATP-dependent activity of type II topoisomerases, e.g., to prevent DNA polymerase stalling. This requirement may explain why certain type II topoisomerases have been designed by Nature to unwind stable left-handed braids much more efficiently than unstable right-handed braids (53,54).
Interestingly, the crossover angle at which topoisomerase IV (type II topoisomerase) has the highest activity (54) corresponds to the most energetically favorable crossover calculated for oligonucleotides (26). The average crossover angle 2α in braids of long DNA molecules is smaller than the value predicted for short, straight oligonucleotides, because the elastic cost of double-helix bending in braids increases as α4 (see Eq. 8). Note that smaller crossover angles are indeed observed in single-molecule braiding experiments (53,55). However, the most favorable local crossover angle upon the enzyme binding might correspond to that for short oligonucleotides (13), particularly after the two strands are cut and the bending constraint is relieved.
Homologous double helices might spontaneously form braided pairs in monovalent salt solutions
Finally, the energy benefit from left-handed braiding might explain the recently observed (7) selective pairing of homologous DNA molecules in monovalent salt solutions (see Fig. 4 A).
Spontaneous pairing of DNA molecules with uncorrelated sequences requires compensation of at least ∼65% of phosphate charges by bound counterions (see Fig. 4 A). Our theory may not be sufficiently accurate to predict the exact charge-compensation threshold. Nevertheless, it is reasonable to expect that the threshold needed for the pairing of uncorrelated sequences can be exceeded only in the presence of divalent or more highly charged counterions. Indeed, in a simple polyelectrolyte model of DNA, the phosphate charge compensation by condensed monovalent ions at experimentally relevant salt concentrations (>10 mM) is expected to be ∼60% or less (16).
Spontaneous pairing of homologs is more favorable and requires <∼60% compensation of the phosphate charges by bound counterions (see Fig. 4 A). The actual charge-compensation threshold for pairing may be even lower, e.g., due to distribution of adsorbed/condensed counterions between the major and minor grooves (see Fig. S2) and/or lower effective dielectric constant of water inside the braid (see Fig. 3 C, inset). Thus, monovalent counterion binding might be sufficient to exceed this threshold and explain the stable pairing of 1–5 kb homologs as reported by Danilowicz et al. (7). For instance, the association energy of such homologs at 60% phosphate charge compensation may be as large as ∼60–300 kcal/mol (Fig. 4 A).
The observed features of the homolog pairing reported by Danilowicz et al. (7), counterintuitive at a first glance, are in fact consistent with the interpretation suggested by our theory. In particular: 1), the observed increase of the strength of the pairing with increasing salt concentrations in monovalent salt is what the theory predicts at <80% compensation of the phosphate charge (Fig. 5). As we noted above, lower charge compensation is expected for monovalent salt solutions; 2), more efficient pairing in MgCl2 compared to NaCl or KCl may be explained by stronger counterion binding to DNA and therefore higher charge compensation (see Fig. 4 A); 3), subtle differences in the pairing efficiency in NaCl and KCl solutions may be related to differences in the partitioning of these counterions between the minor and major grooves and their localization within the grooves (see Fig. S2); and 4), lower bending rigidity of DNA reduces the elastic energy cost of braiding and facilitates the pairing. The decrease in DNA bending rigidity may thus contribute to the observed increase in the pairing efficiency at higher temperatures, up to ∼40°C. The increase in thermal torsional and stretching fluctuations, which weaken the pairing, may overwhelm the bending rigidity effect above 40°C, rationalizing the observed decrease in the pairing efficiency.
Note that this theory suggests how homologous DNA pairing might occur in monovalent salt solutions, but it is not accurate enough for more definite predictions. The features of the pairing observed by Danilowicz et al. (7) might also have alternative interpretations, some of which were discussed by the authors of the study. Thus, further experimental and theoretical studies are needed to confirm such pairing, test its molecular mechanism, and to systematically characterize the role of electrostatic interactions in DNA braiding. Such studies are currently under way in our and other laboratories.
Conclusions
-
1.
We have built a theory of DNA braids, incorporating chiral electrostatic interactions between helical patterns of discrete charges on DNA surface, DNA elasticity, and sequence-related and thermal distortions that affect DNA surface charge patterns.
-
2.
This theory predicts the self-assembly of two DNA molecules with uncorrelated sequences into left-handed braided pairs upon neutralization of as little as ∼65% of the phosphate charge by counterions bound in DNA grooves.
-
3.
DNA molecules with homologous sequences may self-assemble into a stable braided pair already at 60% and even lower phosphate charge neutralization, potentially explaining a recent observation of stable pairing of homologous molecules in NaCl and KCl solutions.
-
4.
Stabilization of left-handed braids by chiral electrostatic interactions may contribute to a variety of biologically significant phenomena.
Acknowledgments
The authors are thankful to G. S. Baldwin, G. van der Heiden, A. Korte, V. A. Parsegian, M. Prentiss, D. C. Rau, J. M. Schurr, J. M. Seddon, and E. Starostin for stimulating discussions.
This work was supported by the United Kingdom Engineering and Physical Sciences Research Council (grant No. EP/H004319/1), the Human Frontiers Science Program (grant No. RGP0049/2010-C102), and the Intramural research program of The Eunice Kennedy Shriver National Institute of Child Health and Human Development, National Institutes of Health.
Contributor Information
Ruggero Cortini, Email: ruggero.cortini@gmail.com.
Alexei A. Kornyshev, Email: a.kornyshev@imperial.ac.uk.
Dominic J. Lee, Email: domolee@hotmail.com.
Sergey Leikin, Email: leikins@mail.nih.gov.
Supporting Material
References
- 1.Barzel A., Kupiec M. Finding a match: how do homologous sequences get together for recombination? Nat. Rev. Genet. 2008;9:27–37. doi: 10.1038/nrg2224. [DOI] [PubMed] [Google Scholar]
- 2.Zickler D., Kleckner N. Meiotic chromosomes: integrating structure and function. Annu. Rev. Genet. 1999;33:603–754. doi: 10.1146/annurev.genet.33.1.603. [DOI] [PubMed] [Google Scholar]
- 3.Aragón-Alcaide L., Strunnikov A.V. Functional dissection of in vivo interchromosome association in Saccharomyces cerevisiae. Nat. Cell Biol. 2000;2:812–818. doi: 10.1038/35041055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Molnar M., Kleckner N. Examination of interchromosomal interactions in vegetatively growing diploid Schizosaccharomyces pombe cells by Cre/loxP site-specific recombination. Genetics. 2008;178:99–112. doi: 10.1534/genetics.107.082826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kornyshev A.A., Leikin S. Sequence recognition in the pairing of DNA duplexes. Phys. Rev. Lett. 2001;86:3666–3669. doi: 10.1103/PhysRevLett.86.3666. [DOI] [PubMed] [Google Scholar]
- 6.Baldwin G.S., Brooks N.J., Kornyshev A.A. DNA double helices recognize mutual sequence homology in a protein free environment. J. Phys. Chem. B. 2008;112:1060–1064. doi: 10.1021/jp7112297. [DOI] [PubMed] [Google Scholar]
- 7.Danilowicz C., Lee C.H., Prentiss M. Single molecule detection of direct, homologous, DNA/DNA pairing. Proc. Natl. Acad. Sci. USA. 2009;106:19824–19829. doi: 10.1073/pnas.0911214106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cherstvy A.G., Kornyshev A.A., Leikin S. Torsional deformation of double helix in interaction and aggregation of DNA. J. Phys. Chem. B. 2004;108:6508–6518. doi: 10.1021/jp0380475. [DOI] [PubMed] [Google Scholar]
- 9.Kornyshev A.A., Lee D.J., Wynveen A. Structure and interactions of biological helices. Rev. Mod. Phys. 2007;79:943–996. [Google Scholar]
- 10.Wang J.C. Cellular roles of DNA topoisomerases: a molecular perspective. Nat. Rev. Mol. Cell Biol. 2002;3:430–440. doi: 10.1038/nrm831. [DOI] [PubMed] [Google Scholar]
- 11.Wang J.C. DNA topoisomerases. Annu. Rev. Biochem. 1996;65:635–692. doi: 10.1146/annurev.bi.65.070196.003223. [DOI] [PubMed] [Google Scholar]
- 12.Cozzarelli N.R. DNA gyrase and the supercoiling of DNA. Science. 1980;207:953–960. doi: 10.1126/science.6243420. [DOI] [PubMed] [Google Scholar]
- 13.Timsit Y., Várnai P. Helical chirality: a link between local interactions and global topology in DNA. PLoS ONE. 2010;5:e9326. doi: 10.1371/journal.pone.0009326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Marguet E., Forterre P. DNA stability at temperatures typical for hyperthermophiles. Nucleic Acids Res. 1994;22:1681–1686. doi: 10.1093/nar/22.9.1681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lee D.J., Wynveen A., Leikin S. Undulations enhance the effect of helical structure on DNA interactions. J. Phys. Chem. B. 2010;114:11668–11680. doi: 10.1021/jp104552u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Netz R.R., Orland H. Variational charge renormalization in charged systems. Eur. Phys. J E Soft Matter. 2003;11:301–311. doi: 10.1140/epje/i2002-10159-0. [DOI] [PubMed] [Google Scholar]
- 17.Charvin G., Vologodskii A., Croquette V. Braiding DNA: experiments, simulations, and models. Biophys. J. 2005;88:4124–4136. doi: 10.1529/biophysj.104.056945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Marko J. Supercoiled and braided DNA under tension. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1997;55:1758–1772. [Google Scholar]
- 19.Boles T.C., White J.H., Cozzarelli N.R. Structure of plectonemically supercoiled DNA. J. Mol. Biol. 1990;213:931–951. doi: 10.1016/S0022-2836(05)80272-4. [DOI] [PubMed] [Google Scholar]
- 20.Strick T.R., Allemand J.F., Croquette V. Behavior of supercoiled DNA. Biophys. J. 1998;74:2016–2028. doi: 10.1016/S0006-3495(98)77908-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Cherstvy A.G. Torque-induced deformations of charged elastic DNA rods: thin helices, loops, and precursors of DNA supercoiling. J. Biol. Phys. 2011;37:227–238. doi: 10.1007/s10867-010-9211-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Clauvelin N., Audoly B., Neukirch S. Elasticity and electrostatics of plectonemic DNA. Biophys. J. 2009;96:3716–3723. doi: 10.1016/j.bpj.2009.02.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Maffeo C., Schöpflin R., Seidel R. DNA-DNA interactions in tight supercoils are described by a small effective charge density. Phys. Rev. Lett. 2010;105:158101. doi: 10.1103/PhysRevLett.105.158101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Fogg J.M., Catanese D.J., Zechiedrich L. Differences between positively and negatively supercoiled DNA that topoisomerases may distinguish. In: Benham C.J., Harvey S., Olson W.K., Sumners D.W., Swigon D., editors. Mathematics of DNA Structure, Function and Interactions. Springer; New York: 2009. pp. 73–121. [Google Scholar]
- 25.Kornyshev A.A., Leikin S., Malinin S.V. Chiral electrostatic interaction and cholesteric liquid crystals of DNA. Eur. Phys. J E Soft Matter. 2002;7:83–93. [Google Scholar]
- 26.Várnai P., Timsit Y. Differential stability of DNA crossovers in solution mediated by divalent cations. Nucleic Acids Res. 2010;38:4163–4172. doi: 10.1093/nar/gkq150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Yakushevich L. Vch Verlagsgesellschaft Mbh; Weinheim, Germany: 2004. Nonlinear Physics of DNA. [Google Scholar]
- 28.Gorin A.A., Zhurkin V.B., Olson W.K. B-DNA twisting correlates with base-pair morphology. J. Mol. Biol. 1995;247:34–48. doi: 10.1006/jmbi.1994.0120. [DOI] [PubMed] [Google Scholar]
- 29.Mitchell J.S., Laughton C.A., Harris S.A. Atomistic simulations reveal bubbles, kinks and wrinkles in supercoiled DNA. Nucleic Acids Res. 2011;39:3928–3938. doi: 10.1093/nar/gkq1312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.DeRouchey J., Parsegian V.A., Rau D.C. Cation charge dependence of the forces driving DNA assembly. Biophys. J. 2010;99:2608–2615. doi: 10.1016/j.bpj.2010.08.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rau D.C., Parsegian V.A. Direct measurement of temperature-dependent solvation forces between DNA double helices. Biophys. J. 1992;61:260–271. doi: 10.1016/S0006-3495(92)81832-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Rau D.C., Parsegian V.A. Direct measurement of the intermolecular forces between counterion-condensed DNA double helices. Evidence for long range attractive hydration forces. Biophys. J. 1992;61:246–259. doi: 10.1016/S0006-3495(92)81831-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Todd B.A., Parsegian V.A., Rau D.C. Attractive forces between cation condensed DNA double helices. Biophys. J. 2008;94:4775–4782. doi: 10.1529/biophysj.107.127332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kornyshev A.A., Leikin S. Theory of interaction between helical molecules. J. Chem. Phys. 1997;107:3656–3674. [Google Scholar]
- 35.Hagerman P.J. Flexibility of DNA. Annu. Rev. Biophys. Biophys. Chem. 1988;17:265–286. doi: 10.1146/annurev.bb.17.060188.001405. [DOI] [PubMed] [Google Scholar]
- 36.Wynveen A., Lee D.J., Leikin S. Helical coherence of DNA in crystals and solution. Nucleic Acids Res. 2008;36:5540–5551. doi: 10.1093/nar/gkn514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kornyshev A.A., Leikin S. Electrostatic interaction between long, rigid helical macromolecules at all interaxial angles. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 2000;62(2 Pt B):2576–2596. doi: 10.1103/physreve.62.2576. [DOI] [PubMed] [Google Scholar]
- 38.Wong G.C.L., Pollack L. Electrostatics of strongly charged biological polymers: ion-mediated interactions and self-organization in nucleic acids and proteins. Annu. Rev. Phys. Chem. 2010;61:171–189. doi: 10.1146/annurev.physchem.58.032806.104436. [DOI] [PubMed] [Google Scholar]
- 39.Grosberg A.Y., Nguyen T.T., Shklovskii B.I. Colloquium: the physics of charge inversion in chemical and biological systems. Rev. Mod. Phys. 2002;74:329–345. [Google Scholar]
- 40.Netz R., Orland H. Beyond Poisson-Boltzmann: fluctuation effects and correlation functions. Eur. Phys. J E Soft Matter. 2000;1:203–214. [Google Scholar]
- 41.Hud N., editor. Nucleic Acid-Metal Ion Interactions. The Royal Society of Chemistry; Cambridge, UK: 2009. [Google Scholar]
- 42.Kornyshev A.A., Leikin S. Electrostatic zipper motif for DNA aggregation. Phys. Rev. Lett. 1999;82:4138–4141. [Google Scholar]
- 43.Bloomfield V.A. DNA condensation. Curr. Opin. Struct. Biol. 1996;6:334–341. doi: 10.1016/s0959-440x(96)80052-2. [DOI] [PubMed] [Google Scholar]
- 44.Pelta J., Jr., Durand D., Livolant F. DNA mesophases induced by spermidine: structural properties and biological implications. Biophys. J. 1996;71:48–63. doi: 10.1016/S0006-3495(96)79232-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Pelta J., Livolant F., Sikorav J.L. DNA aggregation induced by polyamines and cobalthexamine. J. Biol. Chem. 1996;271:5656–5662. doi: 10.1074/jbc.271.10.5656. [DOI] [PubMed] [Google Scholar]
- 46.Li L., Pabit S.A., Pollack L. Double-stranded RNA resists condensation. Phys. Rev. Lett. 2011;106:108101. doi: 10.1103/PhysRevLett.106.108101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bai Y., Das R., Doniach S. Probing counterion modulated repulsion and attraction between nucleic acid duplexes in solution. Proc. Natl. Acad. Sci. USA. 2005;102:1035–1040. doi: 10.1073/pnas.0404448102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Timsit Y., Moras D. DNA self-fitting: the double helix directs the geometry of its supramolecular assembly. EMBO J. 1994;13:2737–2746. doi: 10.1002/j.1460-2075.1994.tb06567.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Xu Y.C., Bremer H. Winding of the DNA helix by divalent metal ions. Nucleic Acids Res. 1997;25:4067–4071. doi: 10.1093/nar/25.20.4067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Gore J., Bryant Z., Bustamante C. DNA overwinds when stretched. Nature. 2006;442:836–839. doi: 10.1038/nature04974. [DOI] [PubMed] [Google Scholar]
- 51.Champoux J.J. DNA topoisomerases: structure, function, and mechanism. Annu. Rev. Biochem. 2001;70:369–413. doi: 10.1146/annurev.biochem.70.1.369. [DOI] [PubMed] [Google Scholar]
- 52.Crisona N.J., Strick T.R., Cozzarelli N.R. Preferential relaxation of positively supercoiled DNA by E. coli topoisomerase IV in single-molecule and ensemble measurements. Genes Dev. 2000;14:2881–2892. doi: 10.1101/gad.838900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Stone M.D., Bryant Z., Cozzarelli N.R. Chirality sensing by Escherichia coli topoisomerase IV and the mechanism of type II topoisomerases. Proc. Natl. Acad. Sci. USA. 2003;100:8654–8659. doi: 10.1073/pnas.1133178100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Neuman K.C., Charvin G., Croquette V. Mechanisms of chiral discrimination by topoisomerase IV. Proc. Natl. Acad. Sci. USA. 2009;106:6986–6991. doi: 10.1073/pnas.0900574106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Charvin G., Bensimon D., Croquette V. Single-molecule study of DNA unlinking by eukaryotic and prokaryotic type-II topoisomerases. Proc. Natl. Acad. Sci. USA. 2003;100:9820–9825. doi: 10.1073/pnas.1631550100. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


