Bayesian Modeling for Genetic Anticipation in Presence of Mutational Heterogeneity: A Case-Study in Lynch Syndrome

Summary

Genetic anticipation, described by earlier age of onset (AOO) and more aggressive symptoms in successive generations, is a phenomenon noted in certain hereditary diseases. Its extent may vary between families and/or between mutation sub-types known to be associated with the disease phenotype. In this paper, we posit a Bayesian approach to infer genetic anticipation under flexible random effects models for censored data that capture the effect of successive generations on AOO. Primary interest lies in the random effects. Misspecifying the distribution of random effects may result in incorrect inferential conclusions. We compare the fit of four candidate random effects distributions via Bayesian model fit diagnostics. A related statistical issue here is isolating the confounding effect of changes in secular trends, screening and medical practices that may affect time to disease detection across birth cohorts. Using historic cancer registry data, we borrow from relative survival analysis methods to adjust for changes in age-specific incidence across birth cohorts. Our motivating case-study comes from a Danish cancer register of 124 families with mutations in mismatch repair genes known to cause hereditary non-polyposis colorectal cancer, also called Lynch syndrome. We find evidence for a decrease in AOO between generations in this study. Our model predicts family level anticipation effects which are potentially useful in genetic counseling clinics for high risk families.

1. Introduction

Genetic anticipation is a phenomenon noted in certain hereditary diseases where succeeding generations have decreased age of onset (AOO). It is hypothesized for some familial diseases in which high-penetrance mutations have been identified (Tabori et al., 2007; Nilbert et al., 2009). Data to test for anticipation can be retrospective in nature, where paired data on AOOs for affected parents are compared to their affected children. Appropriate statistical techniques have been developed to adjust for truncation bias, as younger subjects have not experienced their entire “at-risk” period when the data are ascertained (Huang and Vieland, 1997; Rabinowitz and Yang, 1999). See Boonstra et al. (2010) for a review of testing for anticipation with parent-child pair data.

Alternatively, all identified and obligate mutation carriers in high-risk families may be prospectively followed till disease diagnosis or censoring. Standard regression models for censored data allow for estimation of a generational effect on AOO (Hsu et al., 2000). Using data on affected and unaffected family members is a more powerful approach than the naive analysis of parent-child pairs. Robust variance estimates (Daugherty et al., 2005) or random intercepts (Larsen et al., 2009) can account for within-family correlation. If heterogeneity in anticipation exists across carrier families, use of a random slope corresponding to generation may be more appropriate. In this paper we evaluate this random intercept and slope model in the presence of observed and unmeasured familial heterogeneity under a prospective design.

Normality of the random effects is often assumed for convenience. However, there may be heterogeneity in anticipation across mutation subtypes; it is natural to explore models that are able to capture this variation. A latent mixture model can also be envisioned in which the random effects distribution adapts to latent heterogeneity not directly attributable to measured mutation subtypes. Estimates of fixed effects are relatively robust to misspecification of the random effects distribution (Butler and Louis, 1992; Verbeke and Lesaffre, 1997; Neuhaus et al., 2010), but estimates of the random effects themselves are sensitive to model choice (Verbeke and Molenberghs, 2000). When the inferential focus is on the latter, correct specification and appropriate model diagnostic tools become critical. Although individual predictions of the random effects can vary with the assumed distribution, McCulloch and Neuhaus (2010) recently showed that an aggregate measure of predictive accuracy is minimally affected by distributional misspecifications. Our interest is in both the individual and aggregate level, so proper elucidation of the random effects distribution remains an important statistical and biological issue.

There has been substantial work on robust modeling of the random effects. Magder and Zeger (1996) use a smoothed version of the nonparametric mixing distribution proposed by Laird (1978). Verbeke and Lesaffre (1996) employ a mixture of normals, using latent class membership and the expectation-maximization (EM) algorithm to maximize the likelihood. Kleinman and Ibrahim (1998) utilize a Dirichlet Process prior. Zhang and Davidian (2001) assume the random effects have a smooth density determined by a user-specified tuning parameter. We first consider a three-component mixture of normals where class membership is attributed to the three observed mutation subtypes. We then use a mixture of normals with latent classes, both finite mixture, and infinite. The latter is generated by a Dirichlet Process mixture of normals (Escobar and West, 1995). These models are compared to the normal random effects model. The Bayesian paradigm enables us to specify the hierarchical structure on parameters through prior specification and facilitates computation through Markov chain Monte Carlo (MCMC) techniques (Stephens, 2000; Neal, 2000). We modify existing ideas from the Bayesian model diagnostics literature, using the deviance information criterion (Spiegelhalter et al., 2002; Celeux et al., 2006), posterior conditional predictive ordinates (Geisser, 1980), and a Bayesian analogue of a scoring method proposed by Brier (1950).

Additionally, because we have posterior draws of all model parameters and random effects, these models can easily provide clinical quantities of interest, like the probability that a specific family's level of anticipation exceeds a certain number of years. These tools can be employed in counseling families at high-risk familial cancer genetics clinics.

We also address another major statistical issue in the anticipation literature for which no proper solution has been thus far proposed. Later generations typically have access to better medical care, more sensitive diagnostic techniques and are perhaps more knowledgeable on lifestyle changes which decrease risk of disease. Without independently estimating and adjusting for this cohort effect, generational changes in AOO will be the aggregate effect of anticipation, if it exists, plus these secular changes. Using birth cohort in the model may lead to instability in parameter estimates due to its strong correlation with generation, the primary variable of interest. Daugherty et al. (2005) include a time-varying indicator term reflecting a change in hazard before and after a specific year. In their case-study, upon the addition of this indicator term to the model, the effect of anticipation lost statistical significance. Nilbert et al. (2009) alternatively conduct analysis stratified by birth cohort. Neither of the above two approaches is effcient as a general modeling strategy. Our solution to this problem borrows from the concept of relative survival analysis (Ederer et al., 1961). We use external registry data to estimate this secular change in AOO; the residual effect beyond this estimated trend effect can then be attributed to anticipation.

1.1 A case-study of genetic anticipation in Lynch syndrome

A disease in which the presence of anticipation is disputed is Lynch Syndrome (Larsen et al., 2009; Tsai et al., 1997). First described as a cancer family syndrome by Warthin (1913) and later called hereditary non-polyposis colon cancer (HNPCC), Lynch syndrome (Lynch et al. (1966)), is characterized by early onset of gastrointesinal, uterine and other cancers and has a genetic basis in germline mutations to various mismatch repair (MMR) genes (hMLH1, hMSH2, hMSH6 being the most common).

The dataset we use, originally considered in Larsen et al. (2009), consists of 816 individuals from 124 families (median family size was 6 with a range of 1 to 23) ascertained over 1991–2006 via the population-based HNPCC register in Denmark. The register contains data on all Danish families identified with hereditary colorectal cancer. The current cohort was defined as 124 families who went through genetic counseling and testing and were found to carry HNPCC predisposing mutations in one of the MMR genes: hMLH1 (43 families), hMSH2 (59), or hMSH6 (22). Families with at least two Lynch-related cancers were included. The chosen cohort thus consists of high-risk Lynch families enriched for multiple cancers. Consequently, all results are subject to this multiplex ascertainment bias. All “at-risk” proven mutation carriers in these 124 families were followed prospectively, with the event of interest being diagnosis of a Lynch-related cancer. Individuals were censored administratively in December 2007 (202 individuals), upon detection of adenoma (a benign tumor, 37), cancer not related to Lynch syndrome (7), or upon death (2). We assume independent censoring in our formulation of the problem (this was likely violated for the 37 individuals who had adenoma detected, a limitation in our approach). Besides AOO and the censoring indicator, gender, year of birth, mutation, and generation are available. Descriptive summaries are presented in Table 1. Consistent with the regression approach to testing anticipation, Larsen et al. propose a normal random intercept model with a fixed effect for the difference in mean AOO between consecutive generations. We consider extensions of this model. Lynch et al. (2006) provide an overview of various, potentially latent, heterogeneities which may appear between Lynch families (apart from known mutational heterogeneity). Some examples are etiology based in recurrent versus founder mutations, the geographical location of the affected family, and access to/compliance with regular colonoscopy. This suggests that the anticipation effect might be more adequately modeled as a random effect with a flexible distribution. A further benefit of this approach is that families can get a “personalized” estimate of anticipation.

Table 1.

Descriptive summary of the Danish HNPCC data, containing 43 hMLH1 families, 59 hMSH2 families, and 22 hMSH6 families. The first column denotes total numbers of individuals, the second column gives numbers of individuals who have been diagnosed with a Lynch Syndrome (LS) cancer, and the third and fourth columns give summary statistics corresponding to the ages of onset (AOO) of affected individuals.

	# Subjects	# LS cancers	mean (AOO)	sd (AOO)
Males	392	263	47.0	13.0
Females	424	305	46.6	11.7
gen= 1	196	190	53.0	11.9
gen = 2	345	274	45.2	11.0
gen = 3	234	100	40.0	11.0
gen = 4	41	4	25.0	13.6
hMLH1	279	194	45.4	12.8
hMSH2	402	289	46.3	11.5
hMSH6	135	85	51.6	13.1

The rest of the paper is organized as follows. We introduce the original model from Larsen et al. (2009) and then present the Bayesian specification of proposed candidate models in Section 2. Section 3 discusses model diagnosis strategies using newly proffered criteria as well as standard posterior predictive checks. Section 4 presents an application of the methods to the Danish HNPCC data. Finally, we close with a discussion in Section 5.

2. Model Specification

2.1 A Random intercept model for Genetic Anticipation

Let i = 1,–, N index families and j = 1,–, n_i index individuals within family i. A linear model with random effects is given as

$$T_{ij}=X_{ij}^{\top }\beta +Z_{ij}^{\top }{b}_i+{∊}_{ij},$$ (1)

where T_ij denotes the AOO (in years) of the jth individual in the ith family (person (i, j)), X_ij and Z_ij are vectors of covariates, β is a length-p vector of fixed effects, b_i a length-q vector of random effects, and ε_ij the error term.

T_ij is right-censored for some individuals at C_ij, so we observe {min(t_ij, c_ij), 1 [t_ij ≤ c_ij]}. This is equivalent to the following notational convention:

$$t_{ij}^L=\min (t_{ij},c_{ij}),t_{ij}^U=\{\begin{array}{c}{t}_{ij}{t}_{ij}\le c_{ij}\hfill \\ \infty c_{ij}<t_{ij}\hfill \end{array}\phantom{\}}.$$

Let gen_ij denote the generation of that individual relative to the oldest member in the pedigree. That is, the oldest person in a pedigree is assigned gen = 1, along with his brothers, sisters, and cousins. All members of the next generation are assigned gen = 2, and so forth. The other two covariates used are 1[male_ij] indicating gender and 1[mut_i = hMLH1], 1[mut_i = hMSH2], and 1[mut_i = hMSH6] indicating mutation type. Beginning from (1), the random intercept model proposed by Larsen et al. (2009) uses $X_{ij}^{\top }\beta \equiv ({\mathrm{gen}}_{ij},1\left[{\mathrm{male}}_{ij}\right],1[{\mathrm{mut}}_i=\mathrm{hMLH}1],1[{\mathrm{mut}}_i=\mathrm{hMSH}2])\times {({\beta }_1,{\beta }_2,{\beta }_3,{\beta }_4)}^{\top }$ and $Z_{ij}^{\top }{b}_i\equiv 1\times b_i$, with $b_i\stackrel{\mathit{iid}}{~}\mathcal{N}({\mu }_b,{\sigma }_b^2)$ and ${∊}_{ij}\stackrel{\mathit{iid}}{~}\mathcal{N}(0,{\sigma }^2)$. Larsen et al. estimate parameters by maximizing the marginal likelihood:

$$\prod _{i=1}^N{\int }_{-\infty }^{\infty }\left\{\prod _{j=1}^{n_i}{\int }_{t_{ij}^L}^{t_{ij}^U}\varphi (t,X_{ij}^{\top }\beta +Z_{ij}^{\top }{b}_i,{\sigma }^2)\mathit{dt}\right\}\varphi (b_i,{\mu }_b,{\sigma }_b^2){\mathit{db}}_i$$

where ϕ(·, m, s²) denotes the density of a normal random variable with mean m and variance s². We use the convention that ${\int }_a^{a}f\left(x\right)\mathit{dx}=f\left(a\right)$. The parameter of interest is β₁, which can be interpreted as the difference in mean AOO between consecutive generations of the same family. In the original paper, the authors find a highly significant effect from anticipation, with ${\widehat{\beta }}_1=-2.95(p<0.001)$ corresponding to the fixed effect of generation.

2.2 Birth cohort adjustment

We first describe the adjustment strategy we adopted to create the pseudo-AOO data upon which the final models were built. As mentioned in Section 1, without adjusting for secular changes in diagnostic techniques and lifestyle, the change in AOO between consecutive generations is the cumulative effect of these changes and any anticipatory effect which may be present. Including a “year of birth” effect in order to capture these secular changes does not solve the problem, as corresponding parameters are only weakly identifiable due to ill-conditioning of the design matrix. A stratified-by-birth-cohort analysis lacks statistical power. As an alternative, this cohort effect may be estimated from external historic data. The Nordic Cancer Registries (NORDCAN, Engholm et al., 2010) provide incidence, mortality and prevalence data on 41 major cancers in the Nordic countries. We estimated the change in AOO between five-year birth cohorts via a two-step process.

First, we accumulated cohort-specific incidence rates of colorectal cancer (and, for women, endometrial cancer, the other major Lynch-related cancer) over five-year periods beginning in 1943, the earliest data available, and ending in 2008. Thus, for a single five-year birth cohort, its estimated hazard function for cancer diagnosis was piecewise-linear, changing at five year knots. Web Figure 1 gives a sample plot of the incidence rates by birth cohort for males. We assumed that there was no hazard for cancer diagnosis before age ten and that it remained constant after age 85. There was also some missing information; e.g., when the Registries began in 1943, there was no information on previous incidence rates for the `1869–1873' birth cohort (70–74 years old at that time). We filled in these missing values with the mean of the age-specific hazards for the next five birth cohorts, `1874–1878',…, `1894–1898', when they were 70–74 years old.

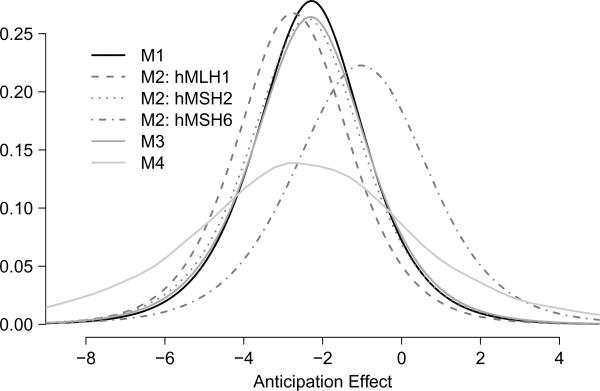
Figure 1.

The top panel presents posterior predictive density of a new pedigree, not present in our dataset, under models M1–M4. The bottom panel presents kernel estimates of the posterior density of three largest families present in our dataset, one from each mutation subtype, under models M1–M4.

Second, we simulated each Danish birth-cohort and exposed it to its cohort-specific hazard. An estimate of each cohort size was obtained from NORDCAN. We then fitted a single survival model with these simulated times-to-event data (S_l, say, for the lth individual) with the corresponding birth cohort as an ordinal covariate. Namely, S_l = γ cohort_l + ε_l, ${∊}_l\stackrel{\mathit{iid}}{~}N(0,{\sigma }_e^2)$. The cohort variable is defined as cohort_l = 0, if the lth subject is born in the reference cohort 1959–63, cohort_l = 1 if the lth subject is born in 1964–1968, cohort_l = −1, if the lth subject is born in 1954–58, and so on for each five-year cohort. We fitted this trend model stratified by gender: $\widehat{\gamma }$ was −0.215 years for males and −0.176 years for females. Of the two primary sources of variability in these estimates (due to simulation variability and the comprehensiveness of the registry), only the former was quantifiable: 50 simulations saw standard deviations of about 0.008 in these estimates. Given the scale of the variables, this uncertainty was ignored in all subsequent analysis.

Returning to the primary dataset under consideration, to adjust for these estimated secular trends, we transformed the data corresponding to the jth member of the ith family as $t_{ij}^{L\ast }\equiv t_{ij}^L+0.215\times {\left(\mathrm{cohort}\right)}_{ij}$ and $t_{ij}^{U\ast }\equiv t_{ij}^U+0.215\times {\left(\mathrm{cohort}\right)}_{ij}$ (under the convention that ∞ remains unchanged) for males, and similarly for females. For an observed (censored) event time, we can interpret $t_{ij}^{L\ast }$ as the AOO (time of censoring) if that person had experienced the medical technology and lifestyle of someone born in the reference cohort. We now present four alternative models using the adjusted AOO data $(t_{ij}^{L\ast },t_{ij}^{U\ast })$ as our response.

2.3 Alternative Models and Likelihood

Recalling the general structure of (1), the common elements of each model are given as follows. $Z_{ij}^{\top }{b}_i\equiv (1,{\mathrm{gen}}_{ij})\times {(b_{0_i},b_{1_i})}^{\top }$, so that the parameter of interest becomes b_1i, the random slope associated with gen_ij. We interpret b_1i as the change in AOO (in years) between consecutive generations of the ith family after adjusting for cohort effects and other covariates. We use a mixture model for the random effects, namely,

$$b_i\mid {\{{\pi }_{\ell },{\mu }_{\ell },{\Sigma }_{\ell }\}}_{\ell }\stackrel{\mathit{iid}}{~}\sum _{\ell =1}^k{\pi }_{\ell }\mathcal{MVN}({\mu }_{\ell },{\Sigma }_{\ell }).$$ (2)

Let d_i denote cluster membership, so that, for d_i ε {1,–, k}, b_i|d_i, μ_di, ${\Sigma }_{d_i}~\mathcal{MVN}({\mu }_{d_i},{\Sigma }_{d_i})$. The error distribution is assumed to be ${∊}_{ij}\stackrel{\mathit{iid}}{~}{t}_5\left({\sigma }^2\right)$ heavy tails account for outliers we found in preliminary analyses. In all analyses, T_ij is the outcome, as in (1). This choice of untransformed outcome and t-residuals provides significantly improved fit over a model with log-transformed AOO and normal residuals. Moreover, the estimated parameters can be directly interpreted in terms of the number of years increse/decrease in AOO. The unique specifications corresponding to each of the four random effects models are as follows.

Model 1 (M1): Single component multivariate normal

The fixed effects are given by: $X_{ij}^{\top }\beta \equiv$ (1[male_ij], 1[mut_i = hMLH1], 1[mut_i = hMSH2]) × (β₁, β₂, β₃)^⊤. In (2), k = 1, so $b_i\stackrel{\mathit{iid}}{~}\mathcal{MVN}({\mu }_1,{\Sigma }_1)$. Relative to Larsen et al., this model relaxes the constraint of a common anticipation effect across families.

Model 2 (M2): Three distinct multivariate normals assigned by measured mutation subtype

The fixed effects, $X_{ij}^{\top }\beta \equiv 1\left[{\mathrm{male}}_{ij}\right]\times {\beta }_1$. Additionally, d_i = 1[mut_i = hMLH1] + 2 × 1[mut_i = hMSH2] + 3 × 1[mut_i = hMSH6], which implies that cluster membership is known, based on the MMR mutation subtype of each family. Thus, rather than just shifting the mean AOO, as in M1, the mutation subtypes also differ (potentially) in the slope corresponding to gen_ij.

Model 3 (M3): A finite mixture of multivariate normals

As in M1, the fixed effects are $X_{ij}^{\top }\beta \equiv$ (1[male_ij], 1[mut_i = hMLH1], 1[mut_i = hMSH2]) × (β₁, β₂, β₃)^⊤. For the mixture components, both k and {d_i} are unknown parameters. This is a more flexible version of M1; mutation subtypes play the same role of shifting the mean AOO, but the distribution of the random eFFects is not forced to normality.

Model 4 (M4): An infinite mixture of multivariate normals

The fixed effects are as in M1 and M3, but b_i is given a Dirichlet Process mixture (DPM) of normals prior, described by the following hierarchy:

$$b_i\mid d_i,{\mu }_{d_i},{\Sigma }_{d_i}~\mathcal{MVN}({\mu }_{d_i},{\Sigma }_{d_i});{\mu }_{d_i},{\Sigma }_{d_i}^{-1}\mid G~G;G\mid \alpha ,G_0~\mathcal{D}\mathcal{P}(\alpha ,G_0(\mu ,E)).$$

α is a precision parameter and G₀(μ, Σ) is the normal-Wishart base distribution (Escobar and West, 1995). Prior specification on α and G₀ is described in the next section. M3 and M4 are similar, the primary difference in interpretation being that the latter allows for the existence of clusters in the population not found in the study sample, admitting an additional level of uncertainty. Note the increasing order of flexibility as we go from M1 to M4.

We consider the joint likelihood of the data and the random effects as the basis of our inference. The contribution of the ith family to this joint likelihood is given by,

$$L_i=\left\{\prod _{j=1}^{n_i}{\int }_{t_{ij}^{L\ast }}^{t_{ij}^{U\ast }}\tau (t,X_{ij}^{\top }\beta +Z_{ij}^{\top }{b}_i,{\sigma }^2,5)\mathit{dt}\right\}{\varphi }_2(b_i,{\mu }_{d_i},{\Sigma }_{d_i}).$$ (3)

τ(·, m, s², ν) gives the density of a t-distributed scalar with location m, scale s and ν degrees of freedom, ϕ₂(·, M, S) denotes the density of a bivariate normal (BVN) vector with mean vector M and variance matrix S, and ${\int }_a^{a}f\left(x\right)\mathit{dx}=f\left(a\right)$. Quadrature or Monte Carlo methods could be used to integrate the random effects in (3) so as to maximize the marginal likelihood, but a hierarchical Bayesian approach is conceptually and computationally much simpler for the proposed latent mixture models.

2.4 Priors

We next specify the prior distributions on model parameters. In all cases, β is given a uniform prior on $\mathbb{R}$ and σ² is Gamma with shape 1 and rate 0.01.

For M1–M3, μ_ℓ|ξ, κ is BVN with mean ξ and precision matrix κ. The hyperprior on ξ is uniform on $\mathbb{R}$, and κ is assumed Wishart with 2 degrees of freedom (df) and scale matrix (2I_2×2)⁻¹. Finally, ${{\Sigma }_{\ell }}^{-1}\mid \Psi$ is Wishart with 8 df and scale matrix (2Ψ)⁻¹, and the hyperprior on Ψ is Wishart with df 2g and scale matrix (2h)⁻¹. We vary g, h to assess prior sensitivity.

M3 requires two additional priors. The number of mixing components k is assumed a priori Poisson with mean 3, truncated at 20, and the mixing probabilities {π₁, …, π_k}|k are assigned a non-informative discrete Dirichlet (1, 1, …, 1) prior. Inference on k is sensitive to the prior on κ (Richardson and Green, 1997), but, since we are primarily interested in exploring heterogeneity rather than identifying distinct familial clusters, fitting more components than necessary is not a concern in the current application.

For M1–M3, it remains to select g and h. This far down the hierarchy, they cannot be intuited or made sufficiently vague. Moreover, it seems plausible that inference on the random effects could be sensitive to g and h; thus we consider several prior structures. For M3, larger values on the diagonals of h favor many small variance components, yielding undesirable spikes in the density of the random effects. Keeping this in mind, we set g₁ = 2 and h₁ = diag(0.06, 0.12); sampling values of Σ_ℓ from this prior shows that the middle 99% of the density is approximately (0.63, 74.62) and (0.36, 37.94) for he diagonal components, wide intervals that avoid zero. As a sensitivity analysis, we also looked at two other priors: g₂ = 1 and h₂ = diag(0.03, 0.06), which flattens the prior density on Σ_ℓ, and g₃ = 2 and h₃ = diag(0.1, 0.3), which puts more mass closer to zero-values.

For M4, we assume a Gamma prior on α with shape 2 and rate 0.5. This induces a prior mode for the number of clusters k at 10, with about 80% of the prior mass on k < 20. For the parameters of the normal-Wishart base measure G₀(μ, Σ), Σ⁻¹|A is Wishart with 5 df and scale matrix A⁻¹ and μ|ξ, κ₀, Σ is normal with mean ξ and scale matrix ${\left(2I_{2\times 2}\right)}^{-1}$. Finally, ξ is normal with mean (50, 0) and variance diag(30, 10), κ₀ is Gamma with shape 0.05 and rate 0.05, and A|B is Wishart with 5 df and scale matrix B⁻¹. While B roughly corresponds to h above, a direct correspondence can not be drawn between the two hyperparameters. We present results under B = diag(3, 6) and evaluate sensitivity to this prior choice.

2.5 Posterior Sampling

We take a Gibbs sampler/data augmentation approach to handle the censored data likelihood (Tanner and Wong, 1987). The algorithm changes between the four models because k and {d_i} are known for M1 and M2 but not M3 or M4. This also implies that the dimension of the parameter space in M3 and M4 can change across iterations; in the finite mixture case of M3, we use the MCMC scheme developed by Stephens (2000), whereas for M4, we use sampling algorithms proposed by Neal (2000) implemented in the DPpackage in R (Jara, 2007). See Web Appendix A for details of the sampling strategy and full conditionals.

For each pairwise combination of {M1, M2, M3} with {{g₁, h₁}, {g₂, h₂}, {g₃, h₃}} and also M4, we run two independent chains with dispersed starting values. The first 10000 iterations are discarded, with every 10th iteration stored thereafter until 10000 such iterations per chain are collected. Combining the two chains gives 20000 draws from the posterior distribution. Convergence is assessed via trace plots and monitoring the value of the potential scale reduction factor (Gelman and Rubin, 1992).

3. Model Comparison and Assessment

3.1 Model Comparison

Quantitative assessments of model fit and predictive ability of the candidate models are carried out by considering the following three criteria.

Deviance Information Criterion (DIC)

(Spiegelhalter et al., 2002; Celeux et al., 2006). The notion of calculating DIC is not translatable to the case of the DPM model (M4), which has an infinite-dimensional parameter space with unbounded model complexity; the following discussion is relevant to M1–M3. For a generic model, given data y, parameter vector θ, and probability model f(y|θ), Spiegelhalter et al. propose DIC = −4E_θ|y ln f(y|θ) + 2 ln $f(y\mid \tilde{\theta }\left(y\right))$, which is the sum of the posterior mean deviance, −2E_θ|y ln f(y|θ), and the penalty term, −2E_θ|y ln f(y|θ) + 2 ln $f(y\mid \tilde{\theta }\left(y\right))$, where $\tilde{\theta }\left(y\right)$ is some posterior estimate of θ, usually the posterior mean. The penalty term is meant to approximate the dimensionality of the parameter space. Once a focus has been identified, the posterior mean deviance can be estimated by a Monte Carlo average of the log-likelihood, but because of the choice in $\tilde{\theta }\left(y\right)$, there is not a consentient definition of DIC for hierarchical models, especially in the presence of random effects and missing data.

There are additional considerations to be made in our case study. Counting k and {d_i} towards model complexity via the penalty term is asymmetric, as they are known in M1 and M2 and would therefore not contribute to the penalty term, but unknown in M3. M3's DIC should be penalized for its number of components by way of estimating multiple mean vectors and variance matrices; including k and {d_i} would doubly-penalize it. This decision is similar to the EM approach to mixture problems, in which the number of clusters and cluster membership are treated as missing data in the complete likelihood.

Consequently, there is missing data on both sides of the conditioning bar in the likelihood: (3) is really the joint density of $y\equiv \{t_{ij}^{L\ast },t_{ij}^{U\ast }\}$ and U₁ ≡ {b_i} (the latter being unobserved), and U₂ ≡ {k, {d_i}} is observed in M1 and M2 but latent in M3.

Let θ denote all other variables in (3), so that the likelihood can be written as Π_i L_i = f(y, U₁|U₂, θ). Celeux et al. (2006) provides an excellent treatment of DIC in the presence of missing data and random effects but only considers likelihoods with one type of U (either on the left of the conditioning bar [the “complete DIC”] or the right [the “conditional DIC”] but not both). It is a natural extension to hybridize the two corresponding DICs from this paper (DIC₄ and DIC₈) to obtain,

$${\mathrm{DIC}}_{\mathrm{hybrid}}=-4{\mathrm{E}}_{\theta ,U_1,U_2\mid y}\ln f(y,U_1,U_2,\theta )+2{\mathrm{E}}_{U_1,U_2\mid y}\ln f(y,U_1,U_2,E_{\theta \mid y,U_1,U_2}\theta ),$$

which we call the hybrid “conditional-complete DIC”. This definition avoids the unwanted behavior of doubly-penalizing M3 for estimating k and {d_i}, as the expectation over U₂ remains outside of the the log in both terms. The only quantity which is not trivial to estimate via MCMC output is E_θ|y,U1,U2 θ, the conditional expectation of θ for arbitrary values of U₁ and U₂. We instead approximate this quantity at each step in the Gibbs sampler with the mean of the conditional distribution.

Conditional Predictive Ordinate (CPO)

This is a cross-validation assessment originally proposed by Geisser (1980). When $t_{ij}^{L\ast }=t_{ij}^{U\ast }$, it is defined for person (i, j) as ${\mathrm{CPO}}_{ij}\equiv f(t_{ij}^{L\ast }\mid \mathrm{data}(-\left[ij\right]))$, where data(−[ij]) means “data for all but person (i, j)”. Similarly, when $t_{ij}^{L\ast }<t_{ij}^{U\ast }$, ${\mathrm{CPO}}_{ij}\equiv \mathrm{Pr}(T_{ij}^{\ast }>t_{ij}^{L\ast }\mid \mathrm{data}(-\left[ij\right]))$. Thus, a large CPO indicates good fit. The log of the pseudo-marginal likelihood (LPML) is given by Σ_ij log CPO_ij and is a summary of the overall model fit. Alternatively, inspecting the log of the ratio of CPOs from two competing models shows the the preferred model for each individual. Let η represent all variables in the likelihood. For the observed survival times, Gelfand and Dey (1994) propose the approximation ${\mathrm{CPO}}_{ij}\approx {\left\{E_{\eta \mid \mathrm{data}}{f}^{-1}(t_{ij}^{L\ast }\mid \eta )\right\}}^{-1}$, using the Monte Carlo sample to estimate the expectation. A similar technique can be employed for the censored survival times, replacing densities with probabilities, as introduced in Hanson (2006).

Brier score

This measure can be used both for model comparison and verification. It is defined as the average squared difference between the current survival probabilities at time t and the current status; thus a higher score is worse. Graf et al. (1999) redefine it in the presence of right-censoring, the contribution of person (i, j) at time t being

$$B{S}_{ij}\left(t\right)=\{\begin{array}{cc}\frac{{\{1-{\widehat{S}}_{ij}\left(t_{ij}^{L\ast }\right)\}}^2}{\widehat{G}\left(t\right)}\hfill & t<t_{ij}^{L\ast }\hfill \\ \frac{{\{0-{\widehat{S}}_{ij}\left(t_{ij}^{L\ast }\right)\}}^2}{\widehat{G}\left(t\right)}\hfill & t_{ij}^{L\ast }=t_{ij}^{U\ast }\le t\hfill \\ 0,\hfill & t_{ij}^{L\ast }\le t<t_{ij}^{U\ast }\hfill \end{array}\phantom{\}}$$

where ${\widehat{S}}_{ij}$ is the estimated survivor function of person (i, j) (averaged over all Monte Carlo simulations), and $\widehat{G}$ is the Kaplan-Meier estimated distribution of censoring times. The integrated Brier score is given by averaging BS_ij(t) over i and j and integrating over all event and censoring times. We divide each model's integrated Brier score by a reference score (that from plugging in ${\widehat{S}}_{ij}(\cdot )=0.5$), so that any model that improves upon equivocality is in [0, 1]. We call this a scaled integrated Brier score (SIBS).

4. Results applied to Danish HNPCC Data

4.1 Posterior Inference

Features of densities associated with random anticipation effects

We present results under the prior specification {g, h} = {g₁, h₁} and B = diag(3, 6) (placed on the variance components). The top panel of Figure 1 provides the posterior predictive density of the anticipation random effect its interpretation being the predicted density of b_1i for a newly-introduced pedigree. For M2, each mutation group is separate as cluster membership is pre-specified. For M3 we marginalize over the mixture components. The density associated with M4 is a kernel density estimate using new draws of b_1i from each converged iteration of the chain. Details are provided in Web Appendix A.

While M3 shows evidence of multiple clusters (58% of the MCMC iterations estimated k > 1), the impact is only to fatten the tails of M1. M4 has even heavier tails (k exceeded one 83% of the time); the mean anticipation effect in M4 is slightly smaller than M1 and M3. If there are multiple modes to the mixture density, there is not enough information to differentiate between them. With assigned cluster membership, M2 differentiates hMSH6 from the other two mutations. The mean anticipation effect is just greater than 1 year for hMSH6, compared to about 2.5 years for the other mutations, and the distribution has wider spread. Note also that, if no random slope was needed, all these densities would be peaked and concentrated and show no variation, thus there is evidence supporting a random (and not fixed) slope model for generation.

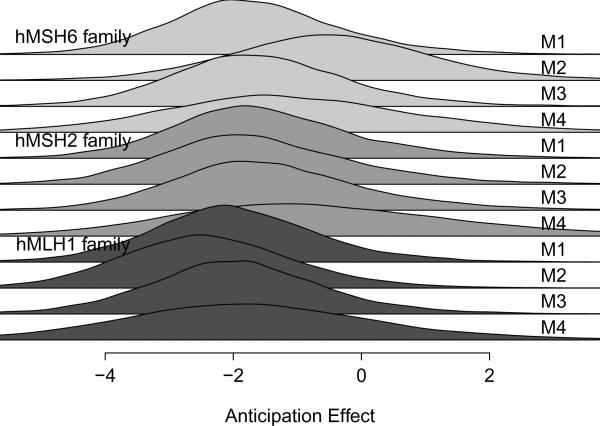
The bottom panel of Figure 1 gives kernel estimates of the posterior density of the random slope corresponding to generation for the largest family from each mutation subtype in our study. For the hMSH2 family, the mean anticipation effect is similar between M1–M4, and only slight differences arise in the hMLH1 family. However, there are differences between the models for the hMSH6 family; the estimated mean effect of anticipation is smaller in M2 and M4 as compared to M1 or M3. M4 again shows the largest variability in all cases. Posterior density estimates for all families are given in Web Figure 2.

Figure 2.

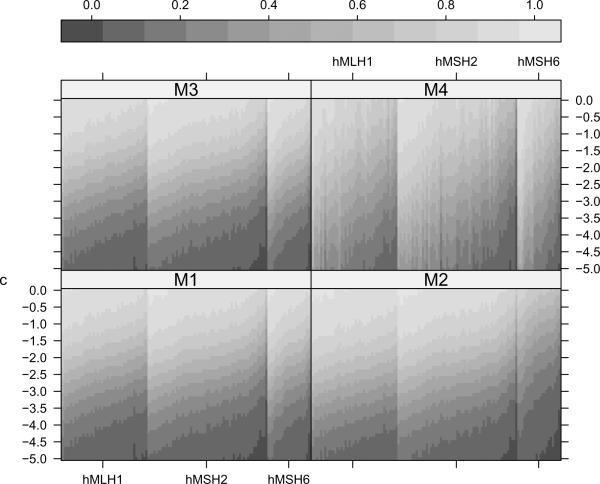
Estimated posterior distribution functions of b_1i, namely $\widehat{\mathrm{Pr}}(b_{1i}<c)$ for i = 1, …, 124, all families in our dataset. The y-axis gives the threshold in years, and the grayscale reflects the corresponding probability. Families (along the x-axis) are ordered first by mutation status (43 hMLH1, 59 hMSH2 and 22 hMSH6 families are represented) and then by the posterior median of b_1i as predicted by M1 within each mutation subtype. c signifies the reduction in number of years in AOO for successive generations. Thus a substantial probability of falling below a negative threshold value indicates evidence of anticipation for that family.

Figure 2, presents estimated posterior distribution functions corresponding to b_{1i, i} = 1, …, 124, in terms of P(b_1i < c) for differing values of c. The value c signifies the decrease in number of years in AOO for successive generations. A significant probability of the random slope being less than −2.0 years say, indicates earlier age of onset in successive generations in that family. We note substantial heterogeneity in these values across families within each mutation subtype. There is more uncertainty in ordering of the families under M4 which is to be expected from the DPM specification. This plot again reiterates the need for a family-specific estimate of anticipation even within a given mutation type.

Parameters of the distributions associated with the random effects

Table 2 presents numerical summaries of the posterior predictive density and moments of the posterior density of the hyperprior parameters corresponding to the random intercept and slope, (b_0i, b_1i). The results are summarized in terms of the median (p₅₀) and equi-tailed 95% credible intervals (p_2.5, p_97.5) based on the draws from the corresponding distributions. Note that mutation subtype is excluded from the fixed covariates in M2, so b_0i and Mean(b_0i) under M2 are not directly comparable to the other models. The estimate of anticipation, as measured by the posterior distribution of the hypermean of the random effects, is identical under M1 and M3 (−2.3 yrs with CI [−3.5,−1.1] yrs) whereas M4 provides a similar estimate with wider CI (−2.5 yrs with CI [−5.6,0.6] yrs). The estimates obtained from M2 illustrates a stronger anticipation effect in hMLH1 and hMSH2 families (−2.8 yrs, CI [−4.3,−1.2] yrs for hMLH1 and −2.5 yrs, CI [−3.8,−1.0] yrs for hMSH2) when compared to hMSH6 (−1.0 yrs, CI [−3.3,1.1] yrs). Similar estimates are obtained from the posterior predictive distribution, but with larger uncertainty owing to individual observations being more variable than the mean estimate. Estimates of the random effects' variance-covariance hyperparameters in Table 2 (last block) are sensitive to prior choices on Σ under the DPM in M4 and produce different results than M1–M3.

Table 2.

Numerical summaries of densities associated with random slopes and intercept estimates. The median (p₅₀) and middle 95% quantiles (p_2.5, p_97.5) based on the generated draws from the corresponding distribution are presented. All results correspond to prior {g, h} = {g1, h1} as described in the text. The b_0i and b_1i columns correspond to the posterior predictive distributions for a new random slope and intercept, respectively. The Mean, Var and Cov columns are derived from the (marginalized over cluster configurations, for M3 and M4) posterior density estimates of the hyperprior parameters corresponding to the random effects.

	p50(p2.5, p97.5)
Fixed Effect Parameters	β1 Gender	β2 hMLH1	β3 hMSH2	σ Error Scale
M1	1.5 (−0.3,3.2)	−6.8 (−9.7,−3.9)	−6.4 (−9.2,−3.7)	9.8 (9.1,10.5)
M2	1.5 (−0.3,3.2)			9.8 (9.1,10.5)
M3	1.5 (−0.3,3.3)	−6.6 (−9.6,−3.7)	−6.3 (−9.1,−3.5)	9.8 (9.1,10.5)
M4	1.5 (−0.3,3.3)	−6.3 (−9.8,-2.6)	−6.1 (−9.4,-2.6)	9.6 (8.9,10.4)

Random Effect Parameters	b0i	b1i	Mean[b0i]	Mean[b1i]
M1	57.3 (50.9,63.9)	−2.3 (−5.7,1.0)	57.4 (54.0,60.7)	−2.3 (−3.5,−1.1)
M2 hMLH1	51.5 (44.9,58.3)	−2.8 (−6.2,0.7)	51.5 (48.4,54.7)	−2.8 (−4.3,−1.2)
M2 hMSH2	51.3 (44.9,57.8)	−2.4 (−6.1,1.1)	51.4 (48.3,54.2)	−2.5 (−3.8,−1.0)
M2 hMSH6	54.0 (46.5,62.2)	−1.1 (−5.3,3.0)	53.9 (49.9,59.1)	−1.0 (−3.3, 1.1)
M3	57.2 (50.4,64.2)	−2.3 (−6.0,1.2)	57.2 (53.8,60.6)	−2.3 (−3.5,−1.1)
M4	57.2 (44.8,69.7)	−2.5 (−10.2,5.2)	57.3 (51.5,62.9)	−2.5 (−5.6, 0.6)

Random Effect Variance Parameters	Var[b0i]	Cov[b0i, b1i]	Var[b1i]
M1	5.6 (0.8, 26.1)	−2.2 (−12.0, 0.4)	1.9 (0.3, 7.2)
M2 hMLH1	6.0 (0.7, 31.0)	−2.2 (−12.0, 0.5)	1.8 (0.3, 7.0)
M2 hMSH2	6.0 (0.7, 27.4)	−2.5 (−13.4, 0.3)	2.1 (0.3, 8.5)
M2 hMSH6	6.4 (0.7, 39.6)	−2.5 (−18.6, 0.5)	2.1 (0.3,11.7)
M3	6.0 (0.7, 25.7)	−2.4 (−11.9, 0.3)	2.0 (0.3, 7.2)
M4	19.0 (2.5,100.9)	−6.7 (−41.4,11.9)	7.0 (1.0,72.6)

Fixed effects estimates

The top panel in Table 2 presents fixed effects estimate corresponding to gender and mutation status (except M2). There is evidence of a later age of onset for males whereas mutation subtype is also a significant factor with hMLH1 and hMSH2 showing earlier mean AOO than hMSH6. However, the effect of mutation status and familial random effects have to be examined and interpreted jointly for each family.

Prior Sensitivity

For M1–M3, results from all three prior specifications were quite similar (results not tabulated). For M1 and M3, the difference between any two priors in the p₅₀ estimate of a newly observed b_1i was never more than 0.07, a small number given the scale. This was also observed in the hMLH1 and hMSH2 subtypes under M2; for hMSH6, the p₅₀ estimates were −1.04, −0.86, and −0.96 for the three prior specifications. Credible intervals for M1, M2, and M3 were similar between the first two priors and narrower under {g₃, h₃}. The DPM in M4 required a more informative prior on the variance components in Σ; vague priors yielded larger credible intervals. In general, M4 exhibits more variability in estimating the hyperparameters on the random effects. The results were robust to prior choice on α.

Clinical Application

Affected families will likely be interested in the family-specific extent of anticipation. Consider the hMSH2 family in the bottom panel of Figure 1, say i = i′. Pr(b_1i′ < 0) = 0.86 and Pr(b_1i′ < −2) = 0.39 for M1 under {g₁, h₁} (M2 and M3 make statements within 0.03 of this probability). This means that the probability that there is some anticipation effect is 0.86 and the probability that the effect from anticipation is at least 2 years is about 0.39. On the other hand, for the hMSH6 family in the Figure (i = i″), Pr(b_1i″ < 0) = 0.89 for M1 but is 0.63 for M2, and Pr(b_1i″ < −2) = 0.42 for M1 but is only 0.16 for M2. Thus, at the level of individual families, the extent of anticipation does depend on the assumed model. Robust choices evoke more confidence in obtained results. However, how strong an anticipation effect is necessary to change prophylactic care for a given family needs to be clinically determined.

4.2 Model Comparison and Assessment

Table 3 provides results from the quantitative comparison techniques discussed in Section 3 under the three prior specifications. Using DIC, there is no consistently preferred model. Estimates of deviance fluctuate markedly between priors. On the other hand, the penalty components are relatively stable, even under M3, with a latent “true” number of parameters.

Table 3.

Assessment of M1–M3 under 3 priors placed on the variance of the mixture components of the random effects distribution: {g₁, h₁} avoids values close to 0, {g₂, h₂} is weaker and “flattens” the prior density relative to {g₁, h₁}, and {g₃, h₃} pushes the density closer to 0. DIC is 'Deviance Information Criterion', p_D is the penalty term (an estimate of model complexity), LPML is the logarithm of the pseudo-marginal likelihood, and SIBS is the scaled integrated Brier score. The results for M4 correspond to the prior specification described in the text. In each column, smaller is better.

Prior	{g1, h1}	{g2, h2}	{g3, h3}
Model		DIC (pD)
M1	2911 (5.9)	2664 (6.2)	2818 (6.2)
M2	2917 (12.3)	2653 (12.6)	2822 (12.6)
M3	2902 (9.4)	2660 (9.7)	2806 (9.4)
		-LPML
M1	1041.2	1038.1	1039.8
M2	1042.7	1038.2	1041.0
M3	1042.2	1039.9	1040.9
M4		1064.6
		SIBS
M1	0.2627	0.2651	0.2641
M2	0.2625	0.2653	0.2641
M3	0.2618	0.2638	0.2632
M4		0.2510

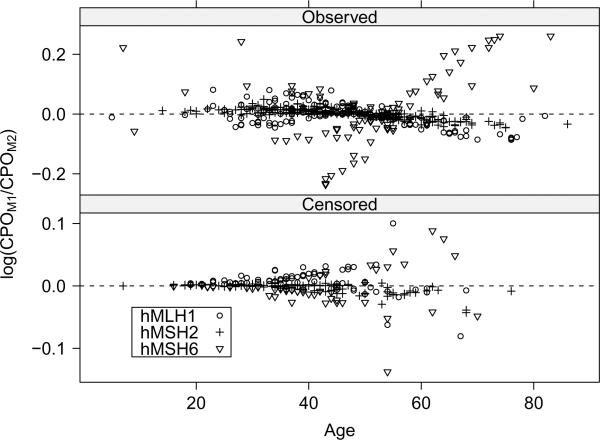
For LPML, differences between M1–M3 are small, but M1 is actually preferred for all three priors; variation of LPML between and within priors was less than that of DIC. Focusing on individuals, Figure 3 gives the log of the ratio of CPOs comparing M1 to M2 under {g₁, h₁} for each individual. This model-to-model comparison is particularly interesting because the general trend is that hMSH6 individuals with late AOOs are fit relatively better by M1 (the log of the ratio being greater than 0) but that M2 offers an improvement in fit for the less extreme event times. We saw similar results when comparing M2 to M3. For hMLH1 and hMSH2 families, results across models are very similar. In terms of LPML, M4 is least favored across the models.

Figure 3.

The logarithm of the ratio of CPOs for M1 (CPO_M1) to M2 (CPO_M2) by most recent age. Individuals are grouped by family mutation and stratified by the censoring indicator. Values greater than 0 favor M1.

Relative to LPML, the order of preferred models is reversed under SIBS. The scale of the between-model differences and between-prior variability is about the same as LPML. In contrast to LPML, M4 slightly improves upon the other models.

For aggregate measures of prediction, there is little difference between models, supporting the findings of McCulloch and Neuhaus (2010). As for individual predictions, there is sensitivity to model choice (Figure 3), and no model is uniformly preferred.

5. Discussion

In this paper we develop the first Bayesian approach to assess genetic anticipation, a problem for which interest lies primarily in prediction of random effects governed by a biologically-plausible non-normal distribution (Lynch et al., 2006). We see additional evidence of its necessity through our work, e.g., Figure 2 indicates substantial familial heterogeneity. We evaluate candidate models which cover a wide range of distributions for the random effects.

The relative survival-type adjustments using historic data provide a systematic approach to adjust for secular trends in AOO, an issue many papers on genetic anticipation have grappled with. While we have tried to mitigate these effects by using external data on all incident cases of colorectal and endometrial cancer, increased awareness of Lynch syndrome may still mean some of the anticipation is diagnostic in nature and not only genetic.

After adjusting for secular trends, there remains evidence of anticipation at both the population and the familial level. The population-level effect size is about 2.5 years across models, 0.5 years less than the original paper (Larsen et al., 2009). The model which constrains cluster membership (M2) identifies one mutation subtype, hMSH6, to be considerably different from the other two. The hMSH6 mutation had the fewest families (22), yielding less precision compared to the other subtypes. It would be worthwhile to posit mechanistic reasons for heterogeneities within hMSH6 families.

The Bayesian simulation methods we use provide direct posterior draws of all parameters, allowing for model assessment and posterior predictions for clinical quantities of interest. As we saw, successfully answering the question, “What is the extent of anticipation in a particular family?”, depends crucially upon properly modeling the anticipation coefficient as well as deciding upon a clinically relevant definition of anticipation.

As a statistical point of interest, this study provides a good forum for the evaluation of Bayesian model comparison techniques. We have a likelihood in which calculation of DIC is not straightforward with current methods. We define a new hybrid complete-conditional DIC, appropriating the ideas of Celeux et al. (2006). It is worthwhile to investigate further this sensitivity of the hybrid DIC to prior specification. To our knowledge, the scaled integrated Brier score has not been used previously in Bayesian analysis of censored data.

The methods and analytic approaches that we develop provide statistical insight into genetic anticipation and also facilitate application in clinical situations. These results are only readily applicable to high-risk Lynch families and generalization to a different population would require further correction for ascertainment bias.