Landscape, Flux, Correlation, Resonance, Coherence, Stability, and Key Network Wirings of Stochastic Circadian Oscillation

Chunhe Li; Erkang Wang; Jin Wang

doi:10.1016/j.bpj.2011.08.012

. 2011 Sep 21;101(6):1335–1344. doi: 10.1016/j.bpj.2011.08.012

Landscape, Flux, Correlation, Resonance, Coherence, Stability, and Key Network Wirings of Stochastic Circadian Oscillation

Chunhe Li ^†,^§, Erkang Wang ^†,^∗∗, Jin Wang ^†,^‡,^∗

PMCID: PMC3177066 PMID: 21943414

Abstract

Circadian rhythms with a period of ∼24 h, are natural timing machines. They are broadly distributed in living organisms, such as Neurospora, Drosophila, and mammals. The underlying natures of the rhythmic behavior have been explored by experimental and theoretical approaches. However, the global and physical natures of the oscillation under fluctuations are still not very clear. We developed a landscape and flux framework to explore the global stability and robustness of a circadian oscillation system. The potential landscape of the network is uncovered and has a global Mexican-hat shape. The height of the Mexican-hat provides a quantitative measure to evaluate the robustness and coherence of the oscillation. We found that in nonequilibrium dynamic systems, not only the potential landscape but also the probability flux are important to the dynamics of the system under intrinsic noise. Landscape attracts the systems down to the oscillation ring while flux drives the coherent oscillation on the ring. We also investigated the phase coherence and the entropy production rate of the system at different fluctuations and found that dissipations are less and the coherence is higher for larger number of molecules. We also found that the power spectrum of autocorrelation functions show resonance peak at the frequency of coherent oscillations. The peak is less prominent for smaller number of molecules and less barrier height and therefore can be used as another measure of stability of oscillations. As a consequence of nonzero probability flux, we show that the three-point correlations from the time traces show irreversibility, providing a possible way to explore the flux from the observations. Furthermore, we explored the escape time from the oscillation ring to outside at different molecular number. We found that when barrier height is higher, escape time is longer and phase coherence of oscillation is higher. Finally, we performed the global sensitivity analysis of the underlying parameters to find the key network wirings responsible for the stability of the oscillation system.

Introduction

Biological oscillations widely exist in living organisms. They have been extensively explored, including cell cycles, circadian clocks, calcium oscillations, and glycolytic oscillations. In the cell, there are intrinsic statistical fluctuations from finite numbers of molecules and the external fluctuations from highly dynamical and inhomogeneous environments (1–8). It is therefore important to investigate robustness and stability of the oscillation under the stochastic fluctuations. The dynamics under extrinsic fluctuations can be studied by the stochastic Langevin dynamics (8). For intrinsic statistical fluctuations, one can explore the probabilistic master equation formalism (9), giving the probability of different states of the system.

Circadian rhythms, with a period of ∼24 h, are natural timing machines, broadly distributed in living organisms. They accommodate to the day-and-night alterations of the earth, adapting to the fluctuating environment. In Neurospora, Drosophila, and mammals, oscillations originated from the negative feedback regulation of the clock genes are developed from the transcription to translation process, which have been modeled at the molecular level. The underlying natures of the rhythmic behavior have been explored by experimental studies and theoretical methods (10–12). However, in exploring the protein networks in a stochastic way, many models can only give local properties of the system. The global and physical natures of the oscillation are still a challenge to see.

Here, we develop a landscape and flux framework (13–15) to explore the global stability and robustness of a circadian oscillation system under intrinsic fluctuations. We directly explore the probabilistic distribution in the whole protein concentration-state space, so that the oscillation system can be investigated globally. Fig. 1 shows a core molecule mechanism of circadian oscillations in Drosophila based on a negative feedback regulation. In this system, Per gene is transcribed to mRNA (Mp) in nucleus, and then transported to cytosol. Next, mRNA is translated into PER protein, which can be reversibly phosphorylated from the form P0 into the forms P1 and P2, successively. The latter form is degraded or transported into the nucleus (PN), which will provide a negative feedback regulation on the expression of its gene (10,11). Therefore, the existence of the negative feedback loop with a delay for this network gives the origin of the oscillations. By means of stochastic simulation method, we obtain the steady-state probability distribution of the system, and further study the underlying global properties of the potential by the relation: U(x) = −lnP_ss(x) (13–20), where P_ss is the steady-state probability in concentration x.

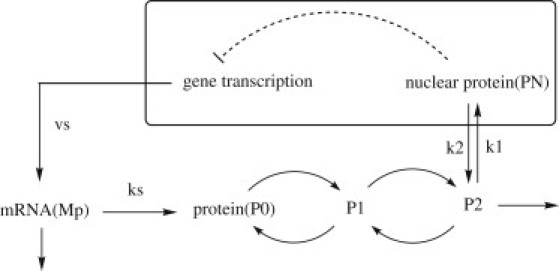
Core wiring diagram for the circadian rhythms network.

The landscape concept has been introduced to ligand binding protein dynamics (21) to explain the existence of the substates. Another success for the landscape concept was from protein folding and the interaction funnel (22,23). These ideas are all based on a gradient dynamics with the equilibrium potentials or energy function known a priori. In the equilibrium systems, only the equilibrium potential or energy function is needed to characterize the global equilibrium properties (equilibrium probability) and local dynamics (gradient) of the whole system. However, in the nonequilibrium systems, both the potential landscape and the associated probabilistic flux are essential to characterize the global steady-state properties (steady-state probability) and the dynamics of the network.

The underlying nature of the rhythmic behavior has been explored by experimental and theoretical approaches. However, the global and physical natures of the oscillation under intrinsic and extrinsic fluctuations are still not very clear. Here we developed a landscape and flux framework to explore the global stability and robustness of a circadian oscillation system. The potential landscape of the network was found to have a global Mexican-hat shape. The height of Mexican hat provides a quantitative measure to evaluate the robustness of the oscillation. We found that in a nonequilibrium open system, both landscape and probability flux are important for the dynamics of the system under intrinsic fluctuations. Landscape attracts the systems down to the oscillation ring while flux drives the coherent oscillations on the ring. We also investigated the phase coherence and entropy production rate of the system at different molecular numbers (leading to different magnitudes of intrinsic fluctuations).

We performed analysis with the two-point autocorrelation function of protein concentration variables. We obtained the corresponding power spectrum and explored the influence of intrinsic statistical fluctuations on the resonance peak for oscillations. The height of the power spectrum of the autocorrelation function measuring the prominence of the resonance peak may provide another way to quantify the stability and coherence of the oscillation system. As a consequence of nonzero probability flux, we show that the three-point correlations from the oscillation time traces show irreversibility, providing an experimental way to explore the flux from time traces of the observations.

Additionally, we investigated the relation of escape time for the system to jump outside with 1), the barrier height; 2), the phase coherence; and 3), the height of the power spectrum of the autocorrelation function. Finally, we performed the global sensitivity analysis of the parameters to find the key network wirings responsible for the stability of the oscillation system.

Materials and Methods

We use the stochastic simulation method (24,25) to solve the dynamics trajectories separately with different initial conditions. We explore the long time steady-state properties and collect the statistics to obtain the steady-state distribution P₀(x) for the state variable x (representing the protein concentrations or numbers of molecule). In the equilibrium systems, the force is a gradient of potential U, and P₀(x) is exponentially related to potential energy function U(x). Therefore, we can obtain the information of potential U by computing equilibrium probability. For the nonequilibrium system, in analogy with the equilibrium system, we can define the generalized potential U for the nonequilibrium case from the steady-state probability (13–20),

P_{0} (x) = \frac{1}{Z} exp {- U (x)},

(1)

with the partition function $Z = \int d x exp {- U (x)}$ . After acquiring the steady-state distribution function, we can thus identify U as the generalized potential energy function of the network system. Accordingly, we map out the potential energy landscape, and we can further discuss the global stability of the protein cellular networks.

Intrinsic fluctuations from limited molecule numbers are usually concentration-dependent. The Langevin equation describing the motion of system is written

\frac{d x}{d t} = F (x) + G \cdot Γ .

(2)

Here, G is a tensor representing the spatial (concentration)-dependent part of the intrinsic noise, and Γ is a vector representing Gaussian white noise corresponding to the time-dependent part of the noise defined as 〈Γ_j (t)〉 = 0 and 〈Γ_i(t)Γ_j(t′)〉 = 2D_iδ_ijδ(t – t′) (δ_ij = 1 for i = j, and δ_ij = 0 for i ≠ j).

The Fokker-Planck diffusion equation emerges from the continuous description of the intrinsic fluctuations with second-order truncations of Taylor series (26) as

\frac{\partial P (x, t)}{\partial t} = - \sum_{i = 1}^{N} \frac{\partial}{\partial x_{i}} F_{i} (x) P (x, t) + \frac{1}{2} \sum_{i = 1, i^{'} = 1}^{N} \frac{\partial^{2}}{\partial x_{i} \partial x_{i^{'}}} D_{i i^{'}} (x) P (x, t) .

(3)

In this equation, x stands for the set {x_i}(i = 1, 2, 3, … N), where N is the number of protein species, and M is the number of chemical reactions. The values F, D, and G are separately defined as

F_{i} (x) = \sum_{j = 1}^{M} v_{j i} a_{j} (x) (i = 1, 2, \dots, N),

D_{i i'} (x) = \sum_{j = 1}^{M} v_{j i} v_{j i'} a_{j} (x) (i, i^{'} = 1, 2, \dots, N),

G_{i j} (x) = v_{j i} \sqrt{a_{j} (x)} (i = 1, 2, \dots N, j = 1, 2, \dots, M) .

The Fokker-Planck diffusion equation can be rewritten into the probability conservation equation as local probability change equal to the in and out flux, $\partial P / \partial t = - \sum_{i}^{N} \partial J_{i} / \partial x_{i}$ , where J_i (x,t) is the probability flux in the N-dimensional space (9): $J_{i} = F_{i} (x) P (x) - \frac{1}{2} \sum_{i^{'} = 1}^{N} \partial / \partial x_{i^{'}} D_{i i^{'}} (x) P (x)$ . The corresponding form in vector is $\partial P / \partial t + \nabla \cdot J (x, t) = 0$ , where $J (x, t) = F \cdot P - 1 / 2 \nabla \cdot (G \cdot G P)$ . Here we will first use the Ito convention. In steady state, $\partial P / \partial t = 0$ , then ∇ · J(x,t) = 0. The divergent free flux implies the rotational nature of the steady-state flux field J_ss. From the definition, $J_{s s} = F \cdot P_{s s} - \frac{1}{2} \nabla \cdot (G \cdot G P_{s s})$ . Hence, the force can be decomposed as

\begin{matrix} F = - \frac{1}{2} D \cdot \frac{\partial}{\partial x} (- ln P_{s s}) + \frac{J_{s s}}{P_{s s}} + G \cdot (\nabla \cdot G) \\ = - \frac{1}{2} D \cdot \frac{\partial}{\partial x} U + \frac{J_{s s}}{P_{s s}} + G \cdot (\nabla \cdot G) \end{matrix} .

Here D is the diffusion coefficient tensor defined as D = G · G^T and P_ss is the steady-state probability distribution. The value U is the generalized potential related to the steady-state probability by U = −lnP_ss. Therefore, in general, the driving force for the dynamical system under intrinsic statistical fluctuations can be decomposed into three terms—the gradient of the potential landscape, the curl flux, and the derivatives of diffusion with respect to concentration mimicking the inhomogeneity of the diffusion.

For the Stratonovich convention (27,28), the diffusion equation with concentration-dependent diffusion can be written as

\frac{\partial P}{\partial t} + \nabla \cdot J (x, t) = 0,

J (x, t) = (F + \frac{1}{2} (G \cdot \nabla) \cdot G) P - \frac{1}{2} \nabla \cdot (G \cdot G P) .

(4)

Now the force can be decomposed as $F = - \frac{1}{2} D \cdot \partial / \partial x U + J_{s s} / P_{s s} + \frac{1}{2} G \cdot (\nabla \cdot G)$ . We can see that Stratonovich formulism and Ito form have similar results for the decomposition of force. We noticed that when the diffusion is homogeneous (diffusion coefficient is constant in concentration x space), the definition of flux is the same as for the external noise (specified as follows) (13,14).

For external noise, flux vector of the system could be defined as (13,14)

J (x, t) = F * P - D * \frac{\partial}{\partial x} P .

(5)

Therefore, by projecting multidimensional force F vector into two dimensions, we can obtain the associated flux vector components in two-dimensional (Mp and PN) protein concentration space. Here, for two-dimensional projection of force F, we approximate the results by computing the mean of $\partial x_{M p} / \partial t$ and $\partial x_{P N} / \partial t$ using trajectories.

Results and Discussion

Landscape and probabilistic curl flux

Table 1 and Table 2 give the reaction steps and parameter values of the circadian network separately, which are decomposed from five deterministic ordinary differential equations (10). With the parameters in Table 2, the corresponding deterministic equations produce a stable limit cycle solution. We used the kinetic Monte Carlo method (24,25) to simulate the reactions and obtain the steady-state probability distribution in terms of the number of different kinds of protein molecules.

Table 1.

Thirty elementary reaction steps

Reaction No.	Reaction step	Probability of reaction
1	G + P_N → [a₁] GP_N	w₁ = a₁ + G × P_N
2	GP_N → [d₁] G + P_N	w₂ = d₁ × GP_N
3	GP_N + P_N → [a₁] GP_N₂	w₃ = a₂ × GP_N × P_N
4	GP_N₂ → [d₂] GP_N + P_N	w₄ = d₂ × GP_N₂
5	GP_N₂ + P_N → [a₃] GP_N₃	w₅ = a₃ × GP_N₂ × P_N
6	GP_N₃ → [d₃] GP_N₂ + P_N	w₆ = d₃ × GP_N₃
7	GP_N₃ + P_N → [a₄] GP_N₄	w₇ = a₄ × GP_N₃ × P_N
8	GP_N₄ → [d₄] GP_N₃ + P_N	w₈ = d₄ × GP_N₄
9	[G, GP_N, GP_N₂, GP_N₃] → [v_s] M_p	w₉ = v_s × (G + GP_N + GP_N₂ +GP_N₃)
10	M_p + E_m → [k_m₁] C_m	w₁₀ = k_m₁ × M_p × E_m
11	C_m → [k_m₂] M_p + E_m	w₁₁ = k_m₂ × C_m
12	C_m → [k_m₃] E_m	w₁₂ = k_m₃ × M_p
13	M_p → [k_s] M_p + P₀	w₁₃ = k_s × C₁
14	P₀ + E₁ → [k₁₁] C₁	w₁₄ = k₁₁ × P₀ × E₁
15	C₁ → [k₁₂] P₀ + E₁	w₁₅ = k₁₂ × C₁
16	C₁ → [k₁₃] P₁ + E₁	w₁₆ = k₁₃ × C₁
17	P₁ + E₂ → [k₂₁] C₂	w₁₇ = k₂₁ × P₁ × E₂
18	C₂ → [k₂₂] P₁ + E₂	w₁₈ = k₂₂ × C₂
19	C₂ → [k₃₂] P₀ + E₂	w₁₉ = k₂₃ × C₂
20	P₁ + E₃ → [k₃₁] C₃	w₂₀ = k₃₁ × P₁ × E₃
21	C₃ → [k₃₂] P₁ + E₃	w₂₁ = k₃₂ × C₃
22	C₃ → [k₃₃] P₂ + E₃	w₂₂ = k₃₃ × C₃
23	P₂ + E₄ → [k₄₁] C₄	w₂₃ = k₄₁ × P₂ × E₄
24	C₄ → [k₄₃] P₁ + E₄	w₂₄ = k₄₂ × C₄
25	C₄ → [k₄₃] P₁ + E₄	w₂₅ = k₄₃ × C₄
26	P₂ + E_d → [k_d₁] C_d	w₂₆ = k_d₁ × P₂ × E_d
27	C_d → [k_d₂] P₂ + E_d	w₂₇ = k_d₂ × C_d
28	C_d → [k_d₃] E_d	w₂₈ = k_d₃ × C_d
29	P₂→ [k₁] P_N	w₂₉ = k₁ × P₂
30	P_N → [k₂] P₂	w₃₀ = k₂ × P_N

Open in a new tab

Table 2.

Parameter values used for stochastic simulations for circadian oscillations

Reaction steps	Parameter values
Steps 1–8	For n = 4:
	a₁ = (1/V) mol⁻¹ h⁻¹, d₁ = 160 h⁻¹
	a₂ = (10/V) mol⁻¹ h⁻¹, d₂ = 100 h⁻¹
	a₃ = (100/V) mol⁻¹ h⁻¹, d₃ = 10 h⁻¹
	a₄ = (100/V) mol⁻¹ h⁻¹, d₄ = 10 h⁻¹
Step 9	v_s = 0.5 mol h⁻¹
Steps 10–12	k_m₁ = (165/V) mol⁻¹ h⁻¹, k_m₂ = 30 h⁻¹, k_m₃ = 3 h⁻¹,E_mtot = E_m + C_m = (0.1 × V) mol
Step 13	k_s = 2.0 h⁻¹
Steps 14–16	k₁₁ = (146.6/V) mol⁻¹ h⁻¹, k₁₂ = 200 h⁻¹, k₁₃ = 20 h⁻¹,E₁tot = E₁ + C₁ = (0.3 × V) mol
Steps 17–19	k₂₁ = (82.5/V) mol⁻¹ h⁻¹, k₂₂ = 150 h⁻¹, k₂₃ = 15 h⁻¹,E₂tot = E₂ + C₂ = (0.2 × V) mol
Steps 20–22	k₃₁ = (146.6/V) mol⁻¹ h⁻¹, k₃₂ = 200 h⁻¹, k₃₃ = 20 h⁻¹,E₃tot = E₃ + C₃ = (0.3 × V) mol
Steps 23–25	k₄₁ = (82.5/V) mol⁻¹ h⁻¹, k₄₂ = 150 h⁻¹, k₄₃ = 15 h⁻¹,E₄tot = E₄ + C₄ = (0.2 × V) mol
Steps 26–28	k_d₁ = (1650/V) mol⁻¹ h⁻¹, k_d₂ = 150 h⁻¹, k_d₃ = 15 h⁻¹,E_dtot = E_d + C_d = (0.1 × V) mol
Steps 29 and 30	k₁ = 2.0 h⁻¹, k₂ = 1.0 h⁻¹

Open in a new tab

In the cell, a small number of molecules provides the origin of intrinsic stochastic fluctuations. There is only a finite number of molecules, typically ∼10³ or less, and fluctuations are proportional to $1 / \sqrt{N}$ (10,29). Therefore, the smaller the total number of molecules is in a system of chemical reactions, the more intrinsic the fluctuations are around the state predicted by the deterministic evolution of this chemical system. Therefore, we define V as the effective dimensionless volume that scales the total molecule number, which characterizes the intrinsic noise of system (10). When V is given, the parameters should be rescaled according to Table 2. After getting the steady-state probability distribution, we can obtain the potential landscape of the network according to U = −lnP_ss, and then explore the global stability and robustness of the system.

For this circadian system, there are 22 different species of molecules. It is hard to visualize the 22-dimensional probability distribution. Therefore, we project the 22-dimensional probability P (G, GP_N…P_N,t → ∞) to only two dimensions (Mp for mRNA in nucleus and PN for Per protein in nucleus) to describe the results, because Mp and PN are two backbone variables in the original five-variable model and extended 22-variable system (10), and they are directly observable in the experiments. From Fig. 2, we can see the shape of the potential landscape is a Mexican hat with an irregular inhomogeneous ring. Inside and outside of the ring, the potential is higher, corresponding to lower probability. Along the ring the potential is lower, and the probability is higher. Therefore, system is attracted to the oscillation ring, and the Mexican-hat-like shape of the landscape guarantees the stability and robustness of the oscillation system.

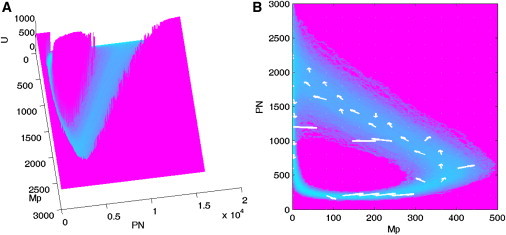
Landscape and flux for V = 200. (A) Three-dimensional landscape for variable Mp (mRNA in nucleus) and PN (per protein in nucleus). (B) Two-dimensional landscape and corresponding probabilistic flux. (*Arrows*) Curl flux vector.

Circadian oscillation system is an open system, which often reaches a nonequilibrium steady state (NESS) by exchanging energy and materials with its environment. Nonzero fluxes and dissipation is one of the distinct features of an NESS (30). Therefore, we not only need the underlying potential landscape, but also the probability flux J, to explore the global properties of the system (13,14). The probability flux of the system in concentration space is given as $J (x, t) = F P - D \cdot \frac{\partial}{\partial x} P$ . Potential landscape and probabilistic flux determine the dynamics and global properties together, and the dynamics of a nonequilibrium network can be described as a spiral curl, unlike the equilibrium case where states only follow the gradient (13,14).

Fig. 2 A shows the three-dimensional landscape for variable Mp and PN, and Fig. 2 B shows the curl flux vector on the two-dimensional landscape of the circadian system. We can see that the direction of the flux is along the oscillation trajectory of the limit cycle. Both the landscape and curl flux are crucial for the dynamics of the oscillation. The landscape attracts the system to the ring valley, and curl flux drives coherent oscillation of the system along the ring.

Barrier height, phase coherence, and entropy production rate for global stability and robust oscillations

In addition, we defined the height of the barrier as U_fix minus U_min_, where U_fix is the potential local maximum inside the close ring (top of the Mexican hat), and U_min is the potential minimum along the ring. Here, the value of the barrier reflects the difficulty for the system to escape from the oscillation attractor to outside.

Fig. 3 A shows the barrier versus the molecular number V. We can see the barrier becomes higher when the molecular number V increases and the fluctuations decrease. It shows that it is harder for the system to go from the ring of attraction to outside because of less fluctuation. The system is thus more stable at large number of molecules (leading to small fluctuations). Therefore, the barrier heights give a quantitative measure to evaluate the robustness and stability of the system.

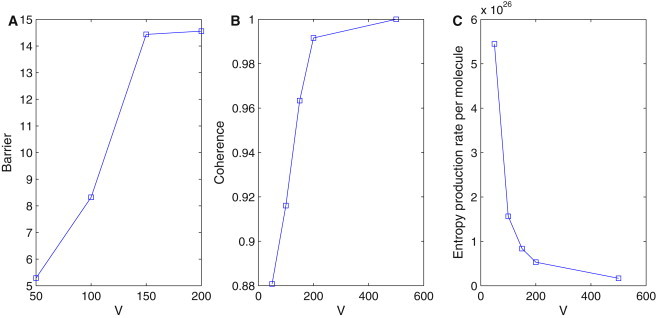
(A) Barrier height versus the molecular number V. (B) Coherence versus the molecular number V. (C) Entropy production rate versus the molecular number V.

The robustness of the oscillation with respect to the molecular number V can be quantified further by the phase coherence ξ, which measures the degree of periodicity of the time evolution of the given concentration variables ((31), and see details in the Supporting Material). The phase coherence ξ quantitatively measures the degree of persistence of the oscillatory phase. In the presence of the fluctuations, the more periodic the time evolution is, the larger the value of ξ. In Fig. 3 B, ξ decreases when V decreases(intrinsic noise increases). This means a small number of molecules or a larger intrinsic fluctuation tends to destroy the coherence of the oscillations, and therefore also destroy its robustness.

The circadian clock is a nonequilibrium open system that can exchange information and energies with outside. In the NESS, the system dissipates energy and entropy that can be determined with the landscape and the flux, and the entropy production rate at the steady state is balanced by the dissipation (32). Thus, by calculating the entropy production rate, and the dissipation, we can obtain a global physical characterization of the nonequilibrium system. The entropy production rate for the whole network (S) includes the contribution from the system (S_sys) (equal to zero in steady state) and the dissipation from the environments (S_dis) (20,29,32),

S = S_{s y s} + S_{d i s} = \sum_{i j} T_{j i} P_{j} ln (\frac{T_{j i} P_{j}}{T_{i j} P_{i}}),

(6)

where T_ij is the transition probability from state i to state j. In Fig. 3 C, we can see the dissipation per molecule (entropy production rate per molecule) decreases when the molecular number V increases, corresponding to fewer intrinsic fluctuations. It shows that a larger number of molecules, or fewer intrinsic fluctuations, produces less dissipation of energy, and the system becomes more stable. Therefore, minimization of the dissipation cost might serve as a design principle for evolution of the network as the entropy production is a global characterization. It is intimately related to the robustness of the network.

Autocorrelation coefficients and resonance peak of the power spectrum and coherence of the oscillation

We computed the autocorrelation function of the variables PN and Mp. Fig. 4 A1 shows the trajectories of PN and Mp for V = 100, and Fig. 4 A2 shows the autocorrelation function versus time interval Δt for these two variables. We can see that autocorrelation functions change periodically with the increase of interval time Δt, and the autocorrelation functions slowly decrease to zero with the time. This shows that the system is oscillatory, and that the correlations between observations in time gradually decay.

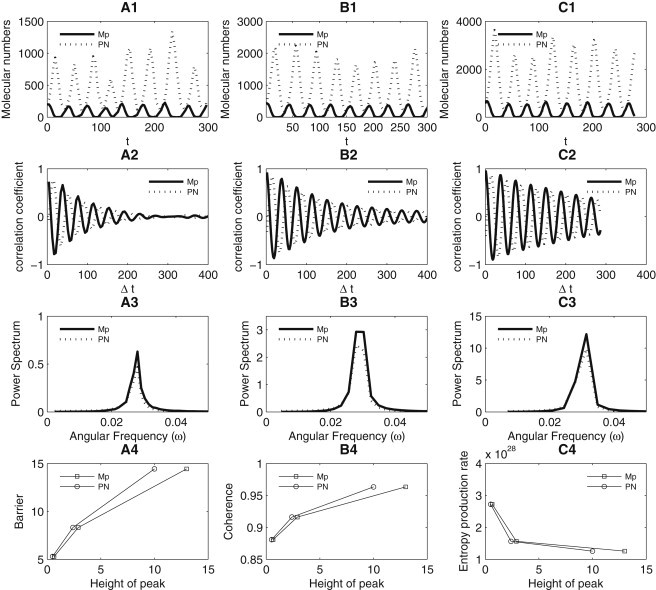
(A1) Trajectories of variables *P_N* and *M_p* for V = 100. (A2) Autocorrelation function versus interval time Δt when V = 100. (A3) Power spectrum of the autocorrelation function in panel A2. (*Solid line*) Mp (mRNA), (*dashed line*) PN (nuclear protein). (B1–B3) Trajectories, autocorrelation function, and the corresponding power spectrum for V = 200, respectively. (C1–C3) Trajectories, autocorrelation function, and the corresponding power spectrum for V = 300, respectively. (A4, B4, and C4) Height of peak of power spectrum of autocorrelation function versus barrier height, coherence, and entropy production rate, respectively.

We also computed the power spectrum by performing the Fourier transform of the autocorrelation function as shown in Fig. 4 A3. There exists a peak in the power spectrum at the frequency of the oscillation. Therefore, the peak can be termed “resonance peak” (33). Changing the molecular number V, we obtained the autocorrelation function and the corresponding power spectrum for V = 200 (Fig. 4, B1–B3) and V = 300 (Fig. 4, C1–C3). Similarly the power spectrum has a peak for both V = 200 and V = 300. Comparing the power spectrum for V = 100, V = 200, and V = 300, we can see that the heights of the peak of the power spectrum are different. This shows how prominent the resonance peak is. In Fig. 4, A4, B4, and C4, we show separately the height of power spectrum versus barrier height, the oscillation coherence, and the entropy production rate.

We can see that the barrier height and coherence increase and the entropy production rate (dissipations) decreases as the resonance peak in the power spectrum becomes more prominent. This is because the large molecular numbers lead to fewer fluctuations and more robust and coherent oscillations, as we discussed. The more prominent the peak, the more likely the system will have only one single frequency dominating the possible oscillations. The system is likely to be more stable with a higher barrier, more coherent oscillations, and fewer dissipations. Therefore, the height of the peak of the power spectrum may provide another way to measure the oscillation robustness. The more stable and coherent oscillation system leads to more prominent peak of the power spectrum and more distinct localized frequency to oscillate.

Three-point correlation functions, their time reversal, and suggested exploration of the nonzero curl flux from the observation of time traces

We also calculated the three-point autocorrelation function in forward and backward time evolution directions: x (t0), x (t0 + t1), and x (t0 + t1 + t2); and x (t0), x (t0 + t2), and x (t0 + t1 + t2). We use f (t1,t2) to denote the former, and g (t1,t2) to denote the latter.

According to the correlation definition,

f (t 1, t 2) = 〈 x (0) x (t 1) x (t 1 + t 2) 〉 = \sum_{i j k} P_{i} x_{i} P_{i j} (t 1) x_{j} P_{j k} (t 2) x_{k},

(7)

where P_i is the probability of state i and P_ij is the transition or jumping probability from state i to state j. If detailed balance is satisfied, the system is in equilibrium. We have P_iP_ij = P_jP_ji, and P_jP_jk = P_kP_kj, then

\begin{matrix} f (t 1, t 2) = 〈 x (0) x (t 1) x (t 1 + t 2) 〉 \\ = \sum_{i j k} P_{j} x_{i} P_{j i} (t 1) x_{j} P_{j k} (t 2) x_{k} \\ = \sum_{i j k} P_{k} x_{i} P_{j i} (t 1) x_{j} P_{k j} (t 2) x_{k} \\ = \sum_{i j k} P_{k} x_{k} P_{k j} (t 2) x_{j} P_{j i} (t 1) x_{i} \\ = 〈 x (0) x (t 2) x (t 1 + t 2) 〉 \\ = 〈 x (t) x (t - t 1) x (t - t 1 - t 2) 〉 = g (t 1, t 2), \end{matrix}

where t = t1 + t2, and g (t1,t2) is the time reversal of f (t1,t2). Therefore, in detailed balance for equilibrium system, f (t1,t2)is equal to its time reversal g (t1,t2). While in nonequilibrium steady state, this relationship will not be satisfied (34).

Fig. 5, A and B, shows the results of f (t1,t2) and g (t1,t2) separately. We can see that Fig. 5 A and Fig. 5 B are obviously different, which can also be found in Fig. 5 C showing the difference of the results of f (t1,t2) and g (t1,t2). This shows that the autocorrelation function is unsymmetrical after the time inversion. This is characteristic of a nonequilibrium steady state. It shows that for nonequilibrium systems, flux is not zero and it is the origin for the asymmetry of the three-point autocorrelation functions. Because the time traces can be measured from experiments, we can infer the nature of the probability flux from the experimental observation. Therefore, high-order correlation analysis may provide a way to directly quantify and validate the concepts of the curl flux introduced (13,14).

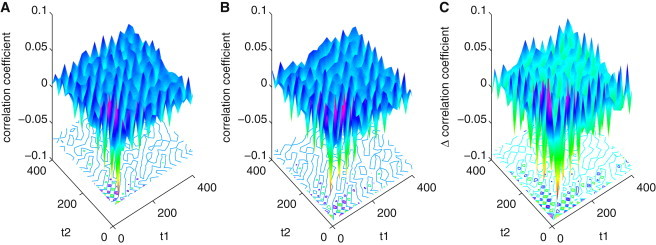
(A and B) Three-point autocorrelation function: x(t0), x(t0 + t1), and x(t0 + t1 + t2) and its time reversal x(t), x(t − t1), and x(t − t1 − t2) for variable Mp (mRNA) when V = 200. From the contour map, it can be seen that the results of correlation function in panels A and B are obviously different, which can also be found in panel C. (C) Difference between panels A and B. It should be noticed that the scales of difference of panels A and B are between −0.1 and 0.1, which approximate the scales of these two correlation functions themselves; they are obviously different.

Escape time for measuring global stability and link to landscape topography and coherence of oscillation

Additionally, we computed the escape time for jumping from the ring valley to outside. Fig. 6 A shows the distribution of escape time for different molecular numbers V. We can see from Fig. 6 A that with the increase of molecular number V, the probability distribution of escape time moves upwards, implying the increase of escape time on average. This is because when the number of molecules increases, the oscillation system becomes more stable accompanied by a deeper ring valley. Therefore, it becomes harder and takes a longer time for the system to jump to the outside from the oscillation ring. Fig. 6, B–D, show separately the barrier height, the phase coherence, and the height of the resonance peak of the power spectrum of autocorrelation function versus the average of escape time. We can see that the average of the escape time increases as the barrier, coherence, and the height of the resonance peak of the power spectrum increase. We can draw the consistent conclusion that larger barrier height corresponding to a more coherent oscillation and a higher peak height of the power spectrum will lead to a longer escape time for the system to jump to the outside from the oscillation ring valley.

(A) Distribution of escape time of jumping to outside from closed ring for different molecular number V. (B–D) Barrier height, the phase coherence, and the height of power spectrum of autocorrelation function versus the average of escape time, respectively.

Because the escape time is a measure of the capability of communicating from one state to another in the system, it provides a global measure of the stability of the system. The faster the escape time, the easier it is to go from one place to another and the less stable the system is. Escape time is a kinetic measure. Because it is correlated with the barrier height, the topography of the underlying landscape can also be used to measure the global stability. Furthermore, the coherence and height of the peak in the power spectrum, which give the quality of the oscillation, all correlate with the escape time monotonically. Therefore, they can also be used as quantitative measures of the global stability and coherence of the oscillations.

Global sensitivity analysis to uncover crucial network wirings for stability and robustness

We also performed a global sensitivity analysis to uncover the key connections or wirings of the circadian network responsible for stability of oscillation as shown in Fig. 7. This is through the changes of the chemical reaction rate constants and explorations of the corresponding effects on barrier heights of oscillation.

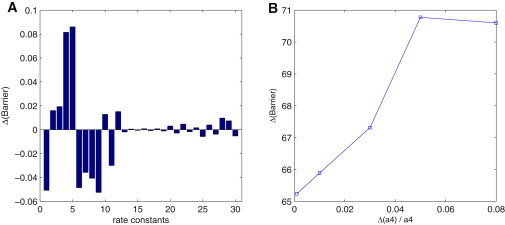
Sensitivity analysis. (A) Effects of parameters on the barrier height at the same perturbation. The x axis represents: 1, v_s; 2, a₁; 3, a₂, 4; a₃, 5, a₄₁; 6, d₁; 7, d₂; 8, d₃; 9, d₄; 10, *k_m*₁; 11, *k_m*₂; 12, *k_m*₃; 13, *k_s*; 14, k₁₁; 15, k₁₂; 16, k₁₃; 17, k₂₁; 18, k₂₂; 19, k₂₃; 20, k₃₁; 21, k₃₂; 22, k₃₃; 23, k₄₁; 24, k₄₂; 25, k₄₃; 26, *k_d*₁; 27, *k_d*₂; 28, *k_d*₃; 29, k₁; and 30, k₂. (B) Effect of parameter a₄ on barrier height. Δa₄/a₄ = percent of parameter increased.

Fig. 7 A shows the influence of the changes in rate constants on barrier height. From such global sensitivity analysis, we found some top rate constants, which influence barrier height more sensitively. These rate constants include a₁, a₂, a₃, and a₄, the increase of which makes the system more stable, as shown by the increase of barrier height. For some other rate constants, d₁, d₂, d₃, and d₄ v_s, the system becomes less stable after these constants are increased.

From the wiring diagram in Fig. 1 and the reaction steps of Table 1, we can see clearly that a₁, a₂, a₃, and a₄ are the rate constants contributing to the repression of protein PN on the promoter G. Therefore, the increase of these constants will make transcription process more difficult due to the decrease of promoter G. This shows that the repression process of promoter by PN is the main process controlling the robustness of system, making the system more stable. According to some recent studies (35), the source of oscillations includes a delay and a negative feedback loop. Therefore, the power of negative feedback being strengthened might be the reason why the oscillation system becomes more robust: when the parameters a₁, a₂, a₃, and a₄ increase, the repression on the promoter G, the most important step of the negative feedback loop, is strengthened.

For the same reason, d₁, d₂, d₃, and d₄ have the opposite effects on the promoter G, therefore, their increases produce the inverse effects to the robustness of the system, and make the oscillation less stable. In Fig. 7 B, we randomly choose one parameter a₄ to see specifically its effect on the barrier height. We can see that the barrier height increases as the parameter a₄ is increased, which is consistent with the results in Fig. 7 A. In the meantime, our method is general and can be used to predict the effects of parameters on the global stability and robustness of the system under intrinsic fluctuations, and furthermore make predictions such as which wirings are important for the experimentalists to verify.

Conclusion

We developed a landscape and flux framework to explore the global stability and robustness of a circadian oscillation system. The potential landscape of the network has been revealed to have a global Mexican-hat shape, and the height of the Mexican hat provides a quantitative measure to evaluate the robustness and coherence of the oscillation. We found that in nonequilibrium dynamic systems, both landscape and flux are important to the dynamics of the system under intrinsic fluctuations. Landscape attracts the systems down to the oscillation ring while flux drives the coherent oscillation on the ring. For dynamical nonequilibrium system, both Yin (potential landscape) and Yang (curl probability flux) duality is needed to describe the underlying global dynamics. We also investigated the entropy production rate of the system at different fluctuations and found that dissipations are less for large number of molecules (with smaller intrinsic fluctuations).

We also found that the power spectrums of autocorrelation functions show a resonance peak at the frequency of coherent oscillations. The peak is less prominent for larger fluctuations and lower barrier height and therefore can be used as another measure of the quality and coherence of oscillations, which is linked with the landscape topography. In addition, as a consequence of nonzero probability flux, we show that the three-point correlations from the time traces show irreversibility, providing a possible way to directly explore the nonzero curl flux from the experimental time traces.

Furthermore, we explored the escape time from the oscillation ring to outside at different molecular number V. Because escape time measures the capability of communication from one state to another, the longer the escape time, the more stable the system. We found that when barrier height is higher, escape time is longer and phase coherence of oscillation is higher. Therefore we can use landscape topography to quantify the global stability.

We performed the global sensitivity analysis of parameters to find the key network wirings responsible for the stability of the oscillation system. This provides a global way to pin down the critical wirings in the network for stability and function, which is potentially useful for synthetic biology and systems biology.

Our landscape and flux framework and the associated analysis is general and can be applied to other complex dynamical and biological systems.

Acknowledgments

C.L. thanks Bo Han for providing the C++ code, upon which modifications were made to implement stochastic simulations.

J.W. acknowledges support from the National Science Foundation. C.L. and E.W. are supported by the National Natural Science Foundation of China (grants 90713022 and 20735003) and 973 Project grants 2009CB930100 and 2010CB933600.

Contributor Information

Erkang Wang, Email: ekwang@ciac.jl.cn.

Jin Wang, Email: jin.wang.1@stonybrook.edu.

Supporting Material

Document S1. One figure and a supporting equation with narrative

mmc1.pdf^{(30.4KB, pdf)}

References

1.McAdams H.H., Arkin A. Stochastic mechanisms in gene expression. Proc. Natl. Acad. Sci. USA. 1997;94:814–819. doi: 10.1073/pnas.94.3.814. [DOI] [PMC free article] [PubMed] [Google Scholar]
2.Elowitz M.B., Leibler S. A synthetic oscillatory network of transcriptional regulators. Nature. 2000;403:335–338. doi: 10.1038/35002125. [DOI] [PubMed] [Google Scholar]
3.Swain P.S., Elowitz M.B., Siggia E.D. Intrinsic and extrinsic contributions to stochasticity in gene expression. Proc. Natl. Acad. Sci. USA. 2002;99:12795–12800. doi: 10.1073/pnas.162041399. [DOI] [PMC free article] [PubMed] [Google Scholar]
4.Thattai M., van Oudenaarden A. Intrinsic noise in gene regulatory networks. Proc. Natl. Acad. Sci. USA. 2001;98:8614–8619. doi: 10.1073/pnas.151588598. [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Vilar J.M.G., Guet C.C., Leibler S. Modeling network dynamics: the lac operon, a case study. J. Cell Biol. 2003;161:471–476. doi: 10.1083/jcb.200301125. [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Paulsson J. Summing up the noise in gene networks. Nature. 2004;427:415–418. doi: 10.1038/nature02257. [DOI] [PubMed] [Google Scholar]
7.Hasty J., Pradines J., Collins J.J. Noise-based switches and amplifiers for gene expression. Proc. Natl. Acad. Sci. USA. 2000;97:2075–2080. doi: 10.1073/pnas.040411297. [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Hasty J., Isaacs F., Collins J.J. Designer gene networks: towards fundamental cellular control. Chaos. 2001;11:207–220. doi: 10.1063/1.1345702. [DOI] [PubMed] [Google Scholar]
9.Van Kampen N.G. North-Holland; Amsterdam, The Netherlands: 1992. Stochastic Processes in Chemistry and Physics. [Google Scholar]
10.Gonze D., Halloy J., Goldbeter A. Robustness of circadian rhythms with respect to molecular noise. Proc. Natl. Acad. Sci. USA. 2002;99:673–678. doi: 10.1073/pnas.022628299. [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Gonze D., Halloy J. BRCA1 protein products: functional motifs. J. Chem. Phys. 2002;116:10997–11010. [Google Scholar]
12.Fall C.P., Marland E.S., Tyson J.J. Springer Verlag; New York: 2002. Computational Cell Biology. [Google Scholar]
13.Wang J., Xu L., Wang E. Potential landscape and flux framework of nonequilibrium networks: robustness, dissipation, and coherence of biochemical oscillations. Proc. Natl. Acad. Sci. USA. 2008;105:12271–12276. doi: 10.1073/pnas.0800579105. [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Wang J., Li C.H., Wang E.K. Potential and flux landscapes quantify the stability and robustness of budding yeast cell cycle network. Proc. Natl. Acad. Sci. USA. 2010;107:8195–8200. doi: 10.1073/pnas.0910331107. [DOI] [PMC free article] [PubMed] [Google Scholar]
15.Li C.H., Wang J., Wang E.K. Landscape and Ux decomposition for exploring global natures of non-equilibrium dynamical systems under intrinsic statistical fluctuations. Chem. Phys. Lett. 2011;505:75–80. [Google Scholar]
16.Qian H., Reluga T.C. Nonequilibrium thermodynamics and nonlinear kinetics in a cellular signaling switch. Phys. Rev. Lett. 2005;94:028101. doi: 10.1103/PhysRevLett.94.028101. [DOI] [PubMed] [Google Scholar]
17.Sasai M., Wolynes P.G. Stochastic gene expression as a many-body problem. Proc. Natl. Acad. Sci. USA. 2003;100:2374–2379. doi: 10.1073/pnas.2627987100. [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Ao P. Potential in stochastic differential equations: novel construction. J. Phys. Math. Gen. 2004;37:L25–L30. [Google Scholar]
19.Hornos J.E., Schultz D., Wolynes P.G. Self-regulating gene: an exact solution. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;72:051907. doi: 10.1103/PhysRevE.72.051907. [DOI] [PubMed] [Google Scholar]
20.Han B., Wang J. Quantifying robustness and dissipation cost of yeast cell cycle network: funneled energy landscape perspectives. Biophys. J. 2007;92:3755–3763. doi: 10.1529/biophysj.106.094821. [DOI] [PMC free article] [PubMed] [Google Scholar]
21.Frauenfelder H., Sligar S.G., Wolynes P.G. The energy landscapes and motions of proteins. Science. 1991;254:1598–1603. doi: 10.1126/science.1749933. [DOI] [PubMed] [Google Scholar]
22.Wolynes P.G., Onuchic J.N., Thirumalai D. Navigating the folding routes. Science. 1995;267:1619–1620. doi: 10.1126/science.7886447. [DOI] [PubMed] [Google Scholar]
23.Wang J., Verkhivker G.M. Energy landscape theory, funnels, specificity, and optimal criterion of biomolecular binding. Phys. Rev. Lett. 2003;90:188101. doi: 10.1103/PhysRevLett.90.188101. [DOI] [PubMed] [Google Scholar]
24.Gillespie D.T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 1976;22:403–434. [Google Scholar]
25.Gillespie D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977;81:2340–2361. [Google Scholar]
26.Gillespie D.T. The chemical Langevin equation. J. Chem. Phys. 2000;113:297–306. [Google Scholar]
27.Riskn H. Springer; Berlin, Germany: 1989. The Fokker-Planck Equation: Methods of Solution and Applications. [Google Scholar]
28.Hu G. Shanghai Scientific and Technological Education Press; Shanghai, China: 1994. Stochastic Forces and Nonlinear Systems. [Google Scholar]
29.Lapidus S., Han B., Wang J. Intrinsic noise, dissipation cost, and robustness of cellular networks: the underlying energy landscape of MAPK signal transduction. Proc. Natl. Acad. Sci. USA. 2008;105:6039–6044. doi: 10.1073/pnas.0708708105. [DOI] [PMC free article] [PubMed] [Google Scholar]
30.Qian H. Open-system nonequilibrium steady state: statistical thermodynamics, fluctuations, and chemical oscillations. J. Phys. Chem. B. 2006;110:15063–15074. doi: 10.1021/jp061858z. [DOI] [PubMed] [Google Scholar]
31.Yoda M., Ushikubo T., Sasai M. Roles of noise in single and coupled multiple genetic oscillators. J. Chem. Phys. 2007;126:115101. doi: 10.1063/1.2539037. [DOI] [PubMed] [Google Scholar]
32.Qian H. Mesoscopic nonequilibrium thermodynamics of single macromolecules and dynamic entropy-energy compensation. Phy. Rev. E. 2001;65:0161021–0161025. doi: 10.1103/PhysRevE.65.016102. [DOI] [PubMed] [Google Scholar]
33.Qian H., Qian M. Pumped biochemical reactions, nonequilibrium circulation, and stochastic resonance. Phys. Rev. Lett. 2000;84:2271–2274. doi: 10.1103/PhysRevLett.84.2271. [DOI] [PubMed] [Google Scholar]
34.Qian H., Elson E.L. Fluorescence correlation spectroscopy with high-order and dual-color correlation to probe nonequilibrium steady states. Proc. Natl. Acad. Sci. USA. 2004;101:2828–2833. doi: 10.1073/pnas.0305962101. [DOI] [PMC free article] [PubMed] [Google Scholar]
35.Mather W., Bennett M.R., Tsimring L.S. Delay-induced degrade-and-fire oscillations in small genetic circuits. Phys. Rev. Lett. 2009;102:068105. doi: 10.1103/PhysRevLett.102.068105. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Document S1. One figure and a supporting equation with narrative

mmc1.pdf^{(30.4KB, pdf)}

[bib1] 1.McAdams H.H., Arkin A. Stochastic mechanisms in gene expression. Proc. Natl. Acad. Sci. USA. 1997;94:814–819. doi: 10.1073/pnas.94.3.814. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib2] 2.Elowitz M.B., Leibler S. A synthetic oscillatory network of transcriptional regulators. Nature. 2000;403:335–338. doi: 10.1038/35002125. [DOI] [PubMed] [Google Scholar]

[bib3] 3.Swain P.S., Elowitz M.B., Siggia E.D. Intrinsic and extrinsic contributions to stochasticity in gene expression. Proc. Natl. Acad. Sci. USA. 2002;99:12795–12800. doi: 10.1073/pnas.162041399. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib4] 4.Thattai M., van Oudenaarden A. Intrinsic noise in gene regulatory networks. Proc. Natl. Acad. Sci. USA. 2001;98:8614–8619. doi: 10.1073/pnas.151588598. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib5] 5.Vilar J.M.G., Guet C.C., Leibler S. Modeling network dynamics: the lac operon, a case study. J. Cell Biol. 2003;161:471–476. doi: 10.1083/jcb.200301125. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib6] 6.Paulsson J. Summing up the noise in gene networks. Nature. 2004;427:415–418. doi: 10.1038/nature02257. [DOI] [PubMed] [Google Scholar]

[bib7] 7.Hasty J., Pradines J., Collins J.J. Noise-based switches and amplifiers for gene expression. Proc. Natl. Acad. Sci. USA. 2000;97:2075–2080. doi: 10.1073/pnas.040411297. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib8] 8.Hasty J., Isaacs F., Collins J.J. Designer gene networks: towards fundamental cellular control. Chaos. 2001;11:207–220. doi: 10.1063/1.1345702. [DOI] [PubMed] [Google Scholar]

[bib9] 9.Van Kampen N.G. North-Holland; Amsterdam, The Netherlands: 1992. Stochastic Processes in Chemistry and Physics. [Google Scholar]

[bib10] 10.Gonze D., Halloy J., Goldbeter A. Robustness of circadian rhythms with respect to molecular noise. Proc. Natl. Acad. Sci. USA. 2002;99:673–678. doi: 10.1073/pnas.022628299. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib11] 11.Gonze D., Halloy J. BRCA1 protein products: functional motifs. J. Chem. Phys. 2002;116:10997–11010. [Google Scholar]

[bib12] 12.Fall C.P., Marland E.S., Tyson J.J. Springer Verlag; New York: 2002. Computational Cell Biology. [Google Scholar]

[bib13] 13.Wang J., Xu L., Wang E. Potential landscape and flux framework of nonequilibrium networks: robustness, dissipation, and coherence of biochemical oscillations. Proc. Natl. Acad. Sci. USA. 2008;105:12271–12276. doi: 10.1073/pnas.0800579105. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib14] 14.Wang J., Li C.H., Wang E.K. Potential and flux landscapes quantify the stability and robustness of budding yeast cell cycle network. Proc. Natl. Acad. Sci. USA. 2010;107:8195–8200. doi: 10.1073/pnas.0910331107. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib15] 15.Li C.H., Wang J., Wang E.K. Landscape and Ux decomposition for exploring global natures of non-equilibrium dynamical systems under intrinsic statistical fluctuations. Chem. Phys. Lett. 2011;505:75–80. [Google Scholar]

[bib16] 16.Qian H., Reluga T.C. Nonequilibrium thermodynamics and nonlinear kinetics in a cellular signaling switch. Phys. Rev. Lett. 2005;94:028101. doi: 10.1103/PhysRevLett.94.028101. [DOI] [PubMed] [Google Scholar]

[bib17] 17.Sasai M., Wolynes P.G. Stochastic gene expression as a many-body problem. Proc. Natl. Acad. Sci. USA. 2003;100:2374–2379. doi: 10.1073/pnas.2627987100. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib18] 18.Ao P. Potential in stochastic differential equations: novel construction. J. Phys. Math. Gen. 2004;37:L25–L30. [Google Scholar]

[bib19] 19.Hornos J.E., Schultz D., Wolynes P.G. Self-regulating gene: an exact solution. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;72:051907. doi: 10.1103/PhysRevE.72.051907. [DOI] [PubMed] [Google Scholar]

[bib20] 20.Han B., Wang J. Quantifying robustness and dissipation cost of yeast cell cycle network: funneled energy landscape perspectives. Biophys. J. 2007;92:3755–3763. doi: 10.1529/biophysj.106.094821. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib21] 21.Frauenfelder H., Sligar S.G., Wolynes P.G. The energy landscapes and motions of proteins. Science. 1991;254:1598–1603. doi: 10.1126/science.1749933. [DOI] [PubMed] [Google Scholar]

[bib22] 22.Wolynes P.G., Onuchic J.N., Thirumalai D. Navigating the folding routes. Science. 1995;267:1619–1620. doi: 10.1126/science.7886447. [DOI] [PubMed] [Google Scholar]

[bib23] 23.Wang J., Verkhivker G.M. Energy landscape theory, funnels, specificity, and optimal criterion of biomolecular binding. Phys. Rev. Lett. 2003;90:188101. doi: 10.1103/PhysRevLett.90.188101. [DOI] [PubMed] [Google Scholar]

[bib24] 24.Gillespie D.T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 1976;22:403–434. [Google Scholar]

[bib25] 25.Gillespie D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977;81:2340–2361. [Google Scholar]

[bib26] 26.Gillespie D.T. The chemical Langevin equation. J. Chem. Phys. 2000;113:297–306. [Google Scholar]

[bib27] 27.Riskn H. Springer; Berlin, Germany: 1989. The Fokker-Planck Equation: Methods of Solution and Applications. [Google Scholar]

[bib28] 28.Hu G. Shanghai Scientific and Technological Education Press; Shanghai, China: 1994. Stochastic Forces and Nonlinear Systems. [Google Scholar]

[bib29] 29.Lapidus S., Han B., Wang J. Intrinsic noise, dissipation cost, and robustness of cellular networks: the underlying energy landscape of MAPK signal transduction. Proc. Natl. Acad. Sci. USA. 2008;105:6039–6044. doi: 10.1073/pnas.0708708105. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib30] 30.Qian H. Open-system nonequilibrium steady state: statistical thermodynamics, fluctuations, and chemical oscillations. J. Phys. Chem. B. 2006;110:15063–15074. doi: 10.1021/jp061858z. [DOI] [PubMed] [Google Scholar]

[bib31] 31.Yoda M., Ushikubo T., Sasai M. Roles of noise in single and coupled multiple genetic oscillators. J. Chem. Phys. 2007;126:115101. doi: 10.1063/1.2539037. [DOI] [PubMed] [Google Scholar]

[bib32] 32.Qian H. Mesoscopic nonequilibrium thermodynamics of single macromolecules and dynamic entropy-energy compensation. Phy. Rev. E. 2001;65:0161021–0161025. doi: 10.1103/PhysRevE.65.016102. [DOI] [PubMed] [Google Scholar]

[bib33] 33.Qian H., Qian M. Pumped biochemical reactions, nonequilibrium circulation, and stochastic resonance. Phys. Rev. Lett. 2000;84:2271–2274. doi: 10.1103/PhysRevLett.84.2271. [DOI] [PubMed] [Google Scholar]

[bib34] 34.Qian H., Elson E.L. Fluorescence correlation spectroscopy with high-order and dual-color correlation to probe nonequilibrium steady states. Proc. Natl. Acad. Sci. USA. 2004;101:2828–2833. doi: 10.1073/pnas.0305962101. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib35] 35.Mather W., Bennett M.R., Tsimring L.S. Delay-induced degrade-and-fire oscillations in small genetic circuits. Phys. Rev. Lett. 2009;102:068105. doi: 10.1103/PhysRevLett.102.068105. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Landscape, Flux, Correlation, Resonance, Coherence, Stability, and Key Network Wirings of Stochastic Circadian Oscillation

Chunhe Li

Erkang Wang

Jin Wang

Abstract

Introduction

Figure 1.

Materials and Methods