Skip to main content
PMC home page
Nucleic Acids Research logoLink to Nucleic Acids Research
. 2011 Jun 21;39(17):7390–7399. doi: 10.1093/nar/gkr395

From face to interface recognition: a differential geometric approach to distinguish DNA from RNA binding surfaces

Shula Shazman 1, Gershon Elber 2, Yael Mandel-Gutfreund 1,*
PMCID: PMC3177183  PMID: 21693557

Abstract

Protein nucleic acid interactions play a critical role in all steps of the gene expression pathway. Nucleic acid (NA) binding proteins interact with their partners, DNA or RNA, via distinct regions on their surface that are characterized by an ensemble of chemical, physical and geometrical properties. In this study, we introduce a novel methodology based on differential geometry, commonly used in face recognition, to characterize and predict NA binding surfaces on proteins. Applying the method on experimentally solved three-dimensional structures of proteins we successfully classify double-stranded DNA (dsDNA) from single-stranded RNA (ssRNA) binding proteins, with 83% accuracy. We show that the method is insensitive to conformational changes that occur upon binding and can be applicable for de novo protein-function prediction. Remarkably, when concentrating on the zinc finger motif, we distinguish successfully between RNA and DNA binding interfaces possessing the same binding motif even within the same protein, as demonstrated for the RNA polymerase transcription-factor, TFIIIA. In conclusion, we present a novel methodology to characterize protein surfaces, which can accurately tell apart dsDNA from an ssRNA binding interfaces. The strength of our method in recognizing fine-tuned differences on NA binding interfaces make it applicable for many other molecular recognition problems, with potential implications for drug design.

INTRODUCTION

The DNA and its RNA messenger encapsulate the essence of life. However, the information encoded in the nucleic acid (NA) molecules cannot be read without the proteins that regulate their expression, namely, DNA and RNA binding proteins. DNA binding proteins play key roles in many biological processes, ranging from DNA packaging, replication, to gene expression control. RNA binding proteins interact with various RNAs at different stages of the gene expression pathway from transcription to translation, as reviewed in ref. (1). Recently, high-throughput methods have shown that the majority of the genome is transcribed, suggesting many new roles for nucleic acid binding proteins (2). Identifying DNA and RNA binding proteins is thus a very important and challenging task. In the last decade many computational methods have been developed for predicting DNA and RNA binding proteins. Several of these methods use sequence features alone as input for the prediction [e.g. (3–5)], while others require knowledge from the three-dimensional (3D) structure (3,6–16). In addition numerous structure- and sequence-based methods were developed for predicting the specific DNA and RNA binding sites (17–27). In general most methods for predicting NA function and NA binding residues based on structure rely on electrostatics and evolutionary conservation. While a number of studies have concentrated on predicting NA binding function (28–30), in the majority of cases the methods cannot tell apart DNA from RNA binding proteins, without relying on homology to a known DNA or RNA binding proteins.

DNA and RNA binding proteins are expected to differ in their structural properties, consistent with the different properties of their natural ligand; DNA usually adopt a classical B-form double-helix while RNA adopts A-form helices frequently interrupted by internal loops and bulges (31). In spite of the clear structural differences between double-stranded DNA (dsDNA) and single-stranded RNA (ssRNA), no apparent differences have been observed between dsDNA and ssRNA binding proteins at their secondary structure level (32,33). Nevertheless, these studies have pointed out distinct features of the NA-protein complexes, including poor packing of the ssRNA–protein complexes and different interaction preferences (32,33). Several recent studies have focused on the structural properties of DNA and RNA binding interfaces (34–36). These studies strongly hint to the role of the geometry and shape of the binding interface for specific recognition of their unique partner (DNA versus RNA); however, they do not discriminate DNA from RNA binding interfaces. Here, we introduce a novel method to uniquely characterize NA binding interfaces based on a differential geometry approach, commonly used in object recognition applications, such as 3D face recognition (37). A distinct differential geometry approach was used previously to dock small ligands to proteins (38). The latter method relies on the existing molecular surface complementarity between a putative ligand and its receptor protein. Here, by exploiting differential geometry, we uniquely describe the molecular surface as a distribution of local surface shapes. The great advantage of the current method is that it can describe any molecular surface shape, regardless of the ligand information, and it is not limited to protein-ligand interactions which follow the ‘lock and key’ paradigm. Overall, using differential geometry attributes (39,40), we were able, for the first time, to successfully distinguish between DNA and RNA binding interfaces. Furthermore, by combining geometric features with electrostatic properties (16), we show that we can uniquely classify dsDNA versus ssRNA binding proteins with 83% accuracy. As we demonstrate for the well-characterized NA binding motif, C2H2 zinc finger, our method does not depend on the binding motif and can successfully distinguish between DNA binding zinc-finger domains and those which bind RNA, even within the same protein. We exemplify this for the RNA polymerase transcription factor III (TFIIIA) which binds both the promoter of the 5S ribosomal gene and the 5S rRNA via separate zinc-finger domains (41). Finally, we show that the method is not sensitive to conformational changes that occur upon NA binding and can correctly predict NA binding properties of proteins in their apo state.

MATERIALS AND METHODS

Data construction

A total of 510 protein–DNA and 190 protein–RNA structures from the Protein Data Bank (PDB) that contained single-chain protein and single-chain DNA/RNA were extracted, including X-ray structures (<3 Å) and structures solved by NMR. Complexes in which the protein was <30 amino acid and the DNA/RNA sequence was <11 nt were removed. The PISCES program http://dunbrack.fccc.edu/PISCES.php was used for extracting a clean protein data set with <30% sequence identity. All structures that contained ssDNA or dsRNA were removed.

The final data set ‘NAbind-130′ consisted of 130 protein–NA complexes (87 protein–DNA complexes and 43 protein–RNA complexes). From this data set, a second data set ‘NAbind-77nr,’ consisting of one representative of each SCOP family, was derived. The ‘NAbind-77nr’ data set consisted of 77 protein–NA complexes (52 protein–DNA complexes and 25 protein–RNA complexes). The subset of unbound proteins structures was obtained from PDB selecting unbound structures with at least 90% sequence identity at the protein level to the proteins in the original ‘NAbind-130′ data set. In addition, eight pairs of apo and holo structures of RNA binding proteins were added from a recent study (42). Overall the data included 32 pairs of proteins for which we had structures available in both holo and apo forms (for details, see Supplementary Data S1).

Interface residues were calculated using the Intervor web server (43) excluding water molecules. The PatchFinder algorithm (44) was applied to extract all continuous positive patches on the protein surface with a cutoff of 2 kT/e. The patches were sorted based on the number of grid points included within the patch, and the largest patch was selected as described in ref. (6). Root mean square deviation (RMSD) between the bound and unbound proteins was calculated using the jCE algorithm, a pre-calculated protein structure alignment tool (45).

Calculating the geometric parameters of the surface using differential geometry

Extracting surface points

Surface points of each protein were computed using the DMS software http://www.cgl.ucsf.edu/Resources/index.html. The DMS program applies the Richards model (46) for obtaining surface accessibility by rolling a ball of radius r along the van der Waals surface of molecule. The surface points are used as an input to the tcocone software (47), which reconstructs the surface based on the Delaunay triangulation algorithm.

Defining the curvature of a surface point

Geometric surface properties were extracted for each protein chain in the database (after removal of the NA chain) using the IRIT modeling package, http://www.cs.technion.ac.il/~irit/. IRIT is a geometric modeling environment that allows one to model basic primitives and perform Boolean operations as well as support freeform surface-based models (39,40). Here, IRIT was employed to extract the curvatures of each surface point defined by DMS. The principal curvatures are denoted as k1, k2 and are defined as the maximum and minimum values of the curvatures of all normal planes of the given surface point, respectively [for details, see ref. (38)].

The Gaussian curvature K is equal to the product of the two principal curvatures K = k1k2. Gaussian curvature is positive for convex and concave parts of the surface, negative at saddle shape parts, and zero for planes, cones and cylinders (developable surfaces).

The Mean curvature H is equal to the average of the principal curvatures H = (k1 + k2)/2. Mean curvature is related to the first variation of surface area. In particular, a minimal surface, such as a soap film, has a zero mean curvature and a soap bubble has a constant mean curvature.

While curvature analysis typically requires C2 continuous surfaces (surfaces with well-defined second-order derivatives), herein we deal with polygonal meshes that are only C0 continuous. Nonetheless, many techniques have been developed in recent years to approximate curvature properties for piecewise linear polygonal meshes; for instance (40), is one short survey on this topic. In this work, the estimation is based on a second-order (quadratic) fit to a small neighborhood of the polygonal mesh centered around a location point p.

Calculating the distribution of local shapes

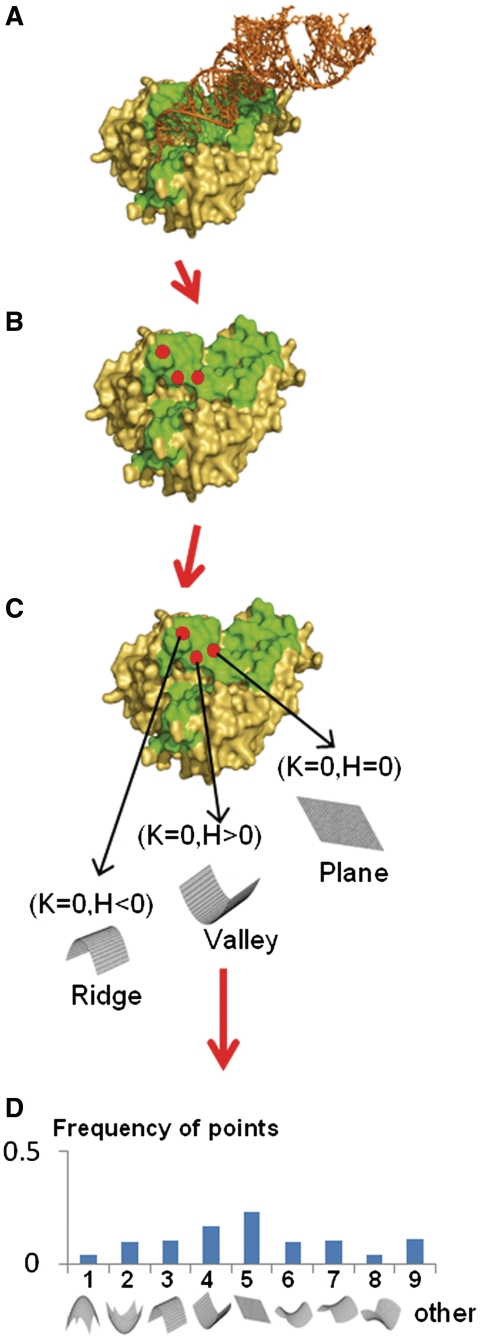
Based on the signs of Gaussian and mean curvatures, every vertex in the triangles’ mesh constructed by the Delaunay triangulations algorithm is classified to one of eight fundamental surface types: Peak, Pit, Ridge, Valley, Flat, Minimal Surface, Saddle Ridge and Saddle Valley (see Supplementary Table S1). The influence of every vertex is then normalized by the effective area of its surrounding triangle. After cataloging each vertex and having its supporting influence, the distribution of the points belonging to the different local geometric shapes are calculated and described as a vector V = {pi, i = 1 … 9}; Σpi = 1, where pi is the probability of interface points belonging to one of the local shapes: 1 = Peak, 2 = Pit, 3 = Ridge, 4 = Valley, 5 = Flat, 6 = Minimal Surface, 7 = Saddle Ridge, 8 = Saddle Valley, 9 = others.

Statistical analysis

Clustering

Data clustering was performed using the MeV software (48), applying hierarchical clustering with average linkage.

Decision Tree

The package rpart from the GNU R software http://cran.r-project.org/web/packages/rpart/index.html was applied to build decision trees based on the CART recursive partitioning algorithm.

Support Vector Machine

Supprt vector machine (SVM) experiments were carried out with Gist program version 2.1.1 (http://microarray.cpmc.columbia.edu/gist/). Input data were normalized by rescaling the columns to values between −1 and 1. A linear kernel was applied for all SVM classifiers. General tests were conducted by using the ‘leave one out’ cross-validation procedure. To evaluate SVM performance, a receiver operating characteristic (ROC) curve, describing the relationship between the false positive rate (FPR) and the true positive rate (TPR), was plotted. The area under ROC curve (AUC) ranged between 0 and 1, and can be interpreted as the probability that when we randomly pick one positive and one negative example, the classifier will assign a higher score to the positive example than to the negative example. The AUCs were reported for each SVM test. Feature selection was performed by starting with the four geometric features (Peak, Pit, Ridge and Valley) and iteratively adding features from the electrostatic and protein features, described in ref. (16). The AUC was calculated successively for each of the testing iterations. In the event that the feature increased the AUC, it was added to the feature set. Iterations were repeated consequently until the SVM converged. The procedure was repeated 100 times, each time with a different seed, and the best results were chosen.

Accuracy and Matthews's Correlation Coefficient (MCC) were calculated using the following formulas:

graphic file with name gkr395um1.jpg
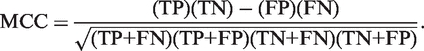graphic file with name gkr395um2.jpg

Availability

A standalone package for predicting dsDNA versus ssRNA interfaces using differential geometry (suitable for linux OS) is available for download.

RESULTS

Characterizing molecular interfaces using differential geometry

In an attempt to uniquely characterize NA binding surfaces, distinguishing the dsDNA from ssRNA binding interfaces, we represent each protein interface (Supplementary Data S1) using a novel differential geometry model, we define the ‘DG model’ (described in Figure 1 and detailed in the ‘Materials and Methods’ section). Briefly, for any given protein we compute the molecule surface based on the well-established Richards algorithm (46). We then reconstruct the surface based on the Delaunay triangulations algorithm using the tcocone software (47). Further, we define the curvature of each surface point (which is represented as the vertices of the Delaunay triangles). In principle, the curvature of a surface point is defined by the degree that a geometric object deviates from being planar (or straight, in the case of a curve) and is closely related to the second-order derivatives of the shape. Two principal curvatures, k1 and k2, fully characterize the second order (bending) behavior of the surface at a certain point and define the Gaussian and mean curvatures, K and H, respectively. The signs of K and H are used to classify the surface points into one of eight fundamental shapes (Supplementary Table S1). Finally, the distribution of the surface points to the local shape is represented by a vector, which characterizes each protein interface (Figure 1).

Figure 1.

Figure 1.

Open in a new tab

A schematic description of the differential geometric model procedure. (A) As an input, a protein nucleic acid complex is obtained from the PDB. (B) The NA-binding interface (green) is extracted using Intervor http://cgal.inria.fr/abs/Intervor/. (C) The Gaussian (K) and mean (H) curvatures of each point on the NA-binding interface is calculated with the IRIT software http://www.cs.technion.ac.il/~irit/ and further assigned to a local geometric shape. (D) The distribution of the interface points relative to the different local geometric shapes is represented as a vector.

Distinguishing NA binding interfaces using geometric features

To explore the potential of the DG model to typify the different biological interfaces, we clustered the vectors using hierarchical clustering. As shown in Figure 2, when classifying the interfaces from the non-redundant ‘NAbind-77nr’ set considering only the four best separating descriptors (Peak, Pit, Ridge and Valley), we observed two distinct clusters. The first cluster was characterized by a high frequency of interface points associated with the valley shape and was comprised mainly of the dsDNA binding interface, and thus was defined the ‘DNA-pattern’. The second cluster was characterized by a relatively high fraction of ridge points and included mainly the ssRNA binding interface, and thus was defined the ‘RNA-pattern’. Overall, based on the hierarchical clustering, 41 out of 52 known dsDNA binding proteins in the ‘NAbind-77nr’ set (79%) were associated with a characteristic ‘DNA-pattern’ while 19 out of 25 known ssRNA binding proteins (76%) were associated with the ‘RNA-pattern’, with an overall MCC of 0.53 (Supplementary Table S2). A similar trend, though less profound, was achieved when clustering the redundant set ‘NAbind-130′ using the four best descriptors (see Supplementary Figure S1). Here, 30/43 ssRNA binding interfaces were associated with the ‘RNA pattern’ and 56/87 dsDNA-binding interfaces were characterized by the ‘DNA pattern’, with an overall MCC of 0.32 (Supplementary Table S2).

Figure 2.

Figure 2.

Open in a new tab

Hierarchal clustering of dsDNA and ssRNA interfaces. Hierarchal clustering of the interface vectors extracted from the ‘NAbind-77nr’ data set. Interfaces are labeled according the NA binding protein label (see Supplementary Data S1), R and D, denote RNA-binding and DNA binding interfaces, respectively. Vectors represent the frequency of the binding interface points related to the local geometric shapes Peak, Pit, Ridge and Valley, extracted from the NA binding interfaces. High frequency is colored red and low frequency colored yellow. Color bar is shown.

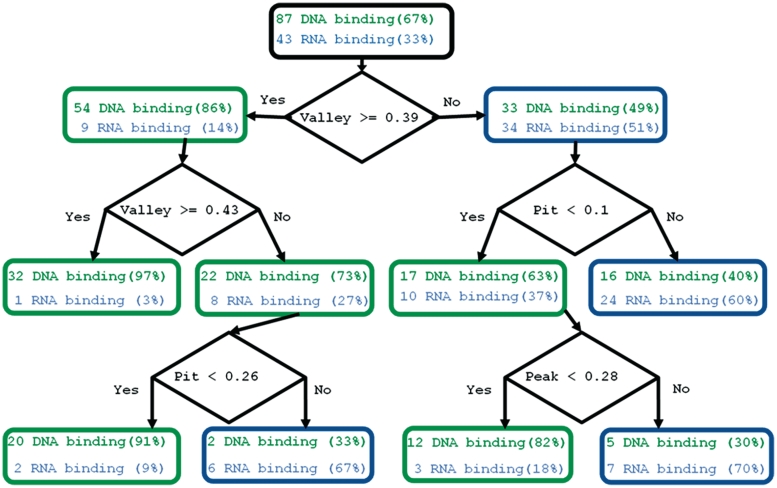
In an attempt to pinpoint the geometric features separating the dsDNA binding interface from the ssRNA binding interface, we employed a Decision Tree algorithm (see ‘Materials and Methods’ section). Using geometric features, the Decision Tree successfully classified the dsDNA versus ssRNA binding interfaces with a MCC of 0.57 and 0.6 for the ‘NAbind-130′ and ‘NAbind-77nr’, respectively (Figure 3). Overall, the prediction accuracy for the dsDNA binding interfaces using the Decision Tree approach was 74% (64/87), which is slightly better than the accuracy achieved using hierarchical clustering. Interestingly, for RNA binding prediction, the Decision Tree achieved significantly higher results with accuracy of 86% (37/43) compared to 70% obtained using hierarchical clustering. As demonstrated in Figure 3, consistent with the hierarchical clustering results, in the Decision Tree the predictor variable ‘valley’ was selected for the first split, resulting in the purest child nodes.

Figure 3.

Figure 3.

Open in a new tab

Separating dsDNA from ssRNA interfaces using a Decision Tree. A Decision Tree was trained on the ‘NAbind-130′ data set. The tree shown represents the results of testing the ‘NAbind-130′ data set using the hold-one-out cross-validation test. The Decision Tree is a binary tree and was constructed by repeatedly splitting a node into two child nodes, beginning with the root node that contains the whole learning sample. The other nodes are colored according to node type, dsDNA binding and ssRNA binding in green and blue, respectively. Node type is determined based on the most frequent class of proteins included in that node. The split rule is represented in the figure by black diamonds. To validate the significance of the results, we generated 1000 shuffled data sets (shuffling the labels of the original data), the probability of getting an MCC of 0.57 or higher was <0.05.

Can geometric features uniquely predict NA binding proteins?

As aforementioned, using the DG model we were able to successfully differentiate between dsDNA and ssRNA binding interfaces. Obviously, the real challenge is to be able to tell whether a given protein will bind dsDNA or ssRNA with no prior knowledge of the binding interface. In previous studies (6,16,44), we showed that the largest electrostatic positive patch is a good predictor for the real interface. Based on the performance of the DG model to distinguish dsDNA from ssRNA interfaces, we were intrigued to examine whether the geometric approach could distinguish between dsDNA and ssRNA binding proteins, when the information of the real binding interface was not considered. To this end, we analyzed the distribution of the local geometric shapes in the largest electrostatic positive patches extracted from the 3D structures of the proteins (see ‘Materials and Methods’ section). Remarkably, the geometric features of the largest electrostatic patches extracted from the dsDNA and the ssRNA binding proteins generated two distinct clusters (Supplementary Figure S2). Consequently, applying a Decision Tree which was trained on the features extracted from real binding interfaces and tested on the features extracted from the electrostatic patches of the proteins, applying hold-one-out cross-validation, achieved an overall 79% accuracy with an MCC of 0.49 for both the ‘NAbind-130′ and ‘NAbind-77nr’ sets. Interestingly, the prediction accuracy based on the largest positive patch was higher for dsDNA binding prediction than for the ssRNA binding prediction (79% versus 76% for DNA and RNA, respectively). These minor differences are in accordance with our previous observations, in which we found an overall lower overlap between the electrostatic patches and the real interfaces for RNA binding interfaces in comparison to DNA binding interfaces (16).

Combining differential geometry with electrostatic features

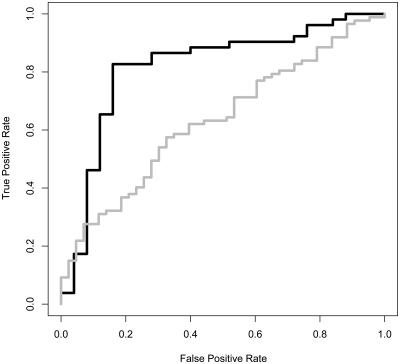
Electrostatic features were previously shown to predict NA binding proteins, distinguishing them from non-NA binding proteins (6,16). Nevertheless, the electrostatic features by themselves were not sufficient to tell apart DNA from RNA binding proteins (16). Here, we applied a machine learning approach, namely SVM, to distinguish automatically between dsDNA and ssRNA, combining the DG model attributes with the electrostatic features extracted from the largest positive patches of the proteins. Using a simple feature selection procedure (described in ‘Materials and Methods’ section), we selected the combination of parameters that best separate the data when applying a cross-validation test on the non-redundant ‘NAbind-77nr’ set. The final set of features was comprised of four DG features; five electrostatic features and one general property of the protein (see Supplementary Table S3). As noticeable, individually, each of the selected features did not show a highly significant difference between the dsDNA and an ssRNA interfaces, however, combining the DG and electrostatic features achieved 83% accuracy with 0.82 AUC (Figure 4). As demonstrated in Figure 4, the latter results depicted by the solid black line are significantly higher than the best results achieved previously (60% and 0.62 for accuracy and AUC, respectively) with the electrostatic and protein features alone (gray line). A detailed summary of the SVM results is provided in Supplementary Table S2. To reassure that these results are not due to over fitting we tested our algorithm on an independent set of proteins. In the recent paper of Zhao et al. (25), they constructed a data set which contains 212 RNA binding and 311 DNA binding domains. From the latter data set we extracted a set of 193 RNA binding chains and 249 DNA binding chains. This data set included dsRNA binding proteins and ssDNA proteins as well proteins which bind as multimeric proteins. Nevertheless, when testing our SVM on the independent data 131 of the 193 RNA binding proteins (68%) were predicted correctly as RNA binding and 195 of 249 (78%) DNA binding proteins were predicted as DNA binding, with an overall 74% accuracy. When selecting the subset of proteins including only ssRNA binding and dsDNA binding proteins which bind as monomers we achieved an overall accuracy of 78% and an MCC value of 0.47 (14/18 predicted correctly as ssRNA binding proteins and 53/69 were predicted correctly as dsDNA binding proteins), similar to the results achieved on the ‘NAbind-130′ set (see Supplementary Table S2). Notably, in comparison to the method of Zhao et al. (25) our method is completely homology independent and thus can be applied ab-initio to proteins which have no fold similarity to the training set.

Figure 4.

Figure 4.

Open in a new tab

Distinguishing dsDNA- from ssRNA-binding proteins using SVM with combined geometric and electrostatics features. A ROC plot summarizing the results of the SVM testing on the ‘NAbind-77nr’ data set using the electrostatic features (gray line) and the combined electrostatic and geometric features (black solid line). As shown the geometric features dramatically improved the SVM prediction achieving and overall 83% accuracy (AUC = 0.82) compared to 60% accuracy (AUC = 0.62) when using the classical features.

The differential geometry approach is not sensitive to conformational changes

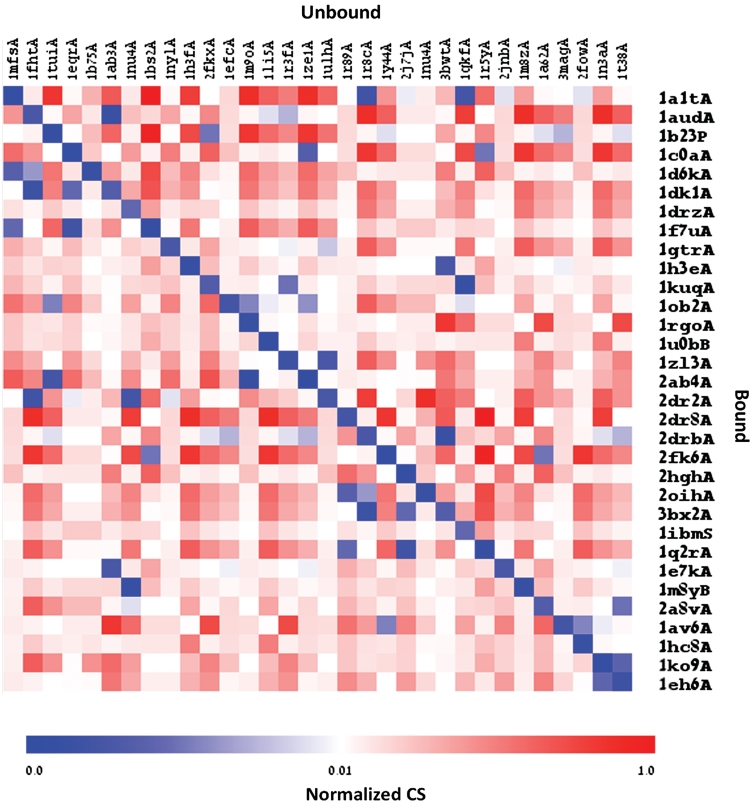
Previous studies on DNA and RNA binding proteins have demonstrated that in the majority of cases, the NA binding interface does not undergo dramatic conformational changes (49,50). To further examine to what extent the differential geometry parameters of the NA binding interfaces change between the bound and unbound states of NA binding proteins, we extracted a set of 32 NA binding proteins for which their structures were available in the apo and holo states (see ‘Material and Methods’ section and Supplementary Data S1 for details). The distributions of surface points in the local geometry shapes were calculated independently for the interfaces of the bound states and their corresponding regions in the unbound states. Subsequently, the vectors were compared to each other using the Euclidian Distance metric, defined as the Correlation Score (CS). The heat map in Figure 5 illustrates the calculated normalized distances between the bound interfaces and unbound corresponding regions (all-against-all). As can be clearly noticed, the lowest CSs (highest correlations between vectors) are observed in the diagonal, demonstrating a very high similarity in the tested regions between the apo and holo states of the same protein. Interestingly, the lowest CSs between the apo and holo structures of the same protein were also obtained for pairs for which conformation changes upon binding are observed. As demonstrated in Supplementary Figure S3, we did not identify a correlation between the RMSD calculated between the bound and unbound proteins and the CSs calculated between the DG vectors of their binding interfaces (Pearson correlation −0.037). Furthermore, the lowest CSs were obtained in cases which were previously demonstrated to undergo a conformational change upon binding, as in the case of the human 8-oxoguanine glycosylase (8OG), which is responsible for the recognition and removal of damaged bases from DNA (PDB 1n3a). Albeit the evident conformational change the protein undergoes upon binding the DNA (51), we still found the interface of the bound protein (PDB 1ko9) most similar to the interface extracted from the unbound structure. Notably, in the case of 8OG, the interface of the bound structure was also correlated, though to a lesser extent, with the interface of the unbound structure of the human O(6)-alkylguanine-DNA alkyltransferase (AGT), which possesses an HTH domain and is also involved in DNA repair, presumably without undergoing a conformational change (52). Overall the comparison between the DG vectors of proteins in the apo and holo states support that the DG method is robust to conformation changes which can occur upon ligand binding. To confirm that the DG method is powerful to predict the binding preference of a protein also in the unbound state we tested the interfaces extracted from the 32 unbound proteins. Consistent with the previous results, 78% of the proteins (25/32) in the unbound state were predicted correctly as ssRNA or dsDNA binding proteins.

Figure 5.

Figure 5.

Open in a new tab

Euclidian distance between the vectors representing the local geometric features of the interfaces extracted from holo and apo structures. The x-axis represents the proteins in the unbound state and the y-axis represents the proteins in the bound state (the interface in the unbound state was defined based on the real NA-interface of the bound state). The color of each cell reflects the normalized Correlation Score between the vectors representing the local geometric features, from dark blue to red. As shown, the Correlation Score between the vectors of the bound and unbound states shown in the diagonal is always the lowest value in the row (colored dark blue).

The zinc finger NA binding motif as a case study

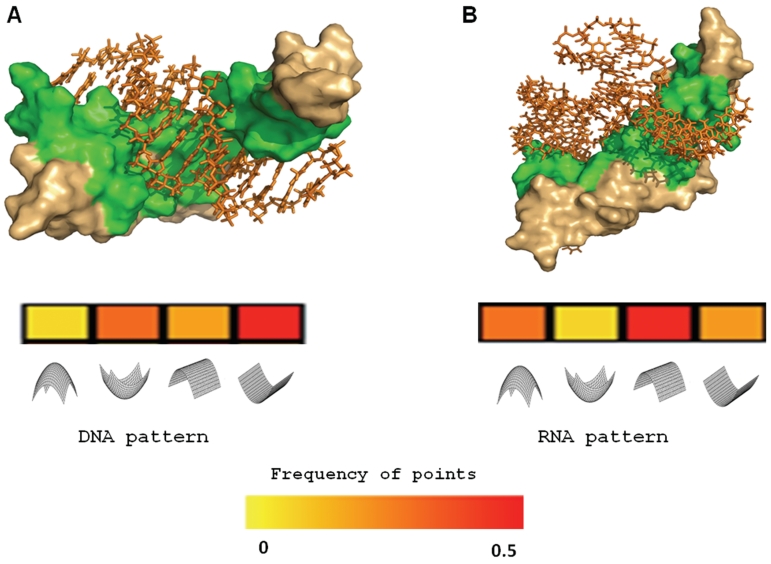
Though all experiments described hitherto were applied on non-redundant data sets (filtered at the level of sequence and family), it is still possible that the differences observed between the two groups relate to the different composition of domains that characterize DNA versus RNA binding proteins. To further test whether the differences in geometric features are associated with the binding domain, we chose the zinc finger domain as a test case. The zinc finger domain is amongst the most abundant DNA binding domains in eukaryotes, found in 3% of the human genome genes (53). However, there is increasing evidence that many RNA binding proteins possess zinc finger domains, including the well-characterized Cys2His2 (C2H2) zinc finger motif, first discovered in the Xenopus transcription factor IIIA (41). Our ‘NAbind-130′ data included 12 zinc finger domains, eight known as DNA binding (solved in complex with DNA) and four known as RNA binding (solved in complex with RNA). As shown in Supplementary Table S4, using our novel method, 6/8 DNA binding domains were successfully predicted as DNA binding while 3/4 RNA binding domains were correctly predicted as RNA binding. We further expanded the data set including a redundant set of 89 zinc-finger domains from PDB. Among the 81 chains of zinc-finger domains annotated as DNA binding, 58 were predicted as DNA binding (72%) and six of eight domains annotated as RNA binding were predicted correctly as RNA binding (75%) (see Supplementary Data S2). Quite incredibly, as demonstrated in Figure 6, fingers 1–3 of TFIIIA (PDB code: 1tf3) that bind DNA (promoter region of the 5S rRNA) (54) were predicted as DNA binding possessing a clear ‘DNA pattern’, while fingers 4–6 of the same protein (PDB code: 2hgh) that bind the 5S rRNA (56) were predicted correctly as RNA binding with a characteristic ‘RNA pattern’. Notably, very similar results were obtained when calculating the DG properties from the calculated binding interfaces and from the largest electrostatic patch extracted directly from the PDB files (data not shown). These results are highly encouraging, as all nine fingers of TFIIIA possess a classical C2H2 motif and can, by no means, be distinguished based on sequence or classical structural features.

Figure 6.

Figure 6.

Open in a new tab

The DG Model can uniquely distinguish DNA from RNA zinc fingers within the same proteins. (A) Fingers 1–3 of TFIIIA in complex with DNA (PDB code 1tf3). (B) Fingers 4–6 of TFIII in complex with RNA (PDB code 2hgh). The vectors representing the frequency of the surface points related to the local geometric shapes are shown as a heat map below each structure. High frequencies are colored red and low frequency colored yellow (color bar is shown). As demonstrated, the frequencies of the interface points from A denote a characteristic ‘DNA pattern’ while the frequencies of the interface points in B show a clear ‘RNA pattern’.

DISCUSSION

Protein-NA recognition is central to various biological processes. Studying the underlining principle that guides these interactions is thus critical for understanding living cells. Despite many similar properties, DNA and RNA possess distinctive entities that are recognized differentially by specialized DNA and RNA binding proteins, respectively. DNA (specifically dsDNA) and RNA (specifically ssRNA) binding interfaces are thus expected to differ in their geometrical features consistent with the different nature of DNA and RNA (31). While the sequence and structural properties of DNA and RNA binding interfaces were extensively studied during the last decade (17–27), to date distinguishing between the DNA and RNA binding interfaces is still an enigma. In this study, we present a novel approach to characterize and classify binding interfaces on proteins, specifically dsDNA and ssRNA interfaces. The method is based primarily on the distribution of geometric surface properties, specifically the Gaussian and mean curvatures (39,40). The uniqueness of the method, which differs from classical methods for classifying protein surfaces (56–59), is that it does not consider the overall concavity of the surface but the variety of local geometric shapes that comprise the entire interface, as commonly used in other applications using DG, such as face recognition (37). Our results show that dsDNA and ssRNA binding interfaces are best distinguished by the high distribution of the valley local shape, which likely accommodate a double-stranded helix whereas the ssRNA binding interfaces are characterized by different local shapes, mainly ridge and peak as well as the valley shape. These results are consistent with the well-established classical notion of DNA being a rigid double-helix molecule while the RNA, specifically ssRNA is much more flexible and dynamic.

A distinct differential geometry approach was used previously to dock small ligands to proteins (38). The advantage of the DG method introduced here over the previous method is that it does not rely on the surface complementarity between the ligand and the binding sites. More so, our method does not depend on either the specific dimension of the ligand (DNA/RNA) or the size of the protein domain and thus is suitable also for characterization of interfaces that bind larger ligands, such as DNA and RNA. In a recent study, Zhao et al. (25) have shown that they can distinguish RNA binding proteins from DNA-binding proteins with very high accuracy, using a structural-based homology approach. While our DG approach did not perform as well on the full-data set from Zhao et al. (25) which includes many dsRNA and ssDNA proteins, we obtained similar results to the results on our ‘NAbind-130′ data set when testing the subset of the data including only ssRNA and dsDNA. It is important to note that the method by Zhao et al. (25) strongly relies on the protein fold and does not attempt to either predict a new RNA or DNA binding domain which is not presented in the current databases or distinguish between the binding preference of domains which can bind both dsDNA and ssRNA, as in the case of the zinc-finger domain (53). During the years since the classical zinc finger motif was first discovered in 1985 by Sir Aaron Klug (41) it has become apparent that the different zinc-finger motifs, bind both DNA and RNA in a specific manner [reviewed in ref. (60)]. As we demonstrate for the well-characterized NA binding motif, C2H2 zinc finger, our method is completely independent of the protein fold and can successfully distinguish between DNA binding zinc-finger domains and those which bind RNA even within the same protein, as in the transcription factor TFIIIA (41). To our knowledge, in spite of the extensive study of these domains (54), our DG approach is the first successful computational method to predict the binding preferences of zinc-finger domains for DNA versus RNA.

In addition to the power of the DG features to distinguish between DNA and RNA binding interfaces (specifically dsDNA versus ssRNA) a great advantage of the method is that it is not highly sensitive to conformation changes of the protein upon binding and could thus be applicable for de-novo prediction of the binding properties of a given protein. We show that by combining differential geometry parameters with electrostatic features, used in our previous studies for NA binding classification (6,16), the method successfully predicts whether a proteins is a dsDNA or a ssRNA binding protein with a very high precision, regardless of the knowledge of the binding interface. Further investigation is required to test the applicability of the method to structural models of proteins for which their 3D structure is yet unavailable. Finally, we propose that the strength of our methods in recognizing fine-tuned differences on binding interfaces can make it applicable for many other molecular recognition problems, with potential implications for drug design.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Funding for open access charge: Supported by the Israeli Science Foundation, ISF (grant number 1297/09 granted to Y.M.G.).

Conflict of interest statement. None declared.

Supplementary Material

Supplementary Data
supp_39_17_7390__index.html (1.4KB, html)

ACKNOWLEDGEMENTS

The authors would like to thank Ron Pinter, who initialized the collaboration between the two groups.

REFERENCES

  • 1.Glisovic T, Bachorik JL, Yong J, Dreyfuss G. RNA-binding proteins and post-transcriptional gene regulation. FEBS Lett. 2008;582:1977–1986. doi: 10.1016/j.febslet.2008.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Kishore S, Luber S, Zavolan M. Deciphering the role of RNA-binding proteins in the post-transcriptional control of gene expression. Brief Funct. Genomics. 2010;9:391–404. doi: 10.1093/bfgp/elq028. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Shanahan HP, Garcia MA, Jones S, Thornton JM. Identifying DNA-binding proteins using structural motifs and the electrostatic potential. Nucleic Acids Res. 2004;32:4732–4741. doi: 10.1093/nar/gkh803. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Yu X, Cao J, Cai Y, Shi T, Li Y. Predicting rRNA-, RNA-, and DNA-binding proteins from primary structure with support vector machines. J. Theor. Biol. 2006;240:175–184. doi: 10.1016/j.jtbi.2005.09.018. [DOI] [PubMed] [Google Scholar]
  • 5.Shao X, Tian Y, Wu L, Wang Y, Jing L, Deng N. Predicting DNA- and RNA-binding proteins from sequences with kernel methods. J. Theor. Biol. 2009;258:289–293. doi: 10.1016/j.jtbi.2009.01.024. [DOI] [PubMed] [Google Scholar]
  • 6.Stawiski EW, Gregoret LM, Mandel-Gutfreund Y. Annotating nucleic acid-binding function based on protein structure. J. Mol. Biol. 2003;326:1065–1079. doi: 10.1016/s0022-2836(03)00031-7. [DOI] [PubMed] [Google Scholar]
  • 7.Gao M, Skolnick J. iAlign: a method for the structural comparison of protein-protein interfaces. Bioinformatics. 2010;26:2259–2265. doi: 10.1093/bioinformatics/btq404. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Gao M, Skolnick J. A threading-based method for the prediction of DNA-binding proteins with application to the human genome. PLoS Comput. Biol. 2009;5:e1000567. doi: 10.1371/journal.pcbi.1000567. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Nimrod G, Szilagyi A, Leslie C, Ben-Tal N. Identification of DNA-binding proteins using structural, electrostatic and evolutionary features. J. Mol. Biol. 2009;387:1040–1053. doi: 10.1016/j.jmb.2009.02.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Robertson TA, Varani G. An all-atom, distance-dependent scoring function for the prediction of protein-DNA interactions from structure. Proteins. 2007;66:359–374. doi: 10.1002/prot.21162. [DOI] [PubMed] [Google Scholar]
  • 11.Chen YC, Wu CY, Lim C. Predicting DNA-binding amino acid residues from electrostatic stabilization upon mutation to Asp/Glu and evolutionary conservation. Proteins. 2007;67:671–680. doi: 10.1002/prot.21366. [DOI] [PubMed] [Google Scholar]
  • 12.Ahmad S, Sarai A. Moment-based prediction of DNA-binding proteins. J. Mol. Biol. 2004;341:65–71. doi: 10.1016/j.jmb.2004.05.058. [DOI] [PubMed] [Google Scholar]
  • 13.Szilagyi A, Skolnick J. Efficient prediction of nucleic acid binding function from low-resolution protein structures. J. Mol. Biol. 2006;358:922–933. doi: 10.1016/j.jmb.2006.02.053. [DOI] [PubMed] [Google Scholar]
  • 14.Bhardwaj N, Langlois R, Zhao G, Lu H. Structure based prediction of binding residues on DNA-binding proteins. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2005;3:2611–2614. doi: 10.1109/IEMBS.2005.1617004. [DOI] [PubMed] [Google Scholar]
  • 15.Jones S, Shanahan HP, Berman HM, Thornton JM. Using electrostatic potentials to predict DNA-binding sites on DNA-binding proteins. Nucleic Acids Res. 2003;31:7189–7198. doi: 10.1093/nar/gkg922. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Shazman S, Mandel-Gutfreund Y. Classifying RNA-binding proteins based on electrostatic properties. PLoS Comput. Biol. 2008;4:e1000146. doi: 10.1371/journal.pcbi.1000146. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Perez-Cano L, Solernou A, Pons C, Fernandez-Recio J. Structural prediction of protein-RNA interaction by computational docking with propensity-based statistical potentials. Pac. Symp. Biocomput. 2009:293–301. doi: 10.1142/9789814295291_0031. [DOI] [PubMed] [Google Scholar]
  • 18.Shulman-Peleg A, Shatsky M, Nussinov R, Wolfson HJ. Prediction of interacting single-stranded RNA bases by protein-binding patterns. J. Mol. Biol. 2008;379:299–316. doi: 10.1016/j.jmb.2008.03.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Maetschke SR, Yuan Z. Exploiting structural and topological information to improve prediction of RNA-protein binding sites. BMC Bioinformatics. 2009;10:341. doi: 10.1186/1471-2105-10-341. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Liu ZP, Wu LY, Wang Y, Zhang XS, Chen L. Prediction of protein-RNA binding sites by a random forest method with combined features. Bioinformatics. 2010;26:1616–1622. doi: 10.1093/bioinformatics/btq253. [DOI] [PubMed] [Google Scholar]
  • 21.Towfic F, Caragea C, Gemperline DC, Dobbs D, Honavar V. Struct-NB: predicting protein-RNA binding sites using structural features. Int. J. Data Min. Bioinform. 2010;4:21–43. doi: 10.1504/ijdmb.2010.030965. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Jeong E, Chung IF, Miyano S. A neural network method for identification of RNA-interacting residues in protein. Genome Inform. 2004;15:105–116. [PubMed] [Google Scholar]
  • 23.Wang L, Brown SJ. Prediction of RNA-binding residues in protein sequences using support vector machines. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2006;1:5830–5833. doi: 10.1109/IEMBS.2006.260025. [DOI] [PubMed] [Google Scholar]
  • 24.Terribilini M, Lee JH, Yan C, Jernigan RL, Honavar V, Dobbs D. Prediction of RNA binding sites in proteins from amino acid sequence. RNA. 2006;12:1450–1462. doi: 10.1261/rna.2197306. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Zhao H, Yang Y, Zhou Y. Structure-based prediction of RNA-binding domains and RNA-binding sites and application to structural genomics targets. Nucleic Acids Res. 2010;39:3017–3025. doi: 10.1093/nar/gkq1266. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Spriggs RV, Jones S. RNA-binding residues in sequence space: conservation and interaction patterns. Comput. Biol. Chem. 2009;33:397–403. doi: 10.1016/j.compbiolchem.2009.07.012. [DOI] [PubMed] [Google Scholar]
  • 27.Perez-Cano L, Fernandez-Recio J. Optimal protein-RNA area, OPRA: a propensity-based method to identify RNA-binding sites on proteins. Proteins. 2010;78:25–35. doi: 10.1002/prot.22527. [DOI] [PubMed] [Google Scholar]
  • 28.Wang L, Brown SJ. BindN: a web-based tool for efficient prediction of DNA and RNA binding sites in amino acid sequences. Nucleic Acids Res. 2006;34:W243–W248. doi: 10.1093/nar/gkl298. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Fujishima K, Komasa M, Kitamura S, Suzuki H, Tomita M, Kanai A. Proteome-wide prediction of novel DNA/RNA-binding proteins using amino acid composition and periodicity in the hyperthermophilic archaeon Pyrococcus furiosus. DNA Res. 2007;14:91–102. doi: 10.1093/dnares/dsm011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Chen YC, Lim C. Common physical basis of macromolecule-binding sites in proteins. Nucleic Acids Res. 2008;36:7078–7087. doi: 10.1093/nar/gkn868. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Draper DE. Themes in RNA-protein recognition. J. Mol. Biol. 1999;293:255–270. doi: 10.1006/jmbi.1999.2991. [DOI] [PubMed] [Google Scholar]
  • 32.Jones S, Daley DT, Luscombe NM, Berman HM, Thornton JM. Protein-RNA interactions: a structural analysis. Nucleic Acids Res. 2001;29:943–954. doi: 10.1093/nar/29.4.943. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Ellis JJ, Broom M, Jones S. Protein-RNA interactions: structural analysis and functional classes. Proteins. 2007;66:903–911. doi: 10.1002/prot.21211. [DOI] [PubMed] [Google Scholar]
  • 34.Bahadur RP, Zacharias M, Janin J. Dissecting protein-RNA recognition sites. Nucleic Acids Res. 2008;36:2705–2716. doi: 10.1093/nar/gkn102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Sonavane S, Chakrabarti P. Cavities in protein-DNA and protein-RNA interfaces. Nucleic Acids Res. 2009;37:4613–4620. doi: 10.1093/nar/gkp488. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Lejeune D, Delsaux N, Charloteaux B, Thomas A, Brasseur R. Protein-nucleic acid recognition: statistical analysis of atomic interactions and influence of DNA structure. Proteins. 2005;61:258–271. doi: 10.1002/prot.20607. [DOI] [PubMed] [Google Scholar]
  • 37.Soldea O, Elber G, Rivlin E. Global segmentation and curvature analysis of volumetric data sets using trivariate B-spline functions. IEEE Trans. Pattern Anal. Mach. Intell. 2006;28:265–278. doi: 10.1109/TPAMI.2006.36. [DOI] [PubMed] [Google Scholar]
  • 38.Goldman BB, Wipke WT. QSD quadratic shape descriptors. 2. Molecular docking using quadratic shape descriptors (QSDock) Proteins. 2000;38:79–94. [PubMed] [Google Scholar]
  • 39.Elaine Cohen RFR, Gershon E. Geometric Modeling with Splines - An Introduction. Natick, Massachusetts: A. K. Peters; 2001. [Google Scholar]
  • 40.Con-Vossen S, Hilbert D. American Mathematical Soc. 1952. Geometry and the Imagination. [Google Scholar]
  • 41.Miller J, McLachlan AD, Klug A. Repetitive zinc-binding domains in the protein transcription factor IIIA from Xenopus oocytes. EMBO J. 1985;4:1609–1614. doi: 10.1002/j.1460-2075.1985.tb03825.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Ahmad S, Sarai A. Analysis of electric moments of RNA-binding proteins: implications for mechanism and prediction. BMC Struct. Biol. 2011;11:8. doi: 10.1186/1472-6807-11-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Cazals F, Proust F, Bahadur RP, Janin J. Revisiting the Voronoi description of protein-protein interfaces. Protein Sci. 2006;15:2082–2092. doi: 10.1110/ps.062245906. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Shazman S, Celniker G, Haber O, Glaser F, Mandel-Gutfreund Y. Patch Finder Plus (PFplus): a web server for extracting and displaying positive electrostatic patches on protein surfaces. Nucleic Acids Res. 2007;35:W526–W530. doi: 10.1093/nar/gkm401. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Prlic A, Bliven S, Rose PW, Bluhm WF, Bizon C, Godzik A, Bourne PE. Pre-calculated protein structure alignments at the RCSB PDB website. Bioinformatics. 2010;26:2983–2985. doi: 10.1093/bioinformatics/btq572. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 46.Richards FM. The interpretation of protein structures: total volume, group volume distributions and packing density. J. Mol. Biol. 1974;82:1–14. doi: 10.1016/0022-2836(74)90570-1. [DOI] [PubMed] [Google Scholar]
  • 47.Dey TK. Tight cocone: a watertight surface reconstructor. J. Comp. Inf. Sci. Eng. 2003;3:302–307. [Google Scholar]
  • 48.Saeed AI, Bhagabati NK, Braisted JC, Liang W, Sharov V, Howe EA, Li J, Thiagarajan M, White JA, Quackenbush J. TM4 microarray software suite. Methods Enzymol. 2006;411:134–193. doi: 10.1016/S0076-6879(06)11009-5. [DOI] [PubMed] [Google Scholar]
  • 49.Ellis JJ, Jones S. Evaluating conformational changes in protein structures binding RNA. Proteins. 2008;70:1518–1526. doi: 10.1002/prot.21647. [DOI] [PubMed] [Google Scholar]
  • 50.Gunther S, Rother K, Frommel C. Molecular flexibility in protein-DNA interactions. Biosystems. 2006;85:126–136. doi: 10.1016/j.biosystems.2005.12.007. [DOI] [PubMed] [Google Scholar]
  • 51.Bjoras M, Seeberg E, Luna L, Pearl LH, Barrett TE. Reciprocal “flipping” underlies substrate recognition and catalytic activation by the human 8-oxo-guanine DNA glycosylase. J. Mol. Biol. 2002;317:171–177. doi: 10.1006/jmbi.2002.5400. [DOI] [PubMed] [Google Scholar]
  • 52.Daniels DS, Mol CD, Arvai AS, Kanugula S, Pegg AE, Tainer JA. Active and alkylated human AGT structures: a novel zinc site, inhibitor and extrahelical base binding. EMBO J. 2000;19:1719–1730. doi: 10.1093/emboj/19.7.1719. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 53.Klug A. The discovery of zinc fingers and their applications in gene regulation and genome manipulation. Annu. Rev. Biochem. 2010;79:213–231. doi: 10.1146/annurev-biochem-010909-095056. [DOI] [PubMed] [Google Scholar]
  • 54.Wuttke DS, Foster MP, Case DA, Gottesfeld JM, Wright PE. Solution structure of the first three zinc fingers of TFIIIA bound to the cognate DNA sequence: determinants of affinity and sequence specificity. J. Mol. Biol. 1997;273:183–206. doi: 10.1006/jmbi.1997.1291. [DOI] [PubMed] [Google Scholar]
  • 55.Lu D, Searles MA, Klug A. Crystal structure of a zinc-finger-RNA complex reveals two modes of molecular recognition. Nature. 2003;426:96–100. doi: 10.1038/nature02088. [DOI] [PubMed] [Google Scholar]
  • 56.Connolly ML. Shape complementarity at the hemoglobin alpha 1 beta 1 subunit interface. Biopolymers. 1986;25:1229–1247. doi: 10.1002/bip.360250705. [DOI] [PubMed] [Google Scholar]
  • 57.Norel R, Lin SL, Wolfson HJ, Nussinov R. Shape complementarity at protein-protein interfaces. Biopolymers. 1994;34:933–940. doi: 10.1002/bip.360340711. [DOI] [PubMed] [Google Scholar]
  • 58.Jiang F, Kim SH. “Soft docking”: matching of molecular surface cubes. J. Mol. Biol. 1991;219:79–102. doi: 10.1016/0022-2836(91)90859-5. [DOI] [PubMed] [Google Scholar]
  • 59.Bacon DJ, Moult J. Docking by least-squares fitting of molecular surface patterns. J. Mol. Biol. 1992;225:849–858. doi: 10.1016/0022-2836(92)90405-9. [DOI] [PubMed] [Google Scholar]
  • 60.Font J, Mackay JP. Beyond DNA: zinc finger domains as RNA-binding modules. Methods Mol. Biol. 2010;649:479–491. doi: 10.1007/978-1-60761-753-2_29. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_39_17_7390__index.html (1.4KB, html)
supp_gkr395_Supplementary_datafileS1.pdf (240.7KB, pdf)
supp_gkr395_Supplementary_datafileS2.pdf (206.8KB, pdf)
supp_gkr395_supp_figures_tables.pdf (411.6KB, pdf)
supp_gkr395_InterFaceDG.zip (697.4KB, zip)

Articles from Nucleic Acids Research are provided here courtesy of Oxford University Press

RESOURCES