Compression and self-entanglement of single DNA molecules under uniform electric field

Abstract

We experimentally study the effects of a uniform electric field on the conformation of single DNA molecules. We demonstrate that a moderate electric field (∼200 V/cm) strongly compresses isolated DNA polymer coils into isotropic globules. Insight into the nature of these compressed states is gained by following the expansion of the molecules back to equilibrium after halting the electric field. We observe two distinct types of expansion modes: a continuous molecular expansion analogous to a compressed spring expanding, and a much slower expansion characterized by two long-lived metastable states. Fluorescence microscopy and stretching experiments reveal that the metastable states are the result of intramolecular self-entanglements induced by the electric field. These results have broad importance in DNA separations and single molecule genomics, polymer rheology, and DNA-based nanofabrication.

The use of electric fields to transport DNA has become an essential technique for a variety of research areas including molecular biology, gene therapy, and fundamental studies of polyelectrolytes (1). In most applications, nonlinear electrokinetics (2) due to the interplay of negatively charged DNA and the electric field are neglected. However, Viovy and coworkers (3, 4) demonstrated the ability of an electric field on order of 100 V/cm to induce strong intermolecular DNA aggregation in a standard electrophoresis buffer in the absence of a sieving matrix. Follow-up studies (5, 6) have attributed the aggregation to an electrohydrodynamic instability triggered by a coupling of macroion (DNA) concentration fluctuations and electric field induced flows beyond the Debye length scale in a moderately concentrated DNA solution (around the DNA overlap concentration c^∗). These results shed light onto why it is so difficult to separate large DNA molecules using capillary electrophoresis.

Over the last decade there has been a shift from techniques measuring ensemble-averaged molecular properties (e.g., the aforementioned capillary electrophoresis experiments), to techniques that manipulate single, dilute DNA molecules in micro/nanofluidic devices or nanopores (7–9). Electric fields are a convenient mode to transport DNA as they scale favorably with device dimensions. The long standing belief in such dilute, single molecule experiments is that uniform DC (direct current) electric fields (up to a few hundred V/cm in standard electrophoresis buffers) do not greatly perturb the conformation of large DNA unless some sort of sieving matrix is used (e.g., gel or microfabricated post array) (1). Numerous fluorescence microscopy experiments confirm this belief to be true [see (10) for a recent review], but are typically limited to field strengths of a few tens of V/cm to avoid image blur. Much larger electric fields give rise to some chain orientation and possibly some slight chain stretching (11), though the stretching is inconclusive because it is not directly measured but must be inferred using models which are not yet agreed upon in the literature. Furthermore, the prior bulk orientation studies of large DNA (40–170 kilobase pairs) (11, 12) were carried out under conditions where chain-chain aggregation was later shown to occur (3). Recent simulations (13) suggest that electric fields beyond those yet experimentally realized (≫1,000 V/cm) could induce both orientation and elongation of the DNA. In striking contrast, here we report that a homogeneous electric field can induce strong isotropic compression, and spontaneous self-entangling and knotting within single DNA molecules in a dilute solution. The compressed molecules exhibit long-lived intermediate conformations that are stabilized by the entanglements during expansion toward equilibrium. This metastable nature of collapsed, strongly entangled polymers has long been suggested by both theories and simulations (14–19), but has been elusive to experimental observation using temperature jump experiments and synthetic polymers (20).

The formation of intramolecular entanglements and knots under electric field is of its own interest. In physics, spontaneous knotting has only been observed for mesoscale vibrated ball-chains (21) or strings (22). In our work, the size of the DNA is on order of microns. DNA knots are also biologically important as they occur naturally and frequently in vivo (23) and have been implicated to hold an active role in gene regulation (24). Previously, knotting of DNA has been experimentally induced using optical tweezers (25), and collisions with local defects inside a nanochannel (26) or gel (27). Here, we provide a much simpler method to generate knots with nearly 100% efficiency and a significantly larger degree of self-entanglement. More importantly, we provide unique insight into how self-entangled DNA relax back to equilibrium via metastable intermediate states.

Results and Discussion

Isotropic Compression of DNA Under Uniform Electric Field.

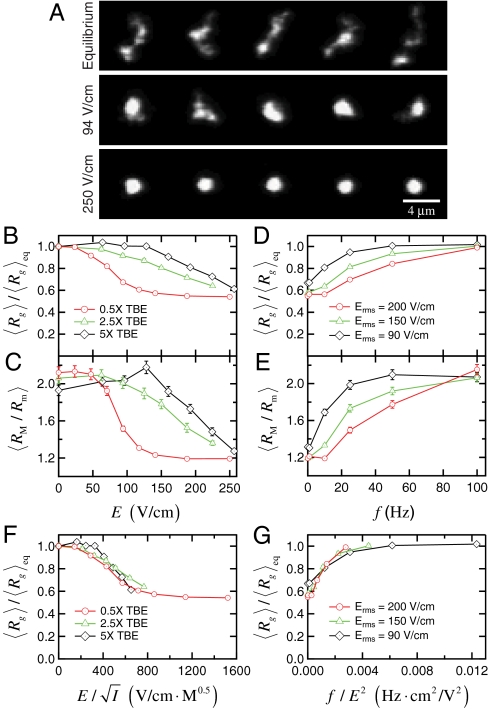
We experimentally examine the conformation of dilute (concentration ≪ c^∗, see SI Text for details) fluorescently labeled DNA molecules under uniform electric fields in 2 μm tall by 200 μm wide straight channels. Fig. 1A shows fluorescent images of individual T4 DNA molecules (165.6 kbp) at equilibrium (i.e., no electric field) and under a uniform DC electric field. Surprisingly, the electric field induces a strong isotropic compression of the DNA: while the equilibrium coil remains relatively extended and highly anisotropic, the T4 DNA becomes significantly more compact under an electric field of 94 V/cm, and is further compressed into a spherical globule by a stronger electric field of 250 V/cm.

Fig. 1.

Electric field induced isotropic compression of T4 DNA. (A) Images of DNA in 0.5 × TBE buffer at equilibrium (top row) and under a uniform DC electric field of E = 94 V/cm (middle row) and E = 250 V/cm (bottom row). For the case of equilibrium, the conformation of one molecule is shown for every 4 s during an observation of 16 s. For each of the two nonzero electric fields, the conformations of five representative DNA are shown. (B) and (C) Conformation of DNA under uniform DC electric fields in three different TBE buffers: (B) ensemble average radius of gyration R_g of DNA (normalized by the equilibrium average 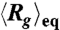) and (C) the corresponding average ratio between the major and minor axes 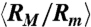as functions of the field strength E. (D) and (E) Conformation of DNA under AC square-wave electric fields in 0.5 × TBE: (D) ensemble average radius of gyration R_g (normalized by the equilibrium average 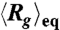) and (E) the corresponding average ratio between the major and minor axes 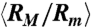as functions of frequency (f) under three different root-mean-square values of field strength. (F) Data of 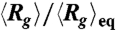shown in (B) vs. 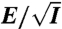. (G) Data of 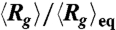shown in (D) vs. f/E².

Fig. 1B displays the ensemble average radius of gyration 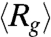of T4 DNA normalized by its equilibrium average (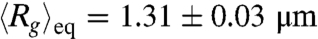) vs. the strength of the DC electric field. Results for three buffers with different ionic strengths (0.5 × TBE, 2.5 × TBE, and 5 × TBE, corresponding ionic strength I ≈ 27 mM, 86 mM, and 155 mM) are shown. A continuous decrease in R_g with increasing field strength is observed. Meanwhile, the DNA molecules become more isotropic as the average ratio between the radii of the major and minor axes 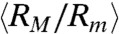of the radius of gyration tensor, a measure of the degree of anisotropy of the DNA (28), decreases simultaneously with 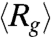(Fig. 1C). Increasing the buffer ionic strength clearly suppresses the compression as the decrease in R_g and R_M/R_m occurs at higher field strength and also becomes more gradual. The compression of T4 DNA induced by DC electric field is also observed in other buffers (see SI Text).

We next subject the T4 DNA to AC (alternating current) square-wave electric field over various frequencies and with three different values of root-mean-square strength: E_rms = 90 V/cm, 150 V/cm, and 200 V/cm. Under all three values of E_rms, the DNA compression is suppressed by increasing the frequency of the AC electric field: both the average radius of gyration (Fig. 1D) and the anisotropic ratio (Fig. 1E) of the DNA increase toward their equilibrium values with increasing frequency. The applied electric field no longer affects the DNA conformation once the frequency exceeds 100 Hz.

As mentioned in the introduction, prior studies might lead one to anticipate minimal chain stretching in our experiments, which is in stark contrast to our observations. However, we realize the strong similarity between the compression observed here for single DNA and the electric field induced intermolecular DNA aggregation in more concentrated (around c^∗) solutions reported in refs. 3, 4. Both phenomena occur under similar field strength and diminish with increasing ionic strength, increasing frequency of the electric field, as well as decreasing DNA molecular weight (see SI Text for the molecular weight dependence). Theories developed by Isambert, et al. (5, 6) attributed the instability to macroion concentration fluctuations, with the DNA coils being the macroion. An electrohydrodynamic flow is setup which drives the macroion rich regions to further concentrate and coalesce. Here we see that due to the fact that individual DNA conformations are inherently anisotropic (29), there will exist similar concentration variations within a single DNA coil.

We further test whether the observed compression is consistent with Isambert’s theory (5, 6) by considering a scaling analysis to collapse the data. The theory predicts that in a DC field the induced hydrodynamic flow, which drives the compression process, scales with ionic strength as v_h ∼ E²/I. Replotting the data in Fig. 1B vs. E/I^0.5 results in data collapse onto a universal curve (Fig. 1F). In AC fields, the theory predicts that v_h ∼ (E²/f)². The AC data also nicely collapse onto a universal curve (Fig. 1G) when rescaling f by E². Given all of these trends in the data, we postulate that the mechanism driving the compaction of single DNA molecules is a nonlinear coupling of the spontaneous macroion segment density fluctuations and a resulting electrohydrodynamic flow that further coarsens the segment rich regions.

Expansion of Compressed T4 DNA.

Because our optical system does not provide the resolution to directly observe the internal conformation of the compressed DNA coils, we examine the expansion dynamics of these DNA back to equilibrium to gain insight into the nature of the compressed state.

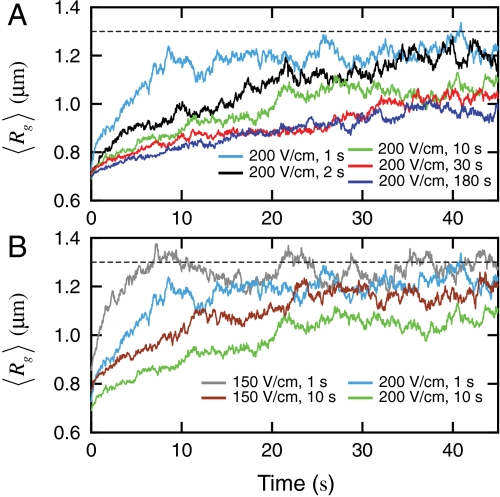
We use an AC square-wave electric field at 10 Hz to compress T4 DNA and then follow the expansion of these initially compressed molecules after switching off the field (Movie S1). Fig. 2 shows time evolution of the ensemble average radius of gyration of DNA after the electric field is switched off. The five 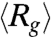traces shown in Fig. 2A correspond to DNA ensembles compressed using an electric field of E_rms = 200 V/cm for five different durations. We observe two striking features of the expansion process. First, none of the five traces appear to have reached the equilibrium average radius of gyration (indicated by the dashed line) after 40 s, a time scale significantly larger than the longest relaxation time of T4 DNA [τ ≈ 1.9 s (30)]. Second, the average expansion slows down as the duration (T_E) of the electric field is increased from 1 s to 30 s. Further increasing T_E from 30 s to 180 s does not result in any evident change in the first 40 s of the 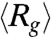data. We note that all five traces shown in Fig. 2A start with similar initial values (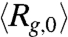, see Table S1), indicating the observed T_E-dependence of the expansion does not result from different extent of DNA compression (that we can resolve).

Fig. 2.

Average expansion of initially compressed T4 DNA in 0.5 × TBE. (A) Traces of the ensemble average radius of gyration 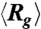of DNA compressed using a 10 Hz square-wave electric field of E_rms = 200 V/cm for five different durations T_E = 1 s, 2 s, 10 s, 30 s, and 180 s. (B) Traces of 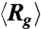of DNA compressed by a 10 Hz square-wave electric field with two different field strengths and durations. The dashed lines indicate the equilibrium average radius of gyration .

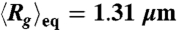Fig. 2B displays traces of 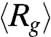of DNA ensembles compressed using two different electric field strengths each for two different durations. It is clearly seen that with the same duration, molecules compressed under the weaker electric field (150 V/cm) show a much faster average expansion. For instance, 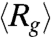of DNA compressed using 150 V/cm for 1 s reaches its equilibrium value within 10 s, while that of DNA compressed using 200 V/cm for 1 s is still below equilibrium after 40 s. We do notice that the initial average sizes of DNA compressed using E_rms = 150 V/cm are about 18% and 12% larger than those of DNA compressed using E_rms = 200 V/cm for 1 s and 10 s, respectively (Table S1). Nonetheless, it is unlikely that such slight differences in the degrees of compression can solely account for the dramatic changes in the expansion process.

Two Types of Expansion Pathways.

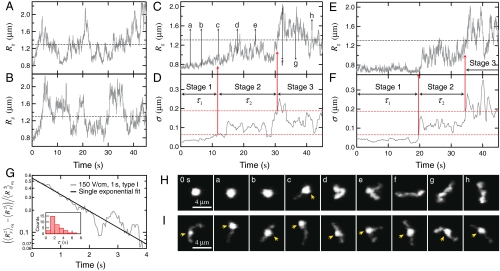
To determine the origin of the slow ensemble average expansion, we examine the dynamics of individual molecules. We discover that the expansion of all the compressed T4 DNA molecules can be categorized into two groups with distinct dynamics which we denote here as type I and type II. Fig. 3 A and B show the time evolution of R_g for two molecules that exhibit representative type I expansion. The key characteristics of this expansion pattern are: (i) the radius of gyration grows smoothly and continuously from the compressed state, and (ii) it returns to the equilibrium average (the black dashed lines in Fig. 3 A and B) usually within 8 s, a time scale corresponding to about four times the longest relaxation time of T4 DNA.

Fig. 3.

Expansion of individual T4 DNA molecules compressed by AC square-wave electric fields in 0.5 × TBE. (A) and (B) Two representative individual traces of R_g vs. time for type I expansion. Both molecules are compressed with E_rms = 150 V/cm, 10 Hz, T_E = 1 s. (C) and (E) Two representative individual traces of R_g for type II expansion. The two molecules are compressed with (C) E_rms = 200 V/cm, 10 Hz, T_E = 30 s, and (E) E_rms = 200 V/cm, 10 Hz, T_E = 10 s. The dashed lines in (A), (B), (C), and (E) indicate the equilibrium average radius of gyration. (D) and (F) The local standard deviation σ of R_g vs. time calculated using a window of 2 s width and the three expansion stages for the R_g traces shown in (C) and (E), respectively. The two red dashed lines in (D) and (F) indicate the two thresholds (σ_t1 = 0.07 μm and σ_t2 = 0.19 μm) used to determine the onset of stage 2 and stage 3. (G) The normalized mean square radius of gyration vs. time for DNA that are compressed with E_rms = 150 V/cm for 1 s and exhibit type I expansion. The black solid line is a single exponential fit to the data which gives a time constant of 1.9 s. Inset is the distribution of the time constant τ obtained by fitting individual trances of 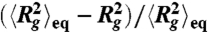to a single exponential. (H) Snap shots of the conformation of the T4 DNA during expansion corresponding to each time points indicated in (C). (I) Representative images of DNA during the second stage of expansion. Each image is a different molecule. The yellow arrows in (H) and (I) point to the compact cores of the DNA.

Fig. 3 D and E show R_g vs. time for two molecules that exhibit representative type II expansion (Movie S2). This expansion pattern not only is much slower but also features a very different kinetic pathway: instead of a continuous expansion, it can be characterized as a three-stage process where individual stages are distinguished by the DNA conformation and magnitude of conformational fluctuations. In the first stage, the molecule stays arrested in the highly compact globular state (Fig. 3H, image 0 s, a, and b). Both the overall increase in size and the conformational fluctuations are extremely limited within this entire stage. In the second stage (Fig. 3H, image c, d, and e), the molecule becomes partially extended and exhibits significantly larger fluctuations. This stage is usually initiated by a nucleation event in which a portion of the DNA (most frequently the end) protrudes out of the globule (Fig. 3H, image c). However, the molecule does not show any further expansion but fluctuates around a certain size smaller than that of the equilibrium coil. At this second arrested state, a majority of the molecules still bear a compact core which is recognized as a bright spot in the images (Fig. 3I). Finally, the compact core of the DNA vanishes as it enters the last stage. The molecule then quickly returns to equilibrium (Fig. 3H, image f, g, and h) and starts to fluctuate in size more vigorously.

The distinct magnitudes of shape fluctuations in the three stages of type II expansion allow us to develop an empirical criterion to determine the durations of the first two stages (τ₁ and τ₂, respectively) in a consistent manner. For each time point, we calculate the standard deviation σ of the local 2 s of R_g data (with a sliding window 1 s ahead to 1 s after). Fig. 3 D and F display the results of σ vs. time for the two R_g traces shown in Fig. 3 C and E, respectively. We identify in both plots three consecutive regions with different magnitudes of σ corresponding to the three expansion stages. The onsets of stage 2 and 3 are determined with two threshold values of σ (the red dashed lines in Fig. 3 D and F) both of which are roughly twice the time average of σ in the previous stage.

We postulate that the physical reason for the two distinct types of expansion dynamics lies in the different initial intramolecular configurations of the compressed DNA. Specifically, the unique three-staged type II expansion results from spontaneously formed self-entanglements of the DNA under the electric field. Several theoretical and simulation studies (15–17, 19) have suggested that intrachain entanglements can topologically constrain the globule from expanding and lead to metastable states, in qualitative agreement with our data. In contrast, the more regular type I expansion corresponds to coils that are free of entanglements or weakly entangled. We use a simple rule to distinguish the two types of expansion: the expansion of a DNA molecule is classified as type I if its radius of gyration reaches the equilibrium average within 8 s. We find the resulting proportion of entangled DNA increases when the ensemble is subject to a longer duration or stronger strength of electric field (Table S1), which explains the observed dependence of the ensemble average expansion on these two factors (Fig. 2).

Expansion of Unentangled DNA.

The expansion of compressed DNA without any self-entanglements has been described using a free energy argument in several studies (17, 31). In brief, for strongly compressed DNA, the initial expansion is driven by the repulsive interactions between segments and the radius of gyration initially increases with time as 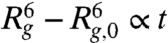where R_g,0 is the initial radius of the compressed molecule. Once the chain has expanded closer to equilibrium, the dynamics are governed by the longest relaxation time of the DNA (32) and the radius of gyration approaches its equilibrium average value as .

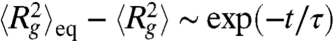We examine the expansion of DNA molecules that are compressed using an electric field of E_rms = 150 V/cm for 1 s and exhibit type I expansion (91% of the ensemble, see Table S1). We do not observe a linear increase of 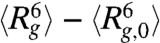with time, suggesting this regime only exits within a short time scale beyond the resolution of our experiments (1/30 s). Instead, the quantity 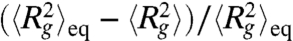is well described by a single exponential decay (Fig. 3G) with a time constant equivalent to the longest relaxation time of T4 DNA in 0.5 × TBE (τ = 1.9 s), consistent with the expected behavior of unentangled DNA near equilibrium. The initial average radius of gyration of these molecules (∼0.86 μm) is more than 30% smaller than that of the equilibrium coil, indicating the expansion becomes governed by the longest relaxation time when the DNA molecules are still significantly compact. This result is analogous to the fact that DNA initially stretched to 30% of complete extension will relax back to a coil in a manner governed by only the slowest relaxation mode.

Expansion of Self-Entangled DNA.

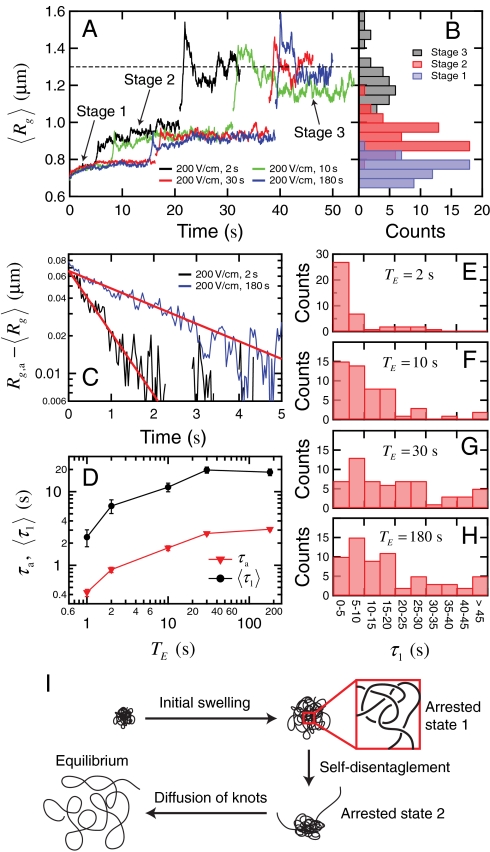
We next probe the ensemble average expansion of self-entangled DNA by calculating the time evolution of the mean radius of gyration in each individual stage during type II expansion (see SI Text). Fig. 4A shows results of 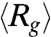for four DNA ensembles compressed under the same electric field strength but for different durations. The three stages of expansion are characterized by distinct values of 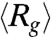, in accord with the very different DNA conformation in each stage. Also, the distributions of the time average radii of gyration of individual molecules in different stages show very little overlap (Fig. 4B), further supporting the three-step nature of the type II expansion process.

Fig. 4.

(A) Ensemble average radius of gyration vs. time in the three stages of type II expansion for four DNA ensembles all compressed under E_rms = 200 V/cm but for different durations. The 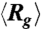traces for the three stages are simply plotted in a consecutive manner for clear illustration. The black dashed line indicates the equilibrium average radius of gyration. (B) Distributions of the time average radii of gyration of individual DNA molecules in each stage of expansion. (C) The quantity 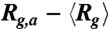as well as the corresponding fitted single exponential function (B exp(-t/τ_a), red lines) with time in stage 1 of the expansion for the DNA ensembles compressed for 2 s and 180 s. (D) The fitted time constant τ_a of the initial swelling process and the ensemble average duration 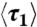of the first stage as functions of T_E. If not visible, the error bar (standard error) is smaller than the symbol size. (E)–(H) Distributions of the duration τ₁ of stage 1 for the four DNA ensembles. (I) Schematic of the expansion pathway of an entangled globule.

In stage 1, we observe a clear saturation of the average DNA size after an initial small degree of swelling for all four DNA ensembles. This provides clear experimental evidence of an “arrested state” during the expansion of entangled polymer globules, which has been suggested by both theories (15, 17) and simulation (16). We use the notion of “entanglement blobs” first introduced in ref. 16 to characterize this arrested state. We assume that a compressed DNA globule contains one self-entanglement every N_e Kuhn segments on average. The initial configuration of the globule is viewed as a network of identical blobs each consisting of n strands of subchain between adjacent entanglements. The blobs are pinned due to the entanglements while inside a blob each subchain behaves like a self-avoiding coil, giving the initial size of the blob 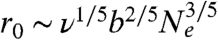where b is the Kuhn length and ν the excluded volume of each Kuhn segment. When the globule is allowed to expand, it first seeks the optimal state compatible with all existing topological constraints, or in other words, each blob swells toward its optimal size r_a under constant values of n and N_e. The free energy of a single blob is given by

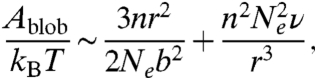[1]

where r is the blob size. Minimizing A_blob yields the optimal blob size: 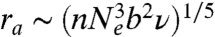. Assuming uniform segment density within the globule, the globule size R_g can be related to the blob size r as R_g ∼ (N/nN_e)^1/3r where N is the total number of Kuhn segments. The DNA size in the arrested state is then given by .

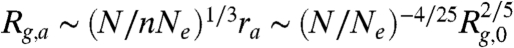During the swelling toward the arrested state, the total driving force, F_exp = -(N/nN_e)(dA_blob/dR_g), is balanced by the viscous drag which is given by F_d ∼ (N/nN_e)(rdR_g/dt) considering no hydrodynamic interactions between blobs. We then arrive at the equation governing the evolution of R_g:

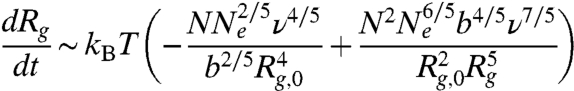[2]

At the very initial stage of the swelling, the repulsive interactions between chain segments primarily account for the driving force and the radius of the globule increases with time as 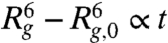. Once the globule becomes close to the arrested state, [2] can be linearized and the resulting radius of gyration follows R_g,a - R_g ∼ exp(-t/τ_a) with the time constant given by

[3]

We now relate the above scalings derived from the blob description of the globule to experimental data. We do not identify an evident initial linear increase of 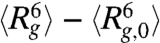with time for any of the DNA ensembles. Instead, all 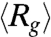traces in stage 1 can be well fitted to the function 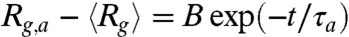(e.g., the two traces shown in Fig. 4C), where R_g,a, B, and τ_a are fitting parameters. The fitted time constant τ_a increases with the duration T_E of the electric field when T_E ≤ 30 s and starts to saturate at T_E > 30 s (Fig. 4D). [3] predicts τ_a to increase with both the total number of entanglements (N/N_e) and the initial DNA size (R_g,0). Because R_g,0 in general would never increase with T_E, the observed T_E-dependence of τ_a is a strong indication of the continuous formation of self-entanglements under electric field until the globule’s internal structure reaches steady state. Following this argument, we expect the DNA size in the arrested state to decrease with increasing T_E. However, the fitted R_g,a remains relatively constant (≈0.77 μm) regardless of T_E. We attribute this partly to the limited optical resolution (28).

To escape from the arrested state in stage 1, the topological constraints inside the globule must be removed through self-disentangling of chain segments. The kinetic pathway of this process has been discussed in ref. 19 and it was suggested that this is a gradual process. In striking contrast, we find it often activated by specific events of chain ends unthreading from the globule, analogous to a nucleation process. The similarity between the unthreading events and nucleation is further realized by looking at the distribution of the duration τ₁ of stage 1 (Fig. 4 E and F). The distribution of expansion times is very broad and flat comparing to the unentangled case in the inset of Fig. 3G (see SI Text for further comparison of statistics), indicating that the unthreading events of entangled DNA molecules occur rather randomly.

Fig. 4A also reveals the existence of a second arrested state after the globule has expanded into stage 2. We believe that this long-lived state is stabilized by the intramolecular knots that are present within the compact cores (Fig. 3I) of the partially extended DNA molecules. Both theory (18) and experiments (25, 26) have previously demonstrated that once a tight knot is formed, it will adopt a metastable configuration and can only be released through diffusion along the DNA contour (i.e., self-reptation of DNA through the knot) toward the ends of the chain. During the slow diffusion process, any further expansion of the DNA molecule is restricted.

We propose a qualitative pathway (Fig. 4I) for the expansion of entangled DNA based on our experimental results. The compressed molecule first expands in a way similar to the swelling of cross-linked gels (33) until it reaches the first arrested state where the DNA conformation is frozen by self-entanglements. Further expansion is activated by “nucleation” events of chain ends disentangling from the globule. The molecule then stays arrested at this partially extended state until most of its intramolecular knots have diffused to either ends of the chain and disappeared. Finally, the molecule becomes unentangled and quickly returns to equilibrium.

Stretching Compressed T4 DNA.

We gain further insight into the internal structure of the compressed T4 DNA by applying forces to deform these globules. We use a planar homogeneous elongational field generated in cross-slot channel to stretch the initially compacted DNA (see SI Text for details and data). We find that the entangled DNA molecules extend dramatically slower comparing to the uncompressed DNA under the same applied force. Furthermore, persistent bright spots are observed when the self-entangled DNA are stretched which are indicative of a knot. These stretching data strongly support the existence of entanglements in the compressed globules.

A Mechanism for Self-Entanglement Under Electric Field.

Finally, we comment on the possible mechanisms for the formation of self-entanglements and knots under moderate electric field. First, entanglements can form due to the increased internal segment concentration when the DNA becomes compressed. The initial radius of gyration of the compressed globule is much larger than the resolution limit set by the point spread function (PSF) of the microscope [the PSF leads to a minimum measurable R_g ≈ 270 nm (28)]. We estimate from the optical size that the DNA concentration inside a globule produced under 200 V/cm is about 7c^∗ (the segment concentration inside a equilibrium DNA coil is c^∗). This concentration is very close to the critical concentration (∼9c^∗) for the onset of entangled regime in semidilute DNA solutions (34) and thus can possibly lead to self-entangling of the molecule. However, an internal DNA concentration of 7c^∗ alone does not give rise to enough entanglements to fully account for the observed slow expansion as it only corresponds to an equilibrium number of entanglements on order of 1 (35). It is useful to compare our results to DNA packaged in a capsid because the knotting observed in this biological context is believed to arise primarily due to confinement effects (36, 37). The smallest initial globule radius observed in our experiments is about 700 nm which is an order of magnitude larger than a typical capsid radius (e.g., λ phage is about 29 nm).

We thus propose a second mechanism that can also promote DNA entangling and knotting under electric field based on our previous postulation on the cause of the compression, namely an electrohydrodynamic instability. These flows not only drive the DNA segments to concentrate, but should also induce some local rotational motion (5, 6) which can lead the DNA to being continually jostled by the flow. Thus the combined affects of increased segment density with a rotationally dominated hydrodynamic flow could lead to the observed strong intrachain entanglements. This mechanism is supported in part by experiments in which it was shown that a tumbled macroscopic string can spontaneously knot (22). These experiments, and subsequent simulations (23), also showed that knot formation is kinetically limited—longer agitation time led to increased knotting probability. These previous results help to explain why in our experiments there is an increase in the percentage of self-entangled molecules as the residence time T_E increases.

Conclusions

We have demonstrated that moderate homogeneous electric fields can lead DNA molecules to compress and self-entangle. Observation of the relaxation process allowed us to clearly identify two metastable arrested states during the relaxation pathway. Our experimental observations thus change the canonical view of how a DNA, or any polyelectrolyte, will change conformation in response to a homogeneous electric field. These results have direct impact in lab on chip devices given the widespread use of electric fields to transport DNA in micro/nanofluidic devices, including very “open” devices designed to sort or position large DNA or chromosomes, and nanopore devices. In fact in recent work on stretching DNA using an electrophoretic contraction (38), we were forced to use high ionic strengths to avoid the formation of persistent “balls” at one end of the DNA which would not unravel in the device. Given the important role of the chain ends in the relaxation process, it will be interesting to perform future experiments with circular DNA. Lastly, electric field induced compaction provides a unique platform to gain fundamental insight into self-entangled molecules.

Materials and Methods

Detailed experimental procedures of channel and DNA preparation, measuring the DNA conformation under electric field, measuring the expansion of compressed T4 DNA, and the DNA stretching experiments are described in SI Text.

Note.

The authors point to a recent report by Riehn et al. (39) on DNA collapse at much larger and only AC electric fields, which was published after the submission of this manuscript.