Abstract
We develop a computational model to compare the relative importance of unbinding and unfolding of actin cross-linking proteins (ACPs) in the dynamic properties of the actin cytoskeleton. We show that in the strain-stiffening regime with typical physiological and experimental strain rates, unbinding events are predominant with negligible unfolding. ACPs unbound by greater forces experience larger displacements, with a tendency to rebind to different filaments. At constant strain, stress relaxes to physiological levels by unbinding only—not unfolding—of ACPs, which is consistent with experiments. Also, rebinding of ACPs dampens full relaxation of stress. When the network is allowed to return to a stress-free state after shear deformation, plastic deformation is observed only with unbinding. These results suggest that despite the possibility of unfolding, unbinding of ACPs is the major determinant for the rheology of the actin network.
Introduction
Cells exhibit a number of interesting dynamic properties in response to external stimuli. Subjected to rapid deformation, the cytoskeleton develops high levels of stress, whereas it can easily deform under low strain rates with relatively little increase in stress (1). At fixed shear strain or stretch, marked stress relaxation is observed (1,2). It is widely believed that the actin cytoskeleton cross-linked by actin binding proteins is primarily responsible for these dynamical properties (3). Reconstituted networks cross-linked by filamin that can both unbind and unfold have drawn attention recently, since they reproduced many of the dynamic properties of cells (4,5). Other experiments (6,7) demonstrate that the unbinding and unfolding behaviors of a single filamin are rate-dependent and can be described by several models for bond rupture or domain unfolding, including Bell's equation (8). Based on these, it was qualitatively predicted that unbinding of filamin would precede unfolding under typical in vitro conditions (9). Numerous recent experiments have focused on elucidating relations between dynamic behaviors of single actin cross-linking proteins (ACPs) and the integrated properties of actin networks (10–13). Computational models have great potential to contribute to understanding of such relations by explicitly relating macroscopic rheological measurements to underlying molecular events. Existing computational approaches to date (14–16), although instructive, do not incorporate ACP unbinding and unfolding simultaneously. Here, we extend our previous model (17) by including these two events. In the strain-stiffening regime, unbinding of ACPs significantly decreases the magnitude of stress at high shear strain, whereas unfolding merely delays the increase of stress to higher values of strain. Frequencies of unbinding and unfolding events depend strongly on the strain rate. At constant strain, stress relaxes to physiological levels only by unbinding, not by unfolding, of ACPs. Finally, plastic deformation, the irreversible reorganization of a network, is observed with unbinding, but not when only unfolding is allowed.
Methods
Model overview
We generate a cross-linked network as in our previous studies (17,18). Briefly, we perform Brownian dynamics simulations on actin monomers, filaments, and ACPs, initially assuming first-order irreversible bond formation. ACPs have a filamin-like V shape and form orthogonal cross-links between filaments during the polymerization process. After growing the network, a coarse-graining procedure is applied to increase length- and timescales of subsequent simulations (17). Mechanical properties of actin filaments and ACPs are characterized by bending and extensional stiffnesses, and thermal fluctuations are included. Steric interactions exist only between actin filaments, preventing them from passing through each other. The measurement of viscoelastic moduli of the networks is performed via bulk rheology in which oscillatory shear strain is applied to the top surface of the cubical simulation box with the bottom surface fixed (17). The small box, whose width is 2.8 μm, allows bulk rheology to effectively capture rheology measured by microprobes as shown in (17). To systematically control and isolate the effects of a given parameter, a geometrically identical network was employed for all measurements. Filament length (Lf) is 1.5 ± 0.65 μm (average ± SD), and the actin concentration (CA) is 12.1 μM. By comparison, the in vitro actin concentration range is 12–74 μM (4,5). Relative concentration of ACP (R = CACP/CA) is 0.020 unless specified.
Dynamic behavior of ACPs
In this model, unbinding/rebinding and unfolding/refolding of ACPs are considered. Experimentally, the force-extension curve of filamin A exhibits a saw-tooth behavior with peak values of 100–200 pN at intervals of ∼30 nm in response to a pulling force (7). When the pulling force is released, it relaxes as a single wormlike chain. To describe such behaviors of filamin A, each arm of ACP is described by a series of wormlike chains and can unfold up to Nuf times according to Bell's equation. Denoting the equilibrium and current length of one ACP arm by r0 and r12, respectively, the force, Fs(r12), and unfolding rate, kuf, are
| (1) |
| (2) |
where p = 0.33 nm is the persistence length, l0,i = (140 + 30 × i) nm (i = 0 − Nuf) is the maximum extension for the ith unfolding, r0 = 105 nm, and κs,ACP is the stiffness of ACP against compression below the equilibrium length, r0. is the zero-force unfolding rate coefficient, and λuf = 6 × 10−10 m is the mechanical compliance. To study the long-time behavior (see below), in different simulations, we rescale with respect to the reference value, = 3.0 × 10−5 s−1. Values of and λuf are set based on previous experiments and Monte Carlo simulations (7). Each unfolding event increases i by 1 while keeping track of the values of r12 at which the ith unfolding occurred, ruf,i. Refolding occurs when r12 decreases below ruf,i, decreasing i by 1. The periods of relaxation and extension are determined by changes in the ACP length during the previous 10 time steps (= 61.7 ns), where a reduction in length for ≥8 of 10 steps is considered relaxation. Once the relaxation period begins, the maximum extension remains constant at the initial l0,i even after i is decreased by refolding. When extension begins again, l0,i instantly changes to a value that corresponds to i, satisfying ruf,i−1 ≤ r12 ≤ ruf,i. This is to capture the behavior observed in AFM experiments (7,19). Simulations conducted with a single ACP at two extension rates are qualitatively similar to results of AFM measurements (Fig. 1).
Figure 1.

Sample force-extension curves of one arm of an ACP with Nuf = 10. Two extension rates are used: 0.3 μm/s (dashed line) and 30 μm/s (solid line). Dotted lines show wormlike chains following Eq. 1.
ACPs unbind in a similar manner but with different parameter values, as follows:
| (3) |
where is the zero-force unbinding rate coefficient, and λub = 1.04 × 10−10 m is the mechanical compliance of the bond for unbinding. The reference value of = 0.115 s−1 is taken from experiment (6). In our model, simultaneous unbinding of both ACP arms is prohibited. We also assume that if an unbinding event occurs on one ACP arm, it completely refolds, and r12 immediately returns to its equilibrium value, r0 (i = 0). Once unbound, the arm of an ACP thermally fluctuates until it rebinds.
Simulation of long-time behaviors
In typical experiments, stress relaxation occurs over timescale longer than seconds (4), which we address in our simulation by employing the following scaling argument. Based on the expectation that network dynamics is governed mainly by the rates of unfolding and unbinding of ACPs, longer-time behaviors may be captured by adjusting the zero-force rate coefficients, and , which we collectively denote as k0. In scaling time by (k0)−1, certain types of time-dependent behaviors could be reduced to a single universal curve. This allows us to predict behaviors at much longer times simply by increasing and and scaling time accordingly. This hypothesis was examined by either increasing shear strain linearly with time (Fig. 2 A) or monitoring stress relaxation under constant strain (Fig. 2 B). Denoting the time over which the shear strain is applied in the first case and that during which stress relaxation is measured in the second as td, all cases with the same values of k0td exhibit similar rheological behaviors.
Figure 2.
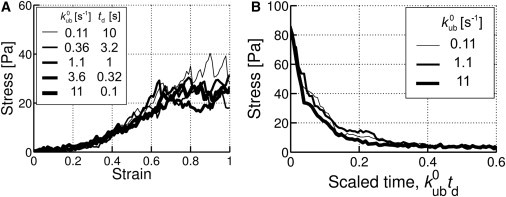
Invariance of rheological behaviors with td fixed. (A) Strain-stiffening. (B) Stress relaxation. (See text for explanation.)
Results and Discussion
Strain-stiffening
With this new model, we first investigated strain-stiffening. A constant shear strain rate is applied to the actin network ( = 10 s−1) with both unbinding and unfolding of ACPs, and the corresponding shear stress is computed. Five different values for the zero-force rates are used (/ = / = n; n = 1–100), each leading to a different effective shear strain rate, = /n based on scaling arguments above. The frequencies of unbinding and unfolding events strongly depend on (Fig. 3 A); at small (<1 s−1), unbinding events dominate, whereas at large (>1 s−1), unfolding dominates. It is important to note that under typical physiological and experimental conditions ( ∼ 0.1 s−1), unbinding/rebinding dominates with far less unfolding/refolding, as qualitatively predicted in (9). The overall shape of the stress-strain curves showing initial stiffening followed by collapse (Fig. 3 B), is consistent with experiments (5,20). The curves also exhibit two distinct power-law regimes before the collapse, which can be well described by the following with c1 = 2.5, c2 = 500, x1 = 0.4, x2 = 4:
| (4) |
where the first and second terms on the righthand side dominate in the low and high γ regimes, respectively. A power-law behavior for τ has been observed in several experiments (10,13,20). To find its origin, we estimated c1, c2, x1, and x2 with the extensional (κs,A) and bending stiffness (κb,A) of actin reduced by up to 0.1. It was observed that κb,A had a noticeable effect on c1 and x1, whereas κs,A strongly influenced c2 and x2 (Fig. 3 C), which agrees with the crossover from bending to stretch-dominated responses of the network (17).
Figure 3.
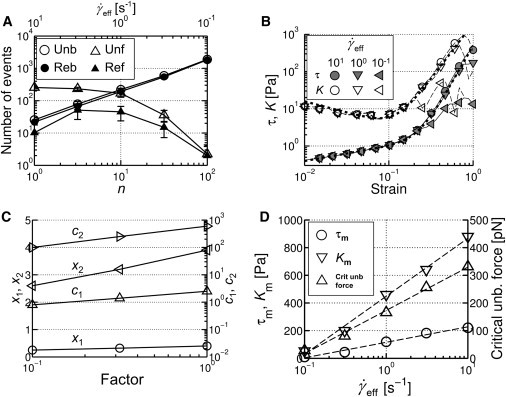
Strain-stiffening behaviors with unbinding and unfolding. (A) The number of various events depending on n (= / = /) with = 10 s−1. = /n on the top horizontal axis is the effective shear strain rate. (B) Stress-strain behaviors and differential modulus, K = dτ/dγ, with different (legend). Thick dotted lines denote the best fits using Eq. 4 and its derivative. (C) Coefficients (c1, triangles; and c2, right-pointing triangles) and exponents (x1, circles; and x2, left-pointing triangles) of Eq. 4 with mechanical stiffness (κb,A for c1 and x1, and κs,A for c2 and x2) reduced by the factor in the x axis. (D) Maximum value of K (Km), the corresponding stress (τm), and critical unbinding force () with different , where indicates the unbinding force of ACP, whose unbinding event initiates a decrease in K at Km.
When unfolding prevails at the highest , the stress level steadily increases. In contrast, when unbinding dominates, stress reaches a level similar to experimental values; stress >100 Pa has rarely been observed in in vitro experiments (3,5). To test hysteresis, an actin network is sheared up to γ = 1.0 and then returned to γ = 0 with three different strain rates ( = 101, 100, 10−1 s−1). The network exhibits greater hysteresis with lower , whereas in a control case without unbinding (very large ), hysteresis is negligible (Fig. S1 in the Supporting Material). This observation is consistent with our findings with regard to plastic deformation, discussed below. Therefore, although unfolding may occur (7), strain-stiffening behaviors of actin-filamin networks are likely governed by unbinding.
Differential modulus, K = dτ/dγ, of the strain-stiffening curves in Fig. 3 B and Fig. S2 A exhibits behaviors similar to those previously observed (10,13): K that remains relatively constant at low γ tends to follow ∼γ3 at γ > ∼0.1, eventually collapsing at high γ. Note that although magnitudes of K are strongly affected by R (Fig. S2 B), as observed in experiment (13), overall tendencies are very similar regardless of R. Both τm (stress at which K is maximal, Km) and (unbinding force of ACP whose unbinding initiates a decrease in K from Km) are both logarithmically dependent on (Fig. 3 D). Considering that both τm and are linearly dependent on , we can infer τm ∼ ; at highly strained states, stress is supported by only a small set of ACPs that experience high tensional forces (17), and therefore τm is expected to be proportional to . In addition, considering for a single molecular bond according to Bell's equation (21), d/dt varies as , as predicted in Lieleg and Bausch (10). Before K reaches a maximum, τ and K are roughly proportional to γ4 (x2 = 3.9 in Fig. 3 C, for the control case of factor n = 1) and γ3, respectively; due to the dependence, Km ∼ , Km varies roughly as (Fig. 3 D).
To further examine how unbinding and subsequent rebinding of ACPs reduce stress, we quantified the displacement between unbinding and rebinding of ACPs (Fig. 4 A, solid circles). ACPs that unbind with larger force tend to be displaced more. We also traced whether or not unbound ACPs rebind to the same filament, assigning turnover values of 1 for ACPs that reattach to a different filament and 0 for those rebinding to the same filament (Fig. 4 A, open circles). Above 20 pN, nearly all unbound ACPs rebind to different actin filaments. Fig. 4 B shows one example of the displacement and turnover of ACPs unbound with ≥20 pN, demonstrating that ACPs tend to rebind to a different filament after a diagonal displacement. Moreover, highly loaded ACPs unbind predominantly from a small fraction of the actin network (supportive framework) that bears most of the load (17). We found that ∼85% of all ACPs that ruptured with ≥20 pN belong to the supportive framework, which constitutes only 25% of the entire network. Immediately after unbinding of such stretched ACPs, the filaments to which the ACPs were originally attached undergo rapid reconfiguration to relieve the load, and they are thus unlikely to remain close to the original ACPs. A cascade of such events will lead to reconfiguration of the network and reduction in stress to levels observed in experiments, ∼10 Pa.
Figure 4.
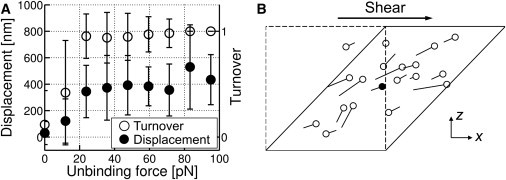
Behaviors of ACPs between unbinding and rebinding events. (A) Distance of travel between unbinding and rebinding (solid circles) and the average turnover, indicating whether or not ACP rebinds to the same filament after unbinding (open circles). The turnover value of 1 indicates rebinding to a different filament, whereas a turnover value of 0 indicates rebinding to the same filament. (B) An example showing displacement and turnover of ACPs unbound with ≥20 pN during shearing of the system from γ = 0 (dashed line) to γ = 1 (solid line). On the xz plane, lines are drawn between unbinding and rebinding locations, with the open and solid symbols indicating rebinding to different or the same filaments, respectively.
Stress relaxation
To study stress relaxation, steady shear stress was first applied to τ0 = 5 Pa with either unbinding (with a rate of ) or unfolding (), followed by holding γ constant for 5 s (Fig. 5). Unfolding induces little stress relaxation with or without refolding, whereas unbinding results in substantial stress relaxation. In the case where both ACP unbinding and rebinding are allowed, stress tends to relax to a finite nonzero value (∼1 Pa). Without rebinding, it continues to decrease nearly to zero, as expected. Only when both unbinding and rebinding are included does the stress relaxation resemble that of reconstituted actin networks cross-linked by filamin (4).
Figure 5.
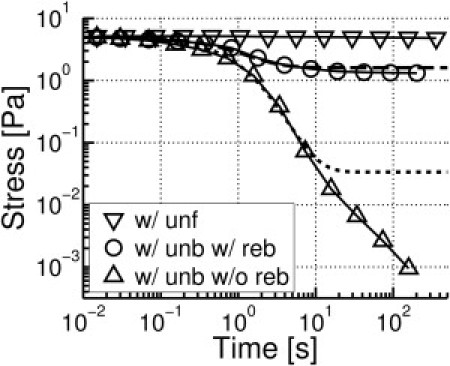
Stress relaxation due to unbinding or unfolding. Time is multiplied by 100 according to the scaling of unbinding/unfolding rates. Dashed and dotted lines are the best fits using Eq. 7.
It was found that the number of intact ACPs forming cross-links (NACP) exponentially decreases at constant γ with unbinding as follows, which is consistent with the kinetics scheme, [actin-ACP] [actin] + [ACP]:
| (5) |
where is the initial number of ACPs that form cross-links, and the factor 2 in the exponent accounts for the possibility of unbinding on either end of an ACP. Although forces acting on ACPs can lead to > , the effect of the forces on NACP seems to be negligible at this low-stress state (τ < 5 Pa). Considering τ ∼ Fub observed in the strain-stiffening behavior, we can assume that each unbinding of an intact ACP bearing Fub reduces τ by an amount proportional to τ (=aτ), and the subsequent rebinding would limit the reduction of τ by b, regardless of Fub. This suggests that
| (6) |
| (7) |
The case without rebinding at t < 10 s (Fig. 5) agrees well with a = 0.006 and b = 0. Since NACP becomes zero at t ∼ 10 s, stress relaxation for t ≥ 10 s in Fig. 5 must originate from a different mechanism, presumably steric interactions between actin filaments. Cases with rebinding are best fitted with a = 0.006 and b = 1.8 Pa.
It was also observed that stress relaxation induces aging of actin networks, similar to that in Lieleg et al. (22); greater relaxation leads to a lower storage modulus, G′, but little affects a loss modulus, G″ (Fig. S3). In our simulation, aging occurs much more quickly, since actin filaments are cross-linked orthogonally by single ACPs, and therefore a large portion of the unbinding events would contribute to the aging. By contrast, in experiments, most unbinding events might have occurred between parallel filaments in bundles, which induces aging very slowly (22). Thus, considering the similarity between the simulations with rebinding and experiments, both unbinding and rebinding of ACPs likely contribute to stress relaxation of actin networks in experiments, but with opposing effects.
Plastic deformation
To study plastic deformation of the network, we applied a constant shear strain rate ( = 10, 1, or 0.1 s−1) up to γ = 1.0, with unbinding/rebinding or unfolding/refolding. The top boundary was then allowed to relax freely (Fig. 6 A). During the free relaxation, it is expected that the shear strain rate is affected by the internal frictional stresses due to viscous drag on the filaments and unbinding/unfolding events. For actin segments clamped to the upper boundary, the restoring force, Fr, will be balanced by the average viscous drag on them, resulting in
| (8) |
Figure 6.
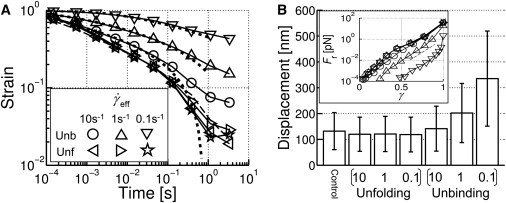
Irreversible deformation of actin networks with unbinding or unfolding. (A) Evolution of shear strain (γ) in time. The top surface of the computational domain was sheared up to γ = 1.0 with various (legend), and then released. Lines represent the control case, with no unbinding or unfolding (dashed line), and fits using Eq. 10 (dotted lines). (B) Average displacements of ACPs between the original network and the network at t = 2 s in A. The numbers on the x axis represent . (inset) The restoring force (Fr) governing dγ/dt during free relaxation is plotted using the same symbols as in A. Dashed line indicates Fr ∼ exp(11.5γ).
With unbinding and high , γ returns close to its initial value (γ = 0). However, with unbinding and low , γ decays more slowly until 0.01 s, and later the rate of relaxation decreases to a level similar to that for high , suggesting that γ may asymptote to a nonzero value. By contrast, in all cases with unfolding, γ rapidly approaches zero. We found that Fr has an exponential dependence on strain during the free relaxation with unbinding, Fr ∼ exp(11.5γ), except at very high γ (Fig. 6 B, inset). Therefore, the temporal profile of γ can be deduced from
| (9) |
| (10) |
where c is a proportionality coefficient, and γ0 = 1.0 is the initial strain for these simulations. The curves for cases with unbinding at = 10, 1, and 0.1 s−1 in Fig. 6 A are fitted by c = 0.11, 0.015, and 0.0005, respectively. On the other hand, the behaviors of Fr(γ) of cases with unfolding and the control case are complicated, precluding a simple expression for γ(t). The difference between unbinding and unfolding can also be seen from displacements of ACPs between their original positions and those at t = 2 s (Fig. 6 B). In cases with unfolding only, average displacements of ACPs are similar to the control case with neither unbinding nor unfolding, whereas unbinding with lower results in larger average displacements, indicating a higher degree of network reorganization.
It is useful to compare the local power exponent in γ ∼ t−x to experimental data, although Eq. 10 does not have an explicit power-law relation. Simulations with unbinding exhibit relatively consistent values in the range, x = 0–0.4. The simulation with = 0.1 s−1 corresponds to typical experimental conditions in terms of and τ(t = 0) = 20 Pa. Its exponent is <0.2, in good agreement with the in vitro (∼0.17 (5)) and in vivo values (1,23,24). Note that the amount of plastic deformation in Gardel et al. (5), where γ falls from the initial value of 0.08 to ∼0.02, might have been greater if the reconstituted actin network had been sheared to a greater extent.
Behavior of the network under oscillatory strain
As explained in the next section, the requirement for sampling many runs and the long simulation time in the presence of the unbinding events of ACPs limit accurate calculation of the complex modulus under oscillatory strain. Despite such limitations, our model semiquantitatively captures experimentally observed behaviors including the hysteresis. Furthermore, behaviors of G′ and G″ at different unbinding rates elucidate a potential mechanism for the power-law behavior (1,23,24). In Fig. S4, A and B, we plot G′ and G″ as a function of at a fixed oscillation frequency of 10 Hz with a prestress of 10 Pa. Note that we did not employ the scaling argument for determining G′ and G″, since neither thermal fluctuation nor diffusion is accelerated, and these phenomena can contribute to G′ and G″ at high frequency. As increases, G′ gradually decreases (Fig. S4 A), which generally follows the density of active ACPs (Fig. S4 B). Thus, at low unbinding rates, energy dissipation should depend more on viscous stress and less on unbinding, which can also be seen in the nearly monotonic increase of the total unbinding energy (total energy dissipated by unbinding of ACPs bearing >1 pN) in Fig. S4 B. On the other hand, G″ reaches a maximum at n = 10, where the oscillation frequency and unbinding rate constants are within about an order of magnitude, that is, when bonds are actively forming and rupturing. As increases further, fewer bonds exist due to the high unbinding rate. Although the total unbinding energy increases monotonically with n (Fig. S4 B), since both the number of active ACPs and G″ fall, the actual contribution to energy dissipation due to rupture appears to fall with n as well. These indicate that the unbinding and rebinding of ACPs contribute to dissipation of energy in a rate-dependent manner. By contrast, viscous dissipation is unlikely to be affected by the rate of unbinding. The rate dependence of energy dissipation could be an important source for the power-law rheology since for a given microstrain, a subset of cross-links with the corresponding binding strength would be the most responsive (1,23,24).
Furthermore, the complex modulus calculated under prestress, τ0, shows behaviors similar to those in experiments. Fig. S5 shows G′ (same as K′ in Kasza et al. (9)) versus τ0 with various R, which remains relatively constant at low τ0 and then increases approximately linearly, consistent with the result of Kasza et al. (9).
Limitations of the model
Although our study faithfully reflects the mechanical and dynamic behaviors of actin filaments and ACPs, it still has several limitations. First, torsional rigidity of actin filaments is neglected, and some of the properties for ACPs were arbitrarily determined. However, the bending forces acting on ACPs can preclude free torsional rotation to some degree. In addition, geometry and the behaviors and rates of unbinding and unfolding are close to those of filamin A at least. Considering simplifications and parameter uncertainty, our network may thus be viewed as one roughly mimicking filamin-cross-linked networks. Second, it has no active molecular motors that generate high internal stress in cells without external stimuli (25). However, it is expected that most of the behaviors observed in this study would appear even with the contractile motors. The motors would be responsible for enhancing the elasticity of actin networks, whereas ACPs mainly govern strain stiffening, stress relaxation, and plastic deformation via unbinding events. A major difference would be that internal stress and strain need to be measured, whereas our study is associated with external ones. In addition, the ability of molecular motors to unbind from actin filaments (26) would increase the complexity of mechanisms governing macroscopic rheological behaviors. Third, the small computational domain prevents the model from probing the rheology of thick actin bundles. Recent in vitro experiments demonstrated that actin networks with large bundles whose mesh size is >10 μm exhibit interesting rheological behaviors (27). Our model has to be coarse-grained much more to simulate such extensive bundles. Last, inclusion of unbinding in our model limits the frequency ranges at which G′ and G″ can be probed. In our previous work with permanent cross-links (17), G′ and G″ at each frequency were obtained clearly and reproducibly even using a single run of simulation. By contrast, with stochastic unbinding events, data from numerous runs for longer duration were required to acquire such clear curves of G′ and G″, greatly elevating computational costs. Thus, frequency range of G′ and G″ covered by our model (10–103 Hz) overlaps only marginally with that in experiments using bulk rheometers. Thus, we focused only on strain-stiffening, stress relaxation, and plastic deformation in this study.
Conclusion
In all cases studied—strain-stiffening, stress relaxation, and plastic deformation—unbinding of ACPs was found to be largely responsible for the behaviors observed under physiological and experimental conditions. With unfolding only, the topology of the network does not change, so the system is unable to adapt to the changes in loading condition. Unbinding of ACPs allows reconfiguration of the supportive framework, the main core of the network responsible for the elastic response (17). Nevertheless, the functional importance of ACP unfolding cannot be ignored. It may assist transient deformation of the actin network, and unfolding of an ACP domain may also play a role in intracellular signaling. Experiments with, e.g., mutant filamin, where domain unfolding is prohibited by disulfide bridges, may help to determine the validity of the results presented here.
We have shown the predominance of unbinding using a computational model incorporating a filamin-like actin cross-linking protein with both unbinding and unfolding events. Incorporating the effects of motor proteins and cell membranes in the model would help to better understand the rich diversity of cellular phenomena.
Acknowledgments
We gratefully acknowledge a fellowship to Taeyoon Kim from the Samsung Scholarship Foundation. We thank H. Lee for insightful discussions.
This work was supported by the National Institutes of Health (GM076689).
Supporting Material
References
- 1.Trepat X., Deng L.H., Fredberg J.J. Universal physical responses to stretch in the living cell. Nature. 2007;447:592–595. doi: 10.1038/nature05824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Matthews B.D., Overby D.R., Ingber D.E. Cellular adaptation to mechanical stress: role of integrins, Rho, cytoskeletal tension and mechanosensitive ion channels. J. Cell Sci. 2006;119:508–518. doi: 10.1242/jcs.02760. [DOI] [PubMed] [Google Scholar]
- 3.Gardel M.L., Nakamura F., Weitz D.A. Stress-dependent elasticity of composite actin networks as a model for cell behavior. Phys. Rev. Lett. 2006;96:088102. doi: 10.1103/PhysRevLett.96.088102. [DOI] [PubMed] [Google Scholar]
- 4.Tseng Y., An K.M., Wirtz D. The bimodal role of filamin in controlling the architecture and mechanics of F-actin networks. J. Biol. Chem. 2004;279:1819–1826. doi: 10.1074/jbc.M306090200. [DOI] [PubMed] [Google Scholar]
- 5.Gardel M.L., Nakamura F., Weitz D.A. Prestressed F-actin networks cross-linked by hinged filamins replicate mechanical properties of cells. Proc. Natl. Acad. Sci. USA. 2006;103:1762–1767. doi: 10.1073/pnas.0504777103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ferrer J.M., Lee H., Lang M.J. Measuring molecular rupture forces between single actin filaments and actin-binding proteins. Proc. Natl. Acad. Sci. USA. 2008;105:9221–9226. doi: 10.1073/pnas.0706124105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Furuike S., Ito T., Yamazaki M. Mechanical unfolding of single filamin A (ABP-280) molecules detected by atomic force microscopy. FEBS Lett. 2001;498:72–75. doi: 10.1016/s0014-5793(01)02497-8. [DOI] [PubMed] [Google Scholar]
- 8.Bell G.I. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 9.Kasza K.E., Koenderink G.H., Weitz D.A. Nonlinear elasticity of stiff biopolymers connected by flexible linkers. Phys. Rev. E. 2009;79:041928. doi: 10.1103/PhysRevE.79.041928. [DOI] [PubMed] [Google Scholar]
- 10.Lieleg O., Bausch A.R. Cross-linker unbinding and self-similarity in bundled cytoskeletal networks. Phys. Rev. Lett. 2007;99:158105. doi: 10.1103/PhysRevLett.99.158105. [DOI] [PubMed] [Google Scholar]
- 11.Lieleg O., Claessens M.M.A.E., Bausch A.R. Transient binding and dissipation in cross-linked actin networks. Phys. Rev. Lett. 2008;101:108101. doi: 10.1103/PhysRevLett.101.108101. [DOI] [PubMed] [Google Scholar]
- 12.Lieleg O., Schmoller K.M., Bausch A.R. Cytoskeletal polymer networks: viscoelastic properties are determined by the microscopic interaction potential of cross-links. Biophys. J. 2009;96:4725–4732. doi: 10.1016/j.bpj.2009.03.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Schmoller K.M., Lieleg O., Bausch A.R. Structural and viscoelastic properties of actin/filamin networks: cross-linked versus bundled networks. Biophys. J. 2009;97:83–89. doi: 10.1016/j.bpj.2009.04.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hoffman B.D., Massiera G., Crocker J.C. Fragility and mechanosensing in a thermalized cytoskeleton model with forced protein unfolding. Phys. Rev. E. 2007;76:051906. doi: 10.1103/PhysRevE.76.051906. [DOI] [PubMed] [Google Scholar]
- 15.Aström J.A., Kumar P.B., Karttunen M. Strain hardening, avalanches, and strain softening in dense cross-linked actin networks. Phys. Rev. E. 2008;77:051913. doi: 10.1103/PhysRevE.77.051913. [DOI] [PubMed] [Google Scholar]
- 16.DiDonna B.A., Levine A.J. Filamin cross-linked semiflexible networks: fragility under strain. Phys. Rev. Lett. 2006;97:068104. doi: 10.1103/PhysRevLett.97.068104. [DOI] [PubMed] [Google Scholar]
- 17.Kim T., Hwang W., Kamm R.D. Computational analysis of viscoelastic properties of crosslinked actin networks. PLOS Comput. Biol. 2009;5:e1000439. doi: 10.1371/journal.pcbi.1000439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kim T., Hwang W., Kamm R.D. Computational analysis of a cross-linked actin-like network. Exp. Mech. 2009;49:91–104. [Google Scholar]
- 19.Schwaiger I., Kardinal A., Rief M. A mechanical unfolding intermediate in an actin-crosslinking protein. Nat. Struct. Mol. Biol. 2004;11:81–85. doi: 10.1038/nsmb705. [DOI] [PubMed] [Google Scholar]
- 20.Wagner B., Tharmann R., Bausch A.R. Cytoskeletal polymer networks: the molecular structure of cross-linkers determines macroscopic properties. Proc. Natl. Acad. Sci. USA. 2006;103:13974–13978. doi: 10.1073/pnas.0510190103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hummer G., Szabo A. Kinetics from nonequilibrium single-molecule pulling experiments. Biophys. J. 2003;85:5–15. doi: 10.1016/S0006-3495(03)74449-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lieleg O., Kayser J., Bausch A.R. Slow dynamics and internal stress relaxation in bundled cytoskeletal networks. Nat. Mater. 2011;10:236–242. doi: 10.1038/nmat2939. [DOI] [PubMed] [Google Scholar]
- 23.Lenormand G., Millet E., Fredberg J.J. Linearity and time-scale invariance of the creep function in living cells. J. R. Soc. Interface. 2004;1:91–97. doi: 10.1098/rsif.2004.0010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Fabry B., Maksym G.N., Fredberg J.J. Scaling the microrheology of living cells. Phys. Rev. Lett. 2001;87:148102. doi: 10.1103/PhysRevLett.87.148102. [DOI] [PubMed] [Google Scholar]
- 25.Schliwa M., Woehlke G. Molecular motors. Nature. 2003;422:759–765. doi: 10.1038/nature01601. [DOI] [PubMed] [Google Scholar]
- 26.Guo B., Guilford W.H. Mechanics of actomyosin bonds in different nucleotide states are tuned to muscle contraction. Proc. Natl. Acad. Sci. USA. 2006;103:9844–9849. doi: 10.1073/pnas.0601255103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Schmoller K.M., Fernández P., Bausch A.R. Cyclic hardening in bundled actin networks. Nat. Commun. 2010;1:134. doi: 10.1038/ncomms1134. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


